1 Introduction

Over the past decades, a great deal of attention in research has been devoted to the fault detection (FD) problem for a lot of control systems due to an increasing demand for higher performance, higher safety, and reliability standards; see, e.g., [1, 2, 15, 19, 23, 24], and the references therein. In practical applications, structures of many systems are usually subject to random variations, which are usually referred to as faults and may result from component and interconnection failures, tracking, parameter shifting, and other sources. For a feedback control system, these faults may possibly result in unsatisfactory performance or even instability when they appear in actuators, sensors, or controllers. In order to maintain the performance of a designed control system, faults and failures have to be detected as quickly as possible. Thus, the basic idea of FD is to construct a residual signal in order to provide a residual evaluation function to compare with a predefined threshold. When the residual evaluation function has a value larger than the threshold, an alarm of fault is engendered. Among many important properties of a FD system, the most important one is that FD systems have to be robust to unavoidable modeling errors or external disturbances that may seriously affect the performance of model-based FD systems. At the same time, FD systems should be sensitive to faults in order to detect faults and failures just in time [4].

Up to now, various kinds of FD techniques, such as unknown input observer approach, parity relations method, optimization-based method, artificial intelligence technique, FD filter approach, and so on, have been extensively utilized in modern manufacturing processes, nuclear engineering, chemical engineering, automotive system, aerospace engineering, etc. [5, 13, 14, 31, 32, 42]. Recently, as an efficient method, \(H_{\infty }\) FD filter method has been investigated by many researchers and a significant body of literature has appeared on both the theoretical research and practical applications; see, e.g., [8, 11, 20, 30, 36, 40, 44, 45], and the references therein. Practically speaking, [45] is the first to take into account the robust \(H_{\infty }\) FD filter design for a class of discrete-time linear Markovian jump systems by using a general observer-based FD filter as residual generator, where the robust FD filter design is formulated as an \(H_{\infty }\)-filtering; [40] investigates the \(H_{\infty }\) FD filtering for a class of discrete-time Markov jump linear system with partially unknown and completely unknown transition probabilities; [8, 36, 44] study the problem of robust \(H_{\infty }\) FD filter design for uncertain systems, Markovian jump singular systems, fuzzy systems, respectively, where missing measurements are all considered and Bernoulli random binary distribution is employed to characterize the data missing phenomenon; and [11, 20, 30] deal with robust \(H_{\infty }\) FD filtering for discrete-time networked systems with global Lipschitz nonlinearities and/or multiple state delays, where random communication delays, data packet dropouts, and signal quantisation are involved.

It is worth noting that, in reality, most physical systems are nonlinear, and thus, how to develop effective FD methods for nonlinear systems is an important and practical problem. It is well known that the Takagi–Sugeno (T–S) fuzzy model has been recognized as a popular and powerful tool in approximating complex nonlinear systems [7]. A T–S fuzzy model is described by a family of fuzzy IF-THEN rules that represent local linear input–output relations of the system. Many results on analysis and synthesis of fuzzy systems can be found in the literature; see, for instance, [9, 10, 16–18, 26], and the references therein. Since T–S fuzzy models have provided a convenient way to study nonlinear systems, a feasible solution of the FD problem for nonlinear systems can be converted to that of FD for T–S fuzzy systems. In recent years, much attention has been paid to the study of FD for fuzzy systems. For example, [2] studies the problem of robust fault detection observer design for T–S models using the descriptor approach; [24] considers the problem of designing a robust FD filter for an uncertain T–S fuzzy models in terms of LMIs; and [44] is concerned with the \(H_{\infty }\) FD filter design for T–S fuzzy systems with intermittent measurements, where the communication links between the plant and the FD filter are assumed to be imperfect, and a stochastic variable satisfying the Bernoulli random binary distribution is used to model the unreliable communication links.

On the other hand, owing to systems in many fields of engineering and science are often disturbed by stochastic noise, the study of stochastic systems has been of great interest; see, e.g., [6, 34, 35, 37], and so on. Very recently, there has been a growing attention on the study of stochastic fuzzy systems. To mention a few, delay-dependent robust control problem for uncertain stochastic fuzzy systems with time-varying delay is investigated in [12]; delay-dependent stabilization problem for a class of time-delay stochastic fuzzy systems is studied in [38]; the stabilization problem for a class of uncertain Itô stochastic fuzzy systems driven by a multidimensional wiener process is considered in [46]; delay-dependent guaranteed cost control for uncertain stochastic fuzzy systems with time delay is discussed in [39]; the robust filtering problem for discrete fuzzy stochastic systems with sensor nonlinearities is studied in [25]; and the robust fuzzy filter design problem for a class of nonlinear stochastic systems is researched in [29], while the robust \(H_{\infty }\) FD filter for a class of It\(\hat{\mathrm{o}}\) stochastic T–S fuzzy systems is discussed in [33], where the time delays and parameter uncertainty are not considered.

Note that time delays and parameter uncertainties arise quite naturally in many practical applications, which are frequently sources of poor performance and instability of various kinds of real systems including stochastic fuzzy systems; see, e.g., [12, 21, 38, 39, 43, 46]. Therefore, it is reasonable and necessary to take into account time delays and parameter uncertainties when investigating robust FD for stochastic fuzzy systems. However, to the best of the authors’ knowledge, so far, there are few research results reported on the FD filtering for uncertain stochastic fuzzy time-delay systems. Thus, the problem of FD filter design for uncertain stochastic fuzzy time-delay systems still remains open and challenging.

It should be pointed out that, for the FD filter design problem of fuzzy systems, there are fuzzy-rule-dependent filter and fuzzy-rule-independent filter. When the premise variable of the original fuzzy model is available in filter implementation, the filter structure will be dependent of the fuzzy rules, which causes the so-called fuzzy-rule-dependent filter [24, 44]. On the contrary, if the premise variable of the fuzzy model is unavailable in filter implementation, then the condition leads to the fuzzy-rule-independent filter [33]. Because the information of the premise variable is fully considered in filter design by applying the fuzzy-rule-dependent line, the result obtained is sure less conservative. However, the filter design will become more complicated by the fuzzy-rule-dependent line [24, 33, 44].

Motivated by the above discussion, this paper considers the robust \(H_{\infty }\) FD problem for a class of uncertain Itô stochastic T–S fuzzy systems with time-varying delays. We deal with the FD by designing fuzzy-rule-independent and fuzzy-rule-dependent FD filters that generate a residual signal to estimate the fault signal. The main idea is to make the error between residual and fault as small as possible. A numerical example and a MSD mechanical system are used to illustrate the usefulness and effectiveness of our method. The main contributions of this paper are summarized as follows: (1) A new class of Itô stochastic T–S fuzzy systems with time-varying delays, norm-bounded parameter uncertainties, which have not been considered in the existing references, is proposed; (2) a Lyapunov–Krasovskii function is constructed to reflect the inherent two time-varying delays in the system itself, and some novel delay-dependent sufficient conditions in terms of linear matrix inequality (LMI) are proposed to guarantee the existence of the desired fuzzy-rule-independent and fuzzy-rule-dependent detection filters; (3) the difficult problem of norm-bounded parameter uncertainties is solved by settling several well-known matrix inequations, and weighting fault signal approach is employed to improve the performance of the FD system; and (4) explicit expression of the desired fuzzy-rule-independent and fuzzy-rule-dependent filter parameters is characterized by congruence transformation, matrix decomposition, and convex optimization technique.

Notation \(\mathbb {R}^{n}\) and \(\mathbb {R}^{n\times m}\) represent, respectively, the \(n\)-dimensional Euclidean space and the set of all \(n\times m\) real matrices. \(M^{\mathrm{T}}\) represents transpose of the matrix \(M; X > Y\) (respectively, \(X\ge Y\)) means that symmetric matrix \(X-Y\) is positive definite (respectively, positive semidefinite). \(I\) and \(O\) refer to the identity matrix and a zero matrix with appropriate dimensions, respectively. The notation \((*)\) represents a term that is induced by symmetry. Let \(\tau >0\) and \(C([-\tau , 0];\mathbb {R}^{n})\) represent the family of continuous functions \(\varphi \) from \([-\tau , 0]\) to \(\mathbb {R}^{n}\) with the norm \(\left\| \varphi \right\| = \mathop {\sup }\nolimits _{ - \tau \le \theta \le 0} | {\varphi (\theta )} |\), where \(| \cdot |\) is the Euclidean norm in \(R^{n}\). \(({\Omega ,\;\mathcal {F},\;{{\{ {{\mathcal {F}_t}} \}}_{t \ge 0}},\;\mathcal {P}})\) is a complete probability space with a filtration \({{{\{ {{\mathcal {F}_t}} \}}_{t \ge 0}}}\) satisfying the usual conditions. \(\mathcal {L}_{{\mathcal {F}_0}}^p({\left[ {-\tau ,\;0} \right] ;\;{\mathbb {R}^n}})\) denotes the family of all \({\mathcal {F}_0}\)-measurable \(C([-\tau , 0];\mathbb {R}^{n})\)-valued random variables \(\varphi = \{ {\varphi (\theta ):\; - \tau \le \theta \le 0} \}\), such that \(\mathop {\sup }\nolimits _{ - \tau \le \theta \le 0} \mathcal {E}{| {\varphi (\theta )} |^p} < \infty \), where \(\mathcal {E}\{ \cdot \}\) refers to the expectation operator with respect to the given probability measure \(\mathcal {P}\). \(\mathcal {L}_{2}[0, \infty )\) is the space of square-integrable vector functions over \([0, \infty ); \left\| \cdot \right\| _{2}\) stands for the usual \(\mathcal {L}_{2}[0, \infty )\) norm, while \(\left\| \cdot \right\| _{\mathcal {E}_{2}}\) denotes the norm in \(\mathcal {L}_{2}((\Omega , \mathcal {F},\mathcal {P}), [0, \infty ))\).

2 Problem Formulation and Preliminaries

We consider a class of nonlinear stochastic systems with parameter uncertainties and time delays described by the following T–S fuzzy stochastic model \((\Sigma )\):

Plant Rule \(i\): IF \({\theta _1}(t)\) is \({\mu _{i1}}\) and \({\theta _2}(t)\) is \({\mu _{i2}}\) and \(\cdots \) and \({\theta _g}(t)\) is \({\mu _{ig}}\), THEN

$$\begin{aligned} \mathrm{d}x(t)&= \left[ {A_i}(t)x(t) + {A_{1i}}(t)x({t - {\tau _1}(t)}) + {B_{0i}}(t)u(t) + {B_i}(t)\omega (t) \right. \nonumber \\&\quad \left. +\,{B_{1i}}(t)f(t) \right] \mathrm{d}t + {E_i}(t)x({t - {\tau _2}(t)})\mathrm{d}\varpi ,\end{aligned}$$
(1)
$$\begin{aligned} \mathrm{d}y(t)&= \left[ {C_i}(t)x(t) + {C_{1i}}(t)x({t - {\tau _1}(t)}) + {D_{0i}}(t)u(t) +{D_i}(t)\omega (t) \right. \nonumber \\&\quad \left. +\, {D_{1i}}(t)f(t) \right] \mathrm{d}t +{F_i}(t)x({t - {\tau _2}(t)} )\mathrm{d}\varpi ,\end{aligned}$$
(2)
$$\begin{aligned} x(t)&= \phi (t),\quad \forall t\in [-\tau ,0],\quad i=1, 2,\ldots , r, \end{aligned}$$
(3)

where \({\mu _{i1}}, {\mu _{i2}}, \ldots , {\mu _{ig}}\) are the fuzzy sets; \(r\) is the number of IF-THEN rules; \(x(t)\in \mathbb {R}^{n}\) is the state vector; \(y(t)\in \mathbb {R}^{p}\) is the measured output; \(u(t)\in \mathbb {R}^{m}\) is the known input; \(\omega (t)\in \mathbb {R}^{q}\) is the unknown disturbance input; \(f(t)\in \mathbb {R}^{l}\) is the fault to be detected; \(u(t), \omega (t)\), and \(f(t)\) belong to \(\mathcal {L}_{2}[0, \infty ); {\theta }(t)=[{\theta _1}(t), {\theta _2}(t), \ldots , {\theta _g}(t)]\) are the premise variables; and \(\phi (t)\) is the initial condition. Throughout this paper, it is assumed that the premise variables do not depend on the input variables \(u(t)\) explicitly. \(\varpi (t)\) is a zero-mean real scalar Brownian motion (Wiener process) on \((\Omega , \mathcal {F}, \mathcal {P})\) relative to an increasing family \((\mathcal {F}_{t})_{t\in [0,\infty )}\) of \(\sigma \)-algebras \(\mathcal {F}_{t}\subset \mathcal {F}\) satisfying

$$\begin{aligned} \mathcal {E}\{{\mathrm{d}}\varpi (t)\} =0,\quad \mathcal {E}\{\mathrm{d}\varpi (t)^{2}\}=\mathrm{d}t. \end{aligned}$$
(4)

\({\tau _1}(t), {\tau _2}(t)\) are the time delays satisfying

$$\begin{aligned} 0 < {\tau _1}(t) \le \tau < \infty ,\;\;0 < {\tau _2}(t) \le \tau < \infty ,\quad {{\dot{\tau }}_1}(t) \le {\mu _1}<1,\;\;{{\dot{\tau }}_2}(t) \le {\mu _2}<1, \nonumber \\ \end{aligned}$$
(5)

where \(\tau , \mu _1\) and \(\mu _2\) are constant scalars. Parameters in system \((\Sigma )\) are described as follows:

$$\begin{aligned} {A_i}(t)&= {A_i} + \Delta {A_i}(t),\;\;\;{A_{1i}}(t) = {A_{1i}} + \Delta {A_{1i}}(t),\;{B_{0i}}(t) = {B_{0i}} + \Delta {B_{0i}}(t),\; \nonumber \\ {B_{1i}}(t)&= {B_{1i}} + \Delta {B_{1i}}(t),\;{E_i}(t) = {E_i} + \Delta {E_i}(t),\;\;\;{C_i}(t) = {C_i} + \Delta {C_i}(t),\; \nonumber \\ {C_{1i}}(t)&= {C_{1i}} + \Delta {C_{1i}}(t),\;{D_{0i}}(t) = {D_{0i}} + \Delta {D_{0i}}(t),{D_{1i}}(t) = {D_{1i}} + \Delta {D_{1i}}(t), \nonumber \\ {F_i}(t)&= {F_i} + \Delta {F_i}(t), \ {B_{i}}(t) = {B_{i}}, \ {D_{i}}(t) = {D_{i}}, \end{aligned}$$
(6)

where \(A_{i}, A_{1i}, B_{0i}, B_{i}, B_{1i}, E_i, C_{i}, C_{1i}, D_{0i}, D_{i}, D_{1i}, F_i\) are known constant matrices with compatible dimensions, and \(\Delta {A_i}(t), \Delta {A_{1i}}(t), \Delta {B_{0i}}(t), \Delta {B_{1i}}(t), \Delta {E_i}(t), \Delta {C_i}(t), \Delta {C_{1i}}(t), \Delta {D_{0i}}(t), \Delta {D_{1i}}(t), \Delta {F_i}(t)\) represent the parameter uncertainties of the system, which are assumed to be of the form

$$\begin{aligned}&\left[ {\begin{array}{lllll} {\Delta {A_i}(t)} &{} {\Delta {A_{1i}}(t)} &{} {\Delta {B_{0i}}(t)} &{} {\Delta {B_{1i}}(t)} &{} {\Delta {E_i}(t)} \\ {\Delta {C_i}(t)} &{} {\Delta {C_{1i}}(t)} &{} {\Delta {D_{0i}}(t)} &{} {\Delta {D_{1i}}(t)} &{} {\Delta {F_i}(t)} \\ \end{array}} \right] \nonumber \\&\quad = \left[ {\begin{array}{c} {{M_{1i}}} \\ {{M_{2i}}} \\ \end{array}} \right] {G_i}(t)\left[ {\begin{array}{lllll} {{N_{1i}}} &{} {{N_{2i}}} &{} {{N_{3i}}} &{} {{N_{4i}}} &{} {{N_{5i}}} \\ \end{array}} \right] , \end{aligned}$$
(7)

where \(M_{1i}, M_{2i}, N_{1i}, N_{2i}, N_{3i}, N_{4i}, N_{5i}\) are known constant matrices with compatible dimensions and \(G_{i}(t)\) are unknown Lebesgue measurable matrix functions satisfying

$$\begin{aligned} G_{i}(t)^{\mathrm{T}}G_{i}(t)\le I,\quad i=1, 2,\ldots , r. \end{aligned}$$
(8)

The parameter uncertainties \(\Delta {A_i}(t), \Delta {A_{1i}}(t), \Delta {B_{0i}}(t), \Delta {B_{1i}}(t), \Delta {E_i}(t), \Delta {C_i}(t),\) \(\Delta {C_{1i}}(t), \Delta {D_{0i}}(t), \Delta {D_{1i}}(t), \Delta {F_i}(t)\) are said to be admissible if both (7) and (8) hold.

Given a pair of \((x(t), u(t))\), by using singleton fuzzier, product inference, and center-average defuzzier, the final output of the fuzzy stochastic system is inferred as follows:

$$\begin{aligned} ({{\Sigma _1}}):\mathrm{d}x(t)&= \sum \limits _{i = 1}^r {{h_i}({\theta (t)})} \left\{ \begin{array}{l} \left[ {A_i}(t)x(t) + {A_{1i}}(t)x({t - {\tau _1}(t)}) + {B_{0i}}(t)u(t) \right. \\ \left. \,+ {B_i}(t)\omega (t) +{B_{1i}}(t)f(t) \right] \mathrm{d}t \\ \,+ {E_i}(t)x({t - {\tau _2}(t)})\mathrm{d}\varpi , \\ \end{array} \right\} \nonumber \\ \mathrm{d}y(t)&= \sum \limits _{i = 1}^r {{h_i}({\theta (t)} )}\left\{ \begin{array}{l} \left[ {C_i}(t)x(t) + {C_{1i}}(t)x({t - {\tau _1}(t)}) + {D_{0i}}(t)u(t) \right. \\ \left. \, + {D_i}(t)\omega (t) + {D_{1i}}(t)f(t) \right] \mathrm{d}t \\ \,+ {F_i}(t)x({t - {\tau _2}(t)})\mathrm{d}\varpi , \\ \end{array}\right\} \qquad \end{aligned}$$
(9)

where \({h_i}({\theta (t)}) = \frac{{{\nu _i}({\theta (t)})}}{{\sum \nolimits _{i = 1}^r {{\nu _i}({\theta (t)})} }},\ {\nu _i}({\theta (t)}) = \prod \nolimits _{j = 1}^g {{\mu _{ij}}({{\theta _j}(t)})}, {{\mu _{ij}}({{\theta _j}(t)})}\), is the grade of membership of \(\theta _{j}(t)\) in \(\mu _{ij}, {\nu _i}({\theta (t)})\ge 0, i=1,2,\ldots , r, \sum \nolimits _{i = 1}^r {{\nu _i}({\theta (t)})} > 0\) for all t. Therefore, \({h_i}({\theta (t)}) \ge 0\), for \(i=1,2,\ldots , r\), and \(\sum \nolimits _{i = 1}^r {{h_i}({\theta (t)})} = 1\) for all t.

Throughout this paper, the nominal system of \(\Sigma _{1}\) in (9) is assumed to be stable. Our FD schemes are concerned with the construction of a residual generator. For the plant represented by (1–9), we consider the following two kinds of FD filters.

2.1 Fuzzy-Rule-Independent Filter

In the case that the premise variable of the original fuzzy model \({\theta }(t)\) is unavailable in filter implementation, the filter structure will have to be independent of the fuzzy rules. Then, the FD filter is designed as the following form.

$$\begin{aligned} ({{\Sigma _c}}):\quad \mathrm{d}{x_c}(t)&= {A_c}{x_c}(t)\mathrm{d}t + {B_c}\mathrm{d}y(t), \nonumber \\ {\chi _c}(t)&= {C_c}{x_c}(t), \end{aligned}$$
(10)

where \({x_c}(t) \in {\mathbb {R}^n}\) is the state vector of the FD filter, \({\chi _c}(t) \in {\mathbb {R}^l}\) is the so-called residual signal, and \({A_c},\;{B_c},\;{C_c}\) are the filter parameters to be designed.

The objective of FD is to identify the fault \(f(t)\) when it appears. To improve the performance of the fault detection system, we add a weighting matrix function into the fault \(f(t)\), i.e., \({f_w}(s) = W(s)f(s)\), where \({f_w}(s)\) and \(f(s)\) denote, respectively, the Laplace transforms of \({f_w}(t)\) and \(f(t)\). One minimal state-space realization of \({f_w}(s)\) and \(f(s)\) can be

$$\begin{aligned} ({{\Sigma _w}}):\quad {{\dot{x}}_w}(t)&= {A_w}{x_w}(t) + {B_w}f(t),\nonumber \\ {f_w}(t)&= {C_w}{x_w}(t) + {D_w}f(t),\nonumber \\ {x_w}(0)&= 0, \end{aligned}$$
(11)

where \({x_w}(t) \in {\mathbb {R}^k}\) is the state vector and \(A_w, B_w, C_w, D_w\) are constant matrices. Denoting \({e_c}(t) \triangleq {\chi _c}(t) - {f_w}(t)\) and augmenting the model of \((\Sigma )\) to include the states of \((\Sigma _{c})\) and \((\Sigma _{w})\), the overall dynamics of the fault detection system is governed by \(({{{\tilde{\Sigma }}_c}})\):

$$\begin{aligned} \mathrm{d}\xi (t)&= \sum \limits _{i = 1}^r {{h_i}({\theta (t)})} \left\{ \begin{array}{l} [ {{\tilde{A}}_i}(t)\xi (t) + {{\tilde{A}}_{1i}}(t)H\xi ({t - {\tau _1}(t)}) + {{\tilde{B}}_i}(t)v(t)]\mathrm{d}t \nonumber \\ + {{\tilde{E}}_i}(t)H\xi ({t - {\tau _2}(t)})\mathrm{d}\varpi \end{array} \right\} , \\ \nonumber \\ {e_c}(t)&\triangleq {\chi _c}(t) - {f_w}(t) = \sum \limits _{i = 1}^r {{h_i}({\theta (t)})} \left\{ {{{\tilde{C}}_i}(t)\xi (t) + {{\tilde{D}}_i}(t)v(t)} \right\} , \end{aligned}$$
(12)

where

$$\begin{aligned} \xi (t)&= \left[ {\begin{array}{c} {x(t)} \\ {{x_c}(t)} \\ {{x_w}(t)} \\ \end{array} } \right] ,\quad v(t) = \left[ {\begin{array}{c} {u(t)} \\ {\omega (t)} \\ {f(t)} \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_i}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{A_{i}} + \Delta {A_{i}}(t)} &{} 0 &{} 0 \\ {{B_c}({{C_i} + \Delta {C_i}(t)})} &{} {{A_c}} &{} 0 \\ 0 &{} 0 &{} {{A_w}} \\ \end{array} } \right] ,\quad H = \left[ {\begin{array}{c@{\quad }c@{\quad }c} I &{} 0 &{} 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_{1i}}(t)&= \left[ {\begin{array}{c} {{A_{1i}} + \Delta {A_{1i}}(t)} \\ {{B_c}({{C_{1i}} + \Delta {C_{1i}}(t)})} \\ 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{B}}_i}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{B_{0i}} + \Delta {B_{0i}}(t)} &{} {{B_i}} &{} {{B_{1i}} + \Delta {B_{1i}}(t)} \\ {{B_c}({{D_{0i}} + \Delta {D_{0i}}(t)})} &{} {{B_c}{D_i}} &{} {{B_c}({{D_{1i}} + \Delta {D_{1i}}(t)})} \\ 0 &{} 0 &{} {{B_w}} \\ \end{array} } \right] , \nonumber \\ {{\tilde{E}}_i}(t)&= \left[ {\begin{array}{c} {{E_i} + \Delta {E_i}(t)} \\ {{B_c}({{F_i} + \Delta {F_i}(t)})} \\ 0 \\ \end{array} } \right] , \quad {{\tilde{C}}_i}(t) \triangleq {{\tilde{C}}_i} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0 &{} {{C_c}} &{} { - {C_w}} \\ \end{array} } \right] , \nonumber \\ {{\tilde{D}}_i}(t)&\triangleq {{\tilde{D}}_i} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} { - {D_w}} \\ \end{array} } \right] ,\nonumber \\ \Delta {{\tilde{A}}_i}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {\Delta {A_{i}}(t)} &{} 0 &{} 0 \\ {{B_c}\Delta {C_i}(t)} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} } \right] ,\quad \Delta {{\tilde{A}}_{1i}}(t) = \left[ {\begin{array}{c} {\Delta {A_{1i}}(t)} \\ {{B_c}\Delta {C_{1i}}(t)} \\ 0 \\ \end{array} } \right] , \nonumber \\ \Delta {{\tilde{B}}_i}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {\Delta {B_{0i}}(t)} &{} 0 &{} {\Delta {B_{1i}}(t)} \\ {{B_c}\Delta {D_{0i}}(t)} &{} 0 &{} {{B_c}\Delta {D_{1i}}(t)} \\ 0 &{} 0 &{} 0 \\ \end{array} } \right] ,\nonumber \\ \Delta {{\tilde{E}}_i}(t)&= \left[ {\begin{array}{c} {\Delta {E_i}(t)} \\ {{B_c}\Delta {F_i}(t)} \\ 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_i}(t)&= {{\tilde{A}}_i} + \Delta {{\tilde{A}}_i}(t),\quad {{\tilde{A}}_{1i}}(t) = {{\tilde{A}}_{1i}} + \Delta {{\tilde{A}}_{1i}}(t), \nonumber \\ {{\tilde{B}}_i}(t)&= {{\tilde{B}}_i} + \Delta {{\tilde{B}}_i}(t),\quad {{\tilde{E}}_i}(t) = {{\tilde{E}}_i} + \Delta {{\tilde{E}}_i}(t). \end{aligned}$$
(13)

2.2 Fuzzy-Rule-Dependent Filter

Now, assume that the premise variable of the fuzzy model \({\theta }(t)\) is available in filter implementation, which implies that \({h_i}({\theta (t)})\) is available for feedback. Suppose that the filter’s premise variable is the same as the plant’s premise variable. Using the parallel distributed compensation (PDC) technique, the fuzzy-rule-dependent filter is designed as follows:

Rule \(i\): IF \({\theta _1}(t)\) is \({\mu _{i1}}\) and \({\theta _2}(t)\) is \({\mu _{i2}}\) and \(\cdots \) and \({\theta _g}(t)\) is \({\mu _{ig}}\), THEN

$$\begin{aligned} \mathrm{d}{x_f}(t)&= {A_{fi}}{x_f}(t)\mathrm{d}t + {B_{fi}}\mathrm{d}y(t), \nonumber \\ {\chi _f}(t)&= {C_{fi}}{x_f}(t),\quad i = 1,2, \ldots ,r \end{aligned}$$
(14)

where \({x_f}(t) \in {\mathbb {R}^n}\) is the state vector , \({\chi _f}(t) \in {\mathbb {R}^l}\) is the so-called residual signal, and \({A_{fi}},\;{B_{fi}},\;{C_{fi}}\) are the filter parameters to be designed. The above filter plant can also be represented by \((\Sigma _{f})\):

$$\begin{aligned} \mathrm{d}{x_f}(t)&= \sum \limits _{i = 1}^r {{h_i}({\theta (t)})} \{ {{A_{fi}}{x_f}(t)\mathrm{d}t + {B_{fi}}\mathrm{d}y(t)} \}, \nonumber \\ {\chi _f}(t)&= \sum \limits _{i = 1}^r {{h_i}({\theta (t)})} {C_{fi}}{x_f}(t). \end{aligned}$$
(15)

Denoting \({e_f}(t) \triangleq {\chi _f}(t) - {f_w}(t)\) and augmenting the model of \((\Sigma )\) to include the states of \((\Sigma _{f})\) and \((\Sigma _{w})\), the fault detection system is described by \(({{{\tilde{\Sigma } }_f}})\):

$$\begin{aligned} \mathrm{d}\zeta (t)&= \sum \limits _{j = 1}^r {\sum \limits _{i = 1}^r {{h_i}({\theta (t)})} {h_j}({\theta (t)})\left\{ \begin{array}{l} \left[ {{\tilde{A}}_{ij}}(t)\zeta (t) +{{\tilde{A}}_{1ij}}(t)H\zeta ({t - {\tau _1}(t)}) \right. \\ \,+ \left. {{\tilde{B}}_{ij}}(t)v(t) \right] \mathrm{d}t \\ \,+ {{\tilde{E}}_{ij}}(t)H\zeta ({t - {\tau _2}(t)})\mathrm{d}\varpi \\ \end{array} \right\} }, \nonumber \\ {e_f}(t)&\triangleq {\chi _f}(t) - {f_w}(t) \nonumber \\&= \sum \limits _{j = 1}^r {\sum \limits _{i = 1}^r {{h_i}({\theta (t)})} {h_j}({\theta (t)})\{ {{{\tilde{C}}_{ij}}(t)\zeta (t) + {{\tilde{D}}_{ij}}(t)v(t)} \}}, \end{aligned}$$
(16)

where

$$\begin{aligned} \zeta (t)&= \left[ {\begin{array}{c} {x(t)} \\ {{x_f}(t)} \\ {{x_w}(t)} \\ \end{array} } \right] , \quad v(t) = \left[ {\begin{array}{c} {u(t)} \\ {\omega (t)} \\ {f(t)} \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_{ij}}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{A_{i}} + \Delta {A_{i}}(t)} &{} 0 &{} 0 \\ {{B_{fj}}({{C_i} + \Delta {C_i}(t)})} &{} {{A_{fj}}} &{} 0 \\ 0 &{} 0 &{} {{A_w}} \\ \end{array} } \right] ,\quad H = \left[ {\begin{array}{c@{\quad }c@{\quad }c} I &{} 0 &{} 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_{1ij}}(t)&= \left[ {\begin{array}{c} {{A_{1i}} + \Delta {A_{1i}}(t)} \\ {{B_{fj}}({{C_{1i}} + \Delta {C_{1i}}(t)})} \\ 0 \\ \end{array} } \right] ,\nonumber \\ {{\tilde{B}}_{ij}}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{B_{0i}} + \Delta {B_{0i}}(t)} &{} {{B_i}} &{} {{B_{1i}} + \Delta {B_{1i}}(t)} \\ {{B_{fj}}({{D_{0i}} + \Delta {D_{0i}}(t)} )} &{} {{B_{fj}}{D_i}} &{} {{B_{fj}}({{D_{1i}} + \Delta {D_{1i}}(t)})} \\ 0 &{} 0 &{} {{B_w}} \\ \end{array} } \right] , \nonumber \\ {{\tilde{E}}_{ij}}(t)&= \left[ {\begin{array}{c} {{E_i} + \Delta {E_i}(t)} \\ {{B_{fj}}({{F_i} + \Delta {F_i}(t)})} \\ 0 \\ \end{array} } \right] , \quad {{\tilde{C}}_{ij}}(t) \triangleq {{\tilde{C}}_{ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0 &{} {{C_{fj}}} &{} { - {C_w}} \\ \end{array} } \right] , \nonumber \\ {{\tilde{D}}_{ij}}(t)&\triangleq {{\tilde{D}}_{ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} { - {D_w}} \\ \end{array} } \right] ,\nonumber \\ \Delta {{\tilde{A}}_{ij}}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {\Delta {A_{i}}(t)} &{} 0 &{} 0 \\ {{B_{fj}}\Delta {C_i}(t)} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} } \right] , \quad \Delta {{\tilde{A}}_{1ij}}(t) = \left[ {\begin{array}{c} {\Delta {A_{1i}}(t)} \\ {{B_{fj}}\Delta {C_{1i}}(t)} \\ 0 \\ \end{array} } \right] , \nonumber \\ \Delta {{\tilde{B}}_{ij}}(t)&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {\Delta {B_{0i}}(t)} &{} 0 &{} {\Delta {B_{1i}}(t)} \\ {{B_{fj}}\Delta {D_{0i}}(t)} &{} 0 &{} {{B_{fj}}\Delta {D_{1i}}(t)} \\ 0 &{} 0 &{} 0 \\ \end{array} } \right] ,\nonumber \\ \Delta {{\tilde{E}}_{ij}}(t)&= \left[ {\begin{array}{c} {\Delta {E_i}(t)} \\ {{B_{fj}}\Delta {F_i}(t)} \\ 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{A}}_{ij}}(t)&= {{\tilde{A}}_{ij}} + \Delta {{\tilde{A}}_{ij}}(t),\quad {{\tilde{A}}_{1ij}}(t) = {{\tilde{A}}_{1ij}} + \Delta {{\tilde{A}}_{1ij}}(t), \nonumber \\ {{\tilde{B}}_{ij}}(t)&= {{\tilde{B}}_{ij}} + \Delta {{\tilde{B}}_{ij}}(t),\quad {{\tilde{E}}_{ij}}(t) = {{\tilde{E}}_{ij}} + \Delta {{\tilde{E}}_{ij}}(t). \end{aligned}$$
(17)

Before proceeding further, we first introduce the following definitions, which will play key roles in deriving our main results in the sequel.

Definition 1

[22] For the uncertain time-delay fuzzy stochastic system \(({{{\tilde{\Sigma } }_c}})\) in (12) with \(v(t) = 0\) and every \(\varphi \in \mathcal {L}_{{\mathcal {F}_0}}^2({[{ -\tau ,\;0}];\;{\mathbb {R}^n}})\), the trivial solution is asymptotically mean square stable if

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } \mathcal {E}{\Vert {\xi ({t,\;\varphi })} \Vert ^2} = 0. \end{aligned}$$

Definition 2

Given a scalar \(\gamma >0\), the fuzzy stochastic system \(({{{\tilde{\Sigma } }_c}})\) in (12) is asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma \) if it is asymptotically mean square stable when \(v(t) = 0\), and under zero initial condition and for all nonzero \(v(t) \in {\mathcal {L}_2}[ {0,\;\infty })\), the following holds:

$$\begin{aligned}&\mathcal {E}\left\{ {\int _0^\infty {{e_c}^\mathrm{T}(t){e_c}(t)\mathrm{d}t} }\right\} < {\gamma ^2}\int _0^\infty {{v^\mathrm{T}}(t)v(t)\mathrm{d}t} \nonumber \\&\quad = {\gamma ^2}\left[ {\int _0^\infty {{u^\mathrm{T}}(t)u(t)\mathrm{d}t} + \int _0^\infty {{\omega ^\mathrm{T}}(t)\omega (t)\mathrm{d}t} + \int _0^\infty {{f^\mathrm{T}}(t)f(t)\mathrm{d}t} } \right] . \end{aligned}$$
(18)

The fault detection problem to be addressed in this paper can be described as the following two steps:

  • Step 1 Design a FD filter and generate a residual signal.

For fuzzy stochastic system \(\Sigma _{1}\) in (9), design a robust \({H_\infty }\) filter in the form of (\(\Sigma _{c}\)) in (10) [or (\(\Sigma _{f}\)) in (15)] to generate a residual signal. Meanwhile, the filter is designed to assure that the resulting FD system \(({{{\tilde{\Sigma } }_c}})\) in (12) [or \(({{{\tilde{\Sigma } }_f}})\) in (16)] is to be asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma >0\).

  • Step 2 Set up a FD measure.

Select an evaluation function and a threshold. In this paper, a residual evaluation function \(J(\chi )\) (where \(\chi \) denotes \({\chi _c}(t)\) or \({\chi _f}(t)\)) and a threshold \(J_\mathrm{th}\) are selected as

$$\begin{aligned} J(\chi )&\triangleq {\left( {\int _{{t_0}}^{{t_0} + {t^ * }} {{\chi ^\mathrm{T}}(t)\chi (t)\mathrm{d}t} } \right) ^{1/2}},\end{aligned}$$
(19)
$$\begin{aligned} {J_\mathrm{th}}&\triangleq \mathop {\sup }\limits _{0 \ne \omega \in {\mathcal {L}_2},\;0 \ne u \in {\mathcal {L}_2},\;f = 0} J(\chi ), \end{aligned}$$
(20)

where \(t_{0}\) denotes the initial evaluation time instant and \(t^{*}\) refers to the evaluation time. Based on the designing, the occurrence of faults can be detected by comparing \(J(\chi )\) and \(J_\mathrm{th}\) according to the following logical relationship:

$$\begin{aligned}&J(\chi ) \leqslant {J_\mathrm{th}} \Longrightarrow no \ \ \mathrm{faults},\\&J(\chi ) > {J_\mathrm{th}} \Longrightarrow \mathrm{with} \ \ \mathrm{faults} \Longrightarrow \mathrm{alarm}. \end{aligned}$$

3 Main Results

Before giving the main results of this paper, we first recall some important lemmas that will be frequently used throughout the proofs.

Lemma 1

([22] Itô differential formula) Let \(x(t)\) be an \(n\)-dimensional Itô process on \(t>0\) with the stochastic differential

$$\begin{aligned} \mathrm{d}x(t) = f(t)\mathrm{d}t + g(t)\mathrm{d}\varpi (t), \end{aligned}$$

where \(f(t) \in {\mathbb {R}^n}\) and \(g(t) \in {\mathbb {R}^{n \times m}}\). Let \(V({x,\;t}) \in {C^{2,1}}({{\mathbb {R}^n} \times {\mathbb {R}^ + };\;{\mathbb {R} }}), {C^{2,1}}({\mathbb {R}^n} \times {\mathbb {R}^ + };\;{\mathbb {R} })\) denotes the family of all real-valued functions defined on \({{\mathbb {R}^n} \times {\mathbb {R}^ + }}\), which are continuously twice differentiable in the first argument and once differentiable in the second argument. Then, \(V({x,\;t})\) is a real-valued Itô process with its stochastic differential given by

$$\begin{aligned} \mathrm{d}V({x,t})&= \mathcal {L}V({x,t})\mathrm{d}t + {V_x}({x,t})g(t)\mathrm{d}\varpi (t),\\ \mathcal {L}V({x,t})&= {V_t}({x,t}) + {V_x}({x,t})f(t) + \frac{1}{2}tr\left( {{g^\mathrm{T}}(t){V_{xx}}({x,t})g(t)}\right) . \end{aligned}$$

Lemma 2

[3] Suppose that matrices \(\{ {{\mathcal {M}_i}} \}_{i = 1}^s \in {\mathbb {R}^{n \times m}}\) and a positive semidefinite matrix \(\mathcal {P} \in {\mathbb {R}^{n \times n}}\) are given. If \(0 \leqslant {h_i} \leqslant 1\) and \(\sum \nolimits _{i = 1}^s {{h_i}} = 1\), then

$$\begin{aligned} {\left( {\sum \limits _{i = 1}^s {{h_i}{\mathcal {M}_i}} }\right) ^\mathrm{T}}\mathcal {P}\left( {\sum \limits _{i = 1}^s {{h_i}{\mathcal {M}_i}} }\right) \leqslant \sum \limits _{i = 1}^s {{h_i}{\mathcal {M}_i}^\mathrm{T}\mathcal {P}{\mathcal {M}_i}}; \end{aligned}$$

[10] For any real matrices \({X_{ij}}, i,j=1,2,\ldots ,s\) and \(\Lambda >0\) with appropriate dimensions, we have

$$\begin{aligned} \sum \limits _{i = 1}^s {\sum \limits _{j = 1}^s {\sum \limits _{k = 1}^s {\sum \limits _{l = 1}^s {{h_i}{h_j}{h_k}{h_l}X_{ij}^\mathrm{T}\Lambda {X_{kl}}} } } } \leqslant \sum \limits _{i = 1}^s {\sum \limits _{j = 1}^s {{h_i}{h_j}X_{ij}^\mathrm{T}\Lambda {X_{ij}}} }, \end{aligned}$$

where \(0 \leqslant {h_i} \leqslant 1\) for \(i=1,2,\ldots ,s\) and \(\sum \nolimits _{i = 1}^s {{h_i}} = 1\).

Lemma 3

[34] Let \(M, N\), and \(F\) be real matrices of appropriate dimensions with \({F^\mathrm{T}}F \leqslant I\), where \(F\) may be time-varying. Then, for any scalar \(\varepsilon \ne 0\), we have

$$\begin{aligned} MFN + {N^\mathrm{T}}{F^\mathrm{T}}{M^\mathrm{T}} \leqslant {\varepsilon ^2}M{M^\mathrm{T}} + {\varepsilon ^{ - 2}}{N^\mathrm{T}}N. \end{aligned}$$

Lemma 4

[35] Let \(\mathcal {A}, \mathcal {D}, \mathcal {S}, \mathcal {W}\), and \(F\) be real matrices of appropriate dimensions such that \(\mathcal {W}>0\) and \({F^\mathrm{T}}F \leqslant I\). Then, for any scalar \(\epsilon > 0\) such that \(\mathcal {W }- \epsilon \mathcal {D}{\mathcal {D}^\mathrm{T}} > 0\), we have

$$\begin{aligned} {({\mathcal {A} + \mathcal {D}F\mathcal {S}})^\mathrm{T}}{\mathcal {W}^{ - 1}}({\mathcal {A} + \mathcal {D}F\mathcal {S}}) \leqslant {\mathcal {A}^\mathrm{T}}{({\mathcal {W }- \epsilon \mathcal {D}{\mathcal {D}^\mathrm{T}}})^{ - 1}}\mathcal {A }+ {\epsilon ^{ - 1}}{\mathcal {S}^\mathrm{T}}\mathcal {S}. \end{aligned}$$

First, we will analyze the stability with an \({H_\infty }\) performance level \(\gamma >0\) of FD system \(({{{\tilde{\Sigma } }_c}})\) in (12) and give the following result.

Theorem 1

Given a scalar \(\gamma >0\), the fuzzy stochastic FD system \(({{{\tilde{\Sigma } }_c}})\) in (12) is asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma \) if there exist scalars \(\varepsilon _{1}>0, \varepsilon _{2}>0\) and matrices \(P>0, Q>0, R>0\) such that the following matrix inequalities hold:

$$\begin{aligned} {{\Upsilon _{i}}}=\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\Upsilon _{11i}}} &{} {{\Upsilon _{12i}}} &{} 0 &{} {{\Upsilon _{14i}}} &{} 0 &{} {{{\tilde{C}}_i}^\mathrm{T}} \\ * &{} {{\Upsilon _{22i}}} &{} 0 &{} {{\Upsilon _{24i}}} &{} 0 &{} 0 \\ * &{} * &{} {{\Upsilon _{33i}}} &{} 0 &{} {\tilde{E}_i^\mathrm{T}} &{} 0 \\ * &{} * &{} * &{} {{\Upsilon _{44i}}} &{} 0 &{} {\tilde{D}_i^\mathrm{T}} \\ * &{} * &{} * &{} * &{} {{\Upsilon _{55i}}} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} { - I} \\ \end{array} } \right] < 0, \end{aligned}$$
(21)

\(i=1,2,\ldots ,r\), where

$$\begin{aligned} {\Upsilon _{11i}}&= P{{\tilde{A}}_i} + {{\tilde{A}}_i}^\mathrm{T}P + {H^\mathrm{T}}({Q+R})H + \varepsilon _1^{-1}P{{\tilde{M}}_{1i}}{{\tilde{M}}^\mathrm{T}}_{1i}P + {\varepsilon _1}{{\tilde{N}}_{1i}}^\mathrm{T}{{\tilde{N}}_{1i}},\\ {\Upsilon _{12i}}&= P{{\tilde{A}}_{1i}} + {\varepsilon _1}{{\tilde{N}}_{1i}}^\mathrm{T}{N_{2i}}, {\Upsilon _{14i}} = P{{\tilde{B}}_i} + {\varepsilon _1}{{\tilde{N}}_{1i}}^\mathrm{T}{\tilde{N}_{3i}}, \\ {\Upsilon _{22i}}&= - ({1 - {\mu _1}})Q + {\varepsilon _1}{N_{2i}}^\mathrm{T}{N_{2i}}, {\Upsilon _{24i}} = {\varepsilon _1}{N_{2i}}^\mathrm{T}{{\tilde{N}}_{3i}},\\ {\Upsilon _{33i}}&= - ({1 - {\mu _2}})R + {\varepsilon _2}{N_{5i}}^\mathrm{T}{N_{5i}}, {\Upsilon _{44i}} = - {\gamma ^2}I + {\varepsilon _1}{{\tilde{N}}_{3i}}^\mathrm{T}{{\tilde{N}}_{3i}}, \\ {\Upsilon _{55i}}&= \varepsilon _2^{-1}{{\tilde{M}}_{1i}}{{\tilde{M}}^\mathrm{T}}_{1i} - {P^{ - 1}}, \end{aligned}$$
$$\begin{aligned} {{\tilde{M}}^\mathrm{T}}_{1i}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{M_{1i}}^\mathrm{T}} &{} {{{({{B_c}{M_{2i}}})}^\mathrm{T}}} &{} 0 \\ \end{array} } \right] ,\ \ {{\tilde{N}}_{1i}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{N_{1i}}} &{} 0 &{} 0 \\ \end{array} } \right] ,\ \ {{\tilde{N}}_{3i}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{N_{3i}}} &{} 0 &{} {{N_{4i}}} \\ \end{array} } \right] ,\qquad \end{aligned}$$
(22)
$$\begin{aligned} {{\tilde{A}}_i}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{A_{i}}} &{} 0 &{} 0 \\ {{B_c}{C_i}} &{} {{A_c}} &{} 0 \\ 0 &{} 0 &{} {{A_w}} \\ \end{array} } \right] , \ \ {{\tilde{A}}_{1i}} = \left[ {\begin{array}{c} {{A_{1i}}} \\ {{B_c}{C_{1i}}} \\ 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{B}}_i}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{B_{0i}}} &{} {{B_i}} &{} {{B_{1i}}} \\ {{B_c}{D_{0i}}} &{} {{B_c}{D_i}} &{} {{B_c}{D_{1i}}} \\ 0 &{} 0 &{} {{B_w}} \\ \end{array} } \right] , \ \ {{\tilde{E}}_i} = \left[ {\begin{array}{c} {{E_i}} \\ {{B_c}{F_i}} \\ 0 \\ \end{array} } \right] . \end{aligned}$$
(23)

Proof

Please see the “Appendix”. \(\square \)

We are now ready to present a solution to the \(H_{\infty }\) FD filter design for \(({{{ \Sigma }_c}})\) in (10).

Theorem 2

For given scalars \(\gamma >0, \varepsilon _{1}>0, \varepsilon _{2}>0\) and matrices \( Q>0, R>0\), suppose there exist matrices \(\mathcal {U}>0, \mathcal {V}>0, V>0, \mathcal {A}_{c}, \mathcal {B}_{c}\), and \(\mathcal {C}_{c}\) such that the following linear matrix inequalities (LMIs) hold as shown in (24) and (25) for all \(i=1,2,\ldots ,r\),

$$\begin{aligned}&\Gamma _{i}=\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\Gamma _{11i}}} &{} {{\Gamma _{12i}}} &{} 0 &{} {{\Gamma _{14i}}} &{} 0 &{} {{\Gamma _{16i}}} &{} {{\Gamma _{17i}}} {{\Gamma _{18i}}} &{} 0 \\ * &{} {{\Gamma _{22}}} &{} 0 &{} {{\Gamma _{24i}}} &{} 0 &{} {{\Gamma _{26i}}} &{} {{\Gamma _{27i}}} {{\Gamma _{28i}}} &{} 0 \\ * &{} * &{} {{\Gamma _{33}}} &{} 0 &{} 0 &{} 0 &{} 0 {{\Gamma _{38i}}} &{} 0 \\ * &{} * &{} * &{} {{\Gamma _{44}}} &{} 0 &{} 0 &{} 0 0 &{} 0 \\ * &{} * &{} * &{} * &{} {{\Gamma _{55}}} &{} 0 &{} 0 0 &{} {{\Gamma _{59i}}} \\ * &{} * &{} * &{} * &{} * &{} { - {\gamma ^2}I} &{} 0 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} { - {\gamma ^2}I} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * { - {\gamma ^2}I} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} { - \mathcal {U}}\\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} * \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} * \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} * \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} * \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} * \\ * &{} * &{} * &{} * &{} * &{} * &{} * * &{} *\\ \end{array} }\right. \nonumber \\&\qquad \qquad \left. {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{114i}}} &{} {{N_{1i}}^\mathrm{T}} \\ 0 &{} {\mathcal {C}_c^\mathrm{T}} &{} 0 &{} 0 &{} {{\Gamma _{214i}}} &{} 0 \\ 0 &{} { - C_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{2i}}^\mathrm{T}} \\ {{\Gamma _{510i}}} &{} 0 &{} {{N_{5i}}^\mathrm{T}} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{3i}}^\mathrm{T}} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} { - D_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} {{N_{4i}}^\mathrm{T}} \\ { - \mathcal {V}} &{} 0 &{} 0 &{} {{\Gamma _{913i}}} &{} 0 &{} 0 \\ { - \mathcal {V}} &{} 0 &{} 0 &{} {{\Gamma _{1013i}}} &{} 0 &{} 0 \\ * &{} { - I} &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} { - \varepsilon _2^{ - 1}I} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} { - {\varepsilon _2}I} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} { - {\varepsilon _1}I} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} { - \varepsilon _1^{ - 1}I} \\ \end{array} } \right] < 0, \end{aligned}$$
(24)
$$\begin{aligned}&\left[ {\begin{array}{c@{\quad }c} \mathcal {U} &{} \mathcal {V } \\ * &{} \mathcal {V } \\ \end{array} } \right] > 0, \end{aligned}$$
(25)

where

$$\begin{aligned} {\Gamma _{11i}}&= {\mathcal {U}{A_i} + {A_i}^\mathrm{T}\mathcal {U} + {\mathcal {B}_c}{C_i} + {C_i}^\mathrm{T}{\mathcal {B}_c}^\mathrm{T} + Q + R},\\ {\Gamma _{12i}}&= {{\mathcal {A}_c} + {A_i}^\mathrm{T}\mathcal {V} + {C_i}^\mathrm{T}{\mathcal {B}_c}^\mathrm{T}} ,{\Gamma _{22}}={{\mathcal {A}_c} + {\mathcal {A}_c}^\mathrm{T}}, \\ {\Gamma _{14i}}&= {\mathcal {U}{A_{1i}} + {\mathcal {B}_c}{C_{1i}} },\ {\Gamma _{24i}}= {\mathcal {V}{A_{1i}} + {\mathcal {B}_c}{C_{1i}}} ,\\ {\Gamma _{16i}}&= {\mathcal {U}{B_{0i}} + {\mathcal {B}_c}{D_{0i}} }, {\Gamma _{17i}}={\mathcal {U}{B_i} + {\mathcal {B}_c}{D_i}}, \\ {\Gamma _{18i}}&= {\mathcal {U}{B_{1i}} + {\mathcal {B}_c}{D_{1i}} } ,\ {\Gamma _{26i}}={\mathcal {V}{B_{0i}} + {\mathcal {B}_c}{D_{0i}}},\\ {\Gamma _{27i}}&= {\mathcal {V}{B_i} + {\mathcal {B}_c}{D_i}}, {\Gamma _{28i}}={\mathcal {V}{B_{1i}} + {\mathcal {B}_c}{D_{1i}} } , \\ {\Gamma _{38i}}&= V{B_w} ,\ {\Gamma _{59i}}={E_i^\mathrm{T}\mathcal {U} + F_i^\mathrm{T}{\mathcal {B}_c}^\mathrm{T}},\\ {\Gamma _{510i}}&= {E_i^\mathrm{T}\mathcal {V} + F_i^\mathrm{T}{\mathcal {B}_c}^\mathrm{T}}, {\Gamma _{114i}}={\Gamma _{913i}}= {\mathcal {U}{M_{1i}} + {\mathcal {B}_c}{M_{2i}}}, \\ {\Gamma _{214i}}&= {\Gamma _{1013i}}= {\mathcal {V}{M_{1i}} + {\mathcal {B}_c}{M_{2i}}},\ {\Gamma _{33}}=V{A_w} + A_w^\mathrm{T}V,\\ {\Gamma _{44}}&= - ({1 - {\mu _1}})Q, {\Gamma _{55}}= - ({1 - {\mu _2}})R. \end{aligned}$$

Then, there exists a fuzzy-rule-independent FD filter \(({{{ \Sigma }_c}})\) in (10) such that the fuzzy stochastic FD system \(({{{\tilde{\Sigma } }_c}})\) in (12) is asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma \). Moreover, if the aforementioned LMI conditions are feasible, then a desired \({H_\infty }\) filer realization is given by

$$\begin{aligned} \left[ {\begin{array}{c@{\quad }c} {{A_c}} &{} {{B_c}} \\ {{C_c}} &{} 0 \\ \end{array} } \right] = \left[ {\begin{array}{c@{\quad }c} {{\mathcal {V}^{ - 1}}} &{} 0 \\ 0 &{} I \\ \end{array} } \right] \left[ {\begin{array}{c@{\quad }c} {{\mathcal {A}_c}} &{} {{\mathcal {B}_c}} \\ {{\mathcal {C}_c}} &{} 0 \\ \end{array} } \right] . \end{aligned}$$
(26)

Proof

Please see the “Appendix”. \(\square \)

Next, we will further consider the fuzzy-rule-dependent case and give the following results.

Theorem 3

Given a scalar \(\gamma >0\), the fuzzy stochastic FD system \(({{{\tilde{\Sigma } }_f}})\) in (16) is asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma \) if there exist scalars \(\varepsilon _{1}>0, \varepsilon _{2}>0\) and matrices \(P>0, Q>0, R>0\) such that the following matrix inequalities hold:

$$\begin{aligned}&{\Upsilon _{ii}} < 0,\quad i = 1,2, \ldots ,r \end{aligned}$$
(27)
$$\begin{aligned}&{\Upsilon _{ij}}+{\Upsilon _{ji}} < 0,\quad 1 \leqslant i < j \leqslant r, \end{aligned}$$
(28)

where

$$\begin{aligned} {{\Upsilon _{ij}}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\Upsilon _{11ij}}} &{} {{\Upsilon _{12ij}}} &{} 0 &{} {{\Upsilon _{14ij}}} &{} 0 &{} {{{\tilde{C}}_{ij}}^\mathrm{T}} \\ * &{} {{\Upsilon _{22ij}}} &{} 0 &{} {{\Upsilon _{24ij}}} &{} 0 &{} 0 \\ * &{} * &{} {{\Upsilon _{33ij}}} &{} 0 &{} {\tilde{E}_{ij}^\mathrm{T}} &{} 0 \\ * &{} * &{} * &{} {{\Upsilon _{44ij}}} &{} 0 &{} {\tilde{D}_{ij}^\mathrm{T}} \\ * &{} * &{} * &{} * &{} {{\Upsilon _{55ij}}} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} { - I} \\ \end{array} } \right] ,\\ {\Upsilon _{11ij}}&= P{{\tilde{A}}_{ij}} + {{\tilde{A}}_{ij}}^\mathrm{T}P + {H^\mathrm{T}}({Q+R})H + \varepsilon _1^{-1}P{{\tilde{M}}_{1ij}}{{\tilde{M}}^\mathrm{T}}_{1ij}P + {\varepsilon _1}{{\tilde{N}}_{1ij}}^\mathrm{T}{{\tilde{N}}_{1ij}}, \\ {\Upsilon _{12ij}}&= P{{\tilde{A}}_{1ij}} + {\varepsilon _1}{{\tilde{N}}_{1ij}}^\mathrm{T}{N_{2ij}}, {\Upsilon _{14ij}} = P{{\tilde{B}}_{ij}} + {\varepsilon _1}{{\tilde{N}}_{1ij}}^\mathrm{T}{\tilde{N}_{3ij}}, \\ {\Upsilon _{22ij}}&= - ({1 - {\mu _1}})Q + {\varepsilon _1}{N_{2ij}}^\mathrm{T}{N_{2ij}}, \ \ {\Upsilon _{24ij}} = {\varepsilon _1}{N_{2ij}}^\mathrm{T}{{\tilde{N}}_{3ij}}, \\ {\Upsilon _{33ij}}&= -({1 - {\mu _2}})R + {\varepsilon _2}{N_{5ij}}^\mathrm{T}{N_{5ij}},\ \ {\Upsilon _{44ij}} = - {\gamma ^2}I + {\varepsilon _1}{{\tilde{N}}_{3ij}}^\mathrm{T}{{\tilde{N}}_{3ij}}, \\ {\Upsilon _{55ij}}&= \varepsilon _2^{-1}{{\tilde{M}}_{1ij}}{{\tilde{M}}^\mathrm{T}}_{1ij} - {P^{ - 1}}, \end{aligned}$$
$$\begin{aligned} {{\tilde{M}}^\mathrm{T}}_{1ij}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{M_{1i}}^\mathrm{T}} &{} {{{({{B_{fj}}{M_{2i}}})}^\mathrm{T}}} &{} 0 \\ \end{array} } \right] ,\quad {{\tilde{N}}_{1ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{N_{1i}}} &{} 0 &{} 0 \\ \end{array} } \right] ,\nonumber \\ {{\tilde{N}}_{3ij}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{N_{3i}}} &{} 0 &{} {{N_{4i}}} \\ \end{array} } \right] ,\quad {N_{2ij}} = {N_{2i}},\ \ {N_{5ij}} = {N_{5i}},\nonumber \\ {{\tilde{A}}_{ij}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{A_{i}}} &{} 0 &{} 0 \\ {{B_{fj}}{C_i}} &{} {{A_{fj}}} &{} 0 \\ 0 &{} 0 &{} {{A_w}} \\ \end{array} } \right] , \quad {{\tilde{A}}_{1ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{A_{1i}}} \\ {{B_{fj}}{C_{1i}}} \\ 0 \\ \end{array} } \right] , \nonumber \\ {{\tilde{B}}_{ij}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{B_{0i}}} &{} {{B_i}} &{} {{B_{1i}}} \\ {{B_{fj}}{D_{0i}}} &{} {{B_{fj}}{D_i}} &{} {{B_{fj}}{D_{1i}}} \\ 0 &{} 0 &{} {{B_w}} \\ \end{array} } \right] , \quad {{\tilde{E}}_{ij}} = \left[ {\begin{array}{c} {{E_i}} \\ {{B_{fj}}{F_i}} \\ 0 \\ \end{array} } \right] . \end{aligned}$$
(29)

Proof

By using Lemmas 1–4 and the same line of the proof of Theorem 1, this theorem can be proved readily, the detailed procedures are omitted here. \(\square \)

Now, we will present a solution to the \(H_{\infty }\) FD filter design for \(({{{ \Sigma }_f}})\) in (15).

Theorem 4

For given scalars \(\gamma >0, \varepsilon _{1}>0, \varepsilon _{2}>0\) and matrices \( Q>0, R>0\), suppose there exist matrices \(\mathcal {U}>0, \mathcal {V}>0, V>0, \mathcal {A}_{fi}, \mathcal {B}_{fi}\), and \(\mathcal {C}_{fi}\) such that (25) and the following LMIs hold:

$$\begin{aligned}&{\Gamma _{ii}} < 0,\quad i = 1,2, \ldots ,r\end{aligned}$$
(30)
$$\begin{aligned}&{\Gamma _{ij}} = \left[ {\begin{array}{c@{\quad }c} {{\Gamma _{1ij}}} &{} {{\Gamma _{2ij}}} \\ * &{} {{\Gamma _{3ij}}} \\ \end{array} } \right] < 0,\quad 1 \leqslant i < j \leqslant r. \end{aligned}$$
(31)

The notations in \({\Gamma _{ii}}\) and \({\Gamma _{ij}}\) of (30)–(31) are given as follows:

$$\begin{aligned} {\Gamma _{11ii}}&= {\mathcal {U}{A_i} + {A_i}^\mathrm{T}\mathcal {U} + {\mathcal {B}_{fi}}{C_i} + {C_i}^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T} + Q + R},\\ {\Gamma _{12ii}}&= {{\mathcal {A}_{fi}} + {A_i}^\mathrm{T}\mathcal {V} + {C_i}^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}} ,\ {\Gamma _{22ii}}={{\mathcal {A}_{fi}} + {\mathcal {A}_{fi}}^\mathrm{T}}, \\ {\Gamma _{14ii}}&= {\mathcal {U}{A_{1i}} + {\mathcal {B}_{fi}}{C_{1i}} },\ {\Gamma _{24ii}}= {\mathcal {V}{A_{1i}} + {\mathcal {B}_{fi}}{C_{1i}}} ,\\ {\Gamma _{16ii}}&= {\mathcal {U}{B_{0i}} + {\mathcal {B}_{fi}}{D_{0i}} },\ {\Gamma _{17ii}}={\mathcal {U}{B_i} + {\mathcal {B}_{fi}}{D_i}}, \\ {\Gamma _{18ii}}&= {\mathcal {U}{B_{1i}} + {\mathcal {B}_{fi}}{D_{1i}}} ,\ {\Gamma _{26ii}}={\mathcal {V}{B_{0i}} + {\mathcal {B}_{fi}}{D_{0i}}},\\ {\Gamma _{27ii}}&= {\mathcal {V}{B_i} + {\mathcal {B}_{fi}}{D_i}},\ {\Gamma _{28ii}}={\mathcal {V}{B_{1i}} + {\mathcal {B}_{fi}}{D_{1i}} } , {\Gamma _{38ii}}=V{B_w} , \\ {\Gamma _{59ii}}&= {E_i^\mathrm{T}\mathcal {U} + F_i^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}},\\ {\Gamma _{510ii}}&= {E_i^\mathrm{T}\mathcal {V} + F_i^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}},\ {\Gamma _{114ii}}={\Gamma _{913ii}}= {\mathcal {U}{M_{1i}} + {\mathcal {B}_{fi}}{M_{2i}}}, \\ {\Gamma _{214ii}}&= {\Gamma _{1013ii}}={\mathcal {V}{M_{1i}} + {\mathcal {B}_{fi}}{M_{2i}}},\ {\Gamma _{33}}=V{A_w} + A_w^\mathrm{T}V,\\ {\Gamma _{44}}&= - ({1 - {\mu _1}})Q,\ {\Gamma _{55}}= - ({1 - {\mu _2}})R. \\ {\Gamma _{11ij}}&= \mathcal {U}{A_i} + {A_i}^\mathrm{T}\mathcal {U} + {\mathcal {B}_{fj}}{C_i} + {C_i}^\mathrm{T}{\mathcal {B}_{fj}}^\mathrm{T} + 2Q + 2R \\&\quad +\, \mathcal {U}{A_j} + {A_j}^\mathrm{T}\mathcal {U} + {\mathcal {B}_{fi}}{C_j} + {C_j}^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}, \\ {\Gamma _{12ij}}&= {\mathcal {A}_{fj}} + {A_i}^\mathrm{T}\mathcal {V} + {C_i}^\mathrm{T}{\mathcal {B}_{fj}}^\mathrm{T} + {\mathcal {A}_{fi}} + {A_j}^\mathrm{T}\mathcal {V} + {C_j}^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T},\\ {\Gamma _{22ij}}&= {\mathcal {A}_{fj}} + {\mathcal {A}_{fj}}^\mathrm{T} + {\mathcal {A}_{fi}} + {\mathcal {A}_{fi}}^\mathrm{T}, \\ {\Gamma _{14ij}}&= \mathcal {U}{A_{1i}} + {\mathcal {B}_{fj}}{C_{1i}} + \mathcal {U}{A_{1j}} + {\mathcal {B}_{fi}}{C_{1j}} , \\ {\Gamma _{24ij}}&= \mathcal {V}{A_{1i}} + {\mathcal {B}_{fj}}{C_{1i}} + \mathcal {V}{A_{1j}} + {\mathcal {B}_{fi}}{C_{1j}}, \\ {\Gamma _{16ij}}&= \mathcal {U}{B_{0i}} + {\mathcal {B}_{fj}}{D_{0i}} + \mathcal {U}{B_{0j}} + {\mathcal {B}_{fi}}{D_{0j}} , \\ {\Gamma _{17ij}}&= \mathcal {U}{B_i} + {\mathcal {B}_{fj}}{D_i} + \mathcal {U}{B_j} + {\mathcal {B}_{fi}}{D_j}, \\ {\Gamma _{26ij}}&= \mathcal {V}{B_{0i}} + {\mathcal {B}_{fj}}{D_{0i}} + \mathcal {V}{B_{0j}} + {\mathcal {B}_{fi}}{D_{0j}}, \\ {\Gamma _{27ij}}&= \mathcal {V}{B_i} + {\mathcal {B}_{fj}}{D_i} + \mathcal {V}{B_j} + {\mathcal {B}_{fi}}{D_j}, \\ {\Gamma _{18ij}}&= \mathcal {U}{B_{1i}} + {\mathcal {B}_{fj}}{D_{1i}} + \mathcal {U}{B_{1j}} + {\mathcal {B}_{fi}}{D_{1j}} , \\ {\Gamma _{28ij}}&= \mathcal {V}{B_{1i}} + {\mathcal {B}_{fj}}{D_{1i}} + \mathcal {V}{B_{1j}} + {\mathcal {B}_{fi}}{D_{1j}} ,\ {\Gamma _{38ij}} = 2V{B_w} , \\ {\Gamma _{59ij}}&= E_i^\mathrm{T}\mathcal {U} + F_i^\mathrm{T}{\mathcal {B}_{fj}}^\mathrm{T} + E_j^\mathrm{T}\mathcal {U} + F_j^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}, \\ {\Gamma _{510ij}}&= E_i^\mathrm{T}\mathcal {V} + F_i^\mathrm{T}{\mathcal {B}_{fj}}^\mathrm{T} + E_j^\mathrm{T}\mathcal {V} + F_j^\mathrm{T}{\mathcal {B}_{fi}}^\mathrm{T}, \\ {\Gamma _{116ij}}&= {\Gamma _{914ij}} = \mathcal {U}{M_{1i}} + {\mathcal {B}_{fj}}{M_{2i}},\quad {\Gamma _{117ji}} = {\Gamma _{915ji}} = \mathcal {U}{M_{1j}} + {\mathcal {B}_{fi}}{M_{2j}}, \\ {\Gamma _{216ij}}&= {\Gamma _{1014ij}} = \mathcal {V}{M_{1i}} + {\mathcal {B}_{fj}}{M_{2i}},\quad {\Gamma _{217ji}} = {\Gamma _{1015ji}} = \mathcal {V}{M_{1j}} + {\mathcal {B}_{fi}}{M_{2j}}. \end{aligned}$$
$$\begin{aligned}&{\Gamma _{1ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\Gamma _{11ij}}} &{} {{\Gamma _{12ij}}} &{} 0 &{} {{\Gamma _{14ij}}} &{} 0 &{} {{\Gamma _{16ij}}} &{} {{\Gamma _{17ij}}} &{} {{\Gamma _{18ij}}} &{} 0 &{} 0 \\ * &{} {{\Gamma _{22ij}}} &{} 0 &{} {{\Gamma _{24ij}}} &{} 0 &{} {{\Gamma _{26ij}}} &{} {{\Gamma _{27ij}}} &{} {{\Gamma _{28ij}}} &{} 0 &{} 0 \\ * &{} * &{} {2{\Gamma _{33}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{38ij}}} &{} 0 &{} 0 \\ * &{} * &{} * &{} {2{\Gamma _{44}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} {2{\Gamma _{55}}} &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{59ij}}} &{} {{\Gamma _{510ij}}}\\ * &{} * &{} * &{} * &{} * &{} { - 2{\gamma ^2}I} &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} { - 2{\gamma ^2}I} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - 2{\gamma ^2}I} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - 2U} &{} { - 2V} \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - 2V} \\ \end{array} } \right] ,\\&{\Gamma _{2ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{116ij}}} &{} {{\Gamma _{117ji}}} &{} {{N_{1i}}^\mathrm{T}} &{} {{N_{1j}}^\mathrm{T}} \\ {C_{fj}^\mathrm{T}} + {C_{fi}^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{216ij}}} &{} {{\Gamma _{217ji}}} &{} 0 &{} 0 \\ { - 2C_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{2i}}^\mathrm{T}} &{} {{N_{2j}}^\mathrm{T}} \\ 0 &{} {{N_{5i}}^\mathrm{T}} &{} {{N_{5j}}^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{3i}}^\mathrm{T}} &{} {{N_{3j}}^\mathrm{T}} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ { - 2D_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{4i}}^\mathrm{T}} &{} {{N_{4j}}^\mathrm{T}} \\ 0 &{} 0 &{} 0 &{} {{\Gamma _{914ij}}} &{} {{\Gamma _{915ji}}} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {{\Gamma _{1014ij}}} &{} {{\Gamma _{1015ji}}} &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} } \right] ,\\ \end{aligned}$$
$$\begin{aligned}&{\Gamma _{3ij}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} { -2I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} { - \varepsilon _2^{ - 1}I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} { - \varepsilon _2^{ - 1}I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} { - {\varepsilon _2}I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} { - {\varepsilon _2}I} &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} { - {\varepsilon _1}I} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} { - {\varepsilon _1}I} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \varepsilon _1^{ - 1}I} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \varepsilon _1^{ - 1}I} \\ \end{array} } \right] ,\\ \end{aligned}$$
$$\begin{aligned}&\Gamma _{ii}=\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\Gamma _{11ii}}} &{} {{\Gamma _{12ii}}} &{} 0 &{} {{\Gamma _{14ii}}} &{} 0 &{} {{\Gamma _{16ii}}} &{} {{\Gamma _{17ii}}} &{} {{\Gamma _{18ii}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{114ii}}} &{} {{N_{1i}}^\mathrm{T}} \\ * &{} {{\Gamma _{22ii}}} &{} 0 &{} {{\Gamma _{24ii}}} &{} 0 &{} {{\Gamma _{26ii}}} &{} {{\Gamma _{27ii}}} &{} {{\Gamma _{28ii}}} &{} 0 &{} 0 &{} {\mathcal {C}_{fi}^\mathrm{T}} &{} 0 &{} 0 &{} {{\Gamma _{214ii}}} &{} 0 \\ * &{} * &{} {{\Gamma _{33}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{38ii}}} &{} 0 &{} 0 &{} { - C_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} {{\Gamma _{44}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{2i}}^\mathrm{T}} \\ * &{} * &{} * &{} * &{} {{\Gamma _{55}}} &{} 0 &{} 0 &{} 0 &{} {{\Gamma _{59ii}}} &{} {{\Gamma _{510ii}}} &{} 0 &{} {{N_{5i}}^\mathrm{T}} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} { - {\gamma ^2}I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{N_{3i}}^\mathrm{T}} \\ * &{} * &{} * &{} * &{} * &{} * &{} { - {\gamma ^2}I} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - {\gamma ^2}I} &{} 0 &{} 0 &{} { - D_w^\mathrm{T}} &{} 0 &{} 0 &{} 0 &{} {{N_{4i}}^\mathrm{T}} \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \mathcal {U}} &{} { - \mathcal {V}} &{} 0 &{} 0 &{} {{\Gamma _{913ii}}} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \mathcal {V}} &{} 0 &{} 0 &{} {{\Gamma _{1013ii}}} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - I} &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \varepsilon _2^{ - 1}I} &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - {\varepsilon _2}I} &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - {\varepsilon _1}I} &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} * &{} { - \varepsilon _1^{ - 1}I} \\ \end{array} } \right] . \end{aligned}$$

Then, there exists a fuzzy-rule-dependent FD filter \(({{{ \Sigma }_f}})\) in (15) such that the fuzzy stochastic FD system \(({{{\tilde{\Sigma } }_f}})\) in (16) is asymptotically mean square stable with an \({H_\infty }\) performance level \(\gamma \). Moreover, if the aforementioned LMI conditions are feasible, then a desired \({H_\infty }\) filer realization is given by

$$\begin{aligned} \left[ {\begin{array}{c@{\quad }c} {{A_{fi}}} &{} {{B_{fi}}} \\ {{C_{fi}}} &{} 0 \\ \end{array} } \right] = \left[ {\begin{array}{c@{\quad }c} {{\mathcal {V}^{ - 1}}} &{} 0 \\ 0 &{} I \\ \end{array} } \right] \left[ {\begin{array}{c@{\quad }c} {{\mathcal {A}_{fi}}} &{} {{\mathcal {B}_{fi}}} \\ {{\mathcal {C}_{fi}}} &{} 0 \\ \end{array} } \right] ,\quad i=1,2,\ldots ,r. \end{aligned}$$
(32)

Proof

This theorem can be proved by employing the same technique of the proof of Theorem 2; the detailed procedures are omitted here. \(\square \)

Remark 1

Note that the obtained conditions in Theorems 2 and 4 are all in LMIs form; desired fuzzy-rule-independent and fuzzy-rule-dependent \(H_{\infty }\) FD filters can be determined by solving the following convex optimization problems:

$$\begin{aligned}&\min {\delta _1} = {\gamma ^2}\quad \mathrm{subject}\;\mathrm{to}\;(24),\;(25); \nonumber \\&\min {\delta _2} = {\gamma ^2}\quad \mathrm{subject}\;\mathrm{to}\;(25),\;(30),\;(31). \end{aligned}$$
(33)

Remark 2

Owing to most physical systems are nonlinear and T–S fuzzy models have provided a convenient way to approximate nonlinear systems, a feasible solution of the FD problem for nonlinear systems can be converted to that of FD for T–S fuzzy systems. By solving the previous convex optimization problems in (33), we can obtain the parameters of the fuzzy-rule-independent and fuzzy-rule-dependent FD filters. Then, the residual signals \({\chi _c}(t)\) and \({\chi _f}(t)\) are generated, and the first step of the FD procedure is thus finished. The next work is to set up a FD measure, as stated in Sect. 2. In Sect. 4, we will provide simulation examples to illustrate the effectiveness of the proposed approach.

4 Simulation Examples

Example 1

Consider the stochastic T–S fuzzy system \(\Sigma _{1}\) in (9) with the number of IF-THEN rules \(r=2\) and the following parameters:

$$\begin{aligned}&{A_{{1}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - 3}}{{.0}}} &{} {{{0}}{{.2}}} &{} {{{0}}{{.4}}} \\ {{{0}}{{.3}}} &{} {{{ - 1}}{{.7}}} &{} {{{0}}{{.5}}} \\ {{{0}}{{.2}}} &{} {{{0}}{{.5}}} &{} {{{ - 2}}{{.5}}} \\ \end{array} } \right] ,\quad {A_{{{11}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.02}}} &{} {{{0}}{{.0}}} &{} {{{ - 0}}{{.1}}} \\ {{{0}}{{.1}}} &{} {{{0}}{{.03}}} &{} {{{0}}{{.1}}} \\ {{{0}}{{.1}}} &{} {{{0}}{{.2}}} &{} {{{0}}{{.1}}} \\ \end{array} } \right] ,\\&{E_{{1}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.02}}} &{} {{0}} &{} {{{0}}{{.01}}} \\ {{{0}}{{.3}}} &{} {{{0}}{{.1}}} &{} {{{0}}{{.2}}} \\ {{{0}}{{.0}}} &{} {{{0}}{{.1}}} &{} {{{0}}{{.2}}} \\ \end{array} } \right] , \\&{A_{{2}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - 2}}{{.7}}} &{} {{{0}}{{.3}}} &{} {{{0}}{{.6}}} \\ {{{0}}{{.2}}} &{} {{{ - 1}}{{.5}}} &{} {{{0}}{{.8}}} \\ {{{0}}{{.3}}} &{} {{{0}}{{.4}}} &{} {{{ - 2}}{{.4}}} \\ \end{array} } \right] ,\quad {A_{{{12}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.0}}} &{} {{{ - 0}}{{.02}}} &{} {{{0}}{{.01}}} \\ {{{0}}{{.0}}} &{} {{{0}}{{.01}}} &{} {{{0}}{{.1}}} \\ {{{0}}{{.2}}} &{} {{{0}}{{.00}}} &{} {{{0}}{{.02}}} \\ \end{array} } \right] ,\\&{E_{{2}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.3}}} &{} {{{0}}{{.1}}} &{} {{{0}}{{.2}}} \\ {{{0}}{{.1}}} &{} {{{0}}{{.2}}} &{} {{{0}}{{.2}}} \\ {{{0}}{{.0}}} &{} {{{0}}{{.3}}} &{} {{{0}}{{.2}}} \\ \end{array} } \right] ,\\&{B_{{{01}}}} \!=\! \left[ {\begin{array}{c} {{{0}}{{.3}}} \\ {{{0}}{{.6}}} \\ {{{0}}{{.5}}} \\ \end{array} } \right] ,\quad \! {B_{{1}}} \!=\! \left[ {\begin{array}{c} {{{0}}{{.5}}} \\ {{{0}}{{.8}}} \\ {{{0}}{{.6}}} \\ \end{array} } \right] ,\quad \! {B_{{{11}}}} = \left[ {\begin{array}{c} {{{0}}{{.4}}} \\ {{{0}}{{.5}}} \\ {{{0}}{{.4}}} \\ \end{array} } \right] ,\quad \! \begin{array}{c} {\;\quad {F_{{1}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.01}}} &{} {{{0}}{{.02}}} &{} {{{0}}{{.004}}} \\ \end{array} } \right] {{,}}\;} \\ {\;{F_{{2}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.01}}} &{} {{{0}}{{.02}}} &{} {{{0}}{{.02}}} \\ \end{array} } \right] {{,}}} \\ \end{array} \\&{B_{{{02}}}} = \left[ {\begin{array}{c} {{{0}}{{.4}}} \\ {{{0}}{{.6}}} \\ {{{0}}{{.7}}} \\ \end{array} } \right] ,\quad {B_{{2}}} = \left[ {\begin{array}{c} {{{0}}{{.5}}} \\ {{{0}}{{.6}}} \\ {{{0}}{{.3}}} \\ \end{array} } \right] ,\quad {B_{{{12}}}} = \left[ {\begin{array}{c} {{{0}}{{.6}}} \\ {{{0}}{{.4}}} \\ {{{0}}{{.3}}} \\ \end{array} } \right] , \\&\begin{array}{c} {{{{C}}_{{1}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{1}}{{.5}}} &{} {{{0}}{{.6}}} &{} {{{1}}{{.3}}} \\ \end{array} } \right] ,\quad {{{C}}_{{{11}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.3}}} &{} {{{0}}{{.2}}} &{} {{{0}}{{.1}}} \\ \end{array} } \right] ,} \\ {{{{C}}_{{2}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{1}}{{.0}}} &{} {{{1}}{{.3}}} &{} {{{0}}{{.7}}} \\ \end{array} } \right] ,\quad {{{C}}_{{{12}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.2}}} &{} {{{0}}{{.4}}} &{} {{{0}}{{.3}}} \\ \end{array} } \right] ,} \\ \end{array} \\&{M_{{{11}}}} = {M_{{{12}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - 0}}{{.2}}} &{} {{0}} &{} {{{0}}{{.1}}} \\ {{0}} &{} {{{0}}{{.1}}} &{} {{0}} \\ {{0}} &{} {{{0}}{{.2}}} &{} {{{0}}{{.2}}} \\ \end{array} } \right] ,\;\;{M_{{{21}}}} = {M_{{{22}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{0}}{{.1}}} &{} 0 &{} {0.3} \\ \end{array} } \right] , \\&{N_{{{11}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - 2}}} &{} 0 &{} {{{0}}{{.1}}} \\ {{{0}}{{.1}}} &{} {{{0}}{{.01}}} &{} {0.02} \\ 0 &{} {0.01} &{} {0.02} \\ \end{array} } \right] {{,}} \quad {N_{{{12}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - 0}}{{.2}}} &{} 0 &{} {{{0}}{{.1}}} \\ {{{0}}{{.1}}} &{} {{{0}}{{.01}}} &{} {0.02} \\ 0 &{} {0.01} &{} {0.02} \\ \end{array} } \right] ,\\&{N_{{{21}}}} = {N_{{{22}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {0.1} &{} {0.02} &{} {0.01} \\ {0.01} &{} {0.03} &{} 0 \\ 0 &{} {0.02} &{} -0.02 \\ \end{array} } \right] , \quad {N_{{{31}}}} = {N_{{{32}}}} = \left[ {\begin{array}{c} {0.03} \\ 0 \\ {0.01} \\ \end{array} } \right] ,\\&{N_{{{41}}}} \!=\! {N_{{{42}}}} \!=\! \left[ {\begin{array}{c} {0.01} \\ {0.02} \\ 0 \\ \end{array} } \right] ,\;\quad \! {N_{{{51}}}} \!=\! \left[ {\begin{array}{c@{\quad }c@{\quad }c} {{{ - }}0.5} &{} {0.9} &{} {0.2} \\ {0.5} &{} {0.5} &{} {0.1} \\ {0.3} &{} 0 &{} {0.1} \\ \end{array} } \right] {{,}}\quad \! {N_{{{52}}}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} {0.5} &{} {0.{{0}}9} &{} {0.2} \\ {0.{{0}}5} &{} {0.5} &{} {0.1} \\ {0.3} &{} 0 &{} {0.1} \\ \end{array} } \right] , \\&{D_{{{01}}}} = {{6}},\quad {D_{{1}}} = {{0}}{{.2}},\quad {D_{{{11}}}} = 5,\quad {D_{{{02}}}} = {{0}}{{.4}},\quad {D_{{2}}} = {{0}}{{.3}},\quad {D_{{{12}}}} = 5, \\&{\mu _1} = 0.1,\;\;{\mu _2} =0.15. \end{aligned}$$

Let \({A_w} = -5,\;\;{B_w} =5,\;\;{C_w}= 1,\;\;{D_w}= 0\) and \({\varepsilon _1} = 0.5,\;\;\;{\varepsilon _2} = 0.{{25}}\); we now consider the fault detection filter design problem.

Case 1. First, we consider the fuzzy-rule-independent filter design problem. Solving LMIs (24), (25) in Theorem 2, we obtain the minimized feasible \(\gamma \) is \(\gamma ^{*}=1.0015\), and

$$\begin{aligned} Q&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0.0774 &{} -0.0226 &{} 0.0504\\ -0.0226 &{} 0.0921 &{} -0.0764\\ 0.0504 &{} -0.0764 &{} 0.1315\\ \end{array} } \right] ,\quad R = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0.2835 &{} -0.0753 &{} 0.0997\\ -0.0753 &{} 0.3368 &{} 0.0442\\ 0.0997 &{} 0.0442 &{} 0.1492\\ \end{array} } \right] ,\\ \mathcal {U}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0.5980 &{} -0.0263 &{} 0.0674\\ -0.0263 &{} 0.3739 &{} -0.0182\\ 0.0674 &{} -0.0182 &{} 0.2954\\ \end{array} } \right] ,\quad \mathcal {V} = \left[ {\begin{array}{c@{\quad }c@{\quad }c} 0.0087 &{} -0.0003 &{} 0.0031\\ -0.0003 &{} 0.0846 &{} -0.0834\\ 0.0031 &{} -0.0834 &{} 0.0898\\ \end{array} } \right] \\ {\mathcal {A}_c}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -0.3001 &{} -0.3440 &{} 0.0975\\ -0.1385 &{} -0.4068 &{} 0.4003\\ -0.1523 &{} 0.0898 &{} -0.3417\\ \end{array} } \right] ,\quad {\mathcal {B}_c} = \left[ {\begin{array}{c} -0.0576\\ -0.0289\\ -0.0275 \\ \end{array} } \right] , \\ {\mathcal {C}_c}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -0.2814&-0.1361&-0.1408 \end{array} } \right] . \end{aligned}$$

Then by solving Eq. (26), we obtain the parameters of the desired filter (10) as follows:

$$\begin{aligned} {A_c}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -25.0278 &{} -29.7755 &{} 10.3045\\ -30.1708 &{} -34.5250 &{} 7.8421\\ -28.8627 &{} -30.0476 &{} 3.1236 \\ \end{array} } \right] ,\quad {B_c} = \left[ {\begin{array}{c} -4.7772\\ -5.9079\\ -5.6305 \\ \end{array} } \right] , \nonumber \\ {C_c}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -0.2814&-0.1361&-0.1408 \end{array} } \right] . \end{aligned}$$
(34)

Case 2 We further consider the fuzzy-rule-dependent filtering problem. By solving LMIs (25), (30), (31), and Eq. (32) in Theorem 4, we get the minimized feasible \(\gamma \) is \(\gamma ^{*}=1.0001\), and

$$\begin{aligned} {A_{f1}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -11.8802 &{} 1.3521 &{} -7.7204\\ -3.1232 &{} -3.8051 &{} -9.9838\\ -6.6983 &{} -0.1698 &{} -13.8786\\ \end{array} } \right] ,\;{B_{f1}} = \left[ {\begin{array}{c} -1.1092\\ -1.3843\\ -1.4897 \\ \end{array} } \right] , \nonumber \\ {C_{f1}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -0.3004&-0.1391&-0.1250 \end{array} } \right] , \nonumber \\ {A_{f2}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -20.5689 &{} 3.6247 &{} -4.9957\\ -3.9684 &{} -0.5830 &{} -9.8952\\ -10.5204 &{} 2.8429 &{} -13.2596\\ \end{array} } \right] ,\quad {B_{f2}} = \left[ {\begin{array}{c} -1.3796\\ -1.2934\\ -1.5144 \\ \end{array} } \right] , \nonumber \\ {C_{f2}}&= \left[ {\begin{array}{c@{\quad }c@{\quad }c} -0.5737&-0.0777&-0.0276 \end{array} } \right] . \end{aligned}$$
(35)

Remark 3

Note that the minimized feasible \(\gamma \) for the fuzzy-rule-independent case is \(\gamma ^{*}=1.0015\), and for the fuzzy-rule-dependent case is \(\gamma ^{*}=1.0001\), which has illustrated that the fuzzy-rule-dependent filter is less conservative than the fuzzy-rule-independent filter in the sense of the disturbance attenuation performance level. However, the fuzzy-rule-dependent filter is more complicated in filter implementation and sometimes that the premise variable of the original fuzzy model \(\theta (t)\) is unavailable, so the fuzzy-rule-independent filter will be more useful under the aforesaid conditions.

To further show the effectiveness of the obtained filters (34) and (35), let the membership function be

$$\begin{aligned} {h_1}({{x_1}(t)})=\frac{{1-\sin ({{x_1}(t)})}}{2},\quad {h_2}({{x_1}(t)} )=\frac{{1+\sin ({{x_1}(t)})}}{2}, \end{aligned}$$

the initial condition be \(x(0)={\left[ {\begin{array}{c@{\quad }c@{\quad }c} {-1} &{} {0.5} &{} 1 \\ \end{array} } \right] ^\mathrm{T}}\). Suppose \({G_1}(t) = {G_2}(t) = I\) and the unknown disturbance input \(\omega (t)\) to be uniformly distributed within \([-1, 1]\) for the time interval \([0, 10]\); the known input is given as \(u(t) = 0.1\sin (t), 0\le t\le 10\); the fault signal is set up as

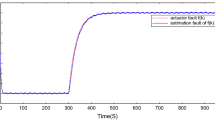
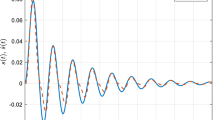
$$\begin{aligned} f(t) = \left\{ \begin{array}{c@{\quad }c} 1, &{} 2.5 \leqslant t \leqslant 5, \\ 0, &{} \mathrm{otherwise}. \\ \end{array} \right. \end{aligned}$$

We select the residual evaluation function and the threshold as (19) and (20); for the designed \( H_{\infty }\) fault detection filter with (34) and (35), the simulation results along an individual discretized Brownian path are given in Figs. 1, 2, 3, and 4. Among them, Fig. 1 depicts the states of the desired fuzzy-rule-independent filter with (34) under zero disturbance and Fig. 2 shows the states of the desired fuzzy-rule-dependent filter with (35) under zero disturbance. Figure 3 presents the generated residual signal of fuzzy-rule-independent filtering problem; Fig. 4 describes the evaluation function of fuzzy-rule-independent filtering problem for both the fault case and the fault-free case. The corresponding simulation results for the fuzzy-rule-dependent filter with (35) can be depicted by the same line.

Fig. 1
figure 1

States of the fault detection filter in (34)

Full size image
Fig. 2
figure 2

States of the fault detection filter in (35)

Full size image
Fig. 3
figure 3

Residual signal of fuzzy-rule-independent case

Full size image
Fig. 4
figure 4

Evaluation function of fuzzy-rule-independent case

Full size image

For the fuzzy-rule-independent case, with the selected threshold \({J_\mathrm{th}} = {\sup _{\omega \ne 0,u \ne 0,f = 0}}{({\int _0^{10} {{{\chi _c} ^\mathrm{T}}(t){\chi _c} (t)} })^{1/2}} = 0.6483\), the results show that \({({\int _0^{2.63} {{\chi _c}^\mathrm{T}(t){\chi _c}(t)} })^{1/2}} = 0.6882 > {J_\mathrm{th}}>{({\int _0^{2.62} {{\chi _c}^\mathrm{T}(t){\chi _c}(t)} })^{1/2}} = 0.6278\). Thus, the appeared fault can be detected after 0.13 s. For the fuzzy-rule-dependent case, with the selected threshold \({J^{*}_\mathrm{th}} = {\sup _{\omega \ne 0,u \ne 0,f = 0}}{({\int _0^{10} {{{\chi _f} ^\mathrm{T}}(t){\chi _f} (t)} })^{1/2}} = 0.5945\), the results show that \({({\int _0^{2.60} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.6007 > {J^{*}_\mathrm{th}}>{({\int _0^{2.59} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.5687\). Then, the appeared fault can be detected after 0.1 s.

Remark 4

From the above results, we know that the better \(H_{\infty }\) performance level the FD system can achieve, the less detection times are needed when \(u(t), \omega (t)\), and \(f(t)\) are given; the similar results can be found in [40]. However, as far as we know, until now, the phenomenon has not been explained comprehensively in theory. Therefore, how to verify the relationship between the detection time and \(H_{\infty }\) performance level from a theoretical perspective is worth forthcoming investigation.

Example 2

Consider the following modified uncertain nonlinear mass-spring-damper (MSD) mechanical system:

$$\begin{aligned} \ddot{ \eta }(t)=-0.225\dot{ \eta }(t)-0.02\eta (t)-0.67\eta ^{3}(t)+u(t), \end{aligned}$$

where \(\eta (t)\in [-1.5, \ 1.5]\) and \(u(t)\) is the force. The practical example is stemmed from [28, 41], which is shown in Fig. 5. It is assumed that the stiffness coefficient of the spring has nonlinearity, and the MSD system itself is disturbed by stochastic process. The aim is to detect the fault appearing on the damper. To illustrate the proposed results, we also assume the state variables and output variables can be measured online and the system output are perturbed by time delay. The corresponding model data presented here were borrowed from [28]; the nonlinear term \(-0.67\eta ^{3}(t)\) can be represented as

$$\begin{aligned} -0.67\eta ^{3}(t)={h_1}({\eta (t)})\cdot 0\cdot \eta ^{3}(t)-{h_2} ({\eta (t)})\cdot 1.5075\eta (t), \end{aligned}$$

where \({h_1}({\eta (t)}), {h_2}({\eta (t)})\in [0, \ 1], {h_1}({\eta (t)})+{h_2}({\eta (t)})=1\). By solving the equations, the membership functions \({h_1}({\eta (t)})\) and \({h_2}({\eta (t)})\) are obtained as follows:

$$\begin{aligned} {h_1}({\eta (t)})=1-\frac{\eta ^{2}(t)}{2.25},\quad {h_2}({\eta (t)})=\frac{\eta ^{2}(t)}{2.25}. \end{aligned}$$

Let \(x_{1}(t)=\dot{ \eta }(t)\) and \(x_{2}(t)= \eta (t)\); the evolution of the state vector and measured output can be described by system (1–3) with the following parameters:

$$\begin{aligned}&{A_1} = \left[ {\begin{array}{c@{\quad }c} -0.225 &{} -0.02 \\ 1 &{} 0 \\ \end{array}} \right] ,\quad {A_2} = \left[ {\begin{array}{c@{\quad }c} -0.225 &{} -1.5275 \\ 1 &{} 0 \\ \end{array}} \right] , \\&A_{11}=A_{12}=0,\quad B_{01}=B_{02}=\left[ {\begin{array}{c} 1 \\ 0 \\ \end{array}} \right] ,\\&B_{1}=\left[ {\begin{array}{c} 0.02 \\ 0.05 \\ \end{array}} \right] ,\quad B_{2}=\left[ {\begin{array}{c} 0.01 \\ 0.06 \\ \end{array}} \right] ,\quad B_{11}=\left[ {\begin{array}{c} 0.4 \\ 0.2 \\ \end{array}} \right] ,\quad B_{12}=\left[ {\begin{array}{c} 0.25 \\ 0.18 \\ \end{array}} \right] , \\&E_{1}=\left[ {\begin{array}{c@{\quad }c} 0.2&{} 0\\ 0.1 &{} 0\\ \end{array}} \right] ,\quad E_{2}=\left[ {\begin{array}{c@{\quad }c} 0.3&{} 0\\ 0.2 &{} 0\\ \end{array}} \right] ,\\&\begin{array}{c} C_{1}=\left[ {\begin{array}{c@{\quad }c} 1.5 &{} 1.3 \\ \end{array}} \right] ,\\ C_{2} =\left[ {\begin{array}{c@{\quad }c} 1.4 &{} 1.2 \\ \end{array}} \right] , \end{array}\quad \begin{array}{c} C_{11}=\left[ {\begin{array}{c@{\quad }c} 0.2 &{} 0.1 \\ \end{array}} \right] ,\\ C_{12}=\left[ {\begin{array}{c@{\quad }c} 0.2 &{} 0.3 \\ \end{array}} \right] , \end{array}\quad \begin{array}{c} F_{1}=\left[ {\begin{array}{c@{\quad }c} 0.01 &{} 0.02 \\ \end{array}} \right] ,\\ F_{2} =\left[ {\begin{array}{c@{\quad }c} 0.01 &{} 0.03 \\ \end{array}} \right] , \end{array}\\&\begin{array}{c} D_{01}=0.6,\\ D_{02}=0.4, \end{array}\quad \begin{array}{c@{\quad }c} D_{1}=0.2,\\ D_{2}=0.3, \end{array}\quad \begin{array}{c@{\quad }c} D_{11}=12,\\ D_{12}=13, \end{array}\\&M_{11} = M_{12} = \left[ {\begin{array}{c@{\quad }c} 0.02 &{} 0.01 \\ 0 &{} -0.01 \\ \end{array}} \right] ,\quad M_{21}=M_{22}=\left[ {\begin{array}{c@{\quad }c} 0.01 &{} 0.03 \\ \end{array}} \right] , \\&\begin{array}{c} N_{11} = N_{12} =\\ N_{51} = N_{52} = \end{array} \left[ {\begin{array}{c@{\quad }c} -0.02 &{} 0.01 \\ 0.01 &{} 0.02 \\ \end{array}} \right] ,\\&N_{21} = N_{22} =0,\quad M_{11} = M_{12} = \left[ {\begin{array}{c@{\quad }c} 0.02 &{} 0.01 \\ 0 &{} -0.01 \\ \end{array}} \right] , \\&N_{31}=N_{32}=\left[ {\begin{array}{c} 0.03 \\ 0.01\\ \end{array}} \right] ,\quad N_{41}=N_{42}=\left[ {\begin{array}{c} 0.01 \\ 0.02\\ \end{array}} \right] ,\\&A_{w} =-5,\quad B_{w} =5,\quad C_{w} =1,\quad D_{w} =0,\quad \mu _{1} =0.4,\nonumber \\&\mu _{2} =0,\quad \varepsilon _{1} =0.05,\quad \varepsilon _{2} =0.3. \end{aligned}$$
Fig. 5
figure 5

Mass-spring-damper system

Full size image

Case 1 Solving LMIs (24), (25) and Eq. (26) in Theorem 2, we obtain the minimized feasible \(\gamma \) is \(\gamma ^{*}=1.0472\), and the parameters of the desired fuzzy-rule-independent filter (10) are as follows:

$$\begin{aligned} {A_c}=\left[ {\begin{array}{c@{\quad }c} -2.7365 &{} 0.0220\\ -0.8023 &{} -1.7364 \\ \end{array} } \right] ,\quad {B_c} \!=\! \left[ {\begin{array}{c} 0.0202\\ -1.1533 \\ \end{array} } \right] ,\quad {C_c} \!=\! \left[ {\begin{array}{c@{\quad }c} -0.0028&-0.0058 \end{array} } \right] .\nonumber \\ \end{aligned}$$
(36)

Case 2 By solving LMIs (25), (30), (31), and Eq. (32) in Theorem 4, we get the minimized feasible \(\gamma \) is \(\gamma ^{*}= 1.0128\) and the parameters of the desired fuzzy-rule-dependent filter (15) as follows:

$$\begin{aligned} {A_{f1}}&= \left[ {\begin{array}{c@{\quad }c} -3.1421 &{} -0.0950\\ 0.0082 &{} -0.9920\\ \end{array} } \right] ,\;{B_{f1}} = \left[ {\begin{array}{c} -0.0594\\ -0.6820 \\ \end{array} } \right] , \nonumber \\ {C_{f1}}&= \left[ {\begin{array}{c@{\quad }c} -0.0033&-0.0064 \end{array} } \right] , \nonumber \\ {A_{f2}}&= \left[ {\begin{array}{c@{\quad }c} -2.8512 &{} -2.9786\\ -7.9889 &{} -28.6139\\ \end{array} } \right] ,\;{B_{f2}} = \left[ {\begin{array}{c} -0.0488\\ -0.3086 \\ \end{array} } \right] , \nonumber \\ {C_{f2}}&= \left[ {\begin{array}{c@{\quad }c} -0.0025&-0.0049 \end{array} } \right] . \end{aligned}$$
(37)

Suppose the initial condition be \(x(0)={\left[ {\begin{array}{c@{\quad }c} -0.1 &{} 0.1 \\ \end{array} } \right] ^\mathrm{T}}, {G_1}(t) = {G_2}(t) = I\), the unknown disturbance input \(\omega (t)\) to be uniformly distributed within \([-1, 1]\) for the time interval \([0, 30]\); the known input is given as \(u(t) = 0.1\sin (t), 0\le t\le 30\); the fault signal is a multicycle incipient fault, which has nonzero value for the time interval \([2, 5]\) and is depicted in Fig. 6. For the designed \( H_{\infty }\) FD filter in (37), Fig. 7 depicts the generated residual signal and Fig. 8 shows the evaluation function for both the fault case and the fault-free case. Then, the selected threshold \({J^{*}_\mathrm{th}} = {\sup _{\omega \ne 0,u \ne 0,f = 0}}{({\int _0^{10} {{{\chi _f} ^\mathrm{T}}(t){\chi _f} (t)} })^{1/2}} = 0.0206\); the results show that \({({\int _0^{2.44} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.0214 > {J^{*}_\mathrm{th}}>{({\int _0^{2.43} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.0205\). Therefore, the appeared fault can be detected after 0.44 s. While when the fault signal is set up as \(f(k) = 0.5, 2 \le k \le 5\), otherwise, \(f(k) = 0\), we get that \({({\int _0^{2.28} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.0215 > {J^{*}_\mathrm{th}}>{({\int _0^{2.27} {{\chi _f}^\mathrm{T}(t){\chi _f}(t)} })^{1/2}} = 0.0205\). The above result means that the fault can be detected after 0.28 s. So the FD time is shorter than the incipient fault case.

Fig. 6
figure 6

Multicycle incipient fault

Full size image
Fig. 7
figure 7

Residual signal of the detection filter in (37)

Full size image
Fig. 8
figure 8

Evaluation function of the detection filter in (37)

Full size image

It should be pointed out that, when a system is subjected to incipient faults and noise outliers, the FD time will be lengthened or even the faults may be undetected due to the relatively low fault currents and short duration ranging [27]. From our examples, it can be shown that the desired FD filters are not only better suited for step faults with relatively long duration and high increment in magnitude, but also suited for incipient faults with relatively low fault currents and short duration ranging.

5 Conclusions

The problem of robust \(H_{\infty }\) FD for a class of Itô stochastic T–S fuzzy systems with time-varying delays and parameter uncertainties has been investigated in this paper. An LMI approach and Lyapunov stability theory have been developed to design fuzzy-rule-independent and fuzzy-rule-dependent FD filters that guarantee the FD system is not only mean square asymptotically stable, but also satisfies a prescribed \( H_{\infty }\)-norm level for all admissible uncertainties. The difficult problem of norm-bounded parameter uncertainties has been solved by settling several well-known matrix inequations. Weighting fault signal approach has been used to improve the performance of the FD system, and explicit expression of the desired filter parameters has been characterized by matrix decomposition, congruence transformation, and convex optimization technique. A numerical example and a MSD mechanical system have been provided to show the effectiveness and usefulness of the proposed method.