Dynamics and delayed feedback control for a 3D jerk system with hidden attractor

Abstract

A 3D jerk system with only one stable equilibria was presented and discussed. Some periodic orbits and chaotic behaviors of this system are obtained. Meanwhile, a delayed feedback control scheme for this system was proposed. By using the method of projection for center manifold computation, Hopf bifurcation for the delayed feedback control system was analyzed and obtained. The simulation results demonstrate the correctness of the Hopf bifurcation analysis and the effectiveness of the proposed delayed feedback control strategy.

1 Introduction

In 1963, Lorenz  [1] constructed a 3D quadratic polynomial ODEs system and found a first chaotic attractor in it. Later, many Lorenz-like systems such as Chen system  [2] and Lü system  [3] were constructed and researched. From the stability of equilibria point of view, these chaotic systems have one saddle and two saddle-foci, and their chaotic attractors are of Shilnikov type [4]. Since the violation of Shilnikov condition for chaotic system with stable equilibria, therefore, it is interesting to ask whether or not there are 3D autonomous chaotic systems with stable equilibria? In 2008, Yang  [5] constructed another chaotic system with one saddle and two stable node-foci and further analyzed in Ref.  [6, 7]. Moreover, the other chaotic system only with two stable node-foci is presented in 2010 by Yang  [8]. For a generic 3D quadratic autonomous system, does there exist chaotic system with none, one equilibrium or any number equilibria? Sprott  [9–11] gave some simple chaotic system with none or one equilibrium by computer search. Subsequently, chaotic systems with one stable equilibrium  [12–16], no equilibria  [17, 18], any number equilibria  [19] and a line equilibrium  [20] have been presented. By the category of chaotic attractors either self-excited or hidden  [21–23], we call the chaotic attractors in dynamical systems with no equilibria or with only stable equilibria hidden attractors. From a computational point of view these hidden attractors cannot be found easily by numerical methods. Furthermore, knowledge about equilibria does not help in the localization of hidden attractors  [20]. Therefore, understanding the local and the global behaviors of chaotic systems with hidden attractors is of great importance.

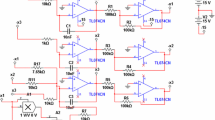
On the other hand, due to unexpected behaviors that may arise from a chaotic system, chaos control and applications have gained increasing attention in the past few decades. Many control techniques have been described and found, such as traditional linear and nonlinear control methods  [24, 25], adaptive control methods  [26, 27], optimal control methods  [28], fuzzy control methods  [29] and delayed feedback control  [30, 31]. These control methods can be classified into two categories, the OGY control and delayed control. The OGY control method is based on the idea of the stabilization of unstable periodic orbits embedded within a strange attractor, and it is achieved by making a small time-dependent perturbation in the form of feedback to an accessible system parameter. However, the changes of the parameter are discrete in time since this method deals with the Poincare map. Furthermore, the OGY control method can stabilize only those periodic orbits whose maximal Lyapunov exponent is small compared with the reciprocal of the time interval between parameter changes. Since the corrections of the parameter are rare and small, the fluctuation noise leads to occasional bursts of the system into the region far from the desired periodic orbit, and these bursts are more frequent for large noise. Considering these limitations, the time-delay control method (also called time-delay autosynchronization method) was introduced by Pyragas  [32] based on a time-continuous control scheme. Choosing proper time delay, the difference of the present state of a given system to its delayed value will vanish if the state to be stabilized is reached. Thus, the method is noninvasive. Moreover, the delayed control has no need for a reference system since it generates the control force from information of the system itself. And, the time delay is an inherent in various biological systems, engineering systems, neuron networks and social sciences. Also, in comparison, the delayed feedback control method is simpler and convenient in controlling chaos for a continuous dynamical system. Following these ideas, and motives by Ref.  [33, 34], this paper analyzes the stability and Hopf bifurcation analysis on a new 3D quadratic jerk system with hidden attractor by using delayed control method

$$\begin{aligned} \frac{{\text {d}x}}{{\text {d}t}} = y, \frac{{\text {d}y}}{{\text {d}t}} = z, \frac{{\text {d}z}}{{\text {d}t}} = -ax-by-cz +y^2+bxy \end{aligned}$$

(1)

with a, b, c are real numbers and $a \ne 0$. The paper is organized as follows: In Sect. 2, some basic dynamics such as the stability of equilibria, Lyapunov exponents spectrum (LES), largest Lyapunov exponent (LLE), periodic orbits and chaotic behaviors of system (1) are presented by numerical simulations. Add a delayed feedback item to the third equation of (1), and a delayed feedback control system is created. The existence of Hopf bifurcation parameters are determined in Sect. 3. In Sect. 4, the direction, stability and the period of the bifurcating solutions are discussed based on the center manifold theorem and the projection method. To verify the theoretic analysis, numerical simulations are given in Sect. 5. Finally, concluding remarks are given in Sect. 6.

2 Dynamical behaviors

2.1 Dissipativity

Since

$$\begin{aligned} \nabla V = \frac{{\partial \dot{x}}}{{\partial x}} + \frac{{\partial \dot{y}}}{{\partial y}} + \frac{{\partial \dot{z}}}{{\partial z}} = - c, \end{aligned}$$

the system (1) is dissipative under the condition $c>0$. It can be easily verified that the exponential contraction term is ${\text {e}^{ - c}}$. This means that a volume $V_0$ is contracted to $V_0\text {e}^{-c}$ in time t, and each volume containing the system trajectory shrinks to zero as $t \rightarrow + \infty$ at an exponential rate $-c$.

2.2 Equilibria and stability

Let $\dot{x} = 0$, $\dot{y} = 0$, $\dot{z} = 0$; system (1) has only one equilibria O(0, 0, 0). The Jacobian matrix of system (1) at O is

$$\begin{aligned} \left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}1&{}0\\ 0&{}0&{}1\\ { - a}&{}{ - b}&{}{ - c} \end{array}} \right) \end{aligned}$$

and the characteristic equation is

$$\begin{aligned} f(\lambda ) = {\lambda ^3} + c{\lambda ^2} + b\lambda + a \end{aligned}$$

In accordance with the Routh–Hurwitz criterion, we can see that the characteristic equation has three negative real parts roots when $c>0$, $a>0$, and $bc-a>0$. Therefore, system (1) has a stable node or stable node-foci. Also by the Routh–Hurwitz criterion, we can see that the system (1) has a saddle-foci when $c>0$, $a>0$, and $bc-a<0$.

2.3 Complex and chaotic behaviors

To further study the dynamics of system (1), numerical simulations have been carried out. Tables 1 and 2 show various phase portraits of system (1) for some fixed parameters.

Table 1 Various phase portraits of system (1) for some fixed parameters with $b=1, c=4$ (PVs parameter values, PPs phase portraits, PS Poincare section)

Table 2 Various phase portraits of system (1) for some fixed parameters with $b=0.6, c=1.7$ (PVs parameter values, PPs phase portraits, PS Poincare section)

Fig. 1

Periodic-1 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 2

Periodic-2 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 3

Periodic-4 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 4

Chaotic attractor of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 5

Periodic-1 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 6

Periodic-2 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 7

Periodic-4 orbit of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 8

Chaotic attractor of system (1) and projection in $x-y$ plane, $y-z$ plane, $z-x$ plane

Fig. 9

Poincare section (1) with different a: a $a=3.31$, b $a=3.35$, c $a=3.36$, d $a=3.4$

Fig. 10

Poincare section (1) with different a: a $a=0.98$, b $a=0.989$, c $a=0.995$, d $a=1$

In addition, we define the Lyapunov dimension by ${D_\lambda } = j + \frac{1}{{\left| {{\lambda _{j + 1}}} \right| }}\sum _{i = 1}^j {{\lambda _i}}$, where j is the largest integer which satisfies $\sum _{i = 1}^j {{\lambda _i}} \ge 0$ and $\sum _{i = 1}^{j+1} {{\lambda _i}} \ge 0$. We can find ${D_\lambda } = 2.015$ for $a=3.4$, $b=1$, $c=4$ and ${D_\lambda } = 2.026$ for $a=1$, $b=0.6$, $c=1.7$.

In order to determine whether the system is chaotic or not, we should calculate the Lyapunov exponents spectrum of system (1) for fixed b, c, and let a varies. When a varies in the interval [3.2, 3.4] and [0.9, 1], Figs.11, 12, 13 and 14 show the Lyapunov exponents spectrum and the largest Lyapunov exponent of system (1) for $b=1$, $c=4$ and $b=0.6$, $c=1.7$, respectively. In order to show chaotic state in a wide parameter region, we calculate the distribution for various attractors such as trivial attractors, periodic attractors, quasiperiodic attractors and chaotic attractors region in a two-parameter space a–b with $c=4$ and $c=1.7$ in Figs. 15 and 16, respectively.

Fig. 11

Lyapunov exponents spectrum of system (1) for $b=1$, $c=4$

Fig. 12

Largest Lyapunov exponent of system (1) for $b=1$, $c=4$

Fig. 13

Lyapunov exponents spectrum of system (1) for $b=0.6$, $c=1.7$

Fig. 14

Largest Lyapunov exponent of system (1) for $b=0.6$, $c=1.7$

Fig. 15

Distribution for various attractors region in two-parameter space a–b, $c=4$, where red solid circle denotes periodic attractor, green solid box denotes quasiperiodic attractor, blue plus denotes chaotic attractor, and black asterisk denotes trivial attractor. (Color figure online)

Fig. 16

Distribution for various attractors region in two-parameter space a–b, $c\,{=}\,1.7$, where red solid circle denotes periodic attractor, green solid box denotes quasiperiodic attractor, blue plus denotes chaotic attractor, and black asterisk denotes trivial attractor. (Color figure online)

3 Existence of Hopf bifurcation for system (1) with time delay

Following the idea of Ref. [35, 36], we add a time-delayed force $k(z(t-\tau )-z(t))$ to the third equation of the system (1), that is, the following delayed feedback control system

$$\begin{aligned}&\dot{x} = y, \dot{y} = z, \nonumber \\&\dot{z} = -ax-by-cy+y^2+bxy+k(z(t-\tau )-z(t)). \end{aligned}$$

(2)

The characteristic equation of the linearized system is

$$\begin{aligned} \det \left( {\begin{array}{c@{\quad }c@{\quad }c} \lambda &{}{ - 1}&{}0\\ 0&{}\lambda &{}{ - 1}\\ a&{}b&{}{\lambda + c + k - k{\text {e}^{ - \lambda \tau }}} \end{array}} \right) = 0. \end{aligned}$$

That the following transcendental equation is obtained

$$\begin{aligned} {\lambda ^3} + (c + k){\lambda ^2} + b\lambda + a - k{\lambda ^2}{\text {e}^{ - \lambda \tau }} = 0. \end{aligned}$$

(3)

According to the Hopf bifurcation theory, we let $\lambda ={\omega }i$, and substituting this into (3), we have

$$\begin{aligned} - {\omega ^3}i - (c + k){\omega ^2} + b\omega i + a + k{\omega ^2}{\text {e}^{ - \omega {\tau }i}} = 0. \end{aligned}$$

Separating the real and imaginary parts, we have

$$\begin{aligned} \left\{ \begin{array}{l} (c + k){\omega ^2} - a = k{\omega ^2}\cos (\omega \tau )\\ b\omega - {\omega ^3} = k{\omega ^2}\sin (\omega \tau ) \end{array} \right. \end{aligned}$$

(4)

By simple calculation, we can get

$$\begin{aligned} {((c + k){\omega ^2} - a)^2} + {(b\omega - {\omega ^3})^2} = {k^2}{\omega ^4}. \end{aligned}$$

(5)

Let $z = {\omega ^2}$, and denote $p={c^2} + 2kc - 2b$, $q={b^2} - 2ac - 2ak$, $r=a^2$; then, Eq. (5) becomes

$$\begin{aligned} h(z)=z^3+pz^2+qz+r. \end{aligned}$$

(6)

Next, we introduce the following results which were proved by  [37, 38].

Proposition 1

(1) If $\varDelta = {p^2} - 3q < 0$, Eq. (6) has no positive roots, i.e., the necessary condition for Eq. (6) to have positive real roots is $\varDelta \ge 0$; (2) , and Eq. (6) has positive roots if and only if $z_1^* = \frac{{ - p + {\sqrt{\varDelta }} }}{3}>0$ and $h(z_1^*) \le 0$; (3) if $b> 0$, $a>0$, $bc-a>0$ and $\varDelta <0$, then Eq. (3) has negative real parts for all $\tau \ge 0$.

Suppose $\varDelta \ge 0$, $z_1^*>0$, $h(z_1^*) \le 0$, without loss of generality, we assume that (6) has three positive roots of Eq. (6) by ${z_j}$, $j=1,2,3$; consequently, Eq. (5) has three positive roots ${\omega _j} = \sqrt{{z_j}}$, $j=1,2,3$. Substituting these into Eq. (4), we have

$$\begin{aligned} \left\{ \begin{array}{l} \textstyle \cos {\omega _j}{\tau _j} = \frac{{(c + k)\omega _j^2 - a}}{{k\omega _j^2}} = P\\ \textstyle \sin {\omega _j}{\tau _j} = \frac{{b{\omega _j} - \omega _j^3}}{{k\omega _j^2}} = Q \end{array} \right. ,\quad j=1,2,3 \end{aligned}$$

(7)

Let

$$\begin{aligned} {\tau _j} = \left\{ \begin{array}{lll} &{}\textstyle \frac{1}{{{\omega _j}}}(\arccos (P) + 2n\pi ), &{}Q\ge 0\\ &{}\textstyle \frac{1}{{{\omega _j}}}(2\pi - \arccos (P) + 2n\pi ),&{}Q<0 \end{array} \right. \end{aligned}$$

where $j = 1,2,3$, $n = 0,1, \cdots$; then, $\pm {\omega _j}i$ is a pair of purely imaginary roots of Eq. (3) with $\tau = {\tau _j}$, $j=1,2,3$.

Theorem 1

Suppose ${z_j} = \omega _j^2$, and ${\left. {\frac{{\text {d}h(z)}}{{\text {d}z}}} \right| _{z = {z_j}}} \ne 0$, if $\varDelta \,{\ge }\, 0$, $z_1^*\,{>}\,0$, $h(z_1^*)\,{\le }\, 0$, then $\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right) } \right] _{\tau = {\tau _j}}^{ - 1} \ne ~0$; moreover, $\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right) } \right] _{\tau = {\tau _j}}^{ - 1}$ and ${\left. {\frac{{\text {d}h(z)}}{{\text {d}z}}} \right| _{z = {z_j}}}$ have the same sign.

Proof

Consider the derivative with respect to $\tau$ of Eq. (3), we can get

$$\begin{aligned} {\left[ {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right] ^{ - 1}} = - \frac{{(3{\lambda ^2} + 2(c + k)\lambda + b){\text {e}^{\lambda \tau }}}}{{k{\lambda ^3}}} + \frac{2}{{{\lambda ^2}}} - \frac{\tau }{\lambda }. \end{aligned}$$

From (7), we have

$$\begin{aligned}&\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right) } \right] _{\tau = {\tau _j}}^{ - 1}\\&\quad = \frac{{(b - 3\omega _j^2)\sin ({\omega _j}{\tau _j}) + 2(c + k){\omega _j}\cos ({\omega _j}{\tau _j})}}{{k\omega _j^3}} - \frac{2}{{\omega _j^2}}\\&\quad = \frac{{(b - 3\omega _j^2)\frac{{b{\omega _j} - \omega _j^3}}{{k\omega _j^2}} + 2(c + k){\omega _j}\frac{{(c + k)\omega _j^2 - a}}{{k\omega _j^2}}}}{{k\omega _j^3}} - \frac{2}{{\omega _j^2}}\\&\quad = \frac{{3\omega _j^4 + 2({c^2} + 2ck - 2b)\omega _j^2 + ({b^2} - 2ac - 2ak)}}{{k\omega _j^4}} \\&\quad = \frac{1}{{k\omega _j^4}}{\left. {\frac{{\text {d}h(z)}}{{\text {d}z}}} \right| _{z = {z_j}}} \ne 0. \end{aligned}$$

Define ${\tau _0} = {\tau _{{j_0}}} = {\min }_{1 \le j \le 3} \{ {\tau _j}\}$, ${\omega _0} = {\omega _{{j_0}}}$, ${z_0} = \omega _0^2$, by the Ref. [37, 38], we have

Proposition 2

• (1) If $b> 0$, $a>0$, $bc-a>0$, $z_1^* >0$, and $h(z_1^*) \le 0$, then Eq. (3) has negative real parts for $\tau \in [0,{\tau _0})$;

• (2) Moreover, if ${\left. {\frac{{\text {d}h(z)}}{{\text {d}z}}} \right| _{z = {z_0}}} \ne 0$, $\tau = {\tau _0}$, then $\pm {\omega _0}i$ is a pair of simple purely imaginary roots of Eq. (3).

Theorem 2

If $b> 0$, $a>0$, $bc-a>0$, $\varDelta \ge 0$, $z_1^* >0$ and $h(z_1^*) \le 0$, then the system (2) undergoes a Hopf bifurcation at the equilibria O when $\tau = {\tau _0}$.

4 Stability of bifurcating periodic solution

In this section, we will analyze the direction of Hopf bifurcation and stability of bifurcating periodic solution of system (2) at $\tau = {\tau _0}$ using the center manifold theorem. Let ${C^m}[ - r,0]$ denote the space of real , m-dimensional vector valued functions on the interval $[-r,0]$ all of whose components have m continuous derivatives. When $m=0$, the superscript will be omitted. For convenience, $t = \tau s$, $\tau = {\tau _0} + \mu$, $\mu \in R$; then, the system (2) can be changed into

$$\begin{aligned} \dot{u}(s) = {L_\mu }u(s) + f(\mu ,u(s)) \end{aligned}$$

(8)

where $s>0$, $\mu \in {R^1}$, ${L_\mu }$ is a one-parameter family of continuous (bounded) linear operators, ${L_\mu }:C[ - 1,0] \rightarrow {R^3}$, the operator $f(\mu ,u(s)):R \times C[ - 1,0] \rightarrow {R^3}$ contains the nonlinear terms, and

$$\begin{aligned} {L_\mu }\varphi (s)= & {} ({\tau _0} + \mu )\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}1&{}0\\ 0&{}0&{}1\\ { - a}&{}{ - b}&{}{ - c - k} \end{array}} \right) \left( {\begin{array}{c} {{\varphi _1}(s)}\\ {{\varphi _2}(s)}\\ {{\varphi _3}(s)} \end{array}} \right) \\&+\, ({\tau _0} + \mu )\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}k \end{array}} \right) \left( {\begin{array}{c} {{\varphi _1}(s - 1)}\\ {{\varphi _2}(s - 1)}\\ {{\varphi _3}(s - 1)} \end{array}} \right) \end{aligned}$$

$$\begin{aligned} f(\mu ,\varphi (s) )= & {} ({\tau _0} + \mu )\left( {\begin{array}{c} 0\\ 0\\ {\varphi _2^2(s) + b{\varphi _1}(s){\varphi _2}(s)} \end{array}} \right) . \end{aligned}$$

Based on the Riesz representation theorem  [36], there is a bounded variation function

$$\begin{aligned} \eta (\mu ,\theta )= & {} ({\tau _0} + \mu )\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}1&{}0\\ 0&{}0&{}1\\ { - a}&{}{ - b}&{}{ - c - k} \end{array}} \right) \delta (\theta )\\&+ \,({\tau _0} + \mu )\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}k \end{array}} \right) \delta (\theta + 1) \end{aligned}$$

where $\delta (\theta )$ is the Dirac delta function, and $\theta \in [ - 1,0]$ such that ${L_\mu }\varphi = \int _{ - 1}^0 {\text {d}\eta (\mu ,\theta )\varphi (\theta ) }$, $\varphi \in C[ - 1,0]$. Next, we define

$$\begin{aligned} A(\mu )\varphi = \left\{ \begin{array}{lll} &{}\textstyle \frac{{\text {d}\varphi (\theta )}}{{\text {d}\theta }},&{}\quad \theta \in [ - 1,0)\\ &{}\textstyle \int _{ - 1}^0 {\text {d}\eta (\mu ,s)\varphi (s)} ,&{}\quad \theta = 0 \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} R(\mu )\varphi = \left\{ \begin{array}{lll} &{}0,&{}\quad \theta \in [ - 1,0)\\ &{}f(\mu ,\varphi ),&{}\quad \theta = 0 \end{array} \right. \end{aligned}$$

for $\varphi \in {C^1}[ - 1,0]$. So we can rewrite system (8) into an operate equation

$$\begin{aligned} \dot{u}(s) = A(\mu )u + R(\mu )u \end{aligned}$$

(9)

where $u(\theta ) = u(s + \theta )$, $\theta \in ( - 1,0]$. For $\phi \in {C^1}[0,1]$, define

$$\begin{aligned} {A^*}(\mu )\varphi = \left\{ \begin{array}{lll} &{}\textstyle - \frac{{\text {d}\phi (\nu )}}{{\text {d}\nu }},&{}\quad \nu \in (0,1]\\ &{}\textstyle \int _{ - 1}^0 {d{\eta ^{\mathrm{T}}}(\mu ,\nu )\varphi ( - \nu )} ,&{}\quad \nu = 0 \end{array} \right. \end{aligned}$$

and a bilinear inner product

$$\begin{aligned} {<}\phi ,\varphi {>}= & {} - \int _{\theta = - 1}^0 {\int _{\nu = 0}^\theta {{{\bar{\phi }}^{\mathrm{T}}}(\nu - \theta )\text {d}\eta (0,\theta )\varphi (\nu )\text {d}\nu } } \\&+\, {{\bar{\phi }}^{\mathrm{T}}}(0)\varphi (0). \end{aligned}$$

Obviously, ${A^*}(0)$ and A(0) are adjoint operators, i.e., if $A(0)q(\theta ) = {\omega _0}{\tau _0}iq(\theta )$, then exists a nonzero vector ${q^*}(\nu )$ such that ${A^*}(0){q^*}(\nu ) = - {\omega _0}{\tau _0}i{q^*}(\nu )$. Let $q(\theta ) = (1,\alpha ,\beta )^{\mathrm{T}}{\text {e}^{i{\omega _0}{\tau _0}\theta }}$, $\theta \in ( - 1,0)$; then,

$$\begin{aligned} {\tau _0}\left( {\begin{array}{c@{\quad }c@{\quad }c} {i{\omega _0}}&{}{ - 1}&{}0\\ 0&{}{i{\omega _0}}&{}{ - 1}\\ a&{}b&{}{i{\omega _0} + c + k - k{\text {e}^{ - i{\omega _0}{\tau _0}}}} \end{array}} \right) q(0) = 0 \end{aligned}$$

Hence, we obtain $q(0) = {\left( {1,i{\omega _0}, - \omega _0^2} \right) ^{\mathrm{T}}}$.

Suppose that the eigenvector ${q^*}(\nu )$ of ${A^*}(0)$ is ${q^*}(\nu ) = \rho {(1,{\alpha ^*},{\beta ^*})^\mathrm{T}}{\text {e}^{i{\omega _0}{\tau _0}\nu }}$, $0 \le \nu < 1$; then,

$$\begin{aligned} {\tau _0}\left( {\begin{array}{c@{\quad }c@{\quad }c} { - i{\omega _0}}&{}0&{}a\\ { - 1}&{}{ - i{\omega _0}}&{}b\\ 0&{}{ - 1}&{}{ - i{\omega _0} + c + k - k{\text {e}^{i{\omega _0}{\tau _0}}}} \end{array}} \right) {q^*}(0) = 0 \end{aligned}$$

Hence, we obtain ${q^*}(0) = {\left( {1,\frac{b}{a} + \frac{i}{{{\omega _0}}},\frac{{i{\omega _0}}}{a}} \right) ^\mathrm{T}}$. Let $< {q^*}(\nu ),q(\theta ) > =1$, one can obtain

$$\begin{aligned}&{<}{q^*}(\nu ),q(\theta ){>} \\&\quad = - \int _{\theta = - 1}^0 {\int _{\nu = 0}^\theta {{{\bar{q}}^*}{^\mathrm{T}}(\nu - \theta )\text {d}\eta (0,\theta )q(\nu )\text {d}\nu } }\\&\qquad +\,{{\bar{q}}^*}{^\mathrm{T}}(0)q(0)\\&\quad = \bar{\rho }(1 + \alpha {{\bar{\alpha }}^*} + \beta {{\bar{\beta }}^*})\\&\qquad - \int _{\theta = - 1}^0 \int _{\nu = 0}^\theta \bar{\rho }(1,{{\bar{\alpha }}^*},{{\bar{\beta }}^*}){\text {e}^{ - i{\omega _0}{\tau _0}(\nu - \theta )}}\text {d}\eta (0,\theta )\\&\qquad \times \left( {\begin{array}{c} 1\\ \alpha \\ \beta \end{array}} \right) {\text {e}^{i{\omega _0}{\tau _0}\nu }}\text {d}\nu \\&\quad = \bar{\rho }(1 + \alpha {{\bar{\alpha }}^*} + \beta {{\bar{\beta }}^*}) \\&\qquad - \int _{\theta = - 1}^0 {\tau _0}\bar{\rho }(1,{{\bar{\alpha }}^*},{{\bar{\beta }}^*})\left[ {\left( {\begin{array}{ccc} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}k \end{array}} \right) \theta \delta (\theta + 1)} \right] \\&\qquad \times \left( {\begin{array}{c} 1\\ \alpha \\ \beta \end{array}} \right) {\text {e}^{i{\omega _0}{\tau _0}\theta }}\text {d}\theta \\&\quad = \int _{\xi = 0}^1 {\tau _0}\bar{\rho }(1,{{\bar{\alpha }}^*},{{\bar{\beta }}^*})\\&\qquad \times \left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}k \end{array}} \right) \delta (\xi )\left( {\begin{array}{c} 1\\ \alpha \\ \beta \end{array}} \right) {\text {e}^{i{\omega _0}{\tau _0}(\xi - 1)}}\text {d}\xi \\&\qquad +\, \bar{\rho }(1 + \alpha {{\bar{\alpha }}^*} + \beta {{\bar{\beta }}^*})\\&\quad = {\tau _0}\bar{\rho }(1,{{\bar{\alpha }}^*},{{\bar{\beta }}^*})\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}k \end{array}} \right) \left( {\begin{array}{c} 1\\ \alpha \\ \beta \end{array}} \right) {\text {e}^{ - i{\omega _0}{\tau _0}}}\\&\qquad +\, \bar{\rho }(1 + \alpha {{\bar{\alpha }}^*} + \beta {{\bar{\beta }}^*})\\&\quad = \bar{\rho }(1 + \alpha {{\bar{\alpha }}^*} + \beta {{\bar{\beta }}^*} + k{\tau _0}\beta {{\bar{\beta }}^*}{\text {e}^{ - i{\omega _0}{\tau _0}}}) = 1 \end{aligned}$$

Hence, we have

$$\begin{aligned} \rho = \frac{1}{{1 + \bar{\alpha }{\alpha ^*} + \bar{\beta }{\beta ^*} + k{\tau _0}\bar{\beta }{\beta ^*}{\text {e}^{i{\omega _0}{\tau _0}}}}}. \end{aligned}$$

Next, we study the stability of bifurcating periodic solutions. We first compute the coordinates to describe the center manifold ${C_0}$. For u(s) a solution of (9) at $\mu = 0$, we define

$$\begin{aligned} z(s) = {<}{q^*}(0),u(s){>} \end{aligned}$$

(10)

and define

$$\begin{aligned} w(s,\theta )= & {} u(s) - z(s)q(\theta ) - \bar{z}(s)\bar{q}(\theta )\nonumber \\= & {} u(s) - 2\mathrm{{Re}}\{ z(s)q(\theta )\}. \end{aligned}$$

(11)

On the manifold ${C_0}$, we suppose

$$\begin{aligned} w(s,\theta )= & {} w(z(s),\bar{z}(s),\theta ) = {w_{20}}(\theta )\frac{{{z^2}}}{2} + {w_{11}}(\theta )z\bar{z}\nonumber \\&+\, {w_{02}}(\theta )\frac{{{{\bar{z}}^2}}}{2} + {w_{30}}(\theta )\frac{{{z^3}}}{6} + \cdots \end{aligned}$$

(12)

In effect, z and ${\bar{z}}$ are local coordinates for ${C_0}$ in C in the directions of ${q^*}(0)$ and ${{\bar{q}}^*}(0)$. Note that w is real if u(s) is, we shall deal with real solutions only. For solutions $u(s) \in {C_0}$ of (9), since $\mu = 0$, we have

$$\begin{aligned} \dot{z}(s)= & {} {<}{q^*}(0),\dot{u}(s){>} \nonumber \\= & {} {<}{q^*}(0),A(0)u(s) + R(0)u{>}\nonumber \\= & {} {<}{q^*}(0),A(0)u(s){>} + {<}{q^*}(0),R(0)u{>} \nonumber \\= & {} {<}{A^*}(0){q^*}(0),u(s){>} + {<}{q^*}(0),R(0)u{>}\nonumber \\= & {} i{\omega _0}{\tau _0}z(s) + \bar{z}(s)\bar{q}(0))\nonumber \\&+\, {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0) + z(s)q(0). \end{aligned}$$

(13)

Let

$$\begin{aligned} g(z,\bar{z})= & {} {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0) + z(s)q(0) + \bar{z}(s)\bar{q}(0))\\= & {} {g_{20}}\frac{{{z^2}}}{2} + {g_{11}}z\bar{z} + {g_{02}}\frac{{{{\bar{z}}^2}}}{2} + {g_{21}}\frac{{{z^2}\bar{z}}}{2} + \cdots \end{aligned}$$

For $\theta = 0$, we have

$$\begin{aligned} u(s)= & {} w(s,0) + z(s)q(0) + \bar{z}(s)\bar{q}(0)\\= & {} \left( {\begin{array}{c} \textstyle {z(s) + \bar{z}(s) + {w_{20,1}}\frac{{{z^2}(s)}}{2} + {o_1}}\\ \textstyle {\alpha z(s) + \bar{\alpha }\bar{z}(s) + {w_{20,2}}\frac{{{z^2}(s)}}{2} + {o_2}}\\ \textstyle {\beta z(s) + \bar{\beta }\bar{z}(s) + {w_{20,3}}\frac{{{z^2}(s)}}{2} + {o_3}} \end{array}} \right) \end{aligned}$$

where

$$\begin{aligned} {o_1}= & {} {w_{11,1}}z(s)\bar{z}(s) + {w_{02,1}}\frac{{{{\bar{z}}^2}(s)}}{2} + {w_{30,1}}\frac{{{z^3}(s)}}{6} + \cdots \\ {o_2}= & {} {w_{11,2}}z(s)\bar{z}(s) + {w_{02,2}}\frac{{{{\bar{z}}^2}(s)}}{2} + {w_{30,2}}\frac{{{z^3}(s)}}{6} + \cdots \\ {o_3}= & {} {w_{11,3}}z(s)\bar{z}(s) + {w_{02,3}}\frac{{{{\bar{z}}^2}(s)}}{2} + {w_{30,3}}\frac{{{z^3}(s)}}{6} + \cdots \end{aligned}$$

then

$$\begin{aligned} \left\{ \begin{array}{l} {g_{20}} = 2\bar{\rho }{\tau _0}{{\bar{\beta }}^*}({\alpha ^2} + b\alpha )\\ {g_{11}} = \bar{\rho }{\tau _0}{{\bar{\beta }}^*}(2\alpha \bar{\alpha }+ b\alpha + b\bar{\alpha })\\ {g_{02}} = 2\bar{\rho }{\tau _0}{{\bar{\beta }}^*}({{\bar{\alpha }}^2} + b\bar{\alpha })\\ {g_{21}} = 2\bar{\rho }{\tau _0}{{\bar{\beta }}^*}(\alpha {w_{11,2}} + \bar{\alpha }{w_{20,2}} \\ \quad +\, b{w_{11,2}} + \frac{{b{w_{20,2}}}}{2} + \frac{{b{w_{20,2}}\bar{\alpha }}}{2}) \end{array} \right. \end{aligned}$$

(14)

From (11), we can know

$$\begin{aligned}&\dot{w}(s,\theta )\nonumber \\&\quad = \dot{u}(s) - \dot{z}(s)q(\theta ) - \dot{\bar{z}}(s)\bar{q}(\theta )\nonumber \\&\quad = -\, [i{\omega _0}{\tau _0}z(s) + {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0) \nonumber \\&\qquad +\, z(s)q(0) + \bar{z}(s)\bar{q}(0))]q(\theta )\nonumber \\&\qquad -\, [ - i{\omega _0}{\tau _0}z(s) + {q^*}{^\mathrm{{T}}}(0)\bar{f}(0,w(s,0) \nonumber \\&\qquad +\, z(s)q(0) + \bar{z}(s)\bar{q}(0))]\bar{q}(\theta )\nonumber \\&\qquad +\,A(0)u(s) + R(0)u(s) \nonumber \\&\quad = A(0)w(s,\theta )\nonumber \\&\qquad + R(0)u(s) - 2\mathrm{{Re}}\{ {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0)\nonumber \\&\qquad +\, z(s)q(0) + \bar{z}(s)\bar{q}(0))q(\theta )\} \nonumber \\&\quad = \left\{ \begin{array}{l} - 2\mathrm{{Re}}\{ {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0) + z(s)q(0) \\ + \bar{z}(s)\bar{q}(0))q(\theta )\} \\ + A(0)w(s,\theta ),\theta \in [ - 1,0)\\ - 2\mathrm{{Re}}\{ {{\bar{q}}^*}{^\mathrm{{T}}}(0)f(0,w(s,0) + z(s)q(0) \\ + \bar{z}(s)\bar{q}(0))q(\theta )\} \\ + A(0)w(s,\theta ) + f(0,u(s)),\theta = 0 \end{array} \right. \end{aligned}$$

(15)

Let

$$\begin{aligned}&h(z,\bar{z},\theta )\nonumber \\&\quad = -2{\mathop {\mathrm{Re}}\nolimits } \{ {{\bar{q}}^*}{^\mathrm{T}}(0)f(0,w(s,0) \nonumber \\&\qquad \;+\, z(s)q(0) + \bar{z}(s)\bar{q}(0))q(\theta )\} + R(0)u(s)\nonumber \\&\quad =\left\{ \begin{array}{l} -2{\mathop {\mathrm{Re}}\nolimits } \{ {{\bar{q}}^*}{^\mathrm{T}}(0)f(0,w(s,0) + z(s)q(0) \\ + \bar{z}(s)\bar{q}(0))q(\theta )\} ,\theta \in [ - 1,0)\\ -2{\mathop {\mathrm{Re}}\nolimits } \{ {{\bar{q}}^*}{^\mathrm{T}}(0)f(0,w(s,0) + z(s)q(0) \\ + \bar{z}(s)\bar{q}(0))q(\theta )\} + f(0,u(s)),\theta = 0 \end{array} \right. \nonumber \\&\quad = {h_{20}}\frac{{{z^2}}}{2} + {h_{11}}z\bar{z} + {h_{02}}\frac{{{{\bar{z}}^2}}}{2} + \cdots \end{aligned}$$

(16)

Then,

$$\begin{aligned} \dot{w}(s,\theta ) = A(0)w(s,\theta ) + h(z,\bar{z},\theta ) \end{aligned}$$

(17)

Substituting (12) into (17), we have

$$\begin{aligned} \dot{w}(s,\theta )= & {} (A(0){w_{20}} + {h_{20}})\frac{{{z^2}}}{2} + (A(0){w_{11}} + {h_{11}})z\bar{z} \nonumber \\&+\, (A(0){w_{02}} + {h_{02}})\frac{{{{\bar{z}}^2}}}{2} + \cdots \end{aligned}$$

(18)

From (12), we can know

$$\begin{aligned}&\dot{w}(s,\theta )\nonumber \\&\quad = {w_z}\dot{z}(s) + w_{\bar{z}}{\dot{\bar{z}}(s)}\nonumber \\&\quad = ({w_{20}}z + {w_{11}}\bar{z} + \cdots )(i{\omega _0}{\tau _0}z(s) + g(z,\bar{z})) \nonumber \\&\qquad +\, ({w_{11}}z + {w_{02}}\bar{z} + \cdots )( - i{\omega _0}{\tau _0}\bar{z}(s) + \bar{g}(z,\bar{z})) \end{aligned}$$

(19)

Comparing the coefficients of (18) and (19), we have

$$\begin{aligned} \left\{ \begin{array}{l} A(0){w_{20}} + {h_{20}} = i2{\omega _0}{\tau _0}{w_{20}}\\ A(0){w_{11}} + {h_{11}} = 0\\ A(0){w_{02}} + {h_{02}} = - 2i{\omega _0}{\tau _0}{w_{02}} \end{array} \right. \end{aligned}$$

(20)

From (16), we can know

$$\begin{aligned}&h(z,\bar{z},\theta )\nonumber \\&\quad = - g(z,\bar{z})q(\theta ) - \bar{g}(z,\bar{z})\bar{q}(\theta ) + R(0)u(s)\nonumber \\&\quad = - \left( {g_{20}}\frac{{{z^2}}}{2} + {g_{11}}z\bar{z} + {g_{02}}\frac{{{{\bar{z}}^2}}}{2} + {g_{21}}\frac{{{z^2}\bar{z}}}{2} + \cdots \right) q(\theta )\nonumber \\&\qquad - \left( {{\bar{g}}_{20}}\frac{{{{\bar{z}}^2}}}{2} + {{\bar{g}}_{11}}z\bar{z} + {{\bar{g}}_{02}}\frac{{{z^2}}}{2} + {{\bar{g}}_{21}}\frac{{{{\bar{z}}^2}z}}{2} + \cdots \right) \bar{q}(\theta )\nonumber \\&\qquad +\, R(0)u(s) \end{aligned}$$

(21)

Since $R(0)u(s) = 0$ for $- 1 \le \theta < 0$,

$$\begin{aligned} \left\{ \begin{array}{l} - {g_{20}}q(\theta ) - {{\bar{g}}_{20}}\bar{q}(\theta ) = {h_{20}}\\ - {g_{11}}q(\theta ) - {{\bar{g}}_{11}}\bar{q}(\theta ) = {h_{11}}\\ - {g_{02}}q(\theta ) - {{\bar{g}}_{02}}\bar{q}(\theta ) = {h_{02}} \end{array} \right. \end{aligned}$$

(22)

Substituting (22) into (20), we have

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{w}}_{20}} = i2{\omega _0}{\tau _0}{w_{20}} + {g_{20}}q(\theta ) + {{\bar{g}}_{20}}\bar{q}(\theta )\\ {{\dot{w}}_{11}} = {g_{11}}q(\theta ) + {{\bar{g}}_{11}}\bar{q}(\theta )\\ {{\dot{w}}_{02}} = - 2i{\omega _0}{\tau _0}{w_{02}} + {g_{02}}q(\theta ) + {{\bar{g}}_{02}}\bar{q}(\theta ) \end{array} \right. \end{aligned}$$

(23)

It is easy to obtain the solutions

$$\begin{aligned} \left\{ \begin{aligned} \textstyle {w_{20}}&\textstyle = \frac{{i{g_{20}}}}{{{\omega _0}{\tau _0}}}q(0){\text {e}^{i{\omega _0}{\tau _0}\theta }} + \frac{{i{{\bar{g}}_{20}}}}{{3{\omega _0}{\tau _0}}}\bar{q}(0){\text {e}^{ - i{\omega _0}{\tau _0}\theta }} \\&\quad + {C_1}{\text {e}^{i2{\omega _0}{\tau _0}\theta }}\\ \textstyle {w_{11}}&\textstyle = - \frac{{i{g_{11}}}}{{{\omega _0}{\tau _0}}}q(0){\text {e}^{i{\omega _0}{\tau _0}\theta }} + \frac{{i{{\bar{g}}_{11}}}}{{{\omega _0}{\tau _0}}}\bar{q}(0){\text {e}^{ - i{\omega _0}{\tau _0}\theta }} \\&\quad + {C_2}\\ \textstyle {w_{02}}&\textstyle = - \frac{{i{g_{02}}}}{{3{\omega _0}{\tau _0}}}q(0){\text {e}^{i{\omega _0}{\tau _0}\theta }} - \frac{{i{{\bar{g}}_{02}}}}{{{\omega _0}{\tau _0}}}\bar{q}(0){\text {e}^{ - i{\omega _0}{\tau _0}\theta }} \\&\quad + {C_3}{\text {e}^{ - i2{\omega _0}{\tau _0}\theta }} \end{aligned} \right. \end{aligned}$$

(24)

Since $R(0)u(s) = f(0,u(s))$ for $\theta = 0$, from (21), we can know

$$\begin{aligned} \left\{ {\begin{array}{l} { - {g_{20}}q(0) - {{\bar{g}}_{20}}\bar{q}(0) + {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2{\alpha ^2} + 2b\alpha } \end{array}} \right) = {h_{20}}}\\ { - {g_{11}}q(0) - {{\bar{g}}_{11}}\bar{q}(0) + {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2\alpha \bar{\alpha }+ b\alpha + b\bar{\alpha }} \end{array}} \right) = {h_{11}}}\\ { - {g_{02}}q(0) - {{\bar{g}}_{02}}\bar{q}(0) + {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2{{\bar{\alpha }}^2} + 2b\bar{\alpha }} \end{array}} \right) = {h_{02}}} \end{array}} \right. \end{aligned}$$

(25)

Substituting (25) into (20), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \textstyle \int _{ - 1}^0 {\text {d}\eta (0,\theta ){w_{20}}} =&{} i2{\omega _0}{\tau _0}{w_{20}}(0) + {g_{20}}q(0) \\ &{}+ {{\bar{g}}_{20}}\bar{q}(0) - {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2{\alpha ^2} + 2b\alpha } \end{array}} \right) \\ \textstyle \int _{ - 1}^0 {\text {d}\eta (0,\theta ){w_{11}}} =&{} {g_{11}}q(0) + {{\bar{g}}_{11}}\bar{q}(0) \\ &{}- {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2\alpha \bar{\alpha }+ b\alpha + b\bar{\alpha }} \end{array}} \right) \\ \textstyle \int _{ - 1}^0 {\text {d}\eta (0,\theta ){w_{02}}} =&{} - i2{\omega _0}{\tau _0}{w_{02}}(0) + {g_{02}}q(0) \\ &{}+ {{\bar{g}}_{02}}\bar{q}(0) - {\tau _0}\left( {\begin{array}{c} 0\\ 0\\ {2{{\bar{\alpha }}^2} + 2b\bar{\alpha }} \end{array}} \right) \end{array} \right. \end{aligned}$$

(26)

Substituting (24) into (26), and noticing that

$$\begin{aligned} \begin{array}{l} \textstyle \int _{ - 1}^0 {\text {d}\eta (0,\theta ){\text {e}^{i{\omega _0}{\tau _0}\theta }}q(0)} = i{\omega _0}{\tau _0}q(0) \\ \textstyle \int _{ - 1}^0 {\text {d}\eta (0,\theta ){\text {e}^{ - i{\omega _0}{\tau _0}\theta }}\bar{q}(0)} = - i{\omega _0}{\tau _0}\bar{q}(0) \end{array} \end{aligned}$$

we have

$$\begin{aligned} {C_1}= & {} {\left( {\begin{array}{c@{\quad }c@{\quad }c} {i2{\omega _0}}&{}{ - 1}&{}0\\ 0&{}{i2{\omega _0}}&{}{ - 1}\\ a&{}b&{}{C_{33}^1} \end{array}} \right) ^{ - 1}}\left( {\begin{array}{c} 0\\ 0\\ {2{\alpha ^2} + 2b\alpha } \end{array}} \right) \end{aligned}$$

(27)

$$\begin{aligned} {C_2}= & {} {\left( {\begin{array}{c@{\quad }c@{\quad }c} 0&{}{ - 1}&{}0\\ 0&{}0&{}{ - 1}\\ a&{}b&{}c \end{array}} \right) ^{ - 1}}\left( {\begin{array}{c} 0\\ 0\\ {2\alpha \bar{\alpha }+ b\alpha + b\bar{\alpha }} \end{array}} \right) \end{aligned}$$

(28)

$$\begin{aligned} {C_3}= & {} {\left( {\begin{array}{c@{\quad }c@{\quad }c} { - i2{\omega _0}}&{}{ - 1}&{}0\\ 0&{}{ - i2{\omega _0}}&{}{ - 1}\\ a&{}b&{}{C_{33}^3} \end{array}} \right) ^{ - 1}}\left( {\begin{array}{c} 0\\ 0\\ {2{{\bar{\alpha }}^2} + 2b\bar{\alpha }} \end{array}} \right) \end{aligned}$$

(29)

where $C_{33}^1 = i2{\omega _0} + c + k - k{\text {e}^{ - i2{\omega _0}{\tau _0}}}$, $C_{33}^3 = - i2{\omega _0} + c + k - k{\text {e}^{i2{\omega _0}{\tau _0}}}$. Hence, we can know ${{w_{20}}}$, ${{w_{11}}}$, consequently, we can know $g_{21}$. By the bifurcation theories in Ref.  [39], we can obtain the following values.

$$\begin{aligned}&{c_1}(0) = \frac{i}{{2{\omega _0}{\tau _0}}}\left( {g_{11}}{g_{20}} - 2{\left| {{g_{11}}} \right| ^2} - \frac{{{{\left| {{g_{02}}} \right| }^2}}}{3}\right) + \frac{{{g_{21}}}}{2}\nonumber \\&{\mu _2} = -\frac{{{\mathop {\mathrm{Re}}\nolimits } \big \{ {c_1}(0)\big \} }}{{{\mathop {\mathrm{Re}}\nolimits } \big \{ {{\left. {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right| }_{\tau = {\tau _0}}}\big \} }},{\beta _2} = 2{\mathop {\mathrm{Re}}\nolimits } \big \{ {c_1}(0)\big \} \nonumber \\&{T_2} = - \frac{{{\mathop {\mathrm{Im}}\nolimits } \big \{ {c_1}(0)\big \} + {\mu _2}{\mathop {\mathrm{Im}}\nolimits } \big \{ {{\left. {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right| }_{\tau = {\tau _0}}}\big \} }}{{{\omega _0}{\tau _0}}} \end{aligned}$$

(30)

Therefore, we have the following result.

Theorem 3

Under the condition of theorem 2,we have the following main results,

• (I) $\mu = 0$ is Hopf bifurcation value of system (8);

• (II) The direction of Hopf bifurcation is determined by the sign of $\mu _2$, if $\mu _2>0$, the Hopf bifurcation is supercritical and the bifurcating periodic solutions exists for $\tau > {\tau _0}$, if $\mu _2<0$, the Hopf bifurcation is subcritical and the bifurcating periodic solutions exists for $\tau < {\tau _0}$.

• (III) The stability of bifurcating periodic solutions is determined by ${\beta _2}$, if ${\beta _2}<0$, the periodic solutions are stable, and if ${\beta _2}>0$, they are unstable.

• (IV) The period of the bifurcating periodic solution is determined by ${T _2}$, if ${T _2}>0$, the period increase, and the period decrease when ${T _2}<0$.

• (V) System (1) can be controlled by the delayed feedback.

5 Numerical simulation

In this section, we apply the results in the previous to system (2) for the purpose of control chaos. We take $a=3.4$, $b=1$, $c=4$, when $\tau =0$ or $k=0$, system (2) is chaotic (see Fig.17), and $p=14+8k$, $q=-26.2-6.8k$, $r=11.56$.

Fig. 17

Chaotic behaviors of system (2) for $k=0$ or $\tau =0$

By proposition 1, proposition 2, $\varDelta \mathrm{{ = }}{(14 + 8k)^2} + 20.4k + 78.6 > 0$ and $z_1^* > 0$ for all $k \in R$, we have the following results.

Conclusion 1

(1) If $k \in ( - \infty , - 0.1263281874]$ or $k \in [0.2076115584, +\infty )$, Eq. (6) has positive roots; (2) If $k \in ( - \infty , - 0.1263281874]$ or $k \in [0.2076115584, +\infty )$, Eq. (3) has negative real parts for $\tau \in [0,{\tau _0})$.

For the purpose of controlling the chaos, we consider $k \in ( - \infty , - 0.1263281874] \cup [0.2076115584, +\infty )$, and in particular, we take $k = 1$, consider the following delayed back control system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = y\\ \dot{y} = z\\ \dot{z} = - 3.4x - y - 4y + {y^2} + xy + (z(t - \tau ) - z(t)) \end{array} \right. \end{aligned}$$

(31)

We can compute $p = 22$, $q = - 33$, $\varDelta = 583$, $h = {z^3} + 22{z^2} - 33z + 11.56$, and ${z_1} \buildrel \textstyle .\over = 0.5824816436$, ${z_2} \buildrel \textstyle .\over = 0.8470555278$, ${\omega _1} \buildrel \textstyle .\over = 0.7632048504$, ${\omega _2} \buildrel \textstyle .\over = 0.9203561962$, ${\tau _1} \buildrel \textstyle .\over = 3.357873552 + \frac{{2n\pi }}{{{\omega _1}}}$, ${\tau _2} \buildrel \textstyle .\over = 0.1814016921 + \frac{{2n\pi }}{{{\omega _2}}}$, $h'({z_1}) = - 6.35295308$, $h'({z_2}) = 6.42295242$; thus, from the Theorem 1, we have $\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right) } \right] _{\tau = {\tau _1}}^{ - 1} < 0$, $\left[ {{\mathop {\mathrm{Re}}\nolimits } \left( {\frac{{\text {d}\lambda }}{{\text {d}\tau }}} \right) } \right] _{\tau = {\tau _2}}^{ - 1} > 0$ for $n=0$.

Conclusion 2

Take ${\tau _0} = {\tau _{20}} = 0.1814016921$; then (1) if we choose $\tau = 0.005 < {\tau _0}$, the zero solution is locally stable(See Fig.18); (2) if we choose $\tau = 1 > {\tau _0}$, the zero solution is locally unstable. (3) By theorem 3, we know that the bifurcating point is subcritical, and the bifurcating periodic solution is unstable.

Fig. 18

Locally stable zero solution of system (2) for $k=1$ and $\tau =0.005$

6 Conclusion

This paper deals with the dynamics and the delayed feedback control of a 3D jerk chaotic system with only one stable equilibrium. The Hopf bifurcation of this system with delayed feedback computed by the method of projection for center manifold, and the subcritical and the supercritical Hopf bifurcation were obtained. Also the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions have been investigated. Numerical simulations confirmed the correctness of the Hopf bifurcation analysis and the efficiency of the delayed feedback control strategy. However, there are still complex dynamics and the topological structure of this system should be exploited. These will be provided in future works.