1 INTRODUCTION

In the last few decades, nonlinear evolution (NLE) equations have been considered by a lot of researchers in the field of mathematical physics. It is known that exact solutions extracted from NLE equations provide comprehensive information about real-world phenomena. For this reason, searching for exact solutions of NLE equations plays a vital role in mathematical physics and is the major topic of many works. An attractive kind of exact solutions is referred to as rational-type solutions which include soliton, lump, lump-kink, breather-wave, and rogue-wave solutions. Because of the importance of these types of exact solutions, a wide range of scholars have devoted their studies to looking for rational-type solutions of nonlinear evolution equations. For example, Wazwaz and El-Tantawy in [1] exerted the simplified Hirota method to seek solitons of \((3+1)\)-dimensional KP\(-\)Boussinesq and BKP\(-\)Boussinesq equations. In another work performed by Manukure et al. [2], lump solutions of a \((2+1)\)-dimensional extended Kadomtsev – Petviashvili equation were obtained by making use of quadratic test functions. Lump-kink solutions to the KP equation were constructed in [3] by considering an ansatz which is a combination of positive quadratic and exponential functions. Lan [4] reported breather-wave and rogue-wave solutions of a generalized \((3+1)\)-dimensional B-type Kadomtsev – Petviashvili equation with the variable coefficient using the homoclinic test technique. For more papers, see [5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36].

The fundamental purpose of the present article is to study a new 3D-HB equation in fluids in the following form:

$$u_{yt}+c_{1}(u_{xxxy}+6u_{x}u_{y}+3u_{xy}u+3u_{xx}\int u_{y}dx)+c_{2}u_{yy}+c_{3}u_{zz}=0,$$
(1.1)

or

$$u_{yt}+c_{1}(u_{xxxy}+6u_{x}u_{y}+3u_{xy}u+3u_{xx}v)+c_{2}u_{yy}+c_{3}u_{zz}=0,u_{y}=v_{x},$$
(1.2)

and to retrieve a bunch of rational-type solutions for it by exerting a number of effective techniques.

It is worthy of note that by considering \(c_{3}=0\), the above new 3D-HB equation is reduced to the 2D-HB equation which has been considered by Hua et al. in [37]. Hua and his collaborators extracted interaction solutions of the 2D-HB equation by utilizing a series of ansatz techniques. Hosseini et al. [38] also found rational wave solutions of the 2D-HB equation with different structures by means of a number of useful approaches.

The structure of this paper is as follows: In Section 2, by using the truncated Painlevé expansion, the Bäcklund transformation and Hirota bilinear form of the new 3D-HB equation are formally derived. In Section 3, a series of test functions is applied to obtain rational-type solutions of the new 3D-HB equation. The last section presents the outcomes of the current article.

2 BÄCKLUND TRANSFORMATION AND HIROTA BILINEAR FORM OF THE MODEL

According to the truncated Painlevé expansion, the Bäcklund transformation of the system (1.2) can be written as

$$u=\frac{{{u}_{0}}}{{{f}^{2}}}+\frac{{{u}_{1}}}{f}+{{u}_{2}},v=\frac{{{v}_{0}}}{{{f}^{2}}}+\frac{{{v}_{1}}}{f}+{{v}_{2}},$$
(2.1)

where \(f\) is a function of variables \(x,y,z,\) and \(t\). The functions \(u_{2}\) and \(v_{2}\) are arbitrary solutions of the new 3D-HB equation and \(u_{0}\), \(u_{1}\), \(v_{0}\), and \(v_{1}\) are unknown functions including the derivatives of \(f\).

Now, by inserting (2.1) into the system (1.2) and solving the resulting system obtained by equating the coefficients of \(f^{-6}\) and \(f^{-3}\) to zero, we obtain

$${{u}_{0}}=-2f_{x}^{2},{{v}_{0}}=-2{{f}_{x}}{{f}_{y}}.$$
(2.2)

Similarly, by considering \(u_{2}=v_{2}=0\), the relations presented in (2.2), and equating the coefficients of \(f^{-5}\) and \(f^{-2}\) to zero, we arrive at a system of nonlinear PDEs whose solution gives

$${{u}_{1}}=2{{f}_{xx}},{{v}_{1}}=2{{f}_{xy}}.$$

Substituting the above results into (2.1) finally results in the following Bäcklund transformation for the new 3D-HB equation:

$$u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}}.$$
(2.3)

Based on the Bäcklund transformation (2.3), Hirota bilinear form corresponding to the new 3D-HB equation can be written as

$$\displaystyle{{B}_{3D-HB}}(f):=({{D}_{y}}{{D}_{t}}+{{c}_{1}}D_{x}^{3}{{D}_{y}}+{{c}_{2}}D_{y}^{2}+{{c}_{3}}D_{z}^{2})f.f=2(f{{f}_{yt}}-{{f}_{y}}{{f}_{t}}+{{c}_{1}}(f{{f}_{xxxy}}-3({{f}_{xxy}}{{f}_{x}}$$
$$\displaystyle-{{f}_{xy}}{{f}_{xx}})-{{f}_{y}}{{f}_{xxx}})+{{c}_{2}}(f{{f}_{yy}}-f_{y}^{2})+{{c}_{3}}(f{{f}_{zz}}-f_{z}^{2}))=0,$$
(2.4)

where \(D_{x},D_{y},D_{y},\) and \(D_{z}\) are Hirota’s bilinear operators.

3 RATIONAL-TYPE SOLUTIONS OF THE NEW 3D-HB EQUATION

In the present section, rational-type solutions of the new 3D-HB equation with different structures are formally established by exerting a number of effective techniques.

3.1 Soliton Solutions

To derive soliton solutions of the governing model, we substitute \(u={{e}^{{{k}_{i}}x+{{\tau}_{i}}y+{{\xi}_{i}}z+{{\varsigma}_{i}}t}}\) into the linear terms of (1.1) and solve the resulting equation for \({\varsigma}_{i}\). After that, the dispersion relation \({\varsigma}_{i}\) can be written as

$${{\varsigma}_{i}}=-\frac{{{c}_{1}}k_{i}^{3}{{\tau}_{i}}+{{c}_{2}}\tau_{i}^{2}+{{c}_{3}}\xi_{i}^{2}}{{{\tau}_{i}}},$$

and so

$${{\theta}_{i}}={{k}_{i}}x+{{\tau}_{i}}y+{{\xi}_{i}}z-\frac{{{c}_{1}}k_{i}^{3}{{\tau}_{i}}+{{c}_{2}}\tau_{i}^{2}+{{c}_{3}}\xi_{i}^{2}}{{{\tau}_{i}}}t,$$

where \(\theta_{i},1\leqslant i\leqslant 3\) are phase variables. Now, by considering the dependent variables

$$u=R{{(\ln f)}_{xx}},v=R{{(\ln f)}_{xy}},$$

and the exponential function

$$f=1+{{e}^{{{k}_{1}}x+{{\tau}_{1}}y+{{\xi}_{1}}z-\frac{{{c}_{1}}k_{1}^{3}{{\tau}_{1}}+{{c}_{2}}\tau_{1}^{2}+{{c}_{3}}\xi_{1}^{2}}{{{\tau}_{1}}}t}},$$

we obtain \(R=2\). Accordingly, the following 1-soliton solution can be obtained:

$$u=2{{\biggl{(}\ln\biggl{(}\!1+{{e}^{{{k}_{1}}x+{{\tau}_{1}}y+{{\xi}_{1}}z-\frac{{{c}_{1}}k_{1}^{3}{{\tau}_{1}}+{{c}_{2}}\tau_{1}^{2}+{{c}_{3}}\xi_{1}^{2}}{{{\tau}_{1}}}t}}\biggr{)}\!\biggr{)}}_{xx}},v=2{{\biggl{(}\!\ln\biggl{(}\!1+{{e}^{{{k}_{1}}x+{{\tau}_{1}}y+{{\xi}_{1}}z-\frac{{{c}_{1}}k_{1}^{3}{{\tau}_{1}}+{{c}_{2}}\tau_{1}^{2}+{{c}_{3}}\xi_{1}^{2}}{{{\tau}_{1}}}t}}\biggr{)}\!\biggr{)}}_{xy}.}$$

Now, we formally take

$$f=1+{{e}^{\theta_{1}}}+{{e}^{{{\theta}_{2}}}}+{{a}_{12}}{{e}^{{{\theta}_{1}}+{{\theta}_{2}}}},$$

as the auxiliary function in order to retrieve the following 2-soliton solution:

$$u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}}.$$

It is noted that the phase variables \(\theta_{i},i=1,2\) are defined as above and the phase shift \(a_{12}\) is given as

$${{a}_{12}}=\frac{-3{{c}_{1}}k_{1}^{2}{{k}_{2}}\tau_{1}^{2}{{\tau}_{2}}+3{{c}_{1}}k_{1}^{2}{{k}_{2}}{{\tau}_{1}}\tau_{2}^{2}+3{{c}_{1}}{{k}_{1}}k_{2}^{2}\tau_{1}^{2}{{\tau}_{2}}-3{{c}_{1}}{{k}_{1}}k_{2}^{2}{{\tau}_{1}}\tau_{2}^{2}+{{c}_{3}}\tau_{1}^{2}\xi_{2}^{2}-2{{c}_{3}}{{\tau}_{1}}{{\tau}_{2}}{{\xi}_{1}}{{\xi}_{2}}+{{c}_{3}}\tau_{2}^{2}\xi_{1}^{2}}{-3{{c}_{1}}k_{1}^{2}{{k}_{2}}\tau_{1}^{2}{{\tau}_{2}}-3{{c}_{1}}k_{1}^{2}{{k}_{2}}{{\tau}_{1}}\tau_{2}^{2}-3{{c}_{1}}{{k}_{1}}k_{2}^{2}\tau_{1}^{2}{{\tau}_{2}}-3{{c}_{1}}{{k}_{1}}k_{2}^{2}{{\tau}_{1}}\tau_{2}^{2}+{{c}_{3}}\tau_{1}^{2}\xi_{2}^{2}-2{{c}_{3}}{{\tau}_{1}}{{\tau}_{2}}{{\xi}_{1}}{{\xi}_{2}}+{{c}_{3}}\tau_{2}^{2}\xi_{1}^{2}}.$$

The special 3-soliton solution of the new 3D-HB equation, namely,

$$\displaystyle u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}},f=1+{{e}^{\theta_{1}}}+{{e}^{{{\theta}_{2}}}}+{{e}^{{{\theta}_{3}}}}+{{a}_{12}}{{e}^{{{\theta}_{1}}+{{\theta}_{2}}}}+{{a}_{13}}{{e}^{{{\theta}_{1}}+{{\theta}_{3}}}}+$$
$$\displaystyle{{a}_{23}}{{e}^{{{\theta}_{2}}+{{\theta}_{3}}}}+a_{12}a_{13}a_{23}e^{\theta_{1}+\theta_{2}+\theta_{3}},$$

where

$$\displaystyle{{\theta}_{i}}={{k}_{i}}x+{{\tau}_{i}}y+{{\xi}_{i}}z-\frac{{{c}_{1}}k_{i}^{3}{{\tau}_{i}}+{{c}_{2}}\tau_{i}^{2}+{{c}_{3}}\xi_{i}^{2}}{{{\tau}_{i}}}t,1\leqslant i\leqslant 3,$$
$$\displaystyle{{a}_{ij}}=\frac{-3{{c}_{1}}k_{i}^{2}{{k}_{j}}\tau_{i}^{2}{{\tau}_{j}}+3{{c}_{1}}k_{i}^{2}{{k}_{j}}{{\tau}_{i}}\tau_{j}^{2}+3{{c}_{1}}{{k}_{i}}k_{j}^{2}\tau_{i}^{2}{{\tau}_{j}}-3{{c}_{1}}{{k}_{i}}k_{j}^{2}{{\tau}_{i}}\tau_{j}^{2}+{{c}_{3}}\tau_{i}^{2}\xi_{j}^{2}-2{{c}_{3}}{{\tau}_{i}}{{\tau}_{j}}{{\xi}_{i}}{{\xi}_{j}}+{{c}_{3}}\tau_{j}^{2}\xi_{i}^{2}}{-3{{c}_{1}}k_{i}^{2}{{k}_{j}}\tau_{i}^{2}{{\tau}_{j}}-3{{c}_{1}}k_{i}^{2}{{k}_{j}}{{\tau}_{i}}\tau_{j}^{2}-3{{c}_{1}}{{k}_{i}}k_{j}^{2}\tau_{i}^{2}{{\tau}_{j}}-3{{c}_{1}}{{k}_{i}}k_{j}^{2}{{\tau}_{i}}\tau_{j}^{2}+{{c}_{3}}\tau_{i}^{2}\xi_{j}^{2}-2{{c}_{3}}{{\tau}_{i}}{{\tau}_{j}}{{\xi}_{i}}{{\xi}_{j}}+{{c}_{3}}\tau_{j}^{2}\xi_{i}^{2}},$$
$$\displaystyle 1\leqslant i,j\leqslant 3,$$

can be achieved if and only if the following 3-soliton condition is satisfied [39, 40]:

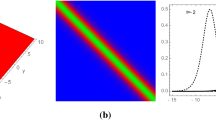
$$\displaystyle\sum\nolimits_{{{\mu}_{1}},{{\mu}_{2}},{{\mu}_{3}}=\pm 1}{P({{\mu}_{1}}{{V}_{1}}+{{\mu}_{2}}{{V}_{2}}+{{\mu}_{3}}{{V}_{3}})}P({{\mu}_{1}}{{V}_{1}}-{{\mu}_{2}}{{V}_{2}})P({{\mu}_{2}}{{V}_{2}}-{{\mu}_{3}}{{V}_{3}})P({{\mu}_{1}}{{V}_{1}}-{{\mu}_{3}}{{V}_{3}})$$
$$\displaystyle=2\sum\nolimits_{({{\mu}_{1}},{{\mu}_{2}},{{\mu}_{3}})\in S}{P({{\mu}_{1}}{{V}_{1}}+{{\mu}_{2}}{{V}_{2}}+{{\mu}_{3}}{{V}_{3}})}P({{\mu}_{1}}{{V}_{1}}-{{\mu}_{2}}{{V}_{2}})P({{\mu}_{2}}{{V}_{2}}-{{\mu}_{3}}{{V}_{3}})P({{\mu}_{1}}{{V}_{1}}-{{\mu}_{3}}{{V}_{3}})=0,$$

in which \(P=yt+c_{1}x^{3}y+c_{2}y^{2}+c_{3}z^{2},V_{i}=(k_{i},\tau_{i},\xi_{i},\varsigma_{i}),\) and \(S=\{(1,1,1),(1,1,-1),(1,-1,1),\) \((-1,1,1)\}.\) The 1-soliton, 2-soliton, and special 3-soliton solutions of the new 3D-HB equation are presented in Figs. 1–3, presenting the behavior of dispersive waves.

Fig. 1
figure 1

1-soliton solution on the \(x-y\) plane for \(k_{1}=1,\tau_{1}=-2,\xi_{1}=2,c_{1}=1,c_{2}=1,c_{3}=2,z=1,\) and \(t=1\).

Full size image
Fig. 2
figure 2

2-soliton solution on the \(x-y\) plane for \(k_{1}=1\), \(\tau_{1}=2\), \(\xi_{1}=-1\), \(k_{2}=-1\), \(\tau_{2}=1\), \(\xi_{2}=2\), \(c_{1}=-1\), \(c_{2}=-2\), \(c_{3}=1\), \(z=1\), and \(t=1\).

Full size image
Fig. 3
figure 3

Special 3-soliton on the \(x-y\) plane for \(k_{1}=-1\), \(\tau_{1}=1\), \(\xi_{1}=2\), \(k_{2}=1\), \(\tau_{2}=-1\), \(\xi_{2}=1\), \(k_{3}=1\), \(\tau_{3}=1\), \(\xi_{3}=1\), \(c_{1}=1\), \(c_{2}=1\), \(c_{3}=1\), \(z=10\), and \(t=1\).

Full size image

3.2 Lump-type Solutions

To retrieve lump-type solutions of the new 3D-HB equation, we exert a test function as follows:

$$f=g^{2}+h^{2}+a_{11},$$
(3.1)

where

$$g=a_{1}x+a_{2}y+a_{3}z+a_{4}t+a_{5},h=a_{6}x+a_{7}y+a_{8}z+a_{9}t+a_{10},$$

and \(a_{i},1\leqslant i\leqslant 11\) are real constants to be computed later. By setting (3.1) in (2.4) and adopting specific operations, we find the following results:

$${{a}_{1}}=-\frac{{{a}_{6}}{{a}_{7}}}{{{a}_{2}}},{{a}_{4}}=-\frac{a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}}}{{{a}_{2}}},{{a}_{8}}=\frac{{{a}_{3}}{{a}_{7}}}{{{a}_{2}}},{{a}_{9}}=-\frac{{{a}_{7}}\left(a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}}\right)}{{{a}_{2}^{2}}}.$$

Now, a lump-type solution is obtained as

$$u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}},$$
(3.2)

such that

$$\displaystyle f=\Bigl{(}\!-\frac{{{a}_{6}}{{a}_{7}}}{{{a}_{2}}}x+{{a}_{2}}y+{{a}_{3}}z-\frac{a_{2}^{2}{{c}_{2}}\!+\!a_{3}^{2}{{c}_{3}}}{{{a}_{2}}}t+{{a}_{5}}\Bigr{)}^{2}\!+{{\Bigl{(}\!{{a}_{6}}x+{{a}_{7}}y+\frac{{{a}_{3}}{{a}_{7}}}{{{a}_{2}}}z-\frac{{{a}_{7}}(a_{2}^{2}{{c}_{2}}\!+\!a_{3}^{2}{{c}_{3}})}{{{a}_{2}^{2}}}t+{{a}_{10}}\Bigr{)}}^{2}}$$
$$\displaystyle+{{a}_{11}}.$$

The lump-type solution of the new 3D-HB equation given by (3.2) is demonstrated in Fig. 4 for a special choice of free parameters.

Fig. 4
figure 4

Lump-type solution on the \(x-y\) plane for \(a_{2}=2,a_{3}=-1,a_{5}=-1,a_{6}=1,a_{7}=1,a_{10}=-0.5,a_{11}=1,c_{2}=1,c_{3}=-1,z=1,\) and \(t=1\).

Full size image

3.3 Interaction Solutions

To derive interaction solutions of the new 3D-HB equation, we employ the following test function:

$$f=g^{2}+h^{2}+ke^{k_{1}x+k_{2}y+k_{3}z+k_{4}t}+a_{11},$$
(3.3)

where

$$g={{a}_{1}}x+{{a}_{2}}y+{{a}_{3}}z+{{a}_{4}}t+{{a}_{5}},h={{a}_{6}}x+{{a}_{7}}y+{{a}_{8}}z+{{a}_{9}}t+{{a}_{10}},$$

and \({{a}_{i}},1\leqslant i\leqslant 11\) and \({{k}_{j}},1\leqslant j\leqslant 4\) are real constants to be calculated, and \(k\) is a positive real constant. By substituting (3.3) into (2.4) and applying specific operations, we find

$$\begin{gathered}\displaystyle{{a}_{1}}=-\frac{{{a}_{6}}{{a}_{7}}}{{{a}_{2}}},\quad{{a}_{4}}=-\frac{a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}}}{{{a}_{2}}},\quad{{a}_{8}}=\frac{{{a}_{3}}{{a}_{7}}}{{{a}_{2}}},\quad{{a}_{9}}=-\frac{{{a}_{7}}\left(a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}}\right)}{{{a}_{2}^{2}}},\\ \displaystyle k_{2}=0,\quad k_{3}=0,\quad k_{4}=-c_{1}k_{1}^{3}.\end{gathered}$$

Now we find the following interaction solution:

$$u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}},$$
(3.4)

in which

$$\displaystyle f=\Bigl{(}\!-\frac{{{a}_{6}}{{a}_{7}}}{{{a}_{2}}}x+{{a}_{2}}y+{{a}_{3}}z-\frac{a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}}}{{{a}_{2}}}t+{{a}_{5}}\Bigr{)}^{2}\!+\!{{\Bigl{(}{{a}_{6}}x+{{a}_{7}}y+\frac{{{a}_{3}}{{a}_{7}}}{{{a}_{2}}}z-\frac{{{a}_{7}}(a_{2}^{2}{{c}_{2}}+a_{3}^{2}{{c}_{3}})}{{{a}_{2}^{2}}}t+{{a}_{10}}\Bigr{)}}^{2}}$$
$$\displaystyle+k{{e}^{{{k}_{1}}x-{{c}_{1}}k_{1}^{3}t}}+{{a}_{11}}.$$

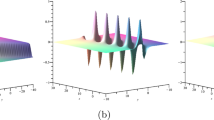
Three-dimensional and density plots of the interaction solution (3.4) are illustrated in Figs. 5 and 6 for different choices of \(t\).

Fig. 5
figure 5

Interaction solution on the \(x-y\) plane for \(a_{2}=-5,a_{3}=1,a_{5}=-1,a_{6}=5,a_{7}=0.1,a_{10}=1,a_{11}=1,k=1,k_{1}=1,c_{1}=-0.2,c_{2}=0.2,c_{3}=0.1,z=1,\) and \(t=-100\).

Full size image
Fig. 6
figure 6

Interaction solution on the \(x-y\) plane for \(a_{2}=-5\), \(a_{3}=1\), \(a_{5}=-1\), \(a_{6}=5\), \(a_{7}=0.1\), \(a_{10}=1\), \(a_{11}=1\), \(k=1\), \(k_{1}=1\), \(c_{1}=-0.2\), \(c_{2}=0.2\), \(c_{3}=0.1\), \(z=1\), and \(t=1\).

Full size image

It is worthy of note that when \(-c_{1}k_{1}^{3}>0\) and \(t\rightarrow+\infty\), the lump-type solution vanishes and the 1-soliton solution stays.

3.4 Breather-wave and Rogue-wave Solutions

To obtain breather-wave solutions of the new 3D-HB equation, we use the following ansatz:

$$f={{e}^{-kg}}+{{b}_{0}}\cos(\tau h)+{{b}_{1}}{{e}^{kg}},$$
(3.5)

where

$$g=a_{1}x+a_{2}y+a_{3}z+a_{4}t+a_{5},h=a_{6}x+a_{7}y+a_{8}z+a_{9}t+a_{10}.$$

By setting (3.5) in (2.4) and applying specific operations, we derive

$${{a}_{2}}=0,{{a}_{4}}=-\frac{{{k}^{2}}a_{1}^{3}{{a}_{7}}{{c}_{1}}+2{{a}_{3}}{{a}_{8}}{{c}_{3}}}{{{a}_{7}}},{{a}_{6}}=0,{{a}_{9}}=-\frac{{{\tau}^{2}}a_{7}^{2}{{c}_{2}}+{{\tau}^{2}}a_{8}^{2}{{c}_{3}}-{{k}^{2}}a_{3}^{2}{{c}_{3}}}{{{\tau}^{2}}{{a}_{7}}},{{b}_{1}}=\frac{1}{4}b_{0}^{2}.$$

Now a breather-wave solution is found as

$$u=2{{(\ln f)}_{xx}},v=2{{(\ln f)}_{xy}},$$

where

$$\displaystyle f={{e}^{-k({{a}_{1}}x+{{a}_{3}}z-\frac{{{k}^{2}}a_{1}^{3}{{a}_{7}}{{c}_{1}}+2{{a}_{3}}{{a}_{8}}{{c}_{3}}}{{{a}_{7}}}t+{{a}_{5}})}}+{{b}_{0}}\cos\left(\tau\left({{a}_{7}}y+{{a}_{8}}z-\frac{{{\tau}^{2}}a_{7}^{2}{{c}_{2}}+{{\tau}^{2}}a_{8}^{2}{{c}_{3}}-{{k}^{2}}a_{3}^{2}{{c}_{3}}}{{{\tau}^{2}}{{a}_{7}}}t+{{a}_{10}}\right)\right)$$
$$\displaystyle+\frac{1}{4}b_{0}^{2}{{e}^{k({{a}_{1}}x+{{a}_{3}}z-\frac{{{k}^{2}}a_{1}^{3}{{a}_{7}}{{c}_{1}}+2{{a}_{3}}{{a}_{8}}{{c}_{3}}}{{{a}_{7}}}t+{{a}_{5}})}}.$$

Now, by assuming \(b_{0}=-2,\tau=k\), and \(k\rightarrow 0\), the following rogue-wave solution can be obtained:

$$u(x,y,z,t)=\frac{4a_{1}^{2}}{{{\theta}^{2}}+{{\nu}^{2}}}-\frac{8a_{1}^{2}{{\theta}^{2}}}{{{({{\theta}^{2}}+{{\nu}^{2}})}^{2}}},v(x,y,z,t)=-\frac{8{{a}_{1}}{{a}_{7}}\theta\nu}{{{({{\theta}^{2}}+{{\nu}^{2}})}^{2}}},$$

where

$$\theta={{a}_{1}}x+{{a}_{3}}z-\frac{2{{a}_{3}}{{a}_{8}}{{c}_{3}}}{{{a}_{7}}}t+{{a}_{5}},\nu={{a}_{7}}y+{{a}_{8}}z-\frac{a_{7}^{2}{{c}_{2}}+a_{8}^{2}{{c}_{3}}-a_{3}^{2}{{c}_{3}}}{{{a}_{7}}}t+{{a}_{10}}.$$

The breather-wave and rogue-wave solutions are formally plotted in Fig. 7 for a special choice of free parameters.

Fig. 7
figure 7

(a) Breather-wave solution on the \(x-y\) plane; (b) Rogue-wave solution on the \(x-y\) plane.

Full size image

4 CONCLUSION

In the present paper, a new \((3+1)\)-dimensional Hirota bilinear equation has been developed and its rational-type solutions have been obtained successfully. In this respect,

  • the truncated Painlevé expansion was utilized to derive the Bäcklund transformation and Hirota bilinear form of the model;

  • soliton solutions were extracted by applying the simplified Hirota method and the 3-soliton condition;

  • the lump-type solution was established by considering two positive quadratic functions as an ansatz;

  • the interaction solution was retrieved by exerting an ansatz composed of two positive quadratic functions and an exponential function;

  • the breather-wave solution and its corresponding rogue-wave solution were constructed by adopting the homoclinic test technique.

In the end, the interaction of lump-type and 1-soliton solutions was studied and some interesting and useful results were presented.