Abstract
The aim of this paper is to present solitary wave solutions of two different forms of Klein–Gordon equations with full nonlinearity. The \(\left( \frac{G'}{G}\right) \)-expansion method is applied to solve the governing equations and then exact 1-soliton solutions are obtained. It is shown that this method provides us with a powerful mathematical tool for solving nonlinear evolution equations in mathematical physics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider the generalized form of Klein–Gordon (KG) equations with full nonlinearity in the form (Biswas et al. 2012; Sassaman and Biswas 2010, 2009; Fabian et al. 2009)
and
where the dependent variable \(q(x,t)\) represents the wave profile. Also, \(k,~a,~b\) and \(c\) are real valued constants and \(m\) is a positive integer with \(m\ge 1.\) In fact, if \(m=1,\) Eq. (2) reduces to the KG equation (Wazwaz 2006)
When \(n=3,\) Eq. (3) becomes the known KG equation with quintic nonlinearity (Wazwaz 2006; Abazari 2013)
The KG equation is one of the most important equations that is studied in the area of quantum physics. This equation appears in relativistic quantum mechanics. The KG equation also appears in relativistic physics and is used to describe dispersive wave phenomena in general. In addition, it appears in nonlinear optics and plasma physics. The KG equation arises in physics in linear and nonlinear forms. The nonlinear form comes from the quantum field theory and describes nonlinear wave interactions (Infeld and Rowlands 2000).
Solving nonlinear evolution equations (NLEEs) is one of the absolute necessities in the area of nonlinear waves. It is difficult to make progress without a closed form analytical solution to these NLEEs. Thus, solving NLEEs is an important task in this area of research. Recently, a new method has been proposed by Wang et al. (2008) called the \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method to study traveling wave solutions of NLEEs. This useful method is developed successfully by many authors (Ebadi and Biswas 2011; Zayed and Gepreel 2009; Zhang et al. 2008; Zhang 2009) and the reference therein. The \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method (Wang et al. 2008; Ebadi and Biswas 2011; Zayed and Gepreel 2009; Zhang et al. 2008; Zhang 2009) is based on the assumptions that the traveling wave solutions can be expressed by a polynomial in \(\left( \frac{G^{\prime }}{G}\right) \) such that \(G=G(\xi )\) satisfies a second order linear ordinary differential equation (ODE). In this paper, we describe the \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method (Zhang 2009) for finding traveling wave solutions of nonlinear partial differential equations (PDEs), the balance numbers of which are not positive integers and then subsequently it will be applied to solve the generalized form of the KG equation with full nonlinearity.
2 The \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method
We suppose that the given NLPDE for \(u(x,t)\) is in the form
where \(P\) is a polynomial. The essence of the \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method can be presented in the following steps:
Step 1. To find the traveling wave solutions of Eq. (5), we introduce the wave variable
Substituting Eq. (6) into Eq. (5), we obtain the following ODE
Step 2. Eq. (7) is then integrated as long as all terms contain derivatives where integration constants are considered zero.
Step 3. Introduce the solution \(U(\xi )\) of Eq. (7) in the finite series form
where \(a_{l}\) are real constants with \(a_{N}\ne 0\) and \(N\) is a positive integer to be determined. The function \(G(\xi )\) is the solution of the auxiliary linear ordinary differential equation
where \(\lambda \) and \(\mu \) are real constants to be determined.
Step 4. Determining \(N\) can be accomplished by balancing the linear term of highest order derivatives with the highest order nonlinear term in Eq. (7).
Step 5. Substituting the general solution of (9) together with (8) into Eq. (7) yields an algebraic equation involving powers of \(\frac{G^{\prime }}{G}\). Equating the coefficients of each power of \(\frac{G^{\prime }}{G}\) to zero gives a system of algebraic equations for \(a_{l},~\lambda ,~\mu \) and \(v.\) Then, we solve the system with the aid of a computer algebra system, such as Maple, to determine these constants. Next, depending on the sign of the discriminant \(\Delta =\lambda ^{2}-4\mu ,\) we get solutions of Eq. (7). So, we can obtain exact solutions of the given Eq. (5).
3 Application to the generalized Klein–Gordon equation with full nonlinearity
Form-I
We first consider the following KG equation:
Suppose that
where \(v\) is a constant to be determined later.
Then Eq. (11) is converted to an ODE
Balancing the \((U^{m})^{\prime \prime }\) with \(U^{2n-m}\) in Eq. (12) gives
We then assume that Eq. (12) has the following formal solutions:
where \(B\) is a constant to be determined later and \(G\) satisfies Eq. (9).
Thus, we obtain
Substituting Eqs. (13)–(15) into Eq. (12) and collecting all terms with the same order of \(\frac{G^{\prime }}{G}\) together, we convert the left-hand side of Eq. (12) into a polynomial in \(\frac{G^{\prime }}{G}\). Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for \(\lambda ,~\mu ,~v\) and \(B:\)
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{m}{n-m}+2}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{m}{n-m}+1}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{m}{n-m}}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{m}{n-m}-1}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{m}{n-m}-2}\) coeff.:
The solution of the above system is
From Eqs. (9), (11), (13) and (17), we obtain the exact traveling wave solution of the KG equation (10) as follows:
where \(c_{1}\) and \(c_{2}\) are arbitrary constants.
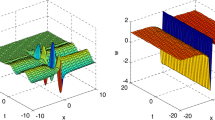
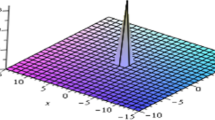
Equation (18) is a new type of exact traveling wave solution to the KG equation (10). Especially, if we choose \(c_{1}=c_{2}\) in (18), we obtain the solitary wave solution of the KG equation (10), namely
Remark 2
In Eqs. (18) and (19), if we take \(m=1,\) then we obtain the following solitary wave solutions
and
Thus, Eqs. (20) and (21) are the solitary wave solutions of the following KG equation
Remark 3
In Eqs. (20) and (21), if we take \(n=3,\) then we obtain the following solitary wave solutions
and
Thus, Eqs. (23) and (24) are the solitary wave solutions of the following KG equation
Remark 4
The exact solutions (21) and (24) that we obtained for the KG equations (22) and (25) are the same as the solutions that were obtained by Wazwaz (2006) who used the tanh method. Form-II
Let us consider the following KG equation:
Using the wave transformation
Eq. (26) is carried out to the following ODE:
Balancing the \((U^{m})^{\prime \prime }\) with \(U^{n+m}\) gives
We then assume that Eq. (28) has the following formal solutions:
where \(H\) is a constant to be determined later and \(G\) satisfies Eq. (9). Therefore, we obtain
Substituting Eqs. (29)–(31) into Eq. (28) and collecting all terms with the same order of \(\frac{G^{\prime }}{G}\) together, we convert the left-hand side of Eq. (28) into a polynomial in \(\frac{G^{\prime }}{G}\). Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for \(\lambda ,~\mu ,~v\) and \(H:\)
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{2m}{n}+2}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{2m}{n}+1}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{2m}{n}}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{2m}{n}-1}\) coeff.:
\(\left( \frac{G^{\prime }}{G}\right) ^{\frac{2m}{n}-2}\) coeff.:
The solution of the above system is
Substituting the solution set (33) into (29), the solution formulae of Eq. (28) can be written as
Substituting the general solutions of second order linear ODE into Eq. (28) gives two types of traveling wave solutions.
Case I When \(\mu <0,\) we obtain the hyperbolic function traveling wave solution
where \(c_{1}\) and \(c_{2}\) are arbitrary constants. On the other hand, assuming \(c_{1}=0\) and \(c_{2}\ne 0,\) the traveling wave solution of (35) can be written as:
Assuming \(c_{2}=0\) and \(c_{1}\ne 0,\) then we obtain
Case II When \(\mu >0,\) we obtain the trigonometric function traveling wave solutions
where \(c_{1}\) and \(c_{2}\) are arbitrary constants. If assume \(c_{1}=0\) and \(c_{2}\ne 0,\) then
and when \(c_{2}=0\) and \(c_{1}\ne 0,\) the solution of Eq. (38) will be
Remark 5
In Eqs. (36), (37), (39) and (40), if we take \(m=1,\) then we obtain the following exact solutions
for \(\frac{a}{v^{2}-k^{2}}<0.\)
for \(\frac{a}{k^{2}-v^{2}}>0.\)
Remark 6
The exact solutions (41)–(44) that we obtained for the KG equations (26) are the same as the solutions that were obtained by Wazwaz (2006) who used the tanh method.
4 Conclusions
Many powerful methods (Biswas et al. 2012; Sassaman and Biswas 2010, 2009; Fabian et al. 2009; Wazwaz 2006; Abazari 2013; Infeld and Rowlands 2000; Wang et al. 2008; Ebadi and Biswas 2011; Zayed and Gepreel 2009; Zhang et al. 2008; Zhang 2009) are used in solitary waves theory to examine exact soliton solutions for nonlinear PDEs. In this paper, we studied the new application of the \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method to derive the exact soliton solutions of the generalized form of KG equations with full nonlinearity. These results will be immensely useful in the area of quantum physics. The \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method is not only efficient, but also has the merit of being widely applicable. The results show that the proposed method is direct, effective and can be applied to many other nonlinear PDEs in mathematical physics.
References
Abazari R (2013) Solitary-wave solutions of the Klein-Gordon equation with quintic nonlinearity. J Appl Mech Tech Phys 54:397–403
Biswas A, Yildirim A, Hayat T, Aldossary OM, Sassaman R (2012) Soliton perturbation theory of the generalized Klein-Gordon equation with full nonlinearity. Proc Romanian Acad Ser A 13:32–41
Ebadi G, Biswas A (2011) The \(\left(\frac{G^{\prime }}{G}\right)\) method and topological soliton solution of the \(K(m, n)\) equation. Commun Nonlinear Sci Numer Simul 16:2377–2382
Fabian AL, Kohl R, Biswas A (2009) Perturbation of topological solitons due to sine-Gordon equation and its type. Commun Nonlinear Sci Numer Simul 14:1227–1244
Infeld E, Rowlands G (2000) Nonlinear waves. Cambridge University Press, Solitons and Chaos, Cambridge
Sassaman R, Biswas A (2009) Topological and non-topological solitons of the generalized Klein-Gordon equations. Appl Math Comput 215:212–220
Sassaman R, Biswas A (2010) Topological and non-topological solitons of the Klein-Gordon equations in 1+2 dimensions. Nonlinear Dyn 61:23–28
Wang ML, Li XZ, Zhang JL (2008) The \(\left(\frac{G^{\prime }}{G}\right)\)- expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A 372(4):417–423
Wazwaz AM (2006) Compactons, solitons and periodic solutions for some forms of nonlinear Klein-Gordon equations. Chaos Solitons Fractals 28:1005–1013
Zayed E, Gepreel KA (2009) Some applications of the \(\left(\frac{G^{\prime }}{G}\right)\)-expansion method to non-linear partial differential equations. Appl Math Comput 212(1):113
Zhang S, Tong JL, Wang W (2008) A generalized \(\left(\frac{G^{\prime }}{G}\right)\)-expansion method for the mKdV equation with variable coefficients. Phys Lett A 372(13):2254–2257
Zhang H (2009) New application of the \(\left(\frac{G^{\prime }}{G}\right)\)-expansion method. Commun Nonlinear Sci Numer Simul 14:3220–3225
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Pierangelo Marcati.
Rights and permissions
About this article
Cite this article
Mirzazadeh, M., Eslami, M. & Biswas, A. Soliton solutions of the generalized Klein–Gordon equation by using \(\left( \frac{G^{\prime }}{G}\right) \)-expansion method. Comp. Appl. Math. 33, 831–839 (2014). https://doi.org/10.1007/s40314-013-0098-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40314-013-0098-3