1 Background

Low weight, simplicity in manufacturing and application, swift response and extreme sensitivity of microelectromechanical systems (MEMS) have led to the widespread use of these systems in the recently developed industrial tools. The mechanical section of these systems consists of fundamental structures like rods, beams, plates, shells and rings. Rectangular and circular cross-sectional microrings, as a type of principal micromechanical elements, are utilized over a large area of engineering affairs. The configuration of rings provides an inimitable opportunity as a rate sensor or gyroscope, which can accurately measure the rotation velocity and rotation rate of MEMS devices. Among the uses of microrings in MEMS, one can mention force sensors [1], dual-mode COMS-MEMS resonators [2], label-free sensors [3, 4], pressure and temperature sensors [5, 6], multi-axis angular velocity sensors [7], vibrating ring gyroscopes [8, 9], rate sensors [10, 11], diaphragm sensors [12], ultrasonic actuators [13, 14], electro-optical modulators [15], etc.

According to various experimental evidence, mechanical elements with micron and submicron dimensions exhibit size-dependent static and dynamic behaviors, so that the classical continuum theory (CCT) is not competent to provide a rationale for this phenomenon in nano- and microstructures. Therefore, several attempts were made to put forward elasticity theories comprising scale parameters. One of the higher-order elasticity theories is the couple stress theory (CST) developed by Mindlin and Tiersten [16] in which two additional scale parameters are exploited to accommodate small-scale effect into constitutive relations. Applying some changes in CST, Yang et al. [17] established the modified couple stress theory (MCST) in which the strain energy includes only a single length scale parameter. In this way, the couple stress tensor will be symmetric, which makes its use much easier. In addition to the mentioned theories, other higher-order elasticity theories such as nonlocal theory [18], strain gradient theory (SGT) [19] and nonlocal strain gradient theory (NSGT) [20] have been suggested to rationalize the size-dependent behavior in micro/nanostructures. In the last decade, many articles have been published in the field of the effect of size on the behavior of different mechanical elements like linear and nonlinear flexural analysis of functionally graded composite microplates with variable thickness [21], vibration of intelligibly designed axially functionally graded (AFG) microtubes [22], free vibration and buckling analysis of FG porous sandwich curved microbeams in thermal environment [23], thermoelastic damping modeling in circular cylindrical nanoshells [24], dynamics of microtubes conveying fluid [25], static analysis of FG composite nanoshells on elastic foundations [26], nonlinear forced vibration analysis of microrotating shaft–disk systems [27], nonlinear buckling analysis of FG porous (FGP) lining reinforced by graphene platelets (GPLs) [28], thermoelastic vibrations of Timoshenko nanobeams [29], quasi-3D nonlinear stability behavior of agglomerated nanocomposite microbeams [30], dynamic analysis of spinning pipes conveying flow with elliptical cross section [31] and forced vibrational analysis of viscoelastic nanotubes conveying fluid subjected to moving load [32].

On the basis of numerous reports from experimental tests, the heat transfer process in certain cases such as the smallness of the structure under study or the short time of heat transfer, such as thermal shocks or laser pulse irradiation, cannot be interpreted through the classical formulation of heat conduction, i.e., the Fourier model. To better expound the heat transfer in such conditions, various nonclassical models have been proposed under the title of generalized thermoelasticity theories. As one of the most basic non-Fourier models, one can refer to the Lord and Shulman (LS) model which consists of only one phase lag parameter or relaxation time [33]. Due to including only one phase lag parameter, this model is also known as single-phase-lag (SPL) model. By incorporation of a term called thermal displacement in the Fourier model, Green and Naghdi established another nonclassical model known as GN-III model [34]. Accounting for nonlocal effect on heat transport and supplementing SPL model, Guyer and Krumhansl [35] propounded nonlocal single-phase-lag (NSPL) thermoelasticity model. To capture the effect of size on the space, Tzou [36] added another phase lag parameter to SPL model, which is known as dual-phase-lag (DPL) model. Incorporating small-scale effect on time into GN-III model, a modified equation called Moore–Gibson–Thompson (MGT) generalized thermoelasticity theory was formulated to give a description of heat transfer procedure in materials [37].

In MEMS resonators, the quality factor (QF) is a sensitive index for estimating the operating efficiency. The higher QF of these small-scaled systems implies the higher sensitivity and lower energy loss during the oscillation. As a major source of energy dissipation at room temperature, thermoelastic damping (TED), which is approximated via the inverse of QF, limits the upper bound of quality factor of vibrating micro/nanostructures. Owing to strain-induced thermoelastic temperature variations in oscillating systems, irreversible heat currents between hot and cold zones are produced, which leads to TED. Thereby, accurate estimation of the magnitude of TED is momentous for optimized design of high QF miniaturized resonators. To establish a theoretical framework for TED in different mechanical elements, two complex frequency (CF) and energy dissipation (ED) methods are mainly used. In CF method, both the motion and heat conduction equations of the structure under investigation should be derived, so that by separating the real and imaginary parts of the complex frequency of the system, a mathematical expression can be reached to describe TED. In ED method, there is no need to derive the equation of motion of the structure, but only by extracting its heat equation and constitutive relations, the amount of dissipated thermal and stored energies in the system can be obtained and through this, the value of TED can be computed. Therefore, ED method has the advantage that it requires fewer calculations due to not needing to derive the equation of motion. The earliest theoretical investigation about TED has been made by Zener [38], who derived an analytical solution for assessment of TED in thin beams within the scope of ED method. Years later, by employing CF method, Lifshitz and Roukes [39] succeeded in providing an explicit solution with a higher accuracy to calculate the value of TED in Euler–Bernoulli beam resonators.

Until today, various analytical studies have been carried out on TED in different structures, which the selected publications in this field are reviewed in the following. Zhou et al. [40] employed CCT as well as SPL model to attain an analytical expression for TED in micro/nanobeams with circular cross section. By making use of ED method, Li et al. [41] evaluated TED in rectangular and circular microplate resonators in the context of CCT and Fourier model. In similar articles, on the basis of CCT, TED in rectangular cross-sectional micro/nanoring resonators within the purview of Fourier model, SPL model and DPL model has been analyzed by Fang and Li [42], Zhou et al. [43] and Zhou and Li [44], respectively. According to CCT, TED in small-sized rings with circular cross section has been examined by Li et al. [45] and Kim and Kim [46] with the help of Fourier and SPL models, respectively. Gu et al. [47] used NSGT together with DPL model to propose a size-dependent model for TED in microbeams. Utilizing DPL model, Shi et al. [48] appraised surface effect on TED in nanobeam resonators in the framework of CF method. In the research of Borjalilou et al. [49], small-scale effects on TED in nanobeams has been modeled by applying NT in conjunction with DPL model. By means of CF method, Singh et al. [50] achieved a closed-form solution for TED in microbeams according to MCST and MGT model. Yang et al. [51] exploited MCST and Fourier model to develop a three-dimensional (3D) model for TED in Kirchhoff rectangular micro/nanoplates. Within the scope of MCST and nonlocal DPL (NDPL) model, Ge and Sarkar [52] presented an analytical solution in the form of infinite series for TED in rectangular cross-sectional micro/nanorings. With the aid of NT and NSPL model, Li et al. [53] provided a size-dependent and model and exact solution for TED in circular cylindrical nanoshells. In the study of Wang et al. [54], CF method has been applied to examine scale effect on TED in circular microplates on the basis of MCST and fractional DPL model.

Based on the above literature review, it was found that thermoelastic damping (TED) is one of the certain causes of energy loss in small-sized structures such as microrings and disruption of their favorable performance. It was also revealed that to scrutinize thermoelastic behavior of microstructures as accurately as possible, size-dependent theories in both structural and thermal areas must be employed. Consequently, theoretical modeling of TED phenomenon in miniaturized mechanical elements like microrings must be performed by accommodating the size effect into both constitutive relations and heat conduction equation. The main objective of the paper at hand is to render a novel size-dependent formulation for TED in rectangular cross-sectional microrings by simultaneous use of MCST and MGT model, something that is lacking in the literature. For fulfillment of this target, the first stage is to extract the nonclassical constitutive relations and heat equation by means of MCST and MGT model. By deriving the temperature field through solving the heat conduction equation, the wasted thermal energy and maximum stored elastic energy are specified. Exploiting the definition of TED corresponding to energy dissipation method, an analytical relationship encompassing the scale parameters of MCST and MGT model is given to anticipate the value of TED. Comparing the results of this model with the ones provided by previous simpler models, the model validation study is done. Preparing a diverse set of graphical data, the impact of some factors like scale parameters of MCST and MGT model, mode number, 1D and 2D models of heat conduction, geometrical parameters and material on TED value is examined.

2 Determination of fluctuation temperature in the ring in the context of MGT model

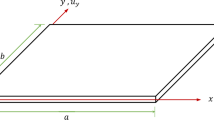
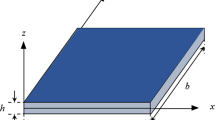
Consider a ring with rectangular cross section similar to that shown in Fig. 1. In this figure, parameters \(R\), \(h\) and \(b\) are symbols of mean radius, radial thickness, and depth of the ring, respectively. The displacement field of the ring can be expressed as follows [55]:

$$\left\{\begin{array}{l}{u}_{r}=u\\ {u}_{\theta }=v+\frac{x}{R}v-\frac{x}{R}\frac{\partial u}{\partial \theta }\\ {u}_{z}=0,\end{array}\right.$$
(1)

in which \(r\), \(\theta\) and \(z\) refer to the radial, peripheral and lateral directions, respectively. Also, \(x\) represents the radial distance of any arbitrary point from the mean radius of the ring. The variables \({u}_{r}\), \({u}_{\theta }\) and \({u}_{z}\) define the displacements of ring in the radial, peripheral and lateral directions, respectively. Moreover, \(u(\theta ,t)\) and \(v(\theta ,t)\) stand for the radial and peripheral displacements of a point located on the centerline of ring. In addition, \(x\) refers to the radial distance of a point from the neutral axis of cross section. Assuming that the peripheral centreline of the ring is inextensible (i.e., \(u=-\partial v/\partial \theta\)), the normal peripheral strain \({\varepsilon }_{\theta \theta }\) can be written as [55]:

Fig. 1
figure 1

Schematic view of a part of a rectangular cross-sectional ring

Full size image
$${\varepsilon }_{\theta \theta }=-\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right).$$
(2)

According to coupled thermoelastic constitutive relation of elasticity, one can write [42]:

$${\sigma }_{\theta \theta }=E\left({\varepsilon }_{\theta \theta }-\alpha T\right),$$
(3)

where \({\sigma }_{\theta \theta }\) is the normal peripheral stress. Parameters \(E\) and \(\alpha\) denote the elasticity modulus and thermal expansion coefficient of the material, respectively. Variable \(T\) represents the difference of current temperature with the reference temperature \({T}_{a}\). On the basis of Hooke's law, for two other normal strains one can write [43]:

$${\varepsilon }_{rr}={\varepsilon }_{zz}=-\nu \frac{{\sigma }_{\theta \theta }}{E}+\alpha T,$$
(4)

in which \({\varepsilon }_{rr}\) and \({\varepsilon }_{zz}\) represent the normal strains in the radial and lateral directions. Additionally, \(\nu\) is the Poisson ratio. Substitution of Eqs. (2) and (3) into Eq. (4) yields:

$${\varepsilon }_{rr}={\varepsilon }_{zz}=\nu \frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)+\left(1+\nu \right)\alpha T.$$
(5)

Within the framework of Moore–Gibson–Thompson (MGT) thermoelasticity theory, the heat conduction is formulated via the following relation [37]:

$$\left(1+\tau \frac{\partial }{\partial t}\right){\varvec{q}}=-k\nabla T-{k}^{*}\nabla \upsilon ,$$
(6)

in which \(q\) represents the vector of heat flux. The variable \(t\) stands for time. Symbol \(\nabla\) refers to the gradient operator. Parameter \(\tau\) is known as relaxation time. Furthermore, \(k\) and \({k}^{*}\) denote the thermal conductivity of the material and thermal conductivity rate, respectively. Additionally, variable \(\upsilon\) is called thermal displacement, which follows the relationship \(T=\partial \upsilon /\partial t\). The energy equation for a thermoelastic solid is expressed by [36]:

$$-\nabla .q=\rho {c}_{v}\frac{\partial T}{\partial t}+\frac{E\alpha {T}_{a}}{1-2\nu }\frac{\partial {\varepsilon }_{V}}{\partial t},$$
(7)

in which material constants \(\rho\) and \({c}_{v}\) refer to the mass density and specific heat per unit mass, respectively. Parameter \({\varepsilon }_{V}\) is also the volumetric strain, which is equal to the trace of strain tensor. Combination of Eqs. (6) and (7) results in the following equation:

$$k\frac{\partial }{\partial t}\left({\nabla }^{2}T\right)+{k}^{*}{\nabla }^{2}T=\left(1+\tau \frac{\partial }{\partial t}\right)\left(\rho {c}_{v}\frac{{\partial }^{2}T}{\partial {t}^{2}}+\frac{E\alpha {T}_{a}}{1-2\nu }\frac{{\partial }^{2}{\varepsilon }_{V}}{\partial {t}^{2}}\right),$$
(8)

where \({\nabla }^{2}=\nabla .\nabla\) represents the Laplace operator. Using Eqs. (2) and (5), one can derive the volumetric strain as follows:

$${\varepsilon }_{V}=\left(2\nu -1\right)\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)+2\left(1+\nu \right)\alpha T.$$
(9)

Placing the above equation in Eq. (8) and sorting the terms, one can get the following equation:

$$\chi \frac{\partial }{\partial t}\left({\nabla }^{2}T\right)+\frac{\chi }{{\tau }_{k}}{\nabla }^{2}T=\left(1+\tau \frac{\partial }{\partial t}\right)\left\{\left[1+\frac{2\left(1+\nu \right)}{1-2\nu }{\Delta }_{E}\right]\frac{{\partial }^{2}T}{\partial {t}^{2}}-\frac{{\Delta }_{E}}{\alpha }\frac{{\partial }^{2}}{\partial {t}^{2}}\left[\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)\right]\right\},$$
(10)

in which

$$\chi =\frac{k}{\rho {c}_{v}},$$
(11a)
$${\tau }_{k}=\frac{k}{{k}^{*}},$$
(11b)
$${\Delta }_{E}=\frac{E{\alpha }^{2}{T}_{a}}{\rho {c}_{v}}.$$
(11c)

At room temperature, in general \(\left[2\left(1+\nu \right)/\left(1-2\nu \right)\right]{\Delta }_{E}\ll 1\) [44]. Therefore, Eq. (10) can be replaced by the following equation:

$$\chi \frac{\partial }{\partial t}\left({\nabla }^{2}T\right)+\frac{\chi }{{\tau }_{k}}{\nabla }^{2}T=\left(1+\tau \frac{\partial }{\partial t}\right)\left\{\frac{{\partial }^{2}T}{\partial {t}^{2}}-\frac{{\Delta }_{E}}{\alpha }\frac{{\partial }^{2}}{\partial {t}^{2}}\left[\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)\right]\right\}.$$
(12)

Supposing harmonic oscillations of the ring, functions \(u\) and \(T\) can be expressed as follows [42]:

$$u\left(\theta ,t\right)={U}_{n}\mathrm{sin}(n\theta ){e}^{i{\omega }_{n}t},$$
(13a)
$$T\left(r,\theta ,z,t\right)={T}_{0}\left(r,\theta ,z\right){e}^{i{\omega }_{n}t},$$
(13b)

where \({U}_{n}\) and \({T}_{0}\) are the amplitudes of fluctuations of radial displacement and temperature increment, respectively. Moreover, \({\omega }_{n}\) addresses the nth vibrational frequency of the ring within the scope of MCST, the value of which can be computed through the following equation for a rectangular cross-sectional ring [56]:

$${\omega }_{n}=\sqrt{1+\frac{6}{1+\nu }{\left(\frac{l}{h}\right)}^{2}}\frac{n\left({n}^{2}-1\right)}{\sqrt{{n}^{2}+1}}\sqrt{\frac{EI}{\rho A{R}^{4}}} \,for\, n\ge 2,$$
(14)

in which \(I=b{h}^{3}/12\) and \(A=bh\). Substituting Eqs. (13a) and (13b) into Eq. (12) and arranging the obtained equation, the heat equation becomes:

$${\nabla }^{2}{T}_{0}+\frac{{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right){\tau }_{k}}{\chi \left(1+i{\omega }_{n}{\tau }_{k}\right)}{T}_{0}=\frac{{\Delta }_{E}}{\alpha }\frac{{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right){\tau }_{k}}{\chi \left(1+i{\omega }_{n}{\tau }_{k}\right)}\frac{x}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}\mathrm{sin}\left(n\theta \right).$$
(15)

Considering that the principal vibrations occur in in-plane directions, heat conduction in the lateral direction \(z\) can be overlooked [42]. Accordingly, one can write:

$${\nabla }^{2}{T}_{0}=\frac{{\partial }^{2}{T}_{0}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial {T}_{0}}{\partial r}+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{T}_{0}}{\partial {\theta }^{2}}.$$
(16)

According to Fig. 1, one can write \(r=R+x\). On the other hand, in thin rings \(R\gg x\). Taking into account these two points, Eq. (16) can be rewritten in a simpler way as below:

$${\nabla }^{2}{T}_{0}=\frac{{\partial }^{2}{T}_{0}}{\partial {x}^{2}}+\frac{1}{R}\frac{\partial {T}_{0}}{\partial x}+\frac{1}{{R}^{2}}\frac{{\partial }^{2}{T}_{0}}{\partial {\theta }^{2}}.$$
(17)

Wong et al. [57] proved that the term \(\left(1/R\right)\left(\partial {T}_{0}/\partial x\right)\) in above equation has a minor role in calculating the value of TED compared to the other two terms. Subsequently, Eq. (17) takes the following form:

$${\nabla }^{2}{T}_{0}=\frac{{\partial }^{2}{T}_{0}}{\partial {x}^{2}}+\frac{1}{{R}^{2}}\frac{{\partial }^{2}{T}_{0}}{\partial {\theta }^{2}}.$$
(18)

Adiabatic thermal boundary conditions are adopted at the inner and outer sides of ring. These boundary conditions can be mathematically expressed as \(\partial {T}_{0}/\partial x=0\) at \(x=\pm h/2\). Considering these conditions as well as Eqs. (15) and (18), the general solution of \({T}_{0}\) can be written as [42]:

$${T}_{0}=\sum\limits_{k=0}^{\infty } \sum\limits_{m=0}^{\infty }{A}_{km}\mathrm{sin}\left(m\theta \right)\mathrm{sin}\left({\beta }_{k}x\right),$$
(19)

where

$${\beta }_{k}=\frac{\left(2k-1\right)\pi }{h}.$$
(20)

Substitution of Eqs. (18) and (19) into Eq. (15) gives:

$$\sum\limits_{k=0}^{\infty } \sum\limits_{m=0}^{\infty }{A}_{km}\left[{\beta }_{k}^{2}+\frac{{m}^{2}}{{R}^{2}}-\frac{{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right){\tau }_{k}}{\chi \left(1+i{\omega }_{n}{\tau }_{k}\right)}\right]\mathrm{sin}\left(m\theta \right)\mathrm{sin}\left({\beta }_{k}x\right)= -\frac{{\Delta }_{E}}{\alpha }\frac{{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right){\tau }_{k}}{\chi \left(1+i{\omega }_{n}{\tau }_{k}\right)}\frac{x}{{R}^{2}}(1-{n}^{2}){U}_{n}\mathrm{sin}\left(n\theta \right).$$
(21)

Multiplying above equation by \(\mathrm{sin}\left(n\theta \right)\mathrm{sin}\left({\beta }_{j}x\right)\), integrating the outcome in the range \(x=-h/2\) to \(x=+h/2\) and \(\theta =0\) to \(\theta =2\pi\), and using the orthogonality property of trigonometric functions, one can attain the coefficient \({A}_{jn}\) as follows:

$${A}_{jn}=\frac{{\Delta }_{E}}{\alpha }\left(1-{n}^{2}\right)\frac{{U}_{n}}{{R}^{2}h}\frac{4{\left(-1\right)}^{j+1}}{{\beta }_{j}^{2}}\frac{{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)-\left(1+{\lambda }_{jn}^{2}\right)\left(1+i{\omega }_{n}{\tau }_{k}\right)},$$
(22)

with

$${\tau }_{j}=\frac{1}{\chi {\beta }_{j}^{2}},$$
(23a)
$${\lambda }_{jn}=\frac{n}{{\beta }_{j}R}=\frac{n}{\left(2j-1\right)\pi }\frac{h}{R}.$$
(23b)

Inserting Eqs. (20) and (22) into Eq. (19), temperature distribution in the ring can be expressed via the following relation:

$${T}_{0}=$$
$$\frac{{\Delta }_{E}}{\alpha } \sum\limits_{j=0}^{\infty } \sum\limits_{n=0}^{\infty }\left(1-{n}^{2}\right)\frac{{U}_{n}h}{{R}^{2}}\frac{4{\left(-1\right)}^{j+1}}{{{\pi }^{2}\left(2j-1\right)}^{2}}\frac{{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)-\left(1+{\lambda }_{jn}^{2}\right)\left(1+i{\omega }_{n}{\tau }_{k}\right)}\mathrm{sin}\left(n\theta \right)\mathrm{sin}\left({\beta }_{j}x\right).$$
(24)

3 Approximating the amount of couple stress-based TED through energy dissipation method

Based on the modified couple stress theory (MCST) developed by Yang et al. [17], the total strain energy \(U\) of an isotropic elastic body occupying region \(\Omega\) in the space is computed by:

$$U=\frac{1}{2}{\iiint }_{\Omega }\left({\sigma }_{ij}{\varepsilon }_{ij}+{m}_{ij}{\gamma }_{ij}^{s}\right)d\Omega .$$
(25)

Here, variables \({\sigma }_{ij}\) and \({m}_{ij}\) define the components of the Cauchy stress tensor \({\varvec{\sigma}}\) and deviatoric part of couple stress tensor \(m\), respectively. Parameters \({\varepsilon }_{ij}\) and \({\gamma }_{ij}^{s}\) are also the components of strain tensor \({\varvec{\varepsilon}}\) and the symmetric part of rotation gradient tensor \({{\varvec{\gamma}}}^{s}\), respectively. The components \({\gamma }_{ij}^{s}\) are calculated via the following relation [17]:

$${\gamma }_{ij}^{s}=\frac{1}{2}\left(\frac{\partial {\phi }_{i}}{\partial {x}_{j}}+\frac{\partial {\phi }_{j}}{\partial {x}_{i}}\right) with {\phi }_{i}=\frac{1}{2}{\left(curl\left({\varvec{u}}\right)\right)}_{i}=\frac{1}{2}\nabla \times {\varvec{u}},$$
(26)

in which \({\varvec{u}}\) denotes the displacement vector. The higher-order constitutive relations within the framework of MCST are expressed by [17]:

$${m}_{ij}=2\mu {l}^{2}{\gamma }_{ij}^{s},$$
(27)

where \(l\) illustrates the characteristic length of MCST. Additionally, material constant \(\mu\) is the shear modulus calculated by \(\mu =E/2\left(1+\nu \right)\).

Use of Eqs. (2) and (3) yields:

$${\sigma }_{\theta \theta }=-\frac{Ex}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)-E\alpha T.$$
(28)

Furthermore, substituting Eq. (1) into Eq. (26) and considering the inextensionality condition of the ring (that is \(u=-\partial v/\partial \theta\)), one can achieve the relation below:

$${\gamma }_{\theta z}^{s}={\gamma }_{z\theta }^{s}=-\frac{1}{2{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right).$$
(29)

Substitution of above equation into Eq. (27) gives:

$${m}_{\theta z}={m}_{z\theta }=-\mu \frac{{l}^{2}}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right).$$
(30)

Within the scope of energy dissipation (ED) method, TED value is given by the following relation [58, 59]:

$${Q}_{TED}^{-1}=\frac{1}{2\pi }\frac{\Delta U}{{U}_{max}},$$
(31)

where \(\Delta U\) and \({U}_{max}\) denote the energy dissipation due to thermoelastic coupling and the peak value of strain energy per cycle of oscillation, respectively. In general, the mentioned variables are calculated through the following relationships [60]:

$$\Delta U=-\pi {\iiint }_{\Omega }{\widehat{\sigma }}_{ij}Im\left({\widehat{\varepsilon }}_{ij}^{th}\right)d\Omega ,$$
(32a)
$${U}_{max}=\frac{1}{2}{\iiint }_{\Omega }\left({\widehat{\sigma }}_{ij}{\widehat{\varepsilon }}_{ij}+{\widehat{m}}_{ij}{\widehat{\gamma }}_{ij}^{s}\right)d\Omega ,$$
(32b)

in which the hat symbol represents the maximum value in a cycle of vibration. In addition, \(Im\left({\varepsilon }_{ij}^{th}\right)\) stands for the imaginary part of thermal strain. For a ring, Eqs. (32a) and (32b) take the following forms:

$$\Delta U=-\pi {\iiint }_{\Omega }{\widehat{\sigma }}_{\theta \theta }Im\left({\widehat{\varepsilon }}_{\theta \theta }^{th}\right)d\Omega ,$$
(33a)
$${U}_{max}=\frac{1}{2}{\iiint }_{\Omega }\left({\widehat{\sigma }}_{\theta \theta }{\widehat{\varepsilon }}_{\theta \theta }+{\widehat{m}}_{\theta z}{\widehat{\gamma }}_{\theta z}^{s}+{\widehat{m}}_{z\theta }{\widehat{\gamma }}_{z\theta }^{s}\right)d\Omega .$$
(33b)

Inserting Eqs. (13a) and (13b) into Eqs. (2), (28), (29) and (30), and disregarding thermal stress due to its slight value, one can get:

$${\widehat{\varepsilon }}_{\theta \theta }=-\frac{x}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}\mathrm{sin}\left(n\theta \right)\, and\, {\widehat{\sigma }}_{\theta \theta }=-\frac{Ex}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}\mathrm{sin}\left(n\theta \right),$$
(34a)
$${\widehat{\gamma }}_{\theta z}^{s}={\widehat{\gamma }}_{z\theta }^{s}=-\frac{1}{2{R}^{2}}\left(1-{n}^{2}\right){U}_{n}\mathrm{sin}\left(n\theta \right)\, and\, {\widehat{m}}_{\theta z}={\widehat{m}}_{z\theta }=-\mu \frac{{l}^{2}}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}\mathrm{sin}\left(n\theta \right).$$
(34b)

Additionally, separating the real and imaginary parts of \({T}_{0}\) in Eq. (24), the relation below can be obtained:

$$Im\left({\widehat{\varepsilon }}_{\theta \theta }^{th}\right)=Im\left(\alpha {T}_{0}\right)=$$
$$\frac{{\Delta }_{E}}{\alpha }\frac{{U}_{n}}{h}\left(1-{n}^{2}\right)\mathrm{sin}\left(n\theta \right) \sum\limits_{j=1}^{\infty }\frac{4{\left(-1\right)}^{j+1}}{{R}^{2}{\beta }_{j}^{2}}\frac{\left(1+{\lambda }_{jn}^{2}\right){\tau }_{j}{\tau }_{k}\left({\tau }_{k}-\tau \right){\omega }_{n}^{3}}{{\left(1+{\lambda }_{jn}^{2}-{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\lambda }_{jn}^{2}\right){\tau }_{k}{\omega }_{n}-{\tau }_{j}{\tau }_{k}\tau {\omega }_{n}^{3}\right]}^{2}}\mathrm{sin}\left({\beta }_{j}x\right).$$
(35)

In rectangular cross-sectional rings, the relation \(d\Omega =b.\left(R+x\right)d\theta .dx\) is established. Therefore, since in thin rings we have \(R\gg x\), the following approximation is valid:

$$d\Omega \approx b.Rd\theta .dx.$$
(36)

Substitution of Eqs. (34a), (35) and (36) into Eq. (33a) and integration in the range of \(-h/2\le x\le h/2\) and \(0\le \theta <2\pi\) gives:

$$\Delta U={\Delta }_{E}{\pi }^{2}E\frac{8b{U}_{n}^{2}}{h{R}^{3}}{\left(1-{n}^{2}\right)}^{2} \sum\limits_{j=1}^{\infty }\frac{1}{{\beta }_{j}^{4}}\frac{\left(1+{\lambda }_{jn}^{2}\right){\tau }_{j}{\tau }_{k}\left({\tau }_{k}-\tau \right){\omega }_{n}^{3}}{{\left(1+{\lambda }_{jn}^{2}-{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\lambda }_{jn}^{2}\right){\tau }_{k}{\omega }_{n}-{\tau }_{j}{\tau }_{k}\tau {\omega }_{n}^{3}\right]}^{2}}.$$
(37)

Moreover, placing Eqs. (34a), (34b) and (36) into Eq. (33b) and integrating the result over \(-h/2\le x\le h/2\) and \(0\le \theta <2\pi\), one can attain the relation below:

$${U}_{max}=\left[1+12\left(\frac{\mu }{E}\right){\left(\frac{l}{h}\right)}^{2}\right]\frac{\pi Eb{h}^{3}}{24{R}^{3}}{\left(1-{n}^{2}\right)}^{2}{U}_{n}^{2}.$$
(38)

Given that \(\mu =E/2\left(1+\nu \right)\), Eq. (38) can be written in the following form:

$${U}_{max}=\left[1+\frac{6}{1+\nu }{\left(\frac{l}{h}\right)}^{2}\right]\frac{\pi Eb{h}^{3}}{24{R}^{3}}{\left(1-{n}^{2}\right)}^{2}{U}_{n}^{2}.$$
(39)

Inserting Eqs. (37) and (39) into Eq. (31), one can achieve the relation below for estimation of TED value in rings with rectangular cross section according to MCST and 2D MGT heat equation:

$${Q}_{TED}^{-1}={\Delta }_{E} \sum\limits_{j=1}^{\infty }{W}_{j}\frac{1}{1+\frac{6}{1+\nu }{\left(\frac{l}{h}\right)}^{2}}\frac{\left(1+{\lambda }_{jn}^{2}\right){\tau }_{j}{\tau }_{k}\left({\tau }_{k}-\tau \right){\omega }_{n}^{3}}{{\left(1+{\lambda }_{jn}^{2}-{\tau }_{j}{\tau }_{k}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\lambda }_{jn}^{2}\right){\tau }_{k}{\omega }_{n}-{\tau }_{j}{\tau }_{k}\tau {\omega }_{n}^{3}\right]}^{2}},$$
(40)

in which the weighting factor \({W}_{j}\) is calculated by:

$${W}_{j}=\frac{96}{{\pi }^{4}{\left(2j-1\right)}^{4}}.$$
(41)

It is worth noting that to arrive at the relation of TED according to CCT, the characteristic length \(l\) must be set to zero. Moreover, in SPL model, the value of \({k}^{*}\) is equal to zero, which according to Eq. (11b) is mathematically equivalent to \({\tau }_{k}\simeq \infty\). Considering these two cases (i.e., \(l=0\) and \({\tau }_{k}\simeq \infty\)) in Eq. (40) and simplifying it, the relation derived in this article is reduced to that reported in the research of Zhou et al. [43], which has been performed in the framework of CCT and SPL model. Additionally, putting \(l=0\), \(\tau =0\) and \({\tau }_{k}\simeq \infty\) in Eq. (40), a relation is obtained that corresponds to that extracted by Fang and Li [42] in the context of CCT and the Fourier model.

Another point that should be mentioned here is that in 1D model of heat conduction, temperature changes in peripheral direction are ignored. Therefore, according to Eq. (18), one can write \({\nabla }^{2}{T}_{0}={\partial }^{2}{T}_{0}/\partial {x}^{2}\). In this way, based on the solution obtained for temperature distribution in Eq. (24), to reach the TED relation in 1D heat conduction model, the terms including \({n}^{2}\) (and in other words, the terms including \({\lambda }_{jn}^{2}\)) should be eliminated from Eq. (40).

4 Validation, numerical examples and discussion

In this section, first, by conducting a comparative study, the validity and accuracy of the developed formulation are examined. For this purpose, the results of this work in specific situations are compared with those published by Zhou et al. [43]. Thus, to make such a comparison, parameters \(l\) and \({k}^{*}\) in the model provided in this article should be omitted. The properties of the studied material at the reference temperature \({T}_{a}=300 K\) are as follows: \(E=160 GPa\), \(\rho =2300 kg/{m}^{3}\), \(\rho {c}_{v}=1.6*{10}^{6} J/{m}^{3}K\), \(k=150 W/mK\), \(\alpha =2.6*{10}^{-6} 1/K\) and \(\tau =4.04 ps\). In Fig. 2, TED versus geometrical ratio \(h/R\) based on the formulation provided by Zhou et al. [43], as well as the formulation derived in this research is displayed. The curves are plotted for a ring with radial thickness \(h=1 \mu m\) and mode number \(n=20\). Considering the perfect compatibility of results extracted from the model presented in the current research with those reported by Zhou et al. [43], it can be concluded that the formulation derived in the framework of MGT model is authoritative.

Fig. 2
figure 2

Validation study by comparing the results of this research with the ones available in the literature

Full size image

In the rest of this section, various graphical data are provided to ascertain the relationship between TED value and nonclassical constants in MCST and MGT model. Apart from the cases in which the role of the type of ring material in TED alterations is investigated, other results are extracted for a gold ring at \({T}_{a}=300 K\). Material constants of gold (Au), silicon (Si) and copper (Cu) at this temperature are given in Table 1 [61, 62]. For different amounts of characteristic length \(l\), the variations of TED according to 2D model with radial thickness \(h\) are illustrated in Fig. 3. To extract these curves, vibration mode number \(n\) is considered equal to 2. Moreover, Figs. 3a, b are drawn for geometrical ratios \(R/h=20\) and \(R/h=100\), respectively. As it is clear, in case \(n=2\), MCST estimates a higher value than CCT for TED. In addition, for larger values of characteristic length \(l\), a greater amount of TED is predicted. This is because with the inclusion of higher-order kinematic variables and stresses in MCST, the amount of energy stored in the system ascends and hence the ratio of wasted thermal energy to strain energy of the system is reduced. It is also evident in both Figs. 3a, b that when the radial thickness of ring enlarges, the estimations of MCST become closer and closer to the predictions of CCT. This outcome is due to the fact that as the dimensions of ring become greater, the size effect gradually disappears.

Table 1 Material constants of gold (Au), silicon (Si) and copper (Cu) at reference temperature \({T}_{a}=300 K\) [61, 62]
Full size table
Fig. 3
figure 3

Effect of characteristic length \(l\) on TED value as a function of the ring thickness \(h\) in vibration mode \(n=2\) a \(R/h=20\) b \(R/h=100\)

Full size image

Figure 4 is depicted under the assumptions of Fig. 3, with the only difference that \(n=100\) is considered. As can be seen, with the increase of vibration mode number \(n\) compared to Fig. 3 (i.e., case \(n=2\)), the impact of characteristic length \(l\) on TED value alters absolutely, so that by increasing the value of \(l\), the amount of TED declines. Of course, in this figure, as in Fig. 3, it is evident that with the increase in radial thickness \(h\), the impact of size and subsequently the difference between the results of MCST and CCT diminishes. In the case of \(n=100\), unlike the case of \(n=2\), TED graph is not completely ascending in terms of \(h\), and the maximum value of TED occurs at a thickness known as the critical thickness, which is a key factor in the optimal design of small-sized basic mechanical elements.

Fig. 4
figure 4

Effect of characteristic length \(l\) on TED value as a function of the ring thickness \(h\) in vibration mode \(n=100\) a \(R/h=20\) b \(R/h=100\)

Full size image

In Fig. 5, by assuming \(R/h=20\), TED calculated based on 1D and 2D models versus vibration mode number \(n\) is shown for different values of characteristic length \(l\). Figures 5a, b is plotted for thicknesses \(h=1 \mu m\) and \(h=10 \mu m\), respectively. According to the curves of Fig. 5, the peak value of TED occurs in a vibration mode located in the middle of the interval under investigation (i.e., \(2\le n\le 1000\)). This outcome can be justified by this fact that the temperature across the thickness of ring reaches equilibrium in a characteristic time \({t}_{eq}\). At small vibration modes which are equivalent to low frequencies, we have \({t}_{eq}\ll {\omega }_{n}^{-1}\). In this case, since the oscillation period is long enough, the vibrating structure is in isothermal state and remains in equilibrium. Thus, the value of energy dissipation is little. At large vibration modes or high frequencies (i.e., in the case \({t}_{eq}\gg {\omega }_{n}^{-1}\)), a period of vibration takes a small amount of time, and the system has not adequate time to relax. Consequently, similar to the case \({t}_{eq}\ll {\omega }_{n}^{-1}\), a negligible value of thermal energy is wasted. Hence, the peak value of energy loss or TED takes place in the case \({t}_{eq}\cong {\omega }_{n}^{-1}\), corresponding to vibration modes that are neither too large nor too small. These curves also corroborate that the influence of characteristic length \(l\) on TED is deeply dependent on the vibration mode number \(n\), so that in low mode numbers, for larger magnitudes of \(l\), a higher TED value is estimated, while in higher mode numbers, as \(l\) enlarges, the amount of TED abates. Another point that is evident in these curves is that as the value of \(l\) gets greater, the peak value of TED happens at a lower mode number. It is also manifest that in low mode numbers, the difference between predictions of 1D and 2D models is trifling, but by increasing \(n\), this difference grows and TED value computed by 2D model becomes higher than that anticipated by 1D model.

Fig. 5
figure 5

Impact of characteristic length \(l\) on 1D and 2D TED value as a function of vibration mode \(n\) in a ring with geometrical ratio \(R/h=20\) a \(h=1 \mu m\) b \(h=10 \mu m\)

Full size image

The graphs in Fig. 6 are drawn with the same conditions as Fig. 5, with the only difference being that the ratio \(R/h\) is supposed to be equal to 100. Compared to Fig. 5, it can be seen that with the increase of the ratio \(R/h\), the peak value of TED emerges in a higher mode number. Besides, the results of 1D and 2D models are almost identical in a wider range of vibration mode numbers. Also, the comparison of Figs. 6a, b indicates that with the increase in the dimensions of ring, the impact of characteristic length \(l\) on TED weakens, so that the difference between the results of MCST and CCT is conspicuously reduced.

Fig. 6
figure 6

Impact of characteristic length \(l\) on 1D and 2D TED value as a function of vibration mode \(n\) in a ring with geometrical ratio \(R/h=100\) a \(h=1 \mu m\) b \(h=10 \mu m\)

Full size image

For a ring with specifications \(l=1 \mu m\) and \(R/h=20\), Fig. 7 displays the alterations of TED with respect to the vibration mode number in the framework of GN-III and MGT models. It is to be noted that Figs. 7a, b are drawn with the assumption of \(h=1 \mu m\) and \(h=10 \mu m\), respectively. According to these curves, in lower mode numbers, the two mentioned models have almost equal estimates of TED, but in higher mode numbers, GN-III model predicts a larger amount for TED than MGT model. The physical interpretation of this result can be that the propagation speed of thermal signals in GN-III model is higher than that in MGT model. Accordingly, heat generated by the nonuniform stress distribution in the context of MGT model has less time to propagate per cycle, which lessens energy loss induced by thermoelastic damping mechanism. In this way, TED value predicted by MGT model is lower than that anticipated by GN-III model. It is also obvious that TED value obtained from 2D model is higher than that estimated by 1D model. The only difference between Fig. 8 and Fig. 7 is that it is drawn for a ring with a geometrical ratio of \(R/h=100\). As it is apparent, in this case as well, with the increase in vibration mode number, the discrepancy between the results of GN-III and MGT models intensifies. In addition, it is clear that as the size of the ring in Fig. 8b becomes larger compared to Fig. 8a, the difference between the predictions of GN-III and MGT models exhibits a noticeable reduction, which emanates from the diminution in size effect.

Fig. 7
figure 7

Comparison of predictions of GN-III and MGT models for variations of TED changes with respect to vibration mode with the assumption of \(l=1 \mu m\) and a ring with a geometric ratio of \(R/h=20\) a \(h=1 \mu m\) b \(h=10 \mu m\)

Full size image
Fig. 8
figure 8

Comparison of predictions of GN-III and MGT models for variations of TED changes with respect to vibration mode with the assumption of \(l=1 \mu m\) and a ring with a geometric ratio of \(R/h=100\) a \(h=1 \mu m\) b \(h=10 \mu m\)

Full size image

Figure 9 is dedicated to investigating the extent and manner of the impact of the material of ring on TED in the context of 2D model. For this purpose, three materials gold (Au), silicon (Si) and copper (Cu) are considered. In this figure, TED as a function of dimensionless ratio \(h/l\) is shown. All the curves in Fig. 9 are extracted for a ring with thickness \(h=2 \mu m\). Besides, in Figs. 9a, b the vibration mode number \(n\) is considered equal to 2 and 100, respectively. Note that in these curves, increasing the ratio of \(h/l\) means decreasing the magnitude of characteristic length \(l\). Hence, Fig. 9a reveals that by decreasing the amount of \(l\), TED value tapers off for all three studied substances. Therefore, in the vibration mode number \(n=2\), including the effect of couple stress in governing equations heightens TED value in all three materials. It can also be observed that in this mode number, the highest amount of TED occurs in Cu-ring and the lowest in Au-ring, although to meticulously compare the amount of TED, it is needful to know the real value of characteristic length \(l\) for each of these materials. It is also manifest in this figure that with the increase of ratio \(h/l\), the small-scale effect gradually shrinks and TED value converges to the estimation of CCT. Figure 9b again signifies that in high vibration modes, the impact of MCST on TED value changes completely, so that the magnitude of TED ascends with the increase of ratio \(h/l\) or the decrease of the value of \(l\). In this figure, it is also clear that to compare the influence of material on the amount of TED (especially for Au and Cu), the actual amount of \(l\) for these materials should be available.

Fig. 9
figure 9

Effect of the material of the ring on the amount of TED in it based on 2D model for a ring with thickness \(h=2 \mu m\) a \(n=2\) b \(n=100\)

Full size image

By adopting the 1D model formulation, Fig. 10 is depicted with the same conditions as Fig. 9. In Fig. 10a, b, the vibration mode number \(n\) is assumed to be 2 and 100, respectively. As can be seen, the curves in Fig. 10 are qualitatively similar to the curves in Fig. 9, and the only difference is that the predicted value of TED in 2D model is higher than that in 1D model (especially in the case of \(n=100\)). Furthermore, it is evident that in the case of \(R/h=100\), because the ring has a larger size than in the case of \(R/h=20\), the impact of size fades in smaller ratios \(h/l\), and the results of MCST converge to those of CCT sooner.

Fig. 10
figure 10

Effect of the material of the ring on the amount of TED in it based on 1D model for a ring with thickness \(h=2 \mu m\) a \(n=2\) b \(n=100\)

Full size image

5 Concluding remarks

In the present research, by incorporating scale effect into both mechanical and thermal scopes, a novel size-dependent formulation has been derived to scrutinize thermoelastic damping (TED) in microring resonators with rectangular cross section. At the first step, the nonclassical constitutive relations and heat equation have been obtained in the purview of modified couple stress theory (MCST) and Moore–Gibson–Thompson (MGT) heat transfer model. By solving heat equation and extracting the fluctuation temperature, the relations of wasted thermal energy and maximum stored elastic energy have been provided. With the help of the relationship defined for TED in the energy dissipation (ED) method, a mathematical formula encompassing the nonclassical parameters of MCST and MGT model has been prepared to determine the amount of TED. Comparing the outcomes of present model with those published in the literature in the framework of simpler models, the validation study has been accomplished. Providing a diverse set of examples, the relationship between TED and some factors such as nonclassical parameters of MCST and MGT model, vibration mode number, 1D and 2D models of heat conduction, geometrical parameters and material value have been clarified. Based on these examples, the following can be enumerated as the key findings of this article:

  • Characteristic length of MCST can have a dual effect on TED, in such a way that it augments TED in low vibration modes and attenuates it in high vibration modes.

  • While the discrepancy between the outputs of 1D and 2D models is trifling in low vibration modes, TED value predicted by 2D model is noticeably higher than that computed by 1D model in high vibration modes.

  • In low vibration modes, the prediction of MGT model for TED value is slightly higher than that of GN-III model, but in high vibration modes, the amount of TED obtained by GN-III model is much higher than that estimated by MGT model.

  • By increasing the dimensions of the ring, the influence of both MCST and MGT model on the magnitude of TED wanes and the results obtained in the framework of the provided formulation converge to those of the classical model.

  • To favorably compare the amount of TED in investigated rings in this study (i.e., gold, silicon and copper), one should know the real value of characteristic length of each material. In addition, in the vibration mode \(n=2\) (\(n=100\)), MCST has an increasing (decreasing) impact on TED value in all three of these materials.