1 Introduction

A ring structure can be a general form to apply for modern MEMS/NEMS devices such as resonator, sensor, etc. And the model is topologically reliable and stable, furthermore the eigenfrequency is much higher than a beam. Additionally, it is easy to manufacture just by bending a micro/nanowire and sticking both ends together with few restriction of the cross-sectional shape. Especially, the long and thin material model with circular-cross-section that forms the source of toroidal ring is easy to obtain. Up to now, (Tao et al. 2011) developed a gyroscope ring model including the piezoelectric effect. Furthermore, (Pauzauskie et al. 2006) represented the triangular-cross-sectional nanowire ring resonator. (Gu et al. 2015) also introduced hybrid plasmonic pseudo-ring resonators by bending a linear wire structure. (Senkal et al. 2014) performed experimental work for an epitaxial silicon encapsulated toroidal ring gyroscope model. (Sederberg et al. 2011) experimentally proved the possibility of the design a plasmonic nano-silicon-ring resonator for optical switching application. In this regard, the toroidal ring for MEMS/NEMS has excellent development potential in the near future.

The thermoelastic dissipation (TED) is one of representative intrinsic damping due to the intermolecular friction heat during the repetitive motion, and is a function of the frequency, temperature, and some other thermal characteristics. While, the attenuation is difficult to control rather than the external-environmental-cause damping mechanisms. (Kim et al. 2010) To ensure the efficiency of the structure as higher quality factor (Q-factor; Q), the TED should be investigated by the classical molecule-scale heat-conduction model. Numerous researchers have studied the dissipation in order to ensure the high-efficiency such as: (Zener 1937) suggested the dissipation as a function of the natural frequency in a yardstick. (Lifshitz and Roukes 2000) proposed the micro-beam model to present the TED effect. Wong et al. (2004),(2006) extended the dissipation mechanism into the micro-ring models using the beam Zener (1937); Lifshitz and Roukes (2000). Li et al. (2016) analyzed the dissipation of the circular-cross-sectional ring structure (Razavilar et al. 2016) presented the TED in a microplate resonator based on the modified plane stress and strain theories. Moreover, Kim and Kim researched the rings with TED for circular- Kim and Kim (2018) cross-section including point masses.

Particularly in the nano-scale, the efficiency can be higher in the ultralow temperature or ultrahigh frequency vibration. For example, the modern devices such as a superconductor or space developments should be designed and analyzed in these extreme environments. Practically, the slow heat flux cannot overcome the fast vibration, thus the delay of the flux occurs in the small structure. In the cryogenic or nano-scaled characteristics, the single-phase-lagging (SPL) can be defined as the time deviation. And thus the delay cannot be investigated by using only the classical principle of Fourier’s heat conduction. Therefore, the thermoelastic attenuation characteristics due to the lagging time are different from classical models should be represented in detail. Moreover, the properties are essential for analysis of NEMS structures which can be applied into mechanical signal processing, ultrasensitive mass detection, or injection probe microscopes, etc. Then, the SPL is a crucial complement to the limitations, and a lot of researches have been continued such as: (Cattaneo 1958) and (Vernotte 1958) independently proposed a model well known as the "CV equation" or “non-Fourier (nF)” to supplement the limitations of the literature using the previous Fourier’s equation. Especially, Lord and Shulman (Lord and Shulman 1967) concretized the CV heat conduction equation for the elastic medium known as “LS” model. (Vitokhin and Ivanova 2017) Moreover, (Khisaeva and Ostoja-Starzewski 2006) examined the damping mechanism of the Euler–Bernoulli nanobeam model during the flexural vibration. (Sharma 2011) studied the vibration for a silicon beam including the frequency shift and dissipation induced by the phase-lagging time. Also, (Zhou and Li 2017) predicted the more accurate characteristics in micro/nano-beams with the TED based on the non-Fourier heat conduction theory. Zhou et al. organized the estimations of the dissipation of the beam with circular- (Zhou et al. 2018) and ring with rectangular- (Zhou et al. 2019) cross-sections, respectively. Moreover, (Kim and Kim 2019) extended the analysis of the dissipation for the cylindrical shell model with the lagging of the heat flux through the thickness direction.

In this work, the TED of the toroidal solid-ring model is investigated including SPL for the MEMS/NEMS structures. Primarily, the eigenfrequency of the ring is obtained during the in-plane and inextensional vibration behavior. Then, the dissipation effect is analyzed for the ring with the phase-lagging by the non-Fourier (nF) heat conduction equation. The 3-dimensional heat conduction is considered with the circular cross-sectional configuration of the model. Thus, the temperature profile is expressed in the analytical form using Bessel functions. Furthermore, quality factor (Q-factor) of the ring is obtained by maximum and dissipated energies in single cycle. Numerical data of Q are compared with the previous experimental literatures, and the temperature distributions are represented graphically. Finally, phase-lagging effect for the normalized cross-section is demonstrated as a function of the frequency and the delaying time.

2 Modeling of the toroidal ring

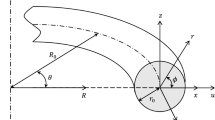
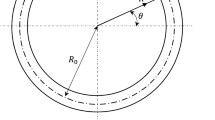
Figure 1 shows a toroidal circular solid ring model with mean radius \(R_{0}\), cross-sectional radius \(r_{0}\), radial coordinate \(x\), and tangential coordinate \(y\). (Li et al. 2016) Additionally, the global and local coordinates are designated as (\(R,\theta ,Z\)), and (\(x,y,z\)) with \(\beta\) as a local angle, respectively.

Fig. 1
figure 1

An imperfect toroidal-solid ring model

Full size image

2.1 Eigenfrequency of the structure

Generally, the ring is sufficiently thin as \(r_{0} \ll R_{0}\), thus Euler–Bernoulli beam model is suitable in this analysis. Additionally, the local distance from the neutral plane in the cross-section is \(\left| x \right| \le \sqrt {r_{o} ^{2} - z^{2} }\). Moreover, the ring is materially homogeneous, isotropic and uniform in the whole structure.

For the nth mode of the in-plane vibration, the shapes in the radial and circumferential directions can be defined as \(\left\{ {u\left( {\theta ,t} \right),v\left( {\theta ,t} \right)} \right\}\) = \(\left\{ {U_{n} \left( \theta \right),V_{n} \left( \theta \right)} \right\} \times \exp \left( {{\text{j}}\omega t} \right)\) = \(\left\{ {\hat{U}_{n} \sin \left( {n\theta } \right),\hat{V}_{n} \cos \left( {n\theta } \right)} \right\} \times \exp \left( {{\text{j}}\omega t} \right)\). In this work, the length of centerline remains constant during the motion known as “inextensional assumption” is introduced into the toroidal ring with \(U_{n} \left( \theta \right) = - \frac{{\partial V_{n} \left( \theta \right)}}{{\partial \theta }}\) and \(\hat{V}_{n} = - \frac{{\hat{U}_{n} }}{n}\) Li et al. (2016); Soedel and Qatu (2005). Thus, the eigenfrequency of the toroidal micro/nano-ring can be obtained as

$$\omega _{{n0}} = \sqrt {\frac{{EI}}{{\rho AR_{0} ^{4} }}\frac{{\left( {n^{2} - 1} \right)^{2} n^{2} }}{{n^{2} + 1}}}$$
(1)

where, \(I = 0.25\pi r_{0} ^{4}\) and \(A = \pi r_{0} ^{2}\) are the moment of inertia and cross-sectional area of a toroidal ring, respectively.

2.2 Non-Fourier heat conduction in 3-dimensional model

To overcome the paradox of infinite speed included in the classical Fourier’s approach of thermal conduction (Khisaeva and Ostoja-Starzewski 2006), the time derivative term should be considered in the general heat flux. Also, delay of the flux is much larger than that of temperature gradient, thus the phase-lagging is considered only into the flux vector. Furthermore, the temperature profile according to local z-axis as well as x-axis and circumferential direction should be considered because the boundary conditions are different from rectangular cross-section (Zhou et al. 2019). Thus, the 2D expression in Zhou et al. (2019) is not valid in this work, therefore the 3D modeling of the TED is suitable for the toroidal ring.

In order to obtain the temperature profile, the solution of the heat conduction model is assumed as (Li et al. 2016)

$$T\left( {R,Z,\theta ,t} \right) = \hat{T}\left( {R,Z,\theta ,t} \right) - \hat{T}_{a} = T_{0} \left( {R,Z,\theta } \right)\exp \left( {\tt j}\omega t \right)$$
(2)

where \(\hat{T}\), \(\hat{T}_{a}\), \({\text{j}}\), \(\omega\), and \(t\) are the instantaneous and ambient temperatures, \(\sqrt { - 1}\), frequency, and time, respectively.

When the temperature deviation is small enough, the coupled heat conduction equation during the relaxation for a single-phase-lag thermoelastic structure, known as Lord-Shulman (LS) model, including the lagging time of heat flux vector \({\tau }_{\mathrm{Q}}\) is (Khisaeva and Ostoja-Starzewski 2006):

$$\left( {1 + \tau _{Q} \frac{\partial }{{\partial t}}} \right) {\bf q} = - k\nabla T$$
(3)

where \(\bf \mathrm{q}\), \(k\), \(\nabla\), and \(T\) are the heat flux vector, constant thermal conductivity, gradient operator, and the absolute temperature, respectively.

Then, the coupled temperature distribution with the strains as in Wong et al. (2006); Kim and Kim (2019) are:

$$\nabla {\bf q} = - C_{v} \frac{{\partial T}}{{\partial t}} - \frac{{E\alpha \hat{T}_{a} }}{{1 - 2}v}\frac{{\partial \hat{e}}}{{\partial t}}$$
(4)

where \(E\), \(\alpha\), \(C_{v}\), \(v\), \(\hat{e} = \varepsilon _{\theta } + \varepsilon _{R} + \varepsilon _{z}\), and \(\nabla ^{2} = \nabla \left( \nabla \right) = \frac{{\partial ^{2} }}{{\partial R^{2} }} + \frac{1}{R}\frac{\partial }{{\partial R}} + \frac{1}{{R^{2} }}\frac{{\partial ^{2} }}{{\partial \theta ^{2} }} + \frac{{\partial ^{2} }}{{\partial z^{2} }}\) are the Young’s modulus, thermal expansion coefficient, specific heat, Poisson’s ratio, cubic dilatation, and the Laplacian operator for the toroidal ring, respectively.

Thus, the coupled heat conduction equation with the lagging time \(\tau _{{\text{Q}}}\) depending on the material property is obtained as:

$$\left( {1 + \tau _{Q} \frac{\partial }{{\partial t}}} \right)\nabla {\bf q } = - k\nabla ^{2} T = \left( {1} + \tau _{Q} \frac{\partial }{{\partial t}} \right)\left( { - C_{v} \frac{{\partial T}}{{\partial t}} - \frac{{E\alpha \hat{T}_{a} }}{{1 - 2}} v\frac{{\partial \hat{e}}}{{\partial t}}} \right)$$
(5)

in here, \({C}_{v}\) and \(\frac{E\alpha {\widehat{T}}_{a}}{1-2v}\) are independent of time.

This equation can be re-arranged as:

$$\left[ {k\nabla ^{2} - C_{v} \left( {\frac{\partial }{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} }}{{\partial t^{2} }}} \right)} \right]T = \frac{{E\alpha \hat{T}_{a} }}{{1 - 2v}}\left( {\frac{\partial }{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} }}{{\partial t^{2} }}} \right)\hat{e}$$
(6)

On the other hand, the thermal strains are

$$\varepsilon _{\theta }^{{\tt thermal}} = \varepsilon _{R}^{{\tt thermal}} = \alpha T\left( {R,\theta ,z,t} \right)$$
(7)

Then using the stress (\(\sigma\))—strain (\(\varepsilon\)) relationships with the thermal effect, components of \(\widehat{e}\) can be written as:

$$\varepsilon _{\theta } = \frac{{\sigma _{\theta } }}{E} + \varepsilon _{\theta }^{{\tt thermal}}$$
(8)
$$\varepsilon _{R} = \varepsilon _{z} = - \frac{{v\sigma _{\theta } }}{E} + \varepsilon _{R}^{{\tt thermal}}$$
(9)

Also, the strain is proportional to \(x\) for the ring, then the inextensional assumption can be adopted into Love’s shell theory. (Soedel and Qatu 2005) For this way, the circumferential strain for in-plane vibration can be obtained as (Wong et al. 2004):

$$\varepsilon _{\theta } = - \frac{x}{{R_{0} ^{2} }}\left( {\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} + u} \right)$$
(10)

Then, the stress \({\sigma }_{\theta }\) including thermal effect is

$$\sigma _{\theta } = - \frac{{Ex}}{{R_{0} ^{2} }}\left( {\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} + u} \right) - \alpha ET$$
(11)

Using Eqs. (7) to (11), the Eq. (6) can be reduced with \(\Delta _{E} = \frac{{E\alpha ^{2} \hat{T}_{a} }}{{C_{v} }} \ll 1\) as:

$$\chi \nabla ^{2} T - \left( {\frac{{\partial T}}{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} T}}{{\partial t^{2} }}} \right) = - \frac{{\Delta _{E} }}{\alpha }\left( {\frac{\partial }{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} }}{{\partial t^{2} }}} \right)\left[ {\frac{x}{{R_{0} ^{2} }}\left( {\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} + u} \right)} \right]$$
(12)

in here, \(\chi = \frac{k}{{C_{v} }}\) is the thermal diffusivity, and \(\Delta _{E}\) is relaxation strength of elastic modulus.

Applying the Laplacian, \(R = R_{0} + x\) for the thin ring, and the Cartesian coordinate \(\left( {x,z} \right)\) can be transformed into the local polar coordinate \(\left( {r,\beta } \right)\) to present the temperature profile in the circular cross-section as (Li et al. 2016).

$$\left\{ {\begin{array}{*{20}c} x \\ z \\ \end{array} } \right\} = r \times \left\{ {\begin{array}{*{20}c} {\sin \left( \beta \right)} \\ {\cos \left( \beta \right)} \\ \end{array} } \right\}$$
(13)

Then, Eq. (12) can be written using the method (Li et al. 2016) with the local polar coordinate as:

$$\chi \left( {\frac{{\partial ^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T}}{{\partial r}} + \frac{1}{r}\frac{{\partial ^{2} T}}{{\partial \beta ^{2} }} + \frac{1}{{R_{0} ^{2} }}\frac{{\partial ^{2} T}}{{\partial \theta ^{2} }}} \right) - \left( {\frac{{\partial T}}{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} T}}{{\partial t^{2} }}} \right) = - \frac{{\Delta _{E} }}{\alpha }\left( {\frac{\partial }{{\partial t}} + \tau _{Q} \frac{{\partial ^{2} }}{{\partial t^{2} }}} \right)\left[ {\frac{{r\sin \left( \beta \right)}}{{R_{0} ^{2} }}\left( {\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} + u} \right)} \right]$$
(14)

2.3 Temperature profile including the TED effect in the ring model

In order to present the TED, the temperature profile using Cartesian coordinate \(\left( {R,Z} \right)\) in Eq. (2) is re-written by the local polar coordinates \(\left( {r,\beta } \right)\) as:

$$T = T\left( {r,\beta ,\theta ,t} \right) = T_{0} \left( {r,\beta ,\theta } \right)\exp \left( {\tt j} \omega t \right)$$
(15)

The boundary condition for adiabatic surface, and the continuity condition in the circumferential direction are \(\frac{{\partial T_{0} }}{{\partial r}} = 0\) at \(r = r_{0}\) and \(T_{0} \left( \theta \right) = T_{0} \left( {\theta + 2\pi } \right)\), respectively.

Using the Eq. (15) with \(\omega\), the differential equation is finally reduced as:

$$\chi \left( {\frac{{\partial ^{2} T_{0} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{0} }}{{\partial r}} + \frac{1}{r}\frac{{\partial ^{2} T_{0} }}{{\partial \beta ^{2} }} + \frac{1}{{R_{0} ^{2} }}\frac{{\partial ^{2} T_{0} }}{{\partial \theta ^{2} }}} \right) - \left( {\tt j} \omega - \tau _{Q} \omega ^{\tt 2} \right)T_{0} = - \left( {{\tt j} \omega - \tau _{Q} \omega ^{\tt 2} } \right)\frac{{\Delta _{E} }}{\alpha }\frac{{r\sin \left( \beta \right)}}{{R_{0} ^{2} }}\left( {1 - n^{2} } \right)\hat{U}_{n} \sin \left( {n\theta } \right)$$
(16)

Using the kth order Bessel function of first kind \({J}_{k}\), the temperature profile can be defined as (Li et al. 2016):

$$T_{0} \left( {r,\beta ,\theta } \right) = \mathop \sum \limits_{{m = 0}}^{{\inf }} \mathop \sum \limits_{{k = 0}}^{{\inf }} \mathop \sum \limits_{{~q = 1}}^{{\inf }} J_{k} \left( {\frac{{a_{{kq}} }}{{r_{0} }}r} \right)\left[ {A_{{kqm}} \sin \left( {k\beta } \right) + B_{{kqm}} \cos \left( {k\beta } \right)} \right]\sin \left( {m\theta } \right)$$
(17)

In here, \(a_{{kq}}\), \(A_{{kqm}}\), \(B_{{kqm}}\) are arbitrary numbers with \(q\) th thermal order.

Then, \({T}_{0}\) can be simplified using Eq. (16) with the boundary and continuous conditions as:

$$T_{0} \left( {r,\beta ,\theta } \right) = \mathop \sum \limits_{{m = 0}}^{{\inf }} \mathop \sum \limits_{{q = 1}}^{{\inf }} J_{1} \left( {\frac{{a_{{1q}} }}{{r_{0} }}r} \right)\left[ {C_{{qm}} \sin \left( \beta \right)} \right]\sin \left( {m\theta } \right)$$
(18)

in here, \(C_{{qm}} = A_{{1qm}}\) is obtained from \(A_{{kqm}}\) for only \(k = 1\), otherwise all \(A_{{kqm}}\) and \(B_{{kqm}}\) can be zero. The methodologies can be similarly referred to Li et al. (2016) easily because the terms including \(\tau _{{\text{Q}}}\) are constant.

In this way, the \(a_{{1q}}\) can be obtained as (Li et al. 2016):

$$\frac{\partial }{{\partial r}}\left[ {J_{1} \left( {\frac{{a_{{1q}} }}{{r_{0} }}r} \right)} \right]_{{r = r_{0} }} = \frac{{a_{{1q}} }}{{2r_{0} }}\left[ {J_{0} \left( {a_{{1q}} } \right) - J_{2} \left( {a_{{1q}} } \right)} \right] = 0$$
(19)

and the results are presented in Table 1.

Table 1 Solutions for the Bessel Function (\(a_{{1q}}\)) in Eq. (19) and the contribution factors (\(b_{{1q}}\))
Full size table

Furthermore, the expressions \(C_{{qm}} = C_{{qn}}\) in the case of \(m=n\) can be obtained from the orthogonality of the Bessel function (Li et al. 2016) as:

$$C_{{qm}} = C_{{qn}} = \frac{{2r_{0} }}{{R_{0} ^{2} }}\frac{{\Delta _{E} \left( {1 - n^{2} } \right)\hat{U}_{n} }}{\alpha }\frac{1}{{\left( {a_{{1q}} ^{2} - 1} \right)J_{1} \left( {a_{{1q}} } \right)}}\frac{{\left( {{\tt j} \omega - \tau _{Q} \omega ^{\tt 2} } \right)\tau _{q} }}{{1 + \gamma ^{2} + \left( {{\tt j} \omega - \tau _{Q} \omega ^{\tt 2} } \right)\tau _{q} }}$$
(20)

Otherwise for \(m\ne n\), all results are zero.

In addition, the thermal relaxation time according to the local radius (Li et al. 2016) is

$$\tau _{q} = \frac{{r_{0} ^{2} }}{{\chi a_{{1q}} ^{2} }}$$
(21)

Moreover, \(\gamma \equiv \gamma \left( {a_{{1q}} ,n,r_{0} ,R_{0} } \right) = \frac{{nr_{0} }}{{a_{{1q}} R_{0} }}\) is a constant according to the heat conduction through the circumferential direction. In other words, \(\gamma\) is an additional attenuation in the 3D model (Li et al. 2016). Then, this work can illustrate the heat conduction along the circumferential direction based on the term \(\frac{1}{{R_{0} ^{2} }}\frac{{\partial ^{2} T_{0} }}{{\partial \theta ^{2} }}\), and also all results are exactly the same as (Li et al. 2016) except \(\tau _{{\text{Q}}}\).

Substituting Eqs. (20)–(21) into (18), the final form of the temperature profile is:

$$T_{0} \left( {r,\beta ,\theta } \right) = \frac{{2r_{0} }}{{R_{0} ^{2} }}\frac{{\Delta _{E} \left( {1 - n^{2} } \right)\hat{U}_{n} }}{\alpha }\sin \left( \beta \right)\sin \left( {n\theta } \right) \times \mathop \sum \limits_{{q = 1}}^{{\inf }} \left[ {\frac{{J_{1} \left( {\frac{{a_{{1q}} }}{{r_{0} }}r} \right)}}{{\left( {a_{{1q}} ^{2} - 1} \right)J_{1} \left( {a_{{1q}} } \right)}}\frac{{\left( {{\tt j} \omega - \tau _{Q} \omega ^{\tt 2} } \right)\tau _{q} }}{{1 + \gamma ^{2} + \left( {{\tt j}\omega - \tau _{Q} \omega ^{\tt 2} } \right)\tau _{q} }}} \right]$$
(22)

In here, the Real and Imaginary parts of \(T_{0} \left( {r,\beta ,\theta } \right)\) are

$$\left\{ {\begin{array}{*{20}c} {\text{Real} \left[ {T_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ {\text{Imag}\left[ {T_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ \end{array} } \right\} = \frac{{2r_{0} }}{{R_{0} ^{2} }}\frac{{\Delta _{E} \left( {1 - n^{2} } \right)\hat{U}_{n} }}{\alpha }\sin \left( \beta \right)\sin \left( {n\theta } \right) \times \mathop \sum \limits_{{q = 1}}^{{\inf }}\left[ {\frac{{J_{1} \left( {\frac{{a_{{1q}} }}{{r_{0} }}r} \right)}}{{\left( {a_{{1q}} ^{2} - 1} \right)J_{1} \left( {a_{{1q}} } \right)}}\frac{1}{{\left\{ {1 + \gamma ^{2} - \tau _{Q} \left( {\omega ^{2} \tau _{q} } \right)} \right\}^{2} + \left( {\omega \tau _{q} } \right)^{2} }} \times \left\{ {\begin{array}{*{20}c} {\Xi _{R} } \\ {\Xi _{I} } \\ \end{array} } \right\}} \right]$$
(23)

where \(\Xi_{R} = - \omega ^{2} \tau _{Q} \tau _{q} \left( {1 + \gamma ^{2} } \right) + \left( {\omega \tau _{q} } \right)^{2} \left\{ {1 + \left( {\omega \tau _{Q} } \right)^{2} } \right\}\) and \(\Xi_{I} = \left( {1 + \gamma ^{2} } \right)\omega \tau _{q}\).

Furthermore, the Q-factor is defined as the ratio of the maximum elastic energy \({W}_{\mathrm{m}\mathrm{a}\mathrm{x}}\) with respect to the energy loss during a single cycle \(\mathrm{\Delta }W\) as (Li et al. 2016):

$$\frac{1}{{Q_{{TED}} }} = \frac{1}{{2\pi }}\frac{{\Delta W}}{{W_{{\max }} }}$$
(24)

In here, the elements in the equation are:

$$W_{{\max }} = \frac{1}{2}\iiint_{{\tt vol}} {\sigma _{\theta } \varepsilon _{\theta } dV} = \frac{1}{2}\iiint_{{\tt vol}} {\sigma _{\theta } \varepsilon _{\theta } \left( {R_{0} + x} \right)dSd\theta }$$
(25)
$$\Delta W = - \pi \iiint_{{\tt vol}} {\sigma _{\theta } \text{Imag}\left[ {\varepsilon _{\theta }^{{\tt thermal}} } \right]dV} = - \pi \iiint_{{\tt vol}} {\sigma _{\theta } \text{Imag}\left[ {\alpha T_{0} } \right]dV}$$
(26)

where \({\text{d}}V\), \({\text{d}}S\), and \({\text{d}}\theta\) are the coefficients of the integral for small volume, surface area, and circumferential angle, respectively.

Also, the TED is sufficiently smaller than the strain and stress, then the simplified expressions are:

$$\varepsilon _{\theta } \approx \frac{{\sigma _{\theta } }}{E},\sigma _{\theta } \approx - \frac{{Ex}}{{R_{0} ^{2} }}\left( {\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} + u} \right)$$
(27)

Therefore, \(W_{{{\text{max}}}}\) and \(\Delta W\) are:

$${W_{\max }} = \int_{x = - {r_0}}^{x = + {r_0}} {\int_{z = - \sqrt {{r_0}^2 - {x^2}} }^{z = + \sqrt {{r_0}^2 - {x^2}} } {\int_{\theta = 0}^{\theta = 2\pi } {\left\{ {{\sigma _\theta }{\varepsilon _\theta }\left( {{R_0} + x} \right)} \right\}d\theta dzdx} } } = \frac{{\pi EI{R_0}}}{2}\left[ {\frac{{\left( {1 - {n^2}} \right){{\hat U}_n}}}{{{R_0}^2}}} \right]$$
(28)
$$\Delta W = - \pi \int_{{x = 0}}^{{x = r_{0} }} \int_{{\beta = 0}}^{{\beta = 2\pi }} \int_{{\theta = 0}}^{{\theta = 2\pi }} \left\{ {\sigma _{\theta } \text{Imag}\left[ {\alpha T_{0} } \right]} \right\}d\theta d\beta dx = \mathop \sum \limits_{{q = 1}}^{{\inf }}\left[ {2\pi \Delta _{E} \frac{8}{{a_{{1q}} ^{2} \left( {a_{{1q}} ^{2} - 1} \right)}}\frac{{\left( {1 + \gamma ^{2} } \right)\omega \tau _{q} }}{{\left\{ {1 + \gamma ^{2} - \tau _{Q} \left( {\omega ^{2} \tau _{q} } \right)} \right\}^{2} + \left( {\omega \tau _{q} } \right)^{2} }}} \right]$$
(29)

Inserting Eqs. (28) and (29) into Eq. (24), the expression of Q-factor can be re-written as:

$$\frac{1}{{Q_{{\tt TED}} }} = \mathop \sum \limits_{{q = 1}}^{{\inf }} \left[ {b_{{1q}} \Delta _{E} \frac{{\left( {1 + \gamma ^{2} } \right)\omega \tau _{q} }}{{\left\{ {1 + \gamma ^{2} - \tau _{Q} \left( {\omega ^{2} \tau _{q} } \right)} \right\}^{2} + \left( {\omega \tau _{q} } \right)^{2} }}} \right] \equiv \mathop \sum \limits_{{q = 1}}^{{\inf }} \frac{1}{{Q_{{{\tt TED}, q}} }}$$
(30)

with the contribution factor of \(q\) th thermal mode \(b_{{1q}} = \frac{8}{{a_{{1q}} ^{2} \left( {a_{{1q}} ^{2} - 1} \right)}}\).

Especially, \(b_{{11}} = 0.987 \approx 1\), and other \(b_{{1q}}\) s (\(q > 1\)) are much smaller than 1 (Li et al. 2016), thus the result can be simplified with only \(q = 1\) as:

$$\frac{1}{{Q_{{{\tt TED}, q = {\tt 1}}} }} = \Delta _{E} \frac{{\left( {1 + \gamma ^{2} } \right)\omega \tau _{1} }}{{\left\{ {1 + \gamma ^{2} - \tau _{Q} \left( {\omega ^{2} \tau _{1} } \right)} \right\}^{2} + \left( {\omega \tau _{1} } \right)^{2} }}$$
(31)

The result is exactly the same as (Li et al. 2016), when \({\tau }_{\mathrm{Q}}\) is zero for toroidal ring based on classical Fourier’s heat conduction model.

3 Numerical simulations and discussions

In this section, the results of the numerical studies are presented for a solid toroidal micro/nano-ring model with the TED effects. The contents are organized as: approximation and normalization by using asymptotic lines, verifications, numerical results for the ring model, and the temperature profiles including the time-lagging.

To consider the TED with non-Fourier heat conduction, single-phase-lag time \({\tau }_{\mathrm{Q}}\) is introduced for the material properties as (Khisaeva and Ostoja-Starzewski 2006)

$$\tau _{Q} = \frac{\chi }{{V_{C} ^{2} /3}} = \frac{\chi }{{\left( {V_{{\tt 2nd}} } \right)^{2} }}$$
(32)

In here, \(V_{C} = \sqrt {E/\rho }\) is the phonon velocity in the medium, well known as “ordinary” or “first” sound velocity. While, the “second” sound velocity \(V_{{2{\text{nd}}}}\) is the finite speed of the heat wave propagation. Additionally, \(V_{{\text{C}}}\) is the RMS value of the 3-dimensional phonon speed, thus \(V_{C} ^{2} = 3 \times \left( {V_{{2{\text{nd}}}} } \right)^{2}\) (Chester 1963). Interestingly, characteristics of both the normally hearable sound and the heat are the similar waves, then \(V_{{2{\text{nd}}}}\) can be considered as another acoustics. Also, this is the crucial difference between the CV’s (i.e. non-Fourier) and classical Fourier’s heat conduction models (Zhou and Li 2017). Moreover, \(\tau _{{\text{Q}}}\) is independent to any geometrical shape, unlike \(\tau _{q}\). Moreover, (Table 2) shows the data of phase-lagging time \(\tau _{{\text{Q}}}\) on NaF based on a curve-fitting from experiment (Kovács and Ván 2016), another method as “RET” (Kovács and Ván 2018), and Eq. (32). In the comparison, the result from Eq. (32) is well matched with existing works, thus the validity of the \(\tau _{{\text{Q}}}\) can be secured for this study.

Table 2 Data of phase-lagging time on NaF with T = 13 [K], E = 79 [GP] and \(\rho\) = 2866 [kg/\({\text{m}}^{3}\)]
Full size table

Table 3 shows the properties of the material under the various ambient temperatures of silicon (Sharma 2011), and the lagging time \({\tau }_{\mathrm{Q}}\) on 40[K] is about 370 times longer than the room temperature. In addition, the Poisson’s ratio \(v\) is 0.22 in all selected temperatures.

Table 3 Material properties of silicon for various temperatures. (Sharma 2011)
Full size table

Furthermore, in order to find the peak value of the \(\left( {Q_{{{\text{TED}}}} } \right)^{{ - 1}}\) with respect to the frequency, the differential expression can be written as:

$$\frac{\partial }{{\partial \omega }}\left( {Q_{{\tt TED}} } \right)^{{ - 1}} = 0$$
(33)

3.1 Asymptotic lines for normalized frequency and quality factor

To compare the TED in beam and previous ring models, the normalized frequency (i.e. \(\hat{\omega }_{{ peak, q}}\)) and peak value of \(\left( {Q_{{{\text{TED}}}} } \right)^{{ - 1}}\) (i.e. \(\left( {\hat{Q}_{{{\text{TED}},{\text{peak}}}} } \right)^{{ - 1}}\)) are introduced according to the non-dimensional lagging time \(\beta _{q} = \frac{{\tau _{{\text{Q}}} }}{{\tau _{q} }}\). Thus, the trends of the data can be simplified into the clear forms, then the easy prediction can be possible for the effect due to the lagging. In this regard, the frequencies of the peak for the [rad/sec] dimension \(\omega _{{{\text{peak}},q}}\) and normalized one \(\hat{\omega }_{{{\text{peak}},q}}\), respectively, are

$$\left( {\hat{\omega }_{{{\tt peak}, q}} } \right)^{2} = \left( {\omega _{{{\tt peak}, q}} \times \tau _{q} } \right)^{2} = \frac{1}{{\beta _{q} ^{2} }}\frac{{f\left( {\beta _{q} } \right)}}{6}$$
(34)

In here, the reasonable expression \(f\left( {\beta _{q} } \right)\) without meaningless negative sqrt term is:

$$f\left( {\beta _{q} } \right) = \left\{ {2\beta _{q} \left( {1 + \gamma ^{2} } \right) - 1} \right\} + \sqrt {\left\{ {2\beta _{q} \left( {1 + \gamma ^{2} } \right) - 1} \right\}^{2} + 12\left( {1 + \gamma ^{2} } \right)^{2} \beta _{q} ^{2} }$$
(35)

Using Eq. (34) into Eq. (30), thus

$$\frac{1}{{\hat{Q}_{{{\tt TED,peak}, q}} }} = \frac{1}{{\left(Q_{{{\tt TED,peak}, q}}\right) \times b_{{1q}} \Delta _{E} }} = \frac{{\beta _{q} \left( {1 + \gamma ^{2} } \right)\sqrt {6f\left( {\beta _{q} } \right)} }}{{6\left\{ {\left( {1 + \gamma ^{2} } \right)\beta _{q} - \frac{{f\left( {\beta _{q} } \right)}}{6}} \right\}^{2} + f\left( {\beta _{q} } \right)}}$$
(36)

In here, \(\left( {\hat{Q}_{{{\text{TED}},{\text{peak}},q}} } \right)^{{ - 1}}\) is no longer \(0.5\Delta _{E}\) Zhou and Li (2017); Zhou et al. (2018),(2019) due to the lagging time effect, rather than classical Fourier’s model Lifshitz and Roukes (2000); Wong et al. (2006). Also, in a sufficiently thin ring when \(\gamma\) is neglected, then the result without \(\gamma\) is equal to the cases of beams Zhou and Li (2017); Zhou et al. (2018) and 1D rectangular-cross-sectional ring cases Zhou et al. (2019). Additionally, \(\left( {\hat{Q}_{{{\text{TED}},{\text{peak}},q}} } \right)^{{ - 1}}\) of the rectangular-cross-sectional ring with 2D heat conduction model Zhou et al. (2019) is much similar to the present work, except \(\gamma\).

Moreover, approximations of Eq. (35) can be obtained by using Taylor’s expansion with much small \(\beta _{q}\), and taking an infinite on the \(\beta _{q}\), respectively, as:

$$f\left( {\beta _{q} } \right) \approx 6\beta _{q} ^{2} \left( {1 + \gamma ^{2} } \right)^{2} {\text{for}\;\text{small}\;} \beta _{q}$$
(37)
$$\mathop {\lim }\limits_{{\beta _{q} \to \inf }} \left\{ {f\left( {\beta _{q} } \right)} \right\} = 6\beta _{q} \left( {1 + \gamma ^{2} } \right)\;{\text{for}}\;{\text{large}}\;\beta _{q}$$
(38)

Substituting these results into Eqs. (34) and (36), thus the normalized peak frequencies and the values of \(\left( {\hat{Q}_{{{\text{TED}},{\text{peak}},q}} } \right)^{{ - 1}}\) s are:

$$\left( {\hat{\omega }_{{{\tt peak}, q}} } \right)^{2} = \left( {1 + \gamma ^{2} } \right)^{2} \;{\text{for}}\;{\text{small}}\;\beta _{q}$$
(39)
$$\left( {\hat{\omega }_{{ peak,q}} } \right)^{2} = \frac{{\left( {1 + \gamma ^{2} } \right)}}{{\beta _{q} }}\;{\text{for}}\;{\text{large}}\;\beta _{q}$$
(40)
$$\frac{1}{{\hat{Q}_{{ TED,peak, q}} }} = \frac{1}{{\left\{ {1 - \beta _{q} \left( {1 + \gamma ^{2} } \right)} \right\}^{2} + 1}}\;{\text{for}}\;{\text{small }}\beta _{q}$$
(41)
$$\frac{1}{{\hat{Q}_{{ TED,peak, q}} }} = \sqrt {\beta _{q} \left( {1+ \gamma ^{2} } \right)} {\text {for}}\;{\text {large}}\;\beta _{q}$$
(42)

Table 4 shows the expressions of the normalized TEDs for classifications of models and cross-sections. Although, the forms of the equations obtained from beams with rectangular-(Zhou and Li 2017), circular-(Zhou et al. 2018) cross-section, and the ring with rectangular-cross-section (Zhou et al. 2019) are much similar to the result of the toroidal ring, but the factors \(\gamma\) and \(b_{{1q}}\) in the calculation are different from existing models. Additionally, there is straight temperature distribution in a rectangular-cross-sectional structure (Wong et al. 2004), thus the \(z\)-direction can be neglected. On the contrary, the temperature profile must exist in a curved pattern except the center for the toroidal ring. Thus there is one more dimension with the \(z\)-coordinate in the circular section. (Li et al. 2016).

Table 4 Comparison of the results for various shapes
Full size table

In other words, the equations themselves can be seen the same as the previous works, but the case of the toroidal-ring model in this work is completely different as shown in here. Especially, \(\gamma\) is the specific term for only ring models rather than beams, and \(b_{{1q}}\) can be grouped by the shape of cross-section. Obviously, \(a_{{1q}}\) is the characteristic of the circular cross-section expressed by Bessel function because the cross-section is circular.

In this regard, normalized results of TED are compared with the previous literatures based on the beam with circular cross-section (Zhou et al. 2018) and ring with rectangular cross-section (Chester 1963). Figure 2(a) shows the plots of \(f\left( {\beta _{q} } \right)\) for \(\gamma ^{2} =\) 0, 0.5, and 1 with the one-term approximations. Moreover, the special term \(\gamma\) for the 3D toroidal ring model can affect the deviation of the \(f\left( {\beta _{q} } \right)\), and the curves are moved toward smaller \(\beta _{q}\). Then, \(f\left( {\beta _{q} } \right)\) can be also applied into small or large \(\beta _{q}\) for the 3D ring. However, the inflection point is nearby \(\beta _{q} \left( {1 + \gamma ^{2} } \right)\), thus checking the range of the curve is necessary to ensure the accuracy of the simplification.

Fig. 2
figure 2

Plots of the (a) \(f\left( {\beta _{q} } \right)\) and asymptotic curves, (b) Normalized values and asymptotic curves of \(\omega _{{{\text{peak}},q}}\), (c) \(\left( {\hat{Q}_{{{\text{TED}},{\text{peak}},q}} } \right)^{{ - 1}}\) according to the normalized lagging time \(\beta _{q}\) and \(\gamma\)

Full size image

Figure 2b, c represent the normalized eigenfrequency \(\hat{\omega }_{{\tt peak},q}\) for the peak of normalized \(\hat{Q}^{{ - 1}}\), and the \(\hat{Q}^{{ - 1}}\) with respect to the non-dimensional lagging time \(\beta _{q}\), including the asymptotic curves based on Eqs. (39–40) and (41–42) respectively. When the ring is sufficiently thin as \(\gamma \to 0\), all asymptotic curves are the same as Zhou and Li (2017); Zhou et al. (2018) for a beam model with circular-cross-section. On the contrary, \(\gamma\) and the peak frequency approach also larger due to the effect of the thickness or high mode numbers. In Fig. 2(c), the normalized \(\hat{Q}^{{ - 1}}\) is nearby \(0.5\Delta _{E}\) when the lagging time is neglected Lifshitz and Roukes (2000); Wong et al. (2004). While, the lagging time is larger, the magnitude of \(\hat{Q}^{{ - 1}}\) approaches extremely larger for the thick model. Generally, \(\hat{\omega }_{{ peak, q}}\) is 1 and the peak of the \(\hat{Q}^{{ - 1}}\) is \(0.5\Delta _{E}\) for the classical Fourier’s heat conduction equation. On the other hand, the peak value is the function of the time-lagging, thus the peak of the \(\hat{Q}^{{ - 1}}\) is no longer \(0.5\Delta _{E}\) and \(\hat{\omega }_{{{\text{peak}},q}}\) cannot be 1 with larger \(\beta _{q}\). The figures can be applied into Zhou and Li (2017); Zhou et al. (2018),(2019), but the application of the data is much different because \(\gamma\) and \(b_{{1q}}\) are not the same as any previous literatures.

3.2 Toroidal ring model considering SPL

In this part, practical parametric studies are shown for the Q-factors of the toroidal silicon ring based on non-Fourier heat conduction. To identify the validity and the trend of the model, Table 5 compares the experimental data (Wong et al. 2004) using COMSOL FEM and analytical form of the rectangular-cross-sectional ring model. (Zhou et al. 2019) The expression of Q for the structure can be obtained by replacing \(\gamma\) and \(b_{{1q}}\) from the toroidal ring in Table 4. Furthermore, the values of the 2D model are a little closer to the experimental and FEM data than 1D as shown in Table 5, thus the present work can be valid to apply into the toroidal ring model. Moreover, the differences in Qs come from the deviation of undamped and damped eigenfrequencies Hossain et al. (2016), and the meshes of the FEM due to the thickness effect. Moreover, the legs of the structure or other sources in vacuum can be neglected for in-plane vibration Wong et al. (2004), then the analytical expressions for 1D and 2D with \(\sum \left( {q = 1\sim 100} \right)\) is reasonable in the verification.

Table 5 Comparison of the data from experimental results
Full size table

Figure 3 shows the effect of TED for various \(n\), \(r_{0}\) and \(R_{0}\) at 293[K] in the model. In (a) and (b), the more peak points appear when \(r_{0}\)/\(R_{0}\) is large due to the thickness of the ring in the non-Fourier heat conduction. Because the thermal propagation cannot catch up with extremely fast vibration, the peaks appear at numerous different values. (Khisaeva and Ostoja-Starzewski 2006) On the other hand, the delay of heat flux is important also, but the 1st term (i.e. \(q = 1\)) is more significant in [\(\mu {\text{m}}\)]-scale rather than [nm]-scale as in (c) and (d). Thus the multiple peaks do not appear in [\(\mu {\text{m}}\)]-scale rather than [nm]-scale. Moreover, the difference of the TED between 2 and 3D rings is larger as increased \(r_{0}\)/\(R_{0}\). This is the reason that the time delay phenomenon is relatively noticeable in thick materials. Furthermore, the increasing values of each \(q\) th order are different due to the properties of circular section in terms of Bessel function. In all cases, more energy losses in 3D than 2D models are observed because the TED of circumferential direction is similarly considered the rectangular-cross-sectional ring with 1D and 2D models (Zhou et al. 2019).

Fig. 3
figure 3

Thermoelastic damping with respect to the mode numbers for 293[K] and (a) \(\left( {r_{0} ,R_{0} } \right)\) = (10,500) (b) (10,\(10^{3}\)), (c) (103,\(5 \times 10^{4}\)), (d) (\(10^{3}\),\(10^{5}\)) [nm]

Full size image

Figure 4 indicates \(Q^{{ - 1}}\) according to the order of \(q\) and summation of \(Q^{{ - 1}}\) for the CV heat conduction model, and the results obtained from classical Fourier’s law (Li et al. 2016) with \(r_{0} = 10\left[ {{\text{nm}}} \right]\), \(R_{0} = 500\left[ {{\text{nm}}} \right]\). In the figure, the \(q\) = 1st thermal order term is significantly dominant for the damping rather than higher \(q\). However, the peak of the higher \(q\) are important in the high mode numbers because the \(q\) th term of the TED is largest in the summation of the dissipation except \(q\) = 1st thermal order. Moreover, the result of the nF heat conduction model can be neglected for the lower-mode of frequency vibration less than \(n\) = 50, thus classical Fourier heat conduction can be valid only in the lower range of \(\omega\). While, the delay of the heat flow should be considered in the higher frequency regions.

Fig. 4
figure 4

Q−1 of q = 1 to 30, and the summation of the Q−1 s with the temperatures as 293 [K] for a ring with \(\left( {r_{0} ,R_{0} } \right)\) = (10,500) [nm]

Full size image

Figure 5 compares the trends of the summation of \(Q^{{ - 1}}\) for the various temperature ranges. For the ultra-low temperature under 100 [K], the peaks appear sufficiently sharp in general. On the contrary, the sharp peaks do not occur in higher temperatures. Strictly speaking, the peak also appears in the high temperature, but \(Q^{{ - 1}}\) is sufficiently smaller in higher order than the case for the \(q\) = 1st order. While, mode numbers according to the peak of the TED are independent of the ambient temperature. In addition, it would be a more reasonable study to predict where peaks will occur, rather than checking the peak values themselves at that time with discrete values of \(n\). But the peak values of the dissipation are more irregular in the lower temperature because the phase-lagging is significant in ultralow temperature. In conclusion, the peaks are the key characteristic of the low temperature or high \(\tau _{q}\), and thus the phase-lagging can be estimated in the region of the higher frequency.

Fig. 5
figure 5

Summation of Q−1 with respect to the various temperatures and frequencies for a ring with \(\left( {r_{0} ,R_{0} } \right)\) = (10, 500) [nm]

Full size image

4 Dimensional temperature profiles

In this section, the normalized temperature profiles with the Real and Imaginary parts are shown to visualize the phase-lagging effects during the motion on the local-radial position in the cross-section. Additionally, the 3D heat conduction model should be used in order to predict the heat conduction through the circumferential direction in toroidal ring. Moreover, the temperature profile can be observed with respect to the local radius on the cross-section by normalization. In this regard, the dimensionless parameters of the frequency and the radii are defined as:

$$\hat{\Omega }_{{nq}} = \omega _{n} \tau _{q} ,\hat{R} = \frac{r}{{r_{0} }}$$
(43)

where \(r\) is the local-radial position through the thickness radius, thus \(0 \le \hat{R} \le 1\) only.

Then, the normalized Real and Imaginary parts by modifying Eq. (23) and using Eq. (43) are:

$${\raise0.5ex\hbox{$\scriptstyle {\left\{ {\begin{array}{*{20}c} {\text{Real}\left[ {\hat{T}_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ {\text{Imag}\left[ {\hat{T}_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\text{Real}\left[ {T_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ {\text{Imag}\left[ {T_{0} \left( {r,\beta ,\theta } \right)} \right]} \\ \end{array} } \right\}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\left( {\frac{{2r_{0} }}{{R_{0} ^{2} }}\frac{{\Delta _{E} \left( {1 - n^{2} } \right)\hat{U}_{n} }}{\alpha }} \right) = \sin \left( \beta \right)\sin \left( {n\theta } \right)\times \mathop \sum \limits_{{q = 1}}^{{\inf }} \left[ {\frac{{J_{1} \left( {a_{{1q}} \hat{R}} \right)}}{{\left( {a_{{1q}} ^{2} - 1} \right)J_{1} \left( {a_{{1q}} } \right)}}\frac{1}{{\left( {1 + \gamma ^{2} - \hat{\Omega }_{{nq}} ^{2} \beta _{q} } \right)^{2} + \hat{\Omega }_{{nq}} ^{2} }} \times \left\{ {\begin{array}{*{20}c} {\hat{\Xi }_{R} } \\ {\hat{\Xi }_{I} } \\ \end{array} } \right\}} \right]}$}}$$
(44)

where \(\hat{\Xi}_{R} = - \hat{\Omega }_{{nq}} ^{2} \beta _{q} \left( {1 + \gamma ^{2} } \right) + \hat{\Omega }_{{nq}} ^{2} \left\{ {1 + \left( {\hat{\Omega }_{{nq}} \beta _{q} } \right)^{2} } \right\}\) and \(\hat{\Xi}_{I} = \left( {1 + \gamma ^{2} } \right)\hat{\Omega }_{{nq}}\).

Figures 6(a) and (b) present the temperature distributions of the ring by Real and Imaginary parts. In order to predict the effect of the lagging clearly and simply, \(\sin \left( \beta \right)\sin \left( {n\theta } \right) = 1\) at \(\hat{R} = 0.1\) are assumed as inner layers. In here, all lines with \(\gamma ^{2} = 0\) can be applied for the beam model with circular section. (Zhou et al. 2018) And although the cross-sectional shape differs from circular to rectangular (Zhou et al. 2019), the equations in Zhou et al. (2019) can be explained by the same figures because the normalized forms are similar as in Table 4. The temperature profile is relatively monotonic for the classical Fourier heat conduction, but is distorted when \(\beta _{q}\) is non-zero based on the CV equation. The negative values within the cases of existing \(\beta _{q}\) s are originated from the time-delay of the heat conduction during the vibration. Moreover, the Real and Imaginary parts of the distribution at \(\hat{R} = 1\) as the surface of the structure are demonstrated in (c) and (d). The multiple peaks can be explained by the mathematical characteristics of the Bessel function as (Zhou et al. 2018). Especially, the toroidal ring stands for the larger discrepancy of the distribution because of the dissipation through the circumferential direction with respect to \(\gamma = \frac{{nr_{0} }}{{a_{{1q}} R_{0} }}\) term. In other words, \(\gamma\) can reinforce the lagging especially in \(0 < \hat{\Omega}_{{nq}} < 1\). Moreover, the peaks with respect to \(\hat{\Omega}_{{nq}}\) are changed due to the term \(\gamma\) in \(\left( {1 + \gamma ^{2} - \hat{\Omega}_{{nq}} ^{2} \beta _{q} } \right)\).

Fig. 6
figure 6

Normalized temperature profiles (a) Real, (b) Imaginary parts at \(\hat{R} = 0.1\), (c) Real, (d) Imaginary parts at \(\hat{R} = 1\)

Full size image

For a case with \(\hat{\Omega}_{{nq}} = 1\), \(\gamma ^{2} = 0.4\) and \(\beta _{q} = 5\), Fig. 7 shows the 3-dimensional temperature profile in the (a) Real and (b) Imaginary parts on the normalized axes of x and z with respect to \(\hat{R}\). As the results, the distorted surface appears when the time-lagging \(\beta _{q}\) exists, then the complicated inflection point indicates the delay based on the finite speed of the propagation in the heat flux. Especially, the peaks due to the phase-lagging on the range for \(\hat{R} < 1\) are changed with respect to the \(\gamma\) as Figs. 6(a) and (b). On the points with \(\hat{R} = 1\) on the neutral plane represented with \(\sin \left( \beta \right)\sin \left( {n\theta } \right) = 1\), the normalized maximum values are the same in Figs. 6(c) and (d).

Fig. 7
figure 7

3Dimensional plots of the normalized temperature fields with \(\beta _{q} = 5\) and \(\hat{\Omega}_{{nq}} = 1\). (a) Real parts (b) Imaginary parts

Full size image

5 Conclusion

In this work, the thermoelastic damping (TED) effect for a toroidal micro/nano-ring model is investigated by using Lord-Shulman (LS) heat conduction equation. The influence of the single-phase-lagging (SPL) of heat flow is analyzed using the polar coordinate during the inextensional and in-plane vibration of the model. In this regard, the TED including the SPL is mainly analyzed according to the geometrical shape, temperature, mode number, etc. The key conclusions are listed as follows:

  1. (A)

    The 3D expression of the temperature profile including SPL is similar to the 1D or 2D beams or ring with rectangular-cross-section. While, the result is much different to the previous models because the governing equation for the ring is solved by Bessel function.

  2. (B)

    In the 3D ring model, the dissipation through the circumferential direction should be considered for higher mode number or large ratio of \(r_{0}\)/\(R_{0}\).

  3. (C)

    The SPL effect is dominant in the lower temperature, nano-scale or higher-mode numbers. Temperature profiles can be normalized with respect to the geometrical shape, mode number, lagging time, etc. On the other hand, the SPL can be sufficiently neglected when the scale is larger then [\(\mu {\text{m}}\)].

  4. (D)

    The lagging can be described by the distorted points through the cross-sectional area. And the size of the peak can be observed by the normalized temperature profile.

  5. (E)

    The final data of this work can be compared with the beams or rectangular-cross-sectional ring including TED with SPL. However, the special characteristics are discussed in detail for the toroidal solid micro/nanoring, which is much different to the previous results.

Thus, the nF heat conduction effect is an important factor in the higher frequencies or ultralow temperature ranges. And this work could be applied for predicting the phenomenon based on the extreme conditions with ultrahigh frequency vibration or cryogenic environments to obtain the environment for operation with high Q of resonator.