Effect of Inclined Mechanical Load on a Rotating Microelongated Two Temperature Thermoelastic Half Space with Temperature Dependent Properties

Abstract

Purpose:

The objective of the present work is to study the disturbances in a rotating microelongated thermoelastic solid half-space with two temperature and temperature dependent properties. The problem has been modeled by employing Lord-Shulman and Green-Lindsay theories to carry out the investigation.

Methods:

To explore the impact of inclined mechanical load on microelongated thermoelastic half space, normal mode technique has been applied and the analytical expressions for the displacement components, stresses, temperature fields and microelongation are obtained.

Results:

In order to illustrate the analytical results, the numerical solution is carried out for aluminum epoxy like material. Influences of rotation, two temperatures, temperature dependent properties and time on the physical quantities are analyzed for Green-Lindsay theory.

Conclusions:

Theoretical and numerical results show the significant dependence of physical fields under consideration on rotation, elongation parameter, temperature dependent properties, two temperature parameter and inclination angle. Also the results of the present study have been compared with the previously published results for validation.

Introduction

The topic of generalized thermoelasticity has received a lot of attention in recent years. The hyperbolic-type heat conduction equations used in the generalized thermoelastic theories allow for thermal signals to travel at finite speeds. By introducing one relaxation time in the Fourier’s law of heat conduction, Lord and Shulman [1] modified the Fourier’s law and developed the first generalized theory of thermoelasticity referred as LS theory. Later on, by incorporating two different relaxation times in the constitutive relations, Green and Lindsay [2] generated a new theory of thermoelasticity, known as temperature rate dependent thermoelasticity and referred as GL theory. On the basis of these theories, a lot of research works have been carried out. The effects of temperature-dependent thermal conductivity on thermoelastic interactions inside a medium with a spherical cavity under a two-temperature Green-Lindsay thermoelasticity theory were analyzed by Kumar et al. [3]. Sheoran et al. [4] examined thermo-mechanical interactions in a rotating non local transversely isotropic material under LS theory. Sadeghi and Kiani [5] reported the generalized magneto thermoelastic response of a layer based on both LS and GL theories.

The microcontinuum field theory [6, 7] is characterized by a fundamental departure from the classical continuum mechanics. In the latter theory, a material particle occupies a certain location within a body at a specific time instant, regardless of orientation. Micropolar material particles, however, can also be oriented. In other words, each micropolar particle’s orientation is determined by an additional characteristic called ‘director’. Comparing a material point with three deformable directors to a particle in the classical theory, there are nine more degrees of freedom. When the directors are characterized by only breathing-type microdeformation, we have microstretch continuum [8, 9] and the number of extra degrees of freedom is reduced to four. In contrary to other microcontinuum field theories, including those for microstretch and micromorphic continua, the directors are rigid in the theory of micropolar continua [10, 11]. Furthermore, when the directors are orthogonal and allow for isotropic expansion or contraction with the exception of no further rotation, this special case is termed as microelongational theory [12].

A microelongated elastic solid acquires four degrees of freedom: three for translation and one for microelongation. According to the microelongation theory, the material particles can execute only volumetric microelongation in addition to classical deformation of the medium. Such a medium allows its material points to expand and contract independently of their translations. Solid-liquid crystals, composite materials reinforced with chopped elastic fibers, porous media with pores filled with non-viscous fluid or gas can be categorized as microelongated medium. The variation due to periodical heat source response in a functionally graded microelongated medium was studied by Shaw and Mukhopadhyay [13]. Shaw and Mukhopadhyay [14] investigated the thermoelastic interactions in the presence of a moving heat source in a homogeneous isotropic microelongated material. The plane strain problem in a thermoelastic microelongated solid with an underlying infinite non-viscous fluid was discussed by Sachdeva and Ailawalia [15]. Using generalized theories of thermoelasticity, Othman et al. [16] examined the effects of initial stress on a microelongated thermoelastic medium when an elastic layer is lying above it. Hilal [17] studied dynamical interactions in a rotating microelongated non local thermoelastic solid with laser pulse. Sharma and Ailawalia [18] focused their attention on two-dimensional deformation in a functionally graded thermoelastic microelongated medium. Othman et al. [19] studied the influence of rotation parameter on a two-dimensional microelongated thermoelastic medium in the context of LS and DPL models.

Chen and Gurtin [20] and Chen et al. [21, 22] constructed a theory of heat conduction in deformable bodies, which depends on two different temperatures, the conductive temperature $\phi$ and the thermodynamical temperature $\theta$. For time-independent situations, the difference between these two temperatures is proportional to the heat supply and in the absence of any heat supply, two temperatures are identical. For time dependent problems, however, for wave propagation problems in particular, two temperatures are generally different, regardless of the presence of heat supply. Warren and Chen [23] studied the wave propagation in the two-temperature theory of thermoelasticity. Youssef [24] extended this concept of two temperature to the generalized thermoelasticity and obtained the uniqueness theorem. Abouelregal et al. [25] investigated a micropolar thermoelasticity theory with a two-phase delay of high-order and two-temperatures. This work examined the microstructure of rotating materials when their atomic or molecular vibrations change under the effects of Hall current.

The elastic modulus is an important physical property of materials reflecting the elastic deformation capacity of the material when subjected to an external load. The material properties are assumed to be constant in most of the investigations. The physical characteristics of engineering materials, however, change with temperature, as is well known. At high temperature, Lomakin [26] observed that the material characteristics such as modulus of elasticity, Poisson’s ratio, coefficient of thermal expansion, thermal conductivity and microelongated parameters are no longer constant. Ezzat et al. [27] solved a problem of generalized thermoelasticity with two relaxation times in an isotropic elastic medium with temperature-dependent mechanical properties. Othman [28] proposed a mathematical model of two-dimensional generalized thermoelasticity with two relaxation times in an isotropic medium with the modulus of elasticity dependent on the reference temperature and solved analytically by applying state-space technique. Aouadi [29] examined the effect of temperature dependency of elastic modulus on the behavior of two-dimensional solutions in micropolar thermoelastic medium. Thermo-mechanical interactions in a generalized thermoelastic medium with gravity and temperature dependent properties under three different theories have been analyzed by Othman et al. [30]. In another article, Othman et al. [31] investigated the disturbances in a homogeneous isotropic temperature dependent magneto-thermo-diffusive medium with fractional order heat transfer. Othman and Said [32] investigated the influence of magnetic field and temperature dependent properties on the plane waves in a fiber-reinforced thermoelastic medium in the context of three-phase-lag theory and Green-Naghdi theory without energy dissipation. Mamen et al. [33] highlighted the influence of porosity on thermodynamic response of FGM beams with effective temperature dependent properties by using a novel integral three variable quasi-3D high order shear deformation theory. The effects of temperature-dependent properties and non local elasticity in the presence of a magnetic field in an infinitely long solid conductive circular cylinder have been studied by Khader et al. [34].

It seems more realistic to analyze the thermo-mechanical disturbances in a rotating medium as most of the large bodies, such as the earth, the moon and other planets have an angular motion. The propagation of waves in a rotating, homogeneous isotropic linear elastic medium had been investigated by Schoenberg and Censor [35]. By employing normal mode technique, Othman [36] investigated a two dimensional thermo-viscoelasticity problem with one relaxation time under the effect of rotation. Bijarnia and Singh [37] examined the propagation of plane waves in a transversely isotropic two temperature generalized thermoelastic solid half space with voids and rotation. Abo-Dahab et al. [38] discussed the effect of rotation and magnetic field on the general model of equations of generalized thermoelasticity for a homogeneous isotropic elastic half-space. Bayones and Abd-Alla [39] employed the linear theory of thermoelasticity to study the effect of rotation in a thermoelastic half-space containing heat sources. The normal mode analysis has been applied and the resulting equations were written in the form of a vector–matrix differential equation, which was then solved by eigenvalue approach. Deswal et al. [40] studied the reflection and transmission phenomena of plane waves between a rotating thermoelastic transversely isotropic solid half space and a fiber-reinforced thermoelastic rotating solid half space in the framework of Lord-Shulman and Green-Lindsay theories.

Although various investigations do exist to observe the disturbances in a homogeneous, isotropic, rotating thermoelastic medium with two temperatures, the work in its present form has not been studied by any researcher till now. The novelty of the present research resides in the fact that it aimed at investigation of dependence of various field quantities on micro-elongation parameter, rotation, temperature dependent properties, two-temperature parameter, inclination angle and their evolution with time. The introduction of these parameters in the thermoelastic medium provides a realistic model for these studies. Since the present work is carried out for a rotating thermoelastic material under the effect of temperature dependent properties and two temperatures, it has many applications for earth and other planetary systems where the occurrence of these parameters is very common. Problem assumes great significance in an earthquake preparation region when we think of the variation in particle motion as a possible precursor for earthquake prediction.

Governing Equations

Following Kiris and Inan [12] and Youssef [24], the constitutive relations and field equations for a rotating microelongated two temperature thermoelastic solid in the context of LS and GL theories of generalized thermoelasticity are given as Constitutive relations:

$$\begin{aligned}{} {} \sigma _{ij}&={\lambda }u_{k,k}\delta _{ij}+\mu (u_{i,j}+u_{j.i})\nonumber \\{} {} &-\beta (1+\nu _0\frac{\partial }{\partial t}){\theta }{\delta _{ij}}+\lambda _0\delta _{ij}\Psi , \end{aligned}$$

(1)

$$\begin{aligned}{} & {} m_{k}=a_{0}{\Psi _{,k}}, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} s-{\sigma }={\lambda _{0}}u_{k,k}+{\lambda _{1}}{\Psi }-{\gamma }{\left( 1+{\nu _{0}}{\frac{\partial }{\partial t}}\right) }{\theta }, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} e_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}). \end{aligned}$$

(4)

Equations of motion

$$\begin{aligned}{} & {} \sigma _{ji,j}={\rho }[{\ddot{u}_{i}}+({\vec {\Omega }}{\times }({\vec {\Omega }}{\times }{\vec {u}}))_{i}+({2\vec {\Omega }}{\times }{\dot{\vec {u}}})_{i}], \end{aligned}$$

(5)

$$\begin{aligned}{} & {} a_{0}{\Psi ,_{ii}}+{\gamma }\left( 1+{\nu _{0}}{\frac{\partial }{\partial t}}\right) {\theta }-{\lambda _{1}}{\Psi }-{\lambda _{0}}u_{j,j}={\frac{1}{2}}{\rho }j_{0}{\ddot{\Psi }}. \end{aligned}$$

(6)

Heat conduction equation

$$\begin{aligned}{} & {} K\phi ,_{ii}={\rho }C_E{\left( 1+{\nu _1}{\frac{\partial }{\partial t}}\right) }{\dot{\theta }}\nonumber \\{} & {} +{\beta }{\left( 1+{n}_0{\nu _1}{\frac{\partial }{\partial t}}\right) }T_{0}{\dot{u}_{i,i}}+{\gamma }T_{0}{\dot{\Psi }}. \end{aligned}$$

(7)

The relation between two temperatures

$$\begin{aligned} {\phi }-{\theta }=a{\phi ,_{ii}}~, \end{aligned}$$

(8)

where $\lambda$, $\mu$ are Lame’s constants, $\beta$ is the thermal elastic coupling tensor, $a_0$, $\lambda _0$, $\lambda _1$ are microelongational constants, $\gamma$ is the microelongational thermal expansion, $u_{i}$ are the displacement components, $\Psi$ is microelongational scalar, $e_{ij}$ are the components of strain, a is the two temperature parameter, $m_{k}$ are the components of microelongation vector, K is the thermal conductivity, $s_{ij}$ are the components of stress tensor, $s=s_{kk}$, $\sigma _{ij}$ are the components of microelongational stress tensor, $\sigma =\sigma _{kk}$, ${\theta }$ is the thermodynamical temperature, $\theta =T-T_0$ where T is the absolute temperature and $T_0$ denotes temperature of the medium in its natural state assumed to be $|\frac{\theta }{T_0}|\ll 1$, $\phi$ is the conductive temperature, $j_{0}$ is microinertia and ${\nu _{0}}, {\nu _{1}}$ are the thermal relaxation times, $C_E$ is the specific heat at constant strain, $\rho$ is the mass density, $\delta _{ij}$ is the Kronecker delta function.

The displacement equation of motion (5) has two additional terms: the centripetal acceleration ${\vec {\Omega }}{\times }({\vec {\Omega }}{\times }{\vec {u}})$ due to time-varying motion only and the Coriolis acceleration ${2\vec {\Omega }}{\times }{\dot{\vec {u}}}$ because of moving reference frame, where $\vec {\Omega }$ is angular velocity (Schoenberg and Censor [35]).

Moreover, the use of the relaxation times ${\nu _{0}}, {\nu _{1}}$ and unifying parameter $n_0$ makes the fundamental equations valid for these theories of generalized thermoelasticity:

(i) Lord and Shulman’s theory [1]

${n_{0}}=1, \nu _{0}=0, \nu _{1}>0$.

(i) Green and Lindsay’s theory [2]

${n_{0}}=0, \nu _{0}> \nu _{1}>0$.

Our goal is to investigate the impact of the material’s temperature dependency on thermo-mechanical interactions. Therefore, one can assume that

$$\begin{aligned}{} & {} ({\lambda }, {\mu }, {\beta }, {\lambda _{0}}, {\lambda _{1}}, {\gamma }, a_{0})\nonumber \\{} & {} \quad =({\lambda ^*}, {\mu ^*}, {\beta ^*}, {\lambda _{0}^*}, {\lambda _{1}^*}, {\gamma ^*}, a_{0}^*)f(T_0), \end{aligned}$$

(9)

where $\lambda ^*$, $\mu ^*$, $\beta ^*$, $\lambda _{0}^*$, $\lambda _{1}^*$, $\gamma ^*$, $a_{0}^*$ are constants and $f(T_0)$ is a given non-dimensional function of reference temperature such that $f(T_0)=(1-{\alpha ^*}T_{0})$, where $\alpha ^*$ is an empirical material constant. In case of temperature independent properties, we have $f(T_0)=1$.

In the aforementioned equations, the superposed dot denotes a partial derivative with respect to time, while the comma notation indicates a derivative with respect to spatial coordinates.

Problem Formulation

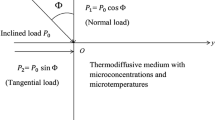
In the framework of the unified LS and GL theories, let us consider an infinite microelongated isotropic thermoelastic solid with rotation. Introducing the rectangular cartesian coordinate system (x, y, z), where the surface of the half-space is represented by the plane $x=0$ and the $x-$axis is displayed pointing vertically downwards into the medium. The surface of the half-space $(x=0)$ is acted upon by an inclined mechanical load (Fig. 1). The current investigation is only allowed to take place in the $xy-$plane and thus all the physical field quantities will be functions of the space variables x, y and time t. The medium is assumed to be rotating with an angular velocity $\vec \Omega =\Omega \hat{n}$, where $\hat{n}$ is a unit vector that represents the direction of rotation.

For a two-dimensional problem in cartesian coordinates x and y, the displacement vector $\vec {u}$ and angular velocity $\vec {\Omega }$ will have the components:

$$\begin{aligned} \vec {u}=(u,v,0),\ \ \vec {\Omega }=(0,0,\Omega ). \end{aligned}$$

(10)

Keeping in view the expression (9), the stresses arising from Eq. (1) in $xy-$plane can be written as:

$$\begin{aligned} {\sigma _{xx}}={} & {} f(T_0)[(\lambda ^*+2\mu ^*){\frac{\partial u}{\partial x}}+{\lambda ^*}{\frac{\partial v}{\partial y}}\nonumber \\{} & {} \quad -{\beta ^*}\left( 1+\nu _{0}{\frac{\partial }{\partial t}}\right) {\theta }+{\lambda _{0}^*}{\Psi }], \end{aligned}$$

(11)

$$\begin{aligned} {\sigma _{yy}}={} & {} f(T_0)[\lambda ^*{\frac{\partial u}{\partial x}}+(\lambda ^*+2\mu ^*){\frac{\partial v}{\partial y}}\nonumber \\{} & {} \quad -{\beta ^*}\left( 1+\nu _{0}{\frac{\partial }{\partial t}}\right) {\theta }+{\lambda _{0}^*}{\Psi }], \end{aligned}$$

(12)

$$\begin{aligned} {\sigma _{xy}}={} & {} f(T_0){\mu ^*}\left( {\frac{\partial u}{\partial y}}+{\frac{\partial v}{\partial x}}\right) . \end{aligned}$$

(13)

Plugging the stress components defined in Eqs. (12), (13) into Eq. (5), we obtain

$$\begin{aligned}{} & {} {f(T_0)}\left[ {(\lambda ^*+2\mu ^*)\frac{\partial ^2 u}{\partial x^2}}+(\lambda ^*+\mu ^*){\frac{\partial ^2 v}{{\partial x}{\partial y}}}+\mu ^*{\frac{\partial ^2 u}{\partial y^2}}\right] \nonumber \\{} & {} \quad -{f(T_0)}{\beta ^*}\left( 1+\nu _{0}{\frac{\partial }{\partial t}}\right) {\frac{\partial {\theta }}{\partial x}}\nonumber \\{} & {} \quad +{f(T_0)}{\lambda _{0}^*}{\frac{\partial {\Psi }}{\partial x}} ={\rho }\left[ {\frac{\partial ^2 u}{\partial t^2}}-{\Omega }^2u-2{\Omega }{\frac{\partial v}{\partial t}}\right] , \end{aligned}$$

(14)

$$\begin{aligned}{} & {} {f(T_0)}\left[ {\mu ^*\frac{\partial ^2 v}{\partial x^2}}+(\lambda ^*+\mu ^*){\frac{\partial ^2 u}{{\partial x}{\partial y}}}+(\lambda ^*+2\mu ^*){\frac{\partial ^2 v}{\partial y^2}}\right] \nonumber \\{} & {} \quad -{f(T_0)}{\beta ^*}\left( 1+\nu _{0}{\frac{\partial }{\partial t}}\right) {\frac{\partial {\theta }}{\partial y}}\nonumber \\{} & {} \quad +{f(T_0)}{\lambda _{0}^*}{\frac{\partial {\Psi }}{\partial y}} ={\rho }\left[ {\frac{\partial ^2 u}{\partial t^2}}-{\Omega }^2u+2{\Omega }{\frac{\partial v}{\partial t}}\right] . \end{aligned}$$

(15)

In view of relations (9) and (10) and using summation convention, Eqs. (6) and (7) take the form respectively:

$$\begin{aligned}{} & {} {f(T_0)}a_0^*\left( {\frac{\partial ^2{\Psi }}{\partial x^2}}+{\frac{\partial ^2{\Psi }}{\partial y^2}}\right) \nonumber \\{} & {}-f(T_0)\gamma ^*\left( 1+\nu _0{\frac{\partial }{\partial t}}\right) \theta -f(T_0)\lambda _1^*\Psi -f(T_0)\lambda _0^*\nonumber \\{} & {} \left( \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) =\frac{1}{2}{\rho }j_0\frac{\partial ^2{\Psi }}{\partial t^2}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} K\left[ \frac{\partial ^2{\phi }}{\partial x^2}+\frac{\partial ^2{\phi }}{\partial y^2}\right] ={\rho }C_E\left( 1+\nu _{1}{\frac{\partial }{\partial t}}\right) \nonumber \\{} & {} \quad {\frac{\partial {\theta }}{\partial t}}+{f(T_0)}{\beta ^*}T_0\left( 1+n_0\nu _{1}{\frac{\partial }{\partial t}}\right) \nonumber \\{} & {} \quad {\frac{\partial }{\partial t}}\left( {\frac{\partial u}{\partial x}}+{\frac{\partial v}{\partial y}}\right) +f(T_0)T_{0}\gamma ^*{\frac{\partial {\Psi }}{\partial t}}. \end{aligned}$$

(17)

In order to get the non-dimensional governing equations, we will make use of the following non-dimensional variables:

$$\begin{aligned}{} & {} (x',y',u',v')=\frac{\omega ^*}{c_1}(x, y, u, v),\nonumber \\{} & {} \quad [t',{\nu _0}',{\nu _1}']=\omega ^*[t,\nu _0,\nu _1],\nonumber \\{} & {} \quad {\sigma _{ij}}'=\frac{\sigma _{ij}}{{\rho }c_{1}^2},\ \ \theta '=\frac{\theta }{T_0},\ \ \phi '=\frac{\phi }{T_0},\nonumber \\{} & {} \quad \Omega '=\frac{\Omega }{\omega ^*},\ \ \Psi '=\frac{\lambda _0^*}{{\beta ^*}T_{0}}\Psi , \end{aligned}$$

(18)

where   $\omega ^*=\frac{{\rho }{C_E}{c_1^2}}{K},\ \ c_{1}^2=\frac{\lambda ^*+2\mu ^*}{\rho }$.

Following Helmholtz decomposition theorem, the relations connecting displacement components and potential functions in dimensionless form are as:

$$\begin{aligned} u=\frac{\partial {\xi }}{\partial x}+\frac{{\partial }\eta }{\partial y},\ \ v=\frac{\partial {\xi }}{\partial y}-\frac{\partial {\eta }}{\partial x}. \end{aligned}$$

(19)

The usage of dimensionless parameters described in (18), the potential functions given by Eq. (19) along with Eqs. (8) and (14)-(17), elicit the following connections by dropping the prime notation

$$\begin{aligned}{} & {} {f(T_0)}\nabla ^2\xi -{\frac{\partial ^2 \xi }{\partial t^2}}+\Omega ^2\xi -2\Omega {\frac{\partial \eta }{\partial t}}\nonumber \\{} & {} \quad -A_3\left( 1+\nu _0{\frac{\partial }{\partial t}}\right) (1-A_{10}\nabla ^2)\phi +A_3\Psi =0, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} 2\Omega {\frac{\partial \xi }{\partial t}}+(f(T_0)-A_1)\frac{\partial ^2\eta }{\partial x^2}\nonumber \\{} & {} \quad +A_2\frac{\partial ^2\eta }{\partial y^2}-{\frac{\partial ^2 \eta }{\partial t^2}}+\Omega ^2\eta =0, \end{aligned}$$

(21)

$$\begin{aligned}{} & {} A_4\nabla ^2\xi -A_5\left( 1+\nu _0{\frac{\partial }{\partial t}}\right) (1-A_{10}\nabla ^2)\phi \nonumber \\{} & {} \quad +A_6{\frac{\partial ^2\Psi }{\partial t^2}}-\nabla ^2\Psi +A_7\Psi =0, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \nonumber A_8\left( 1+n_0\nu _1{\frac{\partial }{\partial t}}\right) {\frac{\partial }{\partial t}}(\nabla ^2\xi )\nonumber \\{} & {} \quad +\left( 1+\nu _1{\frac{\partial }{\partial t}}\right) {\frac{\partial }{\partial t}}(1-A_{10}\nabla ^2)\phi -\nabla ^2\phi \nonumber \\{} & {} \quad +A_9{\frac{\partial \Psi }{\partial t}}=0, \end{aligned}$$

(23)

where

$$\begin{aligned}{} & {} A_1={\frac{f(T_0)( \lambda ^*+\mu ^*)}{( \lambda ^*+2\mu ^*)}}, A_2={\frac{f(T_0)\mu ^*}{(\lambda ^*+2\mu ^*)}}, A_3={\frac{f(T_0)\beta ^*T_0}{( \lambda ^*+2\mu ^*)}},\nonumber \\{} & {} \quad A_4={\frac{{\lambda _{0}^*}^2c_{1}^2}{a_{0}^*\beta ^*T_0{\omega ^*}^2}},A_5={\frac{\gamma ^*{\lambda _{0}^*}c_{1}^2}{a_{0}^*\beta ^*{\omega ^*}^2}},\nonumber \\{} & {} \quad A_6=\frac{{\rho }j_0c_{1}^2}{2f(T_0)a_{0}^*}, A_7={\frac{\lambda _{1}^*{c_{1}^2}}{a_{0}^*{\omega ^*}^2}}, \nonumber \\{} & {} \quad A_8={\frac{f(T_0)\beta ^*c_{1}^2}{K\omega ^*}}, A_9={\frac{f(T_0)\gamma ^*\beta ^*T_0c_{1}^2}{{\lambda _{0}^*}K\omega ^*}},\nonumber \\{} & {} \quad \ A_{10}=\frac{a{\omega ^*}^2}{c_{1}^2}. \end{aligned}$$

Solution Methodology

In the current section, the technique of normal mode analysis is employed. In this technique, the solution of the various physical quantities is divided in terms of normal modes and one gets exact solution without any assumed restrictions on the physical fields that appear in the governing equations of the problem considered. Normal mode analysis considers the assumed solution in Fourier transform domain. The whole dynamics of a complex system can be described in terms of a few generalized coordinates, such as normal modes, which is one of the main objectives of the normal mode technique. So, the physical variables under consideration can be decomposed in terms of normal modes in the following form:

$$\begin{aligned}{} & {} \left[ u, v, \xi , \eta , \phi , \Psi \right] \left( x, y, t\right) \nonumber \\{} & {} \quad =\left[ u^*, v^*, \xi ^*, \eta ^*, \phi ^*, \Psi ^*\right] (x)e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(24)

where $u^*, v^*, \xi ^*, \eta ^*, \phi ^*$ and $\Psi ^*$ are the amplitudes of the physical quantities, $\omega$ is the angular frequency, $\iota$ is the imaginary unit and m is the wave number in $y-$direction.

By owing expression (24), Eqs. (20)-(23) reduce to the following equations:

$$\begin{aligned}{} & {} ({f(T_0)}D^2-B_1)\xi ^*-B_2\eta ^*\nonumber \\{} & {} \quad +(B_{3}D^2-B_4)\phi ^*+A_3\Psi ^*=0, \end{aligned}$$

(25)

$$\begin{aligned}{} & {} B_2\xi ^*+(A_2D^2-B_5)\eta ^*=0, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} (A_4D^2-B_{6})\xi ^*+(B_{7}D^2-B_{8})\phi ^*\nonumber \\{} & {} \quad -(D^2-B_{9})\Psi ^*=0, \end{aligned}$$

(27)

$$\begin{aligned}{} & {} (B_{10}D^2-B_{11})\xi ^*-(B_{12}D^2-B_{13})\phi ^*\nonumber \\{} & {} \quad +B_{14}\Psi ^*=0, \end{aligned}$$

(28)

where

$$\begin{aligned}{} & {} D=\frac{\partial }{\partial x}, B_1=f(T_0)m^2+\omega ^2-\Omega ^2, B_2=2{\omega }{\Omega },\nonumber \\{} & {} \quad B_3=A_3A_{10}(1+\nu _0\omega ),\ B_4=A_3(1+\nu _0\omega )(1+A_{10}m^2),\nonumber \\{} & {} \quad B_5=m^2A_2+\omega ^2-\Omega ^2,\ B_{6}=m^2A_4, \nonumber \\{} & {} \quad B_{7}=A_5A_{10}(1+\nu _0\omega ),\ B_{8}=A_5(1+\nu _0\omega )(1+m^2A_{10}),\nonumber \\{} & {} \quad B_{9}=m^2+A_7+\omega ^2A_6, \ B_{10}=A_8\omega (1+n_0\nu _1\omega ),\nonumber \\{} & {} \quad B_{11}=m^2B_6,\ B_{12}=1+{\omega }A_{10}(1+\nu _1\omega ), \nonumber \\{} & {} \quad B_{13}=m^2+\omega (1+\nu _1\omega )(1+m^2A_{10}),\ B_{14}=A_9\omega . \end{aligned}$$

The non-trivial solution of the system of Eqs. (25)-(28) satisfies the following condition

$$\begin{aligned}{} & {} \left[ D^8-Y_1D^6+Y_2D^4-Y_3D^2+Y_4\right] \nonumber \\{} & {} \quad (\xi ^*(x), \eta ^*(x), \phi ^*(x), \Psi ^*(x))=0, \end{aligned}$$

(29)

where

$$\begin{aligned}{} & {} Y_1=\frac{X_2}{X_1},\ Y_2=\frac{X_3}{X_1},\ Y_3=\frac{X_4}{X_1},\ Y_4=\frac{X_5}{X_1},\\{} & {} X_1=B_{12}F_1+F_4B_{10},\\{} & {} X_2=B_{12}F_2+B_{10}F_5+F_1G_3+F_4G_1,\\{} & {} X_3=B_{12}F_3+B_{10}F_6+F_1G_4+F_2G_3+F_5G_1+F_4G_2, \\{} & {} X_4=F_3G_3+F_2G_4+F_5G_2+F_6G_1,\\{} & {} X_5=F_3G_4+F_6G_2,\ F_1=B_{14}E_1-E_7B_{10}, \\{} & {} F_2=-E_7B_{11}-E_8B_{10}+E_2B_{14}, \ F_3=B_{14}E_3-E_8B_{11}, \\{} & {} F_4=E_7B_{12}+E_4B_{14}, \ F_5=E_7B_{13}+E_8B_{12}+E_5B_{14},\\{} & {} F_6=E_8B_{13}+E_6B_{14},\ G_1=B_{11}+B_9B_{10}-B_{14}A_4, \\{} & {} G_2=B_9B_{11}-B_{6}B_{14},\ G_3=B_{13}+B_9B_{12}+B_{7}B_{14},\\{} & {} G_4=B_9B_{13}+B_{8}B_{14}, \ E_1=f(T_0)A_2,\ E_2=A_2B_1+f(T_0)B_5,\\{} & {} E_3=B_1B_5+B_2^2,\ E_4=A_2B_3, \ E_5=A_2B_4+B_3B_5,\\{} & {} E_6=B_4B_5,\ E_7=A_2A_3,\ E_8=A_3B_5. \end{aligned}$$

The solution of Eq. (29), which is bounded as $x\rightarrow \infty$, is given by

$$\begin{aligned}{} & {} [\xi ^*, \eta ^*, \phi ^*, \Psi ^*](x)\nonumber \\{} & {} \quad =\sum _{i=1}^4[1, H_{1i}, H_{2i}, H_{3i}]M_i(m,\omega )e^{-\lambda _ix}, \end{aligned}$$

(30)

where $\lambda _{i}~(i=1,\ 2,\ 3,\ 4)$ with positive real parts are the characteristic roots of Eq. (29), $M_{i}(m,\omega )~(i=1,\ 2,\ 3,\ 4)$ are arbitrary constants and $H_{1i}, H_{2i}$ and $H_{3i}~(i=1,\ 2,\ 3,\ 4)$ are the coupling parameters directly obtained from Eqs. (25)-(28) as:

$$\begin{aligned}{} & {} H_{1i}=-\frac{B_2}{A_2\lambda _i^2-B_5}, H_{2i}=\frac{B_{10}\lambda _{i}^4-G_1\lambda _{i}^2+G_2}{B_{12}\lambda _{i}^4-G_3\lambda _{i}^2+G_4},\\{} & {} \quad H_{3i}=\frac{(B_{12}\lambda _i^2-B_{13})H_{2i}-(B_{10}\lambda _i^2-B_{11})}{B_{14}}. \end{aligned}$$

Using expressions (24) and (30) in Eqs. (19) and (8), we get

$$\begin{aligned}{}[u^*, v^*, \theta ^*](x)=\sum _{i=1}^4[H_{4i}, H_{5i}, H_{6i}]M_i(m,\omega )e^{-\lambda _ix}, \end{aligned}$$

(31)

where   $H_{4i}=-\lambda _{i}+\iota mH_{1i}, \ \ H_{5i}=\iota m+\lambda _{i}H_{1i},\ \ H_{6i}=[1-A_{10}(\lambda _i^2-m^2)]H_{2i}.$

The usage of non-dimensional quantities given in (18) and normal mode analysis defined in (24), converts the stress expressions (12)-(13) to the form

$$\begin{aligned}{}[\sigma _{xx}^*, \sigma _{yy}^*, \sigma _{xy}^*](x)=\sum _{i=1}^4[L_{1i}, L_{2i}, L_{3i}]M_i(m,\omega )e^{-\lambda _ix}, \end{aligned}$$

(32)

where

$$\begin{aligned}{} & {} L_{1i}=-f(T_0)\lambda _{i}H_{4i}+(A_1-A_2)\iota mH_{5i}-A_3(1+\nu _0\omega )H_{6i}+A_{3}H_{3i},\\& L_{2i}=f(T_0)\iota mH_{5i}-(A_1-A_2)\lambda _iH_{4i}-A_3(1+\nu _0\omega )H_{6i}+A_{3}H_{3i},\\& L_{3i}=A_{2}(\iota mH_{4i}-\lambda _iH_{5i}). \end{aligned}$$

Application: Inclined Mechanical Load on the Surface of half-Space

We take into account a homogeneous, isotropic rotating microelongated thermoelastic half-space with a quiescent initial state occupying the region $x\ge 0$. An inclined mechanical load $R=(R_1,R_2,0)$ with an angle $\delta$, measured from the negative x-axis, is applied to the half-space. The applied load is divided into two components: a normal component $R_1=R$cos$\delta$ and a shear component $R_2=R$sin$\delta$. The elongation scalar function can be freely chosen with the boundary of the half-space being considered to be isothermal. Mathematically, the boundary conditions can be expressed as:

$$\begin{aligned} \sigma _{xx}(0,y,t)= & {} -R_1\psi _1(y,t), \end{aligned}$$

(33)

$$\begin{aligned} \sigma _{xy}(0,y,t)= & {} -R_2\psi _1(y,t), \end{aligned}$$

(34)

$$\begin{aligned} \phi (0,y,t)= & {} 0, \end{aligned}$$

(35)

$$\begin{aligned} \Psi (0,y,t)= & {} 0, \end{aligned}$$

(36)

where $\psi _1=e^{({\omega }t+{\iota }my)}.$

Fig. 1

Geometry of the problem

Inducing non-dimensional variables given by (18) with $\displaystyle R'=\frac{R}{\rho c_1^2}$ and after applying normal mode technique defined in (24), the above boundary conditions reduce to

$$\begin{aligned} \sigma ^*_{xx}(x)= & {} -R_1, \end{aligned}$$

(37)

$$\begin{aligned} \sigma ^*_{xy}(x)= & {} -R_2, \end{aligned}$$

(38)

$$\begin{aligned} \phi ^*(x)= & {} 0, \end{aligned}$$

(39)

$$\begin{aligned} \Psi ^*(x)= & {} 0~~~~~~\textrm{at}~x=0. \end{aligned}$$

(40)

Taking into account the non-dimensional expressions from Eqs. (30) and (32), the above mentioned boundary conditions transform into a set of non-homogeneous system of four equations, which can be simply written in matrix notation as follows:

$$\begin{aligned}{} & {} \left[ \begin{array}{rrrr}L_{11}&{}L_{12}&{}L_{13}&{}L_{14}\\ L_{31}&{}L_{32}&{}L_{33}&{}L_{34}\\ H_{21}&{}H_{22}&{}H_{23}&{}H_{24}\\ H_{31}&{}H_{32}&{}H_{33}&{}H_{34}\end{array}\right] \left[ \begin{array}{rrrr}M_{1}\\ M_{2}\\ M_{3}\\ M_{4}\end{array}\right] =\left[ \begin{array}{rrrr} -R_1 \\ -R_2 \\ 0 \\ 0 \end{array}\right] . \end{aligned}$$

(41)

The expressions of parameters $M_{i}~(i=1,2,3,4)$ can be obtained as a result of solving the system of Eqs. (41):

$$\begin{aligned}{} & {} M_1=\frac{\Delta _1}{\Delta },\ M_2=\frac{\Delta _2}{\Delta },\ M_3=\frac{\Delta _3}{\Delta },\ M_4=\frac{\Delta _4}{\Delta }, \end{aligned}$$

(42)

where

$$\begin{aligned}{} & {} \Delta =H_{21}[H_{32}(L_{13}L_{34}-L_{14}L_{33})-H_{33}(L_{12}L_{34}-L_{14}L_{32})\\{} & {} +H_{34}(L_{12}L_{33}-L_{13}L_{32})] \\{} & {} +H_{22}[H_{31}(L_{14}L_{33}-L_{13}L_{34})+H_{33}(L_{11}L_{34}-L_{14}L_{31})\\{} & {} -H_{34}(L_{11}L_{33}-L_{13}L_{31})] \\{} & {} +H_{23}[H_{31}(L_{12}L_{34}-L_{14}L_{32})-H_{32}(L_{11}L_{34}-L_{14}L_{31})\\{} & {} +H_{34}(L_{11}L_{32}-L_{12}L_{31})] \\{} & {} +H_{24}[H_{31}(L_{13}L_{32}-L_{12}L_{33})-H_{32}(L_{11}L_{33}-L_{13}L_{31})\\{} & {} -H_{33}(L_{11}L_{32}-L_{12}L_{31})],\\{} & {} \Delta _1=H_{22}[H_{33}(L_{14}R_2-L_{34}R_1)-H_{34}(L_{13}R_2-L_{33}R_1)]\\{} & {} +H_{23}[H_{34}(L_{12}R_2-L_{32}R_1)-H_{32}(L_{14}R_2-L_{34}R_1)]\\{} & {} +H_{24}[H_{32}(L_{13}R_2-L_{33}R_1)-H_{33}(L_{13}R_2-L_{32}R_1)],\\{} & {} \Delta _2=H_{21}[H_{34}(L_{13}R_2-L_{33}R_1)-H_{33}(L_{14}R_2-L_{34}R_1)]\\{} & {} +H_{23}[H_{31}(L_{14}R_2-L_{34}R_1)-H_{34}(L_{11}R_2-L_{31}R_1)]\\{} & {} +H_{24}[H_{33}(L_{11}R_2-L_{31}R_1)-H_{31}(L_{13}R_2-L_{33}R_1)],\\{} & {} \Delta _3=H_{21}[H_{32}(L_{14}R_2-L_{34}R_1)-H_{34}(L_{12}R_2-L_{32}R_1)]\\{} & {} +H_{22}[H_{34}(L_{11}R_2-L_{31}R_1)-H_{31}(L_{14}R_2-L_{34}R_1)]\\{} & {} +H_{24}[H_{31}(L_{12}R_2-L_{32}R_1)-H_{32}(L_{11}R_2-L_{31}R_1)],\\{} & {} \Delta _4=H_{21}[H_{33}(L_{12}R_2-L_{32}R_1)-H_{32}(L_{13}R_2-L_{33}R_1)]\\{} & {} +H_{22}[H_{31}(L_{13}R_2-L_{33}R_1)-H_{33}(L_{11}R_2-L_{31}R_1)]\\{} & {} +H_{23}[H_{32}(L_{11}R_2-L_{31}R_1)-H_{31}(L_{12}R_2-L_{32}R_1)]. \end{aligned}$$

Substituting $M_{i}~(i=1,2,3,4)$ from (42) into expressions (30–32) along with (24) to obtain the expressions for field quantities i.e. displacement components, temperature distributions, stresses and microelongation for a homogeneous, isotropic, rotating microelongated thermoelastic medium, one can get

$$\begin{aligned}{} & {} \left[ \xi , \eta , \phi , \Psi \right] (x,y,t)\nonumber \\{} & {} \quad = \frac{1}{\Delta }\sum _{i=1}^4[1, H_{1i}, H_{2i}, H_{3i}]\Delta _{i}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} \left[ u, v, \theta \right] (x,y,t)\nonumber \\{} & {} \quad =\frac{1}{\Delta }\sum _{i=1}^4(H_{4i}, H_{5i}, H_{6i})\Delta _{i}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(44)

$$\begin{aligned}{} & {} \left[ \sigma _{xx}, \sigma _{yy}, \sigma _{xy}\right] (x,y,t)\nonumber \\{} & {} \quad =\frac{1}{\Delta }\sum _{i=1}^4(L_{1i}, L_{2i}, L_{3i})\Delta _{i}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}. \end{aligned}$$

(45)

Special cases

Ignoring rotation effect

In this situation, setting the angular velocity to zero i.e. $\Omega =0$ into the equation of motion to get a different set of equations from (25) and (26). Thus the set of equations analogous to Eqs. (25–28) provide

$$\begin{aligned}{} & {} \left[ D^6-{Y'_1}D^4+{Y'_2}D^2-{Y'_3}\right] (\xi ^*(x), \phi ^*(x), \Psi ^*(x))=0, \end{aligned}$$

(46)

$$\begin{aligned}{} & {} \left[ A_2D^2-B'_2\right] \eta ^*(x)=0. \end{aligned}$$

(47)

Then the corresponding expressions for displacement components, temperature distributions, stresses and microelongation for a homogeneous isotropic microelongated thermoelastic medium are obtained as:

$$\begin{aligned}{} & {} \left[ \xi , \phi , \Psi \right] (x,y,t)\nonumber \\{} & {} \quad = \frac{1}{\Delta '}\sum _{i=5}^7[1, {H'_{1i}}, {H'_{2i}}]{\Delta '_{i}}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(48)

$$\begin{aligned}{} & {} \eta (x,y,t)=\frac{{\Delta '_{8}}}{\Delta '}e^{-\lambda _{8}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(49)

$$\begin{aligned}{} & {} \left[ u, v \right] (x,y,t)=\frac{1}{\Delta '}\sum _{i=5}^8({H'_{3i}}, {H'_{4i}}){\Delta '_{i}}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(50)

$$\begin{aligned}{} & {} \theta (x,y,t)=\frac{1}{\Delta '}\sum _{i=5}^7H'_{5i}{\Delta '_{i}}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(51)

$$\begin{aligned}{} & {} \left[ \sigma _{xx}, \sigma _{yy}, \sigma _{xy}\right] (x,y,t)\nonumber \\{} & {} \quad =\frac{1}{\Delta '}\sum _{i=5}^8({L'_{1i}}, {L'_{2i}}, {L'_{3i}}){\Delta '_{i}}e^{-\lambda _{i}x}e^{({\omega }t+{\iota }my)}, \end{aligned}$$

(52)

where above defined $\lambda _{i} (i=5,6,7)$ are the roots of the characteristic Eq. (46) and $\lambda _8$ is the solution of Eq. (47) with coefficients

$$\begin{aligned}{} & {} {Y'_1}=\frac{X'_2}{X'_1},\ {Y'_2}=\frac{X'_3}{X'_1},\\{} & {} \quad {Y'_3}=\frac{X'_4}{X'_1},\ {B'}_2=m^2A_2+\omega ^2, \end{aligned}$$

where 

$$\begin{aligned}{} {} {X'_1}&=B_3{E'_1}-f(T_0){E'_3},\\{} & {} {X'_2}=B_3{E'_2}+{E'_1}{F'_3}-f(T_0){E'_4}-{F'_1}{E'_3},\\{} {} {X'_3}=\,\,&{E'_2}{F'_3}+{E'_1}{F'_4}-{F'_1}{E'_4}-{F'_2}{E'_3},\\{} & {} {X'_4}={F'_4}{E'_2}-{F'_2}{E'_4},\ E'_1=f(T_0)B_{10}-A_3B_6,\\{} & {} E'_2=B_{10}B'_1-A_3B_7,\ E'_3=B_3B_{10}+A_3B_8,\ E'_4=B_4B_{10}+A_3B_9,\\{} & {} F'_1=B'_1+f(T_0)B_{14}-A_3A_7,\ F'_2=B_{14}B'_1-A_3B_{11},\\{} & {} F'_3=B_4+B_3B_{14}-A_3B_{12}, \ F'_4=B_4B_{14}-A_3B_{13},\\{} & {} {B'}_1=f(T_0)m^2+\omega ^2, \\{} & {} {\Delta '}={H'_{15}}{[H'_{26}}({L'_{17}}{L'_{38}}-{L'_{18}}{L'_{37}})\\{} & {} -{H'_{27}}({L'_{16}}{L'_{38}}-{L'_{18}}{L'_{36}})]\\{} & {} +{H'_{16}}[{H'_{25}}({L'_{18}}{L'_{37}}-{L'_{17}}{L'_{38}})\\{} & {} +{H'_{27}}({L'_{15}}{L'_{38}}-{L'_{18}}{L'_{35}})] \\{} & {} +{H'_{17}}[{H'_{25}}({L'_{16}}{L'_{38}}-{L'_{18}}{L'_{36}})\\{} & {} -{H'_{26}}({L'_{15}}{L'_{38}}-{L'_{18}}{L'_{35}})],\\{} & {} {\Delta '_5}={H'_{16}}{H'_{27}}({L'_{18}}R_2-{L'_{38}}R_1)\\{} & {} -{H'_{17}}{H'_{26}}({L'_{18}}R_2-{L'_{38}}R_1),\\{} & {} {\Delta '_6}=-{H'_{15}}{H'_{27}}({L'_{18}}R_2-{L'_{38}}R_1)]\\{} & {} +{H'_{17}}{H'_{25}}({L'_{18}}R_2-{L'_{38}}R_1),\\{} & {} {\Delta '_7}={H'_{15}}{H'_{26}}({L'_{18}}R_2-{L'_{38}}R_1)\\{} & {} -{H'_{16}}{H'_{25}}({L'_{18}}R_2-{L'_{38}}R_1),\\{} {} {\Delta '_8} &={H'_{15}}[{H'_{27}}({L'_{16}}R_2-{L'_{36}}R_1)\\{} & {} -{H'_{26}}({L'_{17}}R_2-{L'_{37}}R_1)]\\{} & {} +{H'_{16}}[{H'_{25}}({L'_{17}}R_2-{L'_{37}}R_1)-{H'_{27}}({L'_{15}}R_2-{L'_{35}}R_1)]\\{} & {} +{H'_{17}}[{H'_{36}}({L'_{15}}R_2-{L'_{35}}R_1)-{H'_{25}}({L'_{16}}R_2-{L'_{36}}R_1)]. \end{aligned}$$

Coupling parameters in this case are given as:

$$\begin{aligned}{} & {} {H'_{1i}}=-\frac{{E'_1}\lambda _{i}^2-{E'_2}}{{E'_3}\lambda _i^2-{E'_4}},\\{} & {} {H'_{2i}}=-\frac{(f(T_0)\lambda _{i}^2-{B'_1})+(B_3\lambda _i^2-B_4){H'_{1i}}}{A_3},\\{} & {} {H'_{3i}}=-\lambda _i,\ {H'_{4i}}=\iota m,\ {H'_{5i}}=[1-A_{10}(\lambda _i^2-m^2)]{H'_{1i}},\\{} & {} {L'_{1i}}=-f(T_0)\lambda _{i}{H'_{3i}}+(A_1-A_2)\iota m{H'_{4i}}\\{} & {} -A_3(1+\nu _0\omega ){H'_{5i}}+A_{3}{H'_{2i}},\\{} & {} {L'_{2i}}=f(T_0)\iota m{H'_{4i}}-(A_1-A_2)\lambda _i{H'_{3i}}\\{} & {} -A_3(1+\nu _0\omega ){H'_{5i}}+A_{3}{H'_{2i}},\\{} & {} {L'_{3i}}=-2\iota m A_{2}\lambda _i, \ (i=5,6,7),\ {H'_{38}}=\iota m,\ {H'_{48}}=\lambda _8,\\{} & {} {L'_{18}}=\iota m\lambda _8[(A_1-A_2)-1],\\{} & {} {L'_{28}}=-{L'_{18}},\ {L'_{38}}=-A_2(\lambda _8^2+m^2). \end{aligned}$$

Further by ignoring the microelongation effect (i.e. $\lambda _0=\lambda _1=a_0=\gamma =j_0=0$) in this specific case, our results match with those obtained by Othman et al. [41] (after neglecting gravity field and voids) with an appropriate change in the boundary conditions and theory used.

Without Two Temperature

To neglect two temperature effect, it is sufficient to adjust the value of two temperature parameter $a=0$. With this modification, we get the corresponding analytic expressions for all the field variables with one temperature i.e. thermodynamical temperature.

Neglecting Temperature Dependent Properties

In this case, we assume that the material’s constants are independent of temperature. It is sufficient to adjust the value of $\alpha ^*=0$ i.e. $f(T_0)=1$ in the governing equations to obtain the suitable expressions for rotating two temperature microelogated thermoelastic medium under LS and GL theories. If we further consider one temperature case only, then the outcomes coincide with those of Othman et al. [42] (ignoring DPL model), by making suitable changes in the boundary conditions.

Computational Results and Discussion

An analytical numerical procedure is conducted to investigate the effects of rotation, two temperatures, temperature dependence of material’s constants and time on the field variables for GL theory. We have selected a material that resembles aluminum-epoxy for illustrative purposes. The material constants are taken as (Shaw and Mukhopadhyay [14]):

$$\begin{aligned}{} & {} \lambda ^*=7.59\times 10^{10}N/m^2,\ \mu ^*=1.89\times 10^{10}N/m^2,\\{} & {} \beta ^*=\gamma ^*=0.05\times 10^{5}N/m^2K,\\{} & {} \rho =2.19\times 10^3Kg/m^3,\ C_E=966J/KgK,\\{} & {} K=252J/msK,\ j_0=0.196\times 10^{-4}m^2,\\{} & {} \lambda ^*_0=\lambda ^*_1=0.37\times 10^{10}N/m^2,\ a^*_0=0.61\times 10^{-9}N,\\{} & {} T_0=293K,\ a=0.74\times 10^{-15}m^2, \\{} & {} \alpha ^*=0.0001K^{-1},\ \nu _0=0.03s,\ \nu _1=0.01s,\ \Omega =0.3. \end{aligned}$$

Since $\omega =\omega _{0}+\iota \omega _{1}$ is the complex constant term, so that $e^{\omega t}=e^{\omega _{0}t}[\cos (\omega _{1}t)+\iota \sin (\omega _{1}t)]$. When time is small, we might consider $\omega$ to be real i.e. $\omega =\omega _{0}$. The additional material constants used for numerical computation purpose in the problem are taken as: $\omega =5,$$m=1.2$. Adjusting R and $\delta$ with 1 and $60^o$ respectively, we get $R_1=\frac{1}{2}$ and $R_2=\frac{\sqrt{3}}{2}$ from the relation $R_1=R$cos$\delta$ and $R_2=R$sin$\delta$.

With these mentioned numerical data, the values of non-dimensional field variables have been calculated using the MATLAB software and the results are presented in the form of graphs at various points of x at $t=0.1$ and $y=1$. The graphical depiction has been broken into five groups for clarity:

Group I: In Figs. 2, 3, 4, 5, 6 and 7, we have shown the ascendancy of rotation parameter on the various physical fields under GL theory. Here, the solid line indicates the medium rotating with angular velocity ($\Omega =0.3$), the dashed line represents the medium rotating with angular velocity ($\Omega =0.2$) and the dotted line corresponds to the medium rotating with angular velocity ($\Omega =0.1$).

Fig. 2

Impact of rotation on normal displacement distribution

Fig. 3

Impact of rotation on conductive temperature distribution

Fig. 4

Impact of rotation on thermodynamical temperature distribution

Fig. 5

Impact of rotation on normal stress distribution

Fig. 6

Impact of rotation on tangential stress distribution

Fig. 7

Impact of rotation on microelongation distribution

Group II: Figs. 8, 9, 10, 11, 12 and 13 examine the variations of field variables for different values of the inclination angle of load ($\delta =60^o$(solid line), $\delta =30^o$(dashed line), $\delta =0^o$(dotted line)) for GL theory.

Fig. 8

Impact of angle of inclination on normal displacement distribution

Fig. 9

Impact of angle of inclination on conductive temperature distribution

Fig. 10

Impact of angle of inclination on thermodynamical temperature distribution

Fig. 11

Impact of angle of inclination on normal stress distribution

Fig. 12

Impact of angle of inclination on tangential stress distribution

Fig. 13

Impact of angle of inclination on microelongation distribution

Group III: Figs. 14, 15, 16, 17, 18 and 19 are concerned with the investigation of the influence of temperature dependent properties and two temperature parameter on a rotating microelongated solid. Solid line refers to a rotating microelongated solid with two temperature and temperature dependent properties (RMTTTDP). The dashed line shows the rotating microelongated solid with two temperature (RMTT) and dotted line indicates the rotating microelongated solid with temperature dependent properties (RMTDP) for GL theory.

Fig. 14

Impact of two temperature parameter and temperature dependent properties on displacement distribution

Fig. 15

Impact of two temperature parameter and temperature dependent properties on conductive temperature distribution

Fig. 16

Impact of two temperature parameter and temperature dependent properties on thermodynamical temperature distribution

Fig. 17

Impact of two temperature parameter and temperature dependent properties on normal stress distribution

Fig. 18

Impact of two temperature parameter and temperature dependent properties on tangential stress distribution

Fig. 19

Impact of two temperature parameter and temperature dependent properties on microelongation distribution

Group IV: This group consisting of Figs. 20, 21, 22, 23, 24 and 25, displays the impact of three different values of microelongational parameter: $a^*_{0}=0.61\times 10^{-9}$ (solid line), $a^*_{0}=0.61\times 10^{-4}$ (dashed line), $a^*_{0}=0.61\times 10^{-1}$ (dotted line) on all the physical fields.

Fig. 20

Impact of microelongation parameter on displacement distribution

Fig. 21

Impact of microelongation parameter on conductive temperature distribution

Fig. 22

Impact of microelongation parameter on thermodynamical temperature distribution

Fig. 23

Impact of microelongation parameter on normal stress distribution

Fig. 24

Impact of microelongation parameter on tangential stress distribution

Fig. 25

Impact of microelongation parameter on microelongation distribution

Group V: For a wide range of dimensionless variables $x~(0\le x\le 3)$ and $t~(0\le t\le 0.3)$, the solution curves of non-dimensional physical quantities in 3-dimensional variations for GL theory are presented in Figs. 26, 27, 28, 29, 30 and 31.

Fig. 26

Profile of normal displacement distribution

Fig. 27

Profile of conductive temperature distribution

Fig. 28

Profile of thermodynamical temperature distribution

Fig. 29

Profile of normal stress distribution

Fig. 30

Profile of tangential stress distribution

Fig. 31

Profile of microelongation distribution

Group I: Figs. 2, 3, 4, 5, 6 and 7 focus on the variations of all the physical field quantities with distance x for three particular values of rotation parameter (i.e. angular velocity $\Omega =0.3,\ 0.2,\ 0.1$). Figure 2 depicts the spatial variations of normal displacement component for different values of $\Omega$. The figure shows that a decrease in the value of angular velocity results in a decrease in the value of the displacement field, which means that the angular velocity is having a notable increasing impact on the profile of normal displacement. In Fig. 3, effect of variation of $\Omega$ on conductive temperature $\phi$ is depicted. A decrease in angular velocity results in a decrement in the magnitude of conductive temperature. Conductive temperature is having a coincident starting point with a value zero for all the curves, which is in quite good agreement with the boundary condition. All the curves show a similar pattern for all the three values of $\Omega$ and the effect of angular velocity fades as we move away from the boundary. Figure 4 presents the variations of thermodynamical temperature $\theta$ versus distance x for different values of $\Omega$, which decreases with the decrease in the value of angular velocity. The profile of $\theta$ exhibits an increasing effect of angular velocity.

The normal stress variations against location x for different values of angular velocity are shown in Fig. 5. The normal stress component starts with negative values for all the three values of angular velocity and its absolute value decreases with decreasing value of angular velocity. Figure 6 depicts the effect of angular velocity on tangential stress distribution. The nature of tangential stress corresponding to all the three values of angular velocity is same as that of normal stress. Both, normal stress and tangential stress tend to zero after starting with some negative values, which is in favour of boundary conditions and generalized theory of thermoelasticity. Variation in microelongation has been exposed in Fig. 7 for three values of angular velocity. It is observed from the figure that the numerical value of microelongation increases with the decrease in angular velocity. All the solution curves reveal the same behavior with different magnitudes for all the three values of angular velocity.

Group II: Figs. 8, 9, 10, 11, 12 and 13 display the variations of field quantities against the horizontal distance x for different values of the inclination angle ($\delta =60^o, 30^o, 0^o$). In Fig. 8, a similar trend of distribution of normal displacement is observed for the three considered values of inclination angle $\delta$ (i.e., $\delta =60^o, 30^o$ and $0^o$). The figure reveals that the value of normal displacement for inclination angle $30^o$ is higher than that for inclination angle $60^o$. Corresponding to $\delta =0^o$, the inclined load becomes the normal load; therefore normal load has a significant increasing effect on the normal displacement to a specific range of x and has different effects in rest of the domain. The impact of inclination angle on conductive temperature is analyzed through Fig. 9. It can be visualized from the figure that the trend remains same for all the three cases and all the curves have a coincident starting point with value zero, which leads to satisfy the boundary condition. The effect of inclination angle on thermodynamical temperature is shown in Fig. 10. The behavior of the thermodynamical temperature field is almost same for all the considered values of inclination angle and normal load shows a mixed kind of effect against the inclination angle $60^o$.

Fig. 11 clarifies the variations in the normal stress $\sigma _{xx}$ corresponding to different inclination angles. It is observed that the absolute value of normal stress is higher for inclination angle $\delta =30^o$ as compared to $\delta =60^o$ but in case, when the normal load (i.e. $\delta =0^o$) is applied, it provides a mixed kind of effect with respect to inclination angles $60^o$ and $30^o$. The tangential stress experiences a significant impact corresponding to different inclination angles as depicted in Fig. 12. Tangential stress starts with some negative numerical values and then tends to zero as x increases, corresponding to $\delta =60^o$ and $30^o$. As expected, the value of tangential stress starts from zero for normal load and it exhibits extremely small values in comparison with the other curves. Figure 13 provides the detail about the microelongation field variable under different inclination angles. It is manifested from the plot that microelongation starts with a zero value for all the curves, which is in quite a perfect accord with the boundary condition and its magnitude increases with changing inclination angle from $60^o$ to $30^o$.

Group III: In Figs. 14, 15, 16, 17, 18 and 19, we have plotted the solution curves of non dimensional physical quantities for three different cases: (i) Rotating microelongated medium with two temperature and temperature dependent properties (RMTTTDP), (ii) Rotating microelongated medium with two temperature (RMTT), (iii) Rotating microelongated medium with temperature dependent properties (RMTDP). Figure 14 exhibits that the distribution of normal displacement shows a similar pattern for with and without two temperature and also for with and without temperature dependent properties with difference in magnitude. The presence of two temperature and temperature dependent properties increases the magnitude of normal displacement. Figures 15, 16, 17, 18 and 19 indicate that temperature dependent properties have a similar effect (i.e. decreasing) on these field variables. In the absence of two temperature parameter, the conductive temperature becomes the thermodynamical temperature. Thermodynamical temperature firstly undergoes an increasing effect of two temperature parameter in a certain range of distance x and thereafter a reverse pattern of the profile is observed in Fig. 16. Figures 17 and 19 display that two temperature parameter has a numerically decreasing effect on normal stress and microelongation respectively. Tangential stress experiences an absolutely increasing impact in the presence of two temperature, which is shown by Fig. 18. Therefore, the presence of two temperature parameter and temperature dependent properties have a significant impact on all the field quantities.

Group IV: In Figs. 20, 21, 22, 23, 24 and 25, we have explored the effect of elongation parameter by taking three different values of $a^*_{0}$ (i.e. $a^*_{0}=0.61\times 10^{-9}, \ 0.61\times 10^{-4}, \ 0.61\times 10^{-1}$) for GL theory. A comparison of normal displacement profile for different values of $a^*_0$ has been made in Fig. 20. It is evident from the plot that there is an increment in magnitudes of normal displacement with an increasing value of $a^*_0$. Figures 21–23 show the dynamic effects of elongational parameter on conductive temperature, thermodynamical temperature and normal stress. It is found that these fields experience a decreasing effect with $a^*_0$. The behavior of tangential stress and microelongation under the three considered values of $a^*_0$ are observed by Figs. 24 and 25. Tangential stress and microelongation have a notable increasing effect with $a^*_0$. It is also noticed from the figures that all the field variables are following the same trend for the considered values of $a^*_0$.

Group V: We have illustrated the variations of field distributions with distance x and time t by Figs. 26, 27, 28, 29, 30 and 31. From Fig. 26, it is clearly observed that displacement field firstly increases to a small extent and then decreases gradually and tends to zero. The increase in the value of time results in an increase in the numerical values of normal displacement. The variation of conductive temperature versus distance x and time t is depicted in Fig. 27. Numerical values of conductive temperature after starting with value zero increase for some values of x and then decrease towards zero as we move far from the boundary. It also exhibits an increasing effect with time t. Figures 28 and 30 indicate that the numerical values of thermodynamical temperature and tangential stress show the maximum values in the locality of source which decrease with the increase in distance x. Both fields experience an increasing trend with time. From the Figs. 29 and 31, one can observe that the numerical values of normal stress and microelongation firstly increase to a maximum value, then undergo a decreasing pattern and approach to zero for higher x. Normal stress and microelongation also experience an increasing behavior with time t.

Concluding Remarks

The primary objective of the current research is to develop a mathematical model that predicts the behavior of normal displacement, normal stress, tangential stress, temperature distributions and microelongation in a rotating thermoelastic medium with two temperature and temperature dependent properties under the LS and GL theories. The normal mode approach used here provides an exact solution without imposing any assertions on the real physical quantities. It may be used to solve a broad variety of thermodynamic-related issues. Theoretical and numerical findings show that the physical variables under consideration are significantly influenced by rotation, two temperature parameter, temperature dependent properties, inclination angle and elongational parameter. From this research, one can infer that

• The generalized thermoelasticity hypothesis is supported by the fact that all the physical variables have non-zero values only in the small domain of space, which is evident from all the figures.

• It is clearly observed from the figures that all the physical fields satisfy the boundary condition.

• It can be concluded that rotation parameter significantly affects the variations of the obtained physical quantities. Normal displacement, conductive temperature, thermodynamical temperature, normal stress and tangential stress attain an increasing effect in their absolute values with increasing value of rotation parameter.

• All the physical quantities are quite sensitive towards the two temperature parameter. Normal displacement and tangential stress show increasing effect while normal stress and microelongation experience decreasing effect in the presence of two temperature parameter. A mixed kind of effect of two temperature parameter is observed on thermodynamical temperature. Also in the absence of two temperature parameter, the conductive temperature coincides with the thermodynamical temperature which supports the theoretical formulation.

• Temperature dependency of material’s constants strongly affects all the field variables. It has a decreasing effect on conductive temperature, thermodynamical temperature, normal stress, tangential stress and microelongation while an increasing effect is observed on normal displacement distribution.

• All the field variables show a similar pattern for different values of inclination angle $\delta$ of the applied mechanical load except for $\delta =0^o$. With the decrease in the value of angle of inclination from $60^o$ to $30^o$, there can be seen an increase in the magnitude of all the field quantities except tangential stress. Also, in the case of normal load $(\delta =0^o)$, a different behavior of all the field quantities can be observed.

• Changing the value of $a^*_0$ (i.e. elongational parameter) plays an important role in the distribution of the field quantities. Microelongation parameter has an increasing effect on normal displacement, tangential stress, microelongation distribution but a reverse effect is observed on all other distributions.

• A similar pattern of variations of all the physical quantities is observed for different values of time t and an increment in the value of time causes an increment in the magnitude of all the field variables.

The above research is of fundamental importance and finds its applications for experimental researchers/engineers working in the field of geophysics, seismology, material science and earthquake engineering. Microelongated materials can be widely used for various sensors, medical devices, computer processors, accelerometers, inertial sensors and electrical circuits etc.