Generalized Thermoelastic Medium with Temperature-Dependent Properties for Different Theories under the Effect of Gravity Field

Abstract

The problem of the generalized thermoelastic medium for three different theories under the effect of a gravity field is investigated. The Lord–Shulman (L–S), Green–Lindsay (G–L), and classical-coupled (CD) theories are discussed. The modulus of the elasticity is given as a linear function of the reference temperature. The exact expressions for the displacement components, temperature, and stress components are obtained by using normal mode analysis. Numerical results for the field quantities are given in the physical domain and illustrated graphically in the absence and presence of gravity. A comparison also is made between the three theories for the results with and without a temperature dependence.

1 Introduction

The effect of mechanical and thermal disturbances on an elastic body is studied by the theory of thermoelasticity. This theory has two defects. This theory has been studied by Biot [1]. He deals with a defect of the uncoupled theory that mechanical causes have no effect on temperature. This theory predicts an infinite speed of propagation of heat waves which is a defect that it shares with the uncoupled theory. The generalized theories of thermoelasticity are developed to remove this paradox [2]. The first theory was studied by Lord and Shulman (L–S) [3]. They introduced the notation of a time-dependent relaxation time model based on the concept of relaxing of the flux in a classical Fourier’s model for the heat conduction [4]. The second theory was discussed by Green–Lindsay (G–L) [4]. They introduced two different relaxation times in the entropy expression and stress–strain relations [5]. All these theories predict a finite speed of the thermal disturbance propagation.

The thermal stress in a material with temperature-dependent properties was studied extensively by Noda [6]. Material properties such as the modulus of elasticity and the thermal conductivity vary with temperature. When the temperature variation from the initial stress is not strongly varying, the properties of materials are constants. In the refractory industries, the structural components are exposed to a high temperature change. In this case, neglecting the temperature dependence will result in errors in material properties [7]. The dependence of the modulus of elasticity and the thermal conductivity on a reference temperature in the generalized thermoelasticity for an infinite material with a spherical cavity is discussed by Youssef [8]. Othman et al. [9–12] studied the two-dimensional problem of generalized thermoelasticity with temperature-dependent elastic moduli for different theories. However, the effect of gravity on elastic surface waves is discussed by Biot [13]. The force of gravity was assumed to create an initial stress of a hydrostatic nature. Sengupta et al. [14] studied the effect of gravity on some problems of propagation of waves in an anisotropic elastic solid medium. Ahamed [15] investigated the Stoneley waves in a non-homogeneous orthotropic granular medium under the influence of a gravitational field. Vinh and Seriani [16] studied the problem of Rayleigh waves in a non-homogeneous orthotropic elastic medium under the effect of gravity. Abd-Alla et al. [17–21] investigated the influence of gravity for different theories. In seismology and geophysics, the problem of the propagation of Rayleigh waves under the effect of gravity is significant [22].

In the present work, we shall formulate the generalized thermoelastic medium with temperature-dependent properties for three theories under the influence of gravity and solve for the temperature, stress components, and displacement components. The normal mode method is used to obtain the exact expression for the considered variables. A comparison is carried out between the considered variables as calculated from the generalized thermoelasticity based on L–S, G–L, and coupled theories in the absence and presence of gravity. A comparison also is made between the three theories with and without temperature dependence.

2 Formulation of the Problem

We consider a homogeneous isotropic elastic body in a half-space $z \ge 0$ under the effect of a constant gravitational field of acceleration $g$. We are interested in a plane strain in the xz plane with displacement components $u, \,w$ such that

$$\begin{aligned} u=u({x,z,t}), \quad w=w({x,z,t}). \end{aligned}$$

(1)

When the $z$ axis positive downward, the body force components are

$$\begin{aligned} X= 0.\quad Z=g. \end{aligned}$$

(2)

The governing equations of the problem are

• (1) The stress–strain relation may be written as [5]

  $$\begin{aligned} \sigma _{ij}&= 2\mu e_{ij} +\delta _{ij} [\lambda e_{kk} -\nu (\theta +\tau _1 \dot{\theta })] , \end{aligned}$$

  (3)
  $$\begin{aligned} e_{ij}&= \frac{1}{2}\left( {\frac{\partial u_j }{\partial x_i }+\frac{\partial u_i }{\partial x_j }} \right) , \end{aligned}$$

  (4)

  where $\sigma _{ij}$’s are the components of stress, $e_{ij}$’s are the components of strain, $\lambda , \mu$’s are Lame’s constants, $v = (3 \lambda + 2 \mu ) \,a_{t},\, a_{t}$ is the thermal expansion coefficient, $\theta = T - T_{0}$, where $T$ is the temperature above the reference temperature $T_{0}, \,{\tau }_{1}$ is the relaxation time, ${\delta }_{ij}$ is the Kronecker delta, and $i,j=x,\,z$.

• (2) The dynamical equations of an elastic medium are given by [15]

  $$\begin{aligned} \rho \ddot{u}&= \frac{\partial \sigma _{xx} }{\partial x}+\frac{\partial \sigma _{xz} }{\partial z}+\rho g\frac{\partial w}{\partial x}, \end{aligned}$$

  (5)
  $$\begin{aligned} \rho \ddot{w}&= \frac{\partial \sigma _{zx} }{\partial x}+\frac{\partial \sigma _{zz} }{\partial z}-\rho g\frac{\partial u}{\partial x}. \end{aligned}$$

  (6)

• (3) The heat conduction equation is

  $$\begin{aligned} K\theta _{,ii} =\rho C_E [\dot{\theta }+(\tau _0 +\tau _2 )\ddot{\theta }]+\nu T_0 [\dot{e}+\tau _0 \ddot{e}], \end{aligned}$$

  (7)

  where $K$ is the thermal conductivity, $C_{E}$ is the specific heat at constant strain, and ${\tau }_{0}, \,{\tau }_{2}$ are the thermal relaxation times. In the above equations a dot denotes differentiation with respect to time, and a comma followed by a subscript denotes partial differentiation with respect to the corresponding coordinates.

We assume that [23]

$$\begin{aligned} \lambda \!=\!\lambda _0 (1-\alpha ^{{*}}T_0 ) ,\quad \mu \!=\!\mu _0 (1-\alpha ^{{*}}T_0 ) ,\quad \nu =\nu _0 (1-\alpha ^{{*}}T_0 ), \quad \beta =\beta _0 (1-\alpha ^{{*}}T_0 ) ,\nonumber \\ \end{aligned}$$

(8)

where $\lambda _{0},\, \mu _{0}, \,v_{0,} \,{\beta }_{0}$ are constants of the material and ${\alpha }{^*}$ is the linear temperature coefficient. For the case of a modulus of elasticity, the temperature is independent when $\alpha ^{{*}}=0$.

By using Eq. 8 in Eq. 3, we get

$$\begin{aligned} \alpha \sigma _{xx}&= (2\mu _0 +\lambda _0 )e_{xx} +\lambda _0 e_{zz} -\nu _0 (\theta +\tau _1 \dot{\theta }), \end{aligned}$$

(9)

$$\begin{aligned} \alpha \sigma _{zz}&= (2\mu _0 +\lambda _0 )e_{zz} +\lambda _0 e_{xx} -\nu _0 (\theta +\tau _1 \dot{\theta }), \end{aligned}$$

(10)

$$\begin{aligned} \alpha \sigma _{xz}&= 2\mu _0 e_{xz} . \end{aligned}$$

(11)

By substituting from Eqs. 9–11 in Eqs. 5 and 6, we obtain

$$\begin{aligned} \rho \ddot{u}=\frac{1}{\alpha }\left[ {(\mu _0 +\lambda _0)\frac{\partial e}{\partial x}+\mu _0 \nabla ^{2}u-\nu _0 \frac{\partial }{\partial x}(\theta +\tau _1 \dot{\theta })} \right] +\rho g\frac{\partial w}{\partial x}, \end{aligned}$$

(12)

$$\begin{aligned} \rho \ddot{w}=\frac{1}{\alpha }\left[ {(\mu _0 +\lambda _0 )\frac{\partial e}{\partial z}+\mu _0 \nabla ^{2}w-\nu _0 \frac{\partial }{\partial z}(\theta +\tau _1 \dot{\theta })} \right] -\rho g\frac{\partial u}{\partial x}. \end{aligned}$$

(13)

Employing Eq. 7 and using Eq. 8, this yields

$$\begin{aligned} K\theta _{,ii} =\rho C_E [\dot{\theta }+(\tau _0 +\tau _2 )\ddot{\theta }]+\frac{\nu _0 T_0 }{\alpha }[\dot{e}+\tau _0 \ddot{e}]. \end{aligned}$$

(14)

For convenience, the following non-dimensional variables are used:

$$\begin{aligned} ({u}^{\prime },{w}^{\prime })&= \frac{\tilde{\omega }}{c_1 }(u,w),\quad ({x}^{\prime },{z}^{\prime })=\frac{\tilde{\omega }}{c_1 }(x,z),\quad {t}^{\prime }=\tilde{\omega }t,\quad {\tau }^{\prime }_0 =\tilde{\omega }\tau _0 ,\quad {\tau }^{\prime }_1 =\tilde{\omega }\tau _1 ,\nonumber \\ {\tau }^{\prime }_2&= \tilde{\omega }\tau _2 ,\quad {\sigma }^{\prime }_{ij} =\frac{\sigma _{ij} }{\rho c_1^2 },\quad {\theta }^{\prime }=\frac{\nu _0 \theta }{\rho c_1^2 }, \end{aligned}$$

(15)

where $\tilde{\omega }=\frac{\rho C_E c_1^2 }{K}, \quad c_1^2 =\frac{(\lambda _0 +2\mu _0 )}{\rho }$.

In terms of non-dimensional quantities defined in Eq. 15, the above governing equations reduce to (dropping the prime for convenience)

$$\begin{aligned} \ddot{u}&= \frac{1}{\alpha }\left[ {\beta _1 \frac{\partial e}{\partial x}+(1-\beta _1 )\nabla ^{2}u-\frac{\partial }{\partial x}(\theta +\tau _1 \dot{\theta })} \right] +\frac{g}{c_1 \tilde{\omega }}\frac{\partial w}{\partial x}, \end{aligned}$$

(16)

$$\begin{aligned} \ddot{w}&= \frac{1}{\alpha }\left[ {\beta _1 \frac{\partial e}{\partial z}+(1-\beta _1 )\nabla ^{2}w-\frac{\partial }{\partial z}(\theta +\tau _1 \dot{\theta })} \right] -\frac{g}{c_1 \tilde{\omega }}\frac{\partial u}{\partial x}, \end{aligned}$$

(17)

$$\begin{aligned} \nabla ^{2}\theta&= [\dot{\theta }+(\tau _0 +\tau _2)\ddot{\theta }]+\frac{\delta \delta _0 }{\alpha }[\dot{e}+\tau _0 \ddot{e}], \end{aligned}$$

(18)

$$\begin{aligned} \sigma _{xx}&= \frac{1}{\alpha }\left[ {\frac{\partial u}{\partial x}+(2\beta _1 -1)\frac{\partial w}{\partial z}-(\theta +\tau _1 \dot{\theta })} \right] , \end{aligned}$$

(19)

$$\begin{aligned} \sigma _{zz}&= \frac{1}{\alpha }\left[ {\frac{\partial w}{\partial z}+(2\beta _1 -1)\frac{\partial u}{\partial x}-(\theta +\tau _1 \dot{\theta })} \right] , \end{aligned}$$

(20)

$$\begin{aligned} \sigma _{xz}&= \frac{1}{\alpha }(1-\beta _1 )\left[ {\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}} \right] , \end{aligned}$$

(21)

where $\beta _1 =\frac{\mu _0 +\lambda _0 }{\rho c_1^2 },\quad \delta =\frac{\nu _0 }{\rho C_E },\quad \delta _0 =\frac{\nu _0 T_0 }{\rho c_1^2 },\quad \alpha =\frac{1}{1-\alpha ^{{*}}T_0}.$

Now, we introduce the potential functions $\phi (x,z,t)$ and $\psi (x,z,t)$ in non-dimensional form that are given by

$$\begin{aligned} u=\frac{\partial \phi }{\partial x}-\frac{\partial \psi }{\partial z},\quad w=\frac{\partial \phi }{\partial z}+\frac{\partial \psi }{\partial x}. \end{aligned}$$

(22)

By substituting from Eq. 22 in Eqs. 16–18, this yields

$$\begin{aligned} \ddot{\phi }&= \frac{1}{\alpha }[\nabla ^{2}\phi -(\theta +\tau _1 \dot{\theta })]+g\frac{\partial \psi }{\partial x}, \end{aligned}$$

(23)

$$\begin{aligned} \ddot{\psi }&= \frac{1}{\alpha }[(1-\beta _1 )\nabla ^{2}\psi ]-g\frac{\partial \phi }{\partial x}, \end{aligned}$$

(24)

$$\begin{aligned} \nabla ^{2}\theta&= [\dot{\theta }+(\tau _0 +\tau _2) \ddot{\theta }]+\frac{\delta \delta _0 }{\alpha }\left( {\frac{\partial }{\partial t}+\tau _0 \frac{\partial ^{2}}{\partial t^{2}}} \right) \nabla ^{2}\phi . \end{aligned}$$

(25)

3 Solution of the Problem

The solution of the considered physical variables can be decomposed in terms of normal modes and are given in the following form:

$$\begin{aligned}{}[\theta ,\phi ,\psi ,\sigma _{ij} ](x,z,t)=[\theta ^{{*}},\phi ^{{*}},\psi ^{{*}},\sigma _{ij}^{*} ](z){\text{ e }}^{({\text{ i }}cx+\omega t)}, \end{aligned}$$

(26)

where $\omega$ is a complex constant, ${\text{ i }}=\sqrt{-{1}}, \, c$ is the wave number in the $x$-direction, and ${\theta }{^*}(z),\, \varphi ^{{*}}(z),\; \psi ^{{*}}(z),$ and $\sigma _{ij}^{*} (z)$ are the amplitudes of the field quantities.

By substituting from Eq. 26 in Eqs. 23–25, we get

$$\begin{aligned}&(D^{2}-s_1 )\phi ^{{*}}-b_0 \theta ^{{*}}+\text{ i }a_0 g\psi ^{{*}}=0, \end{aligned}$$

(27)

$$\begin{aligned}&(D^{2}-s_2 )\psi ^{{*}}-\text{ i }a_0 a_1 g\phi ^{{*}}=0, \end{aligned}$$

(28)

$$\begin{aligned}&(D^{2}-s_3 )\theta ^{{*}}-s_4 (D^{2}-c^{2})\phi ^{{*}}=0, \end{aligned}$$

(29)

where $s_1 =\alpha \omega ^{2}+c^{2},\quad s_2 =\alpha \omega ^{2}a_1 +c^{2},\quad s_3 =c^{2}+\omega [1+(\tau _0 +\tau _2 )\omega ],$

$$\begin{aligned} s_4 =\frac{\delta \delta _0 }{\alpha }\omega (1+\tau _0 \omega ),\quad a_0 =\frac{\alpha c}{c_1 \tilde{\omega }},\quad b_0 =(1+\tau _1 \omega ),\quad a_1 =[1/(1-\beta _1 )]. \end{aligned}$$

Eliminating $\theta {^*}(z)$, and ${\psi }{^*}(z)$ between Eqs. 27–29, we obtain the sixth-order ordinary differential equation satisfied for $\varphi ^{{*}}(z)$,

$$\begin{aligned} (D^{6}-E_0 D{ }^4+E_1 D^{2}-E_2 )\phi ^{{*}}=0, \end{aligned}$$

(30)

where

$$\begin{aligned} E_0&= s_1 +s_2 +s_3 +b_0 s_4 ,\\ E_1&= s_1 s_2 +s_3 (s_1 +s_2 )-a_0^2 g^{2}a_1 +b_0 s_4 (c^{2}+s_2 ),\\ E_2&= s_3 (s_1 s_2 --a_0^2 g^{2}a_1 )+b_0 s_4 s_2 c^{2} \end{aligned}$$

Similarly, we can show that $\theta {^*}(z)$ and ${\psi }{^*}(z)$, satisfy the equation,

$$\begin{aligned} (D^{6}-E_0 D{ }^4+E_1 D^{2}-E_2 )(\theta ^{{*}},\psi ^{{*}})=0. \end{aligned}$$

(31)

Equation 30 can be factored as

$$\begin{aligned} (D^{2}-k_1^2 )(D^{2}-k_2^2 )(D^{2}-k_3^2 )\phi ^{{*}}=0, \end{aligned}$$

(32)

where $k_n^2 \;\;($n = 1, 2, 3$)$ are the roots of the characteristic equation of Eq. 30,

$$\begin{aligned} m^{6}-E_0 m{ }^4+E_1 m^{2}-E_2 =0. \end{aligned}$$

(33)

The solution of Eq. 30 must be bounded as $z\rightarrow \infty$. Then, it takes the form,

$$\begin{aligned} \phi ^{{*}}=\sum _{n=1}^3 {M_n (c,\omega ) {\text{ e }}^{-k_n z}}. \end{aligned}$$

(34)

Similarly,

$$\begin{aligned} \psi ^{{*}}&= \sum _{n=1}^3 {{M}^{\prime }_n (c,\omega ){\text{ e }}^{-k_n z}}, \end{aligned}$$

(35)

$$\begin{aligned} \theta ^{{*}}&= \sum _{n=1}^3 {{M}^{\prime \prime }_n (c,\omega ){\text{ e }}^{-k_n z}}, \end{aligned}$$

(36)

where $M_n , {M}^{\prime }_n$, and ${M}^{\prime \prime }_n$ are parameters depending on $c$ and $w$.

Substituting from Eqs. 34–36 in Eqs. 28 and 29, this yields

$$\begin{aligned} {M}^{\prime }_n ={\text{ i }}N_n M_n ,\quad {M}^{\prime \prime }_n =G_n M_n, \end{aligned}$$

(37)

where $N_n =\frac{a_0 a_1 g}{(k_n^2 -s_2 )}, \quad G_n =\frac{s_4 (k_n^2 -c^{2})}{(k_n^2 -s_3 )}.$

Thus, we have

$$\begin{aligned} \psi ^{{*}}&= \mathrm{i}\sum _{n=1}^3 {N_n M_n \text{ e }^{-k_n z}}, \end{aligned}$$

(38)

$$\begin{aligned} \theta ^{{*}}&= \sum _{n=1}^3 {G_n M_n {\text{ e }}^{-k_nz}}. \end{aligned}$$

(39)

Using Eqs. 34 and 38 in Eq. 22, we get

$$\begin{aligned} u^{{*}}&= \mathrm{i}\sum _{n=1}^3 {(c+k_n } N_n )M_n {\text{ e }}^{-k_n z}, \end{aligned}$$

(40)

$$\begin{aligned} w^{{*}}&= -\sum _{n=1}^3 {(k_n +c} N_n )M_n {\text{ e }}^{-k_n z}. \end{aligned}$$

(41)

Using Eqs. 22 and 26 in Eqs. 19–21, we obtain

$$\begin{aligned} \sigma _{xx}^{*}&= \frac{1}{\alpha }\left[ {\text{ i }cu^{{*}}+(2\beta _1 -1)Dw^{{*}}-(1+\tau _1 \omega )\theta ^{{*}}} \right] , \end{aligned}$$

(42)

$$\begin{aligned} \sigma _{zz}^{*}&= \frac{1}{\alpha }\left[ {Dw^{{*}}+\text{ i }(2\beta _1 -1)cu^{{*}}-(1+\tau _1 \omega )\theta ^{{*}}} \right] , \end{aligned}$$

(43)

$$\begin{aligned} \sigma _{xz}^{*}&= \frac{1}{\alpha }(1-\beta _1)\left[ {Du^{{*}}+\text{ i }cw^{{*}}} \right] . \end{aligned}$$

(44)

Introducing Eqs. 39–41 in Eqs. 42–44, this yields

$$\begin{aligned} \sigma _{xx}^{*}&= \sum _{n=1}^3 {R_n M_n \text{ e }^{-k_n z}}, \end{aligned}$$

(45)

$$\begin{aligned} \sigma _{zz}^{*}&= \sum _{n=1}^3 {V_n M_n \text{ e }^{-k_n z}}, \end{aligned}$$

(46)

$$\begin{aligned} \sigma _{xz}^{*}&= -i\sum _{n=1}^3 {H_n M_n \text{ e }^{-k_n z}} , \end{aligned}$$

(47)

where

$$\begin{aligned} R_n&= \frac{1}{\alpha }[-c^{2}+2ck_n N_n (\beta _1 -1)+(2\beta _1 -1)k_n^2 -(1+\tau _1 \omega )G_n ], \end{aligned}$$

(48)

$$\begin{aligned} V_n&= \frac{1}{\alpha }[k_n^2 +2ck_n N_n (1-\beta _1)-(2\beta _1 -1)c^{2}-(1+\tau _1 \omega )G_n ], \end{aligned}$$

(49)

$$\begin{aligned} H_n&= \frac{1}{\alpha }(1-\beta _1 )[N_n (k_n^2 +c^{2})+2ck_n ]. \end{aligned}$$

(50)

The normal mode analysis is, in fact, to look for the solution in the Fourier transformed domain, assuming that all the field quantities are sufficiently smooth on the real line such that normal mode analysis of these functions exists.

4 Boundary Conditions

In this section, we need to consider the boundary conditions at $z = 0$, in order to determine the parameter $M_{n}(n = 1, 2, 3)$.

• (1) A thermal boundary condition that the surface of the half-space is subjected to

  $$\begin{aligned} \frac{\partial \theta }{\partial z}=0. \end{aligned}$$

  (51)

• (2) A mechanical boundary condition that the surface of the half-space is traction free

  $$\begin{aligned} \sigma _{xz} =0. \end{aligned}$$

  (52)

• (3) A mechanical boundary condition that the surface of the half-space is subjected to

  $$\begin{aligned} \sigma _{zz} =f(0.y,t)=-f^{*}\text{ e }^{\omega t+\text{ i }cx}. \end{aligned}$$

  (53)

  $f(y, \,t)$ is an arbitrary function of $y$ and $t$; and $f{^*}$ is a constant. Using the expressions of the variables considered into the above boundary conditions (Eqs. 51, 52, and 53) we can obtain the following equations satisfied with the parameters:

  $$\begin{aligned} \sum _{n=1}^3 {k_n G_n } M_n&= 0, \end{aligned}$$

  (54)
  $$\begin{aligned} \sum _{n=1}^3 {H_n } M_n&= 0, \end{aligned}$$

  (55)
  $$\begin{aligned} \sum _{n=1}^3 {V_n } M_n&= -f^{*}. \end{aligned}$$

  (56)

  Solving Eqs. 54–56, we get the parameter $M_{n}\, (n = 1, 2, 3)$ defined as follows:

  $$\begin{aligned} M_1 =\frac{\varDelta _1 }{\varDelta },\quad M_2 =\frac{\varDelta _2}{\varDelta },\quad M_3 =\frac{\varDelta _3 }{\varDelta }, \end{aligned}$$

  (57)

  where

  $$\begin{aligned} \varDelta _1&= (k_3 G_3 H_2 -k_2 G_2 H_3 )f^{*},\quad \quad \quad \varDelta _2 =-(k_3 G_3 H_1 -k_1 G_1 H_3 )f^{*},\\ \varDelta _3&= (k_2 G_2 H_1 -k_1 G_1 H_2 )f^{*}. \end{aligned}$$

5 Numerical Results and Discussion

To illustrate the theoretical results obtained in the preceding section, to compare these in the context of three theories of thermoelasticity, and to study the effect of gravity and temperature on wave propagation in a thermoelastic medium with temperature-dependent properties, we now present some numerical results for the physical constants

$$\begin{aligned} \lambda _0&= 7.76 \times 10^{10} \text{ N }\cdot \text{ m }^{-2},\quad \mu _0 =3.86 \times 10^{10} \text{ N } \cdot \text{ m }^{-{2}},\quad \rho =8954 \text{ kg } \cdot \text{ m }^{-3},\\ \beta _0&= 0.32 \times 10^{9} \text{ N }\cdot \text{ m }^{-2},\quad \text{ K }={386} \;\text{ W }\cdot \text{ m }^{-{1}}\cdot \text{ K }^{-{1}},\quad T_{0} = {293}\, \text{ K, } \\ C_E&= {383.1} \text{ J } \cdot \text{ kg }^{-{1}}\cdot \text{ K }^{-{1}}, \quad \alpha _t ={1.78} \times {10}^{-{4}} \text{ K }^{-{1}},\quad f^{{*}}=1,\\ g&= 9.8 \;\text{ m }\cdot \text{ s }^{-2},\quad \omega =\omega _{0} +\text{ i }\xi ,\quad \omega _{0} ={0.2,}\quad \xi = {0}.9,\quad \text{ c }={0}.9, \\ \tau _{0}&= {0.3 \text{ s },}\quad \tau _{1} =\; 0.9\, \text{ s, } \quad {\uptau }_{2} = \;{0}.6\, \text{ s }. \end{aligned}$$

The computations were carried out for a value of time $t = 0.7$. The numerical technique, outlined above, was used for the distribution of the thermal temperature $\theta$, the displacement components $u, \,w$, and the stress components $\sigma _{xx}, \,\sigma _{zz}$, and $\sigma _{xz}$ for the problem under consideration. All the considered variables depend not only on space $z$ and time $t$ but also on the thermal relaxation times ${\tau }_{0},\, {\tau }_{1}$, and ${\tau }_{2}$. The results are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. The graphs show the six curves predicted by three different theories of thermoelasticity. In these figures, the solid lines represent the solution in the coupled theory, the dotted lines represent the solution in the generalized G–L theory, and the dashed lines represent the solution derived using the L–S theory. Here all the variables are taken in non-dimensional forms and we consider five cases:

• (1) Equations of the coupled thermoelasticity (CD) theory when ${\tau }_{0} = {\tau }_{1} = {\tau }_{2} = 0$.

• (2) Lord and Shulman (L–S) theory when ${\tau }_{1} = {\tau }_{2} = 0,\, {\tau }_{0} > 0$,

• (3) Green and Lindsay (G–L) theory when ${\tau }_{0} = 0,\, {\tau }_{1} \ge {\tau }_{2} > 0$.

• (4) Corresponding equations for the three theories in the absence of a gravity field from the above mentioned cases by taking g = 0.

• (5) Corresponding equations for temperature independence based on the three theories from the above mentioned cases by taking the linear temperature coefficient ${\alpha }{^*} = 0$.

Fig. 1

Horizontal displacement distribution $u$ with temperature dependence and independent of temperature

Fig. 2

Vertical displacement distribution $w$ with temperature dependence and independent of temperature

Fig. 3

Temperature distribution $\theta$ with temperature dependence and independent of temperature

Fig. 4

Distribution of stress component $\sigma _{xx}$ with temperature dependence and independent of temperature

Fig. 5

Distribution of stress component $\sigma _{zz}$ with temperature dependence and independent of temperature

Fig. 6

Distribution of stress component $\sigma _{xz}$ with temperature dependence and independent of temperature

Fig. 7

Horizontal displacement distribution $u$ in the absence and presence of gravity field

Fig. 8

Vertical displacement distribution $w$ in the absence and presence of gravity field

Fig. 9

Temperature distribution $\theta$ in the absence and presence of gravity field

Fig. 10

Distribution of stress component $\sigma _{xx}$ in the absence and presence of gravity field

Fig. 11

Distribution of stress component $\sigma _{zz}$ in the absence and presence of gravity field

Fig. 12

Distribution of stress component $\sigma _{xz}$ in the absence and presence of gravity field

For a value of $x$, namely, $x = 0.7$, this value was substituted in performing the computation. Figures 1, 2, 3, 4, 5, and 6 show comparisons among the displacement components $u, \,w$, the temperature $\theta$, and the stress components $\sigma _{xx}, \,\sigma _{zz}$, and $\sigma _{xz}$ for temperature dependence and independence in the presence of a gravity field.

Figure 1 depicts that the distribution of the horizontal displacement $u$ begins from negative values with temperature dependence, but it begins from positive values independent of temperature. In the context of the three theories with temperature dependence, the values of the horizontal displacement decrease to a minimum value in the range $0 \le z \le 1$, then increase to a maximum value in the range $1 \le z \le 2.9$, and also move in a wave propagation. However, in the context of the three theories independent of temperature, the values of the horizontal displacement decrease to a minimum value in the range $0 \le z \le 1.5$, then increase to a maximum value in the range $1.5 \le z \le 3.8$, and also move in a wave propagation. Figure 2 shows that the distribution of the vertical displacement $w$ always begins from positive values. In the context of the three theories with temperature dependence, the values of the vertical displacement decrease to a minimum value in the range $0 \le z \le 1.5$, then increase in the range $1.5 \le z \le 3$, and also move in a wave propagation. However, in the context of the three theories independent of temperature, the values of the vertical displacement decrease to a minimum value in the range $0 \le z \le 1.9$, then increase to a maximum value in the range $1.9 \le z \le 3.9$, and also move in a wave propagation. The displacements $u$ and $w$ show different behaviors because the elasticity of the solid tends to resist a vertical displacement in the problem under investigation. Figure 3 exhibits that the distribution of the temperature $\theta$ begins from positive values in the context of the G–L theory, but it begins from negative values in the context of the CD and L–S theories dependent on and independent of temperature. In the context of the CD theory with temperature dependence, the values of the temperature increase to a maximum value in the range $0 \le z \le 1.9$, then decrease in the range $1.9 \le z \le 9$. However, in the context of the L–S theory with temperature dependence, the values of the temperature increase to a maximum value in the range $0 \le z \le 2.9$, then decrease in the range $2.9 \le z \le 9$. For the case independent of temperature, in the context of the CD and L–S theories, the values of the temperature increase to a maximum value in the range $0 \le z \le 2.5$, then decrease in the range $2.5 \le z \le 9$. It also shows from the figure that in the context of the G–L theory, the values of the temperature increase to a maximum value in the range $0 \le z \le 1.4$, then decrease in the range $1.4 \le z \le 9$ dependent on and independent of temperature. Figure 4 displays that the distribution of the stress component $\sigma _{xx}$ always begins from positive values. In the context of the CD and G–L theories with temperature dependence, the values of the stress component $\sigma _{xx}$ increase to a maximum value in the range $0 \le z \le 0.1$, then decrease to a minimum value in the range $0.1 \le z \le 1.8$, and also move in a wave propagation. However, in the context of the L–S theory with temperature dependence, the values of the stress component $\sigma _{xx}$ increase to a maximum value in the range $0 \le z \le 0.2$, then decrease to a minimum value in the range $0.2 \le z \le 2$, and also move in a wave propagation. For the case independent of temperature, in the context of the three theories, the values of the stress component $\sigma _{xx}$ increase to a maximum value in the range $0 \le z \le 0.3$, then decrease to a minimum value in the range $0.3 \le z \le 2.8,$ and also move in a wave propagation. Figure 5 exhibits that the distribution of the stress component $\sigma _{zz}$ always begins from a negative value and satisfies the boundary condition at $z = 0$. In the context of the three theories with temperature dependence, the values of the stress component $\sigma _{zz}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase in the range $0.5 \le z \le 2.2$, and also move in a wave propagation. However, in the context of the three theories independent of temperature, the values of the stress component $\sigma _{zz}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase to a maximum value in the range $0.5 \le z \le 2.6$, and also move in a wave propagation. Figure 6 describes the distribution of the stress component $\sigma _{xz}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $z = 0$. In the context of the three theories with temperature dependence, the values of the stress component $\sigma _{xz}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase to a maximum value in the range $0.5 \le z \le 1.8$, and also move in a wave propagation. However, in the context of the three theories independent of temperature, the values of the stress component $\sigma _{xz}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase to a maximum value in the range $0.5 \le z \le 2.2$, and also move in a wave propagation. Figures 1, 2, 3, 4, 5, and 6 demonstrate that the temperature has a significant impact on the physical quantities.

Figures 7, 8, 9, 10, 11, and 12 show comparisons among the displacement components $u, \,w$, the temperature $\theta$, and the stress components $\sigma _{xx}, \,\sigma _{zz}$, and $\sigma _{xz}$ in the absence and presence of a gravity field for the case of a material with temperature dependence.

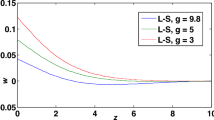
Figure 7 depicts that the distribution of the horizontal displacement $u$ begins from negative values in the presence of a gravity field, but it begins from positive values in the absence of a gravity field. In the context of the three theories and in the absence of a gravity field, the values of the horizontal displacement increase to a maximum value in the range $0 \le z \le 1.2$, then decrease to a minimum value in the range $1.2 \le z \le 3$, and also move in a wave propagation. Figure 8 exhibits that the distribution of the vertical displacement $w$ begins from positive values in the presence of a gravity field while it begins from zero in the absence of a gravity field. In the context of the three theories and in the absence of a gravity field, the values of the vertical displacement decrease to a minimum value in the range $0 \le z \le 1.1$, then increase to a maximum value in the range $1.1 \le z \le 2.9$, and also move in a wave propagation. Figure 9 shows that the distribution of the temperature $\theta$ begins from positive values in the context of the three theories and in the absence and presence of a gravity field except in the context of the CD and L–S theories and in the presence of a gravity field, it begins from negative values. In the context of the CD and L–S theories and in the absence of a gravity field, the values of the temperature increase to a maximum value in the range $0 \le z \le 0.9$, then decrease to a minimum value in the range $0.9 \le z \le 2.8$, and also move in a wave propagation. However, in the context of the G–L theory and in the absence of a gravity field, the values of the temperature increase to a maximum value in the range $0 \le z \le 0.8$, then decrease to a minimum value in the range $0.8 \le z \le 2.5$, and also move in a wave propagation. Figure 10 describes that the distribution of the stress component $\sigma _{xx}$, in the context of the three theories, begins from positive values in the presence of a gravity field, but it begins from negative values in the absence of a gravity field. In the context of the three theories and in the absence of a gravity field, the values of the stress component $\sigma _{xx}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase to a maximum value in the range $0.5 \le z \le 2.5$, and also move in a wave propagation. Figure 11 displays that the distribution of the stress component $\sigma _{zz}$ always begins from a negative value and satisfies the boundary condition at $z = 0$. In the context of the three theories and in the absence of a gravity field, the values of the stress component $\sigma _{zz}$ decrease to a minimum value in the range $0 \le z \le 0.5$, then increase to a maximum value in the range $0.5 \le z \le 2$, and also move in a wave propagation. Figure 12 exhibits the distribution of the stress component $\sigma _{xz}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $z = 0$. In the context of the three theories and in the absence of a gravity field, the values of the stress component $\sigma _{xz}$ increase to a maximum value in the range $0 \le z \le 0.5$, then decrease to a minimum value in the range $0.5 \le z \le 2$, and also move in a wave propagation. Figures 7, 8, 9, 10, 11, and 12 exhibit that the gravity field has an important effect on the physical quantities.

6 Conclusions

By comparing the figures that were obtained for the three thermoelastic theories, important phenomena are observed:

• (1) The curves in the context of the CD, L–S, and G–L theories decrease exponentially with increasing $z$; this indicates that the thermoelastic waves are unattenuated and non-dispersive, while purely thermoelastic waves undergo both attenuation and dispersion.

• (2) The values of all the physical quantities converge to zero with increasing distance $z$, and all functions are continuous.

• (3) It is clear that the gravity field and temperature have important roles on the distribution of the field quantities.

• (4) All the physical quantities satisfy the boundary conditions.

• (5) Analytical solutions based upon normal mode analysis for the thermoelastic problem in solids have been developed and utilized.

• (6) The method that was used in the present article is applicable to a wide range of problems in thermodynamics and thermoelasticity.

• (7) Deformation of the body depends on the nature of the applied forced as well as on the type of boundary conditions.