Effect of Inclined Load and Initial Stress on Plane Waves of Thermoelastic Rotating Medium via Three-Phase-Lag Model

Abstract

In this work, the effect of initial stress and oblique loading on plane waves in thermoelastic media will be investigated in the context of three-phase-lag theory. The entire elastic medium rotates at a uniform angular velocity. The problem is solved numerically by normal modal analysis. Plot and analyze the numerical results for temperature, displacement components, and stress. Graphical results show that the effects of phase delay, tilt angle, and initial stress parameters are evident. Variations in these quantities are plotted in the three-phase hysteresis model (3PHL) and the type III Green and Naghdi theory (G-N III) for insulated boundaries to show the effect of initial stress and angle of inclination in the medium.

1 1 INTRODUCTION

Thermoelasticity is considered an aspect of two main fields of study, the mechanical and the thermal of solids. Both domains have a significant effect on the contraction or expansion of any elastic or inelastic material. Different types of thermo-elasticity include coupled, decoupled, and generalized thermoelasticity. The generalized thermoelastic theory successfully circumvents the infinite propagation velocity of thermal signals predicted in the classical dynamic coupled thermoelastic theory. A coupled thermoelastic model that addresses the first flaw of decoupling theory was developed; however, it also suffers from the second flaw of decoupling theory by Biot [1]. The traditional Fourier’s law by proposing another law of heat transfer, was modified and proposing a generalized theory of thermoelasticity with one relaxation time by Lord and Shulman [2]. This law includes the heat flux vector and its time derivative. A theory that included two constant times acting as relaxation times, modifying not only the heat conduction equation but also all coupled theoretical equations by Green and Lindsay [3]. Green and Naghdi [4] proposed a new generalized theory of thermoelasticity by including thermal displacement gradients in independent constitutive variables. An important feature of this theory that is absent from other theories of thermoelasticity is that it does not take into account the dissipation of thermal energy. Tzou [5] proposed a dual-phase-lag model (DPL) for heat conduction, incorporating the effects of infinitesimal interactions during fast transients of the heat transport mechanism in a macroscopic design. Recently, Choudhuri [6] introduced the heat conduction equation with three-phase-lags, where Fourier’s law of heat conduction is replaced by a modified approximation of Fourier’s law, introducing three different phase-lags for the heat flux vector, the temperature gradient and the thermal displacement gradient. The stability of the heat equation with three-phase-lags was discussed by Quintanilla and Racke [7]. Studies have reported several issues related to thermoelastic three-phase hysteresis models in [8–11]. The strain at each point in the medium is useful for analyzing mining vibrations and drilling the strain field around the crust. It also facilitates theoretical considerations of seismic and volcanic sources, as it can account for the deformation field over the entire volume around the source region. Biot [12] discussed the effect of initial stress on elastic waves. Kuo [13] and Garg et al. [14] discusses the problem of oblique loading in the theory of elastic solids. Under G-N III with oblique loading, [15–17] studied two-dimensional problems for micropolar thermoelastic rotating media with cubic symmetry under different theories and fields. Studying the dynamic response of isotropic generalized thermoelastic solids with additional parameters helps to solve many practical problems. There are many reasons for the initial stress in the medium, which can be traced back to temperature differences, quenching processes, gravity fluctuations, etc. The Earth is believed to be under high initial stress. Therefore, it is of great significance to study the influence of these stresses on the mechanical and thermal state of the medium. Some researchers have studied thermoelastic problems with initial stress effects see [18–26].

In this paper, we study the effects of oblique load and initial stress on plane waves in a thermoelastic rotating medium using a three-phase-lag model. Regular pattern analysis techniques are used to find expressions of the variables under consideration. Some comparative plots were drawn to estimate the effect of initial stress, inclined angle and phase delay parameters for all studied fields.

2 2 FORMULATION OF THE PROBLEM

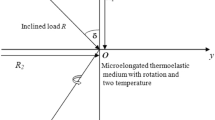
A homogeneous thermoelastic half-space is generated under hydrostatic initial stress and oblique pressure. All quantities considered are functions of time t and coordinates x, z and consider a homogeneous thermoelastic rotating solid in the undeformed state. Take the vertical Cartesian coordinates in which the origin is on the surface y = 0 and the z-axis is perpendicular to the medium, expressed as $z \geqslant 0.$ Assuming that the oblique load F₀ per unit length acts on the y-axis, its inclination angle relative to the z-axis is α₀ (Fig. 1). The analysis can be restricted parallel to $xz -$plane with displacement vector u = (u, 0, w) and rotation vector ${\boldsymbol{\Omega }} = (0,\Omega ,0).$

Fig. 1.

Normal and tangential loadings over a thermoelastic half-space.

System of linear thermoelastic governing equations in a three-phase hysteresis model with rotation, initial stress, and nobody forces and body pairs (Othman et al. [15], Choudhuri [6]).

$${{\sigma }_{{ji,j}}} = \rho [{{u}_{{i,\,tt}}} + {{\{ {\boldsymbol{\Omega }} \times ({\boldsymbol{\Omega }} \times {\mathbf{u}})\} }_{i}} + {{(2{\boldsymbol{\Omega }} \times {{{\mathbf{u}}}_{{,t}}})}_{i}}],$$

(2.1)

$${{\sigma }_{{ij}}} = \lambda {{u}_{{r,r}}}{{\delta }_{{ij}}} + \mu ({{u}_{{i,j}}} + {{u}_{{j,i}}}) - {{\gamma }_{1}}(T - {{T}_{0}}){{\delta }_{{ij}}} - p({{\delta }_{{ij}}} + {{\omega }_{{ij}}}),$$

(2.2)

$$K{\text{*}}{{\nabla }^{2}}T + \tau _{{v}}^{ * }{{\nabla }^{2}}{{T}_{{,t}}} + K{{\tau }_{T}}{{\nabla }^{2}}{{T}_{{,tt}}} = \left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)(\rho {{C}_{E}}{{T}_{{,tt}}} + {{T}_{0}}{{\gamma }_{1}}{{u}_{{i,itt}}}),$$

(2.3)

where, ${{\omega }_{{ij}}} = \frac{1}{2}({{u}_{{j,i}}} - {{u}_{{i,j}}}),$ $\tau _{{v}}^{ * } = K + K{\text{*}}{{\tau }_{{v}}}$ and $0 \leqslant {{\tau }_{{v}}} < {{\tau }_{T}} < {{\tau }_{q}}.$

(i) Three-phase-lag model when $(0 < {{\tau }_{{v}}} < {{\tau }_{T}} < {{\tau }_{q}},$ $K{\text{*}} > 0).$

(ii) L-S theory when $({{\tau }_{T}} = 0,$ $K\text{*} = 0,$ $\tau _{q}^{2} = 0,$ $0 < {{\tau }_{{v}}} < {{\tau }_{q}}).$

(iii) G-N theory (of type III) when (${{\tau }_{{v}}} = {{\tau }_{T}} = {{\tau }_{q}} = 0,$ $K{\text{*}} > 0$).

The constitutive equations can be written as

$${{\sigma }_{{xx}}} = \lambda e + 2\mu \frac{{\partial u}}{{\partial x}} - {{\gamma }_{1}}(T - {{T}_{0}}) - p,$$

(2.4)

$${{\sigma }_{{yy}}} = \lambda e - {{\gamma }_{1}}(T - {{T}_{0}}) - p,$$

(2.5)

$${{\sigma }_{{zz}}} = \lambda e + 2\mu \frac{{\partial w}}{{\partial z}} - {{\gamma }_{1}}(T - {{T}_{0}}) - p,$$

(2.6)

$${{\sigma }_{{xz}}} = \left( {\mu + \frac{p}{2}} \right)\frac{{\partial u}}{{\partial z}} + \left( {\mu - \frac{p}{2}} \right)\frac{{\partial w}}{{\partial x}},$$

(2.7)

$${{\sigma }_{{zx}}} = \left( {\mu + \frac{p}{2}} \right)\frac{{\partial w}}{{\partial x}} + \left( {\mu - \frac{p}{2}} \right)\frac{{\partial u}}{{\partial z}}.$$

(2.8)

Using Eqs. (2.4)–(2.8) into Eqs. (2.1), (2.2), we have

$$\rho [{{u}_{{,tt}}} - {{\Omega }^{2}}u + 2\Omega {{w}_{{,t}}}] = \left( {\lambda + \mu } \right)\frac{{\partial e}}{{\partial x}} + \mu {{\nabla }^{2}}u - {{\gamma }_{1}}\frac{{\partial T}}{{\partial x}} - \frac{p}{2}\frac{\partial }{{\partial z}}\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right),$$

(2.9)

$$\rho [{{w}_{{,tt}}} - {{\Omega }^{2}}w - 2\Omega {{u}_{{,t}}}] = \left( {\lambda + \mu } \right)\frac{{\partial e}}{{\partial z}} + \mu {{\nabla }^{2}}w - {{\gamma }_{1}}\frac{{\partial T}}{{\partial z}} + \frac{p}{2}\frac{\partial }{{\partial x}}\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right),$$

(2.10)

$$K{\text{*}}{{\nabla }^{2}}T + (K + K{\text{*}}{{\tau }_{{v}}}){{\nabla }^{2}}{{T}_{{,t}}} + K{{\tau }_{T}}{{\nabla }^{2}}{{T}_{{,tt}}} = \left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)(\rho {{C}_{E}}{{T}_{{,tt}}} + {{T}_{0}}{{\gamma }_{1}}{{u}_{{i,itt}}}),$$

(2.11)

where $e = \frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}.$

For simplicity, we use thefollowing dimensionless variables

$$(x',z') = \frac{{{{\eta }_{0}}}}{{{{C}_{0}}}}(x,z),\quad (u',w') = \frac{{\rho {{\eta }_{0}}{{C}_{0}}}}{{{{\gamma }_{1}}{{T}_{0}}}}(u,w),\quad (t',\tau _{q}^{'},\tau _{{v}}^{'},\tau _{T}^{'}) = {{\eta }_{0}}\,(t,\,{{\tau }_{q}},{{\tau }_{{v}}},{{\tau }_{T}}),\quad \Omega ' = \frac{\Omega }{{{{\eta }_{0}}}},$$

$$\theta ' = \frac{{T - {{T}_{0}}}}{{{{T}_{0}}}},\quad (\sigma _{{ij}}^{'},p') = \frac{{({{\sigma }_{{ij}}},p)}}{{{{\gamma }_{1}}{{T}_{0}}}},\quad {{\eta }_{0}} = \frac{{\rho {{C}_{E}}C_{0}^{2}}}{K},\quad {{\gamma }_{1}} = \left( {3\lambda + 2\mu } \right){{\alpha }_{t}},\quad C_{0}^{2} = \left( {\lambda + 2\mu } \right){\text{/}}\rho .$$

(2.12)

Equations (2.9)–(2.11) take the following form (dashed lines omitted for simplicity)

$${{u}_{{,tt}}} - {{\Omega }^{2}}u + 2\Omega {{w}_{{,t}}} = \frac{{\lambda + \mu }}{{\rho C_{0}^{2}}}\frac{{\partial e}}{{\partial x}} + \frac{\mu }{{\rho C_{0}^{2}}}{{\nabla }^{2}}u - \frac{{{{\gamma }_{1}}{{T}_{0}}p}}{{2\rho C_{0}^{2}}}\frac{\partial }{{\partial z}}\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right) - \frac{{\partial \theta }}{{\partial x}},$$

(2.13)

$${{w}_{{,tt}}} - {{\Omega }^{2}}w - 2\Omega {{u}_{{,t}}} = \frac{{\lambda + \mu }}{{\rho {{c}_{0}}^{2}}}\frac{{\partial e}}{{\partial z}} + \frac{\mu }{{\rho {{c}_{0}}^{2}}}{{\nabla }^{2}}w - \frac{{\partial \theta }}{{\partial z}} + \frac{p}{2}\frac{{{{\gamma }_{1}}{{T}_{0}}}}{{\rho c_{0}^{2}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right),$$

(2.14)

$$K{\text{*}}{{\nabla }^{2}}\theta + (K{{\eta }_{0}} + K{\text{*}}{{\tau }_{{v}}}){{\nabla }^{2}}{{\theta }_{{,t}}} + K{{\eta }_{0}}{{\tau }_{T}}{{\nabla }^{2}}{{\theta }_{{,tt}}} = \left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {\rho \,C_{0}^{2}{{C}_{E}}{{\theta }_{{,tt}}} + \frac{{\gamma _{1}^{2}{{T}_{0}}}}{\rho }{{u}_{{i,itt}}}} \right).$$

(2.15)

We introduce the displacement potentials $q(x,\,z,\,t)$ and $\boldsymbol\psi (x,\,z,\,t)$ associated with our obtained displacement component $({\mathbf{u}} = \nabla q - \nabla \times \boldsymbol\psi )$

$$u = \frac{{\partial q}}{{\partial x}} + \frac{{\partial \psi }}{{\partial z}},\quad w = \frac{{\partial q}}{{\partial z}} - \frac{{\partial \psi }}{{\partial x}},\quad e = {{\nabla }^{2}}q,\quad \frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}} = {{\nabla }^{2}}\psi .$$

(2.16)

Substituting from Eq. (2.16) into Eqs. (2.13)–(2.15)

$$\left( {{{\nabla }^{2}} - \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{\Omega }^{2}}} \right)q - \theta + 2\Omega \frac{{\partial \psi }}{{\partial t}} = 0,$$

(2.17)

$$\left( {{{a}_{1}}{{\nabla }^{2}} - \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{\Omega }^{2}}} \right)\psi - 2\Omega \frac{{\partial q}}{{\partial t}} = 0,$$

(2.18)

$$K{\text{*}}{{\nabla }^{2}}\theta + (K{{\eta }_{0}} + K{\text{*}}{{\tau }_{{v}}}){{\nabla }^{2}}{{\theta }_{{,t}}} + K{{\eta }_{0}}{{\tau }_{T}}{{\nabla }^{2}}{{\theta }_{{,tt}}} = \left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {\rho \,C_{0}^{2}{{C}_{E}}{{\theta }_{{,tt}}} + \frac{{\gamma _{1}^{2}{{T}_{0}}}}{\rho }\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\nabla }^{2}}q} \right),$$

(2.19)

where ${{a}_{1}} = \frac{{2\mu - {{\gamma }_{1}}{{T}_{0}}p}}{{2\rho C_{0}^{2}}}.$

The solution for the considered physical variables can be decomposed into normal modes method as follows

$$[q,\psi ,\theta ](x,z,t) = [q{\text{*}},\psi {\text{*}},\theta {\text{*}}](z)\exp [i({\kern 1pt} a{\kern 1pt} x - bt)],$$

(2.20)

where b is a complex constant, $i = \sqrt {\, - 1}$ and a is the wavenumber in that x – direction. Using Eq. (2.20) in Eqs. (2.17)–(2.19), then

$$[({{D}^{2}} - {{a}_{2}}]q{\text{*}} - \theta {\text{*}} - {{a}_{3}}\psi {\text{*}} = 0,$$

(2.21)

$$[{{a}_{1}}({{D}^{2}} - {{a}^{2}}) - {{a}_{4}}]\psi {\text{*}} + {{a}_{5}}q \text{*} = 0,$$

(2.22)

$$[{{b}_{1}}{{D}^{2}} - {{b}_{2}}]q{\text{*}} + [{{b}_{3}}{{D}^{2}} - {{b}_{4}}]\theta {\text{*}} = 0.$$

(2.23)

Eliminating $q{\text{*}},\theta {\text{*}},\psi {\text{*}}$ between Eqs. (2.21) and (2.23)

$$({{D}^{6}} - {{L}_{0}}{{D}^{4}} + {{L}_{1}}{{D}^{2}} - {{L}_{2}})\{ q\text{*},\theta \text{*},\psi \text{*}\} = 0,$$

(2.24)

where: ${{a}_{i}},i = 2{\kern 1pt} - {\kern 1pt} 5,$ ${{b}_{j}},j = 1{\kern 1pt} - {\kern 1pt} 13$ and ${{L}_{0}},\;{{L}_{1}},\;{{L}_{2}},$ are given in the Appendix.

The solution of Eq. (2.24), which is bounded for $z \to \infty$

$$q{\text{*}} = \sum\limits_{n = 1}^3 {{{G}_{n}}} {{e}^{{ - {{k}_{n}}z}}},$$

(2.25)

$$\theta {\text{*}} = \sum\limits_{n = 1}^3 {{{H}_{{1n}}}{{G}_{n}}} {{e}^{{ - {{k}_{n}}z}}},$$

(2.26)

$$\psi \text{*} = \sum\limits_{n = 1}^3 {{{H}_{{2n}}}{{G}_{n}}\,{{e}^{{ - {{k}_{n}}z}}}} ,$$

(2.27)

where G_n are some constants, $k_{n}^{2}$ (n = 1, 2) are the roots of Eq. (2.24).

Using formulas (2.16), (2.25), (2.27) on dimensionless boundary conditions, and using Eqs. (2.4)–(2.8), we get the expression of displacement component, stress component and coupled stress distribution of thermoelastic medium

$$u = \sum\limits_{n = 1}^3 {{{H}_{{3n}}}} {{G}_{n}}{{e}^{{ - {{k}_{n}}z}}}{{e}^{{i(ax - bt)}}},$$

(2.28)

$$w = \sum\limits_1^3 {{{H}_{{4n}}}{{G}_{n}}{{e}^{{ - {{k}_{n}}z}}}{{e}^{{i(ax - bt)}}}} ,$$

(2.29)

$${{\sigma }_{{xx}}} = \sum\limits_{n = 1}^3 {{{H}_{{5n}}}{{G}_{n}}{{e}^{{ - {{k}_{n}}z}}}{{e}^{{i(ax - bt)}}}} - p,$$

(2.30)

$${{\sigma }_{{zz}}} = \sum\limits_{n = 1}^3 {{{H}_{{6n}}}{{G}_{n}}{{e}^{{ - {{k}_{n}}z}}}{{e}^{{i(ax - bt)}}}} - p,$$

(2.31)

$${{\sigma }_{{zx}}} = \sum\limits_{n = 1}^3 {{{H}_{{7n}}}{{G}_{n}}{{e}^{{ - {{k}_{n}}z}}}{{e}^{{i(ax - bt)}}}} ,$$

(2.32)

where ${{H}_{{kn}}},k = 1{\kern 1pt} - {\kern 1pt} 7$ are given in the Appendix.

3 3 BOUNDARY CONDITIONS

Consider oblique loads F₀ acting in direction that form an angle α₀ with the z-axis direction

(i). The mechanical boundary conditions

$${{\sigma }_{{zz}}} = {{F}_{1}} = ({{F}_{0}}\cos {{\alpha }_{0}}){{e}^{{i(ax - bt)}}} - p,\quad {{\sigma }_{{zx}}} = {{F}_{2}} = \;({{F}_{0}}\sin {{\alpha }_{0}}){{e}^{{i(ax - bt)}}}.$$

(3.1)

(ii). A thermal boundary condition that the surface of the half-space subjected to thermal shock

$$\theta = {{F}_{3}} = F{\text{*}}{{e}^{{i(ax - bt)}}}.$$

(3.2)

Using boundary conditions (3.1) and (3.2), we obtain a system of three equations. After applying the method of inverse matrix, we obtain the values of the three constants G_n, $n = 1,2,3$.

$$\left( {\begin{array}{*{20}{c}} {{{G}_{1}}} \\ {{{G}_{2}}} \\ {{{G}_{3}}} \end{array}} \right) = {{\left( {\begin{array}{*{20}{c}} {{{H}_{{61}}}}&{{{H}_{{62}}}}&{{{H}_{{63}}}} \\ {{{H}_{{71}}}}&{{{H}_{{72}}}}&{{{H}_{{73}}}} \\ {{{H}_{{11}}}}&{{{H}_{{12}}}}&{{{H}_{{13}}}} \end{array}} \right)}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {{{F}_{0}}\cos {{\alpha }_{0}}} \\ {{{F}_{0}}\sin {{\alpha }_{0}}} \\ {F{\text{*}}} \end{array}} \right).$$

(3.3)

4 4 NUMERICAL RESULTS

The analysiswas performed on magnesium crystal. According to Othman et al. [15] the value of the physical constants are

$${{T}_{0}} = 298\;K^\circ ,\quad \lambda = 9.4 \times {{10}^{{10}}}\,\,N\,\,{{m}^{{ - 2}}},\quad \mu = 4.0 \times {{10}^{{10}}}\,\,N\,\,{{m}^{{ - 2}}},\quad \rho = 1.74 \times {{10}^{3}}\;kg{\text{/}}{{m}^{3}},$$

$${{\gamma }_{1}} = 0.779 \times {{10}^{{ - 9}}}\,\,N,\quad {{C}_{E}} = 1.04 \times {{10}^{3}}\;kg\,\,{{m}^{{ - 3}}},\quad K = 1.7 \times {{10}^{2}}\,\,J{{m}^{{ - 1}}}{{s}^{{ - 1}}}{{\deg }^{{ - 1}}},$$

$${{\alpha }_{t}} = 7.4033 \times {{10}^{{ - 7}}}\,\,{{K}^{{ - 1}}}.$$

The comparisons were carried out for

$$t = 0.1,\quad {{F}_{0}} = 1,\quad F\text{*} = 5,\quad a = 3.8,\quad b = {{b}_{0}} + {{b}_{1}},\quad {{b}_{0}} = 2.5\;rad{\text{/}}\operatorname{s} ,\quad {{b}_{1}} = 0.3\;rad{\text{/}}\operatorname{s} ,$$

$$x = 0.3,\quad 0 \leqslant z \leqslant 2.$$

For the two theoretical problems (3PHL, GN-III) over distance z, numerical techniques are used for the distribution of displacement components $u,w,$ temperature θ and stresses ${{\sigma }_{{xz}}},{{\sigma }_{{zz}}}.$ All variables are assumed to be dimensionless, the results are shown in Figs. 2–11.

Fig. 2.

Variation of displacement u versus z.

Fig. 3.

Variation of displacement w versus z.

Fig. 4.

Variation of temperature distribution θ versus z.

Fig. 5.

Variation of shearing force stress σ_xz versus z.

Fig. 6.

Variation of normal force stress σ_zz versus z.

Fig. 7.

Variation of displacement u versus z.

Fig. 8.

Variation of displacement w versus z.

Fig. 9.

Variation of temperature θ versus z.

Fig. 10.

Variation of shearing force stress σ_xz versus z.

Fig. 11.

Variation of normal force stress σ_zz versus z.

Figures 2–6 show the distributions of $u,w,\theta$ and ${{\sigma }_{{xz}}},{{\sigma }_{{zz}}}$ for two values of the initial stress $(p = 0,1.2).$ Figure 2 shows the distribution of u versus z. It is clear that the value of u in both theories is larger with $p = 1.2$ than without the initial stress $(p = 0),$ starting to reach a maximum at z = 0 and then converging towards the zero range $1 \leqslant z \leqslant 1.5.$

Figure 3 shows the variation of w versus z. It can be seen that the value of w in both theories is larger in the case of p = 0 than in the case of $p = 1.2.$ It takes a maximum value in the range $0 \leqslant z \leqslant 0.5,$ then decreases and converges to zero. Figure 4 shows that the variation of θ starts with positive values, satisfies the boundary conditions at z = 0, reaches a maximum at z = 0, then decreases and converges towards zero. Obviously, the bias voltage does not have much effect on the temperature distribution. Figure 5 shows the distribution of ${{\sigma }_{{xz}}}$ for both theories. It starts at z = 0, then decreases and reaches a minimum in the range $0 \leqslant z \leqslant 0.3.$ But then it increases and converges to zero. The difference in the influence curves of the two theories is more pronounced than the effect of different initial stress values. Figure 6 shows the distribution of ${{\sigma }_{{zz}}},$ it can be seen that the value of ${{\sigma }_{{zz}}},$ in the case of no initial stress is larger than that of $p = 1.2$ in both theories. In both cases, ${{\sigma }_{{zz}}},$ takes a non-positive value. The curve rises and then converges towards zero. In the case of $p = 0$, σ_zz, converges to 0, but in the case of $p = 1.2,$ σ_zz converges to –1.2.

Figures 7–11 represent the variation of $u,w$, $\theta$ and ${{\sigma }_{{xz}}},{{\sigma }_{{zz}}}$ with two theories (3PHL,G-N III) versus z for two values for ${{\alpha }_{0}}$ $({{\alpha }_{0}} = 45^\circ ,60^\circ ).$ Figure 7 shows the distribution of $u$ via z. One observes that; the curves begin from $z = 0$ then decrease and converge to zero. By the increasing of ${{\alpha }_{0}}$ the displacement $u$ increases with the two theories i.e., in the case of ${{\alpha }_{0}} = 60^\circ$ the displacement $u$ is larger than in the case of ${{\alpha }_{0}} = 45^\circ$. Figure 8 shows the variation of $w$ via $z,$ which begins from negative values. It is clear that unlike the distribution of $u$, here in the case of ${{\alpha }_{0}} = 45^\circ$, the displacement $w$ takes larger values than in the case of ${{\alpha }_{0}} = 60^\circ$ and with 3PHL theory it takes values larger than by G-N III. It takes its maximum value at ${{\alpha }_{0}} = 45^\circ$ in 3PHL model. Figure 9 shows the distribution of $\theta$ via $z,$ it starts from its maximum value at $z = 0$ and decreases until converges to zero. One can observe that, by increasing the angle of inclination, θ increases i.e., for ${{\alpha }_{0}} = 60^\circ$ the temperature distribution is larger than at ${{\alpha }_{0}} = 45^\circ$. Figure 10 shows the distribution of ${{\sigma }_{{xz}}}$ via $z,$ it is clear that it begins zero and then decreases in the range $0 \leqslant z \leqslant 0.2$ then increases and converges to zero. We notice that in the range $0.2 \leqslant z \leqslant 1.2,$ ${{\sigma }_{{xz}}}$ takes larger values i.e., for the both theories at ${{\alpha }_{0}} = 45^\circ ,$ while ${{\sigma }_{{xz}}}$ is smaller in the case of ${{\alpha }_{0}} = 60^\circ$. Figure 11 shows that ${{\sigma }_{{zz}}}$ takes negative values, first it decreases in the range $0 \leqslant z \leqslant 0.1$, then it increasing and converges to –1.2. One can notice that by the decreasing of the angle of inclination ${{\sigma }_{{zz}}}$ takes larger values i.e., for the both theories in the case of ${{\alpha }_{0}} = 45^\circ ,$ while in the case of ${{\alpha }_{0}} = 60^\circ ,$ ${{\sigma }_{{zz}}}$ has small values.

Figures 12–14 are giving 3D surface curves for the field quantities i.e. $u,$ $\theta$ and ${{\sigma }_{{zz}}}$ these figures play a crucial role in the identification of physical quantities and their dependency on the vertical component of distance. The varying types of boundary conditions are what determine the nature of applied forces and thus the deformation of the body.

Fig. 12.

Three-dimensional curve distribution of the displacement u versus x, z.

Fig. 13.

Three-dimensional curve distribution of the temperature θ versus x, z.

Fig. 14.

Three-dimensional curve distribution of the stress component σ_zz versus x, z.

5 5 CONCLUSIONS

Analysis of displacements, temperature distribution, normal stressand tangential shear stress due to mechanical load in a semi-infinite generalized thermoelastic medium is an interesting problem of mechanics. A normal mode technique has been used which is applicable to a wide range of problems of thermoelasticity. This method gives exact solutions without any assumed restrictions on the actual physical quantities that appear in the governing equations of the problem considered. The effects of the rotation parameter and angle of inclination as well as initial stress parameter on the field variables are investigated. The results concluded from the above analysis can be summarized as follows:

1. Analytical solutions based upon normal mode analysis for thermoelastic problem in solids have been developed and utilized.

2. The effect of rotation parameter and initial stress parameter on all the studied fields is very much significant.

3. Significant difference in values of the studied fields is noticed for different values of the angle of inclination.

4. The deformation of a body depends on the nature of the applied forces as well as the type of boundary conditions.

5. The value of all physical quantities converges to zero with increase in z and all functions are continuous.

6 NOMENCLATURE

λ, μ	The Lame’s constants	ρ	The material density
x, y, z	The Cartesian coordinates variables	T0	The reference temperature
t	The time variable	σij	Stress tensor components
eij	Strain tensor components	δij	Kronecker delta
K	The additional material constant	K*	Thermal conductivity
CE	he specific heat at constant strain	p	The pressure
τT	The phase-lag of temperature gradient	∇2	Laplace operator
τν	The phase-lag of thermal displacement gradient	τq	The phase-lag of heat flux
${{\gamma }_{1}}\, = \,(3\lambda + 2\mu )\,{{\alpha }_{t}},$ αt	The volume thermal expansion
$\theta = T - {{T}_{0}}$	Absolute temperature (temperature above the reference temperature T0) such that $\left| {{{(T\, - \,{{T}_{0}})} \mathord{\left/ {\vphantom {{(T\, - \,{{T}_{0}})} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right|\, \ll \,1.$

Appendix

${{a}_{2}} = {{a}^{2}} - {{b}^{2}} - {{\Omega }^{2}},$ ${{a}_{3}} = 2ib\Omega ,$ ${{a}_{4}} = - {{\Omega }^{2}} - {{b}^{2}},$ ${{a}_{5}} = 2ib\Omega ,$ ${{b}_{1}} = \;{{b}_{7}}{{b}_{9}},$ ${{b}_{2}} = {{b}_{1}}{{a}^{2}},$ ${{b}_{3}} = K{\text{*}} - ib{{b}_{5}} - {{b}_{6}},$ ${{b}_{4}}\, = \,K{\text{*}}{{a}^{2}} - ib{{b}_{5}}{{a}^{2}} - {{a}^{2}}{{b}_{6}} - {{b}_{7}}{{b}_{8}}$, ${{b}_{5}} = K{{\eta }_{0}} + K{\text{*}}{{\tau }_{\nu }}$, ${{b}_{6}} = K{{\eta }_{0}}{{\tau }_{T}}{{b}^{2}}$, ${{b}_{7}} = 1 - ib{{\tau }_{q}} - \frac{1}{2}{{b}^{2}}\tau _{q}^{2}$, ${{b}_{8}} = \rho C_{0}^{2}{{C}_{E}}{{b}^{2}},$ b₉ = $\frac{{{{\gamma }_{1}}{{T}_{0}}{{b}^{2}}}}{\rho },$ ${{b}_{{10}}} = {{b}_{3}}{{a}_{1}},$ ${{b}_{{11}}} = {{b}_{3}}{{a}_{1}}{{a}^{2}} + {{a}_{4}}{{b}_{3}} + {{b}_{4}}{{a}_{1}} + {{a}_{2}}{{b}_{3}}{{a}_{1}} - {{b}_{1}}{{a}_{1}},$ b₁₂ = ${{b}_{4}}{{a}^{2}}{{a}_{1}}\, + \,{{b}_{4}}{{a}_{4}}\, + \,{{a}_{2}}{{b}_{3}}{{a}_{1}}{{a}^{2}}\, + \,{{a}_{2}}{{b}_{3}}{{a}_{4}}$ + b₄a₂a₁ – ${{a}_{1}}{{a}^{2}}{{b}_{1}}\, - \,{{b}_{1}}{{a}_{4}}\, - \,{{a}_{1}}{{b}_{2}}\, + \,{{a}_{3}}{{a}_{5}}{{b}_{3}},$ ${{b}_{{13}}} = {{b}_{4}}{{a}^{2}}{{a}_{1}}{{a}_{2}} + {{a}_{2}}{{b}_{4}}{{a}_{4}} - {{a}^{2}}{{a}_{1}}{{b}_{2}} - {{b}_{2}}{{a}_{4}} + {{b}_{4}}{{a}_{3}}{{a}_{5}},$ ${{L}_{0}} = \frac{{{{b}_{{11}}}}}{{{{b}_{{10}}}}},$ L₁ = $\frac{{{{b}_{{12}}}}}{{{{b}_{{10}}}}},$ L₂ = $\frac{{{{b}_{{13}}}}}{{{{b}_{{10}}}}},$ H_1n = $\frac{{{{b}_{2}} - {{b}_{1}}k_{n}^{2}}}{{{{b}_{3}}k_{n}^{2} - {{b}_{4}}}},$ H_2n = $- \frac{{{{a}_{5}}}}{{{{a}_{1}}(k_{n}^{2} - {{a}^{2}}) - {{a}_{4}}}},$ H_3n = $ia - {{k}_{n}}{{H}_{{2n}}},$ H_4n = $- ({{k}_{n}} + ia{{H}_{{2n}}}),$ H_5n = $\frac{\lambda }{{\rho {{C}_{0}}^{2}}}(k_{n}^{2} - {{a}^{2}}) - \frac{{2\mu }}{{\rho {{C}_{0}}^{2}}}({{a}^{2}} + ia{{k}_{n}}{{H}_{{2n}}})$ – H_1n, H_6n = $\frac{\lambda }{{\rho {{C}_{0}}^{2}}}(k_{n}^{2} - {{a}^{2}}) + \frac{{2\mu }}{{\rho {{C}_{0}}^{2}}}(k_{n}^{2} + ia{{k}_{n}}{{H}_{{2n}}})$ – H_1n, H_7n = $\frac{\mu }{{\rho C_{0}^{2}}}( - 2{{k}_{n}}ia + {{H}_{{2n}}}k_{n}^{2} + {{a}^{2}}{{H}_{{2n}}}) - \frac{p}{2}\frac{{{{\gamma }_{1}}{{T}_{0}}}}{{\rho C_{0}^{2}}}(k_{n}^{2} - {{a}^{2}}){{H}_{{2n}}}.$