Introduction

Functionally graded materials (FGM) are advanced inhomogeneous materials that due to improving the thermal and mechanical properties of the structure are widely used in engineering structures such as beams and plates. The composite beams made of FGM can be classified into three major classes. The first class involves beams whose material properties vary through the thickness direction and are more commonly known as FGM beams. The second class includes beams in which material properties change along the axial direction and so-called axially functionally graded material (AFGM) beams. The third class consists of beams whose material properties vary in both axial and thickness directions and are well-known as bi-direction functionally graded material (BDFGM) beams. In this study, the behavior of the second class, i.e., AFGM beams is investigated. However, the non-uniform homogeneous beams can be considered the special case of the axially functionally graded (AFG) beams with constant material and variable geometry (Bambaeechee, 2019).

On the other hand, knowing the dynamic behavior of AFGM beams is necessary for the design of these composite beams. In the last decades, the free vibration of FGM beams with the exponential variation of mechanical properties has been investigated widely and is still receiving attention in the literature. Huang and Li, (2010) proposed a new approach for the free vibration of the non-uniform AFGM beams with power law and exponential law gradient. The Rayleigh–Ritz method and the finite element method were applied by Anandakumar and Kim, (2010) to study the modal behavior of a three-dimensional functionally graded (FG) cantilever beam. Ait Atmane et al., (2011) presented the analytical solutions for obtaining the natural frequencies of the exponential FGM beams with varying cross-section and classical boundary conditions.

The exact free vibration of the exponentially AFGM beams with different classical boundary conditions was performed by Li et al., (2013). Accordingly, they studied the effect of the exponential gradient index on the natural frequencies of the beam with various classical end supports. Çallıoğlu et al., (2013) analyzed the free vibration of the symmetric FG sandwich beam with variable cross-section using the mixture rules and laminate theory. The free vibration of AFG non-uniform beams with different boundary conditions was studied by Rajasekaran, (2013) using the differential transformation-based dynamic stiffness approach. Duy et al., (2014) analyzed the free vibration of FGM beams on an elastic foundation and rotational spring supports. Tang et al., (2014) derived the exact frequency equations of the exponentially non-uniform AFG Timoshenko beam with different classical boundary conditions. The analytical solution was developed by Liu and Shu, (2014) to study the free vibration of the exponential FGM beams with single delamination. The exact natural frequencies of simply supported FGM beams with exponentially varying material properties were determined by Celebi and Tutuncu, (2014) using the plane elasticity theory. Kumar et al., (2015) investigated the nonlinear free vibration problem of AFG taper beams with the polynomial and exponential varying materials. Şimşek, (2015) analyzed the free and forced vibration behaviors of the bi-directional FGM Timoshenko beam with various boundary conditions. Ebrahimi and Mokhtari, (2015) investigated the vibration analysis of spinning exponentially FG Timoshenko beams based on the differential transform method.

The non-uniformity effects on the free vibration analysis of the non-uniform FGM beams with the exponential law and power law were discussed by Hosseini Hashemi et al., (2016). A novel method was proposed by Yuan et al., (2016) to obtain the exact solutions to the free vibrations of axially inhomogeneous and non-uniform Timoshenko beams. Wang et al., (2016) analyzed the free vibration of two-directional FGM beams with clamped-free and pinned–pinned end supports. By utilizing the displacement-based semi-analytical method, Lohar et al., (2016) presented the natural frequency and mode shapes of an exponential tapered AFG beam resting on an elastic foundation. Using the methods of initial parameters in differential form, the analysis of the free vibrations of the non-uniform and/or AFG Euler–Bernoulli beams with elastically restrained ends was performed by Shvartsman and Majak, (2016). In that study, the power and exponential functions were utilized for variations of the geometrical and mechanical properties. The free transverse vibration analysis of AFG tapered Euler–Bernoulli beams through the spline finite point method was developed by Liu et al., (2016). They assumed the material types including power law and exponential law and discussed the natural frequencies of the beam with various classical boundary conditions. The analytical and numerical method for the free vibration of double-axially FGM beams with elastic end supports and exponential material properties were performed by Rezaiee-Pajand and Hozhabrossadati (2016a). Moreover, they studied the free vibration analysis of a double-beam system joined by a mass-spring device (Rezaiee-Pajand & Hozhabrossadati, 2016b).

The Chebyshev collocation method was applied by Wattanasakulpong and Mao, (2017) to study stability and vibration analyses of carbon nanotube-reinforced composite beams with elastic boundary conditions. By applying the Chebyshev polynomials, natural frequencies and mode shapes of tapered and AFG Rayleigh beams were examined by He et al., (2017). Using the Adomian decomposition method, the vibration analysis of the exponentially and trigonometrically tapered beams with nonlinearly axial varying FGM properties considering different geometry and material taper ratios was studied by Keshmiri et al., (2018). Karamanlı, (2018) analyzed the free vibration behavior of two-directional FGM beams subjected to various sets of classical boundary conditions by employing a third-order shear deformation theory. By a similar theory, the vibration analysis of FGM beams with elastic support was performed by Wattanasakulpong and Bui, (2018) using the Chebyshev collocation method. In another work, Wattanasakulpong et al., (2018) proposed the Chebyshev collocation approach for vibration analysis of FG porous beams based on third-order shear deformation theory.

The exact natural frequencies and buckling load of the FGM tapered beam-column with elastic supports were presented by Rezaiee-Pajand and Masoodi, (2018). Mahmoud, (2019) proposed a general solution for the free vibration of the non-uniform AFG cantilevers with tip mass at the free end using the transfer matrix method. Based on the new hybrid approach, the free vibration and stability analyses of AFGM Euler–Bernoulli beams with variable cross-sections resting on a uniform Winkler-Pasternak foundation were performed by Soltani and Asgarian, (2019). Avcar, (2019) investigated the free vibration of imperfect sigmoid and power law FG beams with simply supported. The analytical solution was presented by AlSaid-Alwan and Avcar, (2020) to study the free vibration of FG beams utilizing different types of beam theories. By using the Rayleigh–Ritz method, Kumar, (2020) investigated the dynamic behavior of an AFG beam resting on a variable elastic foundation. Erdurcan and Cunedioğlu, (2020) studied the free vibration of an aluminum beam coated with FGM by using a Timoshenko beam and FEM theory for both simply supported and cantilever beams. The Chebyshev spectral collocation method was employed by Sari and Al-Dahidi, (2020) to study the vibration behavior of AFG non-uniform multiple beams. Avcar et al., (2021) analyzed the natural frequencies of sigmoid FG sandwich beams in the framework of high-order shear deformation theory. The continuous elements method was applied by Selmi, (2021) to investigate the free vibration bi-dimensional FGM beams. He considered that the material properties vary exponentially along the beam thickness and length. By a similar approach, Selmi and Mustafa, (2021) analyzed the influences of the gradient indexes and the beam slenderness ratio on the natural frequencies of the exponential BDFGM beams with simple supports. Chen and Chang, (2021) examined the vibration behaviors of BDFGM Timoshenko beams with classical boundary conditions, based on the Chebyshev collocation method. By a similar technique, the flexural vibration analysis of FG sandwich plates resting on an elastic foundation with arbitrary boundary conditions was performed by Tossapanon and Wattanasakulpong, (2020). Recently, the exact solutions for the free transverse vibration of power-law non-uniform AFG beams with endpoint masses and general boundary conditions were presented by Bambaeechee, (2022). Moreover, Zhao et al., (2022) proposed a unified Jacobi–Ritz approach for vibration analysis of FG porous rectangular plate with arbitrary boundary conditions based on a higher-order shear deformation theory.

A comprehensive literature review was completed above based on the focus on the works related to free vibration analysis of the FGM beams with the exponential variation of the material properties. To the best of the authors’ knowledge, there is no reported work on the exact solutions of the free transverse vibration of the exponential AFGM beams with the concentrated tip masses and general boundary conditions. Thus, this study aims to get the closed-form expression for calculating the exact natural frequencies of the exponential AFGM Euler–Bernoulli beams with attached tip masses and general boundary conditions. In the following, the mode shapes and design charts of the AFGM beams can also be obtained. The advantages of the proposed formulations are high accuracy, generality, and simplicity to simulate the various boundary conditions. Also, it can be applied to the purposeful design of vibrating a wide range of uniform beams, non-uniform beams with constant thickness and exponentially decaying width, and composite beams. In addition, a similar strategy can be used for various material distribution. According to the derived formulations, the effects of the elastic supports, attached tip masses, and exponential gradient index on the natural frequencies and mode shapes of the exponential AFGM beams with symmetric and asymmetric boundary conditions are investigated in detail for the first time. Results show they play an important role in the natural frequencies and mode shapes of the AFGM beams. This topic will be very important when the design goal is to achieve or not to achieve a certain frequency. Accordingly, the results of this study can be used for the proper design of the exponential composite beams carrying tip masses with different elastic boundary conditions. Moreover, the proposed method can be applied to study the behavior of the small-scale structures that are governed by the classical Euler–Bernoulli beam theory.

Free vibration analysis

In this work, the analytical solutions to obtain the exact natural frequencies of the exponential AFGM Euler–Bernoulli beam with general boundary conditions and attached tip masses are derived.

AFGM properties

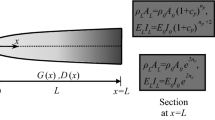
In this study, the material properties, i.e., modulus of elasticity and mass density of the AFGM beam, shown in Fig. 1, are assumed to vary continuously and together in the axial direction according to the exponential functions and defined as (Li et al., 2013):

$$\rho \left( x \right) = \rho_0 e^{2\beta \left( \frac{x}{L} \right)} = \rho_L e^{2\beta \left( {\frac{x}{L} - 1} \right)} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} 0 \le x \le L$$
(1a)
$$E\left( x \right) = E_0 e^{2\beta \left( \frac{x}{L} \right)} = E_L e^{2\beta \left( {\frac{x}{L} - 1} \right)} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} 0 \le x \le L$$
(1b)

where β is the exponential gradient index, x is the axial coordinate, L is the length of the beam, ρ(x) is the volume mass density at position x, and E(x) is the modulus of elasticity at position x. Also, ρ0 and E0, and ρL and EL, are the mass density and modulus of elasticity at x = 0 and x = L, respectively. Here, the subscript “0” means x = 0, and the subscript “L” indicates x = L. As a result, the mass per unit length and flexural rigidity of the exponential AFGM was obtained as:

$$m\left( x \right) = \rho \left( x \right)A = \rho_0 Ae^{2\beta \left( \frac{x}{L} \right)} = \rho_L Ae^{2\beta \left( {\frac{x}{L} - 1} \right)}$$
(2a)
$$K\left( x \right) = E\left( x \right)I = E_0 Ie^{2\beta \left( \frac{x}{L} \right)} = E_L Ie^{2\beta \left( {\frac{x}{L} - 1} \right)}$$
(2b)

where m(x), K(x), A, and I are the mass per unit length, flexural rigidity, cross-section area, and moment of inertia of the AFGM beam, respectively. It should be noted that the exponential gradient index, β, can be any rational number. In addition, when β = 0, the beam is homogeneous.

Fig. 1
figure 1

Schematic of the exponential AFGM beam

Full size image

Governing differential equation

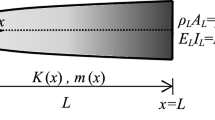
The free lateral vibration differential equation of an AFGM beam of length L with general boundary conditions and tip masses in the framework of the Euler–Bernoulli theory, as shown in Fig. 2, is given by (Rao, 2019):

$$\frac{\partial^2 }{{\partial x^2 }}\left[ {K\left( x \right)\frac{{\partial^2 w\left( {x,t} \right)}}{\partial x^2 }} \right] + m\left( x \right)\frac{{\partial^2 w\left( {x,t} \right)}}{\partial t^2 } = 0,\begin{array}{*{20}c} {} & {} & {} \\ \end{array} 0 \le x \le L$$
(3)

where x is the axial coordinate, t is time, w(x,t) is the lateral deflection of the beam, K(x) is the flexural rigidity of the beam at the position x, and m(x) is the mass per unit length of the beam at the position x.

Fig. 2
figure 2

Schematic of the exponential AFGM beam with general boundary conditions and tip masses

Full size image

Following the separation of variable analogy, the solution of Eq. (3) can be expressed as (Rao, 2019):

$$w_n \left( {x,t} \right) = W_n \left( x \right)\sin \omega_n t$$
(4)

where Wn(x) is the shape function of the lateral motion of the nth vibration mode and ωn is the circular frequency.

Substituting Eq. (4) into Eq. (3), one can get:

$$\frac{{\rm d^2} }{{{\rm d}x^2 }}\left[ {K\left( x \right)\frac{{\rm d^2} W_n \left( x \right)}{{{\rm d}x^2 }}} \right] - m(x)\omega_n^2 W_n \left( x \right) = 0$$
(5)

If Eqs. (2a) and (2b) are inserted into Eq. (5), it can be rewritten as:

$$\frac{{\rm d^2} }{{{\rm d}x^2 }}\left[ {E_0 Ie^{2\beta \left( \frac{x}{L} \right)} \frac{{\rm d^2} W_n \left( x \right)}{{{\rm d}x^2 }}} \right] - \rho_0 Ae^{2\beta \left( \frac{x}{L} \right)} \omega_n^2 W_n \left( x \right) = 0$$
(6)

By deriving from the latter equation, one can get:

$$E_0 Ie^{2\beta \left( \frac{x}{L} \right)} \frac{{\rm d^4} W_n \left( x \right)}{{{\rm d}x^4 }} + 4\beta \frac{E_0 I}{L}e^{2\beta \left( \frac{x}{L} \right)} \frac{{\rm d^3} W_n \left( x \right)}{{{\rm d}x^3 }} + 4\beta^2 \frac{E_0 I}{{L^2 }}e^{2\beta \left( \frac{x}{L} \right)} \frac{{\rm d^2} W_n \left( x \right)}{{{\rm d}x^2 }} - \rho_0 Ae^{2\beta \left( \frac{x}{L} \right)} \omega_n^2 W_n \left( x \right) = 0$$
(7)

or

$$L^4 \frac{{\rm d^4} W_n (x)}{{{\text{d}}x^4}} + 4\beta L^3 \frac{{\rm d^3} W_n \left( x \right)}{{{\text{d}}x^3 }}{ + }4\beta^2 L^2 \frac{{\rm d^2} W_n \left( x \right)}{{{\text{d}}x^2 }}{ - }\omega_n^2 L^4 \frac{\rho_0 A}{{E_0 I}}W_n \left( x \right){ = 0}$$
(8)

Introducing the following quantity

$$X = \frac{x}{L} $$
(9)

and considering in mind that

$${\rm d}x = L{\rm d}X$$
(10)

Equation (8) simplifies as follows:

$$\frac{{\rm d^4} W_n \left( X \right)}{{{\rm d}X^4 }} + 4\beta \frac{{\rm d^3} W_n \left( X \right)}{{{\rm d}X^3 }} + 4\beta^2 \frac{{\rm d^2} W_n \left( X \right)}{{{\rm d}X^2 }} - \Omega_n^2 W_n \left( X \right) = 0$$
(11)

where \(\Omega_n = \omega_n L^2 \sqrt[{}]{{\frac{\rho_0 A}{{E_0 I}}}}\) is the dimensionless natural frequency coefficient of the nth vibration mode.

The general solution of this equation is (Wang & Wang, 2013):

$$W_n \left( X \right) = e^{ - \beta \,X} \left[ {C_1 \cos \,(\delta_1 \,X) + C_2 {\rm sin}\,(\delta_1 \,X) + C_3 {\rm cosh}\,(\delta_2 \,X) + C_4 {\rm sinh}\,(\delta_2 \,X)} \right]\, \begin{array}{*{20}c} {} & {if} \\ \end{array} \,\,\,\,\Omega_n > \beta^2$$
(12a)
$$W_n \left( X \right) = e^{ - \beta \,X} \left[ {C_1 + C_2 X + C_3 {\rm cosh}\,(\delta_2 \,X) + C_4 {\rm sinh}\,(\delta_2 \,X)} \right]\,\,\begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {if} \\ \end{array} \,\,\,\,\Omega_n = \beta^2$$
(12b)
$$W_n \left( X \right)=e^{ - \beta \,X} \left[ {C_1 \cosh \,(\delta_3 \,X) + C_2 {\rm sinh}\,(\delta_3 \,X) + C_3 {\rm cosh}\,(\delta_2 \,X) + C_4 {\rm sinh}\,(\delta_2 \,X)} \right] \begin{array}{*{20}c} {} & {if} \\ \end{array} \,\,\,\,\,\Omega_n < \beta^2$$
(12c)

where \(\delta_1 = \sqrt {\Omega_n - \beta^2 }\), \(\delta_2 = \sqrt {\Omega_n + \beta^2 }\), \(\delta_3 = \sqrt {\beta^2 - \Omega_n }\), and C1, C2, C3, C4 are unknown constants. Although Ωn > β2 in most cases, there are situations where Ωn < β2 (Wang & Wang, 2013). Herein, just investigated the case Ωn > β2 in detail which occurs in most cases.

General boundary conditions and tip masses

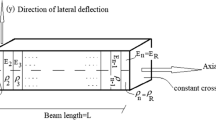
The boundary conditions of the exponential AFGM beam, in the presence of the concentrated tip masses M0 and ML, and constraints with the rotational elastic stiffnesses kR0 and kRL, and lateral translational elastic stiffnesses kT0 and kTL are expressed as:

$$\frac{{\rm d^2} W_n (X)}{{{\rm d}X^2 }} - \frac{{k_{R0} L}}{E_0 I}\frac{{\rm d}W_n (X)}{{{\rm d}X}} = 0$$
(13)
$$\frac{{\rm d^3} W_n (X)}{{{\rm d}X^3 }} + 2\beta \frac{{\rm d^2} W_n (X)}{{{\rm d}X^2 }} + \frac{{\left( {k_{T0} - M_0 \omega_n^2 } \right)L^3 }}{E_0 I}W_n (X) = 0$$
(14)

which refer to the equilibrium of bending and shear at X = 0, respectively, and

$$\frac{{\rm d^2} W_n (X)}{{{\rm d}X^2 }} + \frac{{k_{RL} L}}{E_L I}\frac{{\rm d}W_n (X)}{{{\rm d}X}} = 0$$
(15)
$$\frac{{\rm d^3} W_n (X)}{{{\rm d}X^3 }} + 2\beta \frac{{\rm d^2} W_n (X)}{{{\rm d}X^2 }} + \frac{{\left( {M_L \omega_n^2 - k_{TL} } \right)L^3 }}{E_L I}W_n (X) = 0$$
(16)

which denote the equilibrium of bending and shear at X = 1, respectively.

For simplicity, the following dimensionless mass ratios (α0, αL), stiffness coefficient (KR0, KRL, KT0, and KTL), and stiffness ratios (R0, RL, T0, and TL) are introduced (Rezaiee-Pajand et al., 2015; Šalinić et al., 2018):

$$\begin{gathered} \alpha_0 = \frac{M_0 }{{\rho_0 AL}}, \alpha_L = \frac{M_L }{{\rho_L AL}}, K_{R0} = \frac{{k_{R0} L}}{E_0 I}, K_{T0} = \frac{{k_{T0} L^3 }}{E_0 I}, K_{RL} = \frac{{k_{RL} L}}{E_L I}, K_{TL} = \frac{{k_{TL} L^3 }}{E_L I}, \hfill \\ R_0 = \frac{{K_{R0} }}{{1 + K_{R0} }}, T_0 = \frac{{K_{T0} }}{{1 + K_{T0} }}, R_L = \frac{{K_{RL} }}{{1 + K_{RL} }}, T_L = \frac{{K_{TL} }}{{1 + K_{TL} }}. \hfill \\ \end{gathered}$$
(17)

From above, the corresponding inverse relation between stiffness coefficients and stiffness ratios read:

$$K_{R0} = \frac{R_0 }{{1 - R_0 }}, K_{T0} = \frac{T_0 }{{1 - T_0 }}, K_{RL} = \frac{R_L }{{1 - R_L }}, K_{TL} = \frac{T_L }{{1 - T_L }}.$$
(18)

Accordingly, when the stiffness coefficients (KR0, KRL, KT0, KTL) vary from 0 to ∞, the corresponding stiffness ratios (R0, RL, T0, and TL) take values from 0 to 1. This makes numerical calculations much easier because one avoids seeking the sufficiently large value of spring stiffness coefficients, which would adequately substitute value 1 in specific numerical calculations (Šalinić et al., 2018). As a result, if the stiffness ratios are allowed to become one or zero, then the classical restraints can be easily recovered. Also, the non-classical supports have stiffness ratios between zero and one. For example, the values R0 = T0 = 1 and RL = TL = 0 correspond to the clamped left and the free right end of the beam, respectively. The elastic beam whose stiffness of all elastic supports is 50%, is modeled by considering R0 = T0 = RL = TL = 0.5. Here, the subscript “0” denotes x = 0, and the subscript “L” means x = L.

Substituting the values of X and dimensionless ratios defined as Eq. (17), the boundary conditions of Eqs. (13)–(16) can be expressed by the following dimensionless forms:

$$(1 - R_0 )W^{\prime \prime}_n (0) - R_0 W^{\prime}_n (0) = 0$$
(19)
$$(1 - T_0 )W^{\prime\prime\prime}_n (0) + 2\beta (1 - T_0 )W^{\prime \prime}_n (0) + \left[ {T_0 - \alpha_0 \Omega_n^2 (1 - T_0 )} \right]W_n (0) = 0$$
(20)
$$(1 - R_L )W^{\prime \prime}_n (1) + R_L W^{\prime}_n (1) = 0$$
(21)
$$(1 - T_L )W^{\prime\prime\prime}_n (1) + 2\beta (1 - T_L )W^{\prime \prime}_n (1) + \left[ {\alpha_L \Omega_n^2 (1 - T_L ) - T_L } \right]W_n (1) = 0$$
(22)

where \(W^{\prime}_n (X) = \frac{{\rm d}W_n (X)}{{{\rm d}X}}\), \(W^{\prime \prime}_n (X) = \frac{{\rm d^2} W_n (X)}{{{\rm d} X^2}}\), and \(W^{\prime\prime\prime}_n (X) = \frac{{\rm d^3} W_n (X)}{{{\rm d} X^3}}\).

Determination of the natural frequency

By substituting the general solution (12a) into the dimensionless boundary conditions defined in Eqs. (19)–(22), for the four integration constants, a homogeneous system of four equations can be found as:

$$\left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{13} } & {A_{14} } \\ {A_{21} } & {A_{22} } & {A_{23} } & {A_{24} } \\ {A_{31} } & {A_{32} } & {A_{33} } & {A_{34} } \\ {A_{41} } & {A_{42} } & {A_{43} } & {A_{44} } \\ \end{array} } \right]\left[ \begin{gathered} C_1 \hfill \\ C_2 \hfill \\ C_3 \hfill \\ C_4 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right]$$
(23)

or in compact matrix form as follows:

$$\bf {\text{AC}} = {0}$$
(24)

where the constant coefficients matrix A for the exponential AFGM beams with any rational value of the gradient index is given explicitly in Appendix. To have a non-trivial solution, the determinant of this system must be zero:

$$\det {\textbf{A}} = 0$$
(25)

Consequently, the positive real roots of this equation are the natural frequencies of the AFGM beams with the tip masses and elastic end supports. It should be added, that these are calculated numerically and using the well-known numerical software MAPLE.

Verification and numerical examples

To demonstrate the accuracy and efficiency of the derived formulations, three numerical examples, shown in Fig. 3, are analyzed in this part. The results are compared with those obtained by other researchers in Tables 1, 2, and 3. From Tables 1, 2, and 3, it is observed that the proposed formulations for computing the natural frequencies have high accuracy and are easy to simulate the various classical and non-classical boundary conditions. Moreover, the formulation is applied for a wide range of uniform, non-uniform and composite beams.

Fig. 3
figure 3

Schematic of the exponential AFGM beams with classical boundary conditions and homogeneous beam with symmetric elastic boundary conditions in numerical examples

Full size image
Table 1 The first three dimensionless natural frequencies of cantilever exponential AFGM beam for various β (Example 1)
Full size table
Table 2 The first three dimensionless natural frequencies of simply supported exponential AFGM beam for various β (Example 2)
Full size table
Table 3 The square root of the first three dimensionless natural frequencies of elastic supported homogeneous beam for various R0 = RL = T0 = TL (Example 3)
Full size table

Discussion and parametric studies

The effects of the attached tip masses, elastic supports, and exponential gradient index on the natural frequencies and mode shapes of the AFGM beams with classical and non-classical boundary conditions will be investigated in this section. Accordingly, the schematics of the case studies with non-classical boundary conditions illustrate in Fig. 4. Moreover, several design charts for the fundamental natural frequency of the AFGM beams with various boundary conditions will be presented, for the first time.

Fig. 4
figure 4

Schematic of the exponential AFGM beams with non-classical boundary conditions in parametric studies

Full size image

Effects of the classical boundary conditions with various exponential gradient index and tip mass

In this section, the effects of the exponential gradient index and tip mass at the free end on the natural frequency coefficients Ωn (n = 1,2,3) for beams with symmetric and asymmetric classical boundary conditions, namely, P–P, C–C, F–C, and C–F, are investigated. Here, C means clamped, P denotes pinned, and F indicates free. The numerical values of Ωn (n = 1,2,3) for these cases are tabulated in Table 4. It should be added that according to the same results, depending on the symmetric or asymmetric boundary conditions and the positive or negative sign of the exponential gradient index, this classification is considered.

Table 4 The first three dimensionless natural frequency coefficients Ωn, n = 1, 2, 3 of the exponential AFGM beams with classical supports and various values of β and tip mass
Full size table

From Table 4, it is deduced that the minimum and maximum of the natural frequency occur in the first mode of the uniform beam with C–C and P–P boundary conditions, respectively. Furthermore, for the C–C beam as the absolute value of β increases, the natural frequency coefficients increase. There is a similar situation for the P–P beam, except for the first natural frequency coefficient. On the other hand, as the exponential gradient index increases, the natural frequency coefficients of C–F and F–C beams increase and decrease, respectively. Accordingly, depending on the boundary conditions and mode of the vibration, changing the value of the exponential gradient index can cause a decrease or increase in the natural frequency of the exponential AFGM beam. For example, increasing the value of β from -1 to 1 can raise the fundamental natural frequency coefficient (Ω1) of the F–C AFGM beam to 3.4 times. Although, this effect is lighter for the symmetric beam. Moreover, the natural frequencies of the exponential AFGM beam decrease with the increasing tip mass. Accordingly, the presence of tip mass as much as homogeneous beam mass at the free end can reduce the fundamental natural frequency coefficient (Ω1) of the F–C beam by more than 50%, regardless of β.

Furthermore, Table 4 shows that two symmetric AFGM beams with symmetric exponential gradient indexes have the same natural frequency. On the other hand, two asymmetric AFGM beams with mirror boundary conditions and symmetric exponential gradient indexes have the same natural frequency. It is reminded that the uniform beams with C–F and F–C boundary conditions have the same natural frequencies but for the exponential AFGM beams, the corresponding results are different. The physical reasons for the differences in results for the exponential AFGM beams with C–F and F–C boundary conditions return to the equivalent lateral stiffness and tip mass. Accordingly, for the negative gradient index (corresponding to the trend of decreasing the flexural rigidity), the equivalent lateral stiffness of the C–F beam is larger than the F–C beam. Therefore, the natural frequencies of the C–F beam are larger than F–C beams with a negative gradient index. This phenomenon for the positive gradient index is inverted. In other words, for the positive gradient index (corresponding to the trend of increasing flexural rigidity), the equivalent lateral stiffness of the F–C beam is larger than the C–F beam. Therefore, the natural frequencies of the F–C beam are larger than C–F beams with a negative gradient index. However, the natural frequency decreases in the presence of tip mass, regardless of the boundary conditions.

Effects of the non-classical boundary conditions

In Figs. 5 and 6, variations of the first three dimensionless natural frequencies Ωn (n = 1,2,3) of the exponential AFGM beams (β = 0.5) to various quantities of the rotational and translational stiffness ratios (i.e., T0, R0, TL, and RL) are plotted.

Fig. 5
figure 5

Plot the first three dimensionless natural frequencies in case 1

Full size image
Fig. 6
figure 6

Plot the first three dimensionless natural frequencies in case 2

Full size image

Asymmetric boundary conditions (Case 1)

In this case, the free-supported exponential AFGM beam (β = 0.5) with the translational and rotational springs at x = L (Fig. 4(a)) is studied. As seen in Fig. 5, as the stiffness ratios RL = TL increase from 0 (corresponding to F–F beam) to 1 (corresponding to F–C beam), the natural frequencies of the AFGM beam increase. This effect is more pronounced as the rotational and translational stiffness ratios RL = TL are more than 0.9. In other words, the translational stiffness sensitivity (slope of the TL-Ωn curve) is higher when the stiffness of the translational spring kTL is more than 90%. Accordingly, increasing stiffnesses of the elastic support RL = TL from 10 to 50% and 100% can increase the fundamental frequency of the AFGM beam in case 1 by about 2.95 and 12.33 times, respectively.

Symmetric boundary conditions (Case 2)

In this case, the symmetric elastic supported exponential AFGM beam (β = 0.5) with two translational and rotational springs at x = 0 and x = L (Fig. 4(b)) is investigated. According to Fig. 6, as the stiffness ratios R0 = RL = T0 = TL increase from 0 (corresponding to the F–F beam) to 1 (corresponding to the C–C beam), the natural frequencies of the AFGM beam increase smoothly. Also, the value of Ω1 is almost independent of the rotational stiffness, except in the limit state T0 = TL = 1 (corresponding to the P–P beam). It should be noted that when T0 = TL = 1, the trend of increasing frequencies is more intense and there is a significant difference between the values of Ωn (n = 1,2,3) with other states. Accordingly, increasing stiffnesses of the elastic support R0 = RL = T0 = TL from 10 to 50% and 100% can raise the first dimensionless natural frequency coefficient Ω1 of the AFGM beam in case 2 to 2.99 and 46.40 times, respectively.

From the comparison of Figs. 5 and 6, it is concluded that translational stiffness has relatively more influence on the natural frequencies than rotational stiffness.

Effects of the tip mass with asymmetric boundary conditions (Case 3)

Schematic of the third case study and variations of the first three dimensionless natural frequencies versus the mass ratio, α0, are plotted in Fig. 4(c) and Fig. 7, respectively. Furthermore, the sample results of the corresponding numerical values of Ωn (n = 1,2,3) for this case are listed in Table 5.

Fig. 7
figure 7

Plot the first three dimensionless natural frequencies in case 3

Full size image
Table 5 Sample results of the first three dimensionless natural frequencies for case 3
Full size table

According to Fig. 7, increasing the tip mass ratio causes a reduction in the values of Ωn (n = 1,2,3) of the beam. This effect is more pronounced for the high stiffness and low tip mass ratios. From Fig. 7 and Table 5, it is observed that increasing the tip mass ratio from 0 to 1 can decrease the first dimensionless natural frequency coefficient Ω1 of the AFGM beam for the low, moderate, high, and fully stiffness ratios in case 3 by about 28%, 30%, 42%, and 53%, respectively.

It is reminded that the result, in this case, can be used for the AFGM beam with β = -0.5 and mirror boundary conditions.

Effects of the exponential gradient index with symmetric boundary conditions (Case 4)

In Fig. 4(d) and Fig. 8, respectively, the schematic of the fourth case study and variations of the first three dimensionless natural frequencies versus the exponential gradient index, β, are presented. Moreover, the sample results of the corresponding numerical values of Ωn (n = 1,2,3) for this case are tabulated in Table 6.

Fig. 8
figure 8

Plot the first three dimensionless natural frequencies in case 4

Full size image
Table 6 Sample results of the first three dimensionless natural frequencies for case 4
Full size table

According to Fig. 8 and Table 6, it is deduced that for the AFGM beam with the symmetric elastic boundary conditions and tip masses, the minimum natural frequency always occurs for the homogeneous beam. Also, the variation of the natural frequencies is symmetrical to the variation of the exponential gradient index when the boundary conditions are symmetrical.

Furthermore, it is found that the values of Ωn (n = 1,2) increase as the stiffness and mass ratios increase simultaneously, regardless of β. This trend for the third mode is different and complex. Results show that for a homogeneous beam (β = 0) and AFGM beam (β = 0.5) with the simultaneous increase of each of the values of Ri, Ti, and αi (i = 0, L) from 0.1 to 0.9, the first natural frequency coefficient Ω1 increases by about 5.88 and 5.80 times. Accordingly, the increasing effect of stiffness ratios is greater than the decreasing effect of tip mass ratios. On the other hand, increasing the exponential gradient index from 0 to 1 can increase the value of Ω1 of the symmetric AFGM beam for the low, moderate, and high stiffness ratios by about 10%, 6%, and 4%, respectively.

Effects of the tip masses and various boundary conditions on the mode shapes

The first three mode shapes of the exponential AFGM beam (β = 0.5) in cases 1 through 4 with various values of the variable parameters are plotted in Fig. 9. Those are obtained by solving the Eq. (23) by assuming C1 = 1 and inserting it in Eq. (12a). Figure 9 illustrates that the tip mass (according to cases 1 and 3) and boundary conditions (according to cases 2 and 4) have a significant influence on the mode shapes of the AFGM beam, as expected. Also, the mode shapes of the AFGM beam are always asymmetric because the material distribution is asymmetric.

Fig. 9
figure 9

Plot the first three mode shapes of the AFGM beam (β = 0.5) in a case 1 with RL = TL = 1, b case 2 with R0 = T0 = RL = TL = 1, c case 3 with RL = TL = 1 and α0 = 1, and d case 4 with R0 = T0 = RL = TL = 0.9 and α0 = αL = 0

Full size image

Design charts for various boundary conditions

In this section, the design charts for the fundamental dimensionless natural frequency coefficient of the exponential AFGM beam (β = 0.5) and homogenous beam (β = 0.0) in the range Ω1 = 0.5 to Ω1 = 4 for cases 1 through 4 are illustrated in Fig. 10 and Fig. 11, respectively. Those are degenerated from the characteristic equation (Eq. (25)) assuming a specific value of Ω1. From Figs. 10–11, in addition to confirmation of previous results, the possible combinations of the boundary conditions for specified fundamental natural frequencies are available. For example, the exponential AFGM beam (β = 0.5) in case 1 with RL = 0.2 and TL = 0.6, or RL = 0.8 and TL = 0.4, case 2 with T0 = TL = 0.35, case 3 with RL = TL = 0.6 and α0 = 0.8, and case 4 with R0 = T0 = RL = TL = 0.4 and α0 = αL = 0.2 has the same fundamental natural frequency (Ω1≈1). Moreover, for known boundary conditions, the design charts can be easily used to determine the value of Ω1.

Fig. 10
figure 10

Design charts for the fundamental dimensionless natural frequency (Ω1) of the AFGM beam (β = 0.5) with various boundary conditions

Full size image
Fig. 11
figure 11

Design charts for the fundamental dimensionless natural frequency (Ω1) of the homogeneous beam (β = 0.0) with various boundary conditions

Full size image

By comparison of Fig. 10 and Fig. 11, it is concluded that the design charts of the homogeneous and inhomogeneous beams are very close to each other with symmetric boundary conditions. Nevertheless, there are the main differences between design charts of the homogeneous and inhomogeneous beams with asymmetric boundary conditions.

Conclusions

In this study, the analytical method and design charts for finding the exact solutions to the free transverse vibration of the AFGM beams with attached concentrated tip masses and general boundary conditions were presented in the framework of the Euler–Bernoulli theory. The material properties of AFGM beams were assumed to vary in the axial direction according to the exponential functions. The proposed formulations have high accuracy and efficiency and are usable for uniform, non-uniform, and composite beams. Moreover, a similar strategy could be used for evaluating the other new variables in the free vibration analysis. According to the derived formulations, the effects of elastic supports, attached tip masses, and exponential gradient index on the natural frequencies and mode shapes of the exponential AFGM beams were discussed. Results show those play an important role in the natural frequencies and mode shapes of the AFGM beams. This topic would be very important when the design goal is to achieve or not to achieve a certain frequency. Accordingly, the results and design charts of this study could be used for the proper design of the exponential composite beams and homogeneous beams carrying tip masses with different elastic boundary conditions. Also, the exact solutions were reported in graphical and tabular forms and could be used as the benchmark for FEM and other numerical solutions.

Based on the parametric studies, the following important points are concluded:

  • The natural frequencies of the AFGM beam decrease with the increasing tip mass ratio while increasing with increasing stiffness ratios. However, translational stiffness has relatively more influence than rotational stiffness.

  • Depending on the boundary conditions and mode of the vibration, changing the value of the exponential gradient index β can cause a decrease or increase in the natural frequency of the exponential AFGM beam. Although, this effect is lighter for the symmetric beam.

  • Asymmetric AFGM beams with mirror boundary conditions and mirror gradient index have the same natural frequency. For example, the natural frequencies of the free-clamped beam with exponential gradient index β are equal to the clamped-free beam with exponential gradient index -β.

  • Symmetric AFGM beams for mirror gradient indexes have the same natural frequency. For example, the natural frequencies of the pinned-pinned beam with exponential gradient index β and -β are identical.

  • The presence of tip mass as much as homogeneous beam mass at the free end of the free-clamped AFGM beam can reduce the fundamental natural frequency of the beam by more than 50%.

  • For the symmetric AFGM beam with the non-classical boundary conditions, the minimum natural frequency occurs for the uniform beam. Nevertheless, for the simply supported AFGM beam, the maximum of the first natural frequency takes place in the homogeneous beam.