1 Introduction

Fredholm integral equations are well-known classical relations which have many applications in the engineering problems. The novelty of presented approach in this paper is based on the conversion of governing equation into its weak form. A differential equation includes a function and its derivatives. We obtain the weak form of differential equation through the repetitive integrations according to Fredholm transformation approach. The integration continues till the resulting integral equation and includes only the function itself after the last integration stage; derivatives of function will have been eliminated due to the integration. The solution of weak form of differential equation instead of initial equation has many applications in the finite elements analysis. For example, we consider function \( y(x) \) as a dependent function with the following governing differential equation:

$$ \frac{{{\text{d}}^{4} }}{{{\text{d}}x^{4} }}y + y(x) = 0 $$

in which “x” is independent variable. Since this equation contains \( \left\{ {\frac{{{\text{d}}^{4} }}{{{\text{d}}x^{4} }}y} \right\} \), we need four repetitive integrations with respect to “x” from “0” to “x” to convert this equation into its weak form as follows:

$$ \left\{ \begin{gathered} \frac{{{\text{d}}^{3} }}{{{\text{d}}x^{3} }}y + \int\limits_{0}^{x} {y(s)} {\text{d}}s = C_{1} \hfill \\ \frac{{{\text{d}}^{2} }}{{{\text{d}}x^{2} }}y + \int\limits_{0}^{x} {\left( {x - s} \right)y(s)} {\text{d}}s = C_{1} x + C_{2} \hfill \\ \frac{{\text{d}}}{{{\text{d}}x}}y + \int\limits_{0}^{x} {\frac{{\left( {x - s} \right)^{2} }}{2}y(s)} {\text{d}}s = \frac{{C_{1} }}{2}x^{2} + C_{2} x + C_{3} \hfill \\ y(x) + \int\limits_{0}^{x} {\frac{{\left( {x - s} \right)^{3} }}{6}y(s)} {\text{d}}s = \frac{{C_{1} }}{6}x^{3} + \frac{{C_{2} }}{2}x^{2} + C_{3} x + C_{4} \hfill \\ \end{gathered} \right. $$

The last equation after four repetitive integrations includes only the function y(x) itself, and its derivatives have been eliminated due to integrations process. The last equation is the weak form of governing differential equation. After this transformation, we approximate dependent function y(x) using a power series in order to convert this equation into a solvable one. Also, we apply four independent boundary conditions to calculate the integration constants \( C_{{i\quad i = 1,2,3,4}} \). Functionally graded materials (FGMs) are a new kind of composite materials which are applicable for construction of beams, plates, shells and other engineering structures. The material properties of FGMs can vary continuously along the both cross section and axial direction of structure. The asymptotic development method (ADM) has been utilized to investigate the free vibration of uniform AFG beams with different boundary conditions [1]. The approximation of higher-order linear Fredholm integro-differential-difference equations (IDDEs), with the mixed conditions, has been performed by a new collocation technique based on the balancing polynomials [2]. The rapid stabilization of heat equation on the 1-dimensional torus using the backstepping method with a Fredholm transformation has been studied [3]. Jacobi collocation method for the numerical solution of neutral nonlinear weakly singular Fredholm integro-differential equations has been considered [4]. A direct transcription approach for solving a notable category of optimal control problems governed by nonlinear fractional Fredholm integral equations having delays in both input and output signals has been developed [5]. The best approximate solution of Fredholm integral equations of first kind with some scattered observations has been studied [6]. The harmonic differential quadrature (HDQ) method has been employed by Singh and Sharma [7] to investigate the vibration characteristics of axially functionally graded (AFG) tapered beam. The comparison between the receptance matrices of isotropic homogeneous beam and the axially functionally graded beam carrying concentrated masses has been presented [8]. The symbolic-numeric method of initial parameters (SNMIP) has been applied to study free vibrations of Euler–Bernoulli axially functionally graded tapered, stepped and continuously segmented rods and beams with elastically restrained end with attached masses [9]. The analytical solutions of steady-state dynamic responses of axially functionally graded and non-uniformed beams subjected to harmonic loadings with damping effect have been presented by using the Green’s function element method [10]. Effects of axial load distribution on buckling loads and their modes of functionally graded (FG) beams including a shear effect have been investigated [11]. An effective approximation for free vibration analysis of axially functionally graded material (AFGM) beams based on the Jacobi polynomial theory has been presented [12]. Natural frequencies and mode shapes of un-damped hybrid system are obtained by forming mass and stiffness matrices and solving the eigenvalue problem [13]. The refined plate theory considering the simplified form of governing differential equations has been used by Wankhade and Niyogi [14] to solve the buckling analysis of laminated composite plates. The effects of seismic soil–structure interaction on seismic response of hardening single degree of freedom systems located in diverse geologies have been evaluated by Anand and Satish Kumar [15]. The envelopes of frequency response function (FRF) have been obtained by the experimental modal analysis, and the variation in dynamic property values has been determined from curve fitted FRFs using modal analysis software, and the results have been correlated with the damage level [16]. A simple mathematical method, based on a continuous approach, has been proposed to determine the natural frequencies and mode shapes of trussed-tube systems in tall buildings [17]. The dynamic analysis of soil–structure interaction by using the spectral element method has been presented. In this paper, the partial differential equation governing the motion has been derived and solved by using spectral element method [18]. A general solution for the free transverse vibration of non-uniform, axially functionally graded cantilevers loaded at the tips with point masses has been presented by Mahmoud [19]. The vibration problem of beams with axial functionally graded materials (FGMs) and variable thickness has been investigated by isogeometric analysis (IGA) in conjunction with three-dimensional (3D) theory [20]. The buckling behaviors of axially functionally graded and non-uniform Timoshenko beams have been investigated [21]. The vibration problem of axially functionally graded beams has been investigated using various approaches [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].

2 The equation of motion with bending deformation

In this paper, the vibration of axially functionally graded (AFG) beams is investigated. It is assumed that the beam has a constant cross section along the axial direction, but the material properties of beam have continuous variations along the axial direction of beam. The equation of motion for a beam with varying properties of material along the axial direction of beam is given as follows:

$$ \begin{array}{*{20}c} {\frac{{\partial ^{2} }}{{\partial x^{2} }}\left[ {\bar{E}(x)I\frac{{\partial ^{2} W(x,t)}}{{\partial x^{2} }}} \right] + \bar{\rho }(x)A\frac{{\partial ^{2} W({\text{x}},t)}}{{\partial t^{2} }} = 0} & {0 \le x \le L} \\ \end{array} $$
(1)

in which \( W({\text{x}},t) \) is the lateral deflection of beam, and \( \bar{E}(x) \) and \( \bar{\rho }(x) \) are the functions of modulus of elasticity and mass density of beam material, respectively, that vary along the axial direction of beam. I and A are the moment of inertia and area of cross section of beam which in this paper, and they are assumed to be constant along the axial direction of beam. L is beam length. Figure 1 presents the schematic variations of material properties along the axial direction of beam. It is assumed that beam deflects along the “y” direction; however, deflection along “z” direction can also occur in practical cases. In this paper, the y lateral deflection and z lateral deflection are decoupled.

Fig. 1
figure 1

Variations of material properties along the axial direction

Full size image

In order to compare the results obtained using presented approach in this paper with other available references, the function of variations of material properties is considered as the same with those given in Ref [1]. This function is considered as follows:

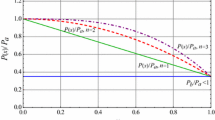
$$ Y(x) = \left\{ {\begin{array}{*{20}l} {Y_{L} \left( {1 - \frac{{e^{{\frac{{\upsilon x}}{L}}} - 1}}{{e^{\upsilon } - 1}}} \right) + Y_{R} \frac{{e^{{\frac{{\upsilon x}}{L}}} - 1}}{{e^{\upsilon } - 1}}} & {\upsilon \ne 0} \\ {Y_{L} \left( {1 - \frac{x}{L}} \right) + Y_{R} \frac{x}{L}} & {\upsilon = 0} \\ \end{array} } \right. $$
(2)

in which YL and YR are the parameters corresponding to properties of material for left and right sides of beam length, respectively. \( \upsilon \) is the gradient parameter describing the intensity of variation of properties along the axial direction. The variations of \( \frac{{Y(x)}}{{Y_{L} }} \) with non-dimensional location parameter \( \xi = \frac{x}{L} \) along the axial direction of beam for \( \frac{{Y_{R} }}{{Y_{L} }} = 3 \) are presented in Fig. 2.

Fig. 2
figure 2

The variations of material properties along the axial direction of beam

Full size image

The lateral vibration of beam is assumed to be a harmonic vibration as follows:

$$ W(x,t) = \phi (x)e^{{i\omega t}} $$
(3)

in which \( \phi (x) \) and \( \omega \) are the mode shape function and natural frequency of vibration, respectively. Considering the non-dimensional location parameter \( \xi = \frac{x}{L} \) and substituting Eq. (3) into Eq. (1) result in the following equation:

$$ \begin{array}{*{20}c} {\frac{{{\text{d}}^{2} }}{{{\text{d}}\xi ^{2} }}\left[ {\bar{E}(\xi )I\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\xi ^{2} }}} \right] - A\omega ^{2} L^{4} \bar{\rho }(\xi )\phi (\xi ) = 0} & {0 \le \xi \le 1} \\ \end{array} $$
(4)

For simplicity of calculations, the following relations are introduced into Eq. (4):

$$ \left\{ \begin{gathered} \bar{E}(\xi ) = E_{L} .E(\xi ) \hfill \\ \bar{\rho }(\xi ) = \rho _{L} .\rho (\xi ) \hfill \\ \lambda ^{2} = \frac{{\rho _{L} A\omega ^{2} L^{4} }}{{E_{L} .I}} \hfill \\ \end{gathered} \right. $$
(5)

The result is the following equation based on the non-dimensional location parameter \( \xi \):

$$ \frac{{{\text{d}}^{2} }}{{{\text{d}}\xi ^{2} }}\left[ {E(\xi )\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\xi ^{2} }}} \right] - \lambda ^{2} \rho (\xi )\phi (\xi ) = 0 $$
(6)

In Eq. (5), \( E_{L} \) and \( \rho _{L} \) are the modulus of elasticity and mass density of left side of beam, respectively (Fig. 1). λ is the non-dimensional natural frequency of vibration. In order to convert Eq. (6) into Fredholm integral equation, both sides of this equation are integrated twice with respect to \( \xi \) within the range 0–\(\xi \). The results are the integral equations as follows:

$$ \frac{{\text{d}}}{{{\text{d}}\xi }}\left[ {E(\xi )\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\xi ^{2} }}} \right] - \lambda ^{2} \int\limits_{0}^{\xi } {\rho (s)\phi (s){\text{d}}s} = C_{1} $$
(7)
$$ E(\xi )\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\xi ^{2} }} - \lambda ^{2} \int\limits_{0}^{\xi } {\left( {\xi - s} \right)\rho (s)\phi (s){\text{d}}s} = C_{1} \xi + C_{2} $$
(8)

Further, integration from both sides of Eq. (8) twice with respect to \( \xi \) from 0 to \( \xi \) yields:

$$ \begin{aligned} & E(\xi )\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} - E^{\prime}(\xi )\phi (\xi ) + \int\limits_{0}^{\xi } {E^{\prime\prime}(s)\phi (s){\text{d}}s} \\ & \quad - \frac{{\lambda ^{2} }}{2}\int\limits_{0}^{\xi } {\left( {\xi - s} \right)^{2} \rho (s)\phi (s){\text{d}}s} = \frac{{C_{1} }}{2}\xi ^{2} + C_{2} \xi + C_{3} \\ \end{aligned} $$
(9)
$$ \begin{aligned} & E(\xi )\phi \left( \xi \right) - 2\int\limits_{0}^{\xi } {E^{\prime}(s)\phi (s)} {\text{d}}s + \int\limits_{0}^{\xi } {\left( {\xi - s} \right)E^{\prime\prime}(s)\phi (s){\text{d}}s} \\ & \quad - \frac{{\lambda ^{2} }}{6}\int\limits_{0}^{\xi } {\left( {\xi - s} \right)^{3} \rho (s)\phi (s){\text{d}}s} = \frac{{C_{1} }}{6}\xi ^{3} + \frac{{C_{2} }}{2}\xi ^{2} + C_{3} \xi + C_{4} \\ \end{aligned} $$
(10)

Equation (10) is Fredholm integral equation of governing equation of motion. \( \left. {C_{i} } \right|_{{i = 1,2,3,4}} \) are the integration constants which are determined through corresponding end boundary conditions of beam. In this paper, the boundary conditions for clamped–free (C–F) beam, simple–simple (S–S) beam, clamped–simple (C–S) beam and clamped–clamped (C–C) beam are considered.

2.1 Clamped–free beam

The following boundary conditions are introduced for a clamped–free beam. It is assumed that the left side of beam is clamped and right side is free.

$$ \left\{ {\begin{array}{*{20}{l}} {\xi = 0}&{\phi = 0,}&{\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} = 0} \\ {\xi = 1}&{\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}} = 0,}&{\frac{{{{\text{d}}^3}\phi }}{{{\text{d}}{\xi^3}}} = 0} \end{array}} \right. $$
(11)

Introducing the boundary conditions (11) into Eqs. (7–10) result in the following integral equation based on the mode shape function \(\phi (\xi ) \):

$$ E(\xi )\phi \left( \xi \right) + \int\limits_0^\xi {{h_1}(\xi ,s)\phi (s)} {\text{d}}s + \int\limits_0^1 {{h_2}(\xi ,s)\phi (s)} {\text{d}}s = 0 $$
(12)

where

$$ \left\{ \begin{gathered} {h_1}(\xi ,s) = - 2E^{\prime}(s) + \left( {\xi - s} \right)E^{\prime\prime}(s) - \frac{{\lambda^2}}{6}{\left( {\xi - s} \right)^3}\rho (s) \hfill \\ {h_2}(\xi ,s) = \frac{{\lambda^2}}{6}{\xi^3}\rho (s) - \frac{{\lambda^2}}{2}{\xi^2}s\rho (s) \hfill \\ \end{gathered} \right. $$
(13)

2.2 Simple–simple beam

When both end conditions of AFG beam are pinned, the following boundary conditions are introduced:

$$ \left\{ {\begin{array}{*{20}{l}} {\xi = 0}&{\phi = 0,}&{\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}} = 0} \\ {\xi = 1}&{\phi = 0,}&{\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}} = 0} \end{array}} \right. $$
(14)

Introducing the boundary conditions (14) into Eqs. (7–10) results in the integral equation introduced in Eq. (12). The resulting integral equation and function \( {h_1}(\xi ,s) \) are exactly the same as what was stated in clamped–free section. The difference, however, is the function \({h_2}(\xi ,s) \). For simple–simple beam, this function is calculated as follows:

$$ \begin{gathered} {h_2}(\xi ,s) = \frac{{\lambda^2}}{6}(1 - s){\xi^3}\rho (s) + 2E^{\prime}(s)\xi - (1 - s)E^{\prime\prime}(s)\xi \hfill \\ \quad + \frac{{\lambda^2}}{6}\xi {(1 - s)^3}\rho (s) - \frac{{\lambda^2}}{6}\xi (1 - s)\rho (s) \hfill \\ \end{gathered} $$
(15)

2.3 Clamped–simple beam

For a beam with clamped–simple boundary conditions, the following relations are considered:

$$ \left\{ {\begin{array}{*{20}{l}} {\xi = 0}&{\phi = 0,}&{\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} = 0} \\ {\xi = 1}&{\phi = 0,}&{\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}} = 0} \end{array}} \right. $$
(16)

Introducing the boundary conditions (16) into Eqs. (7–10) results in the integral equation introduced in Eq. (12). The difference is the function \( {h_2}(\xi ,s) \). For clamped–simple beam, this function is calculated as follows:

$$ {h_2}(\xi ,s) = {g_1}(s){\xi^3} + {g_2}(s){\xi^2} $$
(17)

in which

$$ \left\{ {\begin{array}{*{20}{l}} {{g_1}(s) = - E^{\prime}(s) + \frac{1}{2}(1 - s)E^{\prime\prime}(s) - } \\ {\quad \frac{{\lambda^2}}{12}{{(1 - s)}^3}\rho (s) + \frac{{\lambda^2}}{4}(1 - s)\rho (s)} \\ {{g_2}(s) = - \frac{{\lambda^2}}{4}(1 - s)\rho (s) + 3E^{\prime}(s) - } \\ {\quad \frac{3}{2}(1 - s)E^{\prime\prime}(s) + \frac{{\lambda^2}}{4}{{(1 - s)}^3}\rho (s)} \end{array}} \right. $$
(18)

2.4 Clamped–clamped beam

The following boundary conditions are considered for a clamped–clamed beam:

$$ \left\{ {\begin{array}{*{20}{l}} {\xi = 0}&{\phi = 0,}&{\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} = 0} \\ {\xi = 1}&{\phi = 0,}&{\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} = 0} \end{array}} \right. $$
(19)

Introducing the boundary conditions (19) into Eqs. (7–10) results in the following relation for \({h_2}(\xi ,s) \):

$$ {h_2}(\xi ,s) = {g_1}(s){\xi^3} + {g_2}(s){\xi^2} $$
(20)

in which

$$ \left\{ {\begin{array}{*{20}{l}} {{g_1}(s) = - E^{\prime\prime}(s) + \frac{{\lambda^2}}{2}{{(1 - s)}^2}\rho (s) - 4E^{\prime}(s)} \\ {\quad + 2(1 - s)E^{\prime\prime}(s) - \frac{{\lambda^2}}{3}{{(1 - s)}^3}\rho (s)} \\ {{g_2}(s) = E^{\prime\prime}(s) - \frac{{\lambda^2}}{2}{{(1 - s)}^2}\rho (s) + 6E^{\prime}(s)} \\ {\quad - 3(1 - s)E^{\prime\prime}(s) + \frac{{\lambda^2}}{2}{{(1 - s)}^3}\rho (s)} \end{array}} \right. $$
(21)

3 Shear deformation and axial force effects

The governing equation for AFG beam with effects of axial force and shear deformation is given as follows [25]:

$$ \begin{gathered} \frac{{\partial^2}}{{\partial {x^2}}}\left[ {\overline E (x)I\frac{{{\partial^2}W(x,t)}}{{\partial {x^2}}}} \right] - \frac{\partial }{\partial x}\left[ {\kappa A\overline G (x)\frac{\partial W(x,t)}{{\partial x}}} \right] \hfill \\ \quad + N\frac{{{\partial^2}W(x,t)}}{{\partial {x^2}}} + \overline \rho (x)A\frac{{{\partial^2}W(x,t)}}{{\partial {t^2}}} = 0 \hfill \\ \end{gathered} $$
(22)

in which \( \kappa ,\overline G (x) \) and N are the shear correction factor, shear modules and constant axial compressive force acting on the cross section of beam. The following relations are considered in the later calculations process:

$$ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {W(x,t) = \phi (x){e^{i\omega t}}} \\ {\bar E(\xi ) = {E_L}.E(\xi )} \\ {\overline G (\xi ) = {G_L}.G(\xi )} \\ {\bar \rho (\xi ) = {\rho_L}.\rho (\xi )} \end{array}} \\ {\begin{array}{*{20}{c}} {\xi = \frac{x}{L},}&{{\alpha^2} = \frac{{\kappa A{L^2}{G_L}}}{{{E_L}I}},} \\ {{\beta^2} = \frac{{N{L^2}}}{{{E_L}I}},}&{{\lambda^2} = \frac{{{\rho_L}A{L^4}}}{{{E_L}I}}{\omega^2}} \end{array}} \end{array}} \right. $$
(23)

in which α and β are the non-dimensional parameters corresponding to beam stiffness and axial force acting on the cross section of beam, respectively. \( {G_L} \) is the left side shear modules of beam material (Fig. 1). Substitution of relations (23) into Eq. (22) results in the following governing differential equation based on the non-dimensional location parameter \( \xi \):

$$ \begin{aligned} & \frac{{\text{d}}}{{{\text{d}}\xi }}\left[ {E(\xi )\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\xi ^{2} }}} \right] - \frac{{\text{d}}}{{{\text{d}}\xi }}\left[ {\alpha ^{2} G(\xi )\frac{{{\text{d}}\phi }}{{\partial \xi }}} \right] \\ & \quad + \beta ^{2} \frac{{{\text{d}}^{2} \phi }}{{\partial \xi ^{2} }} - \lambda ^{2} \rho (x)\phi (\xi ) = 0 \\ \end{aligned} $$
(24)

Similar to preceding section, four times repetitive integrations are carried out to convert the governing equation into Fredholm integral equation. The results are as follows:

$$ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}\xi }}\left[ {E(\xi )\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}}} \right] - {\alpha^2}G(\xi )\frac{{{\text{d}}\phi }}{\partial \xi } \hfill \\ \quad + {\beta^2}\frac{{{\text{d}}\phi }}{\partial \xi } - {\lambda^2}\int\limits_0^\xi {\rho (s)\phi (s){\text{d}}s} = {C_1} \hfill \\ \end{gathered} $$
(25)
$$ \begin{gathered} E(\xi )\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}} - {\alpha^2}G(\xi )\phi (\xi ) + {\alpha^2}\int\limits_0^\xi {G^{\prime}(s)\phi (s){\text{d}}s} \hfill \\ \quad + {\beta^2}\phi (\xi ) - {\lambda^2}\int\limits_0^\xi {(\xi - s)\rho (s)\phi (s){\text{d}}s} = {C_1}\xi + {C_2} \hfill \\ \end{gathered} $$
(26)
$$ \begin{gathered} E(\xi )\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} - E^{\prime}(\xi )\phi (\xi ) + \int\limits_0^\xi {E^{\prime\prime}(s)\phi (s){\text{d}}s} - {\alpha^2}\int\limits_0^\xi {G(s)\phi (s)} {\text{d}}s \hfill \\ \quad + {\alpha^2}\int\limits_0^\xi {(\xi - s)G^{\prime}(s)\phi (s){\text{d}}s} + {\beta^2}\int\limits_0^\xi {\phi (s){\text{d}}s} \hfill \\ \quad - \frac{{\lambda^2}}{2}\int\limits_0^\xi {{{(\xi - s)}^2}\rho (s)\phi (s){\text{d}}s} = \frac{{C_1}}{2}{\xi^2} + {C_2}\xi + {C_3} \hfill \\ \end{gathered} $$
(27)
$$ E(\xi )\phi (\xi ) + \int\limits_0^\xi {{h_1}(\xi ,s)\phi (s){\text{d}}s = \frac{{C_1}}{6}{\xi^3} + \frac{{C_2}}{2}{\xi^2} + {C_3}\xi + {C_4}} $$
(28)

Equation (28) is Fredholm integral equation based on the mode shape function \( \phi (\xi ) \). In this equation, \( {h_1}(\xi ,s) \) is calculated as follows:

$$ \begin{gathered} {h_1}(\xi ,s) = - 2E^{\prime}(s) + (\xi - s)E^{\prime\prime}(s) - {\alpha^2}(\xi - s)G(s) \hfill \\ \quad + \frac{{\alpha^2}}{2}{(\xi - s)^2}G^{\prime}(s) + {\beta^2}(\xi - s) - \frac{{\lambda^2}}{6}{(\xi - s)^3}\rho (s) \hfill \\ \end{gathered} $$
(29)

The following boundary conditions are considered for clamped–free beam with axial force effects and shear deformation:

$$ \begin{array}{*{20}{c}} {\xi = 0}&{\phi = 0,}&{\frac{{{\text{d}}\phi }}{{{\text{d}}\xi }} = 0} \end{array} $$
(30)
$$ \begin{array}{*{20}{c}} {\xi = 1}&{\frac{{\text{d}}}{{{\text{d}}\xi }}\left[ {E(\xi )\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}}} \right] - {\alpha^2}G(\xi )\frac{{{\text{d}}\phi }}{\partial \xi } + {\beta^2}\frac{{{\text{d}}\phi }}{\partial \xi } = 0} \end{array} $$
(31)
$$ \begin{array}{*{20}{c}} {\xi = 1}&{E(\xi )\frac{{{{\text{d}}^2}\phi }}{{{\text{d}}{\xi^2}}}} \end{array} $$
(32)

Introducing the boundary conditions (30–32) into Eqs. (25–28) results in the following integral equation:

$$ E(\xi )\phi \left( \xi \right) + \int\limits_0^\xi {{h_1}(\xi ,s)\phi (s)} {\text{d}}s + \int\limits_0^1 {{h_2}(\xi ,s)\phi (s)} {\text{d}}s = 0 $$
(33)

In Eq. (33), \( {h_2}(\xi ,s) \) is calculated as follows:

$$ {h_2}(\xi ,s) = {T_1}(s){\xi^3} + \,{T_2}(s){\xi^2} $$
(34)

in which

$$ \left\{ \begin{gathered} {T_1}(s) = {\kappa_1}\rho (s) \hfill \\ {T_2}(s) = {\kappa_2}\rho (s) + {\kappa_3}{h_1}(1,s) + {\kappa_4}G^{\prime}(s) + {\kappa_5}(1 - s)\rho (s) \hfill \\ \end{gathered} \right. $$
(35)

where

$$ \left\{ \begin{gathered} {\kappa_1} = \frac{{\lambda^2}}{6} \hfill \\ {\kappa_2} = \left[ {\frac{{ - {\lambda^2}{\beta^2} + {\lambda^2}{\alpha^2}G(1) + 6E(1){\lambda^2}}}{{6{\beta^2} - 6{\alpha^2}G(1) - 12E(1)}}} \right] \hfill \\ {\kappa_3} = \left[ {\frac{{ - {\beta^2} + {\alpha^2}G(1)}}{{{\beta^2} - {\alpha^2}G(1) - 2E(1)}}} \right] \hfill \\ {\kappa_4} = \left[ {\frac{{E(1){\alpha^2}}}{{{\beta^2} - {\alpha^2}G(1) - 2E(1)}}} \right] \hfill \\ {\kappa_5} = \left[ {\frac{{E(1){\lambda^2}}}{{ - {\beta^2} + {\alpha^2}G(1) + 2E(1)}}} \right] \hfill \\ \end{gathered} \right. $$
(36)

4 Calculation of natural frequencies

In preceding sections, we convert the governing differential equations of motions into Fredholm integral equation with the following format:

$$ E(\xi )\phi \left( \xi \right) + \int\limits_0^\xi {{h_1}(\xi ,s)\phi (s)} {\text{d}}s + \int\limits_0^1 {{h_2}(\xi ,s)\phi (s)} {\text{d}}s = 0 $$
(37)

The functions \( {h_1}(\xi ,s) \) and \( {h_2}(\xi ,s) \) which are different for each boundary condition have been calculated. The mode shape function \( \phi (\xi ) \) is the only unknown parameter in the resulting integral equations. This function is approximated by a power series as follows:

$$ \phi (\xi ) = \sum\limits_{r = 0}^R {{\xi^r}{C_r}} $$
(38)

where \( {C_r} \) are unknown coefficients to be determined and R is a given positive integer, which is adopted such that the accuracy of results is sustained. Introducing Eq. (38) into integral Eq. (37) leads to:

$$ \sum\limits_{r = 0}^R {\left[ {E(\xi ){\xi^r} + \int\limits_0^\xi {{h_1}(\xi ,s){s^r}{\text{d}}s + \int\limits_0^1 {{h_2}(\xi ,s){s^r}{\text{d}}s} } } \right]} \,{C_r} = 0 $$
(39)

Both sides of Eq. (39) are multiplied by \( {\xi^m} \) and integrated subsequently with respect to \( \xi \) between 0 and 1. This results in a system of equations in \( {C_r} \):

$$ \begin{array}{*{20}{c}} {\sum\limits_{r = 0}^R {\left[ {G(m,r) + {H_1}(m,r) + {H_2}(m,r)} \right]} \,{C_r} = 0}&{m = 0,1,2, \ldots R} \end{array} $$
(40)

in which the functions \( G(m,r),{H_1}(m,r) \) and \( {H_2}(m,r) \) are expressed as follows:

$$ \left\{ \begin{gathered} G(m,r) = \int\limits_0^1 {{\xi^{r + m}}E(\xi )\,{\text{d}}\xi } \hfill \\ {H_1}(m,r) = \int\limits_0^1 {\int\limits_0^\xi {{h_1}(\xi ,s){s^r}{\xi^m}{\text{d}}s\,{\text{d}}\xi \,} } \hfill \\ {H_2}(m,r) = \int\limits_0^1 {\int\limits_0^1 {{h_2}(\xi ,s){s^r}{\xi^m}{\text{d}}s\,{\text{d}}\xi } } \hfill \\ \end{gathered} \right. $$
(41)

The system of linear algebraic Eqs. (40) may be expressed in matrix notations as follows:

$$ {\left[ A \right]_{(R + 1) \times (R + 1)}}{\left[ C \right]_{(R + 1) \times 1}} = {\left[ 0 \right]_{(R + 1) \times 1}} $$
(42)

in which \(\left[ A \right] \) and \( \left[ C \right] \) are the coefficients matrix and unknowns’ vector, respectively. In order to obtain the non-dimensional natural frequencies of beam, functions \( {h_1}(\xi ,s) \) and \( {h_2}(\xi ,s) \) are first obtained. By introducing these functions into (41), the functions \( G(m,r) \),\( {H_1}(m,r) \) and \( {H_2}(m,r) \) associated with the coefficients of matrix [A] are obtained next. The unknown parameter in the coefficients matrix [A] is, therefore, the non-dimensional natural frequency of beam. \( \left[ C \right] = 0 \) is a trivial solution for the resulting system of equations introduced in Eq. (42). The non-dimensional natural frequencies are determined through calculation of a non-trivial solution for resulting system of equations. To achieve this, the determinant of coefficients matrix of system has to be vanished. Accordingly, a frequency equation in \( \lambda \) [which is a polynomial function of order \(2(R + 1)\)] is obtained. Given the fact that the mode shape function is approximated by the power series of (38), the results accuracy is improved if a greater number of series sentences are taken into account. In this case, the order of polynomial is also increased accordingly. Hence, adoption of larger R yields more accurate results.

5 Damping effects

The presented approach in this paper can be used to calculate the natural frequencies of AFG beam with damping effects. Damping effects result in complex natural frequencies. We have investigated damping effects in another published paper [38]. The governing equation of AFG beams with damping term is obtained as follows:

$$ \frac{{\partial ^{2} }}{{\partial x^{2} }}\left[ {\bar{E}\left( x \right)I\frac{{\partial ^{2} }}{{\partial x^{2} }}W(x,t)} \right] + \bar{\rho }\left( x \right)A\frac{{\partial ^{2} }}{{\partial t^{2} }}W(x,t) + \bar{C}\left( x \right)\frac{\partial }{{\partial t}}W(x,t) = 0 $$
(43)

in which \(\overline C (x) = {a_0}\overline m (x)\) is adopted. “\(\overline C \left( x \right)\)” is damping resistance per unit velocity which depends on both coefficients \( {a_0} \) and mass per unit length \(\bar m(x) = \bar \rho (x)A \). “\( {a_0} \)” is called mass proportional damping coefficient and can be calculated as follows:

$$ {a_0} = 2{\zeta_n}{\omega_n} $$
(44)

In relation (44), \( {\zeta_n} \) and \( {\omega_n} \) are damping ratio and natural frequency corresponding to \( n\,{\text{th}} \) mode.

6 Numerical examples

6.1 Verification of presented solution

In order to verify the accuracy of presented approach, the results obtained using presented approach have been compared with those obtained in other available references. The first four non-dimensional natural frequencies of beam with various end boundary conditions have been calculated, and the results have been compared with results of Ref [1] and results of finite elements method. It is assumed that the left side of beam is pure aluminum and the right side is pure zirconia. Table 1 presents the properties of aluminum and zirconia. The variations of material properties along the axial direction of beam are considered as Eq. (2). Table 2 presents the results obtained with \( \upsilon = 3 \) for clamped–free beam, simple–simple beam, clamped–simple beam and clamped–clamped beam.

Table 1 Material properties of AFG beam for left and right sides
Full size table
Table 2 The first four non-dimensional natural frequencies of AFG beam with various boundary conditions
Full size table

The variations of first three non-dimensional natural frequencies with \( \upsilon \) for various end boundary conditions have been calculated. The results are presented in Fig. 3. The results of Fig. 3 present the excellent agreement with those obtained in Ref [1]. The results of Fig. 3 present that the variations pattern for beam with clamped–clamped condition in first mode is different from other ones. Also, the gradient parameter calculated as \( \% {\text{Diff}} = \left[ {\frac{{\lambda _{{\vartheta = 10}} - \lambda _{{\vartheta = - 10}} }}{{\lambda _{{\vartheta = 10}} }}} \right] \times 100 \) for beam with clamped–free condition is more intense and they were calculated equal to 16%, 14% and 13% for first, second and third mode, respectively.

Fig. 3
figure 3

The variations of first three non-dimensional natural frequencies with \(\upsilon \) for various end boundary conditions

Full size image

6.2 Shear deformation and axial force effects

In order to investigate the effects of shear deformation and axial force effects on the natural frequencies of AFG beam, the first three non-dimensional natural frequencies of beam have been calculated in this section. The beam cross section is square with section’s width = 0.5 m. The shear correction factor and beam length are \( \kappa = \frac{5}{6} \) and 3 m, respectively. The axial force acting on the cross section of beam is \( N = 10 \times {10^7}\,kN \). The non-dimensional parameter \( \alpha \) corresponding to stiffness of beam is adopted as \( \alpha = 131.1428 \), and the non-dimensional parameter \( \beta \) corresponding to axial force acting on the cross section of beam is adopted as \( \beta = 50 \). The results are presented in Fig. 4. This figure presents the variations of first three non-dimensional natural frequencies of a clamped–free beam with \( \upsilon \) when the axial force and shear deformation are considered. The results of Fig. 4 present that the variations pattern in first mode is different from other ones. Also, gradient parameter “%Diff” is more intense when the axial force and shear deformation are considered simultaneously. In this case, “%Diff” was calculated equal to %25, %22 and %19 for first, second and third mode, respectively.

Fig. 4
figure 4

The variations of first three non-dimensional natural frequencies of a clamped–free beam with \( \upsilon \) under effects of axial force and shear deformation

Full size image

6.3 Vibration along z direction

Regarding to relations (23), \( \lambda \) is a non-dimensional parameter. Therefore, it is independent from selected moment of inertia. But obviously, it would be interesting to see the original natural frequencies corresponding to y and z lateral directions by selecting different values of \( {I_{yy}} \) and \( {I_{zz}} \). Accordingly, the original natural frequency is calculated as follows:

$$ {\omega^2} = \frac{{{\lambda^2}{E_L}I}}{{{\rho_L}A{L^4}}} $$
(45)

In order to compare the natural frequencies for vibration along the “y” and “z” direction, a clamped–free beam with rectangular cross section is considered. Section’s width = 0.2 m, section’s height = 0.5 m and beam length = 3 m are applied. Regarding Fig. 1, section’s width and section’s height are parallel to “z” and “y” direction, respectively. The variations of original natural frequencies for first three modes with \( \upsilon \) have been calculated, and the results are presented in Fig. 5. The results of Fig. 5 present that the variations pattern with clamped–clamped condition for both \( {I_{yy}} \) and \( {I_{zz}} \) is different from other ones. Also, gradient parameter %Diff for clamped–free and simple–simple conditions is larger from other ones and they were calculated equal to 16% and %15 for C–F and S–S, respectively.

Fig. 5
figure 5

The variations of original natural frequencies for first three modes with \( \upsilon \) applying different values for \( {I_{yy}} \) and \( {I_{zz}} \)

Full size image

7 Conclusion

Application of Fredholm integral equations for free vibration analysis of axially functionally graded beams has been presented. Through repetitive integrations, the governing partial differential equations with variable coefficients have been converted into Fredholm integral equations. In order to solve the resulting integral equations, the mode shape function of vibration has been approximated by a power series and substitution of power series into Fredholm integral equations transformed them into a system of linear algebraic equations. The natural frequencies of AFG beams have been calculated by determination of a non-trivial solution for system of linear algebraic equations. Presented approach has been also used for investigation of axial force effects and shear deformation on the natural frequencies of AFG beams. The accuracy, simplicity and reliability of proposed method are verified thorough several numerical examples. Differences between natural frequencies of proposed method and previous published works are in acceptable ranges. The results of paper present that the variations pattern for beam with clamped–clamped condition in first mode is different from other ones. Also, the gradient parameter calculated for beam with clamped–free condition is more intense. Considering axial force and shear deformation for clamped–free beam, the results present that the variations pattern in first mode is different from other ones. Also, gradient parameter is more intense when the axial force and shear deformation are considered simultaneously. In case of vibration along “y” and “z” lateral direction, the results present that the variations pattern with clamped–clamped condition for both lateral directions is different from other ones. Also, gradient parameter calculated for clamped–free and simple–simple conditions is larger from other.