Buckling and vibration of axially functionally graded nonuniform beams using differential transformation based dynamic stiffness approach

Abstract

The free vibration of axially functionally graded (FG) non-uniform beams with different boundary conditions is studied using Differential Transformation (DT) based Dynamic Stiffness approach. This method is capable of modeling any beam (Timoshenko or Euler, centrifugally stiffened or not) whose cross sectional area, moment of Inertia and material properties vary along the beam. The effectiveness of the method is confirmed by comparing the present results with existing closed form solutions and numerical results. In FG beams, flexural rigidity and mass density may take majority of functions including polynomials, trigonometric and exponential functions (converted to polynomial expressions). DT based Dynamic stiffness approach is proved to be a versatile and simple approach compared to many other methods already proposed.

1 Introduction

There has been a great interest in the analysis of the free vibration characteristics of elastic structures such as turbine, compressor or helicopter blades, spinning spacecraft and satellite booms rotating with constant angular velocity. For a relatively long blade the simplest response is the Euler Bernoulli beam model (EBM). In some cases, these shafts are stubby and when the higher modes in bending vibrations are considered, Timoshenko beam theory (TBT) is employed. The only distinction between the above two theories being shear deformation and rotary inertia are considered in TBT in addition to centrifugal force. With the above, functionally graded material (FGM) complicates the issue.

FGM are multiphase composites with volume fraction of phase varying through a direction. FGM was first proposed by material scientists in Sendai area in Japan in 1984 [1, 2] as thermal barrier material. Since then, these materials have been employed in many engineering application fields such as aircrafts, space vehicles, defense industries, electronic and biomedical sectors. For functionally graded beams, gradient variation may be oriented in cross section, or in the axial direction. But in this research, gradient variation is considered in axial direction.

Semi-inverse method was used to study beam with axially FGM by Elishakoff and his co-workers [3, 4]. Many researchers have used numerical techniques such as Frobenius and Rayleigh-Ritz methods [5–8]. Spectral finite element method (SFEM) also called dynamic stiffness method has been applied by Vinod et al. [9], Doyle [10] to provide a high accuracy using less number of elements. Wright et al. [11] applied the Frobenius method (extended power series method) and solved for natural frequencies of both uniform and tapered rotating beam with cantilever or hinged boundary conditions, in which tapered beam has a linear variation of mass and flexural stiffness along the span of the beam. Huang and Li [12] studied the free vibration of nonuniform axially FG beams by transforming governing equation to Fredholm integral equation.

For Timoshenko beams, Mabie and Rogers [13] solved the differential equation of vibration of a tapered beam by using Bessel functions. Downs [14] employed a dynamic discretization technique to calculate the natural frequency of a tapered Timoshenko beam. Finite element technique was used by Gupta and Rao [15], Dawe [16], To [17], and Lees and Thomas [18] to study the effect of shear deformation and rotary inertia on the modal frequency of a tapered beam. The free vibration characteristics of rotating Timoshenko beams have also been extensively studied by Lee and Lin [19], Du et al. [20], Nagaraj [21] and Lin and Hsiao [22].

The vibration of tapered beams has also been studied by other methods such as the modified differential quadrature method by Choi and Chou 2001 [23], the spline interpolation technique by Irie et al. [24], the transfer matrix approach by Irie et al. [25] and the method of Frobenius by Lee and Lin [26]. Shahba et al. [27] applied FEM using Hermitian polynomials to study the free vibration and stability of tapered axially functionally graded beam. Attarnejad et al. [28] used basic displacement functions (BDF) for free vibration analysis of non-prismatic Timoshenko beams. Attarnejad and Shahba [29, 30] used basic displacement functions to study the free vibration of centrifugally stiffened tapered beams.

In the present paper, we adopt the Differential transformation (DT) based dynamic stiffness method to study the buckling and vibration characteristics of axially FG tapered Euler and Timoshenko beams (centrifugally stiffened or not) by considering four first order differential equations. Zhou [31] was the first one to use differential transformation method (DTM) in engineering applications. Since DTM is an efficient tool for solving nonlinear or parameter varying systems, it has gained much attention by several researchers such as Chen and Ju [32], Arikoglu and Ozhol [33] and Bert and Zeng [34].

However, DT method considered in this paper is much different from other investigators.

• (a) DT based dynamic stiffness method does not pose any restriction on both the type of material gradation and variation of the cross section profile and hence they could cover most of the engineering problems dealing with axially FG beams.

• (b) The technique is directly used to get the shape functions for displacements and bending rotations and hence stiffness, geometric stiffness and mass matrices can be arrived at. Using finite element procedure, these matrices are assembled to form global matrices and applying boundary conditions one can solve for the free and forced vibration and stability problems for the beams and predict the natural frequency and buckling load more precisely in comparison with previous works.

• (c) DT replaces power series in establishing the dynamic stiffness of beams.

2 Governing differential equations

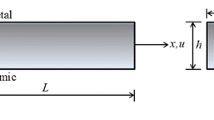
In Fig. 1, a cantilever beam of length L, which is rigidly fixed on the periphery of a rigid hub of radius R is shown. The hub is assumed to rotate about its vertical axis ‘z’ at a constant angular speed Ω. We consider the right hand Cartesian system and the origin is located at the left end of the beam (centre of the hub). The following assumptions are made [35].

• (1) The x axis coincides with the neutral axis of the beam in the un-deformed position.

• (2) The beam cross section is doubly symmetric.

• (3) The out-of-plane displacements are small and neglected.

• (4) The cross sections which are initially perpendicular to the neural axis will remain plane but not perpendicular after deformation for Timoshenko beams.

• (5) Coriolis effects are very small and neglected in case of centrifugally stiffened beam.

Fig. 1

Configuration of functionally graded tapered rotating cantilever beam

Based on Timoshenko beam theory, governing differential equation for free transverse vibration of axially FG tapered rotating beams were derived by Kaya [35] as well as Banerjee [36]. Here we will not repeat the derivation and we give only governing equations and the interested reader may consult Refs. [35, 36].

The shear force $\underline{V} = \underline{V}(x,t)$ at any section including shear deformation is given by

$$ \underline{V}(x,t) = P(x)\frac{\mathrm{d}\underline{w}}{\mathrm{d}x} + K(x) \biggl( \frac{\mathrm{d}\underline{w}}{\mathrm{d}x} - \underline{\theta} \biggr) $$

(1)

where centrifugal force P(x) varies along the span wise direction of the beam and is given by

(2)

where K(x) = shear rigidity given by $K(x)= \kappa \*A(x)G (x)$ only for Timoshenko beams and κ = shear correction factor depending on the cross section (values of κ for circular and rectangular cross section are 2/3 and 5/6). All the notations are defined in Nomenclature.

In case of buckling problems

$$ \underline{V}(x,t) = - P(x)\frac{\mathrm{d}\underline{w}}{\mathrm{d}x} + K(x) \biggl( \frac{\mathrm{d}\underline{w}}{\mathrm{d}x} - \underline{\theta} \biggr) $$

(3)

where P(x) is the compressive load at any section.

The bending moment $\underline{M} = \underline{M}(x,t)$ at any section is given by

$$ \underline{M}(x,t) = d(x)\frac{\mathrm{d}\underline{\theta}}{ \mathrm{d}x} $$

(4)

where d(x)=E(x)I(x), the bending stiffness.

The equations of motion are obtained as

(5)

and

$$ \frac{\mathrm{d}\underline{V}(x,t)}{\mathrm{d}x} - \rho(x)A(x)\underline{\ddot{w}} = p(x,t) $$

(6)

where

$$ \underline{\ddot{\theta}} = \frac{\mathrm{d}^{2}\underline{\theta}}{\mathrm{d}t^{2}} \quad \mbox{and} \quad \underline{\ddot{w}} = \frac{\mathrm{d}^{2}\underline{w}}{\mathrm{d}t^{2}} $$

(7)

Sinusoidal variation for transverse displacement and bending rotation with circular frequency ω (assuming the lateral load, p(x,t)=0) is given by

(8a)

(8b)

where w, θ, M and V are functions of x only and the variables with under score are functions of x and t.

Substituting Eqs. (8a), (8b) in Eqs. (4) and (5) we get

(9a)

(9b)

Equations (1), (3), (9a) and (9b) are written in matrix form as

(10)

In Eq. (10), for buckling problems P(x) is to be substituted as −P(x) where $\nabla = \frac{\mathrm{d}}{\mathrm{d}x}$ with boundary conditions (V=0 or w=0; M=0 or θ=0 at x=0 and x=L). It is to be noted that for a cantilever beam, when the tip mass M _T is added at the free end, the shear at the free end is given by V−ω ² M _T w. Equation (10) can also be written as

(11)

where

$$ \eta^{2} = \varOmega^{2} + \omega^{2} $$

(12)

3 Differential transformation element method (DTEM)

In this section, the required mathematical background for better understanding of DTEM based dynamic stiffness method is presented.

If function y(x) is analytic in domain D; let x=x ₀ represent any point in the domain. Then Taylor’s series expansion is given as

$$ y(x) = \sum_{s = 0}^{\infty} \frac{1}{s!} \biggl\{ \frac{\mathrm{d}^{s}y(x)}{\mathrm{d}x^{s}} \biggr\} \bigg|_{x = x_{0}} (x - x_{0})^{s} $$

(13a)

where s belongs to the set of non-negative integers denoted as S domain.

• (a) Differential transformation DT of y(x) is defined as $\bar{y}[s]$ as

(13b)

It is to be noted that differential transformation of any function is written in square brackets with a bar over the letter as shown in Eqs. (13a) and (13b).

• (b) Inverse differential transformation (IDT): IDT is known as presentation of y(x) by power series using DT of y(x) as

(14a)

In practical problems, Eq. (14a) is replaced by a finite series as

(14b)

where nt (number of terms) is chosen such that $y(x) = \sum_{s = nt + 1}^{\infty} \bar{y}[s](x - x_{0})^{s}$ is negligibly small. In this paper x ₀ is set to zero.

If y(x) is represented as polynomial expression as

$$ y(x) = \sum_{s = 0}^{nt} \mu_{s}(x - x_{0})^{s} $$

(15a)

then one can identify $\bar{y}[0] = \mu_{0},\bar{y}[1] = \mu_{1}\dots\bar{y}[nt] = \mu_{nt}$.

If y(x) is a function $\bar{y}[0],\bar{y}[1],\dots,\bar{y}[nt]$ can be determined using Eq. (13a).

The fundamental theorems of one dimensional differential transformation are

If

(15b)

Consider four first order differential equations over the domain 0≤x≤L. In order to solve the differential equation with Differential Transformation Element Method (DTEM), firstly a recurrent relation is obtained by using the IDT of each term in the differential equation and applying the theorems given above. It is possible to express $\bar{w}[s]$, s=j,j+1,j+2,…,nt in terms of $\bar{\theta} [s]$, $\bar{M}[s]$ and $\bar{V}[s]$, s=0,1,2,…,j−1 and centrifugal force term $\bar{P}[s]$, s=0,1,2,…,j−1 using the recurrent relation. Similarly $\bar{\theta} [s]$, $\bar{M}[s]$ and $\bar{V}[s]$ in terms of other three quantities and centrifugal force term $\bar{P}[s]$.

Assume Young’s modulus E, mass density ρ, breadth of the cross section at any section ‘b’, depth of the section ‘h’ vary with respect to ξ as ($\xi = \frac{x}{L}$)

$$ \begin{aligned}[c] &E(\xi) = \bigl(a_{1} + a_{2}\xi + a_{3} \xi^{2}\bigr);\\\noalign{\vspace{3pt}} &\rho(\xi) = \bigl(b_{1} + b_{2}\xi + b_{3}\xi^{2}\bigr);\\\noalign{\vspace{3pt}} &b(\xi) = (c_{1} + c_{2}\xi), \quad h(\xi) = (h_{1} + h_{2}\xi) \end{aligned} $$

(16)

Hence area and moment of inertia vary as

$$ \begin{aligned}[c] &A(\xi) = \mathit{area} = b(\xi)h(\xi) = \bigl(e_{1} + e_{2}\xi + e_{3}\xi^{2}\bigr);\\\noalign{\vspace{3pt}}& I = \bigl(f_{1} + f_{2}\xi\dots f_{5}\xi^{4}\bigr) \end{aligned} $$

(17)

Flexural rigidity d(x)=E(x)I(x) and ρI(x)=ρ(x)I(x) are given by

(18)

(19)

ρA(x) and K(x) variation is given by

$$ \begin{aligned}[c] & \rho A(\xi) = \bigl(\alpha_{1} + \alpha_{2}\xi\dots \alpha_{5}\xi^{4}\bigr);\\& K(\xi) = \bigl(\beta_{1} + \beta_{2}\xi\dots \beta_{5}\xi^{4}\bigr) \end{aligned} $$

(20)

Centrifugal force at any section is given by

(21)

From the above power series, we obtain

$$ \begin{aligned}[c] & \bar{d}[1] = g_{1}; \qquad \bar{d}[2] = g_{2}\dots \bar{K}[1] = \beta_{1};\\& \bar{K}[2] = \beta_{2}; \qquad \overline{\rho I}[1] = q_{1}; \qquad \overline{\rho I}[2] = q_{2}\\& \overline{\rho A}[1] = \alpha_{1}; \qquad \overline{\rho A}[2] = \alpha_{2}\dots \bar{P}[1] = \gamma_{1};\\& \bar{P}[2] = \gamma_{2}\dots \end{aligned} $$

(22)

In DTEM, the whole domain is firstly divided into ‘ne’ elements as shown in Fig. 2. The solution of the governing differential equation in each element, i.e. w _i (x), θ _i (x), M _i (x) and V _i (x), i=1,2,… ne are sought. The stiffness matrix and the shape functions for lateral displacements and bending rotations are obtained automatically. Assume transverse displacement w(x) and bending rotation θ(x) along the element length could be expressed in terms of nodal ones as

$$ \begin{aligned}[c] & w(x) = \sum_{j = 1}^{4} \psi_{j} \Delta_{j} = \boldsymbol{\psi}^{T}\boldsymbol{\Delta} \\ &\theta(x) = \sum_{j = 1}^{4} \phi_{j}\Delta_{j} = \boldsymbol{\varPhi}^{T}\boldsymbol{ \Delta} \end{aligned} $$

(23)

in which

$$ \Delta = \{ w_{i}\theta_{i}w_{j} \theta_{j} \} $$

(24)

$$ \begin{aligned}[c] & \boldsymbol{\psi} = \{ \psi_{1}\psi_{2}\psi_{3} \psi_{4} \}^{T} \\& \boldsymbol{\varPhi} = \{ \phi_{1}\phi_{2}\phi_{3} \phi_{4} \}^{T} \end{aligned} $$

(25)

where ψ are shown in Fig. 3.

Fig. 2

DTEM model (numbers in circles and beneath the beam respectively denote element and node numbers)

Fig. 3

Shape functions for nodal displacements

With the help of kinetic energy, consistent mass could be derived as

(26)

and geometric stiffness matrix is obtained as

$$ KG_{ij} = \int_{0}^{L_{e}} \biggl( \frac{\mathrm{d}\psi}{\mathrm{d}x} \biggr)_{i}\biggl( \frac{\mathrm{d}\psi}{ \mathrm{d}x} \biggr)_{j}\,\mathrm{d}x $$

(27)

Structural stiffness matrix is automatically obtained in DTEM.

3.1 Derivation of recurrent relation

To get DT of Eq. (11), the following two axioms are used. It is to be noted that from programming point of view s=1 to nt is considered instead of s=0 to nt in the usual way and nt denotes the number of terms. In all the numerical examples investigated, the number of terms considered is 40. The two axioms are

(28)

and

(29)

where B′ denotes $\frac{\mathrm{d}B}{\mathrm{d}x}$. From the last equation of Eq. (11)

$$ - V - K(x)\theta + \bigl(P(x) + K(x)\bigr)\nabla w = 0 $$

(30)

Taking DT of the above equation and using the theorems we get

$$ \bar{w}[s + 1] = \frac{L}{s}\biggl\{ \frac{(\bar{V}[s] + \bar{K}[1] \times \bar{\theta} [s] - s1)}{(\bar{P}[1] + \bar{K}[1])} \biggr\} $$

(31)

s1 in Eq. (31) is given by

(32)

From the third equation of Eqs. (11)

$$ \begin{aligned}[c] &{-} M + E(x)I(x)\nabla\theta = 0; \quad \mbox{or}\\& {-} M + d(x)\nabla\theta = 0 \end{aligned} $$

(33)

Taking DT of the above equation we get

$$ \bar{\theta} [s + 1] = L\bigl\{ \bar{M}[s] - s2\bigr\} /\bigl(s \times\bar{d}[1] \bigr) $$

(34)

where

$$ s2 = \frac{1}{L}\sum_{i = 2}^{k} (s - i + 1)\bar{d}[i] \times\bar{\theta} [s - i + 2] $$

(35)

From the second equation of Eqs. (11)

$$ V + \nabla M + \rho(x)I(x)\eta^{2}\theta - P(x)\nabla w = 0 $$

(36)

Taking DT of the above equation we get

(37)

where

(38)

From the first equation of Eqs. (11)

$$ \nabla V + \omega^{2}\rho(x)A(x)w = 0 $$

(39)

Taking DT of the above equation, we get

$$ \bar{V}[s + 1] = - \omega^{2}L\bigl\{ \overline{\rho A}[1] \times \bar{w}[s] + s4\bigr\} /s $$

(40)

where

$$ \begin{aligned}[c] & s4 = \omega^{2}\sum_{i = 2}^{s} \overline{\rho A}[i] \times\bar{w}[s - i + 1]\\& \rho A(x) = \rho(x)A(x) \end{aligned} $$

(41)

In the above equations $\bar{w}[1]$, $\bar{\theta} [1]$, $\bar{M}[1]$ and $\bar{V}[1]$ denote differential transformation values of deflection, bending rotation, moment and shear at the origin of the element. (In actual DTM, $\bar{w}[0]$, $\bar{\theta} [0]$, $\bar{M}[0]$ and $\bar{V}[0]$ are the deflection, rotation, moment and shear values at the origin of an element.) Using recurrence relation, obtain $\bar{w}[2],\bar{w}[3],\dots ,\bar{w}[nt],\dots, \bar{V}[2],\bar{V}[3], \dots, \bar{V}[\mathit{nt}]$ where ‘nt’ denotes the number of terms.

3.2 DTEM procedure to obtain shape functions, stiffness matrix, geometric stiffness matrix and mass matrices

Transverse displacements w(x) and bending rotation θ(x) along element length could be expressed in terms of nodal ones as given by Eq. (23). Assume we want to get the shape function for w _i =1 and all other displacements as zero. By recurrence relation for $\bar{w}[1] = 1$ and $\bar{M}[1] = 1$; $\bar{V}[1] = 1$ applied independently one can calculate the displacement $w_{j} = \sum_{s = 1}^{nt} \bar{w}[s]$ at the right end of the element as p ₁, y ₁, and z ₁ and calculate the rotation at the right end $\theta_{j} = \sum_{s = 1}^{nt} \bar{\theta} [s]$ for the same $\bar{w}[1] = 1$ and $\bar{M}[1] = 1$; $\bar{V}[1] = 1$ applied independently as p ₂,y ₂, and z ₂ respectively (see Fig. 4). To obtain the shape function for w _i =1 along with the displacement we have transformation for moment M _i and shear V _i which can be obtained from compatibility equation as

$$ \left[ \begin{array}{c@{\quad}c} y_{1} & z_{1} \\ y_{2} & z_{2} \end{array} \right] \left\{ \begin{array}{c} \bar{M}_{i} \\ \bar{V}_{i} \end{array} \right\} + \left\{ \begin{array}{c} p_{1} \\ p_{2} \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ 0 \end{array} \right\} $$

(42)

From Eq. (42) one can solve for $\bar{M}_{i}$, $\bar{V}_{i}$ and hence by knowing $\bar{w}_{1}$, $\bar{M}_{1}$, $\bar{V}_{1}$ one could obtain the shape function ψ by using recurrence relation. The same exercise is repeated for θ _i =1, w _j =1 and θ _j =1. Similarly functions Φ could also be obtained as shape functions for θ

$$ \mathop{\boldsymbol{\psi}}\limits_{4 \times 1} = \mathop{\mathbf{uu}^{T}}\limits_{4 \times \mathit{nt}} \mathop{\mathbf{xi}}\limits_{\mathit{nt}\times 1} $$

(43)

and

$$ \mathop{\boldsymbol{\varPhi}}\limits_{4 \times 1} = \mathop{\boldsymbol{\theta \theta}^{T}}\limits_{4 \times \mathit{nt}} \mathop{\mathbf{xi}}\limits_{\mathit{nt} \times 1} $$

(44)

where

$$ {\mathbf{xi}}^{T} = \bigl\langle 1\ \xi\ \xi^{2}\ \xi^{3} \ \xi^{4}\ \dots \ \xi^{\mathit{nt} - 1} \bigr\rangle $$

(45)

The mass matrix is obtained using Eq. (26) and in that

$$ \rho A(\xi) = \overline{\rho A}[1] + \overline{\rho A}[2]\xi + \overline{\rho A}[3]\xi^{2}\cdots $$

(46)

and

$$ \rho I(\xi) = \overline{\rho I}[1] + \overline{\rho I}[2]\xi + \overline{\rho I}[3]\xi^{2}\cdots. $$

(47)

The first term of the right hand side of Eq. (26) can be written as

(48)

The second term of mass matrix is obtained in a similar manner as

$$ M^{\mathit{II}} = L\sum_{s = 1}^{nt} \overline{\rho I}[s]\boldsymbol{\theta \theta}^{T}\mathbf{ax}^{s} \boldsymbol{\theta \theta} $$

(49)

Combining, the mass matrix is obtained as

(50)

wherein ax ^s

$$ ax(i,j,s) = \frac{1}{(i + j + s - 2)} $$

(51)

$$ \frac{d\psi}{dx} = \frac{1}{L}\mathbf{uu}^{T}\left\{ \begin{array}{c} 0 \\ 1 \\ 2\xi\\ 3\xi^{2} \\ \vdots\end{array} \right\} = \frac{1}{L}\mathbf{uu}^{T}\mathbf{ay}\left\{ \begin{array}{c} 1 \\ \xi\\ \xi^{2} \\ \vdots\\ \vdots\end{array} \right\} $$

(52)

where

$$ \mathbf{ay} = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & \cdots & \cdots & 0 \\ 1 & 0 & \cdots & \cdots & 0 \\ 0 & 2 & \cdots & \cdots & 0 \\ 0 & 0 & 3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots\end{array} \right] $$

(53)

The geometric stiffness matrix is obtained using Eq. (27) as

$$ \mathbf{KG} = \frac{1}{L}\mathbf{uu}^{T}\mathbf{ay} \mathbf{ax}^{1}\mathbf{ay}^{T}\mathbf{uu} $$

(54)

Hence for an element, stiffness matrix [K], geometric stiffness [KG] and mass matrix [M] can be established. The element stiffness matrices are assembled to form global flexural stiffness matrix, global geometric stiffness matrix and global mass matrices. Boundary conditions are applied using Wilson’s Lagrangian multiplier method [37] and the following equations are solved as eigen value problem for natural frequencies and buckling load.

$$ [\mathbf{K}]\{ r\} = \omega^{2}[\mathbf{M}]\{ r\} ; \qquad [\mathbf{K}]\{ r\} = P_{cr}[\mathbf{KG}]\{ r\} $$

(55)

Fig. 4

Deformed shape unit lateral displacement at node i

4 Numerical results and discussion

The following problems can be investigated using the formulation developed in this paper.

• (a) Free vibration of axially functionally graded tapered centrifugally stiffened Timoshenko beams

• (b) Stability analysis of axially functionally graded tapered Timoshenko beams

• (c) Free vibration analysis of axially functionally graded tapered Timoshenko beams

• (d) By assuming very high shear stiffness (say 1e20) and neglecting rotary inertia, all the above three analyses can be carried out for Bernoulli–Euler beams.

4.1 Effects of variable cross section

Consider a tapered beam with a rectangular cross section whose breadth and height both taper vary linearly as

$$ b = b_{0}(1 - c_{b}\xi); \qquad d = d_{0}(1 - c_{h}\xi) $$

(56)

where c _b and c _h are the taper parameters for the breadth and height.

Thus the cross sectional area and moment of inertia vary along the beam axis as (when c _b =c _h =e)

$$ A = A_{0}(1 - e\xi)^{\mathit{mr}}; \qquad I = I_{0}(1 - e \xi)^{\mathit{mr} + 2} $$

(57)

Case A. Depth variation only (mr=1)

$$ A = A_{0}(1 - e\xi); \qquad I = I_{0}(1 - e\xi)^{3} $$

(58)

where $\xi = \frac{x}{L}$ is the non-dimensional longitudinal coordinate along the whole beam, L is the length of whole beam and e is taper ratio and A ₀ and I ₀ are respectively the values of cross-sectional area and moment of inertia at the root where x=0.

Case B. Both depth and breadth variation (mr=2)

$$ A = A_{0}(1 - e\xi)^{2}; \qquad I = I_{0}(1 - e \xi)^{4} $$

(59)

It is instructive to remember that the beam would be uniform when e=0 and it would theoretically taper to a point if e=1 and if e is negative, section depth and breadth increase from x=0, i.e. (ξ=0) to x=L, i.e. (ξ=1).

4.2 Variation of material properties

Moreover, the distribution of modulus of elasticity and mass density are assumed to be respectively varied as power law distribution [38]. It is assumed that the axially FG beams is made of two constituents namely Aluminum and Zirconia with the following properties. (Poisson’s ratio is assumed to be 0.3)

T is a typical material property such as E and ρ which is assumed to vary as

$$ T = (T_{a} - T_{z}) \biggl( \frac{x}{L} \biggr)^{nr} + T_{z} $$

(60)

where the subscripts ‘a’ and ‘z’ refer to the values of the parameters for Aluminum and Zirconia respectively and nr is the material non-homogeneity parameter. The variation of E is depicted for a unit length of beam in Fig. 5 for different values of ‘nr’. It is obvious that the percentage content of Zirconia increases as ‘nr’ increases towards infinity. It is recommended by Nakamura et al. [39] that nr varies in the range of $\frac{1}{3} \le \mathit{nr} \le 3$ and any value out of this range would result into a FG material with too high percentage of one of the constituents, here Zirconia.

Fig. 5

Variation of Young’s modulus along the beam axis with respect to different values of nr

In this section, several numerical examples are provided to demonstrate the competency of the present methods. In order to facilitate the presentation of results, the following dimensionless parameters are introduced as

4.3 Convergence study

The competency of DT based dynamic stiffness (DS) method in free vibration of centrifugally stiffened tapered FG Timoshenko beams is verified through several numerical examples. In what follows, firstly the convergence of the DT based dynamic stiffness method (DT-DS) is examined. Afterwards, the effects of rotation speed, taper ratio, material non-homogeneity parameter on the natural frequencies are investigated.

It is very important to study the convergence characteristics of any numerical method to guarantee the successful application of the method to various engineering problems. For the convergence study of (DT-DS) approach, an axially functionally graded centrifugally stiffened non-prismatic cantilever beam with the following parameters is considered. Since rectangle section is considered, shear correction factor may be assumed as 5/6.

Figure 6 shows the relation between the number of elements in (DT-DS) vs frequency parameter values. Considering four frequency parameters, nt=10 terms would be sufficient to provide satisfactory results. However, for a highly nonlinear problem more number of terms may be necessary to achieve the required accuracy. Considering all the four frequency parameters 10 terms with 40 elements would be sufficient to solve the problem to a desired accuracy.

Fig. 6

Convergence characteristics of Dynamic stiffness method

4.4 Numerical examples

Example 1

(Uniform cantilever Timoshenko beam analysis ($r = \frac{1}{30}$))

The results of Table 1 illustrate the effect of the rotational speed parameter λ, on the fundamental natural frequency of the Timoshenko beam. The fundamental frequency values obtained by Dynamic stiffness method agree with Kaya [35] and Ozgumus and Kaya [40]. All the four fundamental frequencies increase with the increase in speed parameter. The values of ρ, E, A, L are assumed as unity and the shear correction factor κ is assumed as 5/6 and G=0.392E. The hub radius is assumed to be equal to zero.

Table 1 Variation of the fundamental frequency parameters ($\mu = \sqrt{\frac{\rho AL^{4}\omega^{2}}{\mathit{EI}}}$) of a rotating Timoshenko cantilever beam for various value of λ (speed parameter) ($\lambda = \sqrt{\frac{\rho {AL}^{4}\varOmega^{2}}{\mathit{EI}}}$ (δ=0, $r = \frac{1}{30}$, $\frac{{E}}{KG} = 3.059$))

Example 2

Cantilever rotating Timoshenko beam with rotational speed parameter 4 (mr=1; κ=2/3 (circular section); G=0.375E; δ=0; λ=4) is considered. Table 2 illustrates the variation of natural frequencies of a rotating tapered Timoshenko beam with respect to the taper ratio and rotary inertia parameter ‘r’. For e=0, 0.25, 0.5, the frequency parameter values are read approximately from Fig. 4 of Ozgumus and Kaya [40] and compared with the present results in Table 2 and the agreement is quite good. When the rotary inertia parameter increases, the natural frequency parameter μ decreases. Although decreases, the product of μr still increase and hence natural frequency increases. Rotary inertia parameter has dominant effect on higher modes. It is also seen that lower mode frequency parameters are not affected with increase in ‘r’ whereas there is remarkably high decrease in higher mode frequency parameter values. The taper ratio has decreasing effect on natural frequency parameters.

Table 2 Effect of rotary inertia and taper ratio parameters on the first six natural frequency parameters of tapered cantilever rotating Timoshenko beam (λ=4; δ=0; mr=1; κ=2/3; G=0.375E)

Example 3

Consider a tapered axially FG Timoshenko beam with δ=0 rotating with a speed of λ=5. The material follows power law with nr=2. The first four dimensionless natural frequency parameters of the beam are tabulated in Table 3 for mr=2. It can be verified that the frequency parameter values for all types of boundary conditions investigated decrease with taper ratio except for C-F condition where it shows an increasing trend. The first four normalized mode shapes of the beam with taper ratios e=0, 0.8 are given in Fig. 7 for mr=1, nr=2 for C-F boundary conditions and these four normalized mode shapes compare well qualitatively with Fig. 7 of Ref. [41].

Fig. 7

The first four normalized mode shapes (solid line: e=0; dotted line: e=0.8) of an axially graded rotating tapered Timoshenko beam with λ=2; δ=0; and mr=nr=2: Boundary Condition C-F

Table 3 Effect of taper ratio on fundamental frequency parameters of rotating axially FG Timoshenko beam with different BCS (r=0.08; mr=2; nr=2; κ=5/6; G=0.3846E; λ=5)

Example 4

Table 4 shows the buckling loads of a non rotating homogeneous uniform Timoshenko column (r=0.1; κ=5/6; G=0.3846E) and the results agree with Wang et al. [42].

Table 4 Buckling load parameters of homogeneous Timoshenko column for various boundary conditions (r=0.1, G=0.3846E, κ=5/6)

Example 5

Time history analysis of a simply supported Timoshenko beam subjected to step loading at mid span of the beam (L=10 m; b=0.1 m; h=0.1 m; E=2.058×10¹¹ N m⁻², ν=0.3; κ=5/6; ρ=7860 kg m⁻³; F(t)=300 N at mid span of the beam). Figure 8 shows the vertical response at the mid span of the beam for the first 5.0 seconds and compares well qualitatively with the results obtained by Tang [43]. Tang [43] used Leung’s equation to derive the overall mass and stiffness matrix which is more suitable for response analysis than the overall dynamic stiffness matrix. Tang [43] obtained the results of forced vibration of the beam by the precise time integration method of Zhong and Williams [44]. But in the present analysis, considering only first five fundamental modes, the mass and stiffness matrices are reduced to the size of 5×5 and forced vibration analysis is carried out by using Newmark’s linear acceleration method with step size of 0.005 seconds up to 5 seconds. For comparison, forced response for damped system (with damping factor ς=0.05) is also carried out for the same beam and plotted in Fig. 8.

Fig. 8

Forced vibration response of a simply supported Timoshenko beam

Example 6

Consider an axially FG tapered non rotating Timoshenko beam with material non-homogeneity parameter nr=2. The first four frequency parameters of the beam with C-F, H-H; and C-C boundary conditions are given in Table 5. The results agree well with those of Shahba et al. [27].

Table 5 The first four dimensionless frequency parameters and buckling load parameter of an axially FG tapered Timoshenko beam with different BCS (nr=2; mr=2; r=0.1)

Example 7

In this example, we consider a tapered rotating Euler beam with cantilevered boundary conditions. Wright et al. [11] and Hodges and Rutkowski [45] studied the same example. Wang and Wereley [7] used only one single SFEM with 80 terms in the Frobenius power series to obtain the natural frequencies. The mass distribution was assumed to be linear as ρ(x)=ρ ₀(1−0.5ξ) and the flexural stiffness EI(x) as EI(x)=EI ₀(1−0.5ξ)³. This is a depth tapered beam with depth taper ratio as 0.5. All the three modal frequencies as shown in Table 6 exactly match with Wang and Wereley [7] where the rotation speed varies from 0 to 10. Banerjee [8] also studied the same example using uniform rotating dynamic stiffness method where 20 elements were included. In this paper, for a tapered beam exact displacement function is obtained in DT based Dynamic stiffness method.

Table 6 Predictions of non-dimensional natural frequency $\mu^{2} = \frac{\rho A_{0}\omega^{2}L^{4}}{\mathit{EI}_{0}}$ of a tapered cantilever beam under different rotation speeds ρA(x)=ρA ₀(1−0.5x/L); EI(x)=EI ₀(1−0.5x/L) where $\lambda^{2} = \frac{\rho A_{0}\varOmega^{2}L^{4}}{\mathit{EI}_{0}}$

Example 8

(Axially FG beam with δ=0 and λ=2)

The material follows the power law with nr=2. The first four non-dimensional natural frequencies of the beam are tabulated in Table 7 for mr=1 (depth tapered beam) and compared with Zarrinzadeh et al. [46] who solved the problem by Finite element approach and the agreement is very good. It is generally observed that the natural frequencies for all types of boundary conditions decrease with taper ratio with some exceptions. The fundamental frequency increases with respect to taper ratio for C-F condition. These effects are also observed for homogeneous rotating beams by Attarnejad and Shahba [29].

Table 7 Effect of taper ratios on the natural frequency parameters of rotating axially functionally graded Euler beam (mr=1, nr=2, λ=2)

Example 9

Table 8 shows the results of free vibration analysis of axially functionally graded Euler beam (E=E ₀(1+ξ), ρ=ρ ₀(1+ξ+ξ ²)) (mr=2) by (DT-DS) method and compared with Shahba et al. [27]. It is observed that all natural frequencies decrease with the increase in taper ratio except for the fundamental mode of C-F boundary condition. This exception has been also well pointed out by Ozgumus and Kaya [47] for homogeneous tapered beams in the literature.

Table 8 Non-dimensional transverse frequencies ($\mu = \sqrt{\frac{\rho A_{0}L^{4}\omega^{2}}{\mathit{EI}_{0}}}$) for an axially FG tapered beam; Boundary Condition: C-C; Mode: 1–2 (EA=EA ₀(1+ξ); ρA=ρA ₀(1+ξ+ξ ²), mr=2 (μ—frequency parameter); p = buckling load parameter $= \frac{P_{cr}L^{2}}{\mathit{EI}_{0}}$)

Example 10

(Buckling load of axially functionally graded column)

As a comparison, we consider the flexural rigidity of the column is of the form EI(x)=EI ₀(1+ξ−ξ ²) where EI ₀ is the flexural rigidity of the column at ξ=0. Elishakoff [48] has given the exact buckling load as $P_{\mathit{cr}} = \frac{12\mathit{EI}_{0}}{L^{2}}$. But no closed form solution is available for the same column with other boundary conditions. Huang and Li [49] used Fredholm integral equation and obtained the buckling loads for columns with various boundary conditions and the results of the present analysis are compared with Huang and Li [49] in Table 9 and the agreement is quite good.

Table 9 Critical buckling load parameter of a FG Euler column for various BCS

Example 11

(Buckling load of axially functionally graded column)

We consider two special flexural rigidities of polynomial form, one being linearly varying flexural rigidity EI(x)=EI ₀(1+ξ) and the other being parabolically varying flexural rigidity EI(x)=EI ₀(1+ξ)². The results obtained by the present analysis are compared in Table 9 with Huang and Li [49] and they are in excellent agreement with the published results.

5 Conclusions

For uniform Cantilever Timoshenko rotating beam analysis the fundamental frequency parameter values obtained by Dynamic Stiffness method agree with Kaya [35] and Ozgumus and Kaya [40]. All the four fundamental frequencies increase with the increase in speed parameter.

It is also seen that lower mode frequencies are not affected with increase in ‘r’ whereas there is remarkably high decrease in higher mode frequency values. The taper ratio has decreasing effect on natural frequencies.

It can be verified that the frequency values for all types of boundary conditions investigated decrease with taper ratio except for C-F condition where it shows an increasing trend.

For non rotating homogeneous uniform Timoshenko column (r=0.1; κ=5/6; G=0.3846E) the buckling loads calculated agree with Wang et al. [42].

For axially functionally graded Euler beam (E=E ₀(1+ξ), ρ=ρ ₀(1+ξ+ξ ²)) (mr=2) it is observed that all natural frequencies decrease with the increase in taper ratio except for the fundamental mode of C-F boundary condition.

Regarding the DT-DS method the following conclusions are arrived at.

DTM exactly coincides with the traditional Taylor series method when it is applied to problems involving ordinary differential equations [52]. This method captures the effects of variable cross section, centrifugal force and the material non-homogeneity parameter due to axially graded material. Since Wilson’s Lagrangian multiplier method is used, it is easy to incorporate the boundary conditions. DT-DS method considers four first order differential equations instead of one fourth order differential equation and hence writing the Differential transform is an easy task. This method is superior to many other methods because of its simplicity and accuracy in calculating natural frequencies and buckling load and plotting the mode shapes also.

It was shown in the paper that an efficient finite element could be developed based on structural mechanics principles. Instead of assuming shape functions before hand as in classical finite element method, in the DT-DS method proposed, shape functions are derived using DTM satisfying overall equilibrium and compatibility of a beam. Hence they represent real deformations which depend on the variation of material properties such as modulus of elasticity and mass density, variation of geometry (b,h) of the beam. These deformations (shape functions) are substituted in the potential and kinetic energy expressions to derive the stiffness and mass matrices to carry out static and free and forced vibration analysis. Since the new shape functions were derived based on the static deformations, in static problem exact results were obtained by using two elements whereas in dynamic problem at least 10 elements are needed to get the accurate result. Though there are many methods proposed to find the shape functions, a DTM based method is simple, precise and easy to use compared to many other methods developed. Since DT based Dynamic Stiffness method (DT-DS) is efficient tool for solving nonlinear or parameter varying systems, it is expected that this method will find a wide range of applications in structures of functionally graded materials.