Introduction

Beams with a non-uniform and continuous distribution of material and geometrical parameters along the axial direction, namely, non-uniform axially functionally graded (NAFG) beams due to thermal resistance, high stiffness, economic issues, and optimal design are widely utilized in many aerospace, mechanical, electrical, and civil engineering structures. Nevertheless, the non-uniform homogenous beams, i.e., tapered, wedged, stepped, and non-prismatic beams can be considered as the special case of the NAFG beams with constant material and variable geometry [1]. On the other hand, it is important to know the effect of the attached masses on the dynamic behavior and natural frequencies of the NAFG beams, to achieve the proper design of the composite structure. Accordingly, this paper is focused on the free vibration of non-uniform and NAFG beams with attached masses. So far, many reports have been published in these two areas.

About the vibration of non-uniform beams with attached masses, for the first time, Mabie and Rogers [2, 3] derived the exact analytical solutions for the transverse vibrations of tapered and double-tapered cantilever beams with end mass. Based on the finite-element method, the transverse vibration frequencies of a linear tapered beam with one end rotational spring-hinged and carrying a mass at the other free end were studied by Sankaran et al. [4]. Using the analytical approach, Goel [5] investigated the transverse vibrations of the same beam. The closed-form solution in terms of the Bessel functions for the transverse vibrations of a tapered beam carrying a concentrated mass was obtained by Lee [6]. Lau [7, 8] analyzed the first five natural frequencies of non-uniform cantilever beams with a mass at the free end. Utilizing the Rayleigh–Schmidt approach, the fundamental mode of vibration for an elastically restrained cantilever beam with variable cross-section and tip mass was investigated by Laura and Gutierrez [9]. Alvarez et al. [10] obtained an approximate solution for the vibrations of an elastically restrained, non-uniform beam with translational and rotational springs, and with a tip mass using the optimized Rayleigh–Ritz approach. Based on the Bessel functions, the natural frequencies of the same beam were calculated by Yang [11]. An exact analytical solution for the transverse vibrations of a Timoshenko beam of non-uniform thickness clamped at one end and carrying a concentrated mass at the other was presented by Rossi et al. [12]. Lee and Lin [13] derived the exact vibration solutions for non-uniform Timoshenko beams with attachments using the power series method. Utilizing the numerical integration, an approximate method for the vibration analysis of a non-uniform Timoshenko beam with constraint at any point and carrying a heavy tip body was proposed by Matsuda et al. [14]. Based on the characteristics orthogonal polynomials method and the modified Rayleigh–Schmidt method, Grossi et al.[15] studied the vibration of tapered beams with one end spring-hinged and the other end with tip mass. An exact analysis for the transverse vibrations of a linearly tapered cantilever beam with tip mass of rotary inertia, eccentricity, and constraining springs via the Bessel functions was presented by Auciello [16, 17]. Using the same method and Rayleigh–Ritz approach, Auciello and Maurizi [18] investigated the first five natural frequencies of tapered beams with attached mass and inertia elements. The vibrations of a cantilever tapered beam with varying section properties and materials and carrying a mass at the free end utilizing the Bessel functions and Rayleigh–Ritz method were studied by Auciello and Nolè [19]. Wu and Hsieh [20] determined the natural frequencies and corresponding mode shapes of a non-uniform beam carrying multiple point masses using the analytical and numerical combined methods. Using the fundamental solutions and recurrence formulas, a new exact approach for determining the natural frequencies and mode shapes of multistep non-uniform beams with classical and non-classical boundary conditions and concentrated masses was presented by Li [21, 22]. The exact solutions for the natural frequencies and mode shapes of non-uniform beams with multiple spring-mass systems using the numerical assembly method and Bessel functions were performed by Chen and Wu [23]. Karami et al. [24] proposed a differential quadrature element method for the free vibration analysis of arbitrary non-uniform Timoshenko beams with attachments and general boundary conditions. Based on the analytical and numerical combined method, the bending vibrations of wedge beams with any number of point masses were investigated by Wu and Chen [25]. Using a similar approach, Wu and Chiang [26] studied the free vibrations of solid and hollow wedge beams with rectangular or circular cross sections and carrying any number of point masses. Exact free vibration analysis of Euler–Bernoulli tapered beams in the presence of concentrated tip mass and linear dashpot damper in terms of Bessel functions was presented by De Rosa and Maurizi [27]. Wu and Chen [28] obtained an exact solution for the natural frequencies and mode shapes of an immersed elastically restrained wedge beam carrying an eccentric tip mass with the mass moment of inertia. The free and forced vibrations of a tapered cantilever beam carrying multiple point masses were performed by Chen and Liu [29]. Based on the Adomian modified decomposition method, Lai et al. [30] investigated the free vibration of non-uniform Euler–Bernoulli beams with tip mass of rotatory inertia and eccentricity resting on an elastic foundation and subjected to an axial load. An exact solution for the free vibrations of a non-uniform beam carrying multiple elastic-supported rigid bars using the numerical assembly method was determined by Lin [31]. Attarnejad et al. [32] proposed the dynamic basic displacement functions for the free transverse vibration analysis of non-prismatic beams. Moreover, they studied the effect of the tip mass on the natural frequencies. Applying the power series method of Frobenius, the exact solutions for the free vibrations and buckling of double-tapered columns with elastic foundation and tip mass were obtained by Firouz-Abadi et al. [33]. Wang [34] analyzed the vibration of a tapered cantilever of constant thickness and linearly tapered width with tip mass utilizing the initial value numerical method. A numerical finite difference scheme for the free vibration of non-uniform cantilever beams carrying both transversely and axially eccentric tip mass was presented by Malaeke and Moeenfard [35]. The linear and nonlinear frequency characteristics of a non-uniform cantilever beam with tip mass using the Galerkin approximation and the method of multiple scales were studied by Sagar Singh et al. [36]. A new method for the determination of approximate values of natural frequencies of cantilever beams with variable axial parameters with a tip mass and spring was proposed by Nikolić and Šalinić [37]. This technique was based on the replacement of the flexible beam by a rigid multibody system. Torabi et al. [38] presented an exact closed-form solution for the free vibration analysis of conical and tapered beams carrying multiple concentrated masses using the Bessel and Dirac’s delta functions. Based on the theory of the continuous-mass transfer matrix method, Huang et al. [39] derived a formulation for determining the exact natural frequencies and associated mode shapes of a nonlinearly tapered beam carrying various concentrated elements in the arbitrary boundary conditions. A Chebyshev spectral method with a null space approach for investigating the boundary-value problem of a non-prismatic Euler–Bernoulli beam with generalized boundary or interface conditions and tip mass was proposed by Hsu et al. [40].

As regards the vibration of inhomogeneous and functionally graded (FG) beams with attached masses, apparently, the first closed-form solutions of the vibrating inhomogeneous beam and bar with a tip mass via the semi-inverse method were derived by Elishakoff and coworkers [41, 42]. Huang and Li [43] presented a new approach for the free vibration of AFG beams with non-uniform cross-section using the Fredholm integral equations. De Rosa et al. [44] calculated the free vibration frequencies of an Euler–Bernoulli beam with exponentially varying cross-sections, in the presence of concentrated tip mass and linear dashpot damper using the symbolic software Mathematica. Through a finite-element approach, the free vibration and stability analysis of AFG tapered Timoshenko beams were investigated by Shahba et al. [45]. These researchers studied the effects of the attached mass on the natural frequencies. Wang and Wang [46] presented an exact vibration solution for an exponentially tapered cantilever beam with tip mass and including a flexible base modeled by a rotational spring. The exact frequency equations of the free vibration of the exponentially AFG beams with various classical boundary conditions were derived by Li et al. [47]. In another work, Li [48] studied the free vibration of axially loaded shear beams carrying elastically restrained lumped-tip masses via asymptotic Timoshenko beam theory. Based on the Kausel theory, stability and vibration analysis of axially loaded shear beam-columns carrying elastically restrained mass were investigated by Zhang et al. [49]. Tang et al. [50] derived the exact frequency equations of the free vibration of the exponentially non-uniform AFG Timoshenko beams with classical end supports. The vibration of a non-uniform carbon nanotube with attached mass via the nonlocal Timoshenko beam theory using the transfer function method incorporating with the perturbation method was investigated by Tang et al. [51]. Yuan et al. [52] proposed an exact analytical approach to solve the free vibrations of axially inhomogeneous Timoshenko beams with variable cross-section and attached point mass. Based on the initial value method, Chen et al. [53] presented a new approach for determining the natural frequencies of AFG nanowires carrying a nanoparticle at the tip via the Timoshenko beam theory incorporating the surface effects. The free vibration analysis of an FG nano-beam with an attached mass at the tip according to Euler–Bernoulli beam theory was analyzed by Rahmani et al. [54]. Using the rigid multibody method, Nikolić [55] studied the free vibration analysis of NAFG cantilever beams with a tip body. Applying the Ritz method, the free vibrations of AFG cantilever tapered beams carrying attached masses were investigated by Rossit et al. [56]. The transverse vibration of a functionally graded material (FGM) cantilever nano-beam carrying a concentrated mass at the free end applying the analytical solution was studied by Ghadiri and Jafari [57]. A new non-iterative computational technique for the free vibration analysis of NAFG rods and beams via the symbolic-numeric method of initial parameters was proposed by Šalinić et al. [58]. Rossit et al. [59] investigated the effect of considering the theory of Timoshenko on the vibration of AFG cantilever beams carrying concentrated masses using the Rayleigh–Ritz method. Based on the Myklestad method which is also known as the transfer matrix method, Mahmoud [60] presented a general solution for the free transverse vibration of NAFG cantilevers loaded at the tips with point masses. The initial value method was applied by Sun and Li [61] to study the free vibration of NAFG Timoshenko beams. The comparison between the forced vibration of isotropic homogeneous and AFG beams carrying concentrated masses was performed by Nguyen et al. [62]. They investigated the influences of the concentrated masses and the varying of the material properties along the simply supported beam on the receptance matrix. Li et al. [63] developed an analytical solution for the free vibration of exponential FG beams with variable cross-sections resting on Pasternak elastic foundations. A Generalized finite-element approach toward the free vibration analysis of NAFG beams was proposed by Sahu et al. [64]. Recently, Liu et al. [65] presented a closed-form dynamic stiffness formulation for the exact transverse free vibration analysis of linearly tapered and/or NAFG beams based on the Euler–Bernoulli theory.

According to the literature review, there is no published work on the exact solutions of the free transverse vibration of the NAFG beams with end point masses and general boundary conditions. Moreover, there is no comprehensive report on the effects of the attached end point masses on the natural frequencies of the power-law NAFG beams. To overcome these shortages, the analytical approach presented in reference [1] will be extended to obtain the exact natural frequencies of the NAFG Euler–Bernoulli beams with attached end masses and general boundary conditions. In this way, based on the Euler–Bernoulli beam theory, the governing differential equation of motion was solved accurately using the Bessel functions. Then, the constant coefficients matrices of the power-law NAFG beams with the end point masses and general elastic supports were derived by applying the boundary conditions. Accordingly, by taking the constant coefficients matrix determinant equal to zero and calculating the positive real roots, the natural frequencies were obtained. By comparing the responses of the numerical examples with the available solutions, the accuracy, capability, and efficiency of the proposed formulations are demonstrated. Subsequently, the effects of the attached end point masses, rotational and translational elastic supports, and NAFG parameters on the values of the first four natural frequencies of the power-law NAFG beams for the eight parametric cases will be studied comprehensively. It is reminded that the material and geometrical properties of the NAFG beams are assumed to vary continuously and together in the axial length according to the power-law forms. The exact analytical solutions are listed in tabular and graphical forms and can be utilized as the benchmark solutions. Moreover, the results presented herein can be used for the proper design of composite beams carrying end point masses with different elastic boundary conditions.

Free Transverse Vibration Formulation

In this work, the analytical solutions to obtain the exact natural frequencies of the power-law NAFG Euler–Bernoulli beam with attached end point masses and general boundary conditions are presented.

NAFG Material and Geometrical Properties

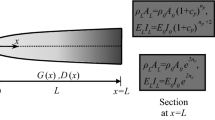
In the present study, the material and geometrical properties, i.e., mass per unit length and flexural rigidity of the NAFG beam, shown in Fig. 1, are assumed to vary continuously and together in the axial direction according to the power-law forms and defined as:

$$m\left( x \right) = \rho \left( x \right)A\left( x \right) = \rho_{0} A_{0} \left( {1 + c\frac{x}{L}} \right)^{p} = \rho_{L} A_{L} \left( {\frac{{1 + c\frac{x}{L}}}{1 + c}} \right)^{p} ,$$
(1a)
$$K\left( x \right) = E\left( x \right)I\left( x \right) = E_{0} I_{0} \left( {1 + c\frac{x}{L}} \right)^{p + 2} = E_{L} I_{L} \left( {\frac{{1 + c\frac{x}{L}}}{1 + c}} \right)^{p + 2} ,$$
(1b)

where x is the axial coordinate, L is the length of the beam, m(x) = ρ(x)A(x) is the unit mass length of the NAFG beam, which is computed by volume mass density ρ(x) and cross-section area A(x), and K(x) = E(x)I(x) is the flexural rigidity of the NAFG beam which is calculated by the modulus of elasticity E(x) and moment of inertia I(x). Also, ρ0, A0, E0, and Io are the mass density, cross-section area, modulus of elasticity, and moment of inertia at x = 0, respectively. Similarly, ρL, AL, EL, and IL are the mass density, cross-section area, modulus of elasticity, and moment of inertia at x = L, respectively. Moreover, p and c are the NAFG parameters that p is an integer quantity and represents the gradient index and c represents the gradient coefficient. It should be noted that the mass per unit length and flexural rigidity of the NAFG beam are positive values and therefore c > − 1. In addition, it is evident that when c = 0.0, the beam is uniform, i.e., the material and geometrical properties are kept constant.

Fig. 1
figure 1

Schematic of the non-uniform axially functionally graded (NAFG) beam with power-law form

Full size image

It is reminded that changing the mass per unit length m(x) and flexural rigidity K(x) can be expressed based on the variations of the material properties or geometrical properties or both of them. According to this point, the tapered, wedged, stepped, and non-prismatic beams can be considered as the special case of the NAFG beams with constant material and variable geometry [1]. For better understanding, the normalized variations of m(x) and K(x) of the NAFG beam, which are normalized by the values of the material and geometrical properties of the beam at x = L, are plotted in Fig. 2 for various values of the gradient index (p) and gradient coefficient (c).

Fig. 2
figure 2

Normalized variations of mass per unit length and flexural rigidity of the NAFG beam: a for various values of gradient index (p) in which c = 0.5; b for various values of gradient coefficient (c) in which p = 2

Full size image

Governing Differential Equation

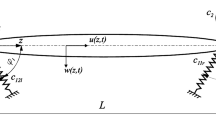
The free transverse vibration differential equation of a NAFG Euler–Bernoulli beam of length L with end point masses and elastic supports, as shown in Fig. 3, is given by [66]:

$$\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {K\left( x \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}} \right] + m\left( x \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }} = 0,\quad 0 < x < L,$$
(2)

where x is the axial coordinate, t is time, w(x,t) is the lateral deflection of the beam, K(x) = E(x)I(x) is the flexural rigidity of the beam at the position x and m(x) = ρ(x)A(x) is the mass per unit length of the beam at the position x.

Fig. 3
figure 3

Schematic of the NAFG beam with end point masses and elastic supports

Full size image

Following the separation of variable analogy, the solution of Eq. (2) can be expressed as [66]:

$$w_{i} \left( {x,t} \right) = W_{i} \left( x \right)e^{{j\omega_{i} t}} \quad (j^{2} = - 1),$$
(3)

where ωi is the circular frequency and Wi(x) is the shape function of the lateral motion of the ith vibration mode.

Substituting the Eq. (3) into Eq. (2), one can get:

$$\frac{{d^{2} }}{{\text{d}x^{2} }}\left[ {K\left( x \right)\frac{{d^{2} W_{i} \left( x \right)}}{{\text{d}x^{2} }}} \right] - m(x)\omega_{i}^{2} W_{i} \left( x \right) = 0.$$
(4)

If Eqs. (1a) and (1b) are inserted into Eq. (4), it can be rewritten as:

$$\begin{gathered} \left( {1 + c\frac{x}{L}} \right)^{p + 2} \frac{{d^{4} W_{i} (x)}}{{\text{d}x^{4} }} + 2\frac{c}{L}(p + 2)\left( {1 + c\frac{x}{L}} \right)^{p + 1} \frac{{d^{3} W_{i} (x)}}{{\text{d}x^{3} }} \hfill \\ + \frac{{c^{2} }}{{L^{2} }}(p + 1)(p + 2)\left( {1 + c\frac{x}{L}} \right)^{p} \frac{{d^{2} W_{i} (x)}}{{\text{d}x^{2} }} - \frac{{\rho_{0} A_{0} \omega_{i}^{2} }}{{E_{0} I_{0} }}\left( {1 + c\frac{x}{L}} \right)^{p} W_{i} (x) = 0. \hfill \\ \end{gathered}$$
(5)

Introducing the following quantity

$$X = \left( {1 + c\frac{x}{L}} \right),$$
(6)

which is equal to 1 at x = 0 and to 1 + c at x = L, and considering in mind that

$$\text{d}x = \left( \frac{L}{c} \right)\text{d}X.$$
(7)

Equation (5) simplifies as follows:

$$X^{p + 2} \frac{{d^{4} W_{i} (X)}}{{\text{d}X^{4} }} + 2(p + 2)X^{p + 1} \frac{{d^{3} W_{i} (X)}}{{\text{d}X^{3} }} + (p + 1)(p + 2)X^{p} \frac{{d^{2} W_{i} (X)}}{{\text{d}X^{2} }} - \frac{{\Omega_{i}^{4} }}{{c^{4} }}X^{p} W_{i} (X) = 0,$$
(8)

where \(\Omega_{i} = \sqrt[4]{{\frac{{\rho_{0} A_{0} \omega_{i}^{2} L^{4} }}{{E_{0} I_{0} }}}}\) is the dimensionless natural frequency coefficient of the ith vibration mode.

The general solution of this equation for the positive gradient coefficient (i.e., c > 0) is [67, 68]:

$$W_{i} \left( X \right) = X^{{ - \frac{p}{2}}} \left[ {C_{1} J_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + } \right.C_{2} Y_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + C_{3} I_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + \left. {C_{4} K_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right)} \right],$$
(9)

where C1, C2, C3, C4 are unknown constants and Jp, Yp, Ip, Kp are, respectively, the Bessel functions of first, second, modified first, and modified second kinds of order p. The detail of the derivation of the general solution Eq. (9) is presented in Appendix A.

It is reminded that the general solution of Eq. (8) for c = 0 (i.e., uniform and isotropic homogenous beam) and negative gradient coefficients (i.e., − 1 < c < 0) are expressed with Eqs. (10) and (11), respectively [68].

$$W_{i} \left( X \right) = C_{1} \sin (X) + C_{2} \cos (X) + C_{3} \sinh (X) + C_{4} \cosh (X),$$
(10)
$$W_{i} \left( X \right) = X^{{ - \frac{p}{2}}} \left[ {C_{1} J_{p} \left( { - \frac{{2\Omega_{i} \sqrt X }}{c}} \right) + } \right.C_{2} Y_{p} \left( { - \frac{{2\Omega_{i} \sqrt X }}{c}} \right) + C_{3} I_{p} \left( { - \frac{{2\Omega_{i} \sqrt X }}{c}} \right) + \left. {C_{4} K_{p} \left( { - \frac{{2\Omega_{i} \sqrt X }}{c}} \right)} \right].$$
(11)

General Boundary Conditions

The boundary conditions, in the presence of end point masses M0, ML and constraints with the rotational elastic stiffnesses kR0, kRL and lateral translational elastic stiffnesses kT0, kTL are expressed as [66]:

$$K(x)\frac{{d^{2} W_{i} (x)}}{{\text{d}x^{2} }} - k_{R0} \frac{{\text{d}W_{i} (x)}}{{\text{d}x}} = 0,$$
(12)
$$\frac{d}{{\text{d}x}}\left[ {K(x)\frac{{d^{2} W_{i} (x)}}{{\text{d}x^{2} }}} \right] + k_{T0} W_{i} (x) - M_{0} \omega_{i}^{2} W_{i} (x) = 0,$$
(13)

which refer to the equilibrium of the bending moment and shear force at x = 0, respectively, and

$$K(x)\frac{{d^{2} W_{i} (x)}}{{\text{d}x^{2} }} + k_{RL} \frac{{\text{d}W_{i} (x)}}{{\text{d}x}} = 0,$$
(14)
$$\frac{d}{{\text{d}x}}\left[ {K(x)\frac{{d^{2} W_{i} (x)}}{{\text{d}x^{2} }}} \right] - k_{TL} W_{i} (x) + M_{L} \omega_{i}^{2} W_{i} (x) = 0,$$
(15)

which denote to the equilibrium of the bending moment and shear force at x = L, respectively.

Substituting Eq. (1b) and utilizing Eqs. (6) and (7), the boundary conditions become:

$$X^{p + 2} \frac{{d^{2} W_{i} (X)}}{{\text{d}X^{2} }} - \frac{{k_{R0} L}}{{E_{0} I_{0} c}}\frac{{\text{d}W_{i} (X)}}{{\text{d}X}} = 0,$$
(16)
$$X^{p + 2} \frac{{d^{3} W_{i} (X)}}{{\text{d}X^{3} }} + (p + 2)X^{p + 1} \frac{{d^{2} W_{i} (X)}}{{\text{d}X^{2} }} + \frac{{\left( {k_{T0} - M_{0} \omega_{i}^{2} } \right)L^{3} }}{{E_{0} I_{0} c^{3} }}W_{i} (X) = 0,$$
(17)

at X = 1 (x = 0), and

$$X^{p + 2} \frac{{d^{2} W_{i} (X)}}{{\text{d}X^{2} }} + \frac{{k_{RL} L}}{{E_{0} I_{0} c}}\frac{{\text{d}W_{i} (X)}}{{\text{d}X}} = 0,$$
(18)
$$X^{p + 2} \frac{{d^{3} W_{i} (X)}}{{\text{d}X^{3} }} + (p + 2)X^{p + 1} \frac{{d^{2} W_{i} (X)}}{{\text{d}X^{2} }} + \frac{{\left( {M_{L} \omega_{i}^{2} - k_{TL} } \right)L^{3} }}{{E_{0} I_{0} c^{3} }}W_{i} (X) = 0,$$
(19)

at X = 1 + c (x = L).

For simplicity, the following dimensionless mass ratios (α0, αL) and stiffness ratios (R0, RL, T0 and TL) are introduced:

$$\begin{gathered} \alpha_{0} = \left. {\frac{{M_{0} }}{{\rho_{0} A_{0} LX^{2} }}} \right|_{X = 1} = \frac{{M_{0} }}{{\rho_{0} A_{0} L}},^{{}} R_{0} = \frac{{k_{R0} L}}{{E_{0} I_{0} }},^{{}} T_{0} = \frac{{k_{T0} L^{3} }}{{E_{0} I_{0} }} \hfill \\ \alpha_{L} = \left. {\frac{{M_{L} }}{{\rho_{L} A_{L} LX^{2} }}} \right|_{X = 1 + c} = \frac{{M_{L} }}{{\rho_{L} A_{L} L(1 + c)^{2} }},^{{}} R_{L} = \frac{{k_{RL} L}}{{E_{L} I_{L} }},^{{}} T_{L} = \frac{{k_{TL} L^{3} }}{{E_{L} I_{L} }}. \hfill \\ \end{gathered}$$
(20)

By replacing the X values and considering the dimensionless natural frequency coefficient, Ωi and dimensionless ratios defined as Eq. (20), the boundary conditions of Eqs. (16)–(19) can be expressed by the following non-dimensional forms:

$$W^{\prime\prime}_{i} (1) - \frac{{R_{0} }}{c}W^{\prime}_{i} (1) = 0,$$
(21)
$$W^{\prime\prime\prime}_{i} (1) + (p + 2)_{{}} W^{\prime\prime}_{i} (1) + \frac{{(T_{0} - \alpha_{0} \Omega_{i}^{4} )}}{{c^{3} }}W_{i} (1) = 0,$$
(22)
$$W^{\prime\prime}_{i} (1 + c) + \frac{{R_{L} }}{c}W^{\prime}_{i} (1 + c) = 0,$$
(23)
$$W^{\prime\prime\prime}_{i} (1 + c) + \frac{(p + 2)}{{(1 + c)}}W^{\prime\prime}_{i} (1 + c) + \frac{{(\alpha_{L} \Omega_{i}^{4} - T_{L} )}}{{c^{3} }}W_{i} (1 + c) = 0,$$
(24)

where \(W^{\prime}_{i} (X) = \frac{{dW_{i} (X)}}{dX}\), \(W^{\prime\prime}_{i} (X) = \frac{{d^{2} W_{i} (X)}}{{d^{2} X}}\), \(W^{\prime\prime\prime}_{i} (X) = \frac{{d^{3} W_{i} (X)}}{{d^{3} X}}\).

Determination of the Natural Frequency

By substituting the general solution (9) into the non-dimensional boundary conditions given in Eqs. (21)–(24), a homogeneous system of four equations for the four integration constants (i.e., C1, C2, C3, C4) can be obtained as:

$$\left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{13} } & {A_{14} } \\ {A_{21} } & {A_{22} } & {A_{23} } & {A_{24} } \\ {A_{31} } & {A_{32} } & {A_{33} } & {A_{34} } \\ {A_{41} } & {A_{42} } & {A_{43} } & {A_{44} } \\ \end{array} } \right]\left[ \begin{gathered} C_{1} \hfill \\ C_{2} \hfill \\ C_{3} \hfill \\ C_{4} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right],$$
(25)

or in compact matrix form as follows:

$${\text{AC}} = 0,$$
(26)

where the constant coefficients matrix A for the NAFG beams with the various gradient coefficient are given explicitly in Appendix B. To have a non-trivial solution, the determinant of this system must be zero:

$$\det {\text{A}} = 0.$$
(27)

Consequently, having the values of p, c, α0, αL, T0, TL, R0, and RL, positive real roots of this equation are the natural frequency coefficients Ωi of the NAFG beams with the end point masses and elastic end supports, shown in Fig. 3. It should be added, these were calculated numerically.

Numerical Examples and Verification

To confirm the accuracy, application, and efficiency of the derived formulations, five numerical examples, shown in Fig. 4a–e, are analyzed in this part. The results are compared with those obtained by other researchers. It should be noted, using the proposed formulations, one can find the exact natural frequencies of the NAFG beams with attached masses and general boundary conditions at both ends. Accordingly, if the stiffness ratios are allowed to become infinity or zero, then the classical restraints can be easily recovered. For example, if R0 = T0 = ∞ and RL = TL = 0, then the beam is considered as the cantilevered beam. If R0 = RL = 0 and T0 = TL = ∞, then the frequency equation of the simply supported beam is obtained. If R0 = RL = ∞ and T0 = TL = ∞, then the beam is considered as the clamped–clamped beam.

Fig. 4
figure 4

Schematic of the NAFG beams with end point masses and different boundary conditions in numerical examples

Full size image

Example 1. In this sample, the first five dimensionless natural frequency coefficients Ωi, i = 1,2,3,4,5 for the NAFG beam (p = 2, c = var. > 0) with T0 = R0 = αL = 0, TL = RL = ∞ and various values of α0 and c (i.e., Fig. 4a) are calculated and arranged in Table 1. Table 1 shows the results of the present study, as well as those other methods. Based on the data shown in Table 1, it is observed that the proposed formulation for computing the natural frequencies has high accuracy and efficiency.

Table 1 First five dimensionless natural frequency coefficients Ωi, i = 1,2,3,4,5 of the NAFG beam (p = 2, c = var. > 0) for T0 = R0 = αL = 0, TL = RL = ∞ and various values of α0 in Example 1
Full size table

Example 2. In this example, the first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 of the NAFG beam (p = 2, c = 0.4) for R0 = αL = 0, TL = RL = ∞ and various values of T0 and α0 (i.e., Fig. 4b) are computed and presented in Table 2. From Table 2, it is concluded that results of the present method are very close to the values obtained by other techniques.

Table 2 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 of the NAFG beam (p = 2, c = 0.4) for R0 = αL = 0, TL = RL = ∞ and various values of T0 and α0 in Example 2
Full size table

Example 3. In this sample, the first five natural frequencies ωi, i = 1,2,3,4,5 are obtained for the NAFG beam (p = 1, c = 4) with T0 = R0 = ∞, TL = RL = αL = 0 and α0 = 0.6 (i.e., Fig. 4c). It should be noted that the numerical values of the mechanical and geometrical properties of the NAFG beam considered as follows: L = 1.6 m, A0 = b0 × h0 = 0.1 × 0.08, I0 = b0 × h03/12 = 0.1 × 0.083/12, M0 = 60.288 kg, ρ0 = 7850 kg/m3, E0 = 2.051 × 1011 N/m2, α0 = 60.288/(7850 × 0.1 × 0.08 × 1.6) = 0.6, ρ0A0 = 7850 × 9.81 × 0.1 × 0.08 = 616.068 N/m, and E0I0 = 2.051 × 1011 × 0.1 × 0.083/12 = 875,093.3333 N m2 [25]. A comparison of the results with the other approaches is listed in Table 3. According to the findings, the prediction of the proposed technique agree well with those other approaches.

Table 3 First five natural frequencies ωi, i = 1,2,3,4,5 of the NAFG beam (p = 1, c = 4) for T0 = R0 = ∞, TL = RL = αL = 0 and α0 = 0.6 in Example 3
Full size table

Example 4. In this example, the first square six dimensionless natural frequency coefficients Ωi2, i = 1,2,3,4,5,6 of the NAFG beam (p = 0, c = − 0.25) for T0 = R0 = ∞, TL = RL = α0 = 0 and various values of αL (i.e., Fig. 4d) are obtained and arranged in Table 4. Table 4 shows the results of the present method, as well as the recent work of Mahmoud [60].

Table 4 First square six dimensionless natural frequency coefficients Ωi2, i = 1,2,3,4,5,6 of the NAFG beam (p = 0, c = − 0.25) for T0 = R0 = ∞, TL = RL = α0 = 0 and various values of αL in Example 4
Full size table

Example 5. In this sample, the first square three dimensionless natural frequency coefficients Ωi2, i = 1,2,3 are calculated for the NAFG beam (p = 1, c = var. < 0) with T0 = ∞, TL = RL = α0 = 0 and various values of R0, αL, and c (i.e., Fig. 4(e)). A comparison of the results with those computed by [34] is listed in Table 5. According to the results, the proposed approach gives a high accuracy prediction. Note that, in Table 5, the results from Çelik [69] are given in square brackets.

Table 5 First square three dimensionless natural frequency coefficients Ωi2, i = 1,2,3 of the NAFG beam (p = 1, c = var. < 0) for T0 = ∞, TL = RL = α0 = 0 and various values of R0 and αL in Example 5
Full size table

Parametric Studies and Discussion

In this section, eight parametric cases, as shown in Fig. 5a–h, with the classical and non-classical boundary conditions will be considered and the effects of the attached end masses, elastic supports, and NAFG parameters on the first four natural frequencies of them will be investigated comprehensively. It should be noted that the NAFG parameters in all cases, except case 8, are considered identical to compare the results of one case with other cases. In other words, in these cases, the dynamic behavior of the NAFG beams with p = 2 and c = 0.5 are studied.

Fig. 5
figure 5

Schematic of the NAFG beams with end point masses and different boundary conditions in parametric studies

Full size image

Effects of the End Mass with Different Elastic Boundary Conditions (Case 1 up to Case 6)

In Figs. 6 through 11, the effects of the end mass ratios (i.e., α0 and αL) with the various rotational and translational stiffness ratios (i.e., R0, T0, RL, and TL), on the first four dimensionless natural frequency coefficients Ωi (i = 1,2,3,4) for the NAFG beams (p = 2, c = 0.5) introduced as case 1 up to case 6 are investigated, respectively. Moreover, the corresponding numerical values of Ωi (i = 1,2,3,4) for these cases are tabulated in Tables 6 through 11, respectively.

Fig. 6
figure 6

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 1

Full size image
Fig. 7
figure 7

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 2

Full size image
Table 6 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 1
Full size table
Table 7 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 2
Full size table

Case 1

Based on data shown in Table 6, it is concluded that for the free supported NAFG beam with the translational spring at x = 0, rotational spring at x = L, and attached point mass at x = 0 (Fig. 5a), as the end mass ratio α0 increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 0.4930, 1.4212, 5.3358 and 8.7880, and tend to 0.4407, 1.1083, 4.4127 and 7.8922 for the low stiffness ratios (T0 = RL = 0.1), respectively. Also, for the moderate stiffness ratios (T0 = RL = 10) in case 1, increasing α0 from 0.0 to 1.0, causes reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 1.4040, 3.1853, 6.1207 and 9.4310, and approach 1.3233, 2.2333, 5.2170 and 8.5506, respectively. Furthermore, when the end mass ratio α0 in this case changes, the first four dimensionless natural frequency coefficients of the NAFG beam remain almost constant for the high stiffness ratios (T0 = RL = 105). In other words, this latter state corresponds to a pinned-guided beam, and evidently, the effect of α0 on the natural frequencies of the beam is very insignificant.

According to Fig. 6 and Table 6, it is observed that increasing the end mass ratio α0 always causes a decrease in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the stiffness ratios. On average and based on the amounts of Ωi (i = 1,2,3,4), Ω1 and Ω2, in this case, have the lowest and highest sensitivity to the variation of the end mass ratio, respectively. Accordingly, the second dimensionless natural frequency coefficient in case 1 can reduce by nearly 31% whenever the end mass ratio α0 increases from 0.0 to 1.0 for T0 = RL = 50. On the other hand, by increasing the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increases, irrespective of the amount of the end mass ratio. At the most sensitive state, increasing T0 and RL from the low stiffness ratios (T0 = RL = 0.1) to the high stiffness ratios (T0 = RL = 105) for α0 = 1.0, can raise the quantity of Ω2 for the NAFG beam in case 1 by about 4.8 times.

Case 2

By observing data in Table 7, it is founded that for the free-pinned supported NAFG beam with the translational spring at x = 0, rotational spring at x = L, and attached point mass at x = 0 (Fig. 5b), when the end mass ratio α0 increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 1.0869, 4.5849, 7.9935 and 11.4515, and tend to 0.8009, 3.7027, 7.1045 and 10.5630 for the low stiffness ratios (T0 = RL = 0.1), respectively. In addition, for the moderate stiffness ratios (T0 = RL = 10) in case 2, increasing α0 from 0.0 to 1.0, causes reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 2.7866, 5.2765, 8.4984 and 11.8510, and approach 1.9490, 4.3986, 7.6248 and 10.9774, respectively. Besides, as the end mass ratio α0 in this case varies, the first four dimensionless natural frequency coefficients of the NAFG beam stay almost constant for the high stiffness ratios (T0 = RL = 105). In other words, this latter state corresponds to a pinned-fixed beam, and clearly, the effect of α0 on the natural frequencies of the beam is very negligible.

As seen in Fig. 7 and Table 7, it is concluded that increasing the end mass ratio α0 always causes a decrease in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the stiffness ratios. On the average and about the quantities of Ωi (i = 1,2,3,4), changing of the end mass ratio α0 has the minimum and maximum influences on the values of Ω1 and Ω4 for this case, respectively. However, the second dimensionless natural frequency coefficient in case 2 can reduce by about 31% whenever the end mass ratio α0 increases from 0.0 to 1.0 for T0 = RL = 500. On the other hand, by increasing the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increases, irrespective of the value of the end mass ratio. At the most sensitive state, increasing T0 and RL from the low stiffness ratios (T0 = RL = 0.1) to the high stiffness ratios (T0 = RL = 105) for α0 = 1.0, can raise the quantity of Ω1 for the NAFG beam in case 2 by nearly 5.7 times.

Case 3

From data reported in Table 8, it is observed that for the free supported NAFG beam with two translational springs at x = 0 and x = L, and attached point mass at x = 0 (Fig. 5c), as the end mass ratio α0 increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 0.6808, 1.0411, 5.3058 and 8.7703, and tend to 0.5137, 0.9657, 4.3737 and 7.8723 for the low stiffness ratios (T0 = TL = 0.1), respectively. As well, for the moderate stiffness ratios (T0 = TL = 10) in case 3, increasing α0 from 0.0 to 1.0, causes reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 2.0948, 3.2328, 5.5103 and 8.8167, and approach 1.6202, 2.8681, 4.6347 and 7.9149, respectively. Moreover, when the end mass ratio α0 in this case changes, the first four dimensionless natural frequency coefficients of the NAFG beam remain almost constant for the high stiffness ratios (T0 = TL = 105). In other words, this latter state corresponds to a pinned–pinned beam, and obviously, the effect of α0 on the natural frequencies of the beam is very negligible.

Table 8 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 3
Full size table

From Fig. 8 and Table 8, it is concluded that increasing the end mass ratio α0 always causes decrease in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the amounts of the stiffness ratios. On the average and based on the amounts of Ωi (i = 1,2,3,4), Ω4 and Ω3 of this case have the lowest and highest sensitivity with respect to the variation of the end mass ratio, respectively. However, the second dimensionless natural frequency coefficient in the case 3 can reduce by nearly 28% whenever the end mass ratio α0 increases from 0.0 to 1.0 for T0 = TL = 100. On the other hand, by increasing in the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increase, irrespective of the value of the end mass ratio. At the most sensitive state, increasing T0 and TL from the low stiffness ratios (T0 = TL = 0.1) to the high stiffness ratios (T0 = TL = 105) for α0 = 1.0, can raise the quantity of Ω2 for the NAFG beam in case 3 by about 7.2 times.

Fig. 8
figure 8

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 3

Full size image

Case 4

Based on data shown in Table 9, it is founded the free-guided supported NAFG beam with two translational springs at x = 0 and x = L, and attached point mass at x = 0 (Fig. 5d), when the end mass ratio α0 increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 0.7864, 2.9795, 6.2937 and 9.7279, and tend to 0.6944, 2.1862, 5.4114 and 8.8400 for the low stiffness ratios (T0 = TL = 0.1), respectively. Also, for the moderate stiffness ratios (T0 = TL = 10) in case 4, increasing α0 from 0.0 to 1.0, causes reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 2.4178, 3.4960, 6.3757 and 9.7506, and approach 1.9114, 2.8715, 5.4761 and 8.8547, respectively. Furthermore, as the end mass ratio α0 in this case varies, the first four dimensionless natural frequency coefficients of the NAFG beam stay almost constant for the high stiffness ratios (T0 = TL = 105). In other words, this latter state corresponds to a pinned-fixed beam, and evidently, the effect of α0 on the natural frequencies of the beam is very insignificant.

Table 9 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 4
Full size table

According to Fig. 9 and Table 9, it is observed that increasing the end mass ratio α0 always causes a reduction in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the stiffness ratios. On the average and concerning the quantities of Ωi (i = 1,2,3,4), changing of the end mass ratio α0 has the minimum and maximum effects on the values of Ω4 and Ω2 for this case, respectively. Accordingly, the second dimensionless natural frequency coefficient in case 4 can reduce by about 28% whenever the end mass ratio α0 increases from 0.0 to 1.0 for T0 = TL = 500. On the other hand, by increasing the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increases, irrespective of the amount of the end mass ratio. At the most sensitive state, increasing T0 and TL from the low stiffness ratios (T0 = TL = 0.1) to the high stiffness ratios (T0 = TL = 105) for α0 = 1.0, can raise the quantity of Ω1 for the NAFG beam in case 4 by nearly 6.5 times.

Fig. 9
figure 9

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 4

Full size image

By comparing the results of Tables 6, 7, 8 and 9 (i.e., cases 1 to 4), it is concluded that the effect of the translational springs on the natural frequencies of the NAFG is more significant than the rotational springs, regardless of the attached tip mass. In other words, the sensitivity of the natural frequencies to the variation of the translational stiffness ratios is greater than the rotational stiffness ratios.

Case 5

By observing data in Table 10, it is founded that for the free supported NAFG beam with the translational and rotational springs at x = L, and attached point mass at x = 0 (Fig. 5e), as the end mass ratio α0 increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 0.7174, 1.4647, 5.3364 and 8.7881, and tend to 0.6026, 1.2149, 4.4150 and 7.8926 for the low stiffness ratios (RL = TL = 0.1), respectively. In addition, for the moderate stiffness ratios (RL = TL = 10) in case 5, increasing α0 from 0.0 to 1.0, causes reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 2.0450, 3.2691, 6.1357 and 9.4364, and approach 1.5175, 2.8583, 5.3094 and 8.5744, respectively. Besides, when the end mass ratio α0, in this case, increases from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 2.4937, 5.5291, 8.9233 and 12.3591, and tend to 1.6868, 4.6819, 8.0428 and 11.4774 for the high stiffness ratios (RL = TL = 105), respectively. This latter state corresponds to a free-clamped beam, and clearly, the effect of α0 on the natural frequencies of the beam is significant for this case.

Table 10 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 5
Full size table

As seen in Fig. 10 and Table 10, it is observed that increasing the end mass ratio α0 always causes a decrease in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the stiffness ratios. On average and based on the amounts of Ωi (i = 1,2,3,4), Ω4 and Ω1, in this case, have the lowest and highest sensitivity to the variation of the end mass ratio, respectively. Accordingly, the first dimensionless natural frequency coefficient in case 5 can reduce by nearly 32% whenever the end mass ratio α0 increases from 0.0 to 1.0 for RL = TL = 105. On the other hand, by increasing the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increases, irrespective of the value of the end mass ratio. At the most sensitive state, increasing RL and TL from the low stiffness ratios (RL = TL = 0.1) to the high stiffness ratios (RL = TL = 105) for α0 = 1.0, can raise the quantity of Ω2 for the NAFG beam in case 5 by about 3.9 times.

Fig. 10
figure 10

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 5

Full size image

Case 6

From data reported in Table 11, it is concluded that for the free supported NAFG beam with two translational springs and two attached point masses at x = 0 and x = L (Fig. 5f), as the end mass ratios α0 = αL increase from 0.0 up to 1.0, the first four dimensionless natural frequency coefficients of the NAFG beam decrease from 0.6808, 1.0411, 5.3058 and 8.7703, and tend to 0.5136, 0.7533, 3.8761 and 7.2400 for the low stiffness ratios (T0 = TL = 0.1), respectively. As well, for the moderate stiffness ratios (T0 = TL = 10) in case 6, increasing α0 = αL from 0.0 to 1.0, cause reduce in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 2.0948, 3.2328, 5.5103 and 8.8167, and approach 1.6197, 2.3621, 3.9183 and 7.2425, respectively. Moreover, when the end mass ratios α0 = αL in this case change, the first four dimensionless natural frequency coefficients of the NAFG beam remain almost constant for the high stiffness ratios (T0 = TL = 105). In other words, this latter state corresponds to a pinned–pinned beam, and obviously, the effect of α0 and αL on the natural frequencies of the beam are very negligible.

Table 11 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 6
Full size table

From Fig. 11 and Table 11, it is observed that increasing the end mass ratios α0 = αL always causes a reduction in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the stiffness ratios. On average and about the quantities of Ωi (i = 1,2,3,4), changing of the end mass ratios α0 = αL have the lowest and highest effect on the values of Ω1 and Ω3 in this case, respectively. Accordingly, the third dimensionless natural frequency coefficient in case 6 can reduce by nearly 33% whenever the end mass ratios α0 = αL increase from 0.0 to 1.0 for T0 = TL = 50. On the other hand, by increasing the stiffness ratios, Ωi (i = 1,2,3,4) of the beam always increases, irrespective of the values of the end mass ratios. At the most sensitive state, increasing T0 and TL from the low stiffness ratios (T0 = TL = 0.1) to the high stiffness ratios (T0 = TL = 105) for α0 = αL = 1.0, can raise the quantity of Ω2 for the NAFG beam in case 6 by about 9.3 times.

Fig. 11
figure 11

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 6

Full size image

Effects of the Symmetric Elastic Boundary Conditions with End Masses (Case 7)

The effects of the non-classical symmetric rotational and translational stiffness ratios (i.e., R0, T0, RL, and TL) with end mass ratios (i.e., α0 and αL), on the first four dimensionless natural frequency coefficients Ωi (i = 1,2,3,4) for the NAFG beam (p = 2, c = 0.5) introduced as case 7 are depicted in Fig. 12. Moreover, the corresponding numerical values of Ωi (i = 1,2,3,4) for this case are arranged in Tables 12.

Fig. 12
figure 12

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 7

Full size image
Table 12 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 7
Full size table

Based on data shown in Table 12, it is concluded for the symmetric elastic-supported NAFG beam with two translational and rotational springs at x = 0 and at x = L, and attached point masses at x = 0 and at x = L (Fig. 5g), when the all stiffness ratios R0 = T0 = RL = TL increase from 0.1 (corresponding to low stiffness) up to 105 (corresponding to high stiffness), the first four dimensionless natural frequency coefficients of the NAFG beam without end masses (i.e., α0 = αL = 0) increase considerably from 0.7735, 1.5413, 5.3511 and 8.7984, and tend to 5.2687, 8.7315, 12.2044 and 15.6604, respectively. Also, for the end mass ratios α0 = αL = 1.0 in case 7, increasing R0 = T0 = RL = TL from 0.1 to 105, cause raise in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 0.6266, 1.0391, 3.9183 and 7.2606, and approach 5.2687, 8.7309, 12.1974 and 15.5840, respectively. Note that, in Table 12, the results from [1] are given in square brackets.

According to Fig. 12 and Table 12, it is observed that increasing all stiffness ratios always causes an increase in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantities of the end mass ratios. Based on the slope of the Ωi–stiffness ratios curves, in this case, Ω4 and Ω1 have the lowest and highest sensitivity versus the simultaneous change of the stiffness ratios, respectively. Accordingly, increasing R0 = T0 = RL = TL from the low stiffness ratios (i.e., 0.1) to the high stiffness ratios (i.e., 105) for α0 = 1.0, can raise the quantity of Ω1 for the NAFG beam in case 7 by about 8.4 times. On the other hand, by increasing the end mass ratios, Ωi (i = 1,2,3,4) of the beam always decreases, irrespective of the amount of the stiffness ratios. On average, the first and second dimensionless natural frequency coefficients in case 7 have the lowest and highest variation versus the changing of the end mass ratios, respectively. At the most sensitive state, the quantity of Ω2 for the NAFG beam in the case 7 can reduce by nearly 33% whenever the end mass ratios α0 = αL increase from 0.0 to 1.0 for R0 = T0 = RL = TL = 0.1.

Effects of the NAFG Parameters with End Mass (Case 8)

In Figs. 13 and 14, changing of the first four dimensionless natural frequency coefficients Ωi (i = 1,2,3,4) for the NAFG beam introduced as case 8 to the variation of the NAFG parameters, namely, the gradient index p and gradient coefficient c are investigated, respectively. Moreover, in Tables 13 and 14, the corresponding numerical values of Ωi (i = 1,2,3,4) for this case are presented, respectively.

Fig. 13
figure 13

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 8 with c = 0.50

Full size image
Fig. 14
figure 14

Plot first four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 8 with p = 2

Full size image
Table 13 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 8 with c = 0.50
Full size table
Table 14 First four dimensionless natural frequency coefficients Ωi, i = 1,2,3,4 for Case 8 with p = 2
Full size table

By observing data in Table 13, it is founded that for the free-fixed supported NAFG beam with the translational and rotational springs at x = 0, and attached point mass at x = 0 (Fig. 5h), whereas the gradient index p increases from -1 up to 3, the first four dimensionless natural frequency coefficients of the NAFG beam without end masses (i.e., α0 = αL = 0) increase from 2.0836, 5.2238, 8.7390 and 12.2324, and tend to 2.6398, 5.6361, 8.9967 and 12.4216, respectively. In addition, for the end mass ratio α0 = 1.0 in case 8, increasing p from -1 to 3, causes an increase in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 1.3563, 4.4770, 7.9310 and 11.4057, and approach 1.8079, 4.7539, 8.0905 and 11.5185, respectively. Note that, in Table 13, the results from [1] are given in square brackets.

As seen in Fig. 13 and Table 13, it is observed that increasing the gradient index p always causes an increase linearly in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the quantity of the end mass ratio. This effect is more pronounced for the first natural frequency of the NAFG cantilever beam and negligible for the fourth natural frequency of one. In other words, based on the slope of the Ωi–p curves, in this case, Ω4 and Ω1 have the lowest and highest sensitivity concerning the change of the gradient index, respectively. Accordingly, the first dimensionless natural frequency coefficient in case 8 with c = 0.5, can increase by about 33% whenever the gradient index increases from -1 to 3 for α0 = 1.0. On the other hand, by increasing the mass ratio α0, Ωi (i = 1,2,3,4) of the beam always decreases, irrespective of the value of the gradient index. At the most sensitive state, increasing α0 from 0.0 to 1.0 for p = -1 can reduce the quantity of Ω1 for the NAFG beam in case 8 with c = 0.5 by nearly 35%.

From data reported in Table 14, it is observed that for the free-fixed supported NAFG beam with the translational and rotational springs at x = 0, and attached point mass at x = 0 (Fig. 5h), whenever the gradient coefficient c increases from − 0.50 up to 0.50, the first four dimensionless natural frequency coefficients of the NAFG beam without end masses (i.e., α0 = αL = 0) increase from 1.1393, 3.6311, 6.5187 and 9.2575, and tend to 2.4937, 5.5300, 8.9272 and 12.3697, respectively. As well, for the end mass ratio α0 = 1.0 in case 8, increasing c from -0.50 to 0.50, causes an increase in the values of Ωi (i = 1,2,3,4) of the NAFG beam from 0.7445, 3.1768, 5.9856 and 8.6900, and approach 1.6868, 4.6824, 8.0456 and 11.4859, respectively. Note that, in Table 14, the results from [1] are given in square brackets.

From Fig. 14 and Table 14, it is concluded that increasing the gradient coefficient c always causes an increase almost linearly in the values of Ωi (i = 1,2,3,4) for the beam, regardless of the amount of the end mass ratio α0. Based on the slope of the Ωi–c curves, in this case, Ω1 and Ω4 have the lowest and highest sensitivity versus the change of the gradient coefficient, respectively. Accordingly, the four dimensionless natural frequency coefficient in case 8 with p = 2 can increase by about 32% whenever gradient coefficient c increases from − 0.50 to 0.50 for α0 = 1.0. On the other hand, by increasing the mass ratio α0, Ωi (i = 1,2,3,4) of the beam always decreases, irrespective of the value of the gradient coefficient. At the most sensitive state, increasing α0 from 0.0 to 1.0 for c = − 0.50 can reduce the quantity of Ω1 for the NAFG beam in case 8 with p = 2 by nearly 35%. Moreover, it should be noted that for the same conditions and regardless of the amount of the end mass ratio α0, the natural frequencies of the NAFG cantilever beam with positive and negative gradient coefficient c always are greater and smaller than those of the uniform beam (i.e., c = 0), respectively.

By observing data in Tables 13 and 14 and according to graphs in Figs. 13 and 14, it is found that as the NAFG parameters increase, Ωi (i = 1,2,3,4) for the NAFG cantilever beam always increases. This influence is more considerable whenever the gradient coefficient c increases. In other words, the effect of the gradient coefficient c on the natural frequencies of the NAFG cantilever beam is more significant than the gradient index p. On the other hand, changing the value of c in lower frequencies is considerable while changing the value of p in higher frequencies is significant, irrespective of the amount of the end mass ratio α0. Furthermore, by increasing the mass ratio α0, Ωi (i = 1,2,3,4) of NAFG cantilever beams always decreases, irrespective of the values of NAFG parameters. This effect is more pronounced for the first natural frequency.

Conclusion

The objective of this paper was to present the analytical solutions for investigating the free transverse vibration and obtaining the exact natural frequencies of the power-law NAFG beams with attached end point masses and general boundary conditions. In this way, based on the Euler–Bernoulli beam theory, the governing differential equation of motion was solved accurately using the Bessel functions. Then, the constant coefficients matrices of the power-law NAFG beams for c > 0, c = 0, and c < 0, with the end point masses and general elastic supports were derived by applying the boundary conditions. Accordingly, by taking the constant coefficients matrix determinant equal to zero and calculating the positive real roots, the natural frequencies were obtained. By comparing the responses of the numerical examples with the available solutions, the accuracy, capability, and efficiency of the proposed formulations were demonstrated. Subsequently, the effects of the attached end point masses, rotational and translational elastic supports, and NAFG parameters on the values of the first four natural frequencies of the power-law NAFG beams for the eight parametric cases were studied comprehensively. The analytical solutions were presented in tabular and graphical forms and could be used as either the benchmark problems or proper design of the composite beams with attached end point masses and general boundary conditions.

Based on the results of this research, the following important points are concluded:

  • As the end point mass ratios increase, the natural frequencies of the power-law NAFG beam decrease. Among the cases studied, the natural frequency of the beam can reduce by up to 33% when the end point mass ratios increase.

  • The natural frequencies of the power-law NAFG beam increase, as the stiffness ratios increase. Among the cases studied, the natural frequency of the beam can rise by up to 9.3 times, when the stiffness ratios increase.

  • According to the slope of the Ω-α curves, the mass sensitivity differs from one power-law NAFG beam to another, and from one mode of vibration to another.

  • The sensitivity of the natural frequencies of the beam to the variation of the translational stiffness ratios is greater than the rotational stiffness ratios.

  • As the power-law NAFG parameters increase, the natural frequencies of the cantilever beam increase. Nevertheless, the effect of the gradient coefficient c on the natural frequencies of the beam is more significant than the gradient index p.