Multi-criteria decision-making based on intuitionistic fuzzy exponential knowledge and similarity measure and improved VIKOR method

Abstract

Atanassov intuitionistic fuzzy sets (AIFSs) are substantially more effective at capturing and processing uncertainty than fuzzy sets. More focus has been placed on the knowledge measure or uncertainty measure for building intuitionistic fuzzy sets. One such use is to solve multi-criteria decision-making issues. On the other hand, the entropy of intuitionistic fuzzy sets is used to measure a lot of uncertainty measures. Researchers have suggested many knowledge measures to assess the difference between intuitionistic fuzzy sets, but several of them produce contradictory results in practice and violate the fundamental axioms of knowledge measure. In this research, we not only develop a new AIF-exponential knowledge measure (AEKM) but also broaden the axiomatic description of the knowledge measure (KM) of the intuitionistic fuzzy set. Its usefulness and validity are evaluated using numerical examples. Additionally, the following four measures result from the suggested AIF-exponential knowledge measure (AEKM) are the AIF-exponential accuracy measure (AEAM), information measure (IM), similarity measure (SM), and dissimilarity measure (DSM). The validity of each of these measures is examined, and their characteristics are explained. The suggested accuracy measure is applied in the context of pattern recognition. To resolve a multi-criteria decision-making (MCDM) dilemma in an intuitionistic fuzzy environment, a modified Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) strategy based on the suggested similarity measure is provided. Choosing a suitable adsorbent for removing hexavalent chromium from wastewater is done using the described methodology.

1 Introduction

Researchers have created a wide range of useful tools and approaches to deal with uncertainty and imprecision in decision-making. Making decisions is a part of every aspect of daily life. In a perfect world, each piece of knowledge and information has a clear and distinct value to represent it. Unfortunately, the information we get is frequently poor, i.e., information with ambiguity (Keith and Ahner 2021; Dutt and Kurian 2013; Hariri et al. 2019), due to the unpredictability and complexity of practical application. How to efficiently interpret ambiguous information to increase decision-making efficiency is consequently a significant problem (Li et al. 2012b; Wang and Song 2018; Yager 2017; Zavadskas et al. 2017). Until Prof. Zadeh (1965) ground-breaking invention of fuzzy sets, probability theory was the only tool available to quantify uncertainty and imprecision. To specify the grades, the fuzzy set (Chen and Lee 2010; Chen and Wang 1995; Chen and Lee 2010; Chen et al. 2009, 2019; Chen and Jian 2017; Lin et al. 2006) and allots a membership function to each component of the entire cosmos set in the unit interval. However, the membership and non-membership functions in fuzzy sets are not mutually exclusive because hesitation degrees are present in many real-world circumstances. Many approaches have been put out at the moment to address this issue, including intuitionistic fuzzy sets (Atanassov and Stoeva 1986; Xu et al. 2008; Yager 2009), rough sets (Aggarwal 2017; Ayub et al. 2022; Wei and Liang 2019; Xue et al. 2022), witness theory (Yager 2018; Deng 2020; Ma et al. 2021) and R-number (Seiti et al. 2019, 2021). An extension of fuzzy sets (FSs), Atanassov intuitionistic fuzzy sets (AIFSs), stands out among them for its distinct benefit in handling uncertain information. The key difference between AIFSs and FSs is that AIFSs distinguish between an element’s membership and non-membership grade and more accurately capture hesitation in human conduct. As a result, AIFSs have become very well liked and are now used in a variety of sectors, including pattern categorization (Luo et al. 2018; Kumar and Kumar 2023; Zeng et al. 2022; Ejegwa and Ahemen 2023; Xiao 2019a), medical evaluation (Khatibi and Montazer 2009; Ejegwa et al. 2020; Garg and Kaur 2020), information fusion (Xu and Zhao 2016; Garg 2017; Yu 2013), and others (Gao et al. 2020; Mahanta and Panda 2021; Konwar and Debnath 2018; Rahman et al. 2021; Feng et al. 2018; Castillo and Melin 2022; Močkoř and Hỳnar 2021; Liu et al. 2020; Chen and Randyanto 2013; Zou et al. 2020; Meng et al. 2020; Zhang et al. 2020). For the fuzzy set’s entropy, which has been a focus of ongoing research. Since (Zadeh 1968) originally brought up fuzzy entropy, scientists have become fascinated with it. The fuzzy entropy axiom and its definition using the Shannon function (Shannon 1948) were put out by Termini and Luca (1972). Burillo and Bustince (1996) first axiomatically constructed the measure of intuitionistic entropy, which was only dependent on hesitation degree. In entropy, there are three primary structures that take into account uncertainty, hesitation, modelling of intuition, and the application of the Shannon entropy notion of probability and unreliability (Tran et al. 2022; Yu et al. 2022; Deng 2020). Many researchers comprising (Wang and Xin 2005; Song et al. 2017; Garg 2019) etc. focus on how an AIF-set’s entropy is defined. Accordingly, the notion of knowledge measure may be viewed as a complimentary concept for the total uncertainty measure instead of the entropy measure (Arya and Kumar 2021). So, instead of concentrating on the connection of entropy and knowledge measure in this paper, we build a new axiomatic framework inside the context of knowledge measure to address the issue that entropy is unable to tackle. Szmidt et al. carried out a ground-breaking investigation of the volume of knowledge that AIFSs transfer (Szmidt et al. 2014; Guo 2015; Wu et al. 2021, 2022; Gohain et al. 2021; Garg and Rani 2022b). The term "knowledge" indicates the information which is deemed helpful in a certain setting and is distinguished by consistency, accuracy, and originality. According to Guo (2015), Wang et al. (2018), Garg and Rani (2022a) and Mishra et al. (2021), it is not sufficient to assume that entropy and knowledge measure possess a confident logical basis when discussing AIFSs; rather, knowledge measure needs to be seen from several angles. While certain ideas support information content, many focus more on its intrinsic ambiguity (Nguyen 2015). According to the aforementioned ideas, there is no axiomatic theory of knowledge measure that combines information content with information clarity.

Guo and Xu (2019) highlight and show that, at the very least, information substance and information clarity are connected to AIFSs in the most recent paper findings. Das et al. (2016) discovered that each and every attribute’s weight were determined by applying the knowledge measure to tackle problems related to multi-criterion decision-making (MCDM). Additionally, Das et al. (2017) performed a thorough examination of the conceptual characterizations of AIF-information measures. In an MCDM problem, we look for a specific option from the available alternatives that satisfies the most set criteria. Several researchers have written about this topic, comprising (Hwang et al. 1981; Mareschal et al. 1984; Opricovic 1998; Yager 2020; Ohlan 2022; Gupta and Kumar 2022) and Arora and Naithani (2023). Every conclusion to an MCDM problem comes with a critical word, such as the weights of the criteria. We can decide which option is finest by utilising the weights for the justified criterion. There are various methods for calculating criteria weights. Opricovic (1998) proposed the VIKOR technique as a method for addressing MCDM problems, which can provide a compromise answer. In this method, the optimal alternative is chosen using an accurate assessment of "Closeness" to the perfect solution. Many studies expanded the conventional VIKOR methodology to address MCDM, MADM, and MCGDM issues. Sanayei et al. (2010) used the fuzzy VIKOR technique to tackle the vendor selection problem. Chang (2014) investigated a case to identify Taiwan’s top hospital. The VIKOR technique for choosing the plant’s site was expanded by Gupta et al. (2016). Using the VIKOR technique, Hu et al. (2020) ranked the medical professionals. A set of metrics was proposed by Badi and Abdulshahed (2021) to assess the long-term viability of the iron and steel sector in Libya using a basic AHP model. Initial Public Offerings (IPOs) in India should be ranked based on performance, according to Biswas and Joshi (2023). To determine the VIKOR approach’s highest group benefit and least individual remorse the majority of scientists utilised the distance measure. However, we employ the proposed similarity measure in the suggested method and the outcomes are very advantageous. The paper mentioned above indicates that there is still room for discussion regarding AIF-knowledge measures. A large number of studies linked to AIF-knowledge and information measures focuses largely on distinguishing between AIF-sets and its complementary. Nguyen (2015) invented this innovative method of studying AIF-knowledge measures, but more study is needed to improve it and create a useful measure that will determine every penny of knowledge of a particular AIF-set. Several important findings from the research on AIF-information and knowledge measures encounter various challenges and are unable to completely handle specific issues in intuitionistic fuzzy environments. In the current work, we describe an approach for solving MCDM issues using proposed AIF-exponential knowledge and similarity measures. Many useful findings on AIF-information measures may not fully resolve the decision-making issues and face many difficulties. Below are some motivating factors that encouraged us to conduct this study:

• Most AIF-knowledge and information measures fail to conform order necessary for linguistic analysis. On the other hand, the proposed AIF-exponential knowledge measure achieves preferred ranking (see Example 1).

• While computing uncertainty between various AIF-sets, most of the estimates of AIF-knowledge and information measurements that are reported in the literature yield ludicrous results (see Example 2).

• Most AIF-knowledge and information measures calculates identical criteria weights across numerous substitutes, whereas suggested AIF-exponential knowledge measure computes distinct criteria weights for various alternatives (see Example 3).

• In an intuitionistic fuzzy environment, a great deal of similarity and dissimilarity measures are unable to identify a pattern among the possible patterns. However, the suggested AIF-accuracy measure distinctly recognises the pattern among the given patterns (see Example 4).

In this paper, we suggested an efficient AIF-exponential knowledge measure based on these findings. The suggested AIF-exponential knowledge measure fixes all the issues with various measures that have been documented in the literature. It also offers correct results when dealing with ambiguity calculations, and attribute weights, and gives satisfactory results in linguistic comparisons. the following are the significant contribution of the present study:

• We present an AIF-exponential knowledge measure and discuss its properties.

• To demonstrate how the proposed AIF-knowledge measure improves upon some of the existing AIF-knowledge and information measures’ shortcomings, we give numerical examples.

• We developed novel accuracy, information, similarity, and dissimilarity measures in an intuitionistic context that is fuzzy depending on the suggested exponential knowledge measure. Additionally, some properties are covered.

• In pattern recognition, a suggested accuracy measure is employed. The effectiveness of the suggested accuracy measure in recognising patterns is shown through a comparison with other measures.

• A modified VIKOR strategy is provided for tackling an MCDM problem. In the suggested method, the proposed AIF-similarity is used instead of the distance measure.

• In the MCDM problem, we also demonstrate the effectiveness of the suggested method for choosing finest adsorbent to remove the hexavalent chromium from the wastewater.

The main points of this paper are in the following way: Sect. 1 detailed the main goal of this paper and relevant publications. The necessity for this study and its primary significance will be addressed. Numerous essential definitions are presented in Sect. 2. An AIF-exponential knowledge measure is proposed in Sect. 3 and its validity is examined. Its characteristics are discussed, and its comparison with numerous different measures are provided. On the basis of the suggested AIF-exponential knowledge measure, we constructed a total of four additional measures in Sect. 4. They are verified, and their characteristics are addressed. The suggested accuracy measure is contrasted to certain other pattern recognition measures that are already in use. Section 5 provides an updated VIKOR technique based on suggested similarity measure to resolve the MCDM problem. The suggested strategy is contrasted against previously proposed methods in the literature using a numerical instance to address the MCDM difficulties. Section 6 contains the conclusion and suggestions for additional research.

2 Preliminaries

Within this section, we briefly review some background material on AIF-sets to facilitate the presentation that follows.

Suppose that

$$\begin{aligned}{} & {} \Upsilon _{s} = \left\{ T = (t_1,t_2,t_3,...t_s)|\sum _{i=1}^{s} t_i = 1\ \textrm{where} \ 0\right. \nonumber \\{} & {} \left. \quad \le t_i\le 1\ \forall i = 1,2,...,s\right\} , \end{aligned}$$

(1)

is the collection of total probability distribution for $t\ge 2$.

The entropy measure defined by Shannon (1948) is

$$\begin{aligned} K(T) = -\sum _{i=1}^{s} t_i\ \textrm{log}\left( t_i\right) ; \end{aligned}$$

(2)

where $T\in \Upsilon _{s}$. The literature has demonstrated generalised entropies in a number of ways. Many fields, including finance, statistics, data mining, and computing, have discovered applications for Shannon entropy.

Rényi (1961) served as the foundation for Shannon entropy generalisation of order-$\gamma$, offered by

$$\begin{aligned} K_\gamma (T) = \dfrac{1}{1-\gamma }\log \left[ \sum _{i=1}^{s}\left( t_i\right) ^\gamma \right] , \gamma \ne 1,\gamma >0. \end{aligned}$$

(3)

Exponential entropy was proposed by Pal and Pal (1989, 1991) another measure based on these considerations is given by

$$\begin{aligned} A_X(T) = \sum _{i=1}^{s}t_i \left( e^{(1-t_i)}-1 \right) . \end{aligned}$$

(4)

Shannon’s Entropy is pointed out be advantaged over by the exponential entropy by these authors. For example, with regard to uniform probability distribution $T = \bigg (\dfrac{1}{t},\dfrac{1}{t},...,\dfrac{1}{t}\bigg )$ exponential entropy possesses fixed upper bound.

$$\begin{aligned} \lim _{t \rightarrow \infty } {A_X}\left( \dfrac{1}{t}, \dfrac{1}{t},...,\dfrac{1}{t}\right) = e-1; \end{aligned}$$

(5)

and that Shannon’s entropy does not in this instance. Termini and Luca (1972) defined fuzzy entropy for a fuzzy set ${\bar{G}}$ corresponding to Eq. (2) as

$$\begin{aligned} K({\bar{G}})= & {} -\dfrac{1}{t}\sum _{i=1}^{s}\left[ \mu _{{\bar{G}}}(z_i)\textrm{log}\left( \mu _{{\bar{G}}}(z_i)\right) \right. \nonumber \\{} & {} \left. + \left( 1-\mu _{{\bar{G}}}(z_i)\right) \textrm{log} \left( 1-\mu _{{\bar{G}}}(z_i)\right) \right] . \end{aligned}$$

(6)

A study on information measure on fuzzy sets was conducted by Bhandari and Pal (1993) giving some measure of fuzzy entropy. In accordance with Eq. (3), they have recommended the following action:

$$\begin{aligned} K_\gamma ({\bar{G}})= & {} -\dfrac{1}{(1-\gamma )}\sum _{i=1}^{s}\textrm{log}\nonumber \\{} & {} \left[ \mu _{{\bar{G}}}^\gamma (z_i) + \left( 1-\mu _{{\bar{G}}}(z_i)\right) ^\gamma \right] , \gamma \ne 1, \gamma >0. \end{aligned}$$

(7)

Definition 1

(Zadeh 1965) Consider a finite set $Z(\ne \phi )$. A fuzzy set ${\bar{G}}$ defined on Z is given by

$$\begin{aligned} {\bar{G}} = \left\{ <z_i,\mu _{{\bar{G}}}(z_i)>:z_i \in Z\right\} ; \end{aligned}$$

(8)

where $\mu _{{\bar{G}}}:Z\rightarrow [0,1]$ represents a membership function for ${\bar{G}}$.

Definition 2

(Atanassov and Stoeva 1986) Consider a finite set $Z(\ne \phi )$. An AIF-set G defined on Z is given by

$$\begin{aligned} G = \{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\}; \end{aligned}$$

(9)

where $\mu _{G}:Z\rightarrow [0,1]$ and $v_{G}:Z\rightarrow [0,1]$ are membership degree and non-membership degree respectively, with the condition

$$\begin{aligned} 0\le \mu _{G}(z_i) + v_{G}(z_i)\le i, \forall \ z_i\ \in Z. \end{aligned}$$

(10)

The hesitation degree of AIF-set G defined in Z is denoted by $(\pi _G)$ $\forall \ z_i\ \in Z,$ and the hesitation degree is calculated by the expression that follows:

$$\begin{aligned} \pi _G(z_i) = 1 - \mu _{G}(z_i) - v_{G}(z_i);\forall \ z_i\ \in Z. \end{aligned}$$

(11)

It is obvious that $\pi _G(z_i) \in [0,1]$ When $\pi _G(z_i) = 0$, the AIF-set degenerates into an ordinary fuzzy set. The greatest AIF-set is one in which each element’s values for the membership and non-membership functions are the same. In most AIF-sets, each element is referred to as an overlap member.

Note: In this work, we will refer to AIFS(Z) as a collection of all AIF-sets defined on Z.

Definition 3

For two AIF-set G and H in Z, the following relations can be defined by

$$\begin{aligned} G = \left\{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\right\} , \\ H = \left\{ <z_i,\mu _{H}(z_i),v_{H}(z_i)>:z_i \in Z\right\} , \end{aligned}$$

then the following are the fundamental AIF-set operations:

$$\begin{aligned} \begin{aligned} G\cap H&= \left\{<z_i,\textrm{min}\left( \mu _{G}(z_i),\mu _{H}(z_i)\right) ,\textrm{max}\left( v_{G}(z_i),v_{H}(z_i)\right) \right. \\&\left. \quad>:z_i \in Z\right\} ;\\ G\cup H&= \left\{<z_i,\textrm{max}\left( \mu _{G}(z_i),\mu _{H}(z_i)\right) ,\textrm{min}\left( v_{G}(z_i),v_{H}(z_i)\right) \right. \\&\left. \quad>:z_i \in Z\right\} ;\\ G^{c}&= \left\{ <z_i, v_{G}(z_i),\mu _{G}(z_i)>:z_i \in Z\right\} ;\\&G\subseteq H \Leftrightarrow {\left\{ \begin{array}{ll} \mu _{G}(z_i)\le \mu _{H}(z_i)\ \textrm{and}\ v_{G}(z_i)\ge v_{H}(z_i)\ \textrm{if}\ \mu _{G}(z_i)\le v_{H}(z_i),\\ \mu _{G}(z_i)\ge \mu _{H}(z_i)\ \textrm{and}\ v_{G}(z_i)\le v_{H}(z_i)\ \textrm{if}\ \mu _{G}(z_i)\ge v_{H}(z_i); \end{array}\right. }\\ {}&G = H \Leftrightarrow G\subseteq H\ \textrm{and}\ H\subseteq G. \end{aligned} \end{aligned}$$

(12)

Definition 4

(Szmidt and Kacprzyk 2001) The following four axioms must be met to define a function $L: AIFS(Z)\rightarrow [0,1]$ as an AIF-information measure:

• (L1) $L(G) = 0$ iff $\mu _{G}(z_i) = 0,$ $v_{G}(z_i) = 1$ or $\mu _{G}(z_i) = 1,$ $v_{G}(z_i) = 0$ $\forall \ z_i\in Z$, i.e., G is a least AIF-set.

• (L2) $L(G) = 1$ iff $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$, i.e., G is a most AIF-set.

• (L3) $L(G)\le L(H)$ iff $G\subseteq H.$

• (L4) $L(G) = L(G^c),$ where $G^c$ is the complement of G.

The Fuzziness of a fuzzy set is determined by the fuzzy entropy. A knowledge measure also establishes the overall amount of knowledge. Singh et al. (2019) claim that these two ideas complement one another.

Definition 5

(Singh et al. 2019) For a function $W: AIFS(Z)\rightarrow [0,1]$ to be considered an AIF-knowledge measure, it needs to meet the four axioms listed below:

• (W1) $W(G) = 1$ iff $\mu _{G}(z_i) = 0,$ $v_{G}(z_i) = 1$ or $\mu _{G}(z_i) = 1,$ $v_{G}(z_i) = 0$ $\forall \ z_i\in Z$, i.e., G is a least AIF-set.

• (W2) $W(G) = 0$ iff $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$, i.e., G is a most AIF-set.

• (W3) $W(G)\ge W(H)$ iff $G\subseteq H.$

• (W4) $W(G) = W(G^c),$ where $G^c$ is the complement of G.

Definition 6

(Hung and Yang 2004; Chen and Chang 2015) Assume G, H, I $\in AIFS(Z)$. The following four axioms must be satisfied for a mapping $A_{m}: AIFS(Z)\times AIFS(Z) \rightarrow [0,1]$ to qualify as an AIF-similarity measure:

• (A1) $0\le A_{m}(G,H)\le 1.$

• (A2) $A_{m}(G,H) = A_{m}(H,G)$.

• (A3) $A_{m}(G,H) = 1 \Leftrightarrow G = H.$

• (A4) $G\subseteq H\subseteq I,$ then $A_{m}(G,H)\ge A_{m}(G,I)$ and $A_{m}(H,I)\ge A_{m}(G,I).$

Definition 7

(Wang and Chang 2005) Let G, H, I $\in AIFS(Z)$. The following four axioms must be satisfied for a mapping $B_{m}: AIFS(Z)\times AIFS(Z) \rightarrow [0,1]$ to qualify as an AIF-dissimilarity measure:

• (B1) $0\le B_{m}(G,H)\le 1.$

• (B2) $B_{m}(G,H) = B_{m}(H,G)$.

• (B3) $B_{m}(G,H) = 0 \Leftrightarrow G = H.$

• (B4) $G\subseteq H\subseteq I,$ then $B_{m}(G,H)\le B_{m}(G,I)$ and $B_{m}(H,I)\le B_{m}(G,I).$

Definition 8

Let G, H $\in AIFS(Z)$. If a mapping $C_{m}: AIFS(Z)\times AIFS(Z) \rightarrow [0,1]$ satisfies all four of the following axioms, it is referred to as an accuracy measure in G w.r.t. H:

• (C1) $C_{m}(G,H)\in [0,1].$

• (C2) $C_{m}(G,H) = 0 \Leftrightarrow \mu _{G}(z_i) = v_{G}(z_i)$.

• (C3) $C_{m}(G,H) = 1$ if $\mu _{G}(z_i) = 0 = \mu _{H}(z_i),$ $v_{G}(z_i) = 1 = v_{H}(z_i)$ or $\mu _{G}(z_i) = 1 = \mu _{H}(z_i),$ $v_{G}(z_i) = 0 = v_{H}(z_i)$ $\forall \ z_i\in Z$, i.e., Both G and H are equal and least AIF-set.

• (C4) $C_{m}(G,H) = W(G)$ if G = H, where W(G) is knowledge measure.

Szmidt and Kacprzyk (1998) described a method for transforming AIF-sets into fuzzy sets, which is briefly detailed here.

Definition 9

(Szmidt and Kacprzyk 1998) Let G $\in AIFS(Z)$, then the membership function $\mu _{{\bar{G}}(z_i)}$ corresponding to fuzzy set ${\bar{G}}$ is given as follow

$$\begin{aligned} \begin{aligned} \mu _{{\bar{G}}}(z_i) =&\ \mu _{G}(z_i) + \dfrac{\pi _{G}(z_i)}{2};\\ {}&= \dfrac{\mu _{G}(z_i) + 1 - v_G(z_i)}{2}, \forall z_i \in Z. \end{aligned} \end{aligned}$$

(13)

3 Proposed intuitionistic fuzzy exponential knowledge measure

In this section, we construct a new AIF-exponential knowledge measure (AEKM) based on Pal and Pal (1989, 1991), fuzzy entropy measure as follows:

$$\begin{aligned} \begin{aligned} D_{H}^{I}(G)&= \dfrac{1}{s\left( 1 - e^{0.75}\right) }\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } \right. \\&\left. \quad - e^{0.75}\right] ; \end{aligned} \end{aligned}$$

(14)

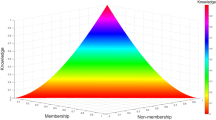
for some G $\in AIFS(Z)$. Figure 1 shows the entire amount of knowledge that the proposed AIF-knowledge measure was able to capture. Now, we investigate the validity of the suggested AEKM $D_{H}^{I}$.

Theorem 1

Suppose $G = \{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\}$ and $H = \{<z_i,\mu _{H}(z_i),v_{H}(z_i)>:z_i \in Z\}$ be the elements of AIFS(Z) for a finite set $Z(\ne \phi )$. Consider a mapping $D_{H}^{I}: AIFS(Z)\rightarrow [0,1]$ given in Eq. (14). Then $D_{H}^{I}$ is a valid AIF-exponential knowledge measure if it fulfils the following properties, (D1)–(D4):

(D1):

$D_{H}^{I}(G) = 1$ iff $\mu _{G}(z_i) = 0,$ $v_{G}(z_i) = 1$ or $\mu _{G}(z_i) = 1,$ $v_{G}(z_i) = 0$ $\forall \ z_i\in Z$, i.e., G is a least AIF-set.

(D2):

$D_{H}^{I}(G) = 0$ iff $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$, i.e., G is a most AIF-set.

(D3):

$D_{H}^{I}(G)\ge D_{H}^{I}(H)$ iff $G\subseteq H.$

(D4):

$D_{H}^{I}(G) = D_{H}^{I}(G^c),$ where $G^c$ is the complement of G.

Proof

(D1).:

First we suppose that $D_{H}^{I}(G) = 1$

$$\begin{aligned}{} & {} \begin{aligned} \Leftrightarrow&\dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] = 1, \end{aligned} \\{} & {} \begin{aligned} \Leftrightarrow&\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) }\right] = 1, \forall \ z_i\in Z, \end{aligned} \end{aligned}$$

$\Leftrightarrow$ $\mu _{G}(z_i) = 0,$ $v_{G}(z_i) = 1$ or $\mu _{G}(z_i) = 1,$ $v_{G}(z_i) = 0$ $\forall \ z_i\in Z$. This validates axiom (D1).

(D2).:

Let us take $D_{H}^{I}(G) = 0$. Then, from Eq. (14), we have

$$\begin{aligned} \begin{aligned}&\dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad - e^{0.75}\right] = 0, \end{aligned} \end{aligned}$$

which gives

$$\begin{aligned} \begin{aligned}&\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) }\right] \\&\quad = e^{0.75}, \forall \ z_i\in Z. \end{aligned} \end{aligned}$$

Thus, we get $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$. Conversely, Let $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$, then Eq. (14) implies $D_{H}^{I}(G) = 0$. This validates axiom (D2).

(D3).:

To validate this axiom, we must first demonstrate that function

$$\begin{aligned} \begin{aligned} g(c,d)&= \left[ \left( \dfrac{c + 1 - d}{2}\right) e^{\left( 1-\left( \dfrac{c + 1 - d}{2}\right) ^2\right) } \right. \\&\left. \quad + \left( \dfrac{1 + d - c}{2}\right) e^{\left( 1-\left( \dfrac{1 + d - c}{2}\right) ^2\right) } - e^{0.75}\right] , \end{aligned} \end{aligned}$$

(15)

is a function that increases with respect to d and decrease with respect to c, where c, d $\in [0,1]$. Differentiating function g partially with respect to c, we obtain

$$\begin{aligned} \begin{aligned}&\dfrac{\partial g(c,d)}{\partial c} = \left[ \frac{1}{2}e^{\left( 1-\left( \dfrac{c + 1 - d}{2}\right) ^2\right) } \right. \\&\left. \quad - \left( \dfrac{c + 1 - d}{2}\right) ^{2}e^{\left( 1-\left( \dfrac{c + 1 - d}{2}\right) ^2\right) }\right. \\&\left. - \frac{1}{2}e^{\left( 1-\left( \dfrac{1 + d - c}{2}\right) ^2\right) }\right. \\&\left. \quad + \left( \dfrac{1 + d - c}{2}\right) ^{2}e^{\left( 1-\left( \dfrac{1 + d - c}{2}\right) ^2\right) }\right] . \end{aligned} \end{aligned}$$

(16)

It is now possible to find critical points of c by entering

$$\begin{aligned} \dfrac{\partial g(c,d)}{\partial c} = 0; \end{aligned}$$

which gives c = d. Here, two cases are mentioned below:

$$\begin{aligned} \dfrac{\partial g(c,d)}{\partial c} = {\left\{ \begin{array}{ll} \textrm{positive}\ \textrm{if}\ c\ge d\\ \textrm{negative}\ \textrm{if}\ c\le d \end{array}\right. } \end{aligned}$$

(17)

i.e., function g is lowering function for $c \le d$ and raising function for $c\ge d$. Likewise, we possess

$$\begin{aligned} \dfrac{\partial g(c,d)}{\partial c} = {\left\{ \begin{array}{ll} \textrm{negative}\ if\ c\ge d\\ \textrm{positive}\ if\ c\le d \end{array}\right. } \end{aligned}$$

(18)

i.e., function g is lowering function for $c \le d$ and raising function for $c\ge d$. Now, take G, H $\in$ AIFS(Z) s.t. $G\subseteq H$. Let $Z_1$ and $Z_2$ are two partitions of Z s.t. Z = $Z_1 \cup Z_2$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{G}(z_i)\le \mu _{H}(z_i) \le v_{G}(z_i)\le v_{G}(z_i) \forall z_i \in Z_1,\\ \mu _{G}(z_i)\ge \mu _{H}(z_i) \le v_{G}(z_i)\ge v_{G}(z_i) \forall z_i \in Z_2.\\ \end{array}\right. } \end{aligned}$$

Thus function g is monotonic and because of Eq. (14), it is thus simple to demonstrate that $D_{H}^{I}(G)\ge D_{H}^{I}(G)$. This validates axiom (D3).

(D4).:

It is simple to observe that

$$\begin{aligned} G^{c} = \left\{ <z_i, v_{G}(z_i),\mu _{G}(z_i)>:z_i \in Z\right\} , \end{aligned}$$

i.e., $\mu _{G^c}(z_i) = v_{G}(z_i)$ and $\mu _{G}(z_i) = v_{G^c}(z_i)$ $\forall z_i \in Z$. Thus, from Eq. (14), we get $D_{H}^{I}(G) = D_{H}^{I}(G^c)$. This validates axiom (D4). As a result, $D_{H}^{I}(G)$ is an accurate AIF-exponential knowledge measure.

Fig. 1

Proposed AIF-exponential knowledge measure

3.1 Properties

In this part, we examine the features of the proposed exponential knowledge measure $D_{H}^{I}(G)$.

Theorem 2

The suggested AIF-exponential knowledge measure $D_{H}^{I}(G)$ satisfies some of the following characteristics.

• (1) $D_{H}^{I}(G)$ attains its highest value for least AIF-set G and attains its lowest value for most AIF-set G.

• (2) $D_{H}^{I}(G\cup H)$ + $D_{H}^{I}(G\cap H)$ = $D_{H}^{I}(G)$ + $D_{H}^{I}(H)$ for any two arbitrary AIF-sets G, H.

• (3) $D_{H}^{I}(G)$ = $D_{H}^{I}(G^c)$.

Proof

• (1). Proof is obvious from axioms (D1) and (D2).

• (2). Let G, H $\in AIF S(Z).$ Divide Z into two parts as follows:

  $$\begin{aligned} Z_1 = \{z_i \in \ Z|G\subseteq H \}, Z_2 = \{z_i \in \ Z|H\subseteq G \}, \end{aligned}$$

  (19)

  i.e.,

  $$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{G}(z_i)\le \mu _{H}(z_i) \le v_{G}(z_i)\le v_{G}(z_i) \forall z_i \in Z_1,\\ \mu _{G}(z_i)\ge \mu _{H}(z_i) \le v_{G}(z_i)\ge v_{G}(z_i) \forall z_i \in Z_2,\\ \end{array}\right. } \end{aligned}$$

  where $\mu _{G}(z_i)$ and $\mu _{H}(z_i)$ are the membership functions and $v_{G}(z_i)$ and $v_{H}(z_i)$ are the non-membership functions for AIF-set G and H, respectively. Now, $\forall z_i \in Z,$

  $$\begin{aligned} \begin{aligned}&D_{H}^{I}(G\cup H) + D_{H}^{I}(G\cap H) = \dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G\cup H}(z_i) + 1 - v_{G\cup H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{G\cup H}(z_i) + 1 - v_{G\cup H}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad + \left( \dfrac{1 + v_{G\cup H}(z_i) - \mu _{G\cup H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G\cup H}(z_i) - \mu _{G\cup H}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \\&\quad + \dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G\cap H}(z_i) + 1 - v_{G\cap H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{G\cap H}(z_i) + 1 - v_{G\cap H}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad + \left( \dfrac{1 + v_{G\cap H}(z_i) - \mu _{G\cap H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G\cap H}(z_i) - \mu _{G\cap H}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \end{aligned} \end{aligned}$$

  which gives

  $$\begin{aligned} \begin{aligned}&\quad D_{H}^{I}(G\cup H) + D_{H}^{I}(G\cap H) = \dfrac{1}{s(1 - e^{0.75})}\sum _{Z_1}\left[ \left( \dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \\&\quad + \dfrac{1}{s(1 - e^{0.75})}\sum _{Z_2}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad +\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \\&\quad + \dfrac{1}{s(1 - e^{0.75})}\sum _{Z_2}\left[ \left( \dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad + \left( \dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \\&\quad + \dfrac{1}{s(1 - e^{0.75})}\sum _{Z_1}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. \quad + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] . \end{aligned} \end{aligned}$$

  On solving, we get

  $$\begin{aligned} D_{H}^{I}(G\cup H) + D_{H}^{I}(G\cap H) = D_{H}^{I}(G) + D_{H}^{I}(H). \end{aligned}$$

  (20)

• (3). Proof is obvious from axioms (D4).

3.2 Comparison analysis

We now compare the proposed AIF-exponential knowledge measure to the other currently in use measures. Using a comparison, the benefits of novel knowledge measure are investigated. We look into these benefits with respect to the manipulation of structured linguistic variables, the estimate of characteristics weights within MCDM problems, as well as the assessment of ambiguity content of AIF-sets. Some of the available measures in literature are (Zeng and Li 2006; Burillo and Bustince (1996; Szmidt and Kacprzyk 2001; Hung and Yang 2006; Zhang and Jiang 2008; Li et al. 2012a; Bajaj et al. 2012; Szmidt et al. 2014; Nguyen 2015; Guo 2015)

$$\begin{aligned} L_{LZ}(G)= & {} 1 - \dfrac{1}{s}\sum _{i=1}^{s}\left| \mu _{G}(z_i) - v_{G}(z_i)\right| ; \end{aligned}$$

(21)

$$\begin{aligned} L_{BB}(G)= & {} \dfrac{1}{s}\sum _{i=1}^{s}\left| 1 - \mu _{G}(z_i) - v_{G}(z_i)\right| ; \end{aligned}$$

(22)

$$\begin{aligned} L_{KS}(G)= & {} \dfrac{1}{s}\sum _{i=1}^{s}\dfrac{\textrm{min}(\mu _{G}(z_i), v_{G}(z_i))+ \pi _{G}(z_i)}{\textrm{max}(\mu _{G}(z_i), v_{G}(z_i))+ \pi _{G}(z_i)}; \end{aligned}$$

(23)

$$\begin{aligned} L_{YH}(G)= & {} \dfrac{1}{s}\sum _{i=1}^{s}(1 - \mu _{G}^{2}(z_i) - v_{G}^{2}(z_i) - \pi _{G}^{2}(z_i)); \end{aligned}$$

(24)

$$\begin{aligned} L_{JZ}(G)= & {} \dfrac{1}{s}\sum _{i=1}^{s}\dfrac{\textrm{min}(\mu _{G}(z_i), v_{G}(z_i))}{\textrm{max}(\mu _{G}(z_i), v_{G}(z_i))}; \end{aligned}$$

(25)

$$\begin{aligned} L_{L}^{q}(G)= & {} 1 - \dfrac{1}{2s}\sum _{i=1}^{s}(|\mu _{G}(z_i) - v_{G}(z_i)|^{q} + |\mu _{G}(z_i) - v_{G}(z_i)|^{3q}),q>0; \end{aligned}$$

(26)

$$\begin{aligned} L_{J}^{y}(G)= & {} \dfrac{y}{s(1 - y)}\sum _{i=1}^{s}(1 - (\mu _{G}^{y}(z_i) + v_{G}^{y}(z_i) + \pi _{G}^{y}(z_i))^{\frac{1}{y}}); \end{aligned}$$

(27)

$$\begin{aligned} W_{S}(G)= & {} 1 - \dfrac{1}{2s}\sum _{i=1}^{s}\left[ \dfrac{\textrm{min}(\mu _{G}(z_i), v_{G}(z_i))+ \pi _{G}(z_i)}{\textrm{max}(\mu _{G}(z_i), v_{G}(z_i))+ \pi _{G}(z_i)} + \pi _{G}(z_i)\right] ; \end{aligned}$$

(28)

$$\begin{aligned} W_{N}(G)= & {} \dfrac{1}{s\sqrt{2}}\sum _{i=1}^{s}\sqrt{\mu _{G}^{2}(z_i) + v_{G}^{2}(z_i) + (\mu _{G}(z_i) + v_{G}(z_i))^{2}}; \end{aligned}$$

(29)

$$\begin{aligned} W_{U}(G)= & {} 1 - \dfrac{1}{2s}\sum _{i=1}^{s}(1 - |\mu _{G}(z_i) \nonumber \\{} & {} \quad - v_{G}(z_i)|)(1 + \pi _{G}(z_i)); \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \begin{aligned} D_{H}^{I}(G)&= \dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } \right. \\&\left. \quad - e^{0.75}\right] ; \end{aligned} ({proposed \,one}). \end{aligned}$$

(31)

3.2.1 Linguistic computation

Linguistic variables are described by the idea of an AIF-set, and actions on an AIF-Set are expressed using linguistic hedges. "MORE”, ”LESS”, ”VERY”, ”FEW”, ”SLIGHTLY”, and ”LESS” are examples of linguistic hedges that are used to represent linguistic variables. In this case, we explored these linguistic hedges and evaluated the effectiveness of the proposed AIF-exponential knowledge measure in comparison to current measures.

Let us take an AIF-set $G = \{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\}$ defined on a finite set $Z(\ne \phi )$ and regard this AIF-set as ”Large” on Z. For $p>0$, De et al. (2000) define the trait of AIF-set G as follow

$$\begin{aligned} G^{p} = \left\{ <z_i,(\mu _{G}(z_i))^{p},1-(1-v_{G})^{p}(z_i)>:z_i \in Z\right\} . \end{aligned}$$

(32)

De et al. (2000) defines the dilation and concentrate for an AIF-set G by

$$\begin{aligned} \begin{aligned}&CO(G) = G^{2},\\ {}&DI(G) = G^{0.5}. \end{aligned} \end{aligned}$$

(33)

Concentration and dilatation are used for trait. We abbreviate the following words for simplicity: L refers to LARGE, V.L. refers to VERY LARGE, L.L. refers to LESS LARGE, Q.V.L. refers to QUITE VERY LARGE and V.V.L. refers to VERY VERY LARGE. The following describes the hedges for AIF-set G:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{L.L.\ stands\ for}\ G^{0.5}\\ \mathrm{L\ stands\ for}\ G\\ \mathrm{V.L.\ stands\ for}\ G^{2}\\ \mathrm{Q.V.L.\ stands\ for\ G}^{3}\\ \mathrm{V.V.L.\ stands\ for\ G}^{4} \\ \end{array}\right. } \end{aligned}$$

(34)

It seems logical that as we move from set $G^{0.5}$ to set $G^{4}$, the quantity of knowledge they express would increase and the uncertainty hidden in them will diminish. information measure L(G) of an AIF-set G has to fulfil the following standards for optimal performance:

$$\begin{aligned} L(\mathrm{V.V.L.})< L(\mathrm{Q.V.L.})< L(\mathrm{V.L.})< L(\textrm{L}) < (\mathrm{L.L.}); \end{aligned}$$

(35)

where L(G) is the information measure of an AIF-set G. However, a knowledge measure must meet the following requirements:

$$\begin{aligned} W(\mathrm{V.V.L.})> W(\mathrm{Q.V.L.})> W(\mathrm{V.L.})> W(\textrm{L}) > W(\mathrm{L.L.}); \end{aligned}$$

(36)

where W(G) is KM of AIF-set G.

Now, to evaluate the effectiveness of the proposed AEKM $D_{H}^{I}(G)$, We utilise the subsequent instance:

Example 1

Let $Z = \{z_i,1\le i\le 5\}$ and Let G be an AIF-set that is defined on Z in the following manner:

$$\begin{aligned} G= & {} \left\{ (z_1,0.105,0.809),(z_2,0.297,0.492),(z_3,0.509,0.482),\right. \nonumber \\{} & {} \left. \quad (z_4,0.906,0.005),(z_5,0.997,0.001)\right\} . \end{aligned}$$

(37)

Using an AIF-set ”G” on Z as ”LARGE” and assuming the linguistic variables in accordance with Eq. (34). We may create the following AIF-sets using Eq. (32).

$$\begin{aligned} \begin{aligned} G^{0.5}&= \{(z_1,0.3240,0.5630),(z_2,0.5450,0.2873),(z_3,0.7134,0.2803),\\&\quad (z_4,0.9518,0.0025),(z_5,0.9985,0.0005)\};\\ G&= \{(z_1,0.1050,0.8090),(z_2,0.2970,0.4920),(z_3,0.5090,0.4820),\\&\quad (z_4,0.9060,0.0050),(z_5,0.9970,0.0010)\};\\ G^{2}&= \{(z_1,0.0110,0.9635),(z_2,0.0882,0.7419),(z_3,0.2591,0.7317),\\&\quad (z_4,0.8208,0.0100),(z_5,0.9940,0.0020)\};\\ G^{3}&= \{(z_1,0.0012,0.9930),(z_2,0.0262,0.8689),(z_3,0.1319,0.8610),\\&\quad (z_4,0.7437,0.0149),(z_5,0.9910,0.0030)\};\\ G^{4}&= \{(z_1,0.0001,0.9987),(z_2,0.0078,0.9334),(z_3,0.0671,0.9280),\\&\quad (z_4,0.6738,0.0199),(z_5,0.9881,0.0040)\}. \end{aligned} \end{aligned}$$

(38)

We now contrasted the effectiveness of the suggested AEKM with that of other measures that have been previously discussed in the literature. Table 1 compares and illustrates the values of the suggested AIF-exponential knowledge measure with those of the existing measures.

Table 1 Comparison between the proposed AIF-exponential knowledge measure and several existing measures

From Table 1, the following observations are drawn:

$$\begin{aligned} \begin{aligned}&L_{LZ}(\mathrm{V.V.L.})<L_{LZ}(\mathrm{Q.V.L.})<L_{LZ}(V.L.)<L_{LZ}(L)>L_{LZ}(\mathrm{L.L.});\\ {}&L_{BB}(\mathrm{V.V.L.})>L_{BB}(\mathrm{Q.V.L.})<L_{BB}(V.L.)<L_{BB}(L)>L_{BB}(\mathrm{L.L.});\\ {}&L_{KS}(\mathrm{V.V.L.})<L_{KS}(\mathrm{Q.V.L.})<L_{KS}(V.L.)<L_{KS}(L)>L_{KS}(\mathrm{L.L.});\\ {}&L_{YH}(\mathrm{V.V.L.})<L_{YH}(\mathrm{Q.V.L.})<L_{YH}(V.L.)<L_{YH}(L)<L_{YH}(\mathrm{L.L.});\\ {}&L_{JZ}(\mathrm{V.V.L.})<L_{JZ}(\mathrm{Q.V.L.})<L_{JZ}(V.L.)<L_{JZ}(L)>L_{JZ}(\mathrm{L.L.});\\ {}&L_{L}^{3}(\mathrm{V.V.L.})<L_{L}^{3}(\mathrm{Q.V.L.})<L_{L}^{3}(V.L.)<L_{L}^{3}(L)>L_{L}^{3}(L.L.);\\ {}&L_{J}^{5}(\mathrm{V.V.L.})<L_{J}^{5}(\mathrm{Q.V.L.})<L_{J}^{5}(V.L.)<L_{J}^{5}(L)>L_{J}^{5}(L.L.);\\ {}&W_{S}(\mathrm{V.V.L.})>W_{S}(\mathrm{Q.V.L.})>W_{S}(\mathrm{V.L.})>W_{S}(L)<W_{S}(\mathrm{L.L.});\\ {}&W_{N}(\mathrm{V.V.L.})>W_{N}(\mathrm{Q.V.L.})>W_{N}(\mathrm{V.L.})>W_{S}(L)<W_{N}(\mathrm{L.L.});\\ {}&W_{U}(\mathrm{V.V.L.})>W_{U}(\mathrm{Q.V.L.})>W_{U}(\mathrm{V.L.})>W_{U}(L)<W_{U}(\mathrm{L.L.});\\ {}&D_{H}^{I}(\mathrm{V.V.L.})>D_{H}^{I}(\mathrm{Q.V.L.})>D_{H}^{I}(\mathrm{V.L.})>D_{H}^{I}(L)>D_{H}^{I}(L.L.).\\ {}&\end{aligned} \end{aligned}$$

(39)

Now, we discovered that not a single knowledge and information measure, with the exception of $L_{YH}(G)$ and $D_{H}^{I}(G)$, match the order suggested by Eqs. (35) and (36). It implies that they are not doing well. Next, we just compare IM $L_{YH}(G)$ and KM $D_{H}^{I}(G)$.

We utilise another AIF-set made by

$$\begin{aligned} G= & {} \left\{ (z_1,0.110,0.798),(z_2,0.280,0.502),(z_3,0.475,0.423),\right. \nonumber \\{} & {} \left. \quad (z_4,0.920,0.019),(z_5,0.981,0.005)\right\} . \end{aligned}$$

(40)

The calculated observed values are shown in Table 2, and the following results are drawn from it:

Table 2 Calculated values for the measures specified in Eq. (24) and (31)

$$\begin{aligned} \begin{aligned}&L_{YH}(\mathrm{V.V.L.})<L_{YH}(\mathrm{Q.V.L.})<L_{YH}(\mathrm{V.L.})<L_{YH}(L)>L_{YH}(\mathrm{L.L.});\\&D_{H}^{I}(\mathrm{V.V.L.})>D_{H}^{I}(\mathrm{Q.V.L.})>D_{H}^{I}(\mathrm{V.L.})>D_{H}^{I}(L)>D_{H}^{I}(\mathrm{L.L.}). \end{aligned} \end{aligned}$$

(41)

In this instance, we can observe that the information measure does not follow the sequence given by Eq. (35). However, the proposed knowledge measure is ordered correctly. As a result, the efficiency of the suggested knowledge measure is quite astounding.

3.2.2 Ambiguity calculation

Different amounts of ambiguity exist between two distinct AIF-sets. On the other hand, certain KM offer the identical ambiguity values that correspond to different AIF-sets. To generalise previously established knowledge measures, a new knowledge measure is needed. The example below shows how the suggested measure works effectively.

Example 2

Define a set $Z = \{z_1,z_2,z_3,z_4\}$ and take $G_1,\ G_2,\ G_3,\ G_4\ \in AIFS(Z)$ as follows:

$$\begin{aligned} \begin{aligned} G_1&= \left\{ (z_1,0.423,0.529),(z_2,0.219,0.421),\right. \\&\left. \quad (z_3,0.231,0.480),(z_4,0.421,0.368)\right\} ;\\ G_2&= \left\{ (z_1,0.320,0.480),(z_2,0.410,0.390),\right. \\&\left. \quad (z_3,0.480,0.320),(z_4,0.319,0.481)\right\} ;\\ G_3&= \left\{ (z_1,0.623,0.077),(z_2,0.619,0.080),\right. \\&\left. \quad (z_3,0.613,0.065),(z_4,0.725,0.002)\right\} ;\\ G_4&= \left\{ (z_1,0.423,0.019),(z_2,0.214,0.523),\right. \\&\left. \quad (z_3,0.329,0.112),(z_4,0.298,0.397)\right\} . \end{aligned} \end{aligned}$$

(42)

We now use various previously published KM and proposed KM to determine the uncertain content of provided AIF-sets. The calculated values are shown in Table 3.

Table 3 Calculation of ambiguity for various AIF-sets defined in Example 2

Table 3 shows that for different AIF-sets, as determined by the existing knowledge measure, the ambiguity content is same. However, the suggested knowledge measure effectively differentiates these AIF-sets.

3.2.3 Assessing attribute weights

In an MCDM situation, the attribute weights play a vital role. Here, attribute weights are calculated use both of the previously established measures and the suggested measure. Here’s an example to illustrate this.

Example 3

Consider a matrix of decisions Z with the set of choices $\{U_1,\ U_2,\ U_3,\ U_4\}$ and set of attributes $\{P_1,\ P_2,\ P_3,\ P_4\}$ developed in an intuitionistic fuzzy environment.

$$\begin{aligned} N = \begin{bmatrix}<0.623,0.077> &{}<0.320,0.480> &{}<0.423,0.019> &{}<0.423,0.529> \\<0.619,0.080> &{}<0.410,0.390> &{}<0.214,0.523> &{}<0.219,0.421> \\<0.613,0.065> &{}<0.480,0.320> &{}<0.329,0.112> &{}<0.231,0.480> \\<0.725,0.002> &{}<0.480,0.320> &{}<0.329,0.112> &{} <0.231,0.480> \\ \end{bmatrix} \end{aligned}$$

The attribute weights are determined using one of the following two methods: (1) entropy-based method: The following formula may be used to determine the weights associated with certain attributes:

$$\begin{aligned} w_j = \dfrac{1 - L(P_j)}{\sum _{j=1}^{t}s-L(P_j)}, j = 1,2,3...s, \end{aligned}$$

(43)

where L denotes information measure corresponding to an AIF-set.

(2) Knowledge-based method: The following formula may be used to determine the weights associated with certain attributes:

$$\begin{aligned} w_j = \dfrac{W(P_j)}{\sum _{j=1}^{t}W(P_j)}, j = 1,2,3...s, \end{aligned}$$

(44)

where W represents the KM associated with an AIF-set.

In this example, we only employ weights that are determined by knowledge measures. Table 4 contains the calculated attribute weights.

Table 4 Assigns weights in accordance with Example 3

Table 4 demonstrates how the attribute weights of some of the available knowledge measures are inconsistent. There are instances where the weights given to certain attributes match. However, the suggested knowledge measure assigns distinct weights to distinct attributes. Consequently, an entirely novel measure for AIF-sets needs to be developed.

4 Deduction

More measures that are generated from the proposed AIF-exponential knowledge measure are suggested in this section.

4.1 Novel AIF-accuracy measure (AEAM)

It is possible to assess the amount of intuitionistic fuzzy knowledge with the amount of intuitionistic fuzzy accuracy. While evaluating the accuracy of one AIF-set H in relation to another AIF-set G, the concept of AIF-accuracy measure is applied. Verma and Sharma (2014) developed the notion of an AIF-set inaccuracy measure derived from fuzzy arrays and gave rise to the following intuitionistic fuzzy Inaccuracy measure:

$$\begin{aligned} I(G,H)= & {} -\dfrac{1}{s}\sum _{i=1}^{s}\left[ \mu _{G}log\left( \dfrac{\mu _{G} + \mu _{H}}{2}\right) + v_{G}log\left( \dfrac{v_{G} + v_{H}}{2}\right) \right. \nonumber \\{} & {} \left. + \pi _{G}log\left( \dfrac{\pi _{G} + \pi _{H}}{2}\right) - \pi _{G}log\pi _{G} - (1-\pi _{G})log(1-\pi _{G}) - \pi _{G}\right] , \end{aligned}$$

(45)

where G,H $\in AIFS(Z).$

Now, corresponding to proposed AIF-exponential knowledge measure $D_{H}^{I}(G)$, we define a new AIF-accuracy measure $D_\textrm{accy}^{I}(G,H)$ of AIF- set H w.r.t. AIF-set G as follows:

$$\begin{aligned} \begin{aligned}&D_\textrm{accy}^{I}(G,H) = \dfrac{1}{2s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. \quad e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] \\&+ \dfrac{1}{2s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \sqrt{\Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\Bigg )}\right. \\&\left. \times e^{\Bigg (1-\Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\Bigg )\Bigg )} \right. \\&\left. \quad + \sqrt{\Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\Bigg )}\right. \\&\left. \times e^{\Bigg (1-\Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\Bigg ) \Bigg )} - e^{0.75}\right] . \end{aligned} \end{aligned}$$

(46)

Now, we look at the validity of the suggested accuracy measure $D_\textrm{accy}^{I}$.

Theorem 3

Let $G = \{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\}$ and $H = \{<z_i,\mu _{H}(z_i),v_{H}(z_i)>:z_i \in Z\}$ are two elements of AIFS(Z) for a finite set $Z(\ne \phi )$. Consider a mapping $D_\textrm{accy}^{I}: AIFS(Z)\times AIFS(Z)\rightarrow [0,1]$ provided in Eq. (46). Thus, $D_\textrm{accy}^{I}(G,H)$ is a legitimate AIF-exponential accuracy measure if it meets the conditions listed below, (E1)–(E4):

(E1):

$D_\textrm{accy}^{I}(G,H) = 1$ if $\mu _{G}(z_i) = \mu _{H}(z_i) = 0,$ $v_{G}(z_i) = v_{H}(z_i) = 1$ or $\mu _{G}(z_i) = \mu _{H}(z_i) = 1,$ $v_{G}(z_i) = v_{H}(z_i) = 0$ $\forall \ z_i\in Z$, i.e., G and H both are equal least AIF-set.

(E2):

$D_{accy}^{I}(G,H) = 0$ $\Leftrightarrow$ $\mu _{G}(z_i) = v_{G}(z_i)$.

(E3):

$D_\textrm{accy}^{I}(G,H)\in [0,1]$.

(E4):

$D_\textrm{accy}^{I}(G,H) = D_{H}^{I}(G)$ if G = H. where $D_{H}^{I}(G)$ is the proposed exponential knowledge measure.

Proof

(E1).:

Let G, H are two least AIF-set are similar. It implies that $\mu _{G}(z_i) = \mu _{H}(z_i) = 0,$ $v_{G}(z_i) = v_{H}(z_i) = 1$ or $\mu _{G}(z_i) = \mu _{H}(z_i) = 1,$ $v_{G}(z_i) = v_{H}(z_i) = 0$. Clearly $D_\textrm{accy}^{I}(G,H) = 1$ in both situations.

(E2).:

Let $D_\textrm{accy}^{I}(G,H) = 0$. i.e.,

$$\begin{aligned} \begin{aligned}&\dfrac{1}{2s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )\right. \\&\left. \quad e^{\Bigg (1-\Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )^2\Bigg )}\right. \\&\left. + \Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )e^{\Bigg (1-\Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )^2\Bigg )} - e^{0.75}\right] \\&+ \dfrac{1}{2s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \sqrt{\Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\Bigg )}\right. \\&\left. \times e^{\Bigg (1-\Bigg (\dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{\mu _{H}(z_i) + 1 - v_{H}(z_i)}{2}\Bigg )\Bigg )}\right. \\&\left. \quad + \sqrt{\Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\Bigg )}\right. \\&\left. \times e^{\Bigg (1-\Bigg (\dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\Bigg )\times \Bigg (\dfrac{1 + v_{H}(z_i) - \mu _{H}(z_i)}{2}\Bigg ) \Bigg )} - e^{0.75}\right] = 0. \end{aligned} \end{aligned}$$

Only positive components are present in the preceding summation, hence the previous equation can only be true if $\mu _{G}(z_i) = v_{G}(z_i),$ $\forall z_i\ \in \ Z.$ Conversely, Let us consider $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall z_i\ \in \ Z,$ which obviously shows $D_\textrm{accy}^{I}(G,H) = 0$.

(E3).:

This is easily demonstrated from Eq. (46).

(E4).:

It is easy to demonstrate $D_\textrm{accy}^{I}(G,H) = D_{H}^{I}(G)$ for G = H using the definition from Eq. (46). Hence, $D_\textrm{accy}^{I}(G,H)$ is a legitimate AIF-exponential accuracy measure.

4.1.1 Pattern detection using the specified accuracy measure

The accuracy measure is now applied in the following manner to address the pattern detection problem with AIF-set. Problem: Consider the AIF-sets used to represent r patterns $M_j = \{<z_i,\mu _{M_j}(z_i),v_{P_j}(z_i)>:z_i\in Z\}$ (j = 1,2,3,...,r) defined over a finite, non-empty set $Z = \{z_1,z_2,z_3,...,z_n\}$. Let $R = \{<z_i,\mu _{R}(z_i),v_{R}(z_i)>:z_i\in Z\}$ is any unidentified pattern. The aim is to categorise pattern R into a known pattern $M_j$.

Here are three approaches to resolving the aforementioned challenge:

.:

${\textbf {Similarity measure strategy: }}$Chen et al. (2016b) If A(G, H) indicates the similarity between pattern G and pattern H, then R is identified as pattern $M_j$, where

$$\begin{aligned} A(R,M_j) = \max _{j=1,2,3,...,r} \left( A\left( R,M_j\right) \right) . \end{aligned}$$

.:

${\textbf {Dissimilarity measure strategy: }}$Kadian and Kumar (2021) If B(G, H) indicates the dissimilarity between pattern G and pattern H, then R is identified as pattern $M_j$, where

$$\begin{aligned} B\left( R,M_j\right) = \min _{j=1,2,3,...,r} \left( B\left( R,M_j\right) \right) . \end{aligned}$$

.:

${\textbf {Accuracy measure strategy: }}$ If C(G, H) indicates the accuracy between pattern G and pattern H, then R is identified as pattern $M_j$, where

$$\begin{aligned} C\left( R,M_j\right) = \max _{j=1,2,3,...,r} \left( C\left( R,M_j\right) \right) . \end{aligned}$$

Boran and Akay (2014) examined pattern detection using similarity measure, whereas (Xiao 2019b) examined pattern detection using dissimilarity measure. We note from comparative studies of similarity and dissimilarity measures that neither a similarity measure nor a dissimilarity measure is suited for every pattern detection issue. Therefore, a different paradigm is needed for problems involving pattern detection. The proposed accuracy measure may be more effective than the existing similarity and dissimilarity measure in specific pattern detecting issues. In the issue of pattern recognition, we contrast the (Boran and Akay 2014) cases to show the efficacy of the suggested AIF-exponential accuracy measure.

Example 4

Consider a finite set $Z = \{z_1,z_2,z_3\}$ which is not empty. Let $F_1, F_2, F_3$ be three patterns as follows:

$$\begin{aligned} F_1 = \left\{ (z_1,0.6,0.1),(z_2,0.5,0.2),(z_3,0.4,0.3),(z_4,0.7,0.2)\right\} ; \\ F_2 = \left\{ (z_1,0.5,0.5),(z_2,0.5,0.3),(z_3,0.6,0.1),(z_4,0.8,0.1)\right\} ; \\ F_3 = \left\{ (z_1,0.0,0.0),(z_2,0.4,0.2),(z_3,0.3,0.3),(z_4,0.5,0.4)\right\} . \end{aligned}$$

Let’s define the unidentified pattern R as follows:

$$\begin{aligned} R = \left\{ (z_1,0.1,0.0),(z_2,0.5,0.2),(z_3,0.4,0.3),(z_4,0.7,0.2)\right\} . \end{aligned}$$

Our present objective is to categorise the unidentified pattern R as one of the patterns $F_1, F_2, F_3$.

Boran and Akay (2014) developed a similarity measure strategy to resolve this pattern recognition issue. Table 5 shows the computed results.

Table 5 Similarity measures between known and undiscovered patterns are provided in Example 4

From Table 5, we discovered the similarity measure $A_{C}$ (Fan and Zhangyan 2001), $A_{HB}$ (Mitchell 2003), $A_{HY}^{1}$ (Hung and Yang 2004), $A_{HY}^{2}$ (Hung and Yang 2004), $A_{HY}^{3}$ (Hung and Yang 2004) are unable to recognise the pattern R, although similarity measure $A_{H}$ (Hong and Kim 1999), $A_{O}$ (Li et al. 2002) and $A_{e}^{P}$ (Liang and Shi 2003) quickly identify the pattern R.

Xiao (2019b) developed a dissimilarity-measure strategy to find the solution of the same example. Table 6 shows the computed results.

Table 6 Dissimilarity measures between known and undiscovered patterns are provided in Example 4

From Table 6, we discovered the similarity measure $B_{eh}$ (Yang and Chiclana 2012), $B_{h}$ (Grzegorzewski 2004) and $B_{Z}^{2}$ (Zhang and Yu 2013) are unable to recognise the pattern R, although similarity measure $B_{E}$ (Wang and Xin 2005), $B_{Z}^{1}$ (Zhang and Yu 2013) and $B_{1}$ (Wang and Xin 2005) quickly identify the pattern R.

The accuracy measure approach is now used, and the recommended accuracy measure is applied to the given patterns. The computed values are: $D_{accy}^{I}(R,F_1) = 0.2914$, $D_{accy}^{I}(R,F_2) = 0.2406$ and $D_{accy}^{I}(R,F_3) = 0.1932$. Pattern R is categorised as part of the pattern $F_1$ utilising the suggested exponential accuracy measure. Therefore, the suggested accuracy measure approach works effectively for this pattern recognition problem.

4.2 AIF-exponential information measure (AEIM)

We are able to define an AIF-exponential information measure $L_{H}^{I}$ for any AIF-set G as follows:

$$\begin{aligned} \begin{aligned} L_{H}^{I}(G)&= 1 - D_{H}^{I}(G),\\&= 1 - \dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{s}\left[ \left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) \right. \\&\left. e^{\left( 1-\left( \dfrac{\mu _{G}(z_i) + 1 - v_{G}(z_i)}{2}\right) ^2\right) }\right. \\&\left. + \left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{G}(z_i) - \mu _{G}(z_i)}{2}\right) ^2\right) } - e^{0.75}\right] . \end{aligned} \end{aligned}$$

(47)

We now examine the validity of the suggested AIF-exponential information measure.

Theorem 4

Let $G = \{<z_i,\mu _{G}(z_i),v_{G}(z_i)>:z_i \in Z\}$ be the element of AIFS(Z) for a finite set $Z(\ne \phi )$. Consider a mapping $L_{H}^{I}: AIFS(Z)\rightarrow [0,1]$ given in Eq. (47). Then $L_{H}^{I}$ is a valid AIF-exponential information measure if it fulfils the following properties, (L1)–(L4):

• (L1) $L_{H}^{I}(G) = 0$ iff $\mu _{G}(z_i) = 0,$ $v_{G}(z_i) = 1$ or $\mu _{G}(z_i) = 1,$ $v_{G}(z_i) = 0$ $\forall \ z_i\in Z$, i.e., G is a least AIF-set.

• (L2) $L_{H}^{I}(G) = 1$ iff $\mu _{G}(z_i) = v_{G}(z_i)$ $\forall \ z_i\in Z$, i.e., G is a most AIF-set.

• (L3) $L_{H}^{I}(G)\le L_{H}^{I}(G)$ iff $G\subseteq H.$

• (L4) $L_{H}^{I}(G) = L_{H}^{I}(G^c),$ where $G^c$ is the complement of G.

Proof

Actually, it is easy to verify that the exponential information measure provided in Eq. (47) complies with the above-mentioned axioms.

4.3 AIF-exponential similarity measure (AESM)

For G, H $\in AIFS(Z)$, we can define a exponential similarity as follows:

$$\begin{aligned} \varpi _m(G,H) = 1 - \left| D_{H}^{I}(G)-D_{H}^{I}(H)\right| . \end{aligned}$$

(48)

We now examine the validity of the suggested AIF-exponential similarity measure.

Theorem 5

Let G, H, I $\in AIFS(Z)$ for a finite set $Z(\ne \phi )$. Consider a mapping $\varpi _m: AIFS(Z)\times AIFS(Z)\rightarrow [0,1]$ given in Eq. (48). If $\varpi _m$ satisfies the four axioms (A1)–(A4) stated below, then $\varpi _m$ is regarded as an AIF-exponential similarity measure.

• (A1) $0\le \varpi _m(G,H)\le 1.$

• (A2) $\varpi _m(G,H) = \varpi _m(H,G)$.

• (A3) $\varpi _m(G,H) = 1 \Leftrightarrow G = H.$

• (A4) If $G\subseteq H\subseteq I,$ then $\varpi _m(G,H)\ge \varpi _m(G,I)$ and $\varpi _m(H,I)\ge \varpi _m(G,I).$

Proof

• (A1) We know that the suggested exponential knowledge measures $D_{H}^{I}(G)$ and $D_{H}^{I}(H)$ have values in the range [0, 1] therefore, $0\le |D_{H}^{I}(G) - D_{H}^{I}(H)|\le 1$, and as a result, the axiom (A1).

• (A2) From Eq. (48), we may infer that $\varpi _m(G,H) = \varpi _m(H,G)$.

• (A3) From Eq. (48), we have

  $$\begin{aligned} \begin{aligned} \varpi _m(G,H) = 1&\Leftrightarrow 1 - \left| D_{H}^{I}(G)-D_{H}^{I}(H)\right| = 1,\\ {}&\Leftrightarrow \left| D_{H}^{I}(G)-D_{H}^{I}(H)\right| = 0,\\ {}&\Leftrightarrow D_{H}^{I}(G) = D_{H}^{I}(H),\\ {}&\Leftrightarrow \mu _G(z_i) = \mu _H(z_i) \textrm{and} v_G(z_i) = v_H(z_i), \forall z_i \in Z,\\ {}&\Leftrightarrow G = H. \end{aligned} \end{aligned}$$
• (A4)
  $$\begin{aligned} \begin{aligned}&\textit{Let}\ G, H, I \in AIFS(Z)\ be\ s.t.\ G\subseteq H\subseteq I,\\ {}&\Rightarrow \mu _G(z_i)\le \mu _H(z_i)\le \mu _I(z_i)\ \textit{and}\ v_G(z_i)\ge v_H(z_i)\ge v_I(z_i),\ \forall z_i \in Z,\\ {}&\Rightarrow D_{H}^{I}(G)\ge D_{H}^{I}(H)\ge D_{H}^{I}(I),\\ {}&\Rightarrow D_{H}^{I}(G) - D_{H}^{I}(I)\ge D_{H}^{I}(G) - D_{H}^{I}(H),\\ {}&\Rightarrow \left| D_{H}^{I}(G) - D_{H}^{I}(I)\right| \ge \left| D_{H}^{I}(G) - D_{H}^{I}(H)\right| ,\\ {}&\Rightarrow 1 - \left| D_{H}^{I}(G) - D_{H}^{I}(I)\right| \le 1 - \left| D_{H}^{I}(G) - D_{H}^{I}(H)\right| ,\\ {}&\Rightarrow \varpi _m(G,H)\ge \varpi _m(G,I).\\ \end{aligned} \end{aligned}$$

  We can also demonstrate that $\varpi _m(H,I)\ge \varpi _m(G,I).$

Consequently, the measure described in Eq. (48) can be reliable SM. When two AIF-sets yield equivalent knowledge, the suggested SM reaches its greatest value, i.e., 1. This established the effectiveness of the suggested AESM.

Example 5

If $Z=\{z\}$ and $G, H\in AIFS(Z)$ s.t. $G = \{z,\mu _{G}(z),v_{G}(z)\}$ and $H = \{0.5,0.5\}$, where $\mu _{G}$ and $v_{G}$ are membership and non-membership function respectively. Figure 2 displays the degree of similarity between AIF-sets G and H for various values of $\mu$ and v. The concepts listed below are simple to understand From Fig. 2:

.:

Boundedness i.e., $0\le \varpi _m(G,H)\le 1.$

.:

$\varpi _m(G,H) = 1\ when\ G = H.$

.:

Symmetry, i.e., $\varpi _m(G,H) =$ $\varpi _m(H,G)$

Fig. 2

Proposed similarity measure

4.4 AIF-exponential dissimilarity measure (AEDSM)

For G, H $\in AIFS(Z)$, we can define a exponential dissimilarity as follows:

$$\begin{aligned} \tau _m(G,H) = \left| D_{H}^{I}(G)-D_{H}^{I}(H)\right| . \end{aligned}$$

(49)

We now examine the validity of the suggested AIF-exponential dissimilarity measure.

Theorem 6

Let G, H, I $\in AIFS(Z)$ for a finite set $Z(\ne \phi )$. Consider a mapping $\tau _m: AIFS(Z)\times AIFS(Z)\rightarrow [0,1]$ given in Eq. (49). If $\tau _m$ satisfies the four axioms (B1)–(B4) stated below, then $\tau _m$ is regarded as an AIF-exponential dissimilarity measure.

• (B1) $0\le \tau _m(G,H)\le 1.$

• (B2) $\tau _m(G,H) = \tau _m(H,G)$.

• (B3) $\tau _m(G,H) = 0 \Leftrightarrow G = H.$

• (B4) $G\subseteq H\subseteq I,$ then $\tau _m(G,H)\le \tau _m(G,I)$ and $\tau _m(H,I)\le \tau _m(G,I).$

Proof

• (B1) We know that the suggested exponential knowledge measures $D_{H}^{I}(G)$ and $D_{H}^{I}(H)$ have values in the range [0, 1] therefore, $0\le |D_{H}^{I}(G) - D_{H}^{I}(H)|\le 1$, and as a result, the axiom (B1).

• (B2) From Eq. (49), we may infer that $\tau _m(G,H) = \tau _m(H,G)$.

• (B3) From Eq. (49), we have

  $$\begin{aligned} \begin{aligned} \tau _m(G,H) = 0&\Leftrightarrow \left| D_{H}^{I}(G)-D_{H}^{I}(H)\right| = 0,\\ {}&\Leftrightarrow D_{H}^{I}(G) = D_{H}^{I}(H),\\ {}&\Leftrightarrow \mu _G(z_i) = \mu _H(z_i) \textrm{and} v_G(z_i) = v_H(z_i), \forall z_i \in Z,\\ {}&\Leftrightarrow G = H. \end{aligned} \end{aligned}$$
• (A4)
  $$\begin{aligned} \begin{aligned}&Let\ G, H, I \in AIFS(Z)\ be\ s.t.\ G\subseteq H\subseteq I,\\ {}&\Rightarrow \mu _G(z_i)\le \mu _H(z_i)\le \mu _I(z_i)\ \textrm{and}\ v_G(z_i)\ge v_H(z_i)\ge v_I(z_i),\ \forall z_i \in Z,\\ {}&\Rightarrow D_{H}^{I}(G)\ge D_{H}^{I}(H)\ge D_{H}^{I}(I),\\ {}&\Rightarrow D_{H}^{I}(G) - D_{H}^{I}(I)\ge D_{H}^{I}(G) - D_{H}^{I}(H),\\ {}&\Rightarrow \left| D_{H}^{I}(G) - D_{H}^{I}(I)\right| \ge \left| D_{H}^{I}(G) - D_{H}^{I}(H)\right| ,\\ {}&\Rightarrow \tau _m(G,H)\le \tau _m(G,I).\\ \end{aligned} \end{aligned}$$

  We can also demonstrate that $\tau _m(H,I)\le \tau _m(G,I).$

Consequently, the measure described in Eq. (49) can be reliable DSM. When two AIF-sets yield equivalent knowledge, the suggested DSM reaches its lowest value, i.e., 0. This established the effectiveness of the suggested AEDSM.

Example 6

If $Z=\{z\}$ and $G, H\in AIFS(Z)$ s.t. $G = \{z,\mu _{G}(z),v_{G}(z)\}$ and $H = \{0.5,0.5\}$, where $\mu _{G}$ and $v_{G}$ are membership and non-membership function respectively. Figure 3 displays the degree of dissimilarity between AIF-sets G and H for various values of $\mu$ and v. The concepts listed below are simple to understand From Fig. 3:

.:

Boundedness i.e., $0\le \tau _m(G,H)\le 1.$

.:

$\tau _m(G,H) = 0\ when\ G = H.$

.:

Symmetry i.e., $\tau _m(G,H) =$ $\tau _m(H,G)$

Fig. 3

Proposed Dissimilarity measure

5 Modified VIKOR technique using proposed Atanassov intuitionistic fuzzy exponential knowledge and similarity measures

This section includes applications of the suggested AEKM and AESM are given in MCDM problems. In MCDM issues, Out of all the alternatives, we want to choose the finest one. Several real-world problems are described using multiple criteria. Following specifications must be met by this model:

i.:

A collection of every possible alternatives.

ii.:

A predefined set of criteria.

iii.:

Weights for the specified Attributes/Criteria.

iv.:

Factors that can influence how much importance is given to every alternative.

5.1 The proposed strategy

Opricovic (1998) examined a method called the VIKOR technique to deal with MCDM difficulties. TOPSIS and VIKOR have different aggregation functions and normalising strategies. When using the TOPSIS method, the optimum option is the one that is the furthest from the negative ideal solution and the closest to the positive ideal solution (Chen et al. 2016a). Making a choice that maximises profit while minimising cost is preferred in this case. Additionally, within VIKOR, the optimal alternative is chosen using an accurate evaluation of "closeness" to the perfect answer.

5.2 Proposed AIF-exponential similarity-based modified VIKOR technique

It is possible to provide the modified VIKOR approach based on similarity for the MCDM problem using the AIF-exponential knowledge measure. It draws inspiration from both the original VIKOR strategy and its adaptations. Take into account an MCDM problem where $T_U = \{U_i\}_{i=1}^{r}$ is a group of all the alternative and $T_P = \{P_j\}_{j=1}^{s}$ is a group of criteria. Let $P_R = \{R_d\}_{d=1}^{n}$ be a group of experts who are asked to weigh in on a potential alternative based on a set of criteria. Let $W_C = \{c_j\}_{j=1}^{s}$ indicate the weight of the criteria that corresponds to attributes $P_j$ s.t. $\sum _{j=1}^{s}c_j = 1$. The steps in the proposed VIKOR method are as follows:

Step 1.:

Construct assessment data: After obtaining the resource individual’s replies for a criterion of a particular alternative, we might develop the following decision matrix (Table 7) in an intuitionistic fuzzy system: where $\mu _{ij}$ is the extent to which the $U_i$ alternative meets $P_j$ criteria and $v_{ij}$ is the extent at which the $U_i$ alternative does not satisfy the $P_j$ criteria.

Step 2.:

Create a normalised decision matrix: The fuzzy decision matrix can be normalised as follows:

$$\begin{aligned} \begin{aligned} S&= \{s_{ij}\},\\ {}&= {\left\{ \begin{array}{ll}<\mu _{ij},v_{ij}>\ \mathrm{Benefit\ criteria}\\ <v_{ij},\mu _{ij}>\ \mathrm{Cost\ criteria}\\ \end{array}\right. } \end{aligned} \end{aligned}$$

(50)

Additionally, Eq. (14) is used to assess the quantity of knowledge that was conveyed. In this equation, we interchange membership, and non-membership values. This is because the highest value for benefit criteria and the lowest value for cost criteria are always desirable.

Step 3.:

Calculate the criterion weights: Two methods are used to determine criteria weights: (i.) For unidentified criterion weights:Chen and Li (2010) offered the following method for calculating the criteria weights:

$$\begin{aligned} c_j^{L} = \dfrac{1 - FL_{j}}{s-\sum _{j=1}^{s}FL_{j}},\forall j = 1,2,3...s, \end{aligned}$$

(51)

where $FL_{j} = \sum _{j=1}^{r}L(U_i,P_j)$ $(\forall j = 1,2,3...s).$ In this instance, $L(U_i,P_j)$ represents the fuzzy IM for an alternative $U_i$ that meets the criterion $P_j$. Knowing that fuzzy knowledge measure and fuzzy information measure are complementary concepts, to determine the criterion weights, we use the formula below:

$$\begin{aligned} c_j^{W} = \dfrac{FW_{ij}}{\sum _{j=1}^{s}FW_{ij}}, j = 1,2,3...s, \end{aligned}$$

(52)

where $FW_{j} = \sum _{j=1}^{r}W(U_i,P_j)$ and $W(U_i,P_j)$ Is the knowledge gleaned from alternative $U_i$ comparable to $P_j$ criteria. (ii.) For criterion weights that are only partially known: In actual situations, resource individuals might not always be able to give their opinions in a vase of specific numbers. Perhaps there is not enough time for this, an inability to comprehend the subject matter, etc. Therefore, in this kind of challenging situation, resource individuals prefer to provide their comments in the form of intervals. We assemble the data provided by the resource people in set ${\bar{O}}$. The formula described below can be used to determine the overall amount of knowledge.

$$\begin{aligned} FW_{j} = \sum _{i=1}^{r}W\left( s_{ij}\right) , \end{aligned}$$

(53)

where

$$\begin{aligned} \begin{aligned} W\left( s_{ij}\right)&= D_{H}^{I}\left( U_i,P_j\right) ,\\&= \dfrac{1}{s(1 - e^{0.75})}\left[ \left( \dfrac{\mu _{ij} + 1 - v_{ij}}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{ij} + 1 - v_{ij}}{2}\right) ^2\right) } \right. \\&\left. \quad + \left( \dfrac{1 + v_{ij} - \mu _{ij}}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{ij} - \mu _{ij}}{2}\right) ^2\right) } - e^{0.75}\right] ,\\&\forall i = 1,2,3...r, j = 1,2,3...s. \end{aligned} \end{aligned}$$

(54)

The following formula is used to obtain the optimal criterion weights.

$$\begin{aligned} \begin{aligned} \max (F)&= \sum _{j=1}^{s}\left( c_{j}^{W}\right) \left( FW_{j}\right) ,\\&= \sum _{j=1}^{s}\left( c_{j}^{W}\sum _{i=1}^{r}W\left( s_{ij}\right) \right) ,\\&= \dfrac{1}{s(1 - e^{0.75})}\sum _{i=1}^{r}\sum _{j=1}^{s}\left[ c_{j}^{W}\left( \left( \dfrac{\mu _{ij} + 1 - v_{ij}}{2}\right) e^{\left( 1-\left( \dfrac{\mu _{ij} + 1 - v_{ij}}{2}\right) ^2\right) } \right. \right. \\&\left. \left. + \left( \dfrac{1 + v_{ij} - \mu _{ij}}{2}\right) e^{\left( 1-\left( \dfrac{1 + v_{ij} - \mu _{ij}}{2}\right) ^2\right) } - e^{0.75}\right) \right] , \end{aligned} \end{aligned}$$

(55)

where $c_{j}^{W}$ $\in {\bar{O}}$ and $\sum _{j=1}^{s} = 1$. As a result, the criterion weights determined by Eq. (55) are as follows.

$$\begin{aligned} argmax(F) = \left( C_1,C_2,...,C_s\right) ^{T}, \end{aligned}$$

(56)

where T is the matrix’s transpose.

Step 4.:

Calculate the finest and worst optimal solutions: We now find the best answers. Let $M = \{M_1,M_2,...,M_s\}$ and $N = \{N_1,N_2,...,N_s\}$ are two distinct sets of optimal solutions, finest and worst, respectively. The finest and worst optimum solutions’ values can be determined as follows:

$$\begin{aligned} M_j= & {} {\left\{ \begin{array}{ll}<\max _{\{i\}}\mu _{ij},\min _{\{i\}}v_{ij}>\mathrm{\ Benefit\ criteria}\\ <\min _{\{i\}}\mu _{ij},\max _{\{i\}}v_{ij}>\mathrm{\ Cost\ criteria} \end{array}\right. } \end{aligned}$$

(57)

$$\begin{aligned} N_j= & {} {\left\{ \begin{array}{ll}<\min _{\{i\}}\mu _{ij},\max _{\{i\}}v_{ij}>\mathrm{\ Benefit\ criteria}\\ <\max _{\{i\}}\mu _{ij},\min _{\{i\}}v_{ij}>\mathrm{\ Cost\ criteria} \end{array}\right. } \end{aligned}$$

(58)

Step 5.:

Calculate the finest and worst optimal similarity matrices: We may calculate the similarity measure of the finest ideal solution M and the normalised decision matrix S for each attribute using the similarity measure formula given in Eq. (48), calculate the similarity measure of the finest ideal solution N and the normalised decision matrix S for each attribute, determine the worst ideal matrix A and finest ideal matrix B using the similarity measure as follows

$$\begin{aligned} A = \{a_{ij}\}_{r\times s}\ and\ B = \{b_{ij}\}_{r\times s}, \end{aligned}$$

(59)

where $a_{ij} = \varpi _m(M_j,s_{ij})$, $b_{ij} = \varpi _m(N_j,s_{ij})$. In this equation, we find the accuracy of each alternative w.r.t. finest as well as worst ideal solution.

Step 6.:

Calculate similarity measure vectors: Identify the similarity measure vectors $O^+$ and $O^-$ that are, for each attribute, the closest and most distant to the optimistic ideal; find the similarity measure vector $I^+$ and $I^-$ that are, for each attribute, the closest and the most distant from the pessimistic ideal.

$$\begin{aligned} \begin{aligned}&O^+ = \left[ o_1^{+} \ o_2^{+} \ \ldots \ o_s^{+}\right] ,\ O^- = \left[ o_1^{-} \ o_2^{-} \ \ldots \ o_s^{-}\right] ;\\ {}&I^+ = \left[ i_1^{+} \ i_2^{+} \ \ldots \ i_s^{+}\right] , \ I^- = \left[ i_1^{-} \ I_2^{-} \ \ldots \ I_s^{-}\right] , \end{aligned} \end{aligned}$$

(60)

where $O^+ = \max _{\{i\}}a_{ij}$, $O^- = \min _{\{i\}}a_{ij}$, $I^+ = \max _{\{i\}}b_{ij}$, $I^- = \min _{\{i\}}b_{ij}$, (j = 1,2,3,...,s). In this equation, we find the vectors that are close as well as far from the finest/worst ideal solutions of similarity matrices.

Step 7.:

Create finest and worst normalised collective utility and individual remorse values: Compute the normalised nearest optimistic ideal collective utility $IK_i$ as well as the normalised nearest optimistic ideal individual remorse $IG_i$ for alternative $U_i$, in order that is:

$$\begin{aligned} \begin{aligned}&IK_i = \sum _{j=1}^{s}{c_{j}^{W}}\dfrac{o_{j}^{+} - a_{ij}^{+}}{o_{j}^{+} - o_{j}^{-}},\\ {}&IG_i = \max _{\{j\}}\left( {c_{j}^{W}}\dfrac{o_{j}^{+} - a_{ij}^{+}}{o_{j}^{+} - o_{j}^{-}}\right) . \forall i = 1,2,3...,r. \end{aligned} \end{aligned}$$

(61)

Likewise, we calculate the normalised closest pessimistic ideal collective efficiency $TK_i$ as well as the normalised nearest pessimistic ideal individual remorse $TR_i$ for alternative $U_i$, in order that is:

$$\begin{aligned} \begin{aligned}&TK_i = \sum _{j=1}^{s}{c_{j}^{W}}\dfrac{i_{j}^{+} - b_{ij}^{+}}{i_{j}^{+} - i_{j}^{-}},\\ {}&TR_i = \max _{\{j\}}\left( {c_{j}^{W}}\dfrac{i_{j}^{+} - b_{ij}^{+}}{i_{j}^{+} - i_{j}^{-}}\right) . \end{aligned} \end{aligned}$$

(62)

Step 8.:

Calculate the nearest optimistic and pessimistic ideal VIKOR indices Calculate the nearest optimistic ideal VIKOR indices $Y_i^{+}$ as well as the nearest pessimistic ideal VIKOR indices $Y_i^{-}$ for alternative $\chi _i$, in order that is:

$$\begin{aligned} \begin{aligned}&Y_i^{+} = \delta \dfrac{IK_{i} - IK^{*}}{IK^{-} - IK^{*}} + (1 - \delta )\dfrac{IG_{i} - IG^{*}}{IG^{-} - IG^{*}}, \\ {}&Y_i^{-} = \delta \dfrac{TK_{i} - TK^{*}}{TK^{-} - TK^{*}} + (1 - \delta )\dfrac{TR_{i} - TR^{*}}{TR^{-} - TR^{*}}; \end{aligned} \end{aligned}$$

(63)

$$\begin{aligned} where\ IK^{-} = \max _i IK_{i},\ IK^{*} = \min _i IK_{i},\ IG^{-} = \max _i IG_{i},\ IG^{*} = \min _i IG_{i}; \\ TK^{-} = \max _i TK_{i},\ TK^{*} = \min _i TK_{i},\ TR^{-} = \max _i TR_{i},\ TR^{*} = \min _i TR_{i}. \end{aligned}$$

The figures of $\delta$ and $(1 - \delta )$, respectively, indicate the relative importance of the strategies of "the vast majority of attribute" as well as "the individual remorse". In most cases, the worth of $\delta = 0.5$ being used.

Step 9.:

Calculate the proximity correlation coefficient: Compute the relative proximity coefficient $MP_i$ for alternative $U_i$ as follows:

$$\begin{aligned} MP_i = \dfrac{ Y_i^{+}}{Y_i^{+} + Y_i^{-}}, \forall i = 1,2,3...,r. \end{aligned}$$

(64)

After figuring out the correlation factor’s value, we put each alternative’s correlation factor list in ascending order. The better the performance of an alternative, the smaller the value of the correlation factor for that particular choice. Note: Additionally, if we replace the suggested AEDSM for the AESM, the performance of an alternative is improved if the correlation factor is higher.

Table 7 Intuitionistic Fuzzy Decision Matrix $MD_{r\times s}$

5.3 Case study

In the last several decades, adsorption has gained popularity as a method for the purification of wastewater. For extracting Cr(VI) from wastewater, a variety of adsorbent items are available on the market, including activated carbon, home waste, agricultural waste, industrial waste, and more. There might be a lot of adsorbents available to us that can extract Cr(VI) from wastewater. The selection of the ideal adsorbent may be complicated and difficult due to the wide range of alternatives. As a result, choosing the right adsorbent is a time-consuming task. When choosing an adequate adsorbent, several characteristics must be taken into account.

According to the literature, several of the market-available adsorbents are inexpensive and naturally occurring. However, they increase environmental contamination. Both cost-effective and environmentally friendly adsorbents are available. While certain adsorbents have a high capacity for adsorption, others have disposal issues. As a result, there are several factors on which the finest choice will be made. Additionally, we might state that certain qualities may be inherently contradictory, i.e., some attributes demand maximum values, while others require minimum values. Consequently, choosing an adsorbent requires special consideration. Additionally, recovering the chromium found in waterways is a desirable option economically. Adsorption should be a quick, easy, affordable, and environmentally friendly method. Additionally, it ought to be among the most effective and widely applicable technologies that are frequently employed over alternative techniques in the international ecological protection zones. Adsorption provides several advantages over conventional methods, including the capacity to reuse the sorbent, low selectivity for specific metals, lower operating costs, the absence of chemical sludges, and short operation times.

To select the optimal adsorbent, all of the aforementioned parameters are taken into consideration. Additionally, employees decide on a variety of criteria, including temperature, pH level, time of day, stirring rate, and Cr(VI) concentration, among others, to choose the most suitable adsorbent. When there are several available options and different influencing factors, a more appropriate mathematical procedure is needed for the selection of the applicable adsorbent. We chose the suggested method as the finest solution for eliminating Cr(VI) from wastewater.

In this article, we use six commercially accessible adsorbents:

1.:

Aspergillus brasiliensis$(U_1)$,

2.:

Mould biomaterial corolinus varicolor$(U_2)$,

3.:

Verticillate seeds of hydrilla$(U_3)$,

4.:

Candida Sea Strains $(U_4)$,

5.:

Pig Iron Mud$(U_5)$,

6.:

Granule Husk$(U_6)$. To choose the finest choice among these alternative we look at eight criteria (1) Adsorbate Content (in ppm)$(P_1)$, (2) Adsorbent Dosage (in g/L)$(P_2)$, (3) Time of Contact (in minutes)$(P_3)$, (4) pH level$(P_4)$, (5) Acceleration (in RPM)$(P_5)$, (6) Temperature (in ${}^{\circ }$C)$(P_6)$, (7) Environment friendly$(P_7)$, (8) Price$(P_8)$ are described in Table 8. To discover the greatest adsorbent, we enlisted the expertise of 10 specialists from research-related domains. The fundamental structure of the current MCDM problem is shown in Fig. 4.

Table 8 Definition of Criteria

Fig. 4

Basic structure of the presented problem

Now, with the aid of the suggested method, we resolve the stated MCDM problem. The steps in the suggested strategy are as follows:

Case 1: For unidentified criterion weights:

Step 1::

We compile all of the resource people’s comments on a criterion pertaining to a certain alternative. The decision matrix that results from putting together the replies given by all resource people is shown in Table 9. In this matrix, $S = s_{ij} = <\mu _{ij},v_{ij}>$, $\mu _{ij}$ reflects the proportion of all the resource people who prefer alternative $U_{i}$ relative to criterion $P_{j}$ to all the resource people concerned and $v_{ij}$ is the proportion of all the resource people overall who oppose alternative $U_{i}$ in light of criteria $P_{j}$ to all the resource people engaged. Additionally included in Table 9 is the level of knowledge that each individual criterion was able to assess.

Step 2::

Since every criterion involved is a benefit criterion, the normalised matrix remains identical to that seen in Table 9.

Step 3::

We establish the weights for the criterion. Let us say the weights of the criteria are uncertain. Next, use Eq. (52), we obtain

$$\begin{aligned} W_{C} = \{0.0433,0.1754,0.1992,0.0780,0.2641,0.1068,0.0459,0.869\}. \end{aligned}$$

Step 4::

Using Eqs. (57) and (58), we may identify the ideal solutions that are finest and worst, as shown below:

$$\begin{aligned} M= & {} \{<0.6,0.3>,<0.7,0.1>,<0.6,0.3>,<0.6,0.2>,<0.8,0.2>,<0.7,0.2>,<0.6,0.3>,<0.7,0.1>\}. \\ W= & {} \{<0.4,0.5>,<0.4,0.4>,<0.3,0.5>,<0.3,0.5>,<0.3,0.5>,<0.3,0.4>,<0.3,0.5>, <0.3,0.6>\}. \end{aligned}$$

Step 5::

We determine the finest ideal matrices A and worst ideal matrices B based on similarity measure using Eq. (65) as follows: A = $\begin{bmatrix} 0.8950 &{} 0.8669 &{} 0.9421 &{} 1 &{} 0.9718 &{} 0.9007 &{} 0.9069 &{} 0.6109\\ 1 &{} 0.6109 &{} 1 &{} 0.9204 &{} 1 &{} 0.7322 &{} 0.9421 &{} 1\\ 1 &{} 0.6461 &{} 0.8950 &{} 0.8626 &{} 0.9715 &{} 0.7322 &{} 1 &{} 0.5990\\ 0.8950 &{} 0.7039 &{} 0.9069 &{} 0.8315 &{} 0.9718 &{} 1 &{} 0.9421 &{} 0.6150\\ 0.8950 &{} 0.5990 &{} 0..9421 &{} 0.8626 &{} 0.9718 &{} 0.7162 &{} 0.9069 &{} 0.599\\ 0.9069 &{} 0.5990 &{} 0.8950 &{} 0.8155 &{} 0.9930 &{} 0.7633 &{} 0.9069 &{} 0.5990\\ \end{bmatrix}$ and B = $\begin{bmatrix} 0.9861 &{} 0.7162 &{} 1 &{} 0.8626 &{} 0.9648 &{} 0.8274 &{} 0.9648 &{} 0.9069\\ 0.9069 &{} 0.9881 &{} 0.9421 &{} 0.9430 &{} 0.9930 &{} 0.9959 &{} 1 &{} 0.7040\\ 0.9069 &{} 0.9529 &{} 0.9524 &{} 1 &{} 0.9648 &{} 0.9959 &{} 0.9421 &{} 0.8950\\ 0.9881 &{} 0.8951 &{} 0.9648 &{} 0.9648 &{} 0.9648 &{} 0.7281 &{} 1 &{} 0.9110\\ 0.9881 &{} 1 &{} 1 &{} 0.8626 &{} 0.9648 &{} 0.9881 &{} 0.9648 &{} 0.8940\\ 1 &{} 1 &{} 0.9529 &{} 0.9529 &{} 1 &{} 0.7633 &{} 0.9648 &{} 0.8950\\ \end{bmatrix}$

Step 6::

Eq. (60) may be used to get the similarity measure solutions $O^{+}$, $O^{-}$, $I^{+}$, and $I^{-}$, and their values are provided below.

$$\begin{aligned} O^{+}= & {} \{1, 0.8699, 1, 1, 1, 1, 1, 1\}, \\ O^{-}= & {} \{0.8950, 0.5990, 0.8950, 0.8155, 0.9715, 0.7162, 0.9069, 0.5990\}, \\ I^{+}= & {} \{1, 1, 1, 1, 1, 0.9959, 1, 0.9110\}, \\ I^{-}= & {} \{0.9069, 0.7162, 0.9421, 0.8626, 0.9648, 0.7281, 0.9421, 0.7040\}. \end{aligned}$$

Step 7::

The virtues of normalised closest finest ideal collective efficiency $IK_{i}$ and normalised nearest finest ideal individual remorse $IG_{i}$ for each option are determined using Eq. (61) and are displayed below

$$\begin{aligned} IK_{1}= & {} 0.5838, IK_{2} = 0.3695, IK_{3} = 0.8529, IK_{4} \\= & {} 0.7733, IK_{5} = 0.8874, IK_{6} = 0.7775; \\ IG_{1}= & {} 0.2613, IG_{2} = 0.1676, IG_{3} = 0.2641, IG_{4} \\= & {} 0.2611, IG_{5} = 0.2613, IG_{6} = 0.1992. \end{aligned}$$

For each alternative, the estimated values of normalised closest worst ideal group utility $TK_i$ and normalised near worst ideally individuals regret $TR_i$ are presented below using Eq. (62)

$$\begin{aligned} TK_{1}= & {} 0.6197, TK_{2} = 0.4872, TK_{3} = 0.5534, TK_{4} \\= & {} 0.5799, TK_{5} = 0.3433, TK_{6} = 0.3160; \\ TR_{1}= & {} 0.2641, TR_{2} = 0.1992, TR_{3} = 0.2641, TR_{4} \\= & {} 0.2641, TR_{5} = 0.2641, TR_{6} = 0.1620. \end{aligned}$$

Step 8::

The outcomes of the VIKOR indexes $Y^{+}$ and $Y{-}$ for each option, as determined by Eq. (63), are displayed below

$$\begin{aligned} Y_{1}^{+}= & {} 0.6922, Y_{2}^{+} = 0, Y_{3}^{+} = 0.9666, Y_{4}^{+} \\= & {} 0.5946, Y_{5}^{+} = 0.9854, Y_{6}^{+} = 0.5575; \\ Y_{1}^{-}= & {} 1, Y_{2}^{-} = 0.4639, Y_{3}^{-} = 0.8908, Y_{4}^{-} \\= & {} 0.9344, Y_{5}^{-} = 0.5449, Y_{6}^{-} = 0. \end{aligned}$$

Step 9::

Using Eq. (64) the estimated correlation coefficient $MP_{i}$ readings for each possibility are displayed below

$$\begin{aligned} MP_{1}= & {} 0.4090, MP_{2} = 0, MP_{3} = 0.5446, MP_{4} \\= & {} 0.3888, MP_{5} = 0.6439, MP_{6} = 1. \end{aligned}$$

By applying the suggested exponential similarity measure in Table 10, we construct the values of the nearest finest ideal VIKOR indices $Y^{+}_{i}$, closest worse ideal VIKOR indices $Y_{i}^{-}$, correlation factor $MP_{i}$, and rankings for each alternative and all the alternatives with attained ranks are shown with the help of Fig. 5. According to, these alternatives are ranked in order of preference $U_2>U_4>U_1>U_3>U_5>U_6$.

Table 9 Intuitionistic Fuzzy Decision Matrix $MD_{6\times 8}$

Table 10 Generated Ranks, Correlation coefficient, and VIKOR indexes

We now do a sensitivity analysis with regard to various values of weightage $(\lambda )$.The range $\lambda$ value is 0 to 1. We take the various values of $\lambda$, ranging from 0 to 1, with a 0.1 step interval. For various choices of $\lambda$, the correlation factor values in accordance with the suggested exponential similarity measure are displayed in Table 11.

Table 11 Sensitive study for various $\lambda$ values using the suggested exponential similarity measure

Case 2: For criterion weights that are only partially known:

Due to the numerous practical considerations, resource personnel are unable to assign numerical weights to the criteria. Under these conditions, intervals are used to distribute the criterion weights. Let us examine the MCDM issue with partially known criteria weights that was described earlier. Provide the following information when determining the criteria’s weights:

The information in Eq. (65) should be read as follows:

$$\begin{aligned} {\bar{O}} = {\left\{ \begin{array}{ll} 0.02\le c_{1}^{W}\le 0.12, 0.05\le c_{2}^{W}\le 0.16, 0.02\le c_{3}^{W}\le 0.18, 0.08\le c_{4}^{W}\le 0.12,\\ 0.02\le c_{5}^{W}\le 0.06, 0.05\le c_{6}^{W}\le 0.16, 0.05\le c_{7}^{W}\le 0.16, 0.10\le c_{8}^{W}\le 0.14. \end{array}\right. } \end{aligned}$$

(65)

$F_{\max } = 0.0433c_{1}^{W} + 0.1754c_{2}^{W} + 0.1992c_{3}^{W} + 0.0780c_{4}^{W} + 0.2641c_{5}^{W} + 0.1068c_{6}^{W} +0.0459c_{7}^{W} + 0.0869c_{8}^{W}$;

subjected to conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} 0.02\le c_{1}^{W}\le 0.12,\\ 0.05\le c_{2}^{W}\le 0.16\\ 0.02\le c_{3}^{W}\le 0.18,\\ 0.08\le c_{4}^{W}\le 0.12,\\ 0.02\le c_{5}^{W}\le 0.06,\\ 0.05\le c_{6}^{W}\le 0.16,\\ 0.05\le c_{7}^{W}\le 0.16,\\ 0.10\le c_{8}^{W}\le 0.14.\\ \sum _{i=1}^{8} c_{i}^{W}. \end{array}\right. } \end{aligned}$$

(66)

Eq. (66), which is solved using MATLAB software, yields the following result:

$$\begin{aligned} c_{1}^{W}= & {} 0.02, c_{2}^{W} = 0.16, c_{3}^{W} = 0.18, c_{4}^{W} = 0.12, c_{5}^{W} = 0.06, c_{6}^{W} \nonumber \\= & {} 0.16, c_{7}^{W} = 0.16, c_{8}^{W} = 0.14. \end{aligned}$$

(67)

Fig. 5

Nearest finest ideal VIKOR indices, closest worse ideal VIKOR indices, correlation factor, and rankings

By resolving in the same manner as case (1), we are able to obtain $U_2$ as the most preferable alternative once more. The following list of MCDM issues that occur in real-life situations can be resolved using the aforementioned method:

• (a) A person wishes to purchase some real estate. On the market, there are four basic types of properties. A person developed the following criteria: (I) Connection, (II) Geographic location (III) Construct Quality, and (IV) Developer Reputation.

• (b) For a birthday party, a person must choose an eatery inside a city. A person developed the following criteria: (I) Comfortable; (II) Rates; (III) Amenities; (IV) Excellence; and (V) Place.

• (c) A business wants to promote travel to India. There may be some influences on it. They are (I) the interest of the community, (II) the availability of funds, (III) infrastructural development, and (IV) the support from the authorities.

5.4 Comparison and analysis

We employ various established approaches from the literature to resolve the example shown in Table 9 to evaluate the effectiveness of the suggested strategy. The following are some of the common techniques:

.:

Hwang et al. (1981) proposed TOPSIS (Technique for Order Preference by Similarity to Ideal Solutions) strategy.

.:

Ye (2010) suggested Decision-making strategy(DMS).

.:

Verma and Sharma (2014) suggested DMS.

.:

Singh et al. (2020) suggested DMSs by utilising several knowledge measures.

.:

Farhadinia (2020) suggested DMSs by utilising several knowledge measures.

.:

Farhadinia (2020) suggested DMSs by the use of knowledge measures looked at by Nguyen (2015).

.:

Farhadinia (2020) suggested DMSs by the use of knowledge measures looked at by Guo (2015).

In an intuitionistic fuzzy environment, we provide Table 12 to contrast the outcomes of different techniques with those of the suggested methodology.

Table 12 Comparative table

The TOPSIS technique states that the finest option is the one that is most distant from the worst solution and most near the greatest respond. When contrasting the TOPSIS method with the VIKOR methodology, Opricovic and Tzeng (2004) said that it is not always the case that the alternative that is most similar to the greatest solution is also the option that is most dissimilar to the worst solution. Ye (2010) only considered the connections between alternative natives and the ideal alternative. Being close to the best answer could be helpful in certain circumstances, but not always since it could cause you to lose track of crucial facts. Because of this, Ye (2010) technique’s suggested output is not especially reliable. In light of the weighted intuitionistic fuzzy inaccuracy measure, Verma and Sharma (2014) devised a method to tackle MCDM problems in an environment where there is uncertainty. To address MCDM difficulties, Singh et al. (2020) suggested using three alternative KM. Farhadinia (2020) provided a method for resolving the MCDM issue by applying four different approaches. He also employs the methods put out by Nguyen (2015) and Guo (2015) to address the similar MCDM problem. The issue that is being presented offers six potential solutions, with the $U_2$ option being the optimum solution according to all provided methodologies, as stated by Table 12. As a consequence, the proposed approach’s output may be trusted.

6 Conclusion

This work proposes and tests the validity of an AIF-exponential knowledge measure. The AIF-exponential knowledge measure proposed is demonstrated in this paper to be an effective method for addressing problems with organised linguistic variables, figuring out desired weights and ambiguity for two different AIF-sets. A comparison with many well-known AIF-information and knowledge measures is made to illustrate the efficacy of the recommended AIF-exponential knowledge measure. To assess the effectiveness of the suggested AIF-exponential knowledge measure, a trio of instances are given in the current paper. In an intuitionistic fuzzy environment, four new measures—accuracy measure, information measure, similarity measure, and dissimilarity measure—are also presented and verified. To find patterns, we employ the suggested AIF-exponential accuracy measures. Additionally, a pattern identification example is provided to illustrate how different measures stack up against the suggested accuracy measure. A modified VIKOR technique based on knowledge measures and similarity measures is offered to address MCDM difficulties, and it is discussed that the findings were rather positive. Its effectiveness is demonstrated with a numerical example and comparison. The suggested method shows tremendous potential because it can identify an alternative that nearly entirely meets all of the conditions. It also offers experts guidance on what aspects make a specific alternative less effective. Furthermore, the suggested methods make it clear why certain options are better than others from the viewpoint of decision-making. No more tedious calculations are needed in the proposed approach. The proposed approach is used to find the most preferable adsorbent for removing Cr(VI) from wastewater. The suggested method may be evaluated and applied for a variety of intuitionistic fuzzy circumstances and does not call for more difficult computations. Hesitant Fuzzy set; Interval-valued Intuitionistic Fuzzy set; Picture Fuzzy set; and Neutrosophic Fuzzy set are all covered by the proposed measure’s extension. The knowledge, accuracy, and similarity that are indicated can be used in a variety of contexts, such as feature identification, speech recognition, and picture thresholding.