Multi-criteria decision-making based on novel fuzzy generalized divergence and knowledge measures

Abstract

In a number of fuzzy systems, knowledge measures have been extensively investigated. However, no research on knowledge measures derived from divergence for standard fuzzy sets has been done. This study develops and validates a new generalized divergence measure for fuzzy sets based on the mathematical structure of Csiszár’s divergence. Some of its specific cases, mathematical properties, and performance comparisons are discussed. In addition, exploiting Csiszár’s divergence idea, a class of fuzzy knowledge measures has been established. The proposed fuzzy generalized divergence is then used to derive a new fuzzy generalized knowledge measure. Its efficacy in capturing the amount of useful information in fuzzy sets was demonstrated by comparing it to some strategic information measures. In uncertain multi-criteria decision-making (MCDM) situations, fuzzy entropy is typically adopted to compute the objective weights of criteria. However, it frequently provides unsatisfactory results. New optimization models for generating the objective weights based on the two proposed measures are implemented. These models incorporate both the principles of maximizing deviation and knowledge measures. This research also presents a novel approach based on a single ideal point for integrating Gray Relational Analysis (GRA) with VIKOR (Vlsekriterijumska Optimizacija I KOmpromisno Resenje). The developed technique focuses on discovering the most advantageous alternative, whose performance meets almost every benefit criterion, as well as identifying the criteria that make an alternative less effective. The consistency and rationality of the proposed approach are demonstrated through a numerical illustration along with sensitivity and comparative analysis.

1 Introduction

Decision-making processes that are more adaptable and less limited are needed to support growth in a number of crucial industries, including those related to transportation, health, economy, etc. However, experts typically offer evaluations that are sensitive to their subjectivity, resulting in ambiguity. In such cases, standard MCDM approaches fail, and appropriate uncertainty management techniques are always needed. Bellman and Zadeh (1970) extended the fuzzy set theory to MCDM to address the intrinsic subjectivity of decision- makers. Therefore, linguistic concepts that produce fuzzy values or fuzzy sets are employed to describe alternatives performances under criteria. Fuzzy multi-criteria decision-making (FMCDM) may aid in understanding how decision-makers analyze alternatives and select the best one (Wang and Lee 2009). Numerous methods of conventional MCDM have been expanded to fuzzy atmosphere as fuzzy TOPSIS (technique for order preference by similarity to ideal solution) (Chen 2000), fuzzy VIKOR (Wang and Chang 2005), fuzzy MOORA (multi-objective optimization based on ration analysis) (Brauers and Zavadskas 2006), fuzzy AHP (Analytic Hierarchy Process) (Lazarevic 2001), and GRA (gray relational analysis) (Ju-Long 1982). Since then, multiple FMCDM have been extensively researched (e.g.,Chen et al. 2019; Zeng et al. 2010; Shahhosseini and Sebt 2011).

The subjective nature of human perception always generates uncertainties in the information gathered about the importance of criteria while decision-making process. Thus, the criteria are differently estimated by decision-makers. Therefore, they should not consider criteria equally important. In addition, the appropriate assessment of criteria weights is crucial in MCDM problems since weight variations might affect the final ranking of alternatives (Hwang and Yoon 1981). In other words, the optimum solution is inextricably linked to changes in the preference order of criteria. In fact, weighting strategies can have a substantial impact on the final ranking. In this context, objective methods calculate the criteria weighting coefficients based on the information integrated into the decision matrix with mathematical models without considering the decision-maker’s opinions. Among the objective techniques are entropy methods (Xia and Xu 2012; Garg et al. 2015); fuzzy linear programming (Mikhailov 2000); maximizing deviation methods (Xu and Da 2005; Wei 2008). Shannon’s entropy-based technique is the most renowned strategy. Entropy (Shannon 1948) was initially intended to assess the average level of uncertainty embedded in random variable outputs. Zadeh (1968) was the first to quantify the uncertainty of a fuzzy set, describing the entropy of a fuzzy event in terms of its probability distribution and membership function. Based on Shannon’s function, De Luca and Termini (1972) proposed the most well-known formulation of fuzzy entropy as the first attempt to evaluate the uncertainty associated with a fuzzy set in a non-probabilistic environment. Since then, fuzzy entropy has been widely used in weight criterion determination (e.g.,Garg et al. 2015; Wang and Lee 2009). Moreover, Xia and Xu (2012) developed a new approach for evaluating criteria weights based on entropy and fuzzy cross-entropy, also known as discrimination information. Kullback (1951) initiated the concept of cross-entropy to estimate the extent of discrimination between two probability distributions. Subsequently, Bhandari and Pal (1993) proposed a fuzzy discrimination measure to quantify discriminatory information between fuzzy sets in line with the Kullback’s probabilistic discrimination. Its symmetrical expression is called a fuzzy divergence measure. A fuzzy divergence measure is a valuable tool for obtaining discriminating information in a wide range of fields. It can potentially expand experts’ knowledge and skills. In recent year, researchers have developed new fuzzy divergence measures for FMCDM. Ohlan and Ohlan (2016) presented Hellinger’s fuzzy generalized divergence measure based on Hellinger’s generalized divergence measure for the probability distributions reported in Taneja (2013). Verma and Maheshwari (2017) developed a method for solving MCDM problems using a new fuzzy Jensen-exponential divergence measure. Mishra et al. (2018) presented a new divergence measure applied to MCDM in an intuitionistic environment to improve cellular mobile telephone service providers. Kadian and Kumar (2022) proposed a new picture fuzzy divergence measure based on Jensen–Tsallis function between picture fuzzy sets, which is applied in MCDM. Umar and Saraswat (2022) developed a new picture fuzzy divergence and applied it to decision-making in machine learning such as pattern recognition, medical diagnosis and clustering.

According to Arya and Kumar (2020), a knowledge measure may capture some essential information that expresses the amount of certainty or precision in a fuzzy set. That can also be evaluated as the average degree of discrimination between a fuzzy set and the most fuzzy set. Several earlier studies on knowledge measures have been undertaken using intuitionistic fuzzy sets (IFS). Indeed, Szmidt et al. (2011, 2014) questioned the duality of entropy and knowledge measures in an intuitionistic framework and defined a new knowledge measure which is effectively a dual measure of entropy. In addition, based on the distance described in (Szmidt and Kacprzyk 2000) between two IFSs, Nguyen (2015) proposed a novel knowledge-based measure of IFSs as the distance of an IFS from the most intuitionistic fuzzy set. Das et al. (2016) devised a novel technique for estimating the criteria weights based on a new intuitionistic fuzzy knowledge measure. Wan et al. (2016) proposed a new risk attitudinal ranking method of IFSs and applied it to multi-attribute decision-making (MADM) with incomplete weight information using new measures of information amount and reliability of IF values. The concept of knowledge measure was extended to Pythagorean and hesitant fuzzy context (e.g., Singh and Ganie 2022; Wan et al. 2020; Sharma et al. 2022). Recently, Singh et al. (2019) introduced a novel fuzzy knowledge measure and demonstrated its duality to a fuzzy entropy measure in a fuzzy setting. In addition, it was used to determine the objective criteria weights in MCDM. An accuracy measure was also developed and used in image thresholding. Singh et al. (2020) established a generalization of the fuzzy knowledge measure previously proposed in their first paper and integrated it into MCDM for setting criteria weights. A comparison was performed with conventional VIKOR, TOPSIS, and compromise-typed variable weight (Yu et al. 2018). Singh and Ganie (2021) proposed a two-parametric generalized fuzzy knowledge measure and a two-parametric generalized accuracy measure, all of which have been incorporated into the MOORA technique. Joshi (2022) suggested a new entropy-based fuzzy knowledge measure, which has been used to determine objective criteria weights. He also provided some other information measures. The key motivations and contributions for introducing this manuscript are:

• Proximity-based compromise programming approaches are commonly used in MCDM problem-solving. Consequently, developing a versatile and effective fuzzy divergence measure for a wide range of applications is still required. Therefore, based on Csiszár’s work, this study suggests a new generalized f-divergence measure for fuzzy sets.

• A fuzzy knowledge measure is also an important topic in fuzzy information theory and may play an essential role in a variety of study domains. Since it is a dual measure of fuzzy entropy, it can provide accurate information about a fuzzy set. In line with its axiomatic definition, a knowledge measure evaluates the extent to which a fuzzy set deviates from the most fuzzy set. From this standpoint, We suggest developing a new class of knowledge measures based on Csiszár’s divergence. Then, the suggested fuzzy generalized divergence is used to generate a new fuzzy generalized knowledge measure. A comparative analysis was carried out to evaluate each of their performances.

• Although the entropy-based method is the most widely used procedure to determine the objective weights of criteria, in some circumstances it can result in insufficient weights. Therefore, we provide a new objective method that incorporates the suggested fuzzy divergence and the proposed knowledge measure. This methodology aims to accumulate as much information about criterion importance as possible since the suggested divergence can indicate to experts how well a criterion discriminates between alternatives, and the knowledge measures can help experts to increase their understanding of the alternative performance under criteria.

• One of the difficulties in addressing a multi-criteria problem with competing criteria, is finding a solution that meets all the criteria simultaneously. The primary way to illustrate such conditions is through a Pareto proficient solution, which requires that improving one criterion deteriorates at least one other criterion (Pareto et al. 1964). Consistent with the compromise programming concept, this work provides a new fuzzy MCDM strategy that combines GRA and VIKOR, based on the proposed fuzzy generalized divergence and on a single ideal point (positive ideal solution). It consists first of transforming cost criteria into benefit criteria and then determining the reference sequence (ideal point). Second, applying GRA to get gray relational coefficients that express the closeness of each alternative performance to that of the ideal solution under each benefit criterion. Finally, apply VIKOR to the resulting gray relational coefficients table and then explain the findings according to the VIKOR principles. The main goal of this procedure is to determine the optimal alternative whose performance under the criteria is closest to that of the desired reference sequence and can discriminate between high-performing and outstandingly poor-performing alternatives. Furthermore, the suggested integrated GRA and VIKOR requires less processing computation than Kuo and Liang’s. The novel FMCDM technique’s consistency is proved using a real-world scenario, as well as sensitivity analysis for various GRA and VIKOR coefficient values. For comparison, the suggested integrated GRA and VIKOR is applied to the numerical example in Kuo and Liang (2011).

This study is structured into four sections. Section 2 briefly reviews some fundamental concepts related to fuzzy set theory as well as fuzzy information measures. Section  3 introduces a new fuzzy generalized divergence measure of Csiszár’s divergence type with proof of its validity and appropriateness also investigated. Section 4 discusses a new class of knowledge measures for fuzzy sets derived from the Csiszár’s class of divergence, then a new knowledge measure is deduced from the proposed fuzzy divergence. In Sect. 5, we investigate the applicability of both proposed measures to FMCDM problem-solving. Finally, Sect. 6 provided a conclusion to this work.

In the next section, we review some necessary concepts and definitions

2 Necessary theoretical tools

Entropy has been involved in much research since it was established by Shannon (1948) to deal with probabilistic uncertainty. It measures the degree of relative ambiguity caused by a misunderstanding of the occurrence of random experimental results. For any discrete probability distribution P, where

$$\begin{aligned} P \in \varPi _n =\left\{ P=(p_1, p_2,\ldots , p_n)\vert \,\,p_i > 0, \,\,\sum _{i=1}^n p_i=1 \right\} . \end{aligned}$$

(1)

The entropy H(P) is given by:

$$\begin{aligned} H(P)=-\displaystyle \sum _{i=1}^n p_i\log p_i. \end{aligned}$$

(2)

Later, based on Shannon’s entropy, Kullback (1951) defined the concept of relative entropy measure, namely directed divergence, that estimates dissimilarity between two probability distributions $(P,Q)\in \varPi _n \times \varPi _n.$ as:

$$\begin{aligned} D_{KL}(P,Q)=\sum _{i=1}^n p_i \log \frac{p_i}{q_i}. \end{aligned}$$

(3)

Csiszár (1967) introduced an important class of divergence measures for probability distributions named Csiszár’s f-divergence measures defined by a convex function $f: \mathbb {R^+}\rightarrow \mathbb {R^+}$ as follows:

$$\begin{aligned} C_f(P,Q)=\sum _{i=1}^n q_i f\left( \frac{p_i}{q_i}\right) . \end{aligned}$$

(4)

Theorem 1

(Csiszár and Korner 1981) If the function f is a convex and normalized, i.e., $f(1)=0,$ then the f-divergence $C_f(P,Q)$ is non-negative and convex in the pair of probability distributions $(P,Q)\in \Gamma _n \times \Gamma _n.$

The undefined expressions of f are interpreted according to Csiszár and Korner (1981) by:

$$\begin{aligned} \begin{aligned}&f(0)=\displaystyle \lim _{t\rightarrow 0^+}f(t),\,\,\,\,0f\left( \frac{0}{0}\right) =0,\,\,\,\text{ and }\\&0f\left( \frac{a}{0}\right) =a \displaystyle \lim _{t\rightarrow +\infty }\frac{f(t)}{t},\,\,\, a>0. \end{aligned} \end{aligned}$$

(5)

Zadeh (1965) provided mathematical theory and appropriate techniques to set up the groundwork for fuzzy set theory as an extension of Boolean logic, to aid in approaching human perception and account for inaccuracies and uncertainties.

Definition 1

(Zadeh 1965) Let $X=\left\{ x_1,x_2,\ldots ,x_n\right\}$ be a finite universe of discourse. A fuzzy set (FS) A is defined as:

$$\begin{aligned} A=\left\{ (x,\mu _{A}(x))\vert \,\, x\in X \right\} , \end{aligned}$$

where $\mu _{A}:X\rightarrow [0, 1]$ is the membership function of A. The belonging degree of x to A is $\mu _{A}(x) \in [0, 1]$.

If $\mu _{A}(x)=1$, then x belongs to A without ambiguity, and if $\mu _{A}(x))=\frac{1}{2}$ then there is maximum fuzziness or ambiguity whether x belongs to A or not. The family of all fuzzy sets defined on X is denoted F(X). The following are some characterizations of fuzzy sets:

Definition 2

Let A, $B \in F(X)$, then we have:

• 1. $A\subset B$, if and only if $\mu _{A}(x)\le \mu _{ B}(x)$,

• 2. $\mu _{A^c}(x)=1-\mu _A(x),\,\,$ $\forall \,\, x \in X,$ $A^c$ expresses the complement of A,

• 3. $\mu _{A\cup B}(x)=\max \big (\mu _A(x),\, \mu _B(x)\big ),\,\,$ $\forall \,\, x \in X,$

• 4. $\mu _{A\cap B}(x)=\min \big (\mu _A(x),\, \mu _B(x)\big ),\,\, \forall \,\, x \in X,$

• 5. $[a] \in F(X)$  $\left( a\in [0,1]\right)$, $\mu _{[a]}(x)=a$, $\forall x \in X,$

• 6. $A= \left[ \frac{1}{2}\right]$ is called the most fuzzy set.

The most prominent axiomatic definition of the fuzzy entropy measure was developed by De Luca and Termini (1972).

Definition 3

(De Luca and Termini 1972) An entropy on F(X) is a real-valued function $E:F(X)\rightarrow [0,1]$ satisfying the following axioms:

• (e1) For all $A\in F(X)$, $E(A)=0$ if and only if A is a crisp set,

• (e2) $E(A)= 1$ if and only if A is the most fuzzy set,

• (e3) $E(A^*)\le E(A)$ for all $A\in F(X)$, where $A^*$ is the sharpened version of A, 

• (e4) $E(A)=E({A^c})$, $A^c$ denotes the complement of A.

De Luca and Termini (1972) also provided the most renowned statement of fuzzy entropy based on Shannon’s function. It is stated as:

$$\begin{aligned} \displaystyle {\begin{aligned} H(A)&= - \sum _i^n \mu _{A}(x_i)\ln (\mu _{A}(x_i)\big )\\&+\big (1-\mu _A(x_i)\big )\ln \big (1-\mu _A(x_i)\big ). \end{aligned}} \end{aligned}$$

(6)

Given two fuzzy sets A and B Bhandari and Pal (1993) were the first to use Kullback’s probabilistic divergence to evaluate the average fuzzy information for discrimination in favor of A versus B, given by:

$$\begin{aligned} \begin{aligned} I(A,B)=&\sum _{i=1}^n \left[ \mu _A(x_i)\ln \frac{\mu _A(x_i)}{\mu _B(x_i)}\right. \\&\left. +(1-\mu _A(x_i))\ln \frac{1-\mu _A(x_i)}{1-\mu _B(x_i)}\right] .\end{aligned} \end{aligned}$$

(7)

Then, they put forward a fuzzy divergence measure as the total average of fuzzy information for discrimination between A and B, which is the symmetric version of I(A, B) and provided as:

$$\begin{aligned} D_{BH}(A,B)= I(A,B)+I(B,A). \end{aligned}$$

(8)

Afterwards, Montes et al. (2002) established a characterization of a fuzzy divergence, which must validate the following postulates.

Definition 4

(Montes et al. 2002) A mapping $D: F(X)\times F(X)\longrightarrow \mathbb {R^+}$ is a divergence measure between fuzzy sets if for each $A,\,B,\,C\, \in \,F(X),$ it satisfies the following properties:

• (D1) D(A, B) is non-negative,

• (D2) $D(A,B)=0$, if and only if $\mu _{ A}(x_i)=\mu _{ B}(x_i)$,

• (D3) $D(A,B)=D(B,A)$.

• (D4) $max\{D(A\cup C, B\cup C),D(A\cap C, B\cap C)\}\le D(A,B).$

A fuzzy distance measure has become important due to its significant applications in various imprecise frameworks.

Definition 5

(Fan and Xie 1999) A real function $d: F(X)\times F(X)\rightarrow \mathbb {R^+}$ is called a distance measure on F(X), if d satisfies the following properties

• (d1) $d(A,B)= d(B,A)\,\,\forall A, \,\,B\,\, \in \,\,F(X)$,

• (d2) $d(A,A)=0,\,\,\,\forall \,\,A\,\,\in \,\, F(X)$,

• (d3) $d(N,N^c)= \displaystyle \max _{A,B \in F(X)}d(A,B),\,\,N$ is a crisp set,

• (d4) $\forall A,B,C \in \,\,F(X)$, if $A\subset B \subset C$, then $d(A,B)\le d(A,C)$ and $d(B,C)\le d(A,C)$.

Fan and Xie (1999) also investigated the relationship between fuzzy entropy, distance and fuzzy similarity measure where, a similarity measure S defined on F(X) is related to distance (expressed in normalized scale) by the following relationship: $S(A,B)=1-d(A,B)$. It is worth mentioning that a fuzzy similarity measure is extensively studied in multiple fuzzy environments (e.g.,Chen and Chen 2001; Cheng et al. 2015; Chen and Jian 2017).

Recently, Singh et al. (2019) put forward an axiomatic definition of the knowledge measure for fuzzy sets, which behaves as a dual measure of fuzzy entropy. Indeed, this measure is used to evaluate the correctness or precision of fuzzy sets (Arya and Kumar 2020; Singh et al. 2020). From an other point of view, knowledge measure can be considered as discrimination measure between a fuzzy set and the most fuzzy set.

Definition 6

(Singh et al. 2019) Let $A \in F(X)$; a real function $K:F(X)\rightarrow \mathbb {R^+}$ is called a knowledge measure if it satisfies the following four postulates:

• (k1) K(A) is maximum if and only if A is a crisp set,

• (k2) K(A) is minimum if and only if A is the most fuzzy set,

• (k3) $K(A^*) \ge K(A)$, $A^*$ is the sharpened version of A,

• (k4) $K({A^c})=K(A).$, where $A^c$ is the complement of A.

3 A new fuzzy generalized divergence measure

The purpose of this section is to develop a new fuzzy generalized divergence measure of Csiszár’s f-divergence type. A convex and normalized function f must be introduced, according to Theorem  1. Therefore, we proposed the function $f_m$ in Eq. (9) to define the proposed fuzzy generalized divergence. Consider the function $f_m: \mathbb {R+} \rightarrow \mathbb {R_+}$ where:

$$\begin{aligned} f_m(x)= \frac{\left( \sqrt{x}-1\right) ^{2m+2}}{(x+1)^m}, \end{aligned}$$

(9)

verifying $f_m(1)=f'_m(1)=0$ with the undefined expression given as in Eq. (5). It should be noted that $f_m$ was inspired by the generating function of a probabilistic divergence measure defined in Taneja (2013). For two arbitrary fuzzy sets A and B $\in F(X)$, where the membership values are, respectively: $\mu _{A}(x_i)$, and $\mu _{B}(x_i)$, $i=1, 2,\ldots , n$. We get the expression below:

$$\begin{aligned} \begin{aligned} D_{m}(A,B)&= \frac{1}{2n}\sum _{i=1}^n\left[ \frac{\left( \sqrt{\mu _{A}(x_i)}-\sqrt{\mu _{B}(x_i)}\right) ^{2m+2}}{(\mu _{A}(x_i)+\mu _{B}(x_i))^{m}}\right. \\&+\left. \frac{\left( \sqrt{1-\mu _{A}(x_i)}-\sqrt{1-\mu _B(x_i)}\right) ^{2m+2}}{(2-\mu _A(x_i)-\mu _B(x_i))^{m}}\right] , \\&\text{ where }\,\,\, m\in \mathbb {N}. \end{aligned} \end{aligned}$$

(10)

Theorem 2

$D_m(A, B )$ defined in Eq. (10) is a valid fuzzy generalized divergence measure.

Proof

$D_m$ is a divergence measure if it satisfies the properties (D1)–(D4) of Definition 4.

• (D1) For any $A,B \in F(X)$ and for $m\in \mathbb {N}$, we have from Eq. (10) that $D_{m}(A, B)$ is the sum of non-negative terms, thus $D_m(A,B)\ge 0$. This proves (D1)

• (D2) Assume that $D_m(A,B)=O$ thus we get from Eq. (10)

  $$\begin{aligned} \left\{ \begin{array}{lll} &{}\frac{\left( \sqrt{\mu _{A}(x_i)}-\sqrt{\mu _{B}(x_i)}\right) ^{2m+2}}{(\mu _{A}(x_i)+\mu _{B}(x_i))^{m}}=0 \\ &{} \text{ and }\\ &{}\frac{\left( \sqrt{1-\mu _{A}(x_i)}-\sqrt{1-\mu _B(x_i)}\right) ^{2m+2}}{(2-\mu _A(x_i)-\mu _B(x_i))^{m}}=0 \end{array}\right. \end{aligned}$$

  (11)

  Eq. (11) holds if $\mu _{A}(x_i)=\mu _{ B}(x_i)$. Now, it is evident that if $\mu _{ A}(x_i)= \mu _B(x_i)$ this implies $D(A,B)=0$. This proves (D2).

• (D3) It is easy to verify that: $D_m(A , B)=D_m(B,A)$ thus, $D_m$ is symmetric, hence (D3) is satisfied.

• (D4) Let us check (D4) which is equivalent to verify the convexity of $D_m$ in A and B.

  $$\begin{aligned} \begin{aligned} f''_m(x)=&=\frac{(2x+2m\sqrt{x}+2mx^{\frac{3}{2}}+4mx+x^2+1)}{{4x^{\frac{3}{2}}(x+1)^{m+2}}}\\&\times (m+1)(\sqrt{x}-1)^{2m}. \end{aligned} \end{aligned}$$

  (12)

  From Eq. (12), we get $f''_m(x)\ge 0$, $\forall x\in (0, \infty )$, and $\forall m\in \mathbb {N}$, it follows that $f_m$ is a convex function. Thus from Theorem 1, $D_m$ is jointly convex in A and B. (D1)–(D4) are verified, so $D_m$ is a valid fuzzy divergence measure.

$\square$

At particular values of the parameter m, $D_m$ is reduced to some well-known fuzzy divergence measures.

• 1. $m=-1$, $D_{m=-1}(A, B)$ = R(A, B), where R(A, B) is Fuzzy Arithmetic mean divergence measure (Tomar and Ohlan 2014b) given by:

  $$\begin{aligned} R(A,B)=\sum _{i=1}^{n}\left[ \frac{\mu _{A}(x_i)+\mu _{ B}(x_i)}{2}+\frac{2-\mu _{A}(x_i)-\mu _{ B}(x_i)}{2}\right] . \end{aligned}$$

  (13)

• 2. $m=0$, $D_{m=0}(A, B)= 2 h(A,B)$ where h(A, B) is the Hellinger’s fuzzy discrimination (Beran 1977) defined as:

  $$\begin{aligned} \begin{aligned}h(A,B)&=\sum _{i=1}^{n}\left[ \frac{\sqrt{\mu _{ A}(x_i)}-\sqrt{\mu _{ B}(x_i)}}{2}\right. \\&+ \left. \frac{\sqrt{1-\mu _{ A}(x_i)}-\sqrt{1-\mu _{ B}(x_i)}}{2}\right] .\end{aligned} \end{aligned}$$

  (14)

Remarque 1

For $m=1$, $D_{m=1}$ can be expressed as: $D_{m=1}(A, B)= 4h(A, B)-\Delta (A, B),$ where $\Delta (A, B)$ is the fuzzy triangular discrimination measure (Dragomir 2003) given by:

$$\begin{aligned} \begin{aligned} \Delta (A, B)&= \sum _{i=1}^{n}\left( \mu _{ A}(x_i)-\mu _{ B}(x_i)\right) ^{2}\\&\times \left[ \frac{1}{(\mu _{ A}(x_i)+\mu _{ B}(x_i))}+\frac{1}{(2-\mu _{ A}(x_i)-\mu _{ B}(x_i))}\right] .\end{aligned} \end{aligned}$$

(15)

In addition, note that the proposed fuzzy divergence measure satisfies the same properties given in Theorems 4.1–4.3 reported in Verma and Maheshwari (2017).

Theorem 3

The proposed fuzzy divergence $D_m$, is a distance measure if it verifies the following properties :

• 1. $D_m(N, N^c)= \displaystyle \max _{A,B \in F(X)}D_m(A, B)$, where N is a crisp set,

• 2. Let A, B and C $\in F(X)$, if $A\subset B\subset C$,  then $D_m(A , B)\le D_m(A , C)$ and $D_m(B , C)\le D_m(A, C).$

Proof

For $x\in \mathbb {R^+}$ and $m\in \mathbb {N}$, the derivative of f is :

$$\begin{aligned} f'_m(x)=(\sqrt{x}-1)^{2m}(\sqrt{x}-1)\frac{m+x+m\sqrt{x}+1}{\sqrt{x}(x+1)^{m+1}}. \end{aligned}$$

(16)

• 1. From Eq. (16), the sign of $f'_m$ depends on the sign of $(\sqrt{x}-1)$, this implies that $f_m$ is decreasing on (0, 1) and increasing on $(1,+\infty ).$ In addition, let us put $x=\frac{\mu _A(x_i)}{\mu _B(x_i)}$ and from Eq. (5), $x=0$ holds if $\mu _A(x_i)=0$ and $\mu _B(x_i)$ is arbitrary $\in [0,1]$ in particular, if $\mu _B(x_i)=1-\mu _A(x_i)$, from Eq. (9), it is clear that $f_m(0)=1$. On the other hand, when $\mu _A(x_i)=1$ and $\mu _B(x_i)=0$ thus $x \rightarrow \infty$, using Eq. (5), $D_m(A,B)= \frac{1}{n}\sum _{i=1}^n 0f_m\left( \frac{1}{0}\right) =1$. Thus $D_m(N , N^c)=\displaystyle \max _{A,B \in F(X)}D_m(A , B).$

• 2. To prove $D_m(A , B)\le D_m(A , C)$, let us consider $t_1=\frac{\mu _A(x_i)}{\mu _B(x_i)}$ and $t_2= \frac{\mu _A(x_i)}{\mu _C(x_i)}$   and from    $A\subset B\subset C$    we get $\mu _{A}(x_i)\le \mu _{ B}(x_i)\le \mu _C(x_i)\,\,\, \forall x_i \in X$, thus    $0\le t_2\le t_1\le 1$ and since $f_m(x)$ is decreasing on (0, 1) (see Eq. (16)), this gives $f_m(t_1)\le f_m(t_2)$ then $D_m(A, B)\le D_m(A, C).$ In the same manner, to prove that $D_m(B, C)\le D_m(A, C)$, we consider $t_1=\frac{\mu _B(x_i)}{\mu _C(x_i)}$  and   $t_2= \frac{\mu _A(x_i)}{\mu _C(x_i)}$, as $\mu _A(x_i)\le \mu _B(x_i)$ for all $x_i \in X$ then we get $1\ge t_1\ge t_2 \ge 0$, then since $f_m(t)$ is decreasing over (0, 1), this gives $f_m(t_1)\le f_m(t_2)$, that is, $D_m(B, C)\le D_m(A, C)$.

$\square$

3.1 Comparative assessment for the suggested divergence measure

To demonstrate the usability of the proposed divergence $D_m$, it has been compared with some prevalent fuzzy divergence measures given below.

Bajaj and Hooda (2010) proposed a measure of fuzzy directed divergence based on the probabilistic divergence given in Renyi et al. (1961), defined for $m >0$ and $m\ne 1$ as:

$$\begin{aligned} \begin{aligned} d_m(A,B)&= \frac{1}{m-1}\sum _{i=1}^{n} \ln \left[ {\mu _{ A}(x_i)}^{m}{\mu _{B}(x_i)}^{1-m}\right. \\&\left. \,\,\,\,\,+{(1-\mu _{ A}(x_i))}^{m}{(1-\mu _{B}(x_i))}^{1-m}\right] .\end{aligned} \end{aligned}$$

(17)

Bhatia and Singh (2012) developed a new (m, q) class of divergence measure with $m>0 ,\,m \ne 1$ and $q>0,\, q\ne 1$ :

$$\begin{aligned} \begin{aligned} D^{q}_m(A,B)&=\frac{1}{q -1}\sum _{i=1}^{n}\left[ ({\mu ^m_{ A}(x_i)}{\mu ^{1-m}_{ B}(x_i)}\right. \\&\left. \,\,\,\,\,+{(1-\mu _{ A}(x_i))}^{m}{(1-\mu _{ B}(x_i))}^{1-m})^{\frac{q-1}{m-1}}-1\right] ,\\&\,\,\,\,\,m>0 ,\,m \ne 1\,\,\, \text{ and }\,\, \,q>0,\,\,\, q\ne 1. \end{aligned} \end{aligned}$$

(18)

Ohlan (2015) introduced the parametric generalized measure of fuzzy divergence as:

$$\begin{aligned} \begin{aligned}L_m(A,B)&= \sum _{i=1}^{n}\frac{(\mu _A(xi)-\mu _B(x_i))^2}{2^m}\\&\times \left[ \frac{(\mu _A(x_i)+\mu _B(x_i))^m}{(\sqrt{\mu _A(x_i)\mu _B(x_i)})^{m+1}}\right. \\&+\left. \frac{(2-\mu _A(x_i)-\mu _B(x_i))^m}{(\sqrt{(1-\mu _A(x_i))(1-\mu _B(x_i))})^{m+1}}\right] ,\\&m\in \mathbb {N}. \end{aligned} \end{aligned}$$

(19)

Ohlan and Ohlan (2016) proposed the generalized Hellinger’s divergence measure defined by:

$$\begin{aligned} \begin{aligned} h_m(A,B)&= \sum _{i=1}^n \left[ \frac{(\sqrt{\mu _A(x_i)}-\sqrt{\mu _B(x_i)})^{2(m+1)}}{(\sqrt{\mu _A(x_i)\mu _B(x_i)})^m}\right. \\&\,\,\,\,\,+\left. \frac{(\sqrt{1-\mu _A(x_i)}-\sqrt{1-\mu _ B(x_i)})^{2(m+1)}}{(\sqrt{(1-\mu _ A(x_i))(1-\mu _ B(x_i)}))^m}\right] ,\\&\,\,\,\,\,\,n\in \mathbb {N}.\end{aligned} \end{aligned}$$

(20)

Table 1 Results of comparative assessment for $D_m$

Fig. 1

Monotonic behavior of $D_m$ w.r.t m

The analysis is performed using two fuzzy sets defined on the universe of discourse $X=\{1,2,3,4,5\}$, that is A and B given as: $A= \{{0.3, 0.4, 0.2, 0.1, 0.5}\}$, $B=\{{0.2, 0.2, 0.3, 0.4, 0.4 }\}$.

By carefully examining the results in Table 1, it is found that the divergence $D ^ {q=2}_{m}$ is constant for $m > 7$. Concerning $L_m (A, B)$, we note that the disparity values are reasonable when compared with the other measures for a few values of the parameter m (i.e., $m=0,\ldots ,7$). On the other hand, from $m = 38$,   $L_m$ rises quickly, likewise for $d_m$. However, $h_m$ and $D_m$ are more helpful, their efficiency is depicted by the minimization of degrees of divergence (Tomar and Ohlan 2014a). Figure 1 illustrates how $D_m$ is superior to the previously mentioned divergence measures. In fact, the capacity of $D_m$ to detect even the smallest difference between two fuzzy sets increases as m rises.

4 A new class of Csiszáz’s divergence-based knowledge measures

The focus of this section is to develop a novel class of Csiszár’s f-divergence-based knowledge measures and then to deduce a new generalized knowledge measure from the suggested fuzzy divergence $D_m$. Let A and B be two fuzzy sets of F(X), and assume that $D_f$ is a fuzzy Csiszár’s f-divergence characterized by:

$$\begin{aligned} D_f(A,B)=\sum _{i=1}^n q_if\left( \frac{p_i}{q_i}\right) , \end{aligned}$$

(21)

where $f:\mathbb {R^+}\longrightarrow \mathbb {R^+}$ is a convex function and twice differentiable on $\mathbb {R^+}$ with $f(1) =f'(1)=0$, where its undefined expression are interpreted as in Eq. (5). Now, consider $B= [\frac{1}{2}]$ the most fuzzy set In F(X), then in term of membership functions of A and B we get :

$$\begin{aligned} D_f\left( A,\left[ \frac{1}{2}\right] \right) = \sum _{i=1}^n \frac{1}{2} \left[ f(2\mu _{ A}(x_i))+f(2(1-\mu _{ A}(x_i)))\right] . \end{aligned}$$

(22)

Consider the function $g:[0,1]\rightarrow \mathbb {R^+}$, such as

$$\begin{aligned} g(\mu _A(x_i))=\frac{1}{2} \big [ f(\mu _A(x_i))+f(2(1-\mu _A(x_i)))\big ]. \end{aligned}$$

Then for $A \in F(X)$, we define

$$\begin{aligned} K_f(A)=c\sum _{i=1}^n g(\mu _A(x_i)),\,\, \,\, c\in \mathbb {R^+}, \end{aligned}$$

(23)

where c is a constant of normalization.

Theorem 4

$K_f(A)$ in Eq. (23) is a valid fuzzy knowledge measure.

Proof

For more simplicity, Let put $c=1$ and $t_i= \mu _{A}(x_i)$ such as

$$\begin{aligned} g(t_i) =\frac{1}{2} \big [ f(2t_i))+f(2(1-t_i))\big ], \end{aligned}$$

(24)

the derivative of g is:

$$\begin{aligned} g'(t_i)= f'(2t_i)-f'(2(1-t_i)). \end{aligned}$$

(25)

Since, f is convex then $f'$ is increasing on $\mathbb {R^+}$, thus for $t_i \in [0,0.5) \,\, f'(2t_i)< f'(2(1-t_i))\Rightarrow g'(t_i)<0$, and for $t_i \in (0.5,1] \,\, f'(2t_i)> f'(2(1-t_i))\Rightarrow g'(t_i)>0$.

Also, we get $g'(t_i)=0$ at $t_i=0.5$. In addition, note that g is a convex function on [0, 1] thus, g(0.5) is a global minimum of g. On the other hand, g attains its maximum at $t_i=0$ or $t_i=1$, such as $\displaystyle \max _{ [0,1]} g(t_i)=\frac{1}{2}\big [f(0)+f(2)\big ].$

Now, from Definition 6 of knowledge measure on F(X), $K_f(A)$ should verify (k1)-(k4).

• (k1) First, we assume that $K_f(A)$ is maximum, that is, $g(\mu _A(x_i))$ is maximum, this implies that $\mu _A(x_i)=0$ or $\mu _A(x_i)=1$ for all $x_i \in X$. Thus, A is crisp set. Inversely, assume that A is crisp set, that is, $\mu _A(x_i)=1$ or $\mu _A(x_i)=0$, thus $g(\mu _A(x_i))$ is maximum. Hence $K_f(A)$ is maximum. This proves (k1).

• (k2) Since, g attains its unique minimum at $t_i=0.5$, that is, $g(0.5)=0$ since $f(1)=0$. Thus if $A=[\frac{1}{2}]$ for all $x_i \in X$, we get $K_f(A)=0$. Conversely, if $K_f(A)= 0$, this implies that $g(\mu _A(x_i))=0$ this implies that $f(2\mu _A(x_i))= f(2(1-\mu _A(x_i)))=0$ this is holds if $\mu _A(x_i)=\frac{1}{2}$ as $f(1)=0$. Hence (k2) holds.

• (k3) Consider $A^*$ the sharpened version of A, i.e.,

  $$\begin{aligned} \mu _{ A^*}(x_i)\le \mu _{ A}(x_i)\,\,\,\,\text{ if }\,\,\,\, \mu _A(x)\le \frac{1}{2}; \end{aligned}$$

  and

  $$\begin{aligned} \mu _{ A^*}(x_i)\ge \mu _{ A}(x_i)\,\,\,\,\text{ if }\,\,\,\, \mu _A(x)\ge \frac{1}{2}. \end{aligned}$$

  Since, g is decreasing on $[0,\frac{1}{2}]$ and increasing on $[\frac{1}{2},1]$, so $g(\mu _{ A^*}(x_i))\ge g(\mu _A(x_i))$ on $[0,\frac{1}{2}]$ and $g(\mu _{ A^*}(x_i))\ge g(\mu _A(x_i))$ on $[\frac{1}{2},1]$. Hence $K_f(A^*)\ge K_f(A)$. Thus, (k3) is checked.

• (k4) Since for all $t_i\in [0,1]$ we have $g(1-t_i)=g(t_i)$, so (k4) is verified.

As (k1)–(k4) are verified $K_f(A)$ is a valid fuzzy knowledge measure. $\square$

For example, let consider the fuzzy triangular discrimination $\Delta (A,B)$ given in Eq. (15). From the preceding, for this Csiszár’s f-divergence, its deduced knowledge measure is set by:

$$\begin{aligned} K_\Delta (A)=\sum _{i=1}^n \frac{2(2\mu _A(x_i)-1)^2}{(2\mu _A(x_i)+1)(3-\mu _{A}(x_i))}. \end{aligned}$$

(26)

It is obvious that $K_\Delta (A)$ verifies (k1)-(k4). Thus $K_\Delta (A)$ is a valid knowledge measure.

Next, based on Theorem 4, a new fuzzy generalized knowledge measure $K_m$ is inferred from the suggested fuzzy generalized divergence $D_m$, as stated in the following theorem.

Theorem 5

For all $A \in F(X)$,

$$\begin{aligned} \begin{aligned} K_m(A)=\frac{c}{4n}&\sum _{i=1}^n\left[ \frac{(\sqrt{2\mu _A(x_i)}-1)^{2m+2}}{(2\mu _A(x_i)+1)^m}\right. \\&+ \left. \frac{\left( \sqrt{2(1-\mu _A(x_i))}-1\right) ^{2m+2}}{(3-2\mu _A(x_i))^m}\right] , \end{aligned} \end{aligned}$$

(27)

where c and is a constant of normalization, and $m\in \mathbb {N}.$

• 1. $K_m(A)$ is valid generalized knowledge measure on F(X) deduced from $D_m.$

• 2. $K_m(A\cup B)+K_m(A\cap B)=K_m(A)+K_m(B)$, $\forall \, A,B \in F(X).$

For $m=1$ and $A\in F(X)$, we get the knowledge measure:

$$\begin{aligned} \begin{aligned} K_{m=1}(A)=&C \sum _{i=1}^n\left[ \frac{(\sqrt{2\mu _A(x_i)}-1)^4}{2\mu _A(x_i)+1}\right. \\&+\left. \frac{(\sqrt{2(1-\mu _A(x_i))}-1)^4}{3-2\mu _A(x_i)}\right] ,\end{aligned} \end{aligned}$$

(28)

where $C=\frac{3}{((\sqrt{2}-1)^4+3)n}.$ Now, we need to examine the relationship between knowledge measures defined in Eq. (23) and fuzzy entropy. For this, let us recall the following theorem.

Theorem 6

(Ebanks 1983) Let$E:F(X)\rightarrow \mathbb {R^+}$. Then E satisfies (e1)–(e4) if and only if E has the form $E(A)= \sum _{i=1}^n G(\mu _A(x_i))$ for some function $G:[0,1]\rightarrow \mathbb {R^+}$ that satisfies:

• (a) $G(0)=G(1)$, and $G(t)>0$ for all $t\in (0,1)$,

• (b) $G(t)<G(0.5)$ for all $t\in [0,1]-{0.5}$,

• (c) G is non-deceasing on [0, 0.5) and non-increasing on (0.5, 1],

• (d) $G(t)=G(1-t)$ for all $t\in [0,1]$.

Consider a fuzzy Knowledge measure $K_f (A)$ as in Eq. (23) and a fuzzy entropy E(A) defined in Theorem 6. Assume that both of them are normalized (normalized scale), so we get the following relationship between functions G and g, that is, $G (t) = 1-g(t)$. Thus, we may announce this theorem:

Theorem 7

Consider on F(X), an entropy measure E(A) defined as in Theorem  6, and $K_f(A)$ a knowledge measure as in Theorem 4. Then we have :

$$\begin{aligned} E(A)=1- K_f(A). \end{aligned}$$

(29)

4.1 Comparative analysis for the proposed knowledge measure

To assess the capacity and usefulness of the proposed generalized knowledge measure, Km(.) is compared to some prevailing information measures using linguistic hedges. To achieve this, we set its generalization parameter m to 1, 2, 3.

Consider a linguistic variable represented by a fuzzy set V. A linguistic modifier, also known as a hedge, is an operator T that transforms fuzzy set V into another fuzzy set T(V), where $\mu _{T(V)}(x) = \Psi_{T}(\mu_{V}(x))$, and $\Psi _T$ is a mathematical transformation. The first modifiers were introduced by Zadeh (1972) as “very”, “more or less”, “quite very” and “very very”.

Consider a fuzzy set A in $X=\big \{1,2,3,4,5,6\big \}$ defined as:

$$\begin{aligned} A=\big \{{(1,0.15), (2,0.45), (3,0.65),(4,0.25),(5,0.3)}\big \}. \end{aligned}$$

Linguistic hedges on A are: $A^{0.5}$ may be interpreted as “more or less A”, $A^2$ may be interpreted as “very A”, $A^3$ may be interpreted as “Quite very (A)”, and $A^4$ may be interpreted as “very very (A)”. Linguistic hedges appear to reduce the uncertainty of a fuzzy set while increasing the amount of useful information. Thus, an effective fuzzy entropy H or knowledge measure K must meet the following requirements respectively:

$$\begin{aligned} H(A^{0.5})>H(A)>H(A^2)>H(A^3)>H(A^4). \end{aligned}$$

(30)

$$\begin{aligned} K(A^{0.5})<K(A)<K(A^2)<K(A^3)<K(A^4). \end{aligned}$$

(31)

The following are some prevalent information measures utilized in comparative evaluation:

$$\begin{aligned} \begin{aligned} H_{H}(A)=&\frac{1}{n(1-e^{-0.5})}\sum _{i=1}^n\left[ \left( 1-e^{-(1-\mu _A(x_i))}\right) \right. \\&\left. \times I_{[\mu _A(x_i)\ge 0.5]}\right. \\&+\left. \left( 1-e^{-\mu _A(x_i)}\right) I_{[\mu _{ A}(x_i)<0.5]}\right] . \end{aligned}\end{aligned}$$

(32)

(Hwang and Yang 2008)

$$\begin{aligned} \begin{aligned} H_{B}^{\alpha }(A)&=\frac{1}{(1-\alpha )n}\sum _{i=1}^n \ln \left[ \mu ^{\alpha }_A(x_i)+(1-\mu _A(x_i))^{\alpha }\right] \\&\alpha >0 ,\,\,\,\,\alpha \ne 1 \end{aligned} \end{aligned}$$

(33)

(Bhandari and Pal 1993)

$$\begin{aligned} \begin{aligned}H_{PP}(A)&=\frac{1}{n(\sqrt{e}-1)}\sum _{i=1}^n\left[ \mu _A(x_i)e^{1-\mu _A(x_i)}\right. \\&+\left. (1-\mu _A(x_i))e^{\mu _A(x_i)}-1\right] . \end{aligned} \end{aligned}$$

(34)

(Pal and Pal 1989)

$$\begin{aligned} \begin{aligned} H_R^S(A)&=\frac{R\times S}{n(R-S)}\sum _{i=1}^n\left[ \left( \mu _{ A}^S(x_i)+(1-\mu _A(x_i))^S\right) ^{\frac{1}{S}}\right. \\&-\left. \left( \mu _{ A}^R(x_i)+(1-\mu _A(x_i))^R \right) ^{\frac{1}{R}}\right] \\&R>1\,\,\text{ and }\,\,0<S<1 \text{ or }\,\, 0<R<1\,\,\text{ and }\,\, S>1. \end{aligned} \end{aligned}$$

(35)

(Joshi and Kumar 2018)

$$\begin{aligned} K_{SG}(A)= \frac{1}{n}\sum _{i=1}^n2\big [\mu ^2_{A}(x_i)+(1-\mu _A(x_i))^{2}\big ]-1. \end{aligned}$$

(36)

(Singh et al. 2019)

$$\begin{aligned} S(A)=\frac{1}{\ln 2}\ln \left[ \frac{2}{n}\sum _{i=1}^n\mu _{A}(x_i)^2+(1-\mu _A(x_i))^2\right] . \end{aligned}$$

(37)

(Arya and Kumar 2020)

$$\begin{aligned} \begin{aligned} K_{SG}^{\alpha }(A)=\frac{1}{n}&\sum _{i=1}^n 2\big [\mu ^{\alpha }_{A}(x_i)+(1-\mu _A(x_i))^{\alpha }\big ]-1,\\&\,\, \alpha >1.\\ \end{aligned} \end{aligned}$$

(38)

(Singh et al. 2020)

$$\begin{aligned} \begin{aligned} K_m(A)=&\frac{k}{4n}\sum _{i=1}^n\left[ \frac{(\sqrt{2x}-1)^{2m+2}}{(2x+1)^m}\right. \\&\left. + \frac{(\sqrt{2(1-x)}-1)^{2m+2}}{(3-2x)^m}\right] ,\,\, m\in \mathbb {N}.\\&\text{ Our } \text{ generalized } \text{ knowledge } \text{ measure } \end{aligned} \end{aligned}$$

(39)

Table 2 Resulting comparative values

Based on the results in Table 2, we observe that for $a > 2$, $K_{SG}^{\alpha }$ is a non-positive real-valued function. From Tables 2 and  3, the order sequences below indicate that the entropy measures $H_{2}^{0.5}(A)$, $H_{0.5}^{15}(A)$ and $H_{BP}^{2}(A)$ are designed to meet the requirement in Eq. (30). The requirement in Eq. (31) is verified by the proposed knowledge measure $K_{m}(A)$ for $m=1,2,3$.

$$\begin{aligned}\begin{aligned}&H_{2}^{0.5}(A^{0.5})> H_{2}^{0.5}(A)> H_{2}^{0.5}(A^2)>H_{2}^{0.5}(A^3)>H_{2}^{0.5}(A^4),\\&H_{0.5}^{15}(A^{0.5})> H_{0.5}^{15}(A)> H_{0.5}^{15}(A^2)>H_{0.5}^{15}(A^3)>H_{0.5}^{15}(A^4),\\&H_{BP}^{2}(A^{0.5})>H_{BP}^{2}(A)>H_{BP}^{2}(A^2)>H_{BP}^{2}(A^3)>H_{BP}^{2}(A^4),\\&K_{1}(A^{0.5})< K_{1}(A)<K_{1}(A^2)<K_{1}(A^3)<K_{1}(A^4),\\&K_{2}(A^{0.5})< K_{2}(A)<K_{2}(A^2)<K_{2}(A^3)<K_{2}(A^4),\\&K_{3}(A^{0.5})< K_{3}(A)<K_{3}(A^2)<K_{3}(A^3)<K_{3}(A^4). \end{aligned}\end{aligned}$$

Table 3 $K_m(A)$ values for $m=1,2,3$

Now, consider another fuzzy set B defined on $X=\{1,2,3,4,5,6\}$ given by:

$$\begin{aligned} \begin{aligned} B=\big \{&(1,0.08), (2,0.116), (3,0.73),(4,0.85),\\&(5,0.68),(6,0.7),(7,1)\big \}. \\&H_{H}(B^{0.5})< H_{H}(B)< H_{H}(B^2)> H_{H}(B^3)>H_{H}(B^4),\\&H_{PP}(B^{0.5})< H_{PP}(B)< H_{PP}(B^2)> H_{PP}(B^3)> H_{PP}(B^4),\\&H_{BP}^{0.5}(B^{0.5})<H_{PP}^{0.5}(B)>H_{BP}^{0.5}(B^2)>H_{BP}^{0.5}(B^3)>H_{BP}^{0.5}(B^4),\\&K_{SG}(B^{0.5})> K_{SG}(B)> K_{SG}(B^2)< K_{SG}(B^3)<K_{SG}(B^4),\\&S(B^{0.5})> S(B)>S(B^2)>S(B^3)<S(B^4),\\&K_{1}(B^{0.5})< K_{1}(B)<K_{1}(B^2)<K_{1}(B^3)<K_{1}(B^4), \\&K_{2}(B^{0.5})< K_{2}(B)<K_{2}(B^2)<K_{2}(B^3)<K_{2}(B^4),\\&K_{3}(B^{0.5})< K_{3}(B)<K_{3}(B^2)<K_{3}(B^3)<K_{3}(B^4).\end{aligned} \end{aligned}$$

Table 4 The resulting comparative values

Following the values in Table 4, we observe that, consistent with the order sequence above, the entropy measures $H_{HY}(B)$, $H_{BP}(B)$, and $H_{PP}(B)$ do not perform well, nor do the knowledge measures S(B) and $K_{SG}(B)$, since these information measures do not verify the respective order sequence given in Eqs. (30) and (31). Whereas, our proposed knowledge measure $K_m$ performs well and appears to be effective for assessing the useful information.

5 Applicability of the proposed measures in MCDM

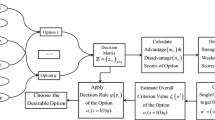
In MCDM, there are two main goals: generating criterion weights and selecting an optimal option from a set of feasible options. Using an appropriate decision-making strategy, on the other hand, may aid in making more rational and relevant conclusions. In this regard, this section provides:first, a new optimization models for determining the objective weights of criteria. Second, a new method for combining GRA and VIKOR techniques. to find the best alternative, which must be both closest to the ideal alternative and perform the best under almost all benefit criteria. In order to understand our method, let us review VIKOR and GRA.

5.1 Gray relational analysis method

Gray Relational Analysis (GRA) is a part of Deng’s gray system theory (Ju-Long 1982; Julong 1989). It is used to investigate problems with complex interrelationships between multiple factors provided as discrete data. GRA has been used successfully in a number of MCDM problems (Olson and Wu 2006; Jiang et al. 2002; Chen et al. 2005). The gray relational (GRA) algorithm transforms the performance $x_{ij}$ of each $A_i$ under criterion $C_j$ into a comparability sequences when ($i=1,\ldots ,p$) and ($j=1,\ldots ,n$):

$$\begin{aligned}&\text{ Lager } \text{ the } \text{ better: }\quad r_{ij}=\frac{x_{ij}-\displaystyle {\min _j(x_{ij})}}{\displaystyle {\max _j (x_{ij})-\min _j(x_{ij})}};\\&\quad \text{ Smaller } \text{ the } \text{ better: }\quad r_{ij}= \frac{\displaystyle \min _j{(x_{ij})}-x_{ij}}{\displaystyle {\max _j {(x_{ij})}-\min _j(x_{ij})}}. \end{aligned}$$

Then, the reference sequence is determined as:

$$\begin{aligned}\begin{aligned}&R=(r^+_1,r^+_2,\ldots ,r^+_n),\,\,\, \text{ where }\,\,\, r^+_j= \displaystyle \max _i (r_{ij})\\&\text{ for }\,\,\, j=1,\ldots ,n. \end{aligned} \end{aligned}$$

Note that the reference sequence can also be any other desired target. further, the gray relational coefficient is given as follows:

$$\begin{aligned} \begin{aligned} \xi _{ij}&= \frac{ \displaystyle {\min _{i} \min _{j}(\delta _{ij})+\rho \displaystyle \max _{i}\max _{j}(\delta _{ij})}}{\delta _{ij}+\rho \displaystyle {\max _{i} \max _{j}(\delta _{ij})}},\\&\text{ where }\quad \delta _{ij}=|r^+_{j}-r_{ij}|, \,\,\, \rho \in [0,1],\\&\rho \quad \text{ is } \text{ a } \text{ resolving } \text{ coefficient. } \end{aligned} \end{aligned}$$

For Each $A_i$, the gray relational degree is computed as:

$$\begin{aligned} \Gamma _i=\sum _{j=1}w_j\xi _{ij}, \end{aligned}$$

$w_j$ is the weight criterion $C_j$. Larger the value of $\Gamma _i$, the better the alternative.

5.2 VIKOR technique

VIKOR is a compromise programming method (Yu 1973), it was originated by Opricovic and Tzeng (2004), and extended to a fuzzy background by Wang and Chang (2005). The VIKOR method is focused on selecting and ranking a set of alternatives subjected to competing criteria. By introducing a raking index based on the particular measure of “closeness” to the ideal “solution” (Tzeng et al. 2005), a compromise ranking list is, thus, produced. The compromise ranking measures are developed from The $L_q$-metric defined by:

$$\begin{aligned} \mathbb {L}_{q,i}=\left\{ \sum _{i=1}^n(\frac{w_j(r^+_{j}-x_{ij})}{r^+_{j}-r^-_{j}})^q \right\} ^{\frac{1}{q}}\,\, \, 1\le q\le \infty . \end{aligned}$$

(40)

The VIKOR technique is conducted as follows:

• (1) For each criterion determine the best and the worst value given, respectively, by: :

  $$\begin{aligned} r^+_j= \displaystyle \max _i x_{ij}\,\,\,\,\,\, \text{ and }\,\,\,\, \,\, r^-_j= \displaystyle \min _i x_{ij}. \end{aligned}$$

• (2) Compute the values of group utility and individual regret over the alternatives $A_i (i = 1, 2,\ldots , p )$ by:

  $$\begin{aligned} \mathbb {L}_{1,i}= & {} S_i=\sum _{j=1}w_j\frac{r^+_j-x_{ij}}{r^+_j-r^-_j},\,\,i=1,\ldots ,n; \end{aligned}$$

  (41)
  $$\begin{aligned} \mathbb {L}_{\infty ,i}= & {} R_i= \displaystyle \max _j (w_j\frac{r^+_j-x_{ij}}{r^+_j-r^-_j}),\,\,i=1,\ldots ,n; \end{aligned}$$

  (42)

• (3) Calculate the compromise measure value $Q_i$ ($i=1,\ldots ,p$) for each option using the given formulae:

  $$\begin{aligned} Q_i=\nu \frac{S_i-S^-}{S^+-S^-}+(1-\nu )\frac{R_i-R^-}{R^+-R^-}, \end{aligned}$$

  (43)

  where $S^-= \displaystyle \min _iS_i$,   $S^+=\displaystyle \max _iS^+$,  $R^-=\displaystyle \min _iR_i$,   $R^+=\displaystyle \max _iR_i$ and $\nu$ is the weight of the strategy of the majority of criteria or the maximum group utility. Without loss of generality, it takes the value 0.5.

• (4) Rank the alternatives $A_i (i = 1, 2,\ldots , p)$ according to the values of $S_i$ , $R_i$ and $Q_i$. The results are three ranking lists.

• (5) Determinate the best solution or a compromise solution. It is clear that the smaller the value of $Q_i$, the better the solution is. To ensure the uniqueness of the optimal option, the following two qualifications must be satisfied simultaneously: (ACDV) Acceptable advantage:  $Q(A^{(2)})-Q( A^{(1)})\ge DQ$ where $DQ= \frac{1}{p-1}$, p is the number of options and $A^{(1)}$ and $A^{(2)}$ are the alternatives with the first and second positions, respectively, in the ranking list $Q_i$ . (ACST) Acceptable Stability:  $A^{(1)}$ should also be the best ranked by $S_i$ and $R_i$. Nevertheless, these two requirements are frequently not achieved simultaneously. Thus, a set of compromise solutions are derived. If the condition (ACDV) is not met, then we shall explore the maximum value of m according to the equation: $Q(A^{(m)}) - Q( A^{(1)})<DQ .$ All the alternatives $A^{(i)}(i = 1,2,\ldots , m)$ are the compromise solutions. If the condition (ACST) is not satisfied, then the alternatives $A^{(1)}$ and $A^{(2)}$ are the compromise solutions.

5.3 A novel MCDM method based on the suggested measures

For the following, consider alternatives $A_1, A_2,\ldots ,A_p$ and $C_1,C_2,\ldots ,C_n$ are competing criteria, where $a_{ij}$ denotes the performance of each alternative $A_i$ under criterion $C_j$, which is weighted $w_ j$, verifying that $w_ j>0$ for all ${j=1,2,\ldots ,n}$ and $\sum _{i=1}^nw_j=1$.

Most multi-criteria methods require a definition of quantitative weights for the different criteria to assess their relative importance (Opricovic and Tzeng 2004). In addition, the proper assessment of weights of criteria plays an important role in (MCDM), since the variation of weights may affect the final ranking of alternatives (Hwang and Yoon 1981). Here, we present a new procedure, involving the two proposed measure $D_m$ and $K_m$ to determine criteria weights based on the idea of maximum deviation (Wei 2008). The steps below illustrate the novel approach.

Step 1:

Formulate the decision-making problem and then create the comparability sequence. Let $\mathfrak {A}=\{ A_1, A_2,\ldots ,A_p\}$ to be a set of alternatives, $\mathfrak {C}=\{C_1, C_2,\ldots ,C_n\}$ be a set of conflicting criteria. Each option $A_i$ is characterized in terms of criterion $C_j$ by the following fuzzy set:

$$\begin{aligned} A_i= & {} \{(C_j, a_{ij}), C_j\in \mathfrak {C}\}\\ \forall \,\,\,\, i= & {} 1,2,3.\ldots , p,\,\,\,\forall \,\,\,\, j=1,2,3,\ldots ,n. \end{aligned}$$

$a_{ij}$ evaluates how much $A_i$ satisfies the criterion $C_j$. Assume that $\mathbf{w}=(w_1,w_2,\ldots ,w_n)^T$ is the weighting vector of criteria, where $0<w_j<1$, $\sum _{j=1}^n w_j=1$. The decision matrix is given by $M=[a_{ij}],\, i=1,\ldots ,p, \,\, j=1,\ldots ,n.$ Criteria can be classified into two types: benefit and cost. Depending on the nature of the criteria, we convert the cost criterion into the benefit criterion (Ohlan and Ohlan 2016). This is accomplished by transforming the fuzzy decision matrix M into a normalized fuzzy decision matrix R by vector normalization, as shown in Eq. 44.

$$\begin{aligned} A_{ij}=\left\{ \begin{array}{ll} \frac{a_{ij}}{\sqrt{\sum _{i=1}^n a_{ij}^2}}\,\,\,\,\,\,\,\,\,\text{ for } \text{ benefit } \text{ criteria }\\ 1-\frac{a_{ij}}{\sqrt{\sum _{i=1}^n a_{ij}^2}}\,\,\,\,\,\,\text{ for } \text{ cost } \text{ criteria }.\\ \end{array} \right. \end{aligned}$$

(44)

Step 2:

a new way of generating criteria weights Due to time constraints and limitations on the expert’s skill, information on the criteria weights may be inadequate or completely unknown. Therefore, developing optimal optimization models is required to discover the objective weight vector. A number of strategies have been devised. Wei (2008) proposed a method which aims to maximize the divergence between all available options across a criterion. Ye (2010) created an approach based on the entropy/cross-entropy model. Wu et al. (2021) provided a model that calculates attribute weights in an intuitionistic setting, utilizing both distance and knowledge measures based on the techniques in Xia and Xu (2012). A knowledge measure is an important tool in information theory because it can provide some useful information about criteria that have insufficient weight information. A fuzzy divergence measure also informs experts about how successfully a criterion discriminates between options; a criterion with a high degree of divergence should be given the highest weight. Given the foregoing, we set up a model that combines the proposed divergence and knowledge measures into a single objective function for providing objective criteria weights. For the criterion $C_j$, the average amount divergence of the alternative $A_i$ to all the other options is given by:

$$\begin{aligned} \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj}) \end{aligned}$$

(45)

and the total divergence between all alternatives under the criterion $C_j$, is provided as:

$$\begin{aligned} \displaystyle \sum _{i=1}^p \left( \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right) . \end{aligned}$$

(46)

The total amount of knowledge with respect to criterion $C_j$ is:

$$\begin{aligned} \displaystyle \sum _{i=1}^p K_m(A_{ij}). \end{aligned}$$

(47)

As previously stated, if a criterion gives a large amount of knowledge across options, this signifies that the information provided is more useful for decision-making and should be given greater weight. Otherwise, it should be given the lowest weight. So, when combining these two factors we get:

$$\begin{aligned} \displaystyle \sum _{i=1}^p\left( K_m(A_{ij})+ \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right) . \end{aligned}$$

(48)

Therefore, based on this association in Eq. (48), to generate the weight vector $\mathbf{w}$ in the case where the information about criterion weights is completely unknown, we put forward a non-linear programming model expressed by:

$$\begin{aligned} \text{(I) }\left\{ \begin{array}{ll} \begin{aligned} \max F(\mathbf{w})&{}=\sum _{j=1}^n w_j \left[ \sum _{i=1}^p (K_m(A_{ij})\right. \\ &{} +\left. \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right] \end{aligned} \\ \text{ s.t }\,\,\, w_j\ge 0,\,\, j=1,2, \ldots,n,\,\,\, \displaystyle \sum _{j=1}^n w_j^2=1. \end{array}\right. \end{aligned}$$

(49)

The unique solution to the optimization problem in Eq. (49) is given by:

$$\begin{aligned} w_j=\frac{\displaystyle \sum _{i=1}^p\left[ K_m(A_{ij})+ \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right] }{\sqrt{\displaystyle \sum _{j=1}^n\left[ \displaystyle \sum _{i=1}^p K_m(A_{ij})+\frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right] ^2}}. \end{aligned}$$

(50)

According to the constraint in the model (I), we get the normalized weight $w_j$ as:

$$\begin{aligned} w^*_j=\frac{\displaystyle \sum _{i=1}^p\left[ K_m(A_{ij})+ \frac{1}{p-1} \displaystyle \sum _{k=1}^pD_m(A_{ij}, A_{kj})\right] }{\displaystyle \sum _{j=1}^n\displaystyle \sum _{i=1}^p\left[ K_m(A_{ij})+ \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right] }. \end{aligned}$$

(51)

However, in instances where the information about the weight vector is partially available, we develop a linear programming model (II) based on the set of the known weight information $\Omega$, which is also a collection of restriction requirements that the weight value wj must meet in real-world scenarios.

$$\begin{aligned} \text{(II) }\left\{ \begin{array}{ll} \begin{aligned} \max F(\mathbf{w})&{}= \sum _{j=1}^n w_j \left[ \sum _{i=1}^pK_m(A_{ij})\right. \\ &{} + \left. \frac{1}{p-1} \displaystyle \sum _{k=1}^p D_m(A_{ij}, A_{kj})\right] \end{aligned} \\ \text{ s.t }\,\,\, \mathbf {w}\in \Omega ,\,\, \,\, w_j\ge 0,\,\,j=1,2,\ldots ,n,\,\,\, \displaystyle \sum _{j=1}^n w_j=1. \end{array}\right. \end{aligned}$$

(52)

By solving the problem in (II), we get the optimal vector weight $\mathbf {w}=(w_1,w_2,\ldots ,w_n)^T$.

Step 3:

A new combination of GRA and VIKOR Construct the weighted normalized fuzzy decision matrix given by:

$$\begin{aligned} \displaystyle \vartheta _{ij}= A_{ij}\,wj\,\,\,\,\,i=1,2,\ldots ,p\,\,\,\,, j=1,2,\ldots ,n. \end{aligned}$$

(53)

Then determine the reference sequence as:

$$\begin{aligned} \begin{aligned}&A^+=(\vartheta ^+_{01},\vartheta ^+_{02},\ldots ,\vartheta ^+_{0n}),\\ \text{ where }\quad \,\,\,\,\,\,\,\,\,\,&\vartheta ^+_{0j}= \displaystyle \max _i \vartheta _{ij},\\&\forall j=1,2,\ldots ,n. \end{aligned} \end{aligned}$$

(54)

Step 4:

Calculate the gray relational coefficient of $A_i,\,\, i=1,\dots ,p$, using Eq. 55

$$\begin{aligned} \xi _{ij}=\frac{\displaystyle {\min _{i}\min _{j}(D_m(\vartheta {ij}, \vartheta ^+_{0j} ))+\rho \max _i \max _j(D_m(\vartheta {ij}, \vartheta ^+_{0j} ))}}{\displaystyle { D_m(\vartheta {ij}, \vartheta ^+_{0j})+\rho \max _i \max _j(D_m(\vartheta {ij}, \vartheta ^+_{0j} ))}}, \end{aligned}$$

(55)

where $\rho$ is the resolving coefficient defined in the range $0 < \rho \le 1$, and it is generally taken equal to 0.5. Note that gray relational coefficients $\xi _{ij}$ are calculated to reflect correlations between existent and desired option evaluations.

Step 5:

Determine the best and worst gray relational coefficient for each criterion. It is worth mentioning that a gray relation coefficient attains its best level when $\xi _{ij}=1$ and its worst level when $\xi _{ij}$ approaches 0. Hence using Eq. (55) the best and worst level of gray relational coefficient $\xi ^*_j$ and $\xi ^-_j$ are, respectively, given as:

$$\begin{aligned} \xi ^*_j=\displaystyle \max _i(\xi _{ij})\,\,\,\,\,\,\text{ and }\,\,\,\,\,\, \xi ^-_j=\displaystyle \min _i(\xi _{ij}). \end{aligned}$$

Step 6:

In general, the greater the degree of discrimination between $A_{ij}$ and $A^+_j$, that is, $\xi _{ij}$ approaches zero, the poorer the $A_{ij}$ is (i.e., $A_i$ performs poorly under criterion $C_j$); the less the degree of discrimination between $A_{ij}$ and $A^+_j$, that is, $\xi _{ij}$ approaches one, the better the $A_{ij}$ is (i.e., $A_i$ has excellent performance under $C_j$). According to the forgoing. Calculate the group utility $S_i$, individual regret $R_i$ and compromise measure $Q_i$ which are given for each alternative $A_i (i=1,\ldots ,p)$ by:

$$\begin{aligned} S_i= & {} \sum _{j=1}^n w_j\frac{\xi ^*_j-\xi _{ij}}{\xi ^*_j-\xi ^-_j},\,\,\,\, R_i= \displaystyle \max _j(w_j\frac{\xi ^*_j-\xi _{ij}}{\xi ^*_j-\xi ^-_j}),\nonumber \\&\quad \text{ for }\,\,\,\, i=1,2,\ldots ,p,\,\,\, \,\,\, j=1,2,\ldots ,n, \end{aligned}$$

(56)

$$\begin{aligned} Q_i= & {} \nu \left( \frac{S^--S_i}{S^*-S^-}\right) +(1-\nu ) \left( \frac{R^*-R_i}{R^*-R^-}\right) ,\nonumber \\&\quad \text{ for } \,\,\,\, i=1,2,\ldots ,p, \end{aligned}$$

(57)

where    $S^*=\displaystyle \max _i S_i$,   $S^-= \displaystyle \min _i S_i$,   $R^*=\displaystyle \max _i R_i$,    $R^-=\displaystyle \min _iR_i$. The parameter $\nu \in [0,1]$ represents the weight of the strategy of maximum group utility, while $(1-\nu )$ is the weight of individual regret. The $\nu$ value is adjusted with respect to the nature of the MCDM issue. In general, to determine the compromise solution, ($\nu =0.5$) is preferred to incorporate both aspects of maximum group utility and minimum regret.

Step 7:

Rank the alternatives. Sort the decreasing values of $S_i$, $R_i$, and $Q_i$ to obtain the alternative rank. The best option is indicated by the smallest value of the compromise measure, $Q_i$. To ensure that the best option is unique, determine the best compromise solution. If the following two conditions are met, $Q_i$ recommends the best-ranked alternative $A^{(1)}$, as a compromise solution. (ACDV) Acceptable advantage: $Q(A^{(2)})-Q(A^{(1)}\ge DQ$, where $DQ=\frac{1}{p-1}$ and $A^{(2)}$ is the alternative of second position in the ranking list by $Q_i$ and p is the number of alternatives. (ACST) Acceptable stability in decision-making: Alternative $A^{(1)}$ must also be the best ranked by S or/and R. This compromise solution is stable within a decision-making process, which could be “voting by majority rule” (when $\nu >0.5$ is needed), or “by consensus” $\nu \approx 0.5$, or “with veto” ($\nu <0.5$). If one of the conditions is not met, then a set of compromise solutions is proposed. It consists of Alternatives $A^{(1)}$ and $A^{(2)}$, if only the requirement (ACST) is not satisfied, or of Alternatives $A^{(1)},A^{(2)},A^{(3)}$,$\ldots ,A^{(M)}$, if the requirement (ACDV) is not satisfied, where $A^{(M)}$ is determined by the relation $Q(A^{(M)})-Q(A^{(1)}) < DQ$ for maximum M (the positions of these alternatives are “in closeness”).

5.4 Numerical illustration

The numerical example is from Joshi and Kumar (2014).

The applicability of The proposed approach is tested in ranking four organizations (alternatives), Bajaj Steel ($A_1$); H.D.F.C Bank ($A_2$); Tata Steel ($A_3$); InfoTech Enterprises ($A_4$). The alternatives are rated on five criteria such as: Earnings per share(EPS) ($C_1$); Face value ($C_2$); P/C (Put-Call) Ratio ($C_3$); Dividend ($C_4$); P/E (Price-to-earnings) ratio ($C_5$) . It is worth noting that $C_1$ and $C_2$ are benefit criteria; a high value indicates a positive growth outlook, whereas the others are cost criteria; a low value indicates a positive growth perspective.

the efficiency of the suggested method is examined for two values $m=1$ and $m=2$ of the generalization parameter of the generalized fuzzy $D_m$ and $K_m$, respectively.

Case 1. Criteria weights are completely unknown In this instance, we can find the best possible alternative by following the procedures below.

Step 1:

The resulting fuzzy decision matrix is depicted in Table 5 Then, using the vector normalization in Eq. (44) on the data in Table 5, it results in the normalized fuzzy decision matrix given in Table 6.

Step 2:

Use Eqs. (10) and  (27) to get the total divergence between all alternatives under criterion $C_j$, as well as the overall amount of knowledge with respect to the same criterion. Then, to get the optimal weight vector $w^*$ use Eq. (51). The results are summarized in Tables 7 and 8. A detailed analysis of Tables 7 and 8 reveals that criteria that allow for adequate discrimination between alternatives and provide a high level of knowledge about the options are given greater weight than those that do not. Another model (I) outcome is that for $m = 1$ and $m = 2$, the weights are preserved in the same order of importance, highlighting the effectiveness of the proposed model for generating criteria weights and its consistency with the established fuzzy information measures.

Step 3:

By Using Eq. (53), we determine the weighted normalized fuzzy decision matrix given in Table 9.

Step 4:

According to Table 9, a reference sequence $A^+$ is obtained using Eq. (54). Thus, we obtain for $m=1$, $A^+=\left( 0.2083, 0.0513, 0.2745, 0.0742,0.1384 \right) .$ For $m=2$, $A^+ =\left( 0.2109,0.0295, 0.3868,0.0438,0.0862\right) .$

Step 5:

Calculate the gray relational coefficient $\xi _{ij}$ for $A_i$, $i=1,\ldots ,p$ and $j=1,2,\ldots ,n$ by using Eqs. (10) and  (55) and fixing the resolving coefficient value of $\rho$ at 0.5. The results are tabulated in Table 10.

Step 6:

  For each alternative $A_i$, calculate group utility $S_ i$, individual regret $R_i$, and compromise measure $Q_i$ using Eqs. (56) and  (57), with the weight strategy $\nu=0.5$. Table 11 summarizes the findings.

Step 7:

   For $m=1$ and $m=2$, Table 11 yields three ranking lists at $\nu =0.5$, thus based on the ascending values of $Q_i$, the options are ranked from the best to the worst as: $A_3> A_1> A_4 > A_2$. However, to find a compromise solution, the two conditions (ACDV) acceptable advantage and (ACST) acceptable stability in decision-making, must be examined. Indeed, for $m=1$, the condition (ACDV) is not satisfied since, $Q(A^{(2)})-Q(A^{(1)})= 0.18360 <DQ$ as $DQ = 0.3333$. Hence,$A_3$ and $A_1$ are compromise solutions. In addition, $Q(A^{(3)})-Q(A^{(1)})=0.3933$, that is, $A_3$ and $A_4$ are not the same compromise solutions as $DQ\le 0.3933$, and $A_3$ has acceptable advantage over $A_4$ which is not included in the set of compromise solution. The condition (ACST) is confirmed because $A_3$ is ranked highest by $S_i$ and $R_i$, as indicated in Table 11. There is acceptable stability in decision-making by consensus since $A_3$ is better ranked than $A_4$ by $S_i$ and $R_i$. Therefore, a decision-maker can give his preferred rank as : $A_3> A_1> A_4> A_2.$ Furthermore, from Table 10, we observe that for $m=1,2$, option $A_3$ performs better than the other three alternatives, and for $A_2$ the criteria $C_3$ and $C_5$ must be improved, because these criteria make $A_2$ the worst option. As can be seen, the ranking order remained unchanged even though the generalization parameter of the suggested fuzzy divergence was changed. Note that according to the findings for m = 2, the interpretations and ranking are the same as those aforementioned.

Table 5 Fuzzy decision matrix Joshi and Kumar (2014)

Table 6 The normalized fuzzy decision matrix

Table 7 Criteria weights computation for $m=1$

Table 8 Criteria weights computation for $m=2$

Table 9 The weighted normalized fuzzy decision matrix w.r.t m

Table 10 Gray relation coefficients of each alternative (case 1)

Table 11 The ranking results using our method (case1)

Table 12 The ranking results using our method (case2)

Case 2. criteria weights are partially unknown

The relations below give the known weights information:

$$\begin{aligned} & \Omega = \left \{0.25\le w_1\le 0.4,\,\, 0.16\le w_2\le 0.27, \right. \\& 0.15\le w_3\le 0.25,\,\, 0.1\le w_4 \le 0.18, \\& 0.2 \le w_5\le 0.35,\,\, w_1\ge 0.2w_4,\\& w_5-w_2\le w_3,\,\, \sum _{j=1}^n w_j=1,\\ & \left. w_j\ge 0 \,\, \,\forall j=1,\dots 5 \right \}. \end{aligned}$$

(58)

Using model (II), as in Eq. (52) we get For $m=1$,   $\mathbf {w*}=\left( 0.2900,0.1600,0.2500,0.1000, 0.2000\right) ^T.$

For $m=2$, we get the weight vector that follows: $\mathbf {w*}=\left( 0.2080,0.0980,0.3280,0.1280,0.2380\right) ^T$.

By following the steps of the proposed technique in the case where criteria weights are partially unknown, taking the resolving coefficient $\rho =0.5$ and the weight of the decision-making strategy $\nu =0.5$. With respect to $m=1$ and $m=2$, Table 12 indicates that, the condition of acceptable advantage (ACDV) is not verified for $A_1$ and $A_4$. However, condition (ACST) is verified as $A_3$ is the best ranked by $S_i$ and $R_i$. Thus, there is acceptable stability within decision-making by consensus. Consequently, the set of compromise solutions includes $A_3$, $A_1$ and $A_4$. However, the final ranking by order preference can be proposed as:

$$\begin{aligned} A_3>A_1>A_4>A_2. \end{aligned}$$

The consistency of the outcomes in the two scenarios where the criterion weights are totally or partially unknown indicates the robustness of the suggested technique.

5.5 Sensitivity analysis and comparison

A sensitivity analysis was performed to demonstrate the robustness of the integrated GRA and VIKOR proposed in this work. For this purpose, the gray relational coefficients are determined by varying the value of the resolution coefficient $\rho$ in [0, 1] and setting the generalization parameter of the proposed fuzzy divergence measure m to 1. An attentive examination of Table 13 reveals two rankings related to $\nu$. Accordingly, for $\nu = 0.25$ and $\nu = 0.5$, the final ranking consists of the compromise solutions $A_3$ and $A_1$. The second option is $A_4$, while the worst option is $A_2$. For $\nu = 0.75$ there are a number of compromise solutions, including $A_3$, $A_1$ and $A_4$. The worst is $A_2$. In light of the sensitivity analysis findings, the decision-makers can provide a confident ranking of the options given as: $A_3>A_1>A_4>A_2$. One of the main results of this analysis was that variations in resolution coefficient and strategy weight do not affect the final ranking, as shown in Fig. 2.

Table 13 Compromise measure values Q for different resolving coefficient values $\rho$ and $m=1$

Fig. 2

Sensitivity analysis outcomes related to $\rho$ at $\nu =0.5$

A comparison with some known FMCDM processes was performed to demonstrate the effectiveness of the strategy presented in this work. These procedures are based on the TOPSIS principle. From Table 14 these approaches all resulted in the same final ranking of options, which is also consistent with our proposed strategy. However, unlike our method, these approaches do not examine the advantages that the options have over each other from a decision-making perspective. They also fail to point out the criteria that make some alternatives to be ineffective. Further, some of the algorithms involved in this evaluation, generate the criteria weights by using the entropy method, resulting in weights that do not correctly discriminate between criteria in terms of importance.

Table 14 Comparison of ranking order of options from various procedures

Kuo and Liang (2011) Kuo developed an integrated GRA and VIKOR approach for evaluating airport service quality based on GRA and VIKOR. Aiming to compare our combining GRA and VIKOR with Kuo and Liang’s method, we undertook to apply our technique to the data in Table 6 of Kuo and Liang’s paper. For this, we set the resolving coefficient $\rho$ to 0.5 and the strategy weight $\nu$ to 0, 0.5, and 1. The results in Table 15 suggest that our strategy yields the same ranking of international airports except for HKG and TPE airports, which are positioned 3 and 4 by our strategy, respectively, whereas these same airports are positioned 4 and 3 by Kuo and Liang’s strategy. However, they reported that when applying fuzzy SWA (Chen and Hwang 1992; Triantaphyllou and Lin 1996) and fuzzy TOPSIS (Chen 2000) to the same numerical data, the final ranking for these methods is: $KIX> NRT> HKG> TPE> SEL> SHA > PEK .$ It is worth mentioning that the ranking by fuzzy SWA and fuzzy TOPSIS is the same as final ranking obtained by our combining GRA and VIKOR method. Finally, we should mention that our technique is less computationally demanding than Kuo and Liang’s.

Table 15 The ranking results using our approach on the Kuo and Liang’s example for $\rho =0.5$

6 Conclusion

Conflicting criteria and ambiguous information are typically present in any decision-making process. To be able to process this information, it is crucial to develop powerful tools to deal with uncertainties. In this study, a novel generalized fuzzy divergence measure is proposed and validated for classical fuzzy sets. In addition, to demonstrate the efficacy of the proposed divergence, a comparative analysis is performed using some well-known fuzzy divergence measures as comparative benchmarks. An interesting aspect that emerged from this analysis is that the proposed divergence is extremely sensitive; it is able to detect any discrepancy between two fuzzy sets. This shows its superiority over the other measures of divergence. Furthermore, this work is also innovative as it establishes a new class of fuzzy knowledge measures derived from the Csiszár’s divergence class. Therefore, the suggested fuzzy divergence Dm is used to deduce a new fuzzy generalized knowledge measure, Km, which is compared to some prevalent information measures. The comparative examination demonstrated the applicability of the newly designed knowledge measure for capturing the level of precise information contained in a fuzzy set. Also, two new optimization models for criterion weight computation have been developed using the proposed measures. A numerical illustration shows that neither changing the generalization parameters of the proposed measures nor the lack of information about the weights of the criteria has any effect on the preferential order of the criteria. In addition, to address FMCDM concerns, a novel solution based on the proposed divergence measure was created, including the GRA and VIKOR techniques. To prove its efficiency, a case study, a comparative assessment, and a sensitivity analysis were provided. The proposed FMCDM approach holds a great deal of potential since it can determine the best option that matches almost all benefit criteria and inform professionals about which criterion makes a particular option less efficient. It also makes it simple to understand the advantages of some options over others from a decision-making point of view. This FMCDM technique does not require intensive computations and can be explored and used in a variety of fuzzy circumstances.