Abstract
The differentiation procedure of intuitionistic fuzzy sets (IFSs) is very important in multiple criteria decision-making (MCDM). The aim here is to introduce a fruitful class of knowledge measures related to the information provided in terms of IFSs. We present a class of knowledge measures of IFSs that are based on the two notions: the fuzziness and the intuitionism of an IFS. An experimental problem is employed to illustrate the weight determination method based on the proposed knowledge measures.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Nowadays, social cognitive procedures significantly influence multiple criteria decision-making (MCDM) [1,2,3,4] where the high uncertainty and complexity of socioeconomic environments are taken into consideration. For instance, Yang and Jiang [5] investigated the effect of social cognitive activities on the consistency convergence rate of group decision-making and also the consensus level of that group. Moreover, in order to show the impact of social cognition on the social decision-making, Lee and Harris [6] reviewed and discussed thoroughly a number of decision-making-based studies. Likewise, there have been several other contributions concerning the study of cognitive information of human beings in social cognitive procedures. Furthermore, the theory of cognitive information of fuzzy sets and their extensions has also come to perform important notes in fruitful research. For example, Farhadinia and Xu [4] introduced ordered weighted hesitant fuzzy sets to characterize cognitive information. Meng et al. [7] proposed linguistic interval hesitant fuzzy sets to elicit cognitive information with emphasis on the application of decision-making process. Zhao et al. [8] developed the concept of dual hesitant fuzzy preferences for extracting cognitive information. Moreover, Liu and Tang [9] concluded that interval neutrosophic uncertain linguistic variables can be used in handling the uncertainty in the cognitive processes.
Generally, in a MCDM problem, we are usually interested in finding the optimal alternative among a set of alternatives with reference to a number of criteria. In the decision-making process, the evaluation of criteria weights plays a considerable role, and it definitely impacts on the final ranking of alternatives. Conceptually, the techniques of determining criteria weights can be divided into three known classes on the basis of information acquisition entailing: objective technique, subjective technique and the integrated technique of both objective and subjective decision information. Using the objective technique, we may specify the criteria weights from the objective information involved in a decision matrix. The most applied objective technique is entropy technique [10]. The subjective technique reflects the subjective intuition or judgement in accordance with the preference information of criteria which is provided by the decision-maker employing the trade-off interrogation, questionnaires or interviews. Among a variety of subjective techniques, we may cite analytic hierarchy process (AHP) [11] and linear programming technique for multidimensional analysis of preference (LINMAP) [12]. The integrated technique, indeed, specifies the weights of criteria with the help of both objective and subjective decision information [13]. What should be considered here is the fact that all the above-mentioned classes are mainly based on the decision information provided in the form of real values, while representing the cognitive information in the form of intuitionistic fuzzy sets (IFSs) enables us to cope well with a situation where a decision organization describes uncertain information by the use of membership and nonmembership functions.
Of information measures, the entropy measure [6, 7, 9] is mostly used for determining the weights of criteria, and this is when the entropy measure is not always able to discriminate the information being represented in the form of IFSs. For example, if we consider the IFSs (μA(x1), νA(x1)) = (0.4,0.4) and (μA(x2), νA(x2)) = (0, 0), then the exiting entropy measures of them are all, or mostly, associated with the same result. Meanwhile, the IFS (μA(x2), νA(x2)) = (0, 0) returns no information, that is, we absolutely know nothing about that. It is worth mentioning that the two given IFSs are clearly different from a decision-making viewpoint. However, we observe that the ignorance of such a shortage in the discrimination of information may lead to consider an unreasonable weight for the criteria which results subsequently in unreliable order of alternatives. Such a deficiency was recently solved by Szmidt et al. [14], using an efficient measure known as knowledge measure. Szmidt et al.’s [14] knowledge measure is indeed constructed by taking both the hesitation index and the entropy measure of an IFS into account.
What is needed to be highlighted is that the entropy measure is not indeed the dual form of knowledge measure. This is because, in some cases, the entropy measure does not provide the answer to the question of how the fuzziness is distributed. However, we will be able to solve the complex real-world optimization problems with this accessible knowledge measure more easily. This fact encourages us to develop those weight determination methods which are established on the ground of knowledge measure for IFSs.
Up to now, a number of different kinds of knowledge measures for IFSs have been introduced. Szmidt at el. [14] claimed that the entropy measure may not be seen as the dual form of knowledge measure, and then they secondly introduced a knowledge measure of IFSs involving both the hesitation margin and the entropy measure of IFSs. In this line, Nguyen [15] pointed out that a knowledge measure should describe the difference of an IFS from the most IFS, and then they introduced a knowledge measure of IFSs by taking both the fuzziness and the intuitionism concepts into account. Das et al. [16] categorized some classes of extended forms of Szmidt at el.’s [14] knowledge measure for IFSs, and then they developed a method of determining the criteria weights in cases which information about weights is partly known or completely unknown. Guo [17] presented an axiomatic framework for measuring the amount of knowledge of IFSs, and then he developed the knowledge theory by introducing a robust model based on the distance between an IFS and its complement.
Delving into the exiting axiomatic frameworks for the knowledge measure of IFSs, we can observe that the only difference between them is related to the fourth axiom, and this difference traces back to the considered parameters in defining the knowledge measure of IFSs. In this study, we set out to introduce another kind of axiomatic framework for a knowledge measure of IFSs pertinent to the notions of fuzziness and intuitionism of an IFS. The real fact of the matter is that the fuzziness of an IFS returns the closeness parameter of membership and nonmembership degrees and the intuitionism of an IFS reflects the amount value of hesitancy degree.
This study is mainly structured into the following sections: Section 2 briefly reviews the concept of existing knowledge measures for IFSs with emphasis on their limitations. In Section 3, a class of new knowledge measures for IFSs is presented. Then, we compare the proposed knowledge measures with the existing ones using procedures given in two subsections: Part I and Part II. We provide a MCDM problem in Section 4 to examine the performance of the proposed knowledge measures in a model of optimization. Finally, some conclusions are offered in Section 5.
Existing Knowledge Measures and Their Limitations
Below are some definitions and concepts that can be used to frame the subsequent discussions.
Definition 1 (see, e.g. [11]) Suppose that X is the reference set on which an intuitionistic fuzzy set (IFS) A is defined by:
in which μA : X → [0, 1] and νA : X → [0, 1] denote, respectively, the membership and nonmembership degrees of the object x belonging to A.
Furthermore, the mappings μA and νA satisfy 0 ≤ μA(x) + νA(x) ≤ 1 for any x ∈ X. An intuitionistic index of x ∈ X is generally defined by πA(x) = 1 − μA(x) − νA(x) such that it satisfies the property 0 ≤ πA(x) ≤ 1. Specially, in the case where πA(x) = 0 for any x ∈ X, the corresponding IFS A reduces to a fuzzy set.
Definition 2 (see, e.g. [11]) Suppose that X is the reference set on which the two IFSs: A = {〈x, μA(x), νA(x)〉| x ∈ X} and B = {〈x, μB(x), νB(x)〉| x ∈ X} are to be considered. Then, it is defined:
The concept of entropy for IFSs, which captures the intuitive comprehension of fuzziness degree, was first presented by Szmidt and Kacprzyk [23] as follows:
Definition 3 [18] Suppose that X is the reference set on which the two IFSs A = {〈x, μA(x), νA(x)〉| x ∈ X} and B = {〈x, μB(x), νB(x)〉| x ∈ X} are defined. Then, the real-valued function E which satisfies
(E1) E(A) = 0 if and only if A is a crisp set.
(E2) E(A) = 1 if and only if μA(x) = νA(x) for any x ∈ X.
(E4) E(A) ≤ E(B) if A ⊆ B for μB(x) ≤ νB(x) or B ⊆ A for μB(x) ≥ νB(x) where x ∈ X is defined as the entropy measure of A.
Several studies were conducted regarding the subject of entropy measures for IFSs. Among them, we may refer to the work of Nguyen [15] in which
Although various entropy measures for IFSs have been introduced so far, they suffer some limitations in the comparison framework, specifically, in the case where μA(x) = νA(x) for some x ∈ X. For instance, it is expected that the amount of an entropy measure for two distinct elements (μA(x1), νA(x1)) = (0, 0) (i.e. there is no information at all) and (μA(x2), νA(x2)) = (0.4,0.4) (i.e. there is a positive amount of information as large as negative one) should be different. This is while the existing entropy measures of IFSs cannot differentiate accurately between these two IFSs.
Motivated by this fact, we feel that revisiting the counterpart of entropy measure, known as the knowledge measure, can be still significant and fruitful.
As seen in what follows, we are not able to say that the knowledge measure is the inverse of entropy measure. This is evident from the forth property which varies from one knowledge measure to another.
Nguyen’s Knowledge Measure [15]
Nguyen [15] defined a knowledge measure of IFSs as the normalized Euclidean distance measure from that IFS to the most IFS 〈x, 0, 0〉 in the form of
which satisfies the following axiomatic properties:
(k1) K(A) = 1 if and only if A is a crisp set.
(k2) K(A) = 0 if and only if πA(x) = 1 for any x ∈ X.
(k ′ 4) K(A) ≤ K(B) if and only if A is less fuzzy than B, that is, μA(x) ≤ μB(x) and νA(x) ≤ νB(x) for any x ∈ X.
Remark 1 Taking the property (k’4) into account, one can easily find that the term “is less fuzzy than” is not in accordance with that of “fuzziness” which was explained priory by the property (E4) in Definition 3.
Nguyen [15] also characterized an entropy measure based on its relationship with the knowledge measure KNg given by (12) as:
Keeping Remark 1 into consideration, it is not far from the truth to say that the knowledge-based entropy measure ENg (shown in [15] as the more logical choice of entropy) produces the results that are not completely in accordance with the intuitionism (refers to the last row of Table 1 in the current contribution)
Szmidt et al.’s Knowledge Measure [14]
Das et al. [16] reviewed firstly the following entropy measures of IFSs
where in the first entropy formula, the notation d serves to indicate the following distance measure
Secondly, Das et al. [16] investigated the knowledge measure of IFSs introduced by Szmidt et al. [14] as:
in order for computing the weights of criteria.
Keeping the knowledge measure KSKB in the mind, Das et al. [16] deduced that the bigger knowledge value of a criterion is assigned to that with the more weight.
Guo’s Knowledge Measure [17]
Guo [17] introduced firstly the following axiomatic definition of knowledge measure for IFSs:
(k1) K(A) = 1 if and only if A is a crisp set.
(k2) K(A) = 0 if and only if πA(x) = 1 for any x ∈ X.
(k4) K(A) ≥ K(B) if and only if A ⊆ B for μB(x) ≤ νB(x), or B ⊆ A for μB(x) ≥ νB(x) for any x ∈ X.
It deserves to pay attention that the property (k4) of a knowledge measure is more similar to the property (E4) describing the concept of “fuzziness” for an entropy measure in Definition 2.
Then, Guo [17] defined the following knowledge measure of IFSs:
By using the knowledge measure of Szmidt et al. [14] given by (22), Guo [13] showed that for the two IFSs A = 〈x, 0.0,0.3〉 and B = 〈x, 0.41,0.3〉 where A ⊂ B (that is, μA(x) = 0.0 ≤ μB(x) = 0.41 and νA(x) = 0.3 ≥ μB(x) = 0.3 for μB(x) ≥ νB(x)), it is concluded that
Clearly, the above results imply that the Guo’s [17] property (k4) is not satisfied, and therefore, we cannot judge correctly about the priority of knowledge measure based on the Guo’s axioms.
Moreover, Guo [17] expressed that no fixed numerical relationships exist between knowledge and entropy measures unless the above-mentioned property (k4) is to be satisfied.
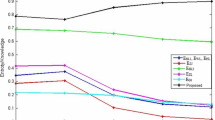
By the way, in the next section, we observe that the counterpart of Guo’s axiom (k4), denoted there by the axiom (K4), is defined differently, and it endows the proposed knowledge measures with the reasonable performance but not like that of the questionable existing knowledge measures. These outcomes have been documented in Table 1.
A New Class of Knowledge Measures for IFSs
Throughout this section, we are going to present a new concept of knowledge measure for IFSs on the basis of known parameters that describe the uncertainty involved in the input variables of a model.
Before any more progress can be made, let us first review some acceptable axioms about a logical definition of knowledge measure for IFSs.
When dealing with a knowledge measure of IFSs, we expect that:
(i) Everything should be known for sure, that is, the knowledge measure should obtain the maximum value 1 in the case where the IFS is crisp, and vice versa.
(ii) In the case where we do not know any more about the IFS, that is, μA(xi) = νA(xi) = 0, the knowledge measure should obtain the minimum value 0.
(iii) The knowledge measure should be symmetrical with respect to any IFS and its complement.
But for stating the property (iv), we cannot certainly say that if an IFS A is “less fuzzy” than an IFS B, then the IFS A possesses a larger amount of knowledge compared to the IFS B.
Up to now, we have formulated two different axioms (k’4) and (k4) which discuss this property from different points of view.
Now, let us develop the concept of knowledge measure for IFSs which satisfies the three first properties (k1), (k2) and (k3) together with a different forth property compared to the above-mentioned ones.
By taking the IFS A = {〈x, μA(x), νA(x)〉| x ∈ X} into account, we introduce the two concepts
where the notations △A and ∇A return the fuzziness and intuitionism of an IFS, respectively.
From the above convention, we observe that the notation △A denotes the closeness parameter of membership and nonmembership degrees and the notation ∇A denotes the amount value of hesitancy degree.
What needs to be highlighted is that the value of \( {\nabla}_A(x)=\frac{\mu_A(x)+{\nu}_A(x)}{2} \) determines only the information concerning on an element x ∈ A, while the amount value of knowledge is expected to be influenced by the amount value of distant measure between μA(x) and νA(x). This is clearly observable from the case where ∇A(x) remains fixed, but the amount value of distant measure is varied. For instance, from the cases μA(x) = 0.4, νA(x) = 0.4, μB(x) = 0.3 and νB(x) = 0.5, we observe that ∇A(x) = 0.4 = ∇B(x), while we expect that the knowledge measure for μA(x) = 0.4 and νA(x) = 0.4 is smaller that for μB(x) = 0.3 and νB(x) = 0.5. This is exactly the reason that we should consider the term △A(x) = ∣ μA(x) − νA(x)∣ in defining the knowledge measure of an IFS A.
Definition 4 Suppose that X is the reference set on which the IFS A = {〈x, μA(x), νA(x)〉| x ∈ X} is defined. Then, we introduce the real-valued function
in which ℵ : [0, 1] × [0, 1] → [0, 1] represents the negation (or the complement) operator, and it satisfies the following axiomatic requirements:
(N1) ℵ(0) = 1 and ℵ(1) = 0.
(N2) If x ≤ y, then ℵ(x) ≥ ℵ(y) for any x, y ∈ [0, 1].
(N3) ℵ(ℵ(x)) = x for any x ∈ [0, 1].
and the functional θ : [0, 1] × [0, 1] → [0, 1] satisfies
(θ1) θ(x, y) = 0 if and only if x = 0 or y = 0;
(θ2) θ(x, y) = 1 if and only if x = 1 and y = 1;
(θ3) θ(x, y) is monotonically non-decreasing in both x, y ∈ [0, 1].
The above measure K, which is defined on a single-element IFS A can be extended to that defined on a general IFS A = {〈xi, μA(xi), νA(xi)〉| xi ∈ X} as the following
It is interesting to note that the above function K satisfies the following axiomatic properties:
Theorem 1 Suppose that X is the reference set on which the IFS
A = {〈x, μA(x), νA(x)〉| x ∈ X} is defined. Then, the real-valued function K introduced by (27) is a knowledge measure of A, and it satisfies
(K1) K(A) = 1 if and only if A is a crisp set;
(K2) K(A) = 0 if and only if πA(x) = 1 for any x ∈ X;
(K4) If ∇A(x) (or △A(x)) is fixed, then K(A) increases as △A(x) (or ∇A(x)) increases.
Proof. We need to prove that the measure K satisfies all the properties (K1)–(K4).
Proof of (K1): From the definition of negation operator, it is easily seen that K(A) = 1 or ℵ[θ(ℵ[∇A(xi)], ℵ[△A(xi)])] = 1 for any xi ∈ X if and only if θ(ℵ[∇A(xi)], ℵ[△A(xi)]) = 0. Thus, from the property (θ1), we conclude that ℵ[∇A(xi)] = 0 or ℵ[△A(xi)] = 0 for any xi ∈ X. These relations are held if and only if ∇A(xi) = 1 or △A(xi) = 1 for any xi ∈ X. Since for any xi ∈ X, we have \( 0\le {\nabla}_A\left({x}_i\right)=\frac{\mu_A\left({x}_i\right)+{\nu}_A\left({x}_i\right)}{2}\le \frac{1}{2} \); hence it must be held △A(xi) = ∣ μA(xi) − νA(xi) ∣ = 1 for any xi ∈ X. Therefore, we result in K(A) = 1 if and only if μA(xi) = 1 and νA(xi) = 0 or μA(xi) = 0 and νA(xi) = 1 for any xi ∈ X which verifies that the IFS A is a crisp set.
Proof of (K2): The relation K(A) = 0 holds if and only if
ℵ[θ(ℵ[∇A(xi)], ℵ[△A(xi)])] = 0 for any xi ∈ X, that is, θ(ℵ[∇A(xi)], ℵ[△A(xi)]) = 1, or by the use of property (θ2), we get ℵ[∇A(xi)] = 1 and ℵ[△A(xi)] = 1. This relation holds if and only if ∇A(xi) = 0 and △A(xi) = 0 for any xi ∈ X which imply that μA(xi) = νA(xi) = 0. That is, it yields that πA(xi) = 1 − μA(xi) − νA(xi) = 1 for any xi ∈ X.
Proof of (K3): From definition of K(A), we can easily find that \( K(A)=\frac{1}{n}\sum \limits_{i=1}^n\aleph \left[\theta \left(\aleph \left[{\nabla}_A\left({x}_i\right)\right],\aleph \left[{\triangle}_A\left({x}_i\right)\right]\right)\right]=\frac{1}{n}\sum \limits_{i=1}^n\aleph \left[\theta \left(\aleph \left[{\nabla}_{A^c}\left({x}_i\right)\right],\aleph \left[{\triangle}_{A^c}\left({x}_i\right)\right]\right)\right]=K\left({A}^c\right). \)
Proof of (K4): Let A = {〈xi, μA(xi), νA(xi)〉| xi ∈ X} and
B = {〈xi, μB(xi), νB(xi)〉| xi ∈ X} be two IFSs such that ∇A(xi) ≤ ∇B(xi) and △A(xi) = △B(xi). Then, we conclude that ℵ[∇A(xi)] ≥ ℵ[∇B(xi)] and ℵ[△A(xi)] = ℵ[△B(xi)]. By the use of property (θ3), we can reach at θ(ℵ[∇A(xi)], ℵ[△A(xi)]) ≥ θ(ℵ[∇B(xi)], ℵ[△B(xi)]) for any xi ∈ X, and further, ℵ[θ(ℵ[∇A(xi)], ℵ[△A(xi)])] ≤ ℵ[θ(ℵ[∇B(xi)], ℵ[△B(xi)])]. This means that K(A) ≤ K(B).
The other assertion which in turn implies ∇A(xi) = ∇B(xi) and △A(xi) ≤ △B(xi) is proved similarly.
Now, we are able to extend the class of knowledge measures by considering the following family of negation operators ℵ and functionals θ:
and
Let us here generate a number of knowledge measures for IFSs by the use of standard complement ℵ(x) = 1 − x together with the latter kinds of operations θ as the followings:
Comparative Study
What needs to be considered here is that the proposed axiomatic framework for measuring the knowledge value of IFSs is independent of the two frameworks given by Szmidt et al. [14] and Guo [17].
If we take a look at the proposed knowledge measures, then it will be obvious that the main intention of presenting such measures is to consider a combination of two acceptable factors, including the degree of fuzziness (i.e. the distance measure of membership and nonmembership) and the lack of knowledge (i.e. the hesitancy or the non-specificity of an IFS). Actually, the first factor, which shows the amount of fuzziness for an IFS, measures how far the distance between the IFS and a crisp set is. The second factor, which shows the amount of non-specificity associated with an IFS, measures how much the unknown data is collected by the use of summation of membership and nonmembership values.
However, in order to draw a complete picture on the implementation of proposed knowledge measures, we divide the comparison section into the following two parts:
Part I
Before going more in details, let us define the following entropy measures which are constructed based on their relationship with the knowledge measures \( {K}_{\theta_1} \), \( {K}_{\theta_2} \), \( {K}_{\theta_3^{\frac{1}{2}}} \) and \( {K}_{\theta_4^2} \) given by (35)–(38):
It is interesting to note that the above entropy measures satisfy the following axiomatic properties:
Theorem 2 Suppose that X is the reference set on which the IFS
A = {〈x, μA(x), νA(x)〉| x ∈ X} is defined. Then, the real-valued functions \( {E}_{\theta_1} \), \( {E}_{\theta_2} \), \( {E}_{\theta_3^{\frac{1}{2}}} \) and \( {E}_{\theta_4^2} \) introduced by (39)–(42) are entropy measures of A, and they satisfy:
Eθ(A) = 0 if and only if A is a crisp set.
Eθ(A) = 1 if and only if πA(x) = 1 for any x ∈ X.
If ∇A(x) (or △A(x)) is fixed, then Eθ(A) increases as △A(x) (or ∇A(x)) decreases.
Proof. The proof of the above axioms are immediate from all the properties (K1)-(K4) in Theorem 3.
In this part, we compare the proposed entropy measures with some existing entropy measures that previously given by (6)–(11) and (13).
Nguyen [15] considered a number of nine single-element IFSs as A1 = 〈x, 0.7,0.2〉, A2 = 〈x, 0.5,0.3〉, A3 = 〈x, 0.5,0〉, A4 = 〈x, 0.5,0.5〉, A5 = 〈x, 0.5,0.4〉, A6 = 〈x, 0.6,0.2〉, A7 = 〈x, 0.4,0.4〉, A8 = 〈x, 1.0,0.0〉 and A9 = 〈x, 0.0,0.0〉.
In order to further analyse, we append to the above set of nine IFSs, another single-element IFS, which has not been considered by Nguyen [15]. This single-element IFS is nothing else except A10 = 〈x, 0.0,1.0〉.
As shown in Table 1, we use the bold type to distinguish the unreasonable cases which are as the followings:
• Measuring Ebb for the IFSs A1 = 〈x, 0.7,0.2〉 and A5 = 〈x, 0.5,0.4〉 results in Ebb(A1) = Ebb(A5) = 0.1, and moreover, measuring Ebb for the IFSs A2 = 〈x, 0.5,0.3〉, A6 = 〈x, 0.6,0.2〉 and A7 = 〈x, 0.4,0.4〉 give rise to Ebb(A2) = Ebb(A6) = Ebb(A7) = 0.2. Furthermore, Ebb cannot differentiate between A9 = 〈x, 0.0,0.0〉 and A10 = 〈x, 0.0,1.0〉, and it returns the same value 1.00 for both of them. These results are unreasonable, and they are come from the fact that the calculation of Ebb is only based on the hesitation margin, and it does not return the relation between membership and nonmembership degrees known as the fuzziness factor;
• Measuring \( {E}_{hc}^{\frac{1}{2}} \) for the IFSs A3 = 〈x, 0.5,0.0〉 and A4 = 〈x, 0.5,0.5〉 results in \( {E}_{hc}^{\frac{1}{2}}\left({A}_3\right)={E}_{hc}^{\frac{1}{2}}\left({A}_4\right)=0.83 \), and moreover, measuring \( {E}_{hc}^{\frac{1}{2}} \) for the IFSs A9 = 〈x, 0.0,0.0〉 and A10 = 〈x, 0.0,1.0〉 give rise to, respectively, \( {E}_{hc}^{\frac{1}{2}}\left({A}_9\right)=0.00 \) and \( {E}_{hc}^{\frac{1}{2}}\left({A}_{10}\right)=2.00 \) which are obviously unreasonable.
Referring again to Table 1, we observe that similar drawback occurs when the entropy measures \( {E}_{hc}^1 \), \( {E}_{hc}^2 \), \( {E}_{hc}^3 \), \( {E}_r^{\frac{1}{3}} \) and \( {E}_r^{\frac{1}{2}} \) are applied to the IFSs A3 = 〈x, 0.5,0.0〉 and A4 = 〈x, 0.5,0.5〉.
• Measuring Esk, Evs1 and Evs2 for the IFSs A4 = 〈x, 0.5,0.5〉 and A7 = 〈x, 0.4,0.4〉 results in the same value of 1, while the IFSs are clearly different. Therefore, the outcomes Esk(A4) = Esk(A7) = 1.00, Evs1(A4) = Evs1(A7) = 1.00 and Evs2(A4) = Evs2(A7) = 1.00 are not rational.
• Measuring ENg for the IFS A10 = 〈x, 0.0,1.0〉 results in the unreasonable outcome ENg(A10) = 0.29.
In view of the above results, one can easily observe that the outcomes of the proposed entropy measures \( {E}_{\theta_1} \), \( {E}_{\theta_2} \), \( {E}_{\theta_3^{\frac{1}{2}}} \) and \( {E}_{\theta_4^2} \) are in agreement with intuition.
Part II
In this part, we consider once again the problem which was examined by Guo [17] and Das et al. [16] to show the performance of proposed knowledge measures compared to the other existing ones.
Suppose that A = {〈x, μA(x), νA(x)〉| x ∈ X} is an IFS whose power of σ is defined by Aσ = {〈x, (μA(x))σ, 1 − (1 − νA(x))σ〉| x ∈ X}. In the case where A is treated as the linguistic variable large, we may thus interpret
• \( {A}^{\frac{1}{2}} \) as the more or less large concept
• A2 as the very large concept
• A3 as the quite very large concept
• A4 as the very large concept
Case 1. Let A = {〈6,0.1,0.8〉, 〈7,0.3,0.5〉, 〈8,0.6,0.2〉, 〈9,0.9,0.0〉, 〈10,1.0,0.0〉} be considered for the price evaluation of five houses indexed by 6, 7, 8, 9 and 10. In this regard, we will be able to form X = {6, 7, 8, 9, 10}. From a mathematical point of view, the ranking order of entropy measures of Aσ should be:
With the above relationship at hand, we are not still able to be assured that there is a reverse order between the amount values of knowledge measure. However, we often expect from the viewpoint of linguistic treating that
Table 2 represents the results of some entropy measures, the existing knowledge measures and the proposed knowledge measures.
Following from Table 2, we observe that the results of entropy measure Esk and knowledge measure KG are quite in accordance with the facts (43) and (44), while the entropy measure EZJ and knowledge measure KSKB do not perform well. This is while all the proposed knowledge measures \( {K}_{\theta_1} \), \( {K}_{\theta_2} \), \( {K}_{\theta_3^{\frac{1}{2}}} \) and \( {K}_{\theta_4^2} \) do as expected of them. As discussed before, here notice that the performance of knowledge measures should not be recognized as a necessity in accordance with the entropy measures.
Case 2. In this case, we only change the middle point of
A = {〈6,0.1,0.8〉, 〈7,0.3,0.5〉, 〈8,0.6,0.2〉, 〈9,0.9,0.0〉, 〈10,1.0,0.0〉} to 〈8,0.5,0.4〉 for reducing the degree of hesitancy of 8, and therefore the resulted IFS will be denoted by
As all we know, the greater amount value of entropy of an IFS results in the higher degree of fuzziness, and conversely, the greater amount value of knowledge of an IFS results in the lower degree of fuzziness. This is exactly what we find in the data provided in Table 3.
Case 3. Again, we change only the middle point of
A = {〈6,0.1,0.8〉, 〈7,0.3,0.5〉, 〈8,0.6,0.2〉, 〈9,0.9,0.0〉, 〈10,1.0,0.0〉} to 〈8,0.5,0.5〉 for reducing the degree of hesitancy of 8, and thus, the resulted IFS is denoted by C = {〈6,0.1,0.8〉, 〈7,0.3,0.5〉, 〈8,0.5,0.5〉, 〈9,0.9,0.0〉, 〈10,1.0,0.0〉}. Similar to Case 2, the behaviour of all data presented in Table 4 are as expected for the value of entropies Esk and EZJ, knowledge measures KSKB and KG, and the proposed knowledge measures \( {K}_{\theta_1} \), \( {K}_{\theta_2} \), \( {K}_{\theta_3^{\frac{1}{2}}} \) and \( {K}_{\theta_4^2} \) at the IFS C.
Determination of Criteria Weights in MCDM with Respect to Knowledge Measures
Here, we are going to investigate a MCDM problem in which a single expert evaluates the alternative A = {A1, …, Am} with respect to the criteria C = {C1, …, Cn} corresponding to the weight w = (w1, …, wn) satisfying 0 ≤ wj ≤ 1 and \( \sum \limits_{j=1}^n{w}_j=1 \). In this regard, the decision matrix is formed as
where \( {d}_{ij}=\left({\mu}_{d_{ij}},{\nu}_{d_{ij}}\right) \) denotes the evaluation value of alternative Ai with respect to the criterion Cj given by the single expert.
In the next step of decision-making process, the aim is to determine the weights of criteria by the use of proposed knowledge measures. To do this end, we suppose that the knowledge-based decision matrix K ≔ K(D) is in the form of
where [kij]m × n ≔ [K(dij)]m × n, and each array kij indicates the knowledge measure value of each IFS dij belonging to the above-mentioned decision matrix D.
What is noteworthy to mention is that the information of criteria weights is usually partly known or even completely unknown. To cope with this situation, we consider here two cases: one is the partly known information case and the other is the case of completely unknown information on criteria weights.
Case of Partly Known Information
In most of the real-world decision-making problem, the decision-maker may access to only partial information about the weights of criteria. In this case, the optimal weights can be obtained using the following knowledge-based optimization problem
where the set of W describes the information on the weights of criteria.
Case of Completely Unknown Information
This case describes the situation where the information on the weights of criteria is completely unknown. In this case, the knowledge-based weights can be determined as
in which 0 ≤ wj ≤ 1 for j = 1, …, n, \( {\sum}_{j=1}^n{w}_j=1 \) and moreover, \( {k}_j={\sum}_{i=1}^m{k}_{ij} \) for j = 1, …, n.
By the weight information at hand, we are now in a position to aggregate all the information on each alternative Ai according to the criteria Cj’s. In the same line of Das et al [16], we are able to implement the weighted intuitionistic fuzzy arithmetic mean operator as the following:
Now, we can derive the priority of alternatives by the help of priority of score functions which are calculated by
Case Study
An investment company is going to invest an amount of money in the best possible option. For this purpose, a number of companies including A1, car company; A2, food company; A3, computer company; and A4, arm company are taken into consideration. In order to assess these alternatives, it needs to consider some criteria including C1, the risk; C2, the growth; C3, the environmental impact; and C4, the social political impact analyses. However, if the above-mentioned alternatives are assessed by IFSs in accordance with the given criteria, then the experts will face to the weights of criteria w = (w1, w2, w3, w4) in the form of partially known or completely unknown.
Let the decision-making matrix be given by:
If we employ the proposed knowledge measures \( {K}_{\theta_1} \), \( {K}_{\theta_2} \), \( {K}_{\theta_3^{\frac{1}{2}}} \) and \( {K}_{\theta_4^2} \) for the above decision matrix D, then we get
For the notational simplicity from now on, we will denote the matrix K∗(D) again by K∗.
Now, by the knowledge measures at hand, we are able to compute the weights of the criteria in the two following situations:
Case of Partly Known Information
In the case where the weights of criteria are partly known, we are able to construct the following linear programming problem
where the set of W is considered as
and further, [kij]m × n ≔ [K(dij)]m × n indicates the knowledge-based decision matrix K ≔ K(D). Here, K could be one of the knowledge measures \( {K}_{\theta_1} \), \( {K}_{\theta_2} \), \( {K}_{\theta_3^{\frac{1}{2}}} \) and \( {K}_{\theta_4^2} \).
The construction of the above linear programming problem is exactly like that considered by Das et al. [16].
Now, with respect to each knowledge measure matrix of those given by (48)–(51), we can calculate \( {k}_j=\sum \limits_{i=1}^4{k}_{ij} \) for j = 1, 2, 3, 4 as the followings:
which each of them gives rise to a linear programming problem in the form of (P) mentioned above. By the way, solving these optimization problems using MATLAB R2016 code “x = linprog(f, A, b, Aeq, beq, lb, ub)” results in the following equal vectors of weights:
Case of Completely Unknown Information
Using the rule described by (45), we can now calculate the weights of the criteria as the followings:
where in all four cases, we have
Now, we are ready to compute the final aggregated values for each alternative according to the rule of (46), and then order them. These results are obtained by taking the two cases of partly known and completely unknown information into account as follows:
Case of partly known information
Since all weight vectors are the same in this case, that is, \( {w}^{K_{\theta_1}}={w}^{K_{\theta_2}}={w}^{K_{\theta_3^{\frac{1}{2}}}}={w}^{K_{\theta_4^2}} \), we then get
Case of Completely Unknown Information
In this case, we have four different sub-cases including:
Case 1. (for \( {w}^{K_{\theta_1}} \))
Case 2. (for \( {w}^{K_{\theta_2}} \))
Case 3. (for \( {w}^{K_{\theta_3^{\frac{1}{2}}}} \))
Case 4. (for \( {w}^{K_{\theta_4^2}} \))
Now, we are in a stage in which the score function of IFSs, denoted here by the notation AGG, can be calculated as the followings:
Case of Partly Known Information
Since in this case we have \( {w}^{K_{\theta_1}}={w}^{K_{\theta_2}}={w}^{K_{\theta_3^{\frac{1}{2}}}}={w}^{K_{\theta_4^2}} \), therefore, the result will be:
which give rise to A1 > A4 > A3 > A2.
Case of Completely Unknown Information
In this case, there exist four distinguished sub-cases which are:
Case 1. (for \( {w}^{K_{\theta_1}} \))
thus A3 > A1 > A4 > A2.
Case 2. (for \( {w}^{K_{\theta_2}} \))
thus A3 > A1 > A4 > A2.
Case 3. (for \( {w}^{K_{\theta_3^{\frac{1}{2}}}} \))
thus A3 > A1 > A4 > A2.
Case 4. (for \( {w}^{K_{\theta_4^2}} \))
thus A3 > A1 > A4 > A2.
Eventually, there is a tendency to compare the results of the proposed knowledge measures with those of the other existing knowledge measures for IFSs which were previously denoted in this contribution as KNg, KSKB and KG. Keeping the statement of problem given in the beginning of Section 5.1 in the mind, we consider the two situations: partly known and completely unknown. Then, the problem is resolved by the use of the knowledge measures KNg, KSKB and KG whose results are compared with that of the proposed knowledge measures in Table 5.
From the data in Table 5, we can observe that most of ranking orders are the same for both cases including partly known and completely unknown weights. The only different results are related to the knowledge measure KSKB, and this is not surprising, because we showed previously that this knowledge measure of Das et al. [16] bears some drawbacks.
Conclusions and Future Works
In this contribution, we defined a class of knowledge measures for IFSs on the basis of different axiomatic framework. Indeed, the proposed knowledge measures have been provided to relate the two notions of fuzziness and intuitionism of an IFS. The former reflects the closeness parameter of membership and nonmembership degrees, and the latter returns the amount value of hesitancy degree. By the use of a practical application, we employed the proposed knowledge measures to deal with a MCDM problem for determining the criteria weights. The results verify that the proposed knowledge measures for IFSs are most accurate and confidential compared to the existing ones and have many possible applications, particularly, in decision-making situations.
References
Farhadinia B. A multiple criteria decision making model with entropy weight in an interval-transformed hesitant fuzzy environment. Cogn Comput. 2017;9:513–25.
Farhadinia B. Determination of entropy measures for the ordinal scale-based linguistic models. Inf Sci. 2016;369:63–79.
Farhadinia B, Herrera-Viedma E. Entropy measures for hesitant fuzzy linguistic term sets using the concept of interval-transformed hesitant fuzzy elements. International Journal of Fuzzy Systems. 2018;20:2122–34.
Farhadinia B, Xu ZS. Distance and aggregation-based methodologies for hesitant fuzzy decision making. Cogn Comput. 2017;9:81–94.
L. Yang, M. Jiang, Dynamic group decision making consistence convergence rate analysis based on inertia particle swarm optimization algorithm. In: International joint conference on artificial intelligence, Hainan Island 2009; 492-496.
Lee VK, Harris LT. How social cognition can inform social decision making. Front Neurosci. 2013;7:259.
Meng FY, Wang C, Chen XH. Linguistic interval hesitant fuzzy sets and their application in decision making. Cogn Comput. 2016;8:52–68.
Zhao N, Xu ZS, Liu FJ. Group decision making with dual hesitant fuzzy preference relations. Cogn Comput. 2016;8:1119–43.
Liu PD, Tang GL. Multi-criteria group decision-making based on interval neutrosophic uncertain linguistic variables and Choquet integral. Cogn Comput. 2016;8:1036–56.
Liu P, Zhang X. Research on the supplier selection of a supply chain based on entropy weight and improved ELECTRE-III method. Int J Prod Res. 2011;49:637–46.
Ishizaka A. Analytic hierarchy process and its extensions, New Perspectives in Multiple Criteria Decision Making, Springer 2019.
Xia HC, Li DF, Zhou JY, Wang JM. Fuzzy LINMAP method for multiattribute decision making under fuzzy environments. J Comput Syst Sci. 2006;72:741–59.
Rao R, Patel B. A subjective and objective integrated multiple attribute decision making method for material selection. Mater Des. 2010;31:4738–47.
Szmidt E, Kacprzyk J, Bujnowski P. How to measure the amount of knowledge conveyed by Atanassov’s intuitionistic fuzzy sets. Inf Sci. 2014;257:276–85.
Nguyen H. A new knowledge-based measure for intuitionistic fuzzy sets and its application in multiple attribute group decision making. Expert Syst Appl. 2015;42:8766–74.
Das S, Dutta B, Guha D. Weight computation of criteria in a decision-making problem by knowledge measure with intuitionistic fuzzy set and interval-valued intuitionistic fuzzy set. Soft Comput. 2016;20:3421–42.
Guo K. Knowledge measure for Atanassov’s intuitionistic fuzzy sets. IEEE Trans Fuzzy Syst. 2016;24:1072–8.
Szmidt E, Kacprzyk J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001;118:467–77.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author declares that he has no conflict of interest.
Human and Animal Rights
This article does not contain any studies with human participants or animals performed by the author.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Farhadinia, B. A Cognitively Inspired Knowledge-Based Decision-Making Methodology Employing Intuitionistic Fuzzy Sets. Cogn Comput 12, 667–678 (2020). https://doi.org/10.1007/s12559-019-09702-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12559-019-09702-7