A Modified Numerical Method Based on Bernstein Wavelets for Numerical Assessment of Fractional Variational and Optimal Control Problems

Abstract

The main idea of this work is to present a novel scheme based on Bernstein wavelets for finding numerical solution of two classes of fractional optimal control problems (FOCPs) and one class of fractional variational problems (FVPs). First, we present an approximation for fractional derivative using the Laplace transform. Then, the obtained integer-order problems are converted into equivalent variational problems. By using the Bernstein wavelets, activation functions and the Gauss–Legendre integration scheme, problems are transformed to algebraic systems of equations. Finally, these systems are solved employing Newton’s iterative scheme. Error bound for the best approximation is given. Also, we propose a scheme to determine the number of basis functions necessary to get a certain precision. In order to verify that the mentioned scheme is applicable and powerful for solving FOCPs and FVP, some numerical experiments have been provided.

1 Introduction

Recently, numerous phenomena in various fields of applied science and engineering have been simulated by fractional differential equations. In detail, these equations have appeared in electromagnetics, viscoelasticity, fluid mechanics, electrochemistry, biological population models, signals processing, continuum, heat transfer in heterogeneous media, ultracapacitor, pharmacokinetics and statistical mechanics (Chen et al. 2013; Jajarmi and Baleanu 2018; Wang and Zhou 2011; Heydari et al. 2016; Popovic et al. 2015).

Therefore, many numerical schemes have been presented for finding numerical solution of these problems, for instance, Adomian decomposition technique (Babolian et al. 2014), variational iteration technique (Yang et al. 2010), bivariate Müntz wavelets technique (Rahimkhani and Ordokhani 2020), fractional alternative Legendre functions technique (Rahimkhani and Ordokhani 2020), fractional Lucas optimization technique (Dehestani et al. 2022), fractional Chelyshkov wavelets technique (Rahimkhani et al. 2019) and orthonormal Bernoulli wavelets neural network technique (Rahimkhani and Ordokhani 2021).

The FOCP are extensions of the classical ones. In such problems, the dynamical system and/or the objective function may be involved with fractional operators. The main reason to study such problems is the fact that there are many problems in which the behavior of their dynamical systems can concisely be expressed in terms of fractional operators, for instance, in the analog fractional-order controller in temperature and motor control applications (Bohannan 2008), fractional control of heat diffusion systems (Suarez et al. 2008), a fractional-order HIV-immune system with memory (Jesus and Machado 2008), a fractional adaptation scheme for lateral control of an autonomous guided vehicle (Ding et al. 2012), mechanical systems (Kiryakova 1994), automotive vehicle design (Bell 2004), manufacturing processes (Samko et al. 1993), transportation systems (Jajarmi and Baleanu 2018), HIV/AIDS epidemic model with random testing and contact tracing (Kiryakova 1994) and physics (Tripathy et al. 2015). FOCPs can be introduced by applying various definitions of fractional derivatives, such as the Caputo fractional derivatives and the Riemann–Liouville. These problems have been studied by many authors; for example, Agrawal (2004) introduced a general formulation and a numerical technique for FOCPs. Lotfi et al. (2013) applied an approximate direct technique for finding solution of a general class of FOCPs. Alipour et al. (2013) investigated multi-dimensional FOCPs by using the Bernstein polynomials. Rabiei et al. (2018a) applied fractional-order Boubaker functions for solving a class of FOCPs. Rahimkhani et al. (2016) used the Bernoulli wavelet method to solve delay FOCPs. Mashayekhi and Razzaghi (2018) proposed a technique based on hybrid of block pulse functions and Bernoulli polynomials for finding approximate solution of FOCPs. Sabermahani et al. (2019) introduced fractional order Lagrange polynomials and used them to solve FOCPs. Rabiei and Parand (2020) investigated the Chebyshev collocation approach for finding numerical solution of FOCPs.

Also, different numerical schemes have been introduced for solving FVPs, for example, Rayleigh–Ritz scheme (Khader 2015), polynomial basis functions scheme (Lotfi and Yousefi 2013), fractional finite element scheme (Agrawal 2008), Müntz–Legendre polynomials scheme (Ordokhani and Rahimkhani 2018), fractional Jacobi functions scheme (Zaky et al. 2018), shifted Chebyshev polynomials scheme (Ezz-Eldien et al. 2018), modified wavelet scheme (Dehestani et al. 2020), etc.

Special kinds of oscillatory functions are wavelets that they have been used in time–frequency analysis, fast algorithms, edge extrapolation, image processing, signal processing and edge extrapolation (Chui 1997). We note that there are some advantages, for instance, compact support, orthogonality and the ability to show the functions at various levels of resolution. Wavelets as a useful class of bases have been applied to solve several problems of the dynamical systems. For example, Haar wavelets have been used to solve of the Riccati differential equation (Li et al. 2014). Müntz–Legendre wavelets have been introduced for finding numerical solution of fractional differential equations (FDEs) with delay (Rahimkhani et al. 2018). Bernoulli wavelets have been used for solving variable FDEs (Soltanpour Moghadam et al. 2020). Genocchi wavelets have been used for solving of various kinds of FDEs with delay (Dehestani et al. 2019). Fractional-order Bernoulli wavelets have been used for numerical analysis of the pantograph FDEs (Rahimkhani et al. 2017). Fractional Chelyshkov wavelets (Rahimkhani et al. 2019) have been introduced for the approximate solution of distributed-order FDEs.

Bernstein wavelets have many useful properties over an interval [0, 1] (we can deduce these properties from the Bernstein polynomials properties Bhatti and Bracken 2007). The Bernstein wavelets bases vanish except the first polynomial at $t=\frac{\hat{n}}{2^{k-1}}$ and the last polynomial at $t=\frac{\hat{n}+1}{2^{k-1}}$, over any interval $[\frac{\hat{n}}{2^{k-1}}, \frac{\hat{n}+1}{2^{k-1}}]$. It also ensures that the sum at any point t of all the Bernstein wavelet is $2^{k-1}\beta _{i, M}$ and every Bernstein wavelets is positive for all real t on the region $t\in (\frac{\hat{n}}{2^{k-1}}, \frac{\hat{n}+1}{2^{k-1}})$. A simple code written in Mathematica or Maple can be applied to obtain all the non-zero Bernstein wavelets of any order m over interval $t\in [\frac{\hat{n}}{2^{k-1}}, \frac{\hat{n}+1}{2^{k-1}}]$. The Bernstein wavelets are advantageous for practical computations, on account of its intrinsic numerical stability. The Bernstein wavelets have many applications for finding numerical solution of different FDEs, fractional integral-differential equations and fractional optimal control problems. Also, the wavelet method is computer oriented; thus, solving higher-order equation becomes a matter of dimension increasing. The solution is convergent, even if the size of increment is large. Wavelet basis has two degrees of freedom which increase the accuracy of the method. The solution is of multiresolution type. Also, they have the following properties (Rahimkhani and Ordokhani 2021):

• The basis set can be improved in an systematic way

• Different resolutions can be used in different regions of space

• The coupling between different resolution levels is easy

• There are few topological constraints for increased resolution regions

• The Laplace operator is diagonally dominant in an appropriate wavelet basis

• The matrix elements of the Laplace operator are very easy to calculate

• The numerical effort scales linearly with respect to system size.

Here our target is to present a new method based on Bernstein wavelets and activation functions for solving of FOCPs and FVP. First, we present an approximation for fractional derivative using the Laplace transform. Then, the under study problems are converted into equivalent variational problems. By using the Bernstein wavelets method and activation functions, the problems are converted to algebraic systems of equations. Finally, these systems are solved employing the Gauss-Legendre integration method and Newton’s iterative technique. Some of the most important advantages of the proposed scheme are listed in the following:

• Easy computation and simple implementation.

• The obtained numerical solution with this method is a continuous and differentiable solution; also these solutions satisfy the initial and boundary conditions.

• We did not use any operational matrix (which reduces the calculation error and CPU time).

• A small value of Bernstein wavelets is needed to achieve high accuracy and satisfactory results.

• By applying this scheme, consideration problems are transformed into a system of algebraic equations that can be solved via a suitable numerical method.

• Used approximate is based on hybrid of Bernstein wavelets and activation functions instead of a linear combination of wavelets, so applied approximate solution is more efficient.

This paper is organized as follows. In Sect. 2, we present some preliminaries about Bernstein wavelets and activation functions. In Sect. 3, we describe the understudy problems. In Sect. 4, we offer a numerical method for finding numerical solution of the fractional optimal control problems and fractional variational problems. In Sect. 5, we propose error bound for the best approximation. In Sect. 6, a criterion for choosing the number of wavelets is presented. In Sect. 7, we report our numerical findings and demonstrate the accuracy of the new numerical scheme by considering six test examples. Finally, concluding remarks are given in Sect. 8.

2 Preliminaries and Notations

2.1 Bernstein Wavelets

The Bernstein wavelets are introduced over [0, 1) as:

$$\begin{aligned} \psi _{n, i, m }(t)= \left\{ \begin{array}{ll} 2^{\frac{k-1}{2}}\beta _{i, m}B_{i,m}(2^{k-1}t-\hat{n}),&\frac{\hat{n}}{2^{k-1}} \le t < \frac{\hat{n}+1}{2^{k-1}},\\ 0, & \text {otherwise}, \end{array} \right. \end{aligned}$$

(1)

with

$$\begin{aligned} \beta _{i,m}= \frac{\sqrt{(2m+1)\left( {\begin{array}{*{5}c} 2m \\ 2i \\ \end{array}} \right) }}{\left( {\begin{array}{*{5}c} m \\ i \\ \end{array}} \right) }, \end{aligned}$$

where k can assume any positive integer that determines the number of subintervals, $n=1, 2, \ldots , 2^{k-1},$ shows the location of a subinterval and refers to the subinterval number, $i=0, 1, \ldots , m, (m=M-1)$ is the order of the Bernstein polynomial and $t \in [0 , 1)$ denotes the time. Also, $B_{i,m}(t)$ are the Bernstein polynomials over [0, 1] , as

$$\begin{aligned} B_{i, m}(t) & = \left( {\begin{array}{*{5}c} m \\ i \\ \end{array}} \right) t^{i} (1-t)^{m-i}\nonumber \\= & \sum _{j=0}^{m-i}\left( {\begin{array}{*{5}c} m \\ i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} m-i \\ j \\ \end{array}} \right) (-1)^{m-i-j}t^{m-j}, 0\le i \le m. \end{aligned}$$

(2)

Bernstein polynomials satisfy the following property (Nemati 2017):

$$\begin{aligned} \int _{0}^{1} B_{i,m}(t) B_{j, n}(t) dt =\frac{ \left( {\begin{array}{*{5}c} m \\ i \\ \end{array}} \right) \left( {\begin{array}{*{5}c} n \\ j \\ \end{array}} \right) }{(m+n+1) \left( {\begin{array}{*{5}c} m+n \\ i+j \\ \end{array}} \right) }. \end{aligned}$$

2.2 Introduction of Activation Functions

In this section, we express a new approximation based on two classes of activation functions for obtaining the numerical solution of FOCP and FVP. This approximation has more ability to solve equations than simple approximations based on wavelets.

The output of hybrid of these activation functions with input data t and parameter C is as

$$\begin{aligned} N(t, C)=AF(\varTheta ). \end{aligned}$$

(3)

Here $\varTheta$ is a linear combination of the Bernstein wavelets as

$$\begin{aligned} \varTheta =\sum _{n=1}^{2^{k-1}}\sum _{i=0}^{M-1}c_{n, i}\varPsi _{n, i, m}(t)=C^{T}\varPsi (t), \end{aligned}$$

(4)

and C vector determined by:

$$\begin{aligned} C= [c_{1,0}, \ldots , c_{1, M-1}, c_{2, 0}, \ldots c_{2, M-1}, \ldots , c_{2^{k-1}, M-1}]^{T}. \end{aligned}$$

(5)

$$\begin{aligned} \varPsi (t)= [\varPsi _{1,0, m}(t), \ldots , \varPsi _{1, M-1,m}(t), \ldots , \varPsi _{2^{k-1}, M-1,m}(t)]^{T}. \end{aligned}$$

(6)

Also, AF(.) is another activation function that affects on the combination of the Bernstein wavelets. Here, we have used functions of tanh(t) and arctan(t) as activation functions. Figure 1 shows structure of hybrid these functions. Also, Fig. 2 shows graphs of $\psi _{n,i, m}(t)$, $arctan(\psi _{n,i, m}(t))$ and $tanh(\psi _{n,i, m}(t))$ for $k=2, M=4$.

Fig. 1

Structure of hybrid of activation functions

Fig. 2

Plots of a $\psi _{n,i, m}(t)$, b $arctan(\psi _{n,i, m}(t))$ and c $tanh(\psi _{n,i, m}(t))$

3 Problem Statement

In this work, we investigate two classes of FOCPs and one class of FVP.

3.1 Type 1

Consider the following FOCP as

$$\begin{aligned} min \quad J[y, z]= \frac{1}{2}\int _{0}^{1} F(t, y(t), z(t)) dt, \end{aligned}$$

(7)

with the following dynamical system

$$\begin{aligned} D^{\nu } y(t)=a(t) y(t) + bz(t)+h(t), \end{aligned}$$

(8)

and the initial condition

$$\begin{aligned} y(0)=\delta _{0}. \end{aligned}$$

(9)

In aforesaid problem, $b \ne 0$ and a(t) and h(t) are continuous functions of t and $D^{\nu } y(t)$ is the Caputo fractional derivative of order $\nu$ as (Rahimkhani and Ordokhani 2020)

$D^{\nu }y(t)=\frac{1}{\Gamma (n- \nu )}\int _{0}^{t}(t-\tau )^{n-\nu -1}y^{(n)}(\tau )d\tau ,$

$n-1 < \nu \le n.$

3.2 Type 2

Consider the following FOCP as

$$\begin{aligned} min \quad J[y, z]= \int _{0}^{1} F(t, y(t), z(t)) dt, \end{aligned}$$

(10)

with the following dynamical system

$$\begin{aligned} Py'(t)+QD^{\nu } y(t)=a(t) y(t) + bz(t)+h(t), \end{aligned}$$

(11)

and the boundary conditions

$$\begin{aligned} y(0)=\delta _{0}, y(1)=\delta _{1}. \end{aligned}$$

(12)

In aforesaid problem $P, Q, b \ne 0$ and a(t) and h(t) are continuous functions of t.

3.3 Type 3

Consider the following FVP as

$$\begin{aligned} min \quad J[y]= \int _{0}^{1} F(t, y(t), D^{\nu }y(t)) dt, \end{aligned}$$

(13)

with the boundary conditions

$$\begin{aligned} y(0)=\delta _{0}, \quad y(1)=\delta _{1}. \end{aligned}$$

(14)

4 The Computational Scheme

Because Caputo fractional derivative is an integral of the solution with respect to time, the numerical method for finding the solution of FDEs requires using the values of all previous time steps. This needs a large size of memory to store the necessary data when computing, which may lead to a memory problem in the computer. Therefore, first, we approximate the Caputo fraction derivative by applying the Laplace transform technique similar to Ren et al. (2016) as follows:

$$\begin{aligned} L \lbrace D^{\nu }y(t)\rbrace =s^{\nu } \hat{y}(s)-s^{\nu -1} y(0)=s^{\nu } [\hat{y}(s) - s^{-1} y(0)], \end{aligned}$$

(15)

where L is Laplace operator. We linearize the term $s^{\nu } (0 < \nu \le 1)$ as

$$\begin{aligned} s^{\nu } \simeq \nu s^{1} +(1- \nu )s^{0}=\nu s +(1- \nu ). \end{aligned}$$

(16)

Replacing Eq. (16) into Eq. (15), we get

$$\begin{aligned} L \lbrace D^{\nu }y(t)\rbrace\simeq & [ \nu s +(1- \nu )] [\hat{y}(s) - s^{-1} y(0)] \nonumber \\= & \nu s [\hat{y}(s) -s^{-1}y(0)]\nonumber \\&+ (1-\nu )[\hat{y}(s)- s^{-1} y(0) ]. \end{aligned}$$

(17)

By using the inverse Laplace transform, we conclude

$$\begin{aligned} D^{\nu }y(t) \simeq \nu y'(t) +(1-\nu )[y(t) -y(0)]. \end{aligned}$$

(18)

4.1 Type 1

For solving problem (7)–(9), we approximate function $D^{\nu }y(t)$ by using Eq. (18) as

$$\begin{aligned} D^{\nu }y(t)\simeq \nu y'(t) +(1-\nu )(y(t) - \delta _{0}). \end{aligned}$$

(19)

Now, we estimate y(t) by hybrid of the activation functions as

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = \delta _{0} +tN(t, C). \end{aligned}$$

(20)

According to Eq. (8), we can write

$$\begin{aligned} z(t)\simeq \tilde{z}(t) & = \frac{1}{b}(\nu {\tilde{y}}{^{\prime}}(t)\nonumber \\&+(1-\nu )({\tilde{y}}(t) - \delta _{0}) - a(t){\tilde{y}}(t)-h(t)). \end{aligned}$$

(21)

By replacing Eqs. (20) and (21) in Eq. (7), we achieve

$$\begin{aligned} J[C] & = \frac{1}{2}\int _{0}^{1} F(t, {\tilde{y}}(t), \frac{1}{b}(\nu {{\tilde{y}}}{^{\prime}}(t)\nonumber \\&+(1-\nu )({\tilde{y}}(t) - \delta _{0}) - a(t){\tilde{y}}(t)-h(t))) dt. \end{aligned}$$

(22)

By employing the above equation and the Gauss–Legendre integration method, we get

$$\begin{aligned} J[C]\simeq & \frac{1}{4}\sum _{j=0}^{\hat{n}}\omega _{j} F\left( \frac{\eta _{j}+1}{2}, {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) , \frac{1}{b}\left( \nu {\tilde{y}}{^{\prime}}\left( \frac{\eta _{j}+1}{2}\right) \right. \right. \nonumber \\&+ (1-\nu )\left( {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) - \delta _{0}\right) \nonumber \\&-a\left. \left. \left( \frac{\eta _{j}+1}{2}\right) {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) -h\left( \frac{\eta _{j}+1}{2}\right) \right) \right) . \end{aligned}$$

(23)

So, to get extremum of J, the following necessary conditions are demonstrated by

$$\begin{aligned} \frac{\partial }{\partial c_{n, i}} J[C]=0, n=1, 2, \ldots , 2^{k-1}; i=0, 1, \ldots , M-1. \end{aligned}$$

(24)

We can solve the previous equations for finding C via Newton’s iterative technique.

4.2 Type 2

For solving problem (10)–(12), we approximate function $D^{\nu }y(t)$ by using Eq. (18) as

$$\begin{aligned} D^{\nu }y(t)\simeq \nu y'(t) +(1-\nu )(y(t) - \delta _{0}). \end{aligned}$$

(25)

Now, we estimate y(t) by the activation functions as

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = \delta _{0}+(\delta _{1} -\delta _{0})t +t(t-1)N(t, C). \end{aligned}$$

(26)

By making use of Eq. (11), we gain

$$\begin{aligned} z(t)\simeq & \tilde{z}(t) = \frac{1}{b}(P{\tilde{y}}{^{\prime}}(t)+ Q(\nu {\tilde{y}}{^{\prime}}(t) \nonumber \\&+(1-\nu ) ({\tilde{y}}(t) - \delta _{0})) -a(t){\tilde{y}}(t)-h(t)). \end{aligned}$$

(27)

By inserting Eqs. (26) and (27) in Eq. (10), we have

$$\begin{aligned} J[C] & = \frac{1}{2}\int _{0}^{1} F(t, {\tilde{y}}(t), \frac{1}{b}(P{\tilde{y}}{^{\prime}}(t)+ Q(\nu {\tilde{y}}{^{\prime}}(t)\nonumber \\&+ (1-\nu )({\tilde{y}}(t) - \delta _{0}))-a(t){\tilde{y}}(t)-h(t)). \end{aligned}$$

(28)

By using the above equation and the Gauss–Legendre integration method, we have

$$\begin{aligned}&J[C]\simeq \frac{1}{4}\sum _{j=0}^{\hat{n}} \omega _{j} F\left( \frac{\eta _{j}+1}{2}, {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) \right. ,\nonumber \\&\quad \frac{1}{b}\left( P{\tilde{y}}{^{\prime}}\left( \left( \frac{\eta _{j}+1}{2}\right) \right. \right. \nonumber \\&\quad +Q\left( \nu {\tilde{y}}{^{\prime}}\left( \frac{\eta _{j}+1}{2}\right) \right. +\left. (1-\nu )\left( {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) - \delta _{0}\right) \right) \nonumber \\&\quad - a\left( \frac{\eta _{j}+1}{2}\right) {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) -h\left( \frac{\eta _{j}+1}{2}\right) \Big)\Big). \end{aligned}$$

(29)

So, to get extremum of J, the following necessary conditions are demonstrated by

$$\begin{aligned} \frac{\partial }{\partial c_{n, i}} J[C]=0, n=1, 2, \ldots , 2^{k-1}; i=0, 1, \ldots , M-1. \end{aligned}$$

(30)

We can solve the previous equations for finding C via Newton’s iterative technique.

4.3 Type 3

For solving problem (13)–(14), we estimate function $D^{\nu }y(t)$ by applying Eq. (18) as

$$\begin{aligned} D^{\nu }y(t)\simeq \nu y'(t) +(1-\nu )(y(t) - \delta _{0}). \end{aligned}$$

(31)

Now, we approximate y(t) by activation functions as

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = \delta _{0}+(\delta _{1} -\delta _{0})t +t(t-1)N(t, C). \end{aligned}$$

(32)

By replacing Eqs. (31) and (32) in Eq. (13), we achieve

$$\begin{aligned} J[C]= \int _{0}^{1}F(t, {\tilde{y}}(t), \nu {\tilde{y}}{^{\prime}}(t) +(1-\nu )({\tilde{y}}(t) - \delta _{0}))dt. \end{aligned}$$

(33)

By employing the Gauss–Legendre integration method and previous equation, we get

$$\begin{aligned} J[C]\simeq & \sum _{j=0}^{\hat{n}}\omega _{j}F\bigg (\frac{\eta _{j}+1}{2}, {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) , \nu {\tilde{y}}{^{\prime}}\left( \frac{\eta _{j}+1}{2}\right) \nonumber \\+ & (1-\nu )\left( {\tilde{y}}\left( \frac{\eta _{j}+1}{2}\right) - \delta _{0}\right) \bigg ). \end{aligned}$$

(34)

So, to get extremum of J, the following necessary conditions are demonstrated by

$$\begin{aligned} \frac{\partial }{\partial c_{n, i}} J[C]=0, n=1, 2, \ldots , 2^{k-1}; i=0, 1, \ldots , M-1. \end{aligned}$$

(35)

We can solve the previous equations for finding C via Newton’s iterative technique.

5 Error Bound for the Best Approximation

The aim of this part is to discuss the error estimate of the current scheme in Sobolev space. The norm of Sobolev ( of integer order $\tau \ge 0$) over (a, b) is given as Rahimkhani et al. (2018)

$$\begin{aligned} \Vert y \Vert _{H^{\tau }(a,b)} & = \bigg (\sum _{j=0}^{\tau }\int _{a}^{b}\vert y^{(j)}(t)\vert dt \bigg )^{\frac{1}{2}}\nonumber \\= & \bigg ( \sum _{j=0}^{\tau } \Vert y^{(j)}(t) \Vert ^{2}_{L^{2}(a,b)}\bigg )^{\frac{1}{2}}, \end{aligned}$$

(36)

where $y^{(j)}$ shows the distributional derivative of order j of y.

Theorem 1

Consider $y \in H^{\tau } (0, 1)$ with $\tau \ge 0$ and $M \ge \tau ,$ and ${\tilde{y}}$ is the best approximation of y that is obtained by applying the activation functions, then we have the following estimations:

$$\begin{aligned} \Vert y -{\tilde{y}} \Vert _{L^{2}(0, 1)} \le c (M-1)^{-\tau }(2^{k-1})^{-\tau } \Vert y ^{(\tau )}\Vert _{L^{2}(0, 1)}, \end{aligned}$$

(37)

and for $1 \le s \le \tau$ we yield

$$\begin{aligned} \Vert y -{\tilde{y}} \Vert _{H^{s}(0, 1)} \le c (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau }\Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}. \end{aligned}$$

(38)

Proof

Consider $y\in H^{\tau } (0, 1)$ with $\tau \ge 0$ and $P_{M-1}^{2^{k-1}}y$ is the best approximation of y that is obtained by using the Müntz–Legendre wavelets over (0, 1), we get Rahimkhani et al. (2018)

$$\begin{aligned} \Vert y - P_{M-1}^{2^{k-1}}y \Vert _{L^{2}(0, 1)} \le c (M-1)^{-\tau }(2^{k-1})^{-\tau } \Vert y ^{(\tau )}\Vert _{L^{2}(0, 1)}, \end{aligned}$$

(39)

for $1 \le s \le \tau$ we have

$$\begin{aligned} \Vert y - P_{M-1}^{2^{k-1}}y\Vert _{H^{s}(0, 1)} \le c (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau } \Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}, \end{aligned}$$

(40)

in above relations, c depends on $\tau$.

Since the best approximation is unique (Kreyszig 1978), it yields

$$\begin{aligned} \Vert y - {\tilde{y}}\Vert _{L^{2}(0, 1)} = \Vert y - P_{M-1}^{2^{k-1}}y \Vert _{L^{2}(0, 1)}, \end{aligned}$$

(41)

$$\begin{aligned} \Vert y- {\tilde{y}}\Vert _{H^{s}(0, 1)} = \Vert y - P_{M-1}^{2^{k-1}}y \Vert _{H^{s}(0, 1)}. \end{aligned}$$

(42)

Therefore, we conclude the desired results.

5.1 Type 1

Theorem 2

Assume that $y \in H^{\tau }(0, 1)$ with $1\le s \le \tau , 0 < \nu \le 1$ and ${\tilde{y}}$ is the best approximation of y that given by the activation functions. If

• F satisfy Lipschitz condition with the Lipschitz constant $\eta$,

• $\frac{1}{\vert b \vert }= \kappa$,

• $\Vert a \Vert _{L^{2}(0, 1)} \le \gamma ,$

then, for the error bound $\Vert E \Vert _{L^{2}(0, 1)}$ we gain

$$\begin{aligned} \Vert E \Vert _{L^{2}(0, 1)}\le & \frac{1}{2}\eta \big ((1+\kappa \gamma ) c (M-1)^{-\tau }(2^{k-1})^{-\tau } \nonumber \\+ & \kappa \frac{c (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau }}{\Gamma (2-\nu )} \big ) \Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}. \end{aligned}$$

(43)

Proof

By using Eqs. (7)–(8) and the aforesaid conditions, we have

$$\begin{aligned}&\Vert E \Vert _{L^{2}(0, 1)} = \Vert J[y, z]- J[{\tilde{y}},\tilde{z}] \Vert _{L^{2}(0, 1)}\nonumber \\&=\frac{1}{2} \Vert \int _{0}^{1} F(t, y(t), z(t)) - F(t, {\tilde{y}}(t), \tilde{ z} (t)) dt \Vert _{L^{2}(0, 1)}\nonumber \\&\le \frac{1}{2}\eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)}+ \frac{1}{2}\eta \Vert z- \tilde{z} \Vert _{L^{2}(0, 1)}\nonumber \\&= \frac{1}{2}\eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)} + \frac{1}{2}\eta \Vert \frac{1}{b}D^{\nu } y- \frac{1}{b} ay- \frac{1}{b} h\nonumber \\&\quad - \frac{1}{b}D^{\nu } {\tilde{y}} + \frac{1}{b} a {\tilde{y}} + \frac{1}{b} h \Vert _{L^{2}(0, 1)} \le \frac{1}{2}\eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)} \nonumber \\&\quad + \frac{1}{2}\eta \kappa \Vert D^{\nu } y - D^{\nu } {\tilde{y}} \Vert _{L^{2}(0, 1)} + \frac{1}{2}\eta \kappa \gamma \Vert y - {\tilde{y}} \Vert _{L^{2}(0, 1)}. \end{aligned}$$

(44)

Consider the following relation

$$\begin{aligned} \Vert u *v \Vert _{p} \le \Vert u \Vert _{1}\Vert v \Vert _{p}. \end{aligned}$$

We obtain

$$\begin{aligned} \Vert D^{\nu }y - D^{\nu }{\tilde{y}} \Vert _{L^{2}(0, 1)}^{2} & = \Vert I^{1-\nu } ( D y - D{\tilde{y}} )\Vert _{L^{2}(0, 1)}^{2}\nonumber \\= & {} \Vert \frac{1}{t^{\nu } \Gamma (1-\nu )}*( D y - D{\tilde{y}} ) \Vert _{L^{2}(0, 1)}^{2} \nonumber \\\le & {} \big ( \frac{1}{(1- \nu ) \Gamma (1-\nu )} \big ) ^{2} \Vert D y - D{\tilde{y}} \Vert _{L^{2}(0, 1)}^{2}\nonumber \\\le & {} \big ( \frac{1}{ \Gamma (2-\nu )} \big ) ^{2} \Vert y - {\tilde{y}} \Vert ^{2}_{H^{s}(0, 1)}; \end{aligned}$$

(45)

by using Eq. (38), we have

$$\begin{aligned} \Vert D^{\nu }y - D^{\nu }{\tilde{y}} \Vert _{L^{2}(0, 1)} \le \frac{c (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau }}{\Gamma (2-\nu )}\Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}. \end{aligned}$$

(46)

By considering (45)–(46) and Eq. (37), we conclude the required results.

5.2 Type 2

Theorem 3

Let $y \in H^{\tau }(0, 1)$ with $1\le s \le \tau , 0 < \nu \le 1$. If the assumptions in Theorem 2 are established and

$$\begin{aligned} \vert \frac{P}{b} \vert = \kappa _{1}, \vert \frac{Q}{b} \vert = \kappa _{2}, \end{aligned}$$

then we get

$$\begin{aligned} \Vert E \Vert _{L^{2}(0, 1)}\le & {} \eta c \big ((1+ \kappa \gamma )(M-1)^{-\tau }(2^{k-1})^{-\tau } \nonumber \\+ & {} (\kappa _{1}+\frac{\kappa _{2}}{\Gamma (2- \nu )}) (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau }\big )\nonumber \\&\Vert y^{(\tau )} \Vert_{L^{2}(0, 1)}. \end{aligned}$$

(47)

Proof

By using Eqs. (10)–(11) and the aforesaid conditions, we have

$$\begin{aligned}&\Vert E \Vert _{L^{2}(0, 1)} = \Vert J[y, z]- J[{\tilde{y}},\tilde{z}] \Vert _{L^{2}(0, 1)}\nonumber \\&= \Vert \int _{0}^{1} F(t, y(t), z(t)) - F(t, {\tilde{y}}(t), \tilde{ z} (t)) dt \Vert _{L^{2}(0, 1)}\nonumber \\&\le \eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)}+ \eta \Vert z- \tilde{z} \Vert _{L^{2}(0, 1)}\nonumber \\&= \eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)}+\eta \Vert \frac{P}{b} y'+ \frac{Q}{b}D^{\nu } y- \frac{1}{b} ay\nonumber \\&\quad - \frac{1}{b} h-\frac{P}{b} {\tilde{y}}{^{\prime}}- \frac{Q}{b}D^{\nu } {\tilde{y}} + \frac{1}{b} a {\tilde{y}} + \frac{1}{b} h \Vert _{L^{2}(0, 1)}\nonumber \\&\le \eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)}+\eta \kappa _{1} \Vert y'- {\tilde{y}}{^{\prime}} \Vert _{L^{2}(0, 1)} \nonumber \\&\quad + \eta \kappa _{2}\Vert D^{\nu }y- D^{\nu }{\tilde{y}} \Vert _{L^{2}(0, 1)}+\frac{1}{b}\eta \kappa \gamma \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)}.\nonumber \\ \end{aligned}$$

(48)

Due to the definition of Sobolev norm for $1\le s \le \tau$, we get

$$\begin{aligned} \Vert y'- {\tilde{y}}{^{\prime}} \Vert _{L^{2}(0, 1)}\le \Vert y- {\tilde{y}} \Vert _{H^{s}(0, 1)}. \end{aligned}$$

(49)

By applying Eqs. (38) and (49), yields

$$\begin{aligned} \Vert y'- {\tilde{y}}{^{\prime}} \Vert _{L^{2}(0, 1)}\le c (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau }\Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}. \end{aligned}$$

(50)

By considering (37), (46) and Eq. (48), we conclude the required results.

5.3 Type 3

Theorem 4

Let $y \in H^{\tau }(0, 1)$ with $1\le s \le \tau , 0 < \nu \le 1$. If the assumptions in Theorem 2 are established, then we achieve

$$\begin{aligned} \Vert E \Vert _{L^{2}(0, 1)}\le & {} \eta c \big ( (M-1)^{-\tau }(2^{k-1})^{-\tau } \nonumber \\+ & {} (M-1)^{2s -\frac{1}{2}-\tau } (2^{k-1})^{s-\tau } \big ) \Vert y^{(\tau )} \Vert _{L^{2}(0, 1)}.\nonumber \\ \end{aligned}$$

(51)

Proof

By using Eqs. (13), we have

$$\begin{aligned} \Vert E \Vert _{L^{2}(0, 1)}& = \Vert J[y]- J[{\tilde{y}}] \Vert _{L^{2}(0, 1)} = \Vert \int _{0}^{1} F(t, y(t), D^{\nu }y(t)) \nonumber \\- & {} F(t, {\tilde{y}}(t), D^{\nu }{\tilde{y}}(t)) dt \Vert _{L^{2}(0, 1)}\nonumber \\\le & {} \eta \Vert y- {\tilde{y}} \Vert _{L^{2}(0, 1)} + \eta \Vert D^{\nu }y- D^{\nu } {\tilde{y}} \Vert _{L^{2}(0, 1)}.\nonumber \\ \end{aligned}$$

(52)

From Eqs. (37), (46) and above equation, the desired result is deduced.

6 A Criterion for Choosing the Number of Wavelets

In this part, we introduce a algorithm for choosing the number of basis functions (k, M). For this aim, we assume $y(.) \in C^{2\hat{n}}([0, 1)).$

6.1 Type 1

By applying the error of $\hat{n}$-point Legendre–Gauss quadrature formula given in Morgado et al. (2017), the exact solution of problem (7)–(9) satisfies the following relation as

$$\begin{aligned} J[C] & = \frac{1}{2}\bigg [ \frac{1}{2} \sum _{j=1}^{\hat{n}}\omega _{j} F\left( \frac{\eta _{j}+1}{2}, y\left( \frac{\eta _{j}+1}{2}\right) , \frac{1}{b}\left( \nu y'\left( \frac{\eta _{j}+1}{2}\right) \right. \right. \nonumber \\&+ (1-\nu )\left(y \left( \frac{\eta _{j}+1}{2}\right) - \delta _{0}\right) \nonumber \\&-a\left. \left. \left( \frac{\eta _{j}+1}{2}\right) y\left( \frac{\eta _{j}+1}{2}\right) -h\left( \frac{\eta _{j}+1}{2}\right) \right) \right) \nonumber \\&+ \mathcal {R} _{\hat{n}} (H)\bigg ], \end{aligned}$$

(53)

where

$$\begin{aligned} \mathcal {R} _{\hat{n}} (H)= \frac{(\hat{n}!)^{4}}{(2\hat{n}+1)(2\hat{n}!)^{4}} \frac{\partial ^{2\hat{n}}}{\partial t^{2\hat{n}}}H(t, y(t)), \end{aligned}$$

and

$$\begin{aligned} H_{1}(t, y(t))& = F\left( \frac{t+1}{2}, y\left( \frac{t+1}{2}\right) , \frac{1}{b}\left( \nu y'\left( \frac{t+1}{2}\right) \right. \right. \nonumber \\&+ (1-\nu )\left( y\left( \frac{t+1}{2}\right) -\delta _{0}\right) \nonumber \\&-a\left. \left. \left( \frac{t+1}{2}\right) y\left( \frac{t+1}{2}\right) -h\left( \frac{t+1}{2}\right) \right) \right) . \end{aligned}$$

(54)

Let

$$\begin{aligned} \sigma _{1}= max \lbrace \vert \frac{\partial ^{2\hat{n}}}{\partial t^{2\hat{n}}}H_{1}(t, y(t)) \vert ; 0 \le t \le 1\rbrace , \end{aligned}$$

and $Y^{1}_{k, M}(t)=\delta _{0} +tN(t, C)$ be the numerical solution of problem (7)–(9) given via the mentioned scheme in Sect. 4.

Therefore, for a given $\epsilon > 0$, we can choose k, M such that the following criterion holds:

$$\begin{aligned}&\frac{1}{4} \bigg \vert \sum _{j=1}^{\hat{n}}\omega _{j} F\left( \frac{\eta _{j}+1}{2}, Y^{1}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) \right. , \frac{1}{b}\left( \nu Y^{1'}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) \right. \nonumber \\&\quad +(1-\nu )\left( Y^{1}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) - \delta _{0}\right) \nonumber \\&\quad -a\left( \frac{\eta _{j}+1}{2}\right) Y^{1}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) \nonumber \\&\quad -h\left. \left. \left( \frac{\eta _{j}+1}{2}\right) \right) \right) \bigg \vert + \frac{(\hat{n}!)^{4}}{2 (2\hat{n}+1)(2\hat{n}!)^{4}}\sigma _{1}\le \epsilon . \end{aligned}$$

(55)

6.2 Type 2

Similar to type 1, we let

$$\begin{aligned} H_{2}(t, y(t)) & = F\left( \frac{t+1}{2}, y\left( \frac{t+1}{2}\right) , \frac{1}{b}\left( Py'\left( \left( \frac{t+1}{2}\right) \right. \right. \right. \nonumber \\&+Q\left( \nu y'\left( \frac{t+1}{2}\right) \right. \nonumber \\&+(1-\nu \left. )\left( y\left( \frac{t+1}{2}\right) - \delta _{0}\right) \right) \nonumber \\&- a\left. \left. \left( \frac{t+1}{2}\right) y\left( \frac{t+1}{2}\right) -h\left( \frac{t+1}{2}\right) \right) \right) , \end{aligned}$$

(56)

$$\begin{aligned} \sigma _{2} = max \lbrace \vert \frac{\partial ^{2\hat{n}}}{\partial t^{2\hat{n}}}H_{2}(t, y(t)) \vert ; 0 \le t \le 1\rbrace , \end{aligned}$$

and $Y^{2}_{k, M}(t)=\delta _{0}+(\delta _{1} -\delta _{0})t +t(t-1)N(t, C)$ is the numerical solution of problem (10)–(12).

So, for a given $\epsilon > 0$, we can choose k, M such that the following criterion holds:

$$\begin{aligned}&\frac{1}{4} \bigg \vert \sum _{j=1}^{\hat{n}} \omega _{j} F\left( \frac{\eta _{j}+1}{2}, Y^{2}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) \right. , \frac{1}{b}\left( PY^{2'}_{k, M}\left( \left( \frac{\eta _{j}+1}{2}\right) \right. \right. \nonumber \\&\quad +Q\left( \nu Y^{2'}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) +(1-\nu )\left( Y^{2}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) \right. \right. \nonumber \\&\quad - \left. \left. \left. \left. \delta _{0}\right) \right) - a\left( \frac{\eta _{j}+1}{2}\right) Y^{2}_{k, M}\left( \frac{\eta _{j}+1}{2}\right) -h\left( \frac{\eta _{j}+1}{2}\right) \right) \right) \bigg \vert \nonumber \\&+ \frac{(\hat{n}!)^{4}}{2 (2\hat{n}+1)(2\hat{n}!)^{4}}\sigma _{2}\le \epsilon . \end{aligned}$$

(57)

Remark 1

For Type 3, we can obtain a criterion for choosing k, M similar to type 1 and type 2.

7 Numerical Investigation of the Mentioned Method

In the current part, we implement the activation functions scheme for finding numerical solution of FOCP and FVP, which justify the applicability and accuracy of the mentioned scheme. The reported numerical results were done on a personal computer, and the codes are written in Mathematica 10.

7.1 Type 1

Example 1

Consider the following FOCP as (Alizadeh et al. 2017)

$$\begin{aligned} J= \frac{1}{2}\int _{0}^{1}[y^{2}(t) + z^{2}(t)]dt, \end{aligned}$$

(58)

with the dynamics system

$$\begin{aligned} D^{\nu }y(t)=-0.25(y(t)-z(t))+t^{\nu }, \end{aligned}$$

(59)

$$\begin{aligned} y(0)=1. \end{aligned}$$

(60)

The aforesaid problem has the following exact solution for $\nu =1$:

$$\begin{aligned} y(t) & = \frac{(\sqrt{2}e ^{\frac{\sqrt{2} t}{4}}-e ^{\frac{\sqrt{2} t}{4}})(9e ^{\frac{-\sqrt{2} }{4}}+2\sqrt{2} +2 )}{(\sqrt{2}-1)e ^{\frac{-\sqrt{2} }{4}}+(\sqrt{2}+1)e ^{\frac{\sqrt{2} }{4}}}\nonumber \\&- \frac{(\sqrt{2}e ^{\frac{-\sqrt{2} t}{4}}+e ^{\frac{-\sqrt{2} t}{4}})(-9e ^{\frac{\sqrt{2} }{4}}+2\sqrt{2} -2)}{(\sqrt{2}-1)e ^{\frac{-\sqrt{2} }{4}}+(\sqrt{2}+1)e ^{\frac{\sqrt{2} }{4}}}\nonumber \\&+2t-8, \end{aligned}$$

(61)

$$\begin{aligned} z(t) = \frac{e ^{\frac{\sqrt{2} t}{4}}(9e ^{-\frac{\sqrt{2} }{4}}+2\sqrt{2} +2)+e ^{- \frac{\sqrt{2} t}{4}}(-9e ^{\frac{\sqrt{2} }{4}} +2\sqrt{2} -2)}{(\sqrt{2}-1)e ^{-\frac{\sqrt{2} }{4}} +(\sqrt{2}+1)e ^{\frac{\sqrt{2} }{4}}}-2t. \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function arctan(.). The state and control variables are approximated by

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = 1+t N(t, C), \\ z(t) \simeq \tilde{z}(t) =4(D^{\nu } {\tilde{y}}(t)-t^{\nu })+ {\tilde{y}}(t). \end{aligned}$$

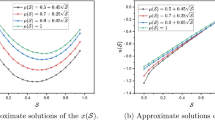
Absolute errors of y(t) and z(t) via $k=1, \nu =1$ and various choices M are expressed in Table 1. From this table, we notice that both the state and the control variables converge as M is increased. Also, the optimal values of cost function and CPU times for $k=1, M=10$ are compared with Alizadeh et al. (2017) in Table 2. Numerical results of the state and control variables with various cases of $\nu$ are portrayed in Fig. 3. From this figure, we conclude that by approaching the values of $\nu$ to 1, the numerical result is convergent to the exact solution.

Table 1 Absolute errors of y(t) and z(t) for $k=1, \nu =1$, (Example 1)

Table 2 Optimal values of J and CPU times for $k=1, M=10$, (Example 1)

Fig. 3

Approximate results for various cases of $\nu$, a y(t), b z(t) (Example 1)

Example 2

Consider the following FOCP as (Sahu and Saha Ray (2018))

$$\begin{aligned} J= \frac{1}{2}\int _{0}^{1}[(y(t)-t^{\nu })^{2} + (z(t)-t^{\nu } - \Gamma (\nu +1))^{2}]dt, \end{aligned}$$

(62)

with the dynamics system

$$\begin{aligned} D^{\nu }y(t)= -y(t) + z(t), \end{aligned}$$

(63)

$$\begin{aligned} y(0)=0. \end{aligned}$$

(64)

The aforesaid problem has the following exact solution:

$$\begin{aligned} y(t)= t^{\nu }, z(t)= t^{\nu }+\Gamma (\nu +1), J=0. \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function tanh(.). The state and control variables are approximated as

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = t N(t, C), z(t) \simeq \tilde{z}(t) =D^{\nu } {\tilde{y}}(t)+ {\tilde{y}}(t). \end{aligned}$$

In Table 3, we report the optimal values of J and CPU times of the presented scheme with $k=2, M=3, \nu =1$, LWM, Chebyshev wavelet method (CWM), Laguerre wavelet method (LaWM) and CASWM (Sahu and Saha Ray 2018). By using Table 3, we conclude that the mentioned method is more accurate than other methods in Sahu and Saha Ray (2018). Also, numerical results of the state and control variables for different choices of $\nu$ are plotted in Fig. 4.

Table 3 Optimal values of J and CPU times for $k=2, M=3$ and $\nu =1$, (Example 2)

Fig. 4

Approximate results for various cases of $\nu$, a y(t), b z(t) (Example 2)

7.2 Type 2

Example 3

Consider the following FOCP as (Rabiei et al. 2018b)

$$\begin{aligned} J= \int _{0}^{1}[z(t) - y(t)]^{2}dt, \end{aligned}$$

(65)

with the dynamics system

$$\begin{aligned} y'(t)+D^{\nu }y(t)= z(t)-y(t) + t^{3}+\frac{6t^{\nu +2}}{\Gamma (\nu +3)}, \end{aligned}$$

(66)

$$\begin{aligned} y(0)=0, y(1)=\frac{6}{\Gamma (\nu +4)}. \end{aligned}$$

(67)

The aforesaid problem has the following exact solution:

$$\begin{aligned} y(t)= \frac{6t^{\nu +3}}{\Gamma (\nu +4)}, z(t)= \frac{6t^{\nu +3}}{\Gamma (\nu +4)}. \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function tanh(.). The state and control variables are approximated by

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) =\frac{6}{\Gamma (\nu +4)}t+ t(t-1) N(t, C), \\ z(t) \simeq \tilde{z}(t) ={\tilde{y}}{^{\prime}}(t)+ D^{\nu } {\tilde{y}}(t)+ {\tilde{y}}(t)-t^{3}-\frac{6t^{\nu +2}}{\Gamma (\nu +3)}. \end{aligned}$$

The optimal values of J and CPU times of the presented scheme with $k=2, M=8$ and Rabiei et al. (2018b) are illustrated in Table 4. In Table 5, we report the absolute errors of y(t) and z(t) for $k=1, \nu =1$ and different cases M. From this table, we notice that by increasing the number of basis functions, the absolute error tends to zero. Diagrams of numerical results of the state and control variables for $k=1, M=10$ and several cases of $\nu$ are shown in Fig. 5.

Table 4 Optimal values of cost function and CPU times for $k=2, M=8$, (Example 3)

Table 5 Absolute errors of y(t) and z(t) for $k=1, \nu =1$ M, (Example 3)

Fig. 5

Approximate results for various cases of $\nu$, a y(t), b z(t) for (Example 3)

Example 4

Consider the following FOCP as (Rabiei et al. (2018b))

$$\begin{aligned} J= \int _{0}^{1}[tz(t) -(\nu +2) y(t)]^{2}dt, \end{aligned}$$

(68)

with the dynamics system

$$\begin{aligned} y'(t)+D^{\nu }y(t)= z(t) + t^{2}, \end{aligned}$$

(69)

$$\begin{aligned} y(0)=0, y(1)=\frac{2}{\Gamma (\nu +3)}. \end{aligned}$$

(70)

The aforesaid problem has the following exact solution:

$$\begin{aligned} y(t)= \frac{2t^{\nu +2}}{\Gamma (\nu +3)}, z(t)= \frac{2t^{\nu +1}}{\Gamma (\nu +2)}. \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function arctan(.). The state and control variables are approximated by

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) =\frac{2}{\Gamma (\nu +3)}t+ t(t-1) N(t, C), \\ z(t) \simeq \tilde{z}(t) ={\tilde{y}}{^{\prime}}(t)+ D^{\nu } {\tilde{y}}(t)+ {\tilde{y}}(t)-t^{2} \end{aligned}$$

The optimal values of J and CPU times of the proposed scheme with $k=1, M=15$ and Rabiei et al. (2018b) for several cases of $\nu$ are summarized in Table 6. In Table 7, we report values of absolute errors of the state variable, the optimal values of cost function and CPU times for $\nu =1, k=1$ and various choices M. From this Table, it is clear that when the number of base functions increases, the absolute error tends to zero. Graphs of numerical results of the state and control variables with $k=1, M=15$ and various cases of $\nu$ are illustrated in Fig. 6.

Table 6 Optimal values of J and CPU times for $k=1, M=15$, (Example 4)

Table 7 Absolute errors of state variable, the optimal values of cost function and CPU times for $k=1, \nu =1$, (Example 4)

Fig. 6

Approximate results for various cases of $\nu$, a y(t), b z(t) (Example 4)

7.3 Type 3

Example 5

Consider the following FVP as

$$\begin{aligned} J=\int _{0}^{1}\left[\frac{1}{2} ( D^{\nu }y(t) )^{2}-y(t)\right]dt, \end{aligned}$$

(71)

with the boundary conditions as

$$\begin{aligned} y(0)= \quad y(1)=0. \end{aligned}$$

(72)

The aforesaid problem has the following exact solution for $\nu =1$:

$$\begin{aligned} y(t)= (1-t)(\frac{t}{2}). \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function arctan(.). The state and control variables are approximated by

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) =t(t-1)N(t, C). \end{aligned}$$

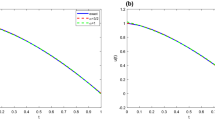
The absolute error behavior for $k=1, M=2$ is demonstrated in Fig. 7. Also, Fig. 8 demonstrates the behavior of numerical results with $M=2, k=1$ and different cases of $\nu$ and the exact solution. This figure demonstrates that the numerical solution is convergent to the exact solution as the value of $\nu$ approaches 1.

Fig. 7

Absolute error for $k=1, M=2$, (Example 5)

Fig. 8

a Approximate results for various cases of $\nu$, b the exact and approximate results for $\nu =1$, (Example 5)

Example 6

Consider the following FVP as (Ordokhani and Rahimkhani 2018; Dehestani et al. 2020; Razzaghi and Yousefi 2000)

$$\begin{aligned} J=\int _{0}^{1}[ ( D^{\nu }y(t) )^{2}+tD^{\nu }y(t) +y^{2}(t)]dt, \end{aligned}$$

(73)

with the boundary conditions as

$$\begin{aligned} y(0)=0, \quad y(1)=\frac{1}{4}. \end{aligned}$$

(74)

The aforesaid problem has the following exact solution for $\nu =1$:

$$\begin{aligned} y(t)= (1-t)(\frac{t}{2}). \end{aligned}$$

We solve the aforesaid problem via the mentioned technique in Sect. 4 with activation function tanh(.). The state and control variables are approximated by

$$\begin{aligned} y(t) \simeq {\tilde{y}}(t) = \frac{1}{4}t+ t(t-1)N(t, C). \end{aligned}$$

The values of approximate solution of y(t) and the optimal values of cost function of the proposed scheme with $k=1, M=4$ and LWM (Razzaghi and Yousefi 2000), Müntz–Legendre method (MLM) (Ordokhani and Rahimkhani 2018), modified wavelet method (MWM) (Dehestani et al. 2020) are summarized in Table 8. Also, the approximate solutions of y(t) for different choices of $\nu$ are demonstrated in Fig. 9. This figure demonstrates that the numerical solution is convergent to the exact solution as the value of $\nu$ approaches 1.

Table 8 Approximate results (${\tilde{y}}(t)$) and the optimal values of cost function, (Example 6)

Fig. 9

Approximate results for various cases of $\nu$, (Example 6)

8 Conclusion and Future Work

In this study, two classes of FOCPs and one class of FVP have been investigated. A novel method based on Bernstein wavelets and activation functions was used for numerical solution of such problems. By applying the Laplace transform, fractional-order problems are converted into integer-order problems. Then, we use hybrid of the Bernstein wavelets and activation functions, Gauss–Legendre integration method and Newton’s iterative method for obtaining numerical solution of such problems. The accuracy of the mentioned scheme has been examined on different numerical examples. The obtained results confirmed that the established technique for solving the intended problems is extremely effective and powerful, even when using a limited number of bases Bernstein wavelets. We plan to do the following works in the future:

• This method can be used to solve different problems such as fractional partial differential equations, two-dimensional FOCP, fractal-fractional differential equations, fractal-fractional OCP, inverse problems etc.

• Wavelets base can be combined with neural network, least squares-support vector regression etc.

• Stability analysis of the suggested scheme for numerical approximation of FOCP is an interesting problem for future work.