Fractional-Lucas optimization method for evaluating the approximate solution of the multi-dimensional fractional differential equations

Abstract

The paper investigates the numerical solution of the multi-dimensional fractional differential equations by applying fractional-Lucas functions (FLFs) and an optimization method. First, the FLFs and their properties are introduced. Then, according to the pseudo-operational matrix of derivative and modified operational matrix of fractional derivative, we present the framework of numerical technique. Also, for computational technique, we evaluate the upper bound of error. As a result, we expound the proposed scheme by solving several kinds of problems. Our computational results demonstrate that the proposed method is powerful and applicable for nonlinear multi-order fractional differential equations, time-fractional convection–diffusion equations with variable coefficients, and time-space fractional diffusion equations with variable coefficients.

1 Introduction

In recent years, fractional calculus has generated tremendous interest in various fields in sciences and engineering. For instance, this topic has been used in modeling the nonlinear oscillation of earthquake, fluid-dynamic traffic, continuum, and statistical mechanics, signal processing, control theory, heat transfer in heterogeneous media, the ultracapacitor, and beam heating [1,2,3,4,5].

Among the fractional-order problems, solving fractional partial differential equations has received considerable attention from many researchers. The solution to most problems cannot be easily obtained by the analytical methods. Therefore, many researchers considered the numerical approach to gain the approximate solution of the proposed problems. The wide type of numerical methods has been introduced such as radial basis functions method [6], adaptive finite element method [7], and optimization method [8].

During recent years, the fractional-order functions have received considerable attention in dealing with various fractional problems. These functions have many advantages which greatly simplify the numerical technique to achieve the approximate solution with high precision. These functions have drawn the attention of many mathematicians and lead to the emersion of flexible approaches for solving fractional-order problems such as fractional-order generalized Laguerre functions [9], fractional-order Genocchi functions [10], fractional-order Legendre functions [11], fractional-order Legendre–Laguerre functions [12], Fractional-order Bessel wavelet functions [13] and Genocchi-fractional Laguerre functions [14]. For some other papers on this subject, see [15, 16].

This paper includes the numerical optimization technique for solving nonlinear multi-order fractional differential equations and time-space fractional diffusion equations. To get the desired goal, we applied FLFs together with an optimization method. It is worthwhile to mention that one of the advantages of these functions is integer coefficients of individual terms, which are effective in computational error. Fractional-Lucas functions features and operational matrices create good conditions to get appropriate results.

The current paper is arranged as follows: In Sect. 2, we describe the fractional-Lucas functions and their properties, and also function approximations. Sections 3 and 4 are devoted to the technique of obtaining a modified operational matrix of the derivative and pseudo-operational matrix of the fractional derivative. The procedure of implementing the proposed method for two classes of the problems is presented in Sect. 5. Convergence analysis and error estimate for the proposed method are discussed in Sect. 6. Section 7 contains some numerical experiments to demonstrate the accuracy of the proposed algorithms. The conclusion is summarized in the last section.

In this paper, we consider two classes of the fractional differential equations:

• Nonlinear multi-order fractional differential equations [17, 18]:

  $$\begin{aligned}&D^{\nu }u(x)+D^{\gamma }u(x)={\mathcal {F}}(x,u,u'),\nonumber \\&\quad 0\le x \le 1,\quad1<\nu \le 2,\quad0<\gamma \le 1, \end{aligned}$$

  (1)

  with the initial conditions

  $$\begin{aligned} u(0)=u_{0}, \quad u'(0)=u_{1}, \end{aligned}$$

  where the parameters $u_{0}$ and $u_{1}$ are constants and ${\mathcal {F}}$ is linear or nonlinear known function.

• Nonlinear time-space fractional diffusion equations [19]:

  $$\begin{aligned}&D^{\nu }_{t}u(x,t)+D^{\gamma }_{x}u(x,t) ={\mathcal {G}}(x,t,u,\frac{\partial u}{\partial x},\frac{\partial ^{2} u}{\partial x^{2}}), \nonumber \\&\quad 0\le x, t\le 1,\quad0<\nu \le 1,\quad 0<\gamma \le 2, \end{aligned}$$

  (2)

  with the initial and boundary conditions

  $$\begin{aligned}&u(x,0)=f_{0}(x),\quad 0\le x \le 1,\\&u(0,t)=\varphi _{0}(t),u(1,t)=\varphi _{1}(t), \quad 0\le t \le 1, \end{aligned}$$

  where $f_{0}(x),$ $\varphi _{0}(t)$ and $\varphi _{1}(t)$ are known functions.

Here also, $D^{\nu }$ and $D^{\gamma }$ denote the Caputo fractional derivatives that this operator is defined as follows [12]:

$$\begin{aligned} D^{\nu }u(x)=\left\{ \begin{array}{ll} \frac{1}{\Gamma (q-\nu )}\int _{0}^{x}(x-t)^{q-\nu -1}u^{(q)}(t){\text {d}}t ,&{} q-1<\nu < q,\\ u^{(q)}(x),&{} \nu =q. \end{array} \right. \end{aligned}$$

2 Fractional-Lucas functions

Fractional-Lucas functions are constructed explicitly by applying the change of variable role $x \rightarrow x^{\alpha }\,(\alpha >0)$, on Lucas polynomials [20] on the interval [0, 1] as

$$\begin{aligned} {\mathbf {FL}}_{m}^{\alpha }(x)=\sum _{k=0}^{[\frac{m}{2}]}\frac{m}{m-k} \displaystyle {m-k\atopwithdelims ()k} x^{(m-2k)\alpha }. \end{aligned}$$

(3)

These functions are defined by the following second-order linear recursive formulas:

$$\begin{aligned} {\mathbf {FL}}^{\alpha }_{m}(x)=\left\{ \begin{array}{ll} 2,&{} m=0,\\ x^{\alpha },&{} m=1,\\ x^{\alpha } {\mathbf {FL}}^{\alpha }_{m-1}(x)+{\mathbf {FL}}^{\alpha }_{m-2}(x),&{} m\ge 2. \end{array} \right. \end{aligned}$$

(4)

A given function f belonging to $L^{2}([0,1])$ can be expanded by FLFs as:

$$\begin{aligned} f(x)=\sum _{m_{1}=0}^{\infty } f_{m_{1}} {\mathbf {FL}}^{\alpha }_{m_{1}}(x). \end{aligned}$$

By truncating the above series, we have

$$\begin{aligned} f(x)\simeq \sum _{m_{1}=0}^{{\mathfrak {M}}_{1}} f_{m_{1}} {\mathbf {FL}}^{\alpha }_{m_{1}}(x)=F^{T}{\mathbf {FL}}^{\alpha }(x), \end{aligned}$$

$$\begin{aligned} {\mathbf {FL}}^{\alpha }(x)=[{\mathbf {FL}}^{\alpha }_{0}(x),{\mathbf {FL}}^{\alpha }_{1}(x),\dots ,{\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}}(x)]^{T}, \end{aligned}$$

(5)

and the coefficients vector are computed as follows:

$$\begin{aligned} F=D^{-1}\langle f(x), {\mathbf {FL}}^{\alpha }(x) \rangle , \quad D= \langle {\mathbf {FL}}^{\alpha }(x), {\mathbf {FL}}^{\alpha }(x) \rangle . \end{aligned}$$

(6)

3 Modified operational matrix of derivative

Throughout this section, we present the technique of calculating the modified operational matrix of the derivative. This issue is discussed in the following theorem.

Theorem 1

Let ${\mathbf {FL}}^{\alpha }(x)$ be the fractional-Lucas vector given in Eq. (5), then the modified operational matrix of the derivative for $\alpha =1$ is defined as:

$$\begin{aligned} ({\mathbf {FL}}^{\alpha }(x))'= {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x), \end{aligned}$$

(7)

where ${\mathbf {\Upsilon }}(\alpha ,x)$ is the $({\mathfrak {M}}_{1}+1)\times ({\mathfrak {M}}_{1}+1)$ modified operational matrix of the derivative for FLFs.

Proof

The following relation for FLFs holds [21]:

$$\begin{aligned} ({\mathbf {FL}}^{\alpha }_{m+1}(x))'=\frac{m+1}{2} \left[ {\mathbf {FL}}^{\alpha }_{m}(x)+\frac{x}{m} ({\mathbf {FL}}^{\alpha }_{m}(x))' \right] . \end{aligned}$$

(8)

Due to the above relation, we have

$$\begin{aligned} ({\mathbf {FL}}^{\alpha }_{0}(x))'= & {} 0,\nonumber \\ ({\mathbf {FL}}^{\alpha }_{1}(x))'= & {} \frac{1}{2} {\mathbf {FL}}^{\alpha }_{0}(x),\nonumber \\ ({\mathbf {FL}}^{\alpha }_{2}(x))'= & {} \left[ {\mathbf {FL}}^{\alpha }_{1}(x)+\frac{x}{2} {\mathbf {FL}}^{\alpha }_{0}(x) \right] ,\nonumber \\ ({\mathbf {FL}}^{\alpha }_{3}(x))'= & {} \frac{3}{2} \left[ {\mathbf {FL}}^{\alpha }_{2}(x)+\frac{x}{2} {\mathbf {FL}}^{\alpha }_{1}(x)+\frac{x^{2}}{4} {\mathbf {FL}}^{\alpha }_{0}(x) \right] ,\nonumber \\ ({\mathbf {FL}}^{\alpha }_{4}(x))'= & {} 2 \left[ {\mathbf {FL}}^{\alpha }_{3}(x)+\frac{x}{2} {\mathbf {FL}}^{\alpha }_{2}(x)+\frac{x^{2}}{4} {\mathbf {FL}}^{\alpha }_{1}(x) \right. \nonumber \\&\quad \left. +\frac{x^{3}}{8} {\mathbf {FL}}^{\alpha }_{0}(x) \right] ,\nonumber \\&\vdots&\nonumber \\ ({\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}}(x))'= & {} \frac{{\mathfrak {M}}_{1}}{2} \left[ {\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}-1}(x)+\frac{x}{2}{\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}-2}(x)\right. \nonumber \\&+\frac{x^{2}}{4} {\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}-3}(x)+\frac{x^{3}}{8} {\mathbf {FL}}^{\alpha }_{{\mathfrak {M}}_{1}-4}(x) \nonumber \\&\left. +\dots + \frac{x^{{\mathfrak {M}}_{1}-1}}{2^{{\mathfrak {M}}_{1}-1}} {\mathbf {FL}}^{\alpha }_{0}(x) \right] . \end{aligned}$$

(9)

Therefore, the modified operational matrix is obtained as follows:

$$\begin{aligned}&{\mathbf {\Upsilon }}(\alpha ,x)\\&\quad =\left[ \begin{array}{cccccccc} 0&{}0&{}0&{}0&{}\dots &{}0&{}0\\ \frac{1}{2}&{}0&{}0&{}0&{}\dots &{}0&{}0\\ \frac{x}{2}&{}1&{}0&{}0&{}\dots &{}0&{}0\\ \frac{3x^{2}}{8}&{}\frac{3x}{4}&{}\frac{3}{2}&{}0&{}\dots &{}0&{}0\\ \frac{2x^{3}}{8}&{}\frac{2x^{2}}{4}&{}\frac{2 x }{2}&{}2&{}\dots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ \frac{{\mathfrak {M}}_{1} x^{{\mathfrak {M}}_{1}-1 }}{2^{{\mathfrak {M}}_{1}}}&{} \frac{{\mathfrak {M}}_{1} x^{{\mathfrak {M}}_{1}-2 }}{2^{{\mathfrak {M}}_{1}-1}}&{} \frac{{\mathfrak {M}}_{1} x^{{\mathfrak {M}}_{1}-3 }}{2^{{\mathfrak {M}}_{1}-2}}&{} \frac{{\mathfrak {M}}_{1} x^{{\mathfrak {M}}_{1}-4 }}{2^{{\mathfrak {M}}_{1}-3}} &{}\dots &{}\frac{{\mathfrak {M}}_{1}}{2} &{} 0 \\ \end{array} \right] . \end{aligned}$$

$\square$

4 Pseudo-operational matrix of the fractional derivative

In the present section, the methodology of obtaining the pseudo-operational matrix of the fractional derivative in Caputo sense of order $q-1<\nu \le q$ is presented. Thus, we define

$$\begin{aligned} D^{\nu } ({\mathbf {FL}}^{\alpha }(x))= {\mathbf {\Theta }}^{q}(\alpha ,\nu ,x) {\mathbf {FL}}^{\alpha }(x), \end{aligned}$$

(10)

where

$$\begin{aligned}&{\mathbf {\Theta }}^{q}(\alpha ,\nu ,x)=x^{q \alpha -\nu } \left[ \theta _{m,k,i}^{\alpha ,\nu } \right] ,\quad i=0,1,\dots ,{\mathfrak {M}}_{1},\\&\quad m=0,1,\dots ,{\mathfrak {M}}_{1}. \end{aligned}$$

According to properties of the Caputo fractional derivative, we have

$$\begin{aligned} D^{\nu } ({\mathbf {FL}}_{m}^{\alpha }(x))=0,\quad m=0,1,\dots ,\lceil \frac{\nu }{\alpha } \rceil -1. \end{aligned}$$

Using the properties of the Caputo fractional derivative for $m=\lceil \frac{\nu }{\alpha } \rceil ,\dots ,{\mathfrak {M}}_{1}$, each component of the pseudo-operational matrix of the fractional derivative ${\mathbf {\Theta }}^{q}(\alpha ,\nu ,x)$ is computed as follows:

$$\begin{aligned}&D^{\nu } ({\mathbf {FL}}_{m}^{\alpha }(x))\nonumber \\&\quad =D^{\nu } \left( \sum _{k=0}^{[\frac{m}{2}]}\frac{m}{m-k} \displaystyle {m-k\atopwithdelims ()k} x^{(m-2k)\alpha } \right) \nonumber \\&\quad =\sum _{k=0}^{[\frac{m}{2}]}\frac{m}{m-k} \displaystyle {m-k\atopwithdelims ()k} D^{\nu } \left( x^{(m-2k)\alpha } \right) \nonumber \\&\quad = \sum _{k=\lceil \frac{m\alpha -\nu }{2\alpha } \rceil }^{[\frac{m}{2}]}\frac{m}{m-k} \displaystyle {m-k\atopwithdelims ()k}\nonumber \\&\qquad \frac{\Gamma ((m-2k)\alpha +1)}{\Gamma ((m-2k)\alpha +1-\nu )} x^{(m-2k)\alpha -\nu } \nonumber \\&\quad = x^{q \alpha -\nu } \sum _{k=\lceil \frac{m\alpha -\nu }{2\alpha } \rceil }^{[\frac{m}{2}]} \lambda ^{\alpha ,\nu }_{m,k} x^{(m-2k-q)\alpha }, \end{aligned}$$

(11)

where

$$\begin{aligned} \lambda ^{\alpha ,\nu }_{m,k}=\frac{m}{m-k} \displaystyle {m-k\atopwithdelims ()k} \frac{\Gamma ((m-2k)\alpha +1)}{\Gamma ((m-2k)\alpha +1-\nu )}. \end{aligned}$$

Next, by expanding $x^{(m-2k-q)\alpha }$ with ${\mathfrak {M}}_{1}$-terms of FLFs, we get

$$\begin{aligned} x^{(m-2k-q)\alpha }=\sum _{i=0}^{{\mathfrak {M}}_{1}} b_{i} {\mathbf {FL}}^{\alpha }_{i}(x). \end{aligned}$$

Employing the two above relations, then we have

$$\begin{aligned}&D^{\nu } ({\mathbf {FL}}_{m}^{\alpha }(x)) \nonumber \\&\quad = x^{q \alpha -\nu } \sum _{k=\lceil \frac{m\alpha -\nu }{2\alpha } \rceil }^{[\frac{m}{2}]} \lambda ^{\alpha ,\nu }_{m,k} \left( \sum _{i=0}^{{\mathfrak {M}}_{1}} b_{i} {\mathbf {FL}}^{\alpha }_{i}(x) \right) \nonumber \\&\quad = x^{q \alpha -\nu } \sum _{i=0}^{{\mathfrak {M}}_{1}} \left( \sum _{k=\lceil \frac{m\alpha -\nu }{2\alpha } \rceil }^{[\frac{m}{2}]} \lambda ^{\alpha ,\nu }_{m,k} b_{i} \right) {\mathbf {FL}}^{\alpha }_{i}(x)\nonumber \\&\quad = x^{q \alpha -\nu } \sum _{i=0}^{{\mathfrak {M}}_{1}} \theta _{m,k,i}^{\alpha ,\nu } {\mathbf {FL}}^{\alpha }_{i}(x), \quad \theta _{m,k,i}^{\alpha ,\nu }=\sum _{k=\lceil \frac{m\alpha -\nu }{2\alpha } \rceil }^{[\frac{m}{2}]} \lambda ^{\alpha ,\nu }_{m,k} b_{i}. \end{aligned}$$

(12)

Accordingly, the vector form of the above formula can be written as follows:

$$\begin{aligned} D^{\nu } ({\mathbf {FL}}_{m}^{\alpha }(x))=x^{q \alpha -\nu } \left[ \begin{array}{cccc} \theta _{m,k,0}^{\alpha ,\nu }&\theta _{m,k,1}^{\alpha ,\nu }&\dots&\theta _{m,k,{\mathfrak {M}}_{1}}^{\alpha ,\nu } \end{array} \right] {\mathbf {FL}}^{\alpha }(x). \end{aligned}$$

In a specific case, for ${\mathfrak {M}}_{1}=2,$ $\alpha =0.5$ and $\nu =0.5$, the pseudo-operational matrix of the fractional derivative is obtained as follows:

$$\begin{aligned}&{\mathbf {\Theta }}^{1}(0.5,0.5,x)\\&\quad =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 4.431134627263790\times 10^{-1}&{} 0 &{} 0\\ 0 &{} 1.128379167095513&{} 0\\ \end{array} \right] . \end{aligned}$$

5 Fractional-Lucas optimization method

In the current section, we present the novel approach for different kinds of fractional differential equations.

5.1 Implementation of the method for fractional differential equations

In this section, we provide an optimization problem for solving the fractional differential equations. For this aim, we expand the function u(x) by FLFs as follows:

$$\begin{aligned} u(x)\simeq U^{T} {\mathbf {FL}}^{\alpha }(x). \end{aligned}$$

(13)

In view of the modified operational matrix of derivative for $\alpha =1,$ we have

$$\begin{aligned} u'(x) \simeq U^{T} {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x). \end{aligned}$$

(14)

And for $0<\alpha <1$, we obtain

$$\begin{aligned} u'(x) \simeq U^{T} {\mathbf {\Theta }}^{1}(\alpha ,1,x) {\mathbf {FL}}^{\alpha }(x). \end{aligned}$$

(15)

On the other hand, according to the pseudo-operational matrix of the fractional derivative, we achieve

$$\begin{aligned} D^{\nu } u(x)\simeq U^{T} {\mathbf {\Theta }}^{2}(\alpha ,\nu ,x) {\mathbf {FL}}^{\alpha }(x),\quad 1<\nu \le 2, \end{aligned}$$

(16)

and

$$\begin{aligned} D^{\gamma } u(x)\simeq U^{T} {\mathbf {\Theta }}^{1}(\alpha ,\gamma ,x) {\mathbf {FL}}^{\alpha }(x),\quad 0< \gamma \le 1. \end{aligned}$$

(17)

By substituting Eqs. (13)–(17) into Eq. (1), the residual function ${\mathbf {R}}(x,U)$ is obtained

$$\begin{aligned}&{\mathbf {R}}(x,U)\nonumber \\&\quad =\left\{ \begin{array}{cc} U^{T} {\mathbf {\Theta }}^{2}(\alpha ,\nu ,x) {\mathbf {FL}}^{\alpha }(x)+U^{T} {\mathbf {\Theta }}^{1}(\alpha ,\gamma ,x) {\mathbf {FL}}^{\alpha }(x)\\ -{\mathcal {F}}\left( x,U^{T} {\mathbf {FL}}^{\alpha }(x),U^{T} {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x) \right) , &{} \alpha =1,\\ \\ U^{T} {\mathbf {\Theta }}^{2}(\alpha ,\nu ,x) {\mathbf {FL}}^{\alpha }(x)+U^{T} {\mathbf {\Theta }}^{1}(\alpha ,\gamma ,x) {\mathbf {FL}}^{\alpha }(x)\\ -{\mathcal {F}}\left( x,U^{T} {\mathbf {FL}}^{\alpha }(x), U^{T} {\mathbf {\Theta }}^{1}(\alpha ,1,x) {\mathbf {FL}}^{\alpha }(x) \right) ,&{}0<\alpha <1. \end{array} \right. \end{aligned}$$

(18)

Thus, using the above relation and initial conditions, the following optimization problem is attained for $\alpha =1$:

$$\begin{aligned} & \min \quad {\mathcal {M}}(U)=\int _{0}^{1} {\mathbf {R}}^{2}(x,U) {\text {d}}x,\\ \nonumber&{\text {subject to}} \\ \nonumber&U^{T} {\mathbf {FL}}^{\alpha }(x)-u_{0}=0,\\ \nonumber&U^{T} {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x)-u_{1}=0. \end{aligned}$$

(19)

And for $0<\alpha <1$, we deduce

$$\begin{aligned} & \min \quad {\mathcal {M}}(U)=\int _{0}^{1} {\mathbf {R}}^{2}(x,U) {\text {d}}x,\\ \nonumber&{\text {subject to}} \\ \nonumber&U^{T} {\mathbf {FL}}^{\alpha }(x)-u_{0}=0,\\ \nonumber&U^{T} {\mathbf {\Theta }}^{1}(\alpha ,1,x) {\mathbf {FL}}^{\alpha }(x)-u_{1}=0. \end{aligned}$$

(20)

For solving the above problem and obtaining the optimal value of elements of the unknown vector U, for $\alpha =1$, we consider

$$\begin{aligned}&{\mathcal {J}}(U,\lambda _{1},\lambda _{2})={\mathcal {M}}(U)+\lambda _{1}\left( U^{T} {\mathbf {FL}}^{\alpha }(x)-u_{0} \right) \nonumber \\&\quad +\,\lambda _{2} \left( U^{T} {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x)-u_{1} \right) . \end{aligned}$$

(21)

Also, for $0<\alpha <1$, we get

$$\begin{aligned}&{\mathcal {J}}(U,\lambda _{1},\lambda _{2})={\mathcal {M}}(U)+\lambda _{1}\left( U^{T} {\mathbf {FL}}^{\alpha }(x)-u_{0} \right) \nonumber \\&\quad +\,\lambda _{2} \left( U^{T} {\mathbf {\Theta }}^{1}(\alpha ,1,x) {\mathbf {FL}}^{\alpha }(x)-u_{1} \right) . \end{aligned}$$

(22)

Then, by applying the Lagrange multipliers method, the necessary conditions can be written as:

$$\begin{aligned} \frac{\partial {\mathcal {J}}}{\partial U}=0,\quad \frac{\partial {\mathcal {J}}}{\partial \lambda _{1}}=0,\quad \frac{\partial {\mathcal {J}}}{\partial \lambda _{2}}=0. \end{aligned}$$

(23)

As a result, considering the system of algebraic equations obtained from Eq. (23), the unknown vector U is determined. Accordingly, the approximate solution is obtained.

5.2 Implementation of the method for fractional diffusion equations

This section introduces the numerical optimization technique for fractional diffusion equations. To realize the purpose, we assume

$$\begin{aligned} u(x,t)\simeq {\mathbf {FL}}^{\alpha T}(x) U {\mathbf {FL}}^{\beta }(t). \end{aligned}$$

(24)

Next, we obtain the approximation of other functions by FLFs with the help of the operational matrix of derivative. Therefore, for $\alpha =1$, we have

$$\begin{aligned} \frac{\partial u}{\partial x}(x,t)\simeq {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Upsilon }}^{T}(\alpha ,x) U {\mathbf {FL}}^{\beta }(t), \end{aligned}$$

(25)

and for $0<\alpha <1$, we get

$$\begin{aligned} \frac{\partial u}{\partial x}(x,t)\simeq {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{1 T}(\alpha ,1,x) U {\mathbf {FL}}^{\beta }(t). \end{aligned}$$

(26)

We also have the following approximation for the second-order derivative of the function:

$$\begin{aligned} \frac{\partial ^{2} u}{\partial x^{2}}(x,t) \simeq {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{2 T}(\alpha ,2,x) U {\mathbf {FL}}^{\beta }(t). \end{aligned}$$

(27)

Also, by considering Eq. (24) and pseudo-operational matrix of fractional derivative, we get the following relations:

$$\begin{aligned} D^{\nu }_{t}u(x,t)\simeq {\mathbf {FL}}^{\alpha T}(x) U {\mathbf {\Theta }}^{1}(\beta ,\nu ,t) {\mathbf {FL}}^{\beta }(t),\quad0<\nu \le 1, \end{aligned}$$

(28)

and

$$\begin{aligned} D^{\gamma }_{x}u(x,t) \simeq {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{2T}(\alpha ,\gamma ,x)U {\mathbf {FL}}^{\beta }(t),\quad 0<\gamma \le 2. \end{aligned}$$

(29)

We now introduce the following residual function with the assistance of substituting Eqs. (24)–(29) into Eq. (2), for $\alpha =1$ and $0<\alpha <1$, respectively:

$$\begin{aligned}&{\mathbf {R}}^{*}(x,t,U)\nonumber \\&\quad ={\mathbf {FL}}^{\alpha T}(x) U {\varvec {\Theta }}^{1}(\beta ,\nu ,t) {\mathbf {FL}}^{\beta }(t)+{\mathbf {FL}}^{\alpha T}(x) {\varvec {\Theta }}^{2T}(\alpha ,\gamma ,x)U {\mathbf {FL}}^{\beta }(t)\nonumber \\&\qquad -\,{\mathcal {G}}\left( x,t,{\mathbf {FL}}^{\alpha T}(x) U {\mathbf {FL}}^{\beta }(t),{\mathbf {FL}}^{\alpha T}(x) {\varvec {\Upsilon }}^{T}(\alpha ,x) U {\mathbf {FL}}^{\beta }(t),\right. \nonumber\\ {\mathbf {FL}}^{\alpha T}(x) {\varvec {\Theta }}^{2 T}(\alpha ,2,\left. x) U {\mathbf {FL}}^{\beta }(t) \right) , \end{aligned}$$

(30)

and

$$\begin{aligned} {\mathbf {R}}^{*}(x,t,U)= \,& {} {\mathbf {FL}}^{\alpha T}(x) U {\mathbf {\Theta }}^{1}(\beta ,\nu ,t) {\mathbf {FL}}^{\beta }(t)\nonumber \\&+{\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{2T}(\alpha ,\gamma ,x)U {\mathbf {FL}}^{\beta }(t)\nonumber \\ \nonumber&-\,{\mathcal {G}}\left( x,t,{\mathbf {FL}}^{\alpha T}(x) U {\mathbf {FL}}^{\beta }(t), {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{1 T}(\alpha ,1,x) U {\mathbf {FL}}^{\beta }(t),\right. \nonumber \\&\left. {\mathbf {FL}}^{\alpha T}(x) {\mathbf {\Theta }}^{2 T}(\alpha ,2,x) U {\mathbf {FL}}^{\beta }(t) \right) . \end{aligned}$$

(31)

From the initial and boundary conditions and Eq. (24), we conclude

$$\begin{aligned}&{\mathbf {\Lambda }}_{0}(x)={\mathbf {FL}}^{\alpha T}(x) U {\mathbf {FL}}^{\beta }(0)-f_{0}(x),\quad0\le x \le 1,\\&{\mathbf {\Lambda }}_{1}(t)={\mathbf {FL}}^{\alpha T}(0) U {\mathbf {FL}}^{\beta }(t)-\varphi _{0}(t), \quad 0\le t \le 1,\\&{\mathbf {\Lambda }}_{2}(t)={\mathbf {FL}}^{\alpha T}(1) U {\mathbf {FL}}^{\beta }(t)-\varphi _{1}(t), \quad 0\le t \le 1. \end{aligned}$$

As a result, the following optimization problem is obtained:

$$\begin{aligned} & \min \quad {\mathcal {M}}^{*}(U)=\int _{0}^{1} \int _{0}^{1} {\mathbf {R}}^{*2}(x,t,U) {\text {d}}x {\text {d}}t,\\ \nonumber&{\text {subject to}} \\ \nonumber&{\mathbf {\Lambda }}_{0}(x)=0,\\ \nonumber&{\mathbf {\Lambda }}_{1}(t)=0,\\ \nonumber&{\mathbf {\Lambda }}_{2}(t)=0. \end{aligned}$$

(32)

More precisely, by applying nodal points of Newton–Cotes [12] in conditions, we deduce

$$\begin{aligned} &\min \quad {\mathcal {M}}^{*}(U)=\int _{0}^{1} \int _{0}^{1} {\mathbf {R}}^{*2}(x,t,U) {\text {d}}x {\text {d}}t,\\ \nonumber&{\text {subject to}} \\ \nonumber&{\mathbf {\Lambda }}_{0}(x_{i})=0, \quad i=0,1,\dots ,{\mathfrak {M}}_{1} \\ \nonumber&{\mathbf {\Lambda }}_{1}(t_{j})=0, \quad j=0,1,\dots ,{\mathfrak {M}}_{2}\\ \nonumber&{\mathbf {\Lambda }}_{2}(t_{j})=0. \end{aligned}$$

(33)

Then, for solving the aforesaid minimization problem and evaluating the optimal value of unknown matrix U,  we define

$$\begin{aligned} {\mathcal {J}}^{*}(U,\lambda _{1},\lambda _{2})={\mathcal {M}}^{*}(U)+A {\mathbf {\Lambda }}_{0} +B {\mathbf {\Lambda }}_{1} +C{\mathbf {\Lambda }}_{2}. \end{aligned}$$

(34)

where

$$\begin{aligned} A= & {} \left[ a_{0},a_{1},\dots ,a_{{\mathfrak {M}}_{1}} \right] ^{T},\\ B= & {} \left[ b_{0},b_{1},\dots ,b_{{\mathfrak {M}}_{2}} \right] ^{T},\\ C= & {} \left[ c_{0},c_{1},\dots ,c_{{\mathfrak {M}}_{2}} \right] ^{T}, \end{aligned}$$

and

$$\begin{aligned}&{\mathbf {\Lambda }}_{0}=\left[ {\mathbf {\Lambda }}_{0}(x_{0}),{\mathbf {\Lambda }}_{0}(x_{1}),\dots ,{\mathbf {\Lambda }}_{0}(x_{{\mathfrak {M}}_{1}})\right] ^{T}, \\&{\mathbf {\Lambda }}_{1}=\left[ {\mathbf {\Lambda }}_{1}(t_{0}),{\mathbf {\Lambda }}_{1}(t_{1}),\dots ,{\mathbf {\Lambda }}_{1}(t_{{\mathfrak {M}}_{2}})\right] ^{T}, \\&{\mathbf {\Lambda }}_{2}=\left[ {\mathbf {\Lambda }}_{2}(t_{0}),{\mathbf {\Lambda }}_{2}(t_{1}),\dots ,{\mathbf {\Lambda }}_{2}(t_{{\mathfrak {M}}_{2}})\right] ^{T}. \end{aligned}$$

Next, in order to obtain the unknown matrix U,  we utilize Lagrange multipliers method. So, we consider the necessary conditions below for the extremum of the fractional diffusion equation

$$\begin{aligned} \frac{\partial {\mathcal {J}}^{*}}{\partial U}=0,\quad \frac{\partial {\mathcal {J}}^{*}}{\partial A}=0,\quad\frac{\partial {\mathcal {J}}^{*}}{\partial B}=0,\quad \frac{\partial {\mathcal {J}}^{*}}{\partial C}=0. \end{aligned}$$

As a result, by solving the aforesaid system of algebraic equations, we determine the unknown matrix U. Then, by replacing the obtained matrix into Eq. (24), the approximate solution is obtained.

6 Convergence analysis and error estimate

Overall, this section discusses the convergence analysis and error estimate in Sobolev space. For this purpose, the Sobolev norm of integer order $\mu \ge 0$ in the domain $\Delta =(a,b)^{d}$ in $R^{d}$ for $d=2,3$ is defined [22]

$$\begin{aligned} \Vert u\Vert _{H^{\mu }(a,b)}=\left( \sum _{j=0}^{\mu } \sum _{i=1}^{d} \Vert D^{j}_{i}u\Vert ^{2}_{L^{2}(\Delta )} \right) ^{\frac{1}{2}}, \end{aligned}$$

(35)

where $D^{j}_{i}$ denotes the jth derivative of u relative to the ith variable. To achieve the objectives and simplifying the way of presenting the results, we consider ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}={\mathfrak {M}}$ and $\alpha =\beta$.

Theorem 2

Suppose that $u\in H^{\mu }(\Delta )$, $\mu \ge 0$ and $\Delta =(0,1)^{2}.$ If

$$\begin{aligned} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u=\sum _{m_{1}=0}^{{\mathfrak {M}}} \sum _{m_{2}=0}^{{\mathfrak {M}}} a_{m_{1}m_{2}} {\mathbf {FL}}_{m_{1}}^{\alpha }(x) {\mathbf {FL}}_{m_{2}}^{\alpha }(t), \end{aligned}$$

is the best approximation of u,  then we have the following estimations:

$$\begin{aligned} \Vert u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\Vert _{L^{2}(\Delta )}\le c \alpha ^{1-\mu } {\mathfrak {M}}^{1-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

(36)

and for $1\le r \le \mu ,$

$$\begin{aligned} \Vert u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\Vert _{H^{r}(\Delta )}\le c\alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

(37)

where

$$\begin{aligned} \sigma (r)=\left\{ \begin{array}{ccc} 0,&{}r=0,\\ 2r-\frac{1}{2},&{} r>0, \end{array} \right. \end{aligned}$$

and c depends on $\mu .$ In addition, the symbol on the right-hand side of the above error formulas is defined as follows:

$$\begin{aligned} |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}=\left( \sum _{j=\min (\mu ,{\mathfrak {M}}\alpha +1)}^{\mu } \sum _{i=1}^{d} \Vert D^{j}_{i}u\Vert ^{2}_{L^{2}(\Delta )} \right) ^{\frac{1}{2}}. \end{aligned}$$

Proof

According to results presented in [22] and the known concept which the best approximation is unique [23], the following estimate holds:

$$\begin{aligned}&\Vert u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\Vert _{L^{2}(\Delta )}= \Vert u-{\mathbf {P}}_{{\mathfrak {M}}\alpha }u\Vert _{L^{2}(\Delta )} \nonumber \\&\quad \le c ({\mathfrak {M}}\alpha )^{1-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

(38)

and for $1\le r \le \mu ,$

$$\begin{aligned}&\Vert u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\Vert _{H^{r}(\Delta )}= \Vert u-{\mathbf {P}}_{{\mathfrak {M}} \alpha }u\Vert _{H^{r}(\Delta )} \nonumber \\&\quad \le c ({\mathfrak {M}} \alpha )^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

(39)

Hence, the desired result is deduced. $\square$

Lemma 1

Let $u\in H^{\mu }(\Delta )$, $\mu \ge 0$ and $0<\nu \le 1,$ then we have

$$\begin{aligned}&\Vert D_{t}^{\nu }u-D_{t}^{\nu }({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\Vert _{L^{2}(\Delta )}\nonumber \\&\quad \le \frac{c}{ \Gamma (2-\nu )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

(40)

Proof

Due to the above-mentioned results and property of the norm

$$\begin{aligned} \Vert f*g\Vert _{p} \le \Vert f\Vert _{p} \Vert g\Vert _{1}, \end{aligned}$$

where $*$ is the convolution product and also from Riemann–Liouville fractional integral properties [12], we conclude

$$\begin{aligned}&\left\| D_{t}^{\nu }u-D_{t}^{\nu }({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right\| _{L^{2}(\Delta )}\\&\quad = \left\| I_{t}^{1-\nu }\left[ D_{t}^{1}u-D_{t}^{1}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right] \right\| _{L^{2}(\Delta )}\\&\quad =\left\| \frac{1}{t^{\nu } \Gamma (1-\nu )} *\left[ D_{t}^{1}u-D_{t}^{1}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right] \right\| _{L^{2}(\Delta )}\\&\quad \le \frac{1}{(1-\nu ) \Gamma (1-\nu )} \left\| D_{t}^{1}u-D_{t}^{1}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u) \right\| _{L^{2}(\Delta )}\\&\quad \le \frac{1}{ \Gamma (2-\nu )} \left\| u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u \right\| _{H^{r}(\Delta )} \\&\quad \le \frac{c}{ \Gamma (2-\nu )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

$\square$

Lemma 2

Let $u\in H^{\mu }(\Delta )$, $\mu \ge 0$ and $1<\gamma \le 2$ , then we have

$$\begin{aligned}&\left\| D_{x}^{\gamma }u-D_{x}^{\gamma }({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le \frac{c}{ \Gamma (3-\gamma )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |D_{x}^{1}u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

(41)

Proof

From the above lemma, we have

$$\begin{aligned}&\left\| D_{x}^{\gamma }u-D_{x}^{\gamma }({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right\| _{L^{2}(\Delta )}\\&\quad = \left\| I_{x}^{2-\gamma }\left[ D_{x}^{2}u-D_{x}^{2}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right] \right\| _{L^{2}(\Delta )}\\&\quad =\left\| \frac{1}{x^{\gamma -1} \Gamma (2-\gamma )} *\left[ D_{x}^{2}u-D_{x}^{2}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right] \right\| _{L^{2}(\Delta )}\\&\quad \le \frac{1}{(2-\gamma ) \Gamma (2-\gamma )} \left\| \left[ D_{x}^{2}u-D_{x}^{2}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u)\right] \right\| _{L^{2}(\Delta )}\\&\quad = \frac{1}{ \Gamma (3-\gamma )} \Vert D_{x}^{1} \left[ D_{x}^{1}u-D_{x}^{1}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u) \right] \Vert _{L^{2}(\Delta )} \\&\quad \le \frac{1}{ \Gamma (3-\gamma )} \Vert D_{x}^{1}u-D_{x}^{1}({\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u) \Vert _{H^{r}(\Delta )} \\&\quad \le \frac{c}{ \Gamma (3-\gamma )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |D_{x}^{1}u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

$\square$

Lemma 3

Let $u\in H^{\mu }(\Delta )$, $\mu \ge 0$ and $1<r \le \mu$ , then we get

$$\begin{aligned}&\left\| \frac{\partial }{\partial x}u - \frac{\partial }{\partial x} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

(42)

and

$$\begin{aligned}&\left\| \frac{\partial ^{2}}{\partial x^{2}}u - \frac{\partial ^{2}}{\partial x^{2}} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } \left| \frac{\partial }{\partial x} u\right| _{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

(43)

Proof

Directly, the results are obtained from Lemma 2. Thus, we have

$$\begin{aligned}&\left\| \frac{\partial }{\partial x}u - \frac{\partial }{\partial x} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\\&\quad \le \left\| u -{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{H^{r}(\Delta )} \\&\quad \le c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

and also

$$\begin{aligned}&\left\| \frac{\partial ^{2}}{\partial x^{2}}u - \frac{\partial ^{2}}{\partial x^{2}} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\\&\quad =\left\| \frac{\partial }{\partial x} \left( \frac{\partial }{\partial x} u\right) - \frac{\partial }{\partial x} \left( \frac{\partial }{\partial x} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right) \right\| _{L^{2}(\Delta )}\\&\quad \le \left\| \frac{\partial }{\partial x}u -\frac{\partial }{\partial x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{H^{r}(\Delta )} \\&\quad \le c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } \left| \frac{\partial }{\partial x} u\right| _{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

$\square$

Corollary 1

Let $u\in H^{\mu }(\Delta )$, $\mu \ge 0$ and $1<r \le \mu .$ If the assumptions in the above theorem and lemmas are established, and Lipschitz condition with the Lipschitz constant $\delta$ is satisfied for${\mathcal {G}},$ then we gain

$$\begin{aligned}&\left\| {\mathbf {R}}^{\alpha }\right\| _{L^{2}(\Delta )} \le c\delta \alpha ^{1-\mu } {\mathfrak {M}}^{1-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\quad +\left[ \frac{1}{ \Gamma (2-\nu )} +\delta \right] c\alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\quad +\left[ \frac{1}{ \Gamma (3-\gamma )}+\delta \right] c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } \left| \frac{\partial }{\partial x} u\right| _{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}, \end{aligned}$$

(44)

where

$$\begin{aligned} {\mathbf {R}}^{\alpha }= {\mathbf {E}}u(x,t)-{\mathbf {E}}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u(x,t). \end{aligned}$$

So that,

$$\begin{aligned} {\mathbf {E}}u(x,t)=D^{\nu }_{t}u(x,t)+D^{\gamma }_{x}u(x,t) -{\mathcal {G}}\left( x,t,u,\frac{\partial }{\partial x} u,\frac{\partial ^{2} }{\partial x^{2}}u\right) , \end{aligned}$$

and

$$\begin{aligned}&{\mathbf {E}}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u(x,t)=D^{\nu }_{t}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u(x,t)+D^{\gamma }_{x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u(x,t)\\&\quad -{\mathcal {G}}(x,t,{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u,\frac{\partial }{\partial x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u,\frac{\partial ^{2}}{\partial x^{2}} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}} u). \end{aligned}$$

Proof

From the results of the above theorem and lemmas, we achieve the following results:

$$\begin{aligned}&\left\| {\mathbf {R}}^{\alpha }\right\| _{L^{2}(\Delta )}\nonumber \\&\quad = \left\| {\mathbf {E}}u-{\mathbf {E}}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le \left\| D^{\nu }_{t}u-D^{\nu }_{t}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u \right\| _{L^{2}(\Delta )}+ \left\| D^{\gamma }_{x}u-D^{\gamma }_{x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u \right\| _{L^{2}(\Delta )}\nonumber \\&\qquad + \left\| {\mathcal {G}}(x,t,u,\frac{\partial }{\partial x} u,\frac{\partial ^{2} }{\partial x^{2}}u)-{\mathcal {G}}(x,t,{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u,\frac{\partial }{\partial x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right. \nonumber \\&\qquad ,\left. \frac{\partial ^{2}}{\partial x^{2}} {\mathbf {P}}^{\alpha }_{{\mathfrak {M}}} u) \right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le \left\| D^{\nu }_{t}u-D^{\nu }_{t}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u \right\| _{L^{2}(\Delta )}+ \left\| D^{\gamma }_{x}u-D^{\gamma }_{x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u \right\| _{L^{2}(\Delta )}\nonumber \\&\qquad + \delta \left\| u-{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}+\delta \left\| \frac{\partial }{\partial x}u-\frac{\partial }{\partial x}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\nonumber \\&\qquad +\delta \left\| \frac{\partial ^{2}}{\partial x^{2}}u-\frac{\partial ^{2}}{\partial x^{2}}{\mathbf {P}}^{\alpha }_{{\mathfrak {M}}}u\right\| _{L^{2}(\Delta )}\nonumber \\&\quad \le \frac{c}{ \Gamma (2-\nu )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\qquad + \frac{c}{ \Gamma (3-\gamma )} \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } \left| \frac{\partial }{\partial x}u\right| _{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\qquad + c\delta \alpha ^{1-\mu } {\mathfrak {M}}^{1-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\quad +c\delta \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\qquad +c\delta \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } \left| \frac{\partial }{\partial x} u\right| _{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\quad =c\delta \alpha ^{1-\mu } {\mathfrak {M}}^{1-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\qquad +\left[ \frac{1}{ \Gamma (2-\nu )} +\delta \right] c\alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}\nonumber \\&\qquad + \left[ \frac{1}{ \Gamma (3-\gamma )}+\delta \right] c \alpha ^{\sigma (r)-\mu } {\mathfrak {M}}^{\sigma (r)-\mu } |\frac{\partial }{\partial x} u|_{H^{\mu ;{\mathfrak {M}}\alpha }(\Delta )}. \end{aligned}$$

(45)

Accordingly, the proof is completed. $\square$

7 Numerical experiments

In this section, we implement the fractional-Lucas optimization method in solving the different classes of fractional differential equations, which justify the accuracy, applicability, and efficiency of the proposed method. The computations were performed on a personal computer, and the codes are written in MATLAB 2016.

7.1 Fractional differential equation

Example 1

For the first example, we consider the following initial value problem [24]:

$$\begin{aligned} D^{\nu }u(x)+3u(x)=3x^{3}+\frac{8}{\Gamma (0.5)}x^{3-\nu },\quad1<\nu \le 2, \end{aligned}$$

with the initial condition $u(0)=0,u'(0)=0.$ The exact solution, when $\nu =\frac{3}{2},$ is $u(x)=x^{3}.$ In Table 1 the value of absolute error for various choices of $\nu$ with $\alpha =1$ and ${\mathfrak {M}}_{1}=3$ is computed. From this table, it can be observed that, as $\nu$ approaches $\frac{3}{2}$, the approximate solution converges to the exact solution. The behavior of the numerical solutions obtained by numerical technique is illustrated in Figs. 1 and 2 for different choices of parameters mentioned in Sect. 5.1.

Table 1 Absolute error for various choices of $\nu$ with $\alpha =1$ and ${\mathfrak {M}}_{1}=3$ of Example 1

Fig. 1

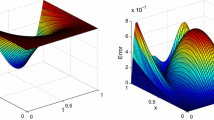
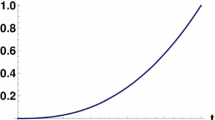
Approximate solution and exact solution for $\nu =1.5,1.4,1.3,1.2$ (left) and absolute error for $\nu =1.5$ (right) with ${\mathfrak {M}}_{1}=3$ and $\alpha =1$ of Example 1

Fig. 2

Approximate solution and exact solution for $\nu =1.5,1.4,1.3,1.2$ (left) and absolute error for $\nu =1.5$ (right) with ${\mathfrak {M}}_{1}=6$ and $\alpha =0.5$ of Example 1

Example 2

Consider the following nonlinear multi-order fractional differential equations [17, 18]:

$$\begin{aligned}&D^{\nu }u(x)+D^{\gamma }u(x)+[u(x)]^{2}\\&\quad =(x^{2}-x)^{2} +\frac{2x^{2-\nu }}{\Gamma (3-\nu )}+\frac{2x^{2-\gamma }}{\Gamma (3-\gamma )}- \frac{x^{1-\gamma }}{\Gamma (2-\gamma )}, \end{aligned}$$

$$\begin{aligned} 1<\nu \le 2,\quad 0<\gamma \le 1, \end{aligned}$$

with the initial conditions $u(0)=0, u'(0)=-1.$ The exact solution for this problem is $u(x)=x^{2}-x.$ In view of the presented method, for $\alpha =1$, we have

$$\begin{aligned} &\min \quad {\mathcal {M}}(U)=\int _{0}^{1} {\mathbf {R}}^{2}(x,U) {\text {d}}x,\\ \nonumber&{\text {subject to}} \\ \nonumber&U^{T} {\mathbf {FL}}^{\alpha }(x)=0,\\ \nonumber&U^{T} {\mathbf {\Upsilon }}(\alpha ,x) {\mathbf {FL}}^{\alpha }(x)+1=0, \end{aligned}$$

and for $0<\alpha <1$, we get

$$\begin{aligned} &\min \quad{\mathcal {M}}(U)=\int _{0}^{1} {\mathbf {R}}^{2}(x,U) {\text {d}}x,\\ \nonumber \, &{\text {subject to}}&\\ \nonumber&U^{T} {\mathbf {FL}}^{\alpha }(x)=0,\\ \nonumber&U^{T} {\mathbf {\Theta }}^{1}(\alpha ,1,x) {\mathbf {FL}}^{\alpha }(x)+1=0, \end{aligned}$$

where

$$\begin{aligned}&{\mathbf {R}}(x,U)=U^{T} {\mathbf {\Theta }}^{2}(\alpha ,\nu ,x) {\mathbf {FL}}^{\alpha }(x)+ U^{T} {\mathbf {\Theta }}^{1}(\alpha ,\gamma ,x) {\mathbf {FL}}^{\alpha }(x)\\&\quad +\left[ U^{T} {\mathbf {FL}}^{\alpha }(x)\right] ^{2}\\&\quad -\left( (x^{2}-x)^{2} +\frac{2x^{2-\nu }}{\Gamma (3-\nu )}+\frac{2x^{2-\gamma }}{\Gamma (3-\gamma )}- \frac{x^{1-\gamma }}{\Gamma (2-\gamma )} \right) . \end{aligned}$$

For $\alpha =\beta =1,$ $\nu =2,\gamma =1,$ and ${\mathfrak {M}}_{1}=2$, we obtain

$$\begin{aligned} u_{1}= & {} -1.0000000000000058,\\ u_{2}= & {} -1,\\ u_{3}= & {} 1.0000000000000058. \end{aligned}$$

Therefore, the approximate solution is

$$\begin{aligned} u(x)=x^{2}-x+1.147943701974890\times 10^{-41}. \end{aligned}$$

And also, for $\alpha =\beta =1,$ $\nu =1.5,\gamma =0.5$ and ${\mathfrak {M}}_{1}=2$, we deduce

$$\begin{aligned} u_{1}= & {} -0.9999999999999976,\\ u_{2}= & {} -1,\\ u_{3}= & {} 0.9999999999999976. \end{aligned}$$

Then,

$$\begin{aligned} u(x)=0.9999999999999976x^{2}-x+1.1021437293\times 10^{-41}. \end{aligned}$$

Also, we compare our results with Chebyshev wavelet methods [17, 18] in Table 2. By comparing these results, it can be seen that there is good agreement between numerical solutions and the exact solution.

Table 2 Comparison of absolute error for $\alpha =1$ with ${\mathfrak {M}}_{1}=2$ of Example 2

Example 3

Consider the following nonlinear fractional differential equations [25]:

$$\begin{aligned} D^{\gamma }u(x)+[u(x)]^{2}=1,\quad 0<\gamma \le 1,\quad0\le x \le 1, \end{aligned}$$

with the initial conditions $u(0)=0.$ The exact solution, when $\gamma =1,$ is $u(x)=\frac{\exp (2x)-1}{\exp (2x)+1}.$ In Tables 3 and 4, the value of absolute error and $L_{2}$-error for various choices of $\alpha ,\gamma$ and ${\mathfrak {M}}_{1}$ is presented. In Table 3 we notice that as the number of base functions ${\mathfrak {M}}_{1}$ increases, the absolute error tends to zero. Also, we show $L_{2}$-error in Table 4 to illustrate the effect of the $\alpha$ and $\gamma$ parameters on the numerical results. In addition, the approximate solution for $\gamma =1,0.95,0.9,0.85,0.8,$ and $\alpha =1$ with ${\mathfrak {M}}_{1}=5$ is plotted in Fig. 3.

Table 3 Absolute error for different choices of ${\mathfrak {M}}_{1}$ with $\alpha =\gamma =1$ of Example 3

Table 4 $L_{2}$-error for different choices of $\alpha ,\gamma$ with ${\mathfrak {M}}_{1}=5$ of Example 3

Fig. 3

Approximate solution for $\gamma =1,0.95,0.9,0.85,0.8,$ and $\alpha =1$ with ${\mathfrak {M}}_{1}=5$ of Example 3

7.2 Fractional diffusion equation

Example 4

Consider the following time-fractional convection–diffusion equation with variable coefficients [26,27,28]

$$\begin{aligned}&D_{t}^{\nu }u(x,t)+x\frac{\partial u(x,t)}{\partial x}+\frac{\partial ^{2} u(x,t)}{\partial x^{2}}=2t^{2\nu }+2x^{2}+2, \\&0<x< 1,\quad 0<t\le 1,\quad 0<\nu \le 1, \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned}&u(x,0)=x^{2},\quad 0<x< 1,\\&u(0,t)=\frac{2\Gamma (\nu +1)}{\Gamma (2\nu +1)}t^{2\nu },\\&u(1,t)=1+\frac{2\Gamma (\nu +1)}{\Gamma (2\nu +1)}t^{2\nu },\quad 0<t\le 1. \end{aligned}$$

The exact solution for this problem is $u(x,t)=x^{2}+\frac{2\Gamma (\nu +1)}{\Gamma (2\nu +1)}t^{2\nu }.$ With the help of the proposed method in previous section, for $\alpha =\beta =\nu =1$ and ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$, we have

$$\begin{aligned}&u_{11}=-1.0000000000000777,\\&u_{12}=-4.7510058418675076\times 10^{-14},\\&u_{13}=0.5000000000000758,\\&u_{21}=-7.578895611098832\times 10^{-14},\\&u_{22}=-4.5370462095201405\times 10^{-14},\\&u_{23}=7.371827437818487\times 10^{-14},\\&u_{31}=0.5000000000000765,\\&u_{32}=4.57701815507234\times 10^{-14},\\&u_{33}=-7.459073413110155\times 10^{-14}. \end{aligned}$$

Therefore, the approximate solution is gained as follows:

$$\begin{aligned}&u(x,t)=4.577018155072\times 10^{-14} tx^{2}- 4.1413634656068944\\&\quad \times 10^{-15} x- 3.4797537359033616\times 10^{-14} t \\&\quad +\, 7.3718274378184873\times 10^{-14} xt^{2} + 1.00000000000000380x^{2} \\&\quad -\, 7.4590734131101545\times 10^{-14} x^{2}t^{2}- 4.5370462095201411\\&\quad \times \,10^{-14} xt + 1.00000000000000247t^{2}\\&\quad +\, 6.501249483589424\times 10^{-17}. \end{aligned}$$

Table 5 contains the comparison of the absolute error obtained by present method for $\alpha =\beta =1,\nu =0.5$ and $t=0.5$ with Haar wavelet method (HWM) [26], Sinc–Legendre method (SLM) [27], and Chebyshev wavelets method (CWM) [28]. It should be noted that our method with the number of base functions less than Chebyshev wavelets method [28] achieved the same results. Also, Figs. 4 and 5 demonstrate the behavior of the numerical technique for different choices of $\alpha ,\beta ,\nu$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$.

Table 5 Comparison of absolute error for $\alpha =\beta =1,\nu =0.5$ with $t=0.5$ of Example 4

Fig. 4

Approximate solution (left) and absolute error (right) for $\nu =\alpha =0.3,\beta =1$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$ of Example 4

Fig. 5

Approximate solution (left) and absolute error (right) for $\nu =\alpha =0.9,\beta =1$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$ of Example 4

Example 5

Consider the following nonlinear time-space fractional advection–diffusion equation [29]

$$\begin{aligned}&D^{\nu }_{t}u(x,t)+u(x,t)\frac{\partial u(x,t)}{\partial x}=x+xt^{2}, \\&\quad 0\le x\le 1,\quad t >0, \quad 0< \nu \le 1, \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned}&u(x,0)=0,\quad 0<x<1,\\&u(0,t)=0,\quad u(1,t)=t,\quad t >0. \end{aligned}$$

The exact solution, when $\nu =1,$ is $u(x,t)=xt.$ According to the method presented in the earlier section, by taking ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=1$ and $\alpha =\beta =\nu =1,$ we get

$$\begin{aligned}&U=\left[ \begin{array}{cccc} 7.771561172376096\times 10^{-16}&{} 4.440892098500626\times 10^{-16}\\ -3.552713678800501\times 10^{-15}&{} 1.0000000000000078 \end{array} \right] . \end{aligned}$$

Consequently, the approximate solution is obtained as follows:

$$\begin{aligned}&u(x,t)=8.8817841970012\times 10^{-16}t- 7.105427357601001\\&\quad \, \times 10^{-15}x+ xt + 3.10862446895043\times 10^{-15}. \end{aligned}$$

Also, the behavior of the approximate solution for different choices of $\nu$ is illustrated in Fig. 6.

Fig. 6

Exact solution and approximate solutions for $\nu =1,0.9,0.7,0.5$ and $\alpha =\beta =1$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$ and $x=0.5$ of Example 5

Example 6

Consider the following time-space fractional diffusion equation with variable coefficients [30, 31]:

$$\begin{aligned}&D^{\frac{1}{2}}_{t}u(x,t)+xD^{\frac{1}{2}}_{x}u(x,t) =\frac{2xt^{\frac{1}{2}}}{\sqrt{\pi }}+\frac{2x^{\frac{3}{2}}t}{\sqrt{\pi }}, \\&\quad 0\le x \le 2,\quad 0\le t \le 1, \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned}&u(x,0)=0,\quad 0\le x \le 2,\\&u(0,t)=0,\quad0\le t \le 1. \end{aligned}$$

The exact solution for this problem is $u(x,t)=xt.$ Table 6 illustrates comparisons of the absolute errors of the approximate solutions with methods in [30, 31] at various times. The $L_{2}$-error for different values of $\alpha ,\beta$ and ${\mathfrak {M}}_{1},{\mathfrak {M}}_{2}$ at various times on the interval $x\in [0,2]$ is computed in Table 7. We also show the absolute errors for different choices of $\alpha ,\beta$ and ${\mathfrak {M}}_{1},{\mathfrak {M}}_{2}$ in Fig. 7. The computational results on the tables and figures verify the accuracy and efficiency of the proposed method.

Table 6 Comparison of absolute error for $\alpha =\beta =1$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=1$ of Example 6

Table 7 $L_{2}$-error for different choices of $\alpha ,\beta$ and ${\mathfrak {M}}_{1},{\mathfrak {M}}_{2}$ on the interval $x\in [0,2]$ of Example 6

Fig. 7

Absolute error for $\alpha =\beta =0.5$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=2$ (left) and $\alpha =\beta =1$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=1$ (right) of Example 6

Example 7

Consider the following space fractional diffusion equation with variable coefficients [32, 33]:

$$\begin{aligned}&\frac{\partial u(x,t)}{\partial t}= \Gamma (1.2)x^{1.8}D^{1.8}_{x}u(x,t)+(6x^{3}-3x^{2})\exp (-t)\\&\quad 0\le x \le 1,\quad t >0, \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned}&u(x,0)=x^{2}-x^{3},\quad 0<x<1,\\&u(0,t)=u(1,t)=0,\quad t>0. \end{aligned}$$

The exact solution for this problem is $u(x,t)=(x^{2}-x^{3})\exp (-t).$ Table 8 compares the absolute errors at different points of x and t on interval [0, 1] with obtained results in methods [32, 33]. In addition, we display the approximate solution and absolute error for $\alpha =\beta =1$ with ${\mathfrak {M}}_{1}=3,{\mathfrak {M}}_{2}=5$ in Fig. 8. The comparison of the obtained results in table and figure with those based on other methods demonstrates that the proposed scheme is a powerful tool to get the approximate solution with high accuracy.

Table 8 Comparison of the absolute error obtained by the present method with methods in [32, 33] of Example 7

Fig. 8

Approximate solution (left) and absolute error (right) for $\alpha =\beta =1$ with ${\mathfrak {M}}_{1}=3,{\mathfrak {M}}_{2}=5$ of Example 7

Example 8

Consider the following time-space fractional diffusion equation [19]:

$$\begin{aligned}&D^{\nu }_{t}u(x,t)+D^{\gamma }_{x}u(x,t)=\cos (x)+\cos (t), \\&\quad 0\le x,t \le 1, \quad 0< \nu ,\gamma \le 1, \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned}&u(x,0)=\sin (x),\quad 0\le x \le 1,\\&u(0,t)=\sin (t),\quad 0\le t \le 1 \end{aligned}$$

The exact solution, when $\nu =\gamma =1,$ is $u(x,t)=\sin (x)+\sin (t).$ To show the effect of the number of base functions to the accuracy of approximate solution, we exhibit the absolute errors for different values of ${\mathfrak {M}}_{1},{\mathfrak {M}}_{2}$ in Table 9. Besides, the behavior of the approximate solution for different choices of $\nu ,\gamma$ is presented in Figs. 9 and 10. These graphs are plotted to verify the accuracy and efficiency of the proposed method.

Table 9 Absolute errors for different values of ${\mathfrak {M}}_{1},{\mathfrak {M}}_{2}$ with $\nu =\gamma =\alpha =\beta =1$ of Example 8

Fig. 9

Approximate solutions for $\nu =\gamma =1,0.9,0.8,0.7,0.6$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=3,\alpha =\beta =1$ and $t=1$ of Example 8

Fig. 10

Approximate solutions for (blue) $\nu =\gamma =1,$ (orange) $\nu =\gamma =0.8,$ (green) $\nu =\gamma =0.6,$ (pink) $\nu =\gamma =0.4$ with ${\mathfrak {M}}_{1}={\mathfrak {M}}_{2}=3$ and $\alpha =\beta =1$ of Example 8

8 Conclusion

A novel numerical optimization method is constructed for evaluating the approximate solution of various classes of fractional partial differential equations. We first introduce fractional-Lucas functions and then compute the modified operational matrix of the derivative and pseudo-operational matrix of the fractional derivative by applying the properties of FLFs and Caputo fractional derivative. Despite using a few terms of base functions, the numerical results illustrate the excellent behavior of the optimization approach to gain the approximate solution. Also, the trend of the numerical approach illustrates that the method is very effective and accurate.