Modified Pseudo-dynamic Bearing Capacity of Strip Footing Resting on Layered Soil

Abstract

Seismic bearing capacity analysis is an important aspect for the design of foundation in earthquake-prone areas. In this study, an attempt is made to evaluate the seismic bearing capacity of foundation resting on two-layered $c - \phi$ soil using a new pseudo-dynamic limit equilibrium approach considering linear failure surface and the soil supporting as a visco-elastic material. The results are expressed in terms of bearing capacity ratio. A comparison of the present method with other available literatures is presented, which shows the acceptability of the results of the present study. Hence, the results of the present study may be used to design seismically stable shallow strip footing.

1 Introduction

Evaluation of seismic bearing capacity is an integral part of foundation design in the seismically active region. Several researchers have investigated bearing capacity of shallow strip footing using analytical, numerical and experimental methods. Numerous researchers have been analyzing the bearing capacity of shallow strip footing considering the underground soil as single layer of homogeneous soil. However, in nature soil is non-homogeneous and in some cases, different layers overlay to each other.

A innumerable number of researchers investigated the bearing capacity of shallow foundation on layered soil considering static loading condition (Button 1953; Reddy and Srinivasan 1967; Hanna and Meyerhof 1979; Florkiewicz 1989; Michalowski and Shi 1995; Michalowski 2002; Wang and Carter 2002; Kumar et al. 2007; Ghazavi and Eghbali 2008; Benmebarek et al. 2012; Karamitros et al. 2013; Ahmadi and Kouchaki 2016; Haghbin 2016; Khatri et al. 2017; Bera and Sasmal 2017; Biswas and Ghosh 2017; Mosallanezhad and Moayedi 2017; Jahani et al. 2018; Rajaei et al. 2018). To solve this problem, different failure surfaces such as linear, log-spiral are considered in the analysis. A comparison as given in Table 1 shows that there is no such difference in result.

Table 1 Comparison of ultimate bearing capacity between linear and log-spiral failure surfaces $\gamma$ = 18 kN/m³, q = 18 kN/m², c = 15 kN/m², B₀ = 2.5 m

Drominex and Pecker (1995), Soubra (1997) have developed the seismic bearing capacity factors for strip footings using upper-bound limit analysis. Many researchers have analyzed the seismic bearing capacity using the limit equilibrium method (Richards et al. 1993; Budhu and Al-Karni 1993; Saran and Agarwal 1991; Choudhury and Subba Rao 2006; Ghosh and Debnath 2017; Debnath and Ghosh 2018). In all the mentioned seismic analyses, the researchers have considered pseudo-static inertia forces, which are very crude approximation of earthquake dynamic forces where the time and phase lag are not considered. Jadar and Ghosh (2017), Saha and Ghosh (2015, 2019) have considered simultaneous resistance of unit weight, surcharge and cohesion to evaluate the bearing capacity of shallow strip footing. As an improvement of pseudo-static method, Steedman and Zeng (1990) have proposed a simple pseudo-dynamic method to analyze a vertical retaining wall in which only horizontal inertia force is considered. The proposed method is extensively used by numerous researchers (Choudhury and Nimbalkar 2005; Ghosh 2008; Saha and Ghosh 2015). However, pseudo-dynamic method lacks in certain aspects. For example, pseudo-dynamic method does not satisfy the boundary condition. It considers only incidental waves traveling upward through a linear elastic soil surface, resulting in a violation of the free-surface boundary condition. Pseudo-dynamic method follows a simple approach to consider the acceleration amplification. Linear variation of the acceleration is considered in this analysis. Also, the pseudo-dynamic method does not consider the damping properties of the soil. Whereas Bellezza (2014) has proposed a new pseudo-dynamic approach that considers the boundary condition, Pain et al. (2015) have showed that the wall–soil interaction in various seismic conditions may or may not be in phase for maximum sliding of the wall under active mode of failure. The researchers assumed a planar rupture surface. Pain et al. (2017) have applied this method to compute the passive earth pressure to take into account the negative wall friction angle under seismic loading conditions. Bellezza (2015) has taken into account the effect of both horizontal and vertical seismic accelerations to estimate the seismic active thrust assuming the soil as a Kelvin–Voigt solid. So, it is seen that new pseudo-dynamic method has advantages over pseudo-static and pseudo-dynamic, which is yet to be applied to solve foundation-related problems resting on two-layered soil.

Hence, in the present study, an attempt is made to use this new pseudo-dynamic approach to evaluate the seismic bearing capacity of shallow strip footing resting on two-layered $c - \phi$ soil. Particle swarm optimization algorithm is used for optimization. Bearing capacity is evaluated as a single coefficient for the simultaneous action of unit weight, surcharge and cohesion, which is more practical to simulate the field situation.

2 Model Definition

A strip footing having a width of $B_{0}$ is assumed to be on the top of a two-layered $c - \phi$ soil as shown in Fig. 1. The water table is assumed to be well below the footing. The bearing capacity of a strip footing, $q_{\text{ult}}$, is normally computed using the following formulation

$$q_{\text{ult}} = \frac{1}{2}\gamma B_{0} N_{{\gamma^{\prime \prime } }} ,$$

whereas $N_{{\gamma^{\prime \prime } }}$ is the single bearing capacity coefficient for simultaneous resistance of unit weight, surcharge and cohesion.

Fig. 1

Geometry of footing on two-layered

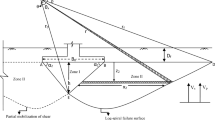
The failure surfaces are adopted as shown in Fig. 2. These were adopted by other investigators (Richards et al. 1993). As shown in Fig. 2, face BDF perpendicular to the base of the foundation is assumed to act like a retaining wall on which, at failure stage, active pressures resulting from $q_{\text{ult}}$, the weight of wedge ABDEF as soil pressure, are applied to the left side. On the right-hand side, surcharge $q_{1} = \gamma_{1} D_{\rm f}$ and the weight of wedge BJKFD generate passive resistances on the vertical wall. At equilibrium, both these active pressure and passive resistances are equal.

Fig. 2

Failure mechanism and wedges assumed in the present analysis

3 Wave Propagation for Visco-Elastic Material

Consider P and S waves traveling along the visco-elastic soil layer in the upward direction and approaching an interface between two different soil layers as shown in Fig. 3. Since these waves traveling toward the interface, it will be referred to as an incident waves. When the incident waves reaches at the interface, the part of its energy will be transmitted through the interface to continue traveling in the upward direction through layer 1. The remainder will be reflected at the interface and will travel back through layer 2 in the downward direction as a reflected wave.

Fig. 3

Wave propagation on two-layered soil

The reflected and refracted waves produced by incident P wave, S wave at interface are shown in Fig. 3. Table 2 shows the relation between amplitudes of different waves and angles formed by the waves with normal to the plane.

Table 2 Types of wave amplitude and angle with normal plane

From Snell’s Law, $\frac{\sin a}{X} = \frac{\sin b}{Y} = \frac{\sin c}{X} = \frac{\sin d}{Y} = \frac{\sin e}{V} = \frac{\sin f}{Z}$ [For details-NPTEL-Geotechnical Earthquake Engineering, Module 2, Wave Propagation; Lecture 7–9].

The related terms in Snell’s law are given in Table 2.

Assuming that the displacement associated with incident, reflected and transmitted waves are of same harmonic form and so writing down the corresponding displacement, acceleration and stress Eqs. acceleration amplitude is represented as:

$$\therefore \;a_{\rm r} = \frac{{1 - \alpha_{z} }}{{1 + \alpha_{z} }}a_{\rm i}$$

(1)

$$\therefore \;a_{\rm t} = \frac{2}{{1 + \alpha_{z} }}a_{\rm i}$$

(2)

where

$$\alpha_{z} = \frac{{\rho_{1} v_{1} }}{{\rho_{2} v_{2} }}$$

Here, $a_{\rm r}$ = acceleration amplitude due to reflected wave $a_{\rm i}$ = acceleration amplitude due to incident wave $a_{\rm t}$ = acceleration amplitude due to transmitted wave

The equation of motion for stress waves traveling through a visco-elastic medium was first proposed by Yuan et al. (2006). In vector form, the equation may be written as:

$$\rho \frac{{\partial^{2} u}}{{\partial t^{2} }} = \left\{ {(\lambda + G) + (\eta_{\text{l}} + \eta_{\text{s}} )\frac{\partial }{\partial t}} \right\}{\text{grad}}(\kappa ) + \left( {G + \eta_{\text{s}} \frac{\partial }{\partial t}} \right)\nabla^{2} \bar{u}$$

(3)

where $\rho$ = density, $\lambda$ = Lame constant; G  = shear modulus; $\eta_{\text{s}}$ and $\eta_{\text{l}}$ = viscosities of the soil; $\bar{u}$ = displacement vector; and $\kappa$ = div ($\bar{u}$).

The solution of a plane wave propagating vertically in a Kelvin–Voigt homogeneous medium was given by Bellezza (2015) as follows

$$\rho \frac{{\partial^{2} u_{\text{h}} }}{{\partial t^{2} }} = G\frac{{\partial^{2} u_{\text{h}} }}{{\partial z^{2} }} + \eta_{\rm s} \frac{{\partial^{3} u_{\text{h}} }}{{\partial z^{2} \partial t}}$$

(4)

$$\rho \frac{{\partial^{2} u_{\text{v}} }}{{\partial t^{2} }} = (\lambda + 2G)\frac{{\partial^{2} u_{\text{v}} }}{{\partial z^{2} }} + (\eta_{\rm L} + 2\eta_{\text{s}} )\frac{{\partial^{3} u_{\text{v}} }}{{\partial z^{2} \partial t}}$$

(5)

The stress–strain relationship of Kelvin–Voigt model is given by

$$\tau = \gamma_{\text{s}} G + \eta_{\text{s}} \frac{{\partial \gamma_{\text{s}} }}{\partial t}$$

(6)

$$\eta_{\text{s}} = \frac{2G\xi }{\omega }$$

(7)

where $\tau$ = shear stress; $\gamma_{\text{s}}$ = shear strain; $\eta_{\text{s}}$ = viscosity of soil; G = shear modulus; $\omega$ = angular frequency, $\xi$ = damping ratio.

At the ground surface z = 0, shear stress is zero. Assuming a base displacement, the horizontal displacement can be written as:

$$u_{\text{hb}} = \frac{{u_{{{\text{h}}0}} }}{{c_{\text{s}}^{2} + s_{\text{s}}^{2} }}[(c_{\text{s}} c_{{{\text{s}}z}} + s_{\text{s}} s_{{{\text{s}}z}} )\cos \omega t + (s_{\text{s}} c_{{{\text{s}}z}} - c_{\text{s}} s_{{{\text{s}}z}} )\sin \omega t]$$

(8)

Horizontal acceleration may be obtained by differentiating Eq. (8) twice with respect to time:

$$a_{\text{h}} (z,t) = \frac{{k_{\text{h}} g}}{{c_{\text{s}}^{2} + s_{\text{s}}^{2} }}\left[ {(c_{\text{s}} c_{{{\text{s}}z}} + s_{\text{s}} s_{{{\text{s}}z}} )\cos \omega t + (s_{\text{s}} c_{{{\text{s}}z}} - c_{\text{s}} s_{{{\text{s}}z}} )\sin \omega t} \right]$$

(9)

Similarly, vertical acceleration may be expressed as:

$$a_{\text{v}} (z,t) = \frac{{k_{\text{h}} g}}{{c_{\text{p}}^{2} + s_{\text{p}}^{2} }}\left[ {(c_{\text{p}} c_{{{\text{p}}z}} + s_{\text{p}} s_{{{\text{p}}z}} )\cos \omega t + (s_{\text{p}} c_{{{\text{p}}z}} - c_{\text{p}} s_{{{\text{p}}z}} )\sin \omega t} \right]$$

(10)

H is the total thickness of homogeneous soil layer.

4 Procedure of Analysis

To solve the problem using new pseudo-dynamic method, the following assumptions are made.

• a. The soil in each layer is homogeneous and isotropic.

• b. The weight of the soil above the base of the foundation has been replaced by a uniform surcharge.

• c. The failure mechanism consists of two active wedge angles and passive wedge angles, which are admitted as the variable of this present analysis.

To determine the bearing capacity coefficient, the geometry of the problem is depicted in Figs. 4, 5, 6 and 7. Parameters involved in the present study are as follows:

Fig. 4

Active wedge in the top layer

Fig. 5

Active wedge in the bottom layer

Fig. 6

Passive wedge in the top layer

Fig. 7

Passive wedge in the bottom layer

$c_{1}$ = cohesion of soil in top layer, $c_{2}$ = cohesion of soil in bottom layer, $\phi_{1}$ = angle of friction of soil in top layer, $\phi_{2}$ = angle of friction of soil in bottom layer, $\gamma_{1}$ = unit weight of soil in top layer,$\gamma_{2}$ = unit weight of soil in bottom layer, $\xi_{1}$ = damping ratio in top soil layer, $\xi_{2}$ = damping ratio in bottom soil layer, $\alpha_{{{\text{A}}1}}$ = angle of slip surface at top layer in active zone,$\alpha_{{{\text{A}}2}}$ = angle of slip surface at bottom layer in active zone,$\alpha_{{{\text{p}}1}}$ = angle of slip surface at top layer in passive zone,$\alpha_{{{\text{p}}2}}$ = angle of slip surface at bottom layer in passive zone, $\delta_{1}$ = friction angle along surface between active and passive zones at the first layer, $\delta_{2}$ = friction angle along surface between active and passive zones at the second layer. The thickness of the second layer contributing the failure wedge $h_{2}$ is expressed as:

$$h_{2} = B_{0} \tan \alpha_{{{\text{A}}2}} - h_{1} \frac{{\tan \alpha_{{{\text{A}}2}} }}{{\tan \alpha_{{{\text{A}}1}} }}\quad \left( {{\text{Ghazavi and Eghbali 2}}00 8} \right)$$

(11)

whereas $h_{1}$ is the thickness of first layer.

Active earth pressure and passive resistance in each layer are given, respectively, by:

4.1 Active Pressure at Top Layer

As shown in Fig. 4, wedge ABDE is known as active wedge. The weight of the wedge

$$W_{\text{A}} = \frac{{2B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} }}{2}h_{1} \gamma_{1}$$

(12)

Total load on the foundation is given by

$$P_{1} = p_{\text{L}} B_{0}$$

(13)

Total cohesive force on slip lines BD, AE and ED is given by

$$C_{{1,{\text{BD}}}} = c_{1} h_{1} ,\,C_{{1,{\text{AE}}}} = c_{1} {\text{AE}} = c_{1} h_{1} \cos ec{\kern 1pt} \alpha_{\rm A1} ,\;C_{{1,{\text{ED}}}} = c_{1} {\text{ED}} = c_{1} \left( {B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} } \right)$$

(14)

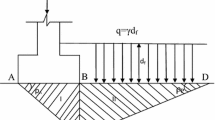
Considering 2:1 distribution, the intensity of load on the face ED is given by Fig. 8

$$p_{{{\text{L}}1}} = \frac{{p_{\text{L}} B_{0} }}{{\left( {B_{0} + h_{1} } \right)}}$$

(15)

Fig. 8

Load spread mechanism

The mass of the strip of thickness ${\text{d}}z_{1}$ (Fig. 4) in the trapezoidal failure wedge ${\text{ABDE}}$ is given by

$$m(z_{1} )_{{({\text{ABDE}})}} = \frac{{\gamma _{1} }}{g}\left( {\frac{{B_{0} \tan \alpha _{{{\text{A}}1}} - z_{1} }}{{\tan \alpha _{{{\text{A}}1}} }}} \right){\text{ d}}z_{1}$$

(16)

Acceleration of transmitted shear wave is given by:

$$a_{{{\text{t}}_{\text{h}} ({\text{ABDE}})}} (z_{1} ,t) = \frac{{a_{{{\text{t}}_{{{\text{h}}_{1} }} 0}} }}{{c_{{{\text{s}}_{1} }}^{2} + s_{{{\text{s}}_{1} }}^{2} }}\left[ {(c_{{{\text{s}}_{1} }} c_{{{\text{s}}_{1} z_{1} }} + s_{{{\text{s}}_{1} }} s_{{{\text{s}}_{1} z_{1} }} )\cos \omega t + (s_{{{\text{s}}_{1} }} c_{{{\text{s}}_{1} z_{1} }} - c_{{{\text{s}}_{1} }} s_{{{\text{s}}_{1} z_{1} }} )\sin \omega t} \right]$$

(17)

where

$$a_{{{\text{t}}_{{{\text{h}}_{1} }} 0}} = \frac{2}{{1 + (\alpha_{z} )_{\rm s} }}a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} ;\;a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} = k_{\text{h}} g;\quad (\alpha_{z} )_{\text{s}} = \frac{{\rho_{1} v_{{{\text{s}}1}} }}{{\rho_{2} v_{{{\text{s}}2}} }}$$

(18)

From Bellezza (2015), $K_{{{\text{s}}_{1} }} ,\,K_{{{\text{s}}_{2} }}$ are the real and imaginary parts of the complex wave no. $K_{\text{s}}^{*}$ is defined as a function of the complex shear modulus $G^{*}$ in particular $K_{\text{s}}^{*} = \omega_{\text{s}} \sqrt {\rho /G^{*} } = K_{{{\text{s}}_{1} }} + iK_{{{\text{s}}_{2} }}$ and $G = G + 2i\xi_{1}$

$$y_{{{\text{s}}_{1} }} = \frac{{\omega_{\text{s}} h_{1} }}{{v_{{{\text{s}}1}} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{1}^{2} } + 1}}{{2(1 + 4\xi_{1}^{2} )}}}$$

(19)

$$y_{{{\text{s}}_{2} }} = - \frac{{\omega h_{1} }}{{v_{{{\text{s}}1}} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{1}^{2} } - 1}}{{2(1 + 4\xi_{1}^{2} )}}}$$

(20)

The horizontal inertia force exerted on the small element due to horizontal earthquake acceleration can be expressed as $m(z_{1} )_{{({\text{ABDE}})}} a_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} (z_{1} ,t)$. The total horizontal inertia force acting in the wedge ${\text{ABDE}}$ may be obtained using the following equations:

$$\begin{aligned} Q_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} & = \int\limits_{0}^{{{\text{h}}_{1} }} {a_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} } (z_{1} ,t){\kern 1pt} m(z_{1} )_{{({\text{ABDE}})}} \\ & = \frac{{a_{{{\text{t}}_{{{\text{h}}_{1} }} 0_{{_{{({\text{ABDE}})}} }} }} \gamma_{1} }}{{g\tan \alpha_{{A_{1} }} }}\left[ {\frac{{c_{{{\text{s}}_{1} }} I_{{{\text{s}}_{1} }} + s_{{{\text{s}}_{1} }} I_{{{\text{s}}_{2} }} }}{{c_{{{\text{s}}_{1} }}^{2} + s_{{{\text{s}}_{1} }}^{2} }}\cos \omega t + \frac{{{\text{s}}_{{{\text{s}}_{1} }} I_{{{\text{s}}_{1} }} - c_{{{\text{s}}_{1} }} I_{{{\text{s}}_{2} }} }}{{c_{{{\text{s}}_{1} }}^{2} + s_{{{\text{s}}_{1} }}^{2} }}\sin \omega t} \right] \\ & = \frac{{a_{{{\text{t}}_{{{\text{h}}_{1} }} 0_{{_{{({\text{ABDE}})}} }} }} \gamma_{1} }}{{g\tan \alpha_{{A_{1} }} }}\left[ {A_{{{\text{h}}_{1} }} \cos \omega t + B_{{{\text{h}}_{1} }} \sin \omega t} \right] \\ \end{aligned}$$

(21)

where $a_{{{\text{t}}_{{{\text{h}}_{1} }} 0}} = \frac{2}{{1 + (\alpha_{z} )_{\text{s}} }}a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} ;\quad a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} = \;k_{\text{v}} g$; $(\alpha_{z} )_{\text{s}} = \frac{{\rho_{1} v_{{{\text{s}}1}} }}{{\rho_{2} v_{{{\text{s}}2}} }}$$A_{{{\text{h}}_{1} }} ,\,B_{{{\text{h}}_{1} }}$ are dimensionless parameters which depend on $y_{{{\text{s}}_{1} }} ,\,y_{{{\text{s}}_{2} }}$

Calculation of $c_{{{\text{s}}_{1} }}$, $c_{{{\text{s}}_{1} z_{1} }}$, $s_{{{\text{s}}_{1} }}$, $s_{{{\text{s}}_{1} z_{1} }}$, $I_{{{\text{s}}_{1} }}$, $I_{{{\text{s}}_{2} }}$, $A_{{{\text{h}}_{1} }} ,\,B_{{{\text{h}}_{1} }}$ is given in “Appendix 1”.

Similarly, the total vertical inertia force $Q_{{{\text{t}}_{{{\text{v}}({\text{ABDE}})}} }}$ can be calculated.

Applying limit equilibrium condition, we get,

$$\begin{aligned} & \sum {V = 0} ; \\ & \Rightarrow C_{{1,{\text{AE}}}} \sin \alpha_{{{\text{A}}1}} {\kern 1pt} + C_{{1,{\text{BD}}}} + R_{{{\text{A}}1}} \cos (\alpha_{{{\text{A}}1}} - \phi_{1} ) + P_{{{\text{A}}1}} \sin \delta_{1} \\ & \quad + \left( {p_{{{\text{L}}1}} + \gamma_{1} h_{1} } \right){\text{ED}}\left( {1 \pm a_{{{\text{i}}_{\text{v}} }} (h_{2} ,t)/g} \right) - P_{1} (1 \pm k_{\text{v}} ) - \left\{ {W_{\text{A}} + Q_{{{\text{t}}_{{{\text{v}}({\text{ABDE}})}} }} } \right\} = 0 \\ \end{aligned}$$

(22)

$$\begin{aligned} & \sum {H = 0} ; \\ & \Rightarrow - C_{{1,{\text{AE}}}} \cos \alpha_{{{\text{A}}1}} + R_{{{\text{A}}1}} \sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right) \\ & \quad - P_{{{\text{A}}1}} \cos \delta_{1} - \left[ {\left( {p_{{{\text{L}}1}} + \gamma_{1} h_{1} } \right){\text{ED}}{\kern 1pt} (a_{{{\text{i}}_{\text{h}} }} (h_{2} ,t)/g)\tan \phi_{2} + c_{{2,{\text{ED}}}} {\text{ED}}} \right] + P_{1} k_{\rm h} + Q_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} = 0 \\ \end{aligned}$$

(23)

After solving Eqs. 22, 23 and simplifying both, we get the active pressure as given below

$$\begin{aligned} P_{{{\text{A}}1}} & =P_{\rm L} B_{0} \left\{ {\frac{{\left\{ {(1 \pm k_{\text{v}} )} \right\}\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right) + k_{\text{v}} \cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}}} \right\} - \left\{ {\frac{{p_{\text{L}} B_{0} }}{{\left( {B_{0} + h_{1} } \right)}}\left( {B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} } \right)} \right\} \\ & \left\{ {\frac{{\left( {1 \pm a_{{{\text{i}}_{\text{v}} }} (h_{2} ,t)/g} \right)\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right) + \left\{ {a_{{{\text{i}}_{\text{h}} }} (h_{2} ,t)/g} \right\}\tan \phi_{2} \cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}}} \right\} + \frac{{2B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} }}{2}h_{1} \gamma_{1} \left\{ {\frac{{\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}}} \right\} \\ & \quad - \gamma_{1} h_{1} \left( {B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} } \right)\left\{ {\frac{{\left( {1 \pm a_{{{\text{i}}_{\text{v}} }} (h_{2} ,t)/g} \right)\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right) + \left\{ {a_{{{\text{i}}_{\text{h}} }} (h_{2} ,t)/g} \right\}\tan \phi_{2} \cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}}} \right\} - 2c_{1} h_{1} \frac{{\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}} \\ & \quad - c_{1} B_{0} \frac{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}} + Q_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} \frac{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}} + Q_{{{\text{t}}_{{{\text{v}}({\text{ABDE)}}}} }} \frac{{\sin \left( {\alpha_{{{\text{A}}1}} - \phi_{1} } \right)}}{{\cos \left( {\alpha_{{{\text{A}}1}} - \phi_{1} - \delta_{1} } \right)}} \\ \end{aligned}$$

(24)

4.2 Active Pressure at Bottom Layer

The weight of the wedge EDF

$$W_{\text{B}} = \frac{1}{2}{\kern 1pt} \left( {B_{0} - h_{1} \cot \alpha_{{{\text{A}}1}} } \right)h_{2} \gamma_{2}$$

(25)

Base shear at the interface between the two layers is given by

$$\left( {p_{{{\text{L}}1}} + \gamma_{1} h_{1} } \right)\left\{ {a_{{{\text{i}}_{\text{h}} }} (h_{2} ,t)/g} \right\}\;\tan \varphi_{2} + c_{2} ,\;\left( {p_{{{\text{L}}1}} + \gamma_{1} h_{1} } \right)\left\{ {a_{{{\text{t}}_{\text{h}} }} (h_{1} ,t)/g} \right\}\;\tan \varphi_{1} + c_{1}$$

(26)

Total cohesive force at slip lines DF and EF is expressed as given below

$$C_{{2,{\text{DF}}}} = c_{2} {\text{DF}} = c_{2} h_{2} ,\;C_{{2,{\text{EF}}}} = c_{2} {\text{EF}} = c_{2} h_{2} \cos ec\alpha_{{{\text{A}}2}} ,\;C_{{1,{\text{ED}}}} = c_{1} {\text{ED}} = c_{1} \left( {B_{0} - h_{1} \cot \alpha_{\text{A1}} } \right)$$

(27)

The mass of the strip of thickness ${\text{d}}z_{2}$ (Fig. 5) in the triangular failure wedge ${\text{EDF}}$ is given by $m(z_{2} )_{{({\text{EDF}})}} = \frac{{\gamma_{2} }}{g}\left( {\frac{{{\text{h}}_{2} - z_{2} }}{{\tan \alpha_{\rm A2} }}} \right){\text{d}}z_{2}$; the acceleration at any depth $z_{2}$ below the first soil layer at time t can be expressed as:

$$a_{{{\text{i}}_{{{\text{h}}({\text{EDF}})}} }} (z_{2} ,t) = \frac{{a_{{{\text{i}}_{{{\text{h}}_{2} }} 0_{{({\text{EDF}})}} }} }}{{c_{{{\text{s}}_{2} }}^{2} + s_{{{\text{s}}_{2} }}^{2} }}\left[ {(c_{{{\text{s}}_{2} }} c_{{{\text{s}}_{2} z_{2} }} + s_{{{\text{s}}_{2} }} s_{{{\text{s}}_{2} z_{2} }} )\cos \omega t + (s_{{{\text{s}}_{2} }} c_{{{\text{s}}_{2} z_{2} }} - c_{{{\text{s}}_{2} }} s_{{{\text{s}}_{2} z_{2} }} )\sin \omega t} \right]$$

(28)

where

$$\begin{aligned} c_{{{\text{s}}_{2} z_{2} }} & = \cos k_{{{\text{s}}_{3} z_{2} }} \cosh k_{{{\text{s}}_{4} z_{2} }} ,\;c_{{{\text{s}}_{2} }} = \cos y_{{{\text{s}}_{3} }} \cosh y_{{{\text{s}}_{4} }} ,\;s_{{{\text{s}}_{2} z_{2} }} = - \sin k_{{{\text{s}}_{3} z_{2} }} \sinh k_{{{\text{s}}_{4} z_{2} }} ,\;s_{{{\text{s}}_{2} }} = - \sin y_{{{\text{s}}_{3} }} \sinh y_{{{\text{s}}_{4} }} \\ & = \cos \left( {\frac{{y_{{{\text{s}}_{3} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\cosh \left( {\frac{{y_{{{\text{s}}_{4} }} z_{2} }}{{{\text{h}}_{2} }}} \right) \\ & = - \sin \left( {\frac{{y_{{{\text{s}}_{3} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\sinh \left( {\frac{{y_{{{\text{s}}_{4} }} z_{2} }}{{{\text{h}}_{2} }}} \right) \\ y_{{{\text{s}}_{3} }} & = \frac{{\omega_{\rm s} h_{2} }}{{v_{\rm s2} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{2}^{2} } + 1}}{{2(1 + 4\xi_{2}^{2} )}}} ,\;y_{{{\text{s}}_{4} }} = - \frac{{\omega h_{2} }}{{v_{\rm s2} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{2}^{2} } - 1}}{{2(1 + 4\xi_{2}^{2} )}}} \\ \end{aligned}$$

(29)

Therefore, the total horizontal inertia force $Q_{{{\text{i}}_{{{\text{h}}({\text{EDF}})}} }}$ acting in the failure wedge ${\text{EDF}}$ is given by

$$\begin{aligned} Q_{{{\text{i}}_{{{\text{h}}({\text{EDF}})}} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {a_{{{\text{i}}_{{{\text{h}}({\text{EDF}})}} }} } (z_{2} ,t){\kern 1pt} m(z_{2} )_{{({\text{EDF}})}} \\ & = \frac{{a_{{{\text{i}}_{{{\text{h}}_{2} }} 0_{{({\text{EDF}})}} }} \gamma_{2} }}{{g\tan \alpha_{{A_{2} }} }}\left[ {A_{{{\text{h}}_{2} }} \cos \omega t + B_{{{\text{h}}_{2} }} \sin \omega t} \right] \\ \end{aligned}$$

(30)

Horizontal inertia force exerted on the small element due to horizontal reflected earthquake wave acceleration can be expressed as $m(z_{2} )_{\text{EDF}} a_{{{\text{r}}_{{{\text{h}}_{{({\text{EDF}})}} }} }} (z_{2} ,t)$. Therefore, the horizontal inertia force $Q_{{{\text{r}}_{{{\text{h}}({\text{EDF}})}} }}$ acting in the failure wedge ${\text{EDF}}$ is given by

$$Q_{{{\text{r}}_{{{\text{h}}({\text{EDF}})}} }} = \int\limits_{0}^{{{\text{h}}_{2} }} {a_{{{\text{r}}_{{{\text{h}}({\text{EDF}})}} }} } (z_{2} ,t){\kern 1pt} m(z_{2} )_{{({\text{EDF}})}}$$

(31)

$$= \frac{{a_{{{\text{r}}_{{{\text{h}}_{2} }} 0_{{({\text{EDF}})}} }} \gamma_{2} }}{{g\tan \alpha_{{A_{2} }} }}\left[ {A_{{{\text{h}}_{2} }} \cos \omega t + B_{{{\text{h}}_{2} }} \sin \omega t} \right]$$

(32)

where

$$a_{{{\text{r}}_{{{\text{h}}_{2} }} 0}} = \frac{{1 - (\alpha_{z} )_{\rm s} }}{{1 + (\alpha_{z} )_{\rm s} }}a_{{{\text{i}}_{{{\text{h}}_{2} }} 0}} ;\;a_{{{\text{i}}_{{{\text{h}}_{2} }} 0}} = \;k_{\rm h} g;\;(\alpha_{z} )_{\rm s} = \frac{{\rho_{1} v_{\rm s1} }}{{\rho_{2} v_{\rm s2} }}$$

(33)

Net horizontal inertia force

$$(Q_{{{\text{h}}_{\rm (EDF)} }} )_{\rm R} = Q_{{{\text{i}}_{\rm h(EDF)} }} - Q_{{{\text{r}}_{\rm h(EDF)} }}$$

(34)

Calculations of $I_{{{\text{s}}_{3} }}$, $I_{{{\text{s}}_{4} }}$, $A_{{{\text{h}}_{2} }} ,\,B_{{{\text{h}}_{2} }}$ are given in “Appendix 1”

Similarly, net vertical inertia force,

$$(Q_{{v_{\rm (EDF)} }} )_{\rm R} \;{\text{can}}\;{\text{be}}\;{\text{calculated}}$$

(35)

Applying to limit equilibrium condition,

$$\begin{aligned} & \sum {V = 0} ; \\ & \quad \Rightarrow C_{{2,{\text{EF}}}} \sin \alpha _{{A2}} + C_{{2,{\text{DF}}}} + R_{{{\text{A}}2}} \cos \left( {\alpha _{{{\text{A}}2}} - \phi _{2} } \right) \\ & \quad + P_{{A2}} \sin \delta _{2} - \left( {p_{{{\text{L}}1}} + \gamma _{1} h_{1} } \right){\text{ED}}\left\{ {1 \pm a_{{\text{t}}_{\rm v}} (h_{1} ,t)/g} \right\} - \left\{ {W_{{\text{B}}} + (Q_{{{\text{v}}_{{({\text{EDF}})}} }} )R} \right\} = 0 \\ \end{aligned}$$

(36)

$$\begin{aligned} & \sum {H = 0} ; \\ & \Rightarrow C_{\rm 1,ED} - C_{\rm 2,EF} \cos \alpha_{\rm A2} + R_{\rm A2} \sin \left( {\alpha_{\rm A2} - \phi_{2} } \right) - P_{\rm A2} \cos \delta_{2} \\ & \quad + \left( {p_{\rm L1} + \gamma_{1} h_{1} } \right){\text{ED}} \left\{ {a_{{\rm t_{\rm h} }} (h_{1} ,t)/g} \right\}\tan \phi_{1} + (Q_{{{\text{h}}_{\rm (EDF)} }} )_{\rm R} = 0 \\ \end{aligned}$$

(37)

Solving Eqs. 36, 37 and simplifying, we get

$$\begin{aligned} P_{{{\text{A2}}}} & = \frac{{p_{{\text{L}}} B_{0} }}{{B_{0} + h_{1} }}\left( {B_{0} - h_{1} \cot \alpha _{{{\text{A1}}}} } \right)\left\{ {\frac{{\left( {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right)\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right) + \left\{ {a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} \cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} \\ & \quad + \frac{1}{2}\left( {B_{0} - h_{1} \cot \alpha _{{{\text{A1}}}} } \right)h_{2} \gamma _{2} \left\{ {\frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} + \gamma _{1} h_{1} \left( {B_{0} - h_{1} \cot \alpha _{{{\text{A1}}}} } \right) \\ & \quad \left\{ {\frac{{\left( {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right)\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right) + \left\{ {a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} \cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} - 2c_{2} h_{2} \frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} \\ & \quad - c_{2} h_{2} \cot \alpha _{{{\text{A2}}}} \frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} - c_{1} \left[ {{\text{h}}_{1} \cot \alpha _{{{\text{A1}}}} \frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} - B_{0} \frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right] \\ & \quad + (Q_{{{\text{h}}_{{({\text{EDF}})}} }} )_{{\text{R}}} \frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} + (Q_{{{\text{v}}_{{({\text{EDF}})}} }} )_{{\text{R}}} \frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} \\ \end{aligned}$$

(38)

Total active pressure from both the layers is given by

$$P_{\rm A} = P_{\rm A1} + P_{\rm A2}$$

(39)

4.3 Passive Resistance at Top Layer

Due to active pressure generated in top layer, passive zone provides the resistance to prevent the movement toward that direction. The weight of the passive wedge BJKD (Fig. 6)

$$W_{\rm c} = \frac{{{\text{h}}_{1} \cot \alpha_{p1} + 2h_{2} \cot \alpha_{\rm p2} }}{2}h_{1} \gamma_{1}$$

(40)

Total surcharge load in top layer of passive zone

$$\begin{aligned} Q_{1} &= q_{1} {\text{BJ}} \hfill \\ & = \,\gamma_{1} D_{\rm f} (h_{1} \cot \alpha_{p1} + h_{2} \cot \alpha_{\rm p2} ) \hfill \\ \end{aligned}$$

(41)

Total cohesive force in slip lines BD and JK of passive wedge

$$C_{1,DK} = c_{1} DK = c_{1} h_{2} \cot \alpha_{\rm p2} ,\;C_{1,BD} = c_{1} BD = c_{1} h_{1} ,\;C_{1,JK} = c_{1} JK = c_{1} h_{1} \cos ec\alpha_{p1}$$

(42)

The mass of the strip of thickness ${\text{d}}z_{1}$(Fig. 6) in the trapezoidal failure wedge ${\text{BJKD}}$ is given by $m(z_{1} )_{\text{BJKD}} = \frac{{\gamma_{1} }}{g}(h_{1} \cot \alpha_{p1} + h_{2} \cot \alpha_{\rm p2} - z_{1} \cot \alpha_{p1} ){\text{d}}z_{1}$, the acceleration at any depth $z_{1}$ below the ground surface and time t can be expressed as:

$$a_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} (z_{1} ,t) = \frac{{a_{{{\text{t}}_{{{\text{h}}_{1} }} 0_{{({\text{BJKD}})}} }} }}{{c_{{{\text{s}}_{3} }}^{2} + s_{{{\text{s}}_{3} }}^{2} }}\left[ {(c_{{{\text{s}}_{3} }} c_{{{\text{s}}_{3} z_{1} }} + s_{{{\text{s}}_{3} }} s_{{{\text{s}}_{3} z_{1} }} )\cos \omega t + (s_{{{\text{s}}_{3} }} c_{{{\text{s}}_{3} z_{1} }} - c_{{{\text{s}}_{3} }} s_{{{\text{s}}_{3} z_{1} }} )\sin \omega t} \right]$$

(43)

where

$$\begin{aligned} c_{{{\text{s}}_{3} z_{1} }} & = \cos k_{{{\text{s}}_{5} z_{1} }} \cosh k_{{{\text{s}}_{6} z_{1} }} \\ & = \cos \left( {\frac{{y_{{{\text{s}}_{5} }} z_{1} }}{{{\text{h}}_{1} }}} \right)\cosh \left( {\frac{{y_{{{\text{s}}_{6} }} z_{1} }}{{{\text{h}}_{1} }}} \right) \\ c_{{{\text{s}}_{3} }} & = \cos y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} \\ s_{{{\text{s}}_{3} z_{1} }} & = - \sin k_{{{\text{s}}_{5} z_{1} }} \sinh k_{{{\text{s}}_{6} z_{1} }} \\ & = - \sin \left( {\frac{{y_{{{\text{s}}_{5} }} z_{1} }}{{{\text{h}}_{1} }}} \right)\sinh \left( {\frac{{y_{{{\text{s}}_{6} }} z_{1} }}{{{\text{h}}_{1} }}} \right)s_{{{\text{s}}_{3} z_{1} }} = - \sin k_{{{\text{s}}_{5} z_{1} }} \sinh k_{{{\text{s}}_{6} z_{1} }} \\ & = - \sin \left( {\frac{{y_{{{\text{s}}_{5} }} z_{1} }}{{{\text{h}}_{1} }}} \right)\sinh \left( {\frac{{y_{{{\text{s}}_{6} }} z_{1} }}{{{\text{h}}_{1} }}} \right) \\ \end{aligned}$$

$$s_{{{\text{s}}_{3} }} = - \sin y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }}$$

$$y_{{{\text{s}}_{5} }} = \frac{{\omega_{\rm s} h_{1} }}{{v_{\rm s1} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{1}^{2} } + 1}}{{2(1 + 4\xi_{1}^{2} )}}} ,\quad y_{{{\text{s}}_{6} }} = - \frac{{\omega_{\rm s} h_{1} }}{{v_{\rm s1} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{1}^{2} } - 1}}{{2(1 + 4\xi_{1}^{2} )}}} ,$$

(44)

The horizontal—due to horizontal earthquake acceleration—can be expressed as $m(z_{1} )_{\text{BJKD}} a_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} (z_{1} ,t)$. Therefore, the total horizontal inertia force $Q_{{{\text{t}}_{\text{h}} ({\text{BJKD}})}}$ acting in the failure wedge $BJKD$ is given by

$$\begin{aligned} Q_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {a_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} {\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} } (z_{1} ,t) m(z_{1} )_{{({\text{BJKD}})}} \\ & = \frac{{a_{{{\text{t}}_{{{\text{h}}_{1} }} 0_{{({\text{BJKD}})}} }} \gamma_{2} }}{{g\tan \alpha_{{p_{2} }} }}\left[ {A_{{{\text{h}}_{3} }} \cos \omega t + B_{{{\text{h}}_{3} }} \sin \omega t} \right] \\ \end{aligned}$$

(45)

where

$$a_{{{\text{t}}_{{{\text{h}}_{1} }} 0}} = \frac{2}{{1 + (\alpha_{z} )_{\text{s}} }}a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} ;\quad a_{{{\text{i}}_{{{\text{h}}_{1} }} 0}} = \;k_{\text{h}} g;\;(\alpha_{z} )_{\text{s}} = \frac{{\rho_{1} v_{{{\text{s}}1}} }}{{\rho_{2} v_{{{\text{s}}2}} }}$$

(46)

Detailed calculations of $I_{{{\text{s}}_{{\text{5}}} }}$,$I_{{{\text{s}}_{{\text{6}}} }}$,$A_{{{\text{h}}_{3} }} ,\,B_{{{\text{h}}_{3} }}$ are given in “Appendix 2”.

Similarly, the total vertical inertia force, $Q_{{{\text{t}}_{{{\text{v}}({\text{BJKD}})}} }}$ acting in the failure wedge ${\text{BJKD}}$ can be evaluated.

Using limit equilibrium condition,

$$\begin{aligned} & \sum {V = 0} ; \\ & \Rightarrow - C_{{1,{\text{BD}}}} - C_{{1,{\text{JK}}}} \sin \alpha _{{p1}} + R_{{p1}} \cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right) - P_{{{\text{p}}1}} \sin \delta _{1} + \left( {q_{2} + \gamma _{1} h_{1} } \right){\text{DK}}\left\{ {1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g} \right\} - \left( {Q_{1} } \right)\left\{ {1 \pm k_{{\text{v}}} } \right\} - \left\{ {W_{{\text{c}}} + Q_{{{\text{t}}_{{{\text{v(BJKD)}}}} }} } \right\} = 0 \Rightarrow - C_{{1,{\text{BD}}}} - C_{{1,{\text{JK}}}} \sin \alpha _{{p1}} + R_{{p1}} \cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right) - P_{{{\text{p}}1}} \sin \delta _{1} + \left( {q_{2} + \gamma _{1} h_{1} } \right){\text{DK}}\left\{ {1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g} \right\} - \left( {Q_{1} } \right)\left\{ {1 \pm k_{{\text{v}}} } \right\} - \left\{ {W_{{\text{c}}} + Q_{{{\text{t}}_{{{\text{v(BJKD)}}}} }} } \right\} = 0 \\ \end{aligned}$$

(47)

$$\begin{aligned} & \sum {H = 0} ; \\ & \Rightarrow - C_{{{\text{1}},{\text{JK}}}} \cos \alpha _{{{\text{p1}}}} + C_{{{\text{1}},{\text{DK}}}} - R_{{{\text{p1}}}} \sin \left( {\phi _{1} + \alpha _{{{\text{p1}}}} } \right) \\ & \quad + P_{{{\text{p1}}}} \cos \delta _{1} + \left( {q_{2} + \gamma _{1} h_{1} } \right){\text{DK}}\left\{ {a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g} \right\}\tan \phi _{2} + Q_{1} k_{{\text{h}}} + Q_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} = 0 \\ \end{aligned}$$

(48)

Solving Eqs. 47, 48 and after simplification, passive resistance can be expressed as:

$$\begin{aligned} P_{{{\text{p1}}}} & = \frac{{{\text{h}}_{1} \cot \alpha _{{p1}} + 2h_{2} \cot \alpha _{{{\text{p2}}}} }}{2}h_{1} \gamma _{1} \left\{ {\frac{{\sin \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}}} \right\} \\ & \quad - \gamma _{1} h_{1} h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\left\{ {1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g} \right\}\sin \left( {\phi _{1} + \alpha _{{p1}} } \right) + \left\{ {a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g} \right\}\tan \phi _{2} \cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}}} \right\} - \gamma _{1} D_{{\text{f}}} \frac{{\left( {{\text{h}}_{1} \cot \alpha _{{p1}} + h_{2} \cot \alpha _{{{\text{p2}}}} } \right)}}{{\left( {{\text{h}}_{1} + h_{1} \cot \alpha _{{p1}} + h_{2} \cot \alpha _{{{\text{p2}}}} } \right)}}h_{2} \cot \alpha _{{{\text{p2}}}} \\ & \left\{ {\frac{{1 \pm a_{{\text{i}}} v(h_{2} ,t)/g\sin \left( {\phi _{1} + \alpha _{{p1}} } \right) + a_{{{\text{i}}_{{\text{h}}} }} h(h_{2} ,t)/g\tan \phi _{2} \cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}}} \right\} + \gamma _{1} D_{{\text{f}}} \left( {{\text{h}}_{1} \cot \alpha _{{{\text{p}}1}} + h_{2} \cot \alpha _{{{\text{p2}}}} } \right) \\ & \left\{ {\frac{{\left( {1 \pm k_{{\text{v}}} } \right)\sin \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right) - k_{{\text{h}}} \cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\} + 2c_{1} h_{1} \left\{ {\frac{{\sin \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\} + c_{1} \left[ {{\text{h}}_{1} \cot \alpha _{{{\text{p}}1}} \left\{ {\frac{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\} - h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\}} \right] \\ & \quad - Q_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} \frac{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}} + Q_{{{\text{t}}_{{{\text{v}}({\text{BJKD}})}} }} \frac{{\sin \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} \\ \end{aligned}$$

(49)

4.4 Passive Resistance at Bottom Layer

Total weight of the passive wedge DKF is shown in Fig. 7

$$W_{\rm D} = \frac{1}{2}h_{2}^{2} \cot \alpha_{\rm p2} \gamma_{2}$$

(50)

According to $2:1$, load distribution method intensity of surcharge load at depth $h_{1}$ can be written (Fig. 8)

$$q_{2} = \frac{{q_{1} \text{DK}}}{{\left( { \text{DK} + h_{1} } \right)}} = \frac{{q_{1} \left( {{\text{h}}_{1} \cot \alpha_{p1} + h_{2} \cot \alpha_{\rm p2} } \right)}}{{\left( {{\text{h}}_{1} + h_{1} \cot \alpha_{p1} + h_{2} \cot \alpha_{\rm p2} } \right)}}$$

(51)

Base shear between two passive wedges can be written as

$$\left( {q_{2} + \gamma_{1} h_{1} } \right)\left\{ {a_{{{\text{i}}_{h} }} (h_{2} ,t)/g} \right\}\;\tan \phi_{2} + c_{2} ,\;\left( {q_{2} + \gamma_{1} h_{1} } \right)\left\{ {a_{{\rm t_{\rm h} }} (h_{1} ,t)/g} \right\}\;\tan \phi_{1} + c_{1} ,$$

(52)

Cohesive forces in slip lines DF, KF and DK are given by, respectively

$$C_{{2,{\text{DF}}}} = c_{2} {\text{DF}} = c_{2} h_{2} ,\;C_{{2,{\text{KF}}}} = c_{2} {\text{KF}} = c_{2} h_{2} \cos ec\alpha_{\rm p2} ,\;C_{{1,{\text{DK}}}} = c_{1} h_{2} \cot \alpha_{\rm p2}$$

The mass of the strip of thickness ${\text{d}}z_{4}$ (Fig. 7) in the triangular failure wedge ${\text{DKF}}$ is given by $m(z_{4} )_{\rm DKF} = \frac{{\gamma_{2} }}{g}\left( {C_{1,DK} = c_{1} h_{2} \cot \alpha_{\rm p2} } \right){\text{d}}z_{4}$, the acceleration at any depth $z_{4}$ below the first soil layer and time can be expressed as:

$${\text{a}}_{{{\text{i}}_{\text{h(DKF)}} }} (z_{2} ,t) = \frac{{a_{{i{}_{{{\text{h}}_{2} }}0_{\rm (DKF)} }} }}{{c_{{{\text{s}}_{4} }}^{2} + s_{{{\text{s}}_{4} }}^{2} }}\left[ {(c_{{{\text{s}}_{4} }} c_{{{\text{s}}_{4} z_{2} }} + s_{{{\text{s}}_{4} }} s_{{{\text{s}}_{4} z_{2} }} )\cos \omega t + (s_{{{\text{s}}_{4} }} c_{{{\text{s}}_{4} z_{2} }} - c_{{{\text{s}}_{4} }} s_{{{\text{s}}_{4} z_{2} }} )\sin \omega t} \right]$$

(53)

where

$$\begin{aligned} c_{{{\text{s}}_{4} z_{2} }} & = \cos k_{{{\text{s}}_{7} z_{2} }} \cosh k_{{{\text{s}}_{8} z_{2} }} \\ & = \cos \left( {\frac{{y_{{{\text{s}}_{7} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\cosh \left( {\frac{{y_{{{\text{s}}_{8} }} z_{2} }}{{{\text{h}}_{2} }}} \right),\;c_{{{\text{s}}_{4} }} = \cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} \\ s_{{{\text{s}}_{4} z_{2} }} & - \sin \left( {\frac{{y_{{{\text{s}}_{7} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\sinh \left( {\frac{{y_{{{\text{s}}_{8} }} z_{2} }}{{{\text{h}}_{2} }}} \right),\;s_{{{\text{s}}_{4} }} = - \sin y_{{{\text{s}}_{7} }} \sinh y_{{{\text{s}}_{8} }} \\ y_{{{\text{s}}_{7} }} & = \frac{{\omega_{\rm s} h_{2} }}{{v_{\rm s2} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{2}^{2} } + 1}}{{2(1 + 4\xi_{2}^{2} )}}} ,\;y_{{{\text{s}}_{8} }} = - \frac{{\omega h_{2} }}{{v_{\rm s2} }}\sqrt {\frac{{\sqrt {1 + 4\xi_{2}^{2} } - 1}}{{2(1 + 4\xi_{2}^{2} )}}} \\ \end{aligned}$$

The horizontal inertia force exerted on the small element due to horizontal incidental shear wave acceleration can be expressed as $m(z_{2} )_{\rm DKF} a_{{{\text{i}}_{{{\text{h}}({\text{DKF}})}} }} (z_{2} ,t)$. Therefore, the total horizontal inertia force $Q_{{ih_{\rm (DKF)} }}$ acting in the failure wedge ${\text{EDF}}$ is given by

$$\begin{aligned} Q_{{{\text{i}}_{{{\text{h}}({\text{DKF}})}} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {a_{{{\text{i}}_{{{\text{h}}({\text{DKF}})}} }} } (z_{2} ,t)m(z_{2} )_{{({\text{DKF}})}} \\ & = \frac{{a_{{{\text{i}}_{{h2}} 0_{{({\text{DKF}})}} }} \gamma _{2} }}{{g\tan \alpha _{{{\rm p}_{2} }} }}\left[ {\frac{{c_{{{\text{s}}_{4} }} I_{{{\text{s}}_{7} }} + s_{{{\text{s}}_{4} }} I_{{{\text{s}}_{{\text{8}}} }} }}{{c_{{{\text{s}}_{4} }}^{2} + s_{{{\text{s}}_{4} }}^{2} }}{\text{ }}\cos \omega t + \frac{{{\text{s}}_{{{\text{s}}_{4} }} I_{{{\text{s}}_{{\text{7}}} }} 7 - c_{{{\text{s}}_{4} }} I_{{{\text{s}}_{{\text{8}}} }} }}{{c_{{{\text{s}}_{4} }}^{2} + s_{{{\text{s}}_{4} }}^{2} }}\sin \omega t} \right] \\ & = \frac{{a_{{{\text{i}}_{{{\text{h}}2}} 0_{{({\text{DKF}})}} }} \gamma _{2} }}{{g\tan \alpha _{{{\text{p}}_{2} }} }}\left[ {A_{{{\text{h}}_{4} }} \cos \omega t + B_{{{\text{h}}_{4} }} \sin \omega t} \right] \\ \end{aligned}$$

(54)

The horizontal inertia force exerted on the small element due to reflected shear wave acceleration can be expressed as:

$$\begin{aligned} Q_{{{\text{r}}_{h(DKF)} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {a_{{{\text{r}}_{{h({\text{DKF}})}} }} } (z_{2} ,t) m(z_{2} )_{{({\text{DKF}})}} \\ & = \frac{{a_{{{\text{r}}_{h2} 0_{\rm (DKF)} }} \gamma_{2} }}{{g\tan \alpha_{{{\rm p}_{2} }} }}\left[ {A_{{{\text{h}}_{4} }} \cos \omega t + B_{{{\text{h}}_{4} }} \sin \omega t} \right] \\ \end{aligned}$$

(55)

where $a_{{{\text{r}}_{{{\text{h}}_{2} }} 0}} = \frac{{1 - (\alpha_{z} )_{\rm s} }}{{1 + (\alpha_{z} )_{\rm s} }}a_{{{\text{i}}_{{{\text{h}}_{2} }} 0}} ;\;a_{{{\text{i}}_{{{\text{h}}_{2} }} 0}} = \;k_{h} g$; $(\alpha_{z} )_{\rm s} = \frac{{\rho_{1} v_{\rm s1} }}{{\rho_{2} v_{\rm s2} }}$

Net horizontal inertia force

$$(Q_{{{\text{h}}_{{({\text{DKF}})}} }} )_{\rm R} = Q_{{{\text{i}}_{{{\text{h}}({\text{DKF}})}} }} - Q_{{{\text{r}}_{{{\text{h}}({\text{DKF}})}} }}$$

(56)

Detailed calculation of equations $I_{{{\text{s}}_{{\text{7}}} }}$, $I_{{{\text{s}}_{{\text{8}}} }}$, $A_{{{\text{h}}_{4} }} ,\,B_{{{\text{h}}_{4} }}$ is given in “Appendix 2”

Similarly, the net vertical inertia force $(Q_{{{\rm v}_{\rm (DKF)} }} )_{\rm R}$ can be calculated

Applying equilibrium conditions,

$$\begin{aligned} & \sum {V = 0} ; \\ & \Rightarrow \; - C_{{{\text{2}},{\text{DF}}}} - C_{{{\text{2}},{\text{KF}}}} \sin \alpha _{{{\text{p2}}}} + R_{{{\text{p2}}}} \cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) - P_{{{\text{p2}}}} \sin \delta _{2} - \left( {q_{2} + \gamma _{1} h_{1} } \right){\text{DK}}\left\{ {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right\} - \left\{ {W_{{\text{D}}} + (Q_{{{\text{v}}_{{({\text{DKF}})}} }} )_{{\text{R}}} } \right\} = 0 \\ \end{aligned}$$

(57)

$$\begin{aligned} & \sum {H = 0} ; \\ & \Rightarrow - C_{{{\text{1}},{\text{DK}}}} - C_{{{\text{2}},{\text{KF}}}} \cos \alpha _{{{\text{p2}}}} - R_{{{\text{p2}}}} \sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) + P_{{{\text{p2}}}} \cos \delta _{2} - \left( {q_{2} + \gamma _{1} h_{1} } \right){\text{DK}}\left\{ {a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} + (Q_{{{\text{h}}_{{({\text{DKF}})}} }} )_{{\text{R}}} = 0 \\ \end{aligned}$$

(58)

Solving Eqs. (57) and (58), it can be expressed as

$$\begin{aligned} P_{{{\text{p2}}}} = \frac{1}{2}h_{2}^{2} \cot \alpha _{{{\text{p2}}}} \gamma _{2} \left\{ {\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} + \gamma _{1} h_{1} h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\left\{ {1 \pm a_{{t_{v} }} (h_{1} ,t)/g} \right\}\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) + \left\{ {a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} \cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}} \right\} \\ & \quad + \gamma _{1} D_{{\text{f}}} \frac{{\left( {{\text{h}}_{1} \cot \alpha _{{{\text{p}}1}} + h_{2} \cot \alpha _{{{\text{p2}}}} } \right)}}{{\left( {{\text{h}}_{1} + h_{1} \cot \alpha _{{{\text{p}}1}} + h_{2} \cot \alpha _{{{\text{p2}}}} } \right)}}h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\left\{ {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right\}\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) + \left\{ {a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} \cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} \\ & \quad + 2c_{2} h_{2} \left\{ {\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} + c_{1} h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} + c_{2} h_{2} \cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} + (Q_{{{\text{v}}_{{({\text{DKF}})}} }} )_{{\text{R}}} \frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} \\ & \quad - (Q_{{{\text{h}}_{{({\text{DKF}})}} }} )_{{\text{R}}} \frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} \\ \end{aligned}$$

(59)

Total passive resistance from the two wedges can be expressed as

$$P_{\rm p} = P_{p1} + P_{\rm p2}$$

(60)

In Fig. 2, it is seen that line BF can be thought as a retaining wall with the total active lateral thrust $P_{\rm A}$ from two layers of soil pushing against the passive resistance $P_{\rm p}$. At equilibrium, the components of two active force and passive resistance are equal. Thus, equating Eqs. 39 and 60, the final expression reduces to the form of Eq. 62

$$P_{\rm A} = P_{\rm p}$$

(61)

$$p_{\rm L} = \frac{1}{2}\bar{\gamma }N_{{\gamma^{\prime \prime } }}$$

(62)

$N_{{\gamma^{\prime \prime } }}$ is a single bearing capacity coefficient for the simultaneous resistance of cohesion, unit weight and surcharge. In seismic condition, $N_{{\gamma^{\prime \prime } }}$ is expressed as $N_{\gamma E}$ and static condition $N_{\gamma S}$$\bar{\gamma }$ is the equivalent unit weight and is given by,

$$\bar{\gamma } = \frac{{A_{1} \gamma_{1} + A_{2} \gamma_{2} }}{{A_{1} + A_{2} }}$$

(63)

where $A_{1}$ and $A_{2}$ are the effective area of each layer in breach zone and dependent on $h_{1}$ and $h_{2}$. Bearing capacity coefficient $(N_{{\gamma^{\prime\prime}}} )$ is a function of several parameters including cohesion, surcharge and unit weight. It can be expressed as

$$N_{{\gamma^{\prime \prime } }} = \left( {\frac{{a_{1} }}{{e_{1} }} + \frac{{b_{1} }}{{e_{1} }} + \frac{{2\bar{c}}}{{\bar{\gamma }B_{0} }}\;\frac{{d_{1} }}{{e_{1} }}} \right)$$

(64)

where $\bar{c}$ is defined as the weighted averaged cohesion showing the proportion of each layer in the slip line and is given by

$$\bar{c} = \frac{{c_{1} h_{1} + c_{2} h_{2} }}{{{\text{h}}_{1} + h_{2} }}$$

(65)

The detail equations for $a_{1}$, $b_{1}$, $d_{1}$ and $e_{1}$ are given in “Appendix 3”, and the flowchart of the present methodology is shown in Fig. 9.

Fig. 9

Flowchart to calculate bearing capacity coefficient $N_{{\gamma^{\prime \prime } }}$

Since the heuristic algorithms give us low ramification and high execution, these methods are relatively new and can be applied in the geotechnical problem. Out of these methods, a brief discussion on particle swarm optimization is given here as it is used in the analysis.

5 Particle Swarm Optimization

Kennedy and Eberhart (1995) have developed PSO as a stimulation of birds swarm. Swarm is a group of individuals with defined rules for individual behaviors and communications. The ability of each individual to deal with the previous experiences of the swarm is called swarm intelligence. This capability guides the swarm toward its optimum goal. PSO is a population-based search technique where a population of particles starts their journey in a space with respect to the current best position (Hossain and El-Shafie 2014). Reynolds (1987) described three simple rules for the behavior of individuals inside a swarm which are used as one of the basic concepts of PSO by Kennedy and Eberhart (1995). Although these simple rules model the behavior of individuals, their combination produces a complicated behavior for the swarm:

• a. Individuals avoid collision with others

• b. Individuals go toward the goal of swarm

• c. Individuals go to the center of swarm

The process of decision making related to individuals is other basic concept of PSO. Each individual of the swarm makes decision based on the following two factors:

1. The own experiences of individual that is its best results so far 2. The experiences of other individuals in the swarm that is the best results in the whole swarm. Figure 10 illustrates one flowchart to optimize a problem using PSO. At the starting step of the original PSO, a certain number of individuals, called particles, are distributed in the search space by using a random pattern (Kennedy and Eberhart 1995; Cheng et al. 2007). Each particle is a representative of a feasible solution. Figure 11 shows the schematic structure of a particle in PSO involving three divided parts as its current position, best position, and velocity. The current position, best position and velocity of particles record, respectively, the current coordinates, best coordinates and velocity vectors of a particle in D-dimensional space, where D starts from one (Kalatehjari 2013). Consequently, for a particle in D-dimensional space, a 3-dimensional particle is desirable. The aim of PSO is to meet the termination criteria which are defined as the criteria for terminating the iterative search process. To select an appropriate termination criterion, it should be noted that the termination condition does not cause a prematurely converge and it should protect against oversampling of the fitness (Engelbrecht 2007). The following termination criteria are frequently used in PSO: 1. Termination when the maximum number of iterations is exceeded 2. Termination when a satisfactory solution is found based on the condition of each problem 3. Termination when no improvement is achieved over a certain number of iterations. These criteria are applied to ensure that PSO is able to converge on a feasible solution. In fact, PSO tries to make the objective function as minimum or maximum depend to the problem to be solved. To lead the swarm toward this aim, the fitness value of each particle is determined by evaluating its current position by the objective function. After evaluating the fitness of all particles, Eq. 66 (velocity equation) is used to calculate the velocity of particles based on their best position and the position of the best particle in the swarm. Using Eq. 67, particle positions can be updated according to their current positions and velocities. This iterative process continues until reaching the termination criteria. Equations 66 and 67 are as follows (Kennedy and Eberhart 1995):

Fig. 10

Flowchart of PSO algorithm

Fig. 11

Schematic structure of a particle in PSO (Kalatehjari 2013)

Let $X$ and $V$ denote a particle’s position and velocity in a search space. Then, the ith particle can be interpreted as $X_{i} = (x_{\rm i1} ,x_{\rm i2} ,x_{i3,} \ldots \ldots \ldots \ldots \ldots.,x_{\rm id} )$ and the velocity of the ith particle is delimited by $V_{i} = \left( {v_{\rm i1} ,v_{\rm i2} ,v_{\rm i3} ,\ldots.,v_{\rm id} } \right)$, $d$ comprises the dimension of the problem. The best previous particle of the ith particle is recorded and represented as $P_{i} = \left( {p_{\rm i1} ,p_{\rm i2} ,p_{\rm i3} ,\ldots \ldots \ldots \ldots \ldots \ldots \ldots,p_{\rm id} } \right)$, the index of the best particle among all the particles is comprised by $P_{g} = \left( {p_{\rm g1} p_{\rm g2} p_{\rm g3} \ldots \ldots \ldots..p_{\rm gd} } \right)$. The velocity and position of each particle can be wangled according to the following equation:

$$V_{\text{id}} = \;\bar{\omega } * V_{\text{id}} + \bar{c}_{1} * {\text{rand}} * \left( {P_{\text{id}} - X_{\text{id}} } \right) + \bar{c}_{2} * {\text{rand}} * \left( {P_{\text{gd}} - X_{\text{id}} } \right)$$

(66)

$$X_{\rm id} = X_{\rm id} + V_{\rm id}$$

(67)

whereas $\bar{c}_{1}$ and $\bar{c}_{2}$ are position constants known as acceleration coefficient, $\bar{\omega }$ is the inertia weight coefficient; rand is a random number within the range $\left[ {0,\;1} \right]$. In the present analysis $\bar{\omega }$ is characterized by $\bar{\omega }({\text{gn}}) = \bar{\omega }_{{{\text{max}}}} - \frac{{\bar{\omega }_{{{\text{max}}}} - \bar{\omega }_{{{\text{min}}}} }}{{NI}}*{\text{gn}}$, where $gn$ is the generation.

6 PSO Application in Geotechnical Engineering

Complexity of analysis of geotechnical behavior is due to multivariable dependencies of soil and rock responses. Most of the materials that geotechnical engineers deal with show uncertain behavior in consequence of the complex formation of these materials. Therefore, in some geotechnical engineering problems, the objective function is non-convex and discontinuous. Consequently, simple optimization techniques may have difficulties in finding the global optimum solution due to getting trapped in local solutions. To overcome this limitation, using a powerful optimization method to obtain the global optimum solution is of interest. In recent years, soft computing techniques have been widely used to predict geotechnical parameters (Singh et al. 2017; Sharma and Singh 2017). Accordingly, as a powerful optimization technique, PSO has entered in the field of geotechnical engineering to solve its problems. Keeping in view of the feasibility of PSO, in the present analysis PSO is applied to optimize the bearing capacity coefficient.

7 Results and Discussion

Subsequently optimization of bearing capacity coefficient $(N_{{\gamma^{\prime \prime } }} )$ w.r.t. variables $\alpha_{\rm A1}$, $\alpha_{\rm A2}$, $\alpha_{p1}$$\alpha_{\rm p2}$, $t/T$ by particle swarm optimization algorithm, optimum $\left( {N_{{\gamma^{\prime\prime}}} } \right)$ can be determined. Minimum value is taken as optimized value. The bearing capacity ratio $\frac{{N_{\gamma E} }}{{N_{\gamma S} }}$ is presented in Tables 3, 4, 5, and 6. Ranges of various parameters are given in below:

$$\begin{array}{*{20}l} {\xi = 10\% ,\quad 20\% \;\frac{{D_{\rm f} }}{{B_{0} }} = 0.25,0.5,1\quad \frac{{\phi_{1} }}{{\phi_{2} }} = 0.6,0.8,1\quad \frac{{\delta_{1} }}{{\delta_{2} }} = 0.6,0.8,1} \hfill \\ {\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.6,0.8,1\quad \frac{{c_{1} }}{{c_{2} }} = 0.6,0.8,1\quad \frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.25,0.5,1\quad k_{v} = 0,\frac{{k_{h} }}{2},k_{h} } \hfill \\ {{\text{h}}_{1} /\lambda ,h_{2} /\lambda = 0.3\quad h_{1} /\eta ,h_{2} /\eta = 0.16\quad \xi_{1} /\xi_{2} = 0.6,\;0.8,\;1\quad \frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8\;\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8} \hfill \\ \end{array}$$

where $\lambda = Tv_{\rm s1} ,\;Tv_{\rm s2}$ and $\eta = Tv_{p1} ,\;Tv_{\rm p2}$

Table 3 Static bearing capacity coefficients $N_{\gamma S}$ minimum

Table 4 Seismic and static bearing capacity coefficients ratio $\frac{{N_{\gamma E} }}{{N_{\gamma S} }}$ minimum

Table 5 Static bearing capacity coefficients $N_{\gamma S}$ minimum

Table 6 Seismic and static bearing capacity coefficients $\frac{{N_{\gamma E} }}{{N_{\gamma S} }}$ minimum

The parametric study is done for the variation of seismic bearing capacity coefficients with the different soil parameters as shown in Figs. 12, 13, 14, 15, 16, 17, 18, 19 and 20.

Fig. 12

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\phi_{1} /\phi_{2} = 0.8$, $\delta_{1} /\delta_{2} = 0.8$, $k_{V} = k_{h} / 2$, $\gamma_{1} /\gamma_{2} = 0.8$, $h_{1} /B_{0} = 0.25$ 2c₂/$B_{0} \gamma_{2} = 0.2$, c₁/c₂ = 0.8, h₁/$\lambda$, h₂/$\lambda$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2, V_p1/V_p2 = 0.8

Fig. 13

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$ $h_{1} /B_{0} = 0.50$, $\phi_{1} /\phi_{2} = 0.8$, $\delta_{1} /\delta_{2} = 0.8$, $k_{V} = k_{h} / 2$, $\gamma_{1} /\gamma_{2} = 0.8$, $\xi_{1} /\xi_{2} = 0.8$, 2c₂/$B_{0} \gamma_{2} = 0.2$, c₁/c₂ = 0, h₁/$\lambda$, h₂/$\lambda$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2, V_p1/V_p2 = 0.8

Fig. 14

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\phi_{1} /\phi_{2} = 0.8$, $\delta_{1} /\delta_{2} = 0.8$, $k_{V} = k_{h} / 2$, $\gamma_{1} /\gamma_{2} = 0.8$, D_f/B₀ = 0.50, 2c₂/$B_{0} \gamma_{2} = 0.2$, c₁/c₂ = 0.8 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2, V_p1/V_p2 = 0.8

Fig. 15

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\phi_{1} /\phi_{2} = 0.8$, D_f/B₀ = 0.8, $k_{V} = k_{h} / 2$, $h_{1} /B_{2} = 0.25$, 2c₂/$B_{0} \gamma_{2} = 0.2$, c₁/c₂ = 0.8 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2, V_p1/V_p2 = 0.8

Fig. 16

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$, $h_{1} /B_{0} = 0.50$ $\delta_{1} /\delta_{2}$ = 0.8, k_v = k_h/2, $\xi_{1} /\xi_{2}$ = 0.8, $\gamma_{1} /\gamma_{2} = 0.8$, D_f/B₀ = 0.50, 2c₂/B₀ $\gamma_{2} = 0$, c₁/c₂ = 0 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2 = 0.8, V_p1/V_p2 = 0.8

Fig. 17

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$, $h_{1} /B_{0} = 0.50$ $\delta_{1} /\delta_{2}$ = 0.8, k_v = k_h/2, $\xi_{1} /\xi_{2}$ = 0.8, $\phi_{1} /\phi_{2} = 0.8$, D_f/B₀ = 0.50, 2c₂/B₀ $\gamma_{2} = 0$, c₁/c₂ = 0 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2 = 0.8, V_p1/V_p2 = 0.8

Fig. 18

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$, $\gamma_{1} /\gamma_{2} = 0.8$ $\delta_{1} /\delta_{2}$ = 0.8, k_v = k_h/2, $\xi_{1} /\xi_{2}$ = 0.8, $\phi_{1} /\phi_{2} = 0.8$, D_f/B₀ = 0.50, 2c₂/B₀ $\gamma_{2} = 0$, c₁/c₂ = 0 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2 = 0.8, V_p1/V_p2 = 0.8

Fig. 19

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$, h₁/B₀ = 0.50 $\delta_{1} /\delta_{2}$ = 0.8, k_v = k_h/2, $\xi_{1} /\xi_{2}$ = 0.8, $\phi_{1} /\phi_{2} = 0.8$, D_f/B₀ = 0.50, 2c₂/B₀ $\gamma_{2} = 0.2$, h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16, V_S1/V_S2 = 0.8, V_p1/V_p2 = 0.8

Fig. 20

Variation of $N_{\gamma E}$ with k_h for $\phi_{2} = 30$°, $\delta_{2} = \phi_{2} /2$, $\xi_{2} = 20\%$, h₁/B₀ = 0.50 $\delta_{1} /\delta_{2}$ = 0.8, k_v = k_h/2, $\xi_{1} /\xi_{2}$ = 0.8, $\phi_{1} /\phi_{2} = 0.8$ D_f/B₀ = 0.50, 2c₂/B₀ $\gamma_{2} = 0$, c₁/c₂ = 0 h₁/$\gamma$, h₂/$\gamma$ = 0.3, h₁/$\eta$, h₂/$\eta$ = 0.16

• i. Variations of seismic bearing capacity coefficient for different values of $\xi_{1} /\xi_{2}$ using particle swarm optimization algorithm:

  Figure 12 depicts the variation of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\xi_{2} = 20\%$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$ $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From this plot, it is seen that coefficient $N_{\gamma E}$ increases with the increase in the value of $\xi_{1} /\xi_{2}$. It is also obvious as increase in damping properties of soil increases the resistance of the soil grains below the foundation and thus increases the bearing capacity.

• ii. Variations of seismic bearing capacity coefficient for different values of $\frac{{D_{\rm f} }}{{B_{0} }}$ using particle swarm optimization algorithm:

  Figure 13 depicts the variations of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30^{0}$, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0.2$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi_{2} = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From this plot, it is seen that coefficient $N_{\gamma E}$ increases with the increase in the value of $\frac{{D_{\rm f} }}{{B_{0} }}$. It is also obvious as increase in depth increases the confinement of the soil grains below the foundation. Thus, by increasing $\frac{{D_{\rm f} }}{{B_{0} }}$ bearing capacity of the foundation increases.

• iii. Variations of seismic bearing capacity coefficient for different values of $k_{v}$ using particle swarm optimization algorithm:

  Figure 14 shows the variations of $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0.2$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the plot, it is seen that $N_{\gamma E}$ decreases with the increase in the value of $k_{v}$. It is obvious because increase in the value of $k_{v}$ will increase the disturbance of base soil, and this result decreases the value of $N_{\gamma E}$.

• iv. Variations of seismic bearing capacity coefficient for different values of $\frac{{\delta_{1} }}{{\delta_{2} }}$ using particle swarm optimization algorithm:

  Figure 15 shows the variations of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.5$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the plot, it is seen that coefficient $N_{\gamma E}$ increases with the increase in the value of $\frac{{\delta_{1} }}{{\delta_{2} }}$. Here, increase in $\delta_{1}$ value is made keeping the $\delta_{2}$ value as a constant. So, obviously due to the increase in $\frac{{\delta_{1} }}{{\delta_{2} }}$ ratio, the value $N_{\gamma E}$ will increase

• v. Variations of seismic bearing capacity coefficient for different values of $\frac{{\phi_{1} }}{{\phi_{2} }}$ using particle swarm optimization algorithm:

  Figure 16 depicts the variations of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the figure, it is seen that coefficient $N_{\gamma E}$ increases with the increase in the value of $\frac{{\phi_{1} }}{{\phi_{2} }}$. Here increase in $\phi_{1}$ value is made keeping the $\phi_{2}$ value as constant.

• vi. Variations of seismic bearing capacity coefficient for different values of $\frac{{\gamma_{1} }}{{\gamma_{2} }}$ using particle swarm optimization algorithm:

  Figure 17 shows the variations of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the figure, it is seen coefficient $N_{\gamma E}$ increases with the increase in the value of $\frac{{\gamma_{1} }}{{\gamma_{2} }}$. Here, $\frac{{\gamma_{1} }}{{\gamma_{2} }}$ ratio is increased keeping $\gamma_{2}$ as constant.

• vii. Variations of seismic bearing capacity coefficient for different values of $\frac{{{\text{h}}_{1} }}{{B_{0} }}$ using particle swarm optimization algorithm:

  Figure 18 shows the variations of seismic bearing capacity coefficient $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{\delta_{1} }}{{\delta_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0$, $\frac{{c_{1} }}{{c_{2} }} = 0$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the figure, it is seen that coefficient $N_{\gamma E}$ decreases with the increase in the value of $\frac{{{\text{h}}_{1} }}{{B_{0} }}$. Here, $h_{1}$ is the depth of the top layer and it is considered in the analysis that it is weaker than the bottom layer. So, weaker layer will provide less resistance and hence increase in the thickness of this layer decreases the value of bearing capacity coefficient.

• viii. Variations of seismic bearing capacity coefficient for different values of $\frac{{c_{1} }}{{c_{2} }}$ using particle swarm optimization algorithm:

  Figure 19 shows the variations of $\left( {N_{\gamma E} } \right)$ with $k_{h}$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0.2$, $k_{v} = \frac{{k_{h} }}{2}$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$. From the plot, it is seen that the coefficient $N_{\gamma E}$ increases with the increase in the values $\frac{{c_{1} }}{{c_{2} }}$. Here, $\frac{{c_{1} }}{{c_{2} }}$ ratio is increased while keeping $c_{2}$ as constant. So, obviously due to the increase in $\frac{{c_{1} }}{{c_{2} }}$ ratio, the value $N_{\gamma E}$ will increase.

• ix. Variations of seismic bearing capacity coefficient for different values of impedance ratio $\alpha_{z}$ using particle swarm optimization algorithm: variations of seismic bearing capacity coefficient for different values of impedance ratio $\alpha_{z}$ using particle swarm optimization algorithm:

  Figure 20 shows the variations of $\left( {N_{\gamma E} } \right)$ at $\phi_{2} = 30$°, $\delta_{2} = \frac{{\phi_{2} }}{2}$, $\frac{{{\text{h}}_{1} }}{{B_{0} }} = 0.50$, $\frac{{\gamma_{1} }}{{\gamma_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\frac{{\phi_{1} }}{{\phi_{2} }} = 0.8$, $\frac{{D_{\rm f} }}{{B_{0} }} = 0.5$, $\frac{{2c_{2} }}{{\gamma_{2} B_{0} }} = 0.2$, $\frac{{c_{1} }}{{c_{2} }} = 0.8$, $k_{v} = \frac{{k_{h} }}{2}$, $\xi = 20\%$, $\xi_{1} /\xi_{2} = 0.8$, $\frac{{v_{\rm s1} }}{{v_{\rm s2} }} = 0.8$, $h_{1} /\lambda ,\,h_{2} /\lambda = 0.3$, $h_{1} /\eta ,\,h_{2} /\eta$ = 0.16, $\frac{{v_{p1} }}{{v_{\rm p2} }} = 0.8$ with $k_{h}$. From the plot, it is seen that the coefficient $N_{\gamma E}$ decreases with the increase in the values $\alpha_{z}$.

• x. From Terzaghi (1943) we know ultimate bearing capacity $q_{ult} = cN_{\rm c} + qN_{q} + 0.5\gamma B_{0} N_{\gamma }$, taking c = 8 kN/m², γ = 19 kN/m³, B₀ = 1.7 m and D_f = 1.3 m, the values of $cN_{\rm c}$, $qN_{q}$ and $0.5\gamma B_{0} N_{\gamma }$ are evaluated at different values of ϕ and plotted in Fig. 21. Also, in the present methodology, if we put all values of h₁ = 0, k_h = k_v = 0, then it will give the bearing capacity ($q_{{{\text{ult}}({\text{P}})}}$) of shallow strip footing resting on single-layered soil under static loading condition, which also is shown in Fig. 21. In the same figure, $q_{{{\text{ult}}({\text{T}})}}$ represents the bearing capacity as obtained using Terzaghi’s equation. From the plot, it is seen that the present method calculates the bearing capacity 26% higher value in comparison with Terzaghi (1943).

  Fig. 21

  

  Variation of bearing capacity coefficients with $\phi$ for $\gamma = 19$ kN/m³, B₀ = 1.7 m, D_f = 1.3 m, c = 8 kN/m²

8 Comparison

A comparison of bearing capacity coefficient values has made for different friction angles. The comparison is made to demonstrate the accuracy of the present methodology. With known formulation for bearing capacity coefficient $N_{{\gamma^{\prime \prime } }}$, a computer programing software ‘MATLAB’ code has been developed using PSO algorithm, which is able to calculate the ultimate bearing capacity, $q_{\text{ult}}$, for various combinations of soil properties in each layer. Table 7 represents a comparison of the present results with the experimental data from Khatri et al. (2017), Kumar et al. (2007) for the strip footing with four different series of experimental data. Table 8 shows a comparison of the present results with corresponding experimental data from Hanna (1981), Khatri et al. (2017) and Farah (2004) for strip footing with $\phi_{1}$ of 47.7°, $\gamma_{1}$ of 16.33 kN/m³, $\phi_{2}$ of 34°, $\gamma_{2}$ of 13.78 kN/m³. It is noteworthy that the values of $\frac{{q_{u} }}{{\gamma_{1} B_{0} }}$ given by Farah (2004) were found to be always greater than those given by Hanna (1981). For $\frac{{{\text{h}}_{1} }}{{B_{0} }}$ values up to 1.0, the values of $N_{\gamma }$ from Hanna(1981), Khatri et al. (2017) and Farah (2004) were found to be closer with the present result. The comparison of the present results with those represented by Hanna (1981) for circular footing is presented in Table 9 with $\phi_{1}$ of 47.7°, $\gamma_{1}$ of 16.33 kN/m³, $\phi_{2}$ of 34°, $\gamma_{2}$ of 13.78 kN/m³.The present values of q_u/γ₁B₀ of h₁/B₀ of 1 or lesser are found to be closer with the corresponding values from Hanna (1981). Table 10 shows comparison between Lotfizadeh and Kamalian (2016) and present analysis. From Table 10, it is seen that the present value gives higher value than Lotfizadeh and Kamalian (2016). A comparison of analytical solution is done with the present analysis. Table 11 represents the comparison between Debnath and Ghosh (2018) and present analysis. Table 12 depicts a comparison between upper and lower bound bearing capacities obtained by Eshkevari et al. (2019) and present analysis. The upper-bound and lower-bound bearing capacities were calculated in a series of analyses where the ratio of thickness of top layer to width of footing ($h_{1} /B_{0}$) and angle of internal friction of bottom layer are increased while keeping rest of the parameter as constant. From the comparison, in Tables 11 and 12, it is seen that the present analysis gives relatively closer value with Eshkevari et al. (2019).

Table 7 Comparison of $\frac{{q_{u} }}{{\gamma_{1} B_{0} }}$ values in four series with experimental data from Kumar et al. (2007) and Khatri et al. (2017) for rough strip footing on two-layered soil

Table 8 Comparison of $\frac{{q_{u} }}{{\gamma_{1} B_{0} }}$ values with data from Hanna (1981), Farah (2004) and Khatri et al. (2017) for rough strip footing on two-layered soil

Table 9 Comparison of $\frac{{q_{u} }}{{\gamma_{1} B_{0} }}$ values with data from Hanna (1981) and Khatri et al. (2017) for rough circular footing on two-layered soil

Table 10 Comparison of $\frac{{q_{u} }}{{\gamma_{1} B_{0} }}$ values with data from Lotfizadeh and Kamalian (2016) for strip footing on two-layered sandy soil

Table 11 Comparison of ${\text{Bearing}}\;{\text{Capacity}}\;{\text{Coefficient}}\;(N_{{\gamma^{\prime \prime } }} )$ values with values from Debnath and Ghosh (2018) for strip footing on two-layered soil

Table 12 Comparison with upper-bound and lower-bound values

8.1 Numerical Example

In this section, a numerical example for the case of weak over strong clay soil is discussed using Eq. (62). The results are compared with the results of available solutions. The numerical solution determines the ultimate bearing capacity of strip footing of 4 m width, positioned on top of a two-layered clayey soil. The soil profile consists of a 2-m deep top layer with an undrained shear strength of 20 kPa and stronger bottom layer with an undrained shear strength of 25 kPa; the angle of internal friction is zero for both layers in the undrained loading condition. The ultimate bearing capacity obtained from the present study is approximately 107 kPa. Ahmadi and Kouchaki (2016) have calculated an ultimate bearing capacity of 105 kPa for this problem, which is (− 1.86%) lower than the present study. Meyerhof and Hanna (1975) calculated an ultimate bearing capacity of 110 kPa (+ 2.803%), which is higher than the present result. Merifield et al. (1999) and Michalowski (2002) have calculated an upper bound of 109.2 kPa (+ 2.06%), which is higher than the present result. Chen (1975) has calculated upper bound value of 115 kPa (+ 7.67%), which is even higher than upper-bound value of Merifield et al. (1999) and Michalowski (2002). Zhu (2004) has evaluated the ultimate bearing capacity of 108.4 kPa (+ 1.30%), whereas Merifield et al. (1999) have calculated a lower-bound value of 100 kPa (− 6.54), which is lower than Ahmadi and Kouchaki (2016). From this numerical example, it is seen that the present study gives values closure to Ahmadi and Kouchaki (2016), Zhu (2004), upper-bound solution of Merifield et al. (1999).

9 Conclusions

The bearing capacity of strip footing resting on two-layered $c - \phi$ soil has been analytically determined by using a new pseudo-dynamic limit equilibrium approach in conjunction with particle swarm optimization. Simultaneous resistance of unit weight, surcharge and cohesion is taken into account to evaluate the new pseudo-dynamic bearing capacity coefficients in which linear failure surface is considered. On the basis of analysis, it is seen that keeping the bottom layer’s value constant, when we increase the corresponding values of upper layer like $\gamma ,c,\phi$, then the values of seismic bearing capacity increase or vice versa. Seismic bearing capacity value decreases if we increase the value of horizontal and vertical seismic acceleration coefficients. The analytical results are presented in terms of single bearing capacity coefficients $(N_{{\gamma^{\prime \prime } }} )$. Results as obtained from the present analysis are well comparable with earlier experimental, numerical and analytical solutions. So, the results obtained from the present analysis as given in tabular form can be used to evaluate the bearing capacity of foundation resting on two-layered soil under seismic loading condition. Further research work can be done for the problem using a new pseudo-dynamic method considering logarithmic failure surface.

Appendices

Appendix 1

$$\begin{aligned} c_{{{\text{s}}_{1} z_{1} }} & = \cos k_{{{\text{s}}_{1} z_{1} }} \cosh k_{{{\text{s}}_{2} z_{2} }} \\ & = \cos \left( {\frac{{y_{{{\text{s}}_{1} }} z_{1} }}{{{\text{h}}_{1} }}} \right)\cosh \left( {\frac{{y_{{{\text{s}}_{2} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\;c_{{{\text{s}}_{1} }} = \cos y_{{{\text{s}}_{1} }} \cosh y_{{{\text{s}}_{2} }} \\ \end{aligned}$$

$$\begin{aligned} s_{{{\text{s}}_{1} z_{1} }} & = - \sin k_{{{\text{s}}_{1} z_{1} }} \sinh k_{{{\text{s}}_{2} z_{2} }} \\ & = \sin \left( {\frac{{y_{{{\text{s}}_{1} }} z_{1} }}{{{\text{h}}_{1} }}} \right)\sinh \left( {\frac{{y_{{{\text{s}}_{2} }} z_{2} }}{{{\text{h}}_{2} }}} \right)\;s_{{{\text{s}}_{1} }} = - \sin y_{{{\text{s}}_{1} }} \sinh y_{{{\text{s}}_{2} }} \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{1} }} & = \int\limits_{0}^{{{\text{h}}_{1} }} {c_{{{\text{s}}_{1} z_{1} }} } (B_{0} \tan \alpha_{{A_{1} }} - z_{1} ){\text{d}}z_{1} \\ & = - \frac{{{\text{h}}_{1}^{2} }}{{\left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)}}\left[ \begin{aligned} - y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} + \cosh (y_{{{\text{s}}_{2} }} )\left\{ {(y_{{{\text{s}}_{1} }}^{2} - y_{{{\text{s}}_{2} }}^{2} )\cos y_{{{\text{s}}_{1} }} + y_{{{\text{s}}_{1} }} (y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\sin y_{{{\text{s}}_{1} }} } \right\} + y_{{{\text{s}}_{2} }} \hfill \\ \left\{ {(y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\cos y_{{{\text{s}}_{1} }} - 2y_{{{\text{s}}_{1} }} \sin y_{{{\text{s}}_{1} }} } \right\}\sinh (y_{{{\text{s}}_{2} }} ) \hfill \\ \end{aligned} \right] \\ & \quad + \frac{{B_{0} h_{1} \tan \alpha_{{A_{1} }} \left\{ {y_{{{\text{s}}_{1} }} \cosh y_{{{\text{s}}_{2} }} \sin y_{{{\text{s}}_{1} }} + y_{{{\text{s}}_{2} }} \cos y_{{{\text{s}}_{1} }} \sinh y_{{{\text{s}}_{2} }} } \right\}}}{{(y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )}} \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{2} }} & = \int\limits_{0}^{{{\text{h}}_{1} }} {{\text{s}}_{{{\text{s}}_{1} z_{1} }} } (B_{0} \tan \alpha_{{A_{1} }} - z_{1} ){\text{d}}z_{1} \\ & = \frac{{{\text{h}}_{1}^{2} }}{{\left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)}}\left[ \begin{aligned} - 2y_{{{\text{s}}_{1} }} y_{{{\text{s}}_{2} }} + y_{{{\text{s}}_{2} }} \cosh (y_{{{\text{s}}_{2} }} )\left\{ {2y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} + (y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\sin y_{{{\text{s}}_{1} }} } \right\} - \hfill \\ \left\{ {y_{{{\text{s}}_{1} }} (y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\cos y_{{{\text{s}}_{1} }} + (y_{{{\text{s}}_{1} }}^{2} - y_{{{\text{s}}_{2} }}^{2} )\sin y_{{{\text{s}}_{1} }} } \right\}\sinh (y_{{{\text{s}}_{2} }} ) \hfill \\ \end{aligned} \right] \\ & & \quad + \frac{{B_{0} h_{1} \tan \alpha_{{A_{1} }} \left\{ { - y_{{{\text{s}}_{2} }} \cosh y_{{{\text{s}}_{2} }} \sin y_{{{\text{s}}_{1} }} + y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} \sinh y_{{{\text{s}}_{2} }} } \right\}}}{{(y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )}} \\ \end{aligned}$$

$$\begin{aligned} A_{{{\text{h}}_{1} }} & = \frac{{{\text{h}}_{1}^{2} }}{{\left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)}}\left[ \begin{aligned} \left( {y_{{{\text{s}}_{2} }}^{2} - y_{{{\text{s}}_{1} }}^{2} } \right)\left( {\cos^{2} y_{{{\text{s}}_{1} }} + \sinh^{2} y_{{{\text{s}}_{2} }} } \right) - y_{{{\text{s}}_{1} }} \left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)\sin y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} \hfill \\ - y_{{{\text{s}}_{2} }} \left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)\sinh y_{{{\text{s}}_{2} }} \cosh y_{{{\text{s}}_{2} }} + 2y_{{{\text{s}}_{1} }} y_{{{\text{s}}_{2} }} \sin y_{{{\text{s}}_{1} }} \sinh y_{{{\text{s}}_{2} }} - \left( {y_{{{\text{s}}_{2} }}^{2} - y_{{{\text{s}}_{1} }}^{2} } \right)\cos y_{{{\text{s}}_{1} }} \cosh y_{{{\text{s}}_{2} }} \hfill \\ \end{aligned} \right] \\ & \quad + \frac{{B_{0} h_{1} \tan \alpha_{{A_{1} }} (y_{{{\text{s}}_{1} }} \sin y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} + y_{{{\text{s}}_{2} }} \cosh y_{{{\text{s}}_{2} }} \sinh y_{{{\text{s}}_{2} }} }}{{\left( {y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} } \right)}} \\ \end{aligned}$$

$$\begin{aligned} B_{{{\text{h}}_{1} }} & = \frac{{{\text{h}}_{1}^{2} }}{{(y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )}}\left[ \begin{aligned} y_{{{\text{s}}_{1} }} (y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\sinh y_{{{\text{s}}_{2} }} \cosh y_{{{\text{s}}_{2} }} - y_{{{\text{s}}_{2} }} (y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )\sin y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} - 2y_{{{\text{s}}_{1} }} y_{{{\text{s}}_{2} }} \left( {\cos^{2} y_{{{\text{s}}_{1} }} + \sinh^{2} y_{{{\text{s}}_{2} }} } \right) \hfill \\ + 2y_{{{\text{s}}_{1} }} y_{{{\text{s}}_{2} }} \cos y_{{{\text{s}}_{1} }} \cosh y_{{{\text{s}}_{2} }} + (y_{{{\text{s}}_{2} }}^{2} - y_{{{\text{s}}_{1} }}^{2} )\sin y_{{{\text{s}}_{1} }} \sinh y_{{{\text{s}}_{2} }} \hfill \\ \end{aligned} \right] \\ & \quad + \frac{{B_{0} h_{1} \tan \alpha_{{A_{1} }} (y_{{{\text{s}}_{2} }} \sin y_{{{\text{s}}_{1} }} \cos y_{{{\text{s}}_{1} }} - y_{{{\text{s}}_{1} }} \cosh y_{{{\text{s}}_{2} }} \sinh y_{{{\text{s}}_{2} }} )}}{{(y_{{{\text{s}}_{1} }}^{2} + y_{{{\text{s}}_{2} }}^{2} )}} \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{3} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {c_{{{\text{s}}_{2} z_{2} }} } (h_{2} - z_{2} ){\text{d}}z_{2} \\ & = - \frac{{{\text{h}}_{2}^{2} }}{{\left( {y_{{{\text{s}}_{3} }}^{2} + y_{{{\text{s}}_{4} }}^{2} } \right)^{2} }}\left[ {2y_{{{\text{s}}_{3} }} y_{{{\text{s}}_{4} }} \sin y_{{{\text{s}}_{3} }} \sinh y_{{{\text{s}}_{4} }} + \left( {y_{{{\text{s}}_{3} }}^{2} - y_{{{\text{s}}_{4} }}^{2} } \right) - \left( {y_{{{\text{s}}_{3} }}^{2} - y_{{{\text{s}}_{4} }}^{2} } \right)\cos y_{{{\text{s}}_{3} }} \cosh y_{{{\text{s}}_{4} }} } \right] \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{4} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {{\text{s}}_{{{\text{s}}_{2} z_{2} }} } (h_{2} - z_{2} ){\text{d}}z_{2} \\ & = \frac{{{\text{h}}_{2}^{2} }}{{\left( {y_{{{\text{s}}_{3} }}^{2} + y_{{{\text{s}}_{4} }}^{2} } \right)^{2} }}\left[ {\left( {y_{{{\text{s}}_{3} }}^{2} - y_{{{\text{s}}_{4} }}^{2} } \right)\sin y_{{{\text{s}}_{3} }} \sinh y_{{{\text{s}}_{4} }} + 2y_{{{\text{s}}_{3} }} y_{{{\text{s}}_{4} }} \cos y_{{{\text{s}}_{3} }} \cosh y_{{{\text{s}}_{4} }} - 2y_{{{\text{s}}_{3} }} y_{{{\text{s}}_{4} }} } \right] \\ A_{{{\text{h}}_{2} }} & = \frac{{2y_{{{\text{s}}_{3} }} y_{{{\text{s}}_{4} }} \sin y_{{{\text{s}}_{3} }} \sinh y_{{{\text{s}}_{4} }} + \left( {y_{{{\text{s}}_{3} }}^{2} - y_{{{\text{s}}_{4} }}^{2} } \right)(\cos y_{{{\text{s}}_{3} }} \cosh y_{{{\text{s}}_{4} }} - \cos^{2} y_{{{\text{s}}_{3} }} - \sinh^{2} y_{{{\text{s}}_{4} }} )}}{{(\cos^{2} y_{{{\text{s}}_{3} }} + \sinh^{2} y_{{{\text{s}}_{4} }} )\left( {y_{{{\text{s}}_{3} }}^{2} + y_{{{\text{s}}_{4} }}^{2} } \right)^{2} }} \\ B_{{{\text{h}}_{2} }} & = \frac{{2y_{{{\text{s}}_{3} }} y_{{{\text{s}}_{4} }} (\cos y_{{{\text{s}}_{3} }} \cosh y_{{{\text{s}}_{4} }} - \cos^{2} y_{{{\text{s}}_{3} }} - \sinh^{2} y_{{{\text{s}}_{4} }} ) - \left( {y_{{{\text{s}}_{3} }}^{2} - y_{{{\text{s}}_{4} }}^{2} } \right)\sin y_{{{\text{s}}_{3} }} \sinh y_{{{\text{s}}_{4} }} }}{{\left( {\cos^{2} y_{{{\text{s}}_{3} }} + \sinh^{2} y_{{{\text{s}}_{4} }} } \right)\left( {y_{{{\text{s}}_{3} }}^{2} + y_{{{\text{s}}_{4} }}^{2} } \right)^{2} }} \\ \end{aligned}$$

Appendix 2

$$\begin{aligned} I_{{{\text{s}}_{5} }} & = \int\limits_{0}^{{{\text{h}}_{1} }} {c_{{{\text{s}}_{3} z_{1} }} } (B_{0} \tan \alpha_{{A_{1} }} - z_{1} ){\text{d}}z_{1} \\ & = \frac{{{\text{h}}_{1}^{2} \left( {y_{{{\text{s}}_{5} }}^{2} - y_{{{\text{s}}_{6} }}^{2} } \right)\tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} + \frac{{y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} + y_{{{\text{s}}_{6} }} \sinh y_{{{\text{s}}_{6} }} \cos y_{{{\text{s}}_{5} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)}}(h_{1} h_{2} \tan \alpha_{{p_{1} }} + h_{1}^{2} \tan \alpha_{{p_{2} }} ) \\ & \quad - \frac{{{\text{h}}_{1}^{2} \left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)(y_{{{\text{s}}_{6} }} \cos y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} + y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} )\tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} + \frac{{y_{{{\text{s}}_{6} }} 2h_{1}^{2} y_{{{\text{s}}_{5} }} \sin y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} - h_{1}^{2} \cosh y_{{{\text{s}}_{6} }} \left( {y_{{{\text{s}}_{5} }}^{2} - y_{{{\text{s}}_{6} }}^{2} } \right)\cos y_{{{\text{s}}_{5} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{6} }} & = \int\limits_{0}^{{{\text{h}}_{1} }} {c_{{{\text{s}}_{3} z_{1} }} } (B_{0} \tan \alpha_{{A_{1} }} - z_{1} ){\text{d}}z_{1} \\ & = \frac{{{\text{h}}_{1}^{2} \left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)(y_{{{\text{s}}_{6} }} \cosh y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} - y_{{{\text{s}}_{5} }} \cos y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} )\tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} - \frac{{2h_{1}^{2} y_{{{\text{s}}_{5} }} y_{{{\text{s}}_{6} }} \tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} \\ & \quad + \frac{{{\text{h}}_{1}^{2} \left\{ {2y_{{{\text{s}}_{5} }} y_{{{\text{s}}_{6} }} \cos y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} - \left( {y_{{{\text{s}}_{6} }}^{2} - y_{{{\text{s}}_{5} }}^{2} } \right)\sin y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} } \right\}\tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }} \\ & \quad - \frac{{(y_{{{\text{s}}_{6} }} \cosh y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} - y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} \cos y_{{{\text{s}}_{5} }} )}}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)}}\left( {{\text{h}}_{1} h_{2} \tan \alpha_{{p_{1} }} + h_{1}^{2} \tan \alpha_{{p_{2} }} } \right) \\ \end{aligned}$$

$$\begin{aligned} B_{{{\text{h}}_{3} }} & = - \frac{{{\text{h}}_{1}^{2} \tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }}\left[ {\cos y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} \left( {y_{{{\text{s}}_{5} }}^{2} - y_{{{\text{s}}_{6} }}^{2} } \right)\sin y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} + 2y_{{{\text{s}}_{5} }} y_{{{\text{s}}_{6} }} \cos y_{{{\text{s}}_{5} }} } \right] \\ & \quad + \frac{{[y_{{{\text{s}}_{5} }} \sinh y_{{{\text{s}}_{6} }} \cosh y_{{{\text{s}}_{6} }} - y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} \cos y_{{{\text{s}}_{5} }} (\cosh^{2} y_{{{\text{s}}_{6} }} + \sinh^{2} y_{{{\text{s}}_{6} }} )]}}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)}}(h_{1} h_{2} \tan \alpha_{{p_{1} }} + h_{1}^{2} \tan \alpha_{{p_{2} }} ) \\ & \quad + \frac{{{\text{h}}_{1}^{2} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)}}[y_{{{\text{s}}_{6} }} \sin y_{{{\text{s}}_{5} }} \cos y_{{{\text{s}}_{5} }} (\cosh^{2} y_{{{\text{s}}_{6} }} + \sinh^{2} y_{{{\text{s}}_{6} }} ) - y_{{{\text{s}}_{5} }} \cosh y_{{{\text{s}}_{6} }} \sinh y_{{{\text{s}}_{6} }} \cos 2y_{{{\text{s}}_{5} }} ]\tan \alpha_{{p_{2} }} \\ & \quad + \frac{{{\text{h}}_{1}^{2} \tan \alpha_{{p_{2} }} }}{{\left( {y_{{{\text{s}}_{5} }}^{2} + y_{{{\text{s}}_{6} }}^{2} } \right)^{2} }}\left[ {2y_{{{\text{s}}_{5} }} y_{{{\text{s}}_{6} }} \left\{ {\cos^{2} y_{{{\text{s}}_{6} }} - \sinh^{2} y_{{{\text{s}}_{5} }} (\cosh^{2} y_{{{\text{s}}_{6} }} + \sinh^{2} y_{{{\text{s}}_{6} }} )} \right\}} \right] \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{7} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {c_{{{\text{s}}_{4} z_{2} }} } (h_{2} - z_{2} ){\text{d}}z_{2} \\ & = - \frac{{{\text{h}}_{2}^{2} }}{{\left( {y_{{{\text{s}}_{7} }}^{2} + y_{{{\text{s}}_{8} }}^{2} } \right)^{2} }}\left[ {2y_{{{\text{s}}_{7} }} y_{{{\text{s}}_{8} }} \sin y_{{{\text{s}}_{7} }} \sinh y_{{{\text{s}}_{8} }} + \left( {y_{{{\text{s}}_{7} }}^{2} - y_{{{\text{s}}_{8} }}^{2} } \right) - \left( {y_{{{\text{s}}_{7} }}^{2} - y_{{{\text{s}}_{8} }}^{2} } \right)\cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} } \right] \\ \end{aligned}$$

$$\begin{aligned} I_{{{\text{s}}_{4} }} & = \int\limits_{0}^{{{\text{h}}_{2} }} {{\text{s}}_{{{\text{s}}_{4} z_{2} }} } (h_{2} - z_{2} ){\text{d}}z_{2} \\ & = \frac{{{\text{h}}_{2}^{2} }}{{\left( {y_{{{\text{s}}_{7} }}^{2} + y_{{{\text{s}}_{8} }}^{2} } \right)^{2} }}\left[ {\left( {y_{{{\text{s}}_{7} }}^{2} - y_{{{\text{s}}_{8} }}^{2} } \right)\sin y_{{{\text{s}}_{7} }} \sinh y_{{{\text{s}}_{8} }} + 2y_{{{\text{s}}_{7} }} y_{{{\text{s}}_{8} }} \cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} - 2y_{{{\text{s}}_{7} }} y_{{{\text{s}}_{8} }} } \right] \\ \end{aligned}$$

$$A_{{{\text{h}}_{4} }} = \frac{{2y_{{{\text{s}}_{7} }} y_{{{\text{s}}_{8} }} \sin y_{{{\text{s}}_{7} }} \sinh y_{{{\text{s}}_{8} }} + \left( {y_{{{\text{s}}_{7} }}^{2} - y_{{{\text{s}}_{8} }}^{2} } \right)\left( {\cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} - \cos^{2} y_{{{\text{s}}_{7} }} - \sinh^{2} y_{{{\text{s}}_{8} }} } \right)}}{{\left( {\cos^{2} y_{{{\text{s}}_{7} }} + \sinh^{2} y_{{{\text{s}}_{8} }} } \right)\left( {y_{{{\text{s}}_{7} }}^{2} + y_{{{\text{s}}_{8} }}^{2} } \right)^{2} }}$$

$$B_{{{\text{h}}_{4} }} = \frac{{2y_{{{\text{s}}_{7} }} y_{{{\text{s}}_{8} }} \left( {\cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} - \cos^{2} y_{{{\text{s}}_{7} }} - \sinh^{2} y_{{{\text{s}}_{8} }} \cos y_{{{\text{s}}_{7} }} \cosh y_{{{\text{s}}_{8} }} - \cos^{2} y_{{{\text{s}}_{7} }} - \sinh^{2} y_{{{\text{s}}_{8} }} } \right) - \left( {y_{{{\text{s}}_{7} }}^{2} - y_{{{\text{s}}_{8} }}^{2} } \right)\sin y_{{{\text{s}}_{7} }} \sinh y_{{{\text{s}}_{8} }} }}{{\left( {\cos^{2} y_{{{\text{s}}_{7} }} + \sinh^{2} y_{{{\text{s}}_{8} }} } \right)\left( {y_{{{\text{s}}_{7} }}^{2} + y_{{{\text{s}}_{8} }}^{2} } \right)^{2} }}$$

Appendix 3

$$\begin{aligned} a_{1} & = \left( {\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{p1}} + 2\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{\gamma _{1} }}{{\bar{\gamma }}}\left\{ {\frac{{\sin \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}}} \right\} - 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \\ & \quad \left\{ {\frac{{\left\{ {1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g} \right\}\sin \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right) + \left\{ {a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g} \right\}\tan \phi _{2} \cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}}} \right\} + \left( {\frac{{{\text{h}}_{2} }}{{B_{0} }}} \right)^{2} \cot \alpha _{{{\text{p2}}}} \frac{{\gamma _{2} }}{{\bar{\gamma }}}\left\{ {\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} \\ & \quad + 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) + a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g\tan \phi _{1} \cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} - \left( {2 - \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{\gamma _{1} }}{{\bar{\gamma }}} \\ & \left\{ {\frac{{\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}}} \right\} + 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\left( {1 - \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)\left\{ {\frac{{1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right) + a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g\tan \phi _{2} \cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}}} \right\} \\ & \quad - \left( {1 - \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)\frac{{{\text{h}}_{2} }}{{B_{0} }}\frac{{\gamma _{2} }}{{\bar{\gamma }}}\left\{ {\frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} - 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\left( {1 - \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)\left\{ {\frac{{\left\{ {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right\}\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right) + a_{{\text{t}}} h(h_{1} ,t)/g\tan \phi _{1} \cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} \\ & \quad - 2\frac{{Q_{{{\text{t}}_{{{\text{h}}({\text{BJKD}})}} }} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} + 2\frac{{Q_{{t_{{v(BJKD)}} }} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\sin \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} - 2\frac{{(Q_{{{\text{h}}_{{({\text{DKF}})}} }} )_{{\text{R}}} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} + 2\frac{{(Q_{{v_{{({\text{DKF}})}} }} )_{{\text{R}}} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} \\ & & \quad - 2\frac{{Q_{{{\text{t}}_{{{\text{h}}({\text{ABDE}})}} }} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}} - 2\frac{{(Q_{{{\text{h}}_{{({\text{EDF}})}} }} )_{{\text{R}}} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} + 2\frac{{Q_{{t_{{v(ABDE)}} }} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}} + 2\frac{{(Q_{{v_{{({\text{EDF}})}} }} )_{{\text{R}}} }}{{\bar{\gamma }B_{0}^{2} }}\frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} \\ d_{1} & = 2\frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} + \frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} + \frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}d_{1} = 2\frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\frac{{\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} + \frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} + \frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \frac{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}} \\ & \quad + 2\frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{\sin \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} + \frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{p1}} \frac{{\cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} - \frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \frac{{\cos \left( {\phi _{1} + \alpha _{{p1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{p1}} + \delta _{1} } \right)}} \\ & \quad + 2\frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\frac{{\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}} + \frac{{c_{1} }}{{\bar{c}}}\frac{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}} + 2\frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\frac{{\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} \\ & \quad + \frac{{c_{2} }}{{\bar{c}}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{A2}}}} \frac{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}} - \frac{{c_{1} }}{{\bar{c}}}\frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} + \frac{{c_{1} }}{{\bar{c}}}\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} \frac{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}} \\ \end{aligned}$$

$$\begin{aligned} b_{1} & = 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{D_{{\text{f}}} }}{{B_{0} }}\left( {\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{p}}1}} + \frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)\left\{ {\frac{{\left( {1 \pm k_{{\text{v}}} } \right)\sin \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right) - k_{{\text{h}}} \cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\} \\ & \quad - \left\{ {\frac{{2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{D_{{\text{f}}} }}{{B_{0} }}\left( {\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{p}}1}} + \frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)}}{{\left( {\frac{{{\text{h}}_{1} }}{{B_{0} }} + \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{p}}1}} + \frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)}}} \right\}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g\sin \left( {\phi _{1} + \alpha _{{p1}} } \right) + a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g\tan \phi _{2} \cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} } \right)}}{{\cos \left( {\phi _{1} + \alpha _{{{\text{p}}1}} + \delta _{1} } \right)}}} \right\} \\ \quad + 2\frac{{\gamma _{1} }}{{\bar{\gamma }}}\frac{{D_{{\text{f}}} }}{{B_{0} }}\frac{{\left( {\frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{p}}1}} + \frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)}}{{\left( {\frac{{{\text{h}}_{1} }}{{B_{0} }} + \frac{{{\text{h}}_{1} }}{{B_{0} }}\cot \alpha _{{{\text{p}}1}} + \frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} } \right)}}\frac{{{\text{h}}_{2} }}{{B_{0} }}\cot \alpha _{{{\text{p2}}}} \left\{ {\frac{{1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g\sin \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right) + a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g\tan \phi _{1} \cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} } \right)}}{{\cos \left( {\phi _{2} + \alpha _{{{\text{p2}}}} + \delta _{2} } \right)}}} \right\} \\ e_{1} & = \left\{ {\frac{{\left\{ {(1 \pm k_{{\text{v}}} )} \right\}\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right) + k_{{\text{h}}} \cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}}} \right\} - \left\{ {\frac{{\left( {1 - \frac{{h_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)}}{{1 + \frac{{h_{1} }}{{B_{0} }}}}} \right\} \\ & \quad \left\{ {\frac{{\left( {1 \pm a_{{{\text{i}}_{{\text{v}}} }} (h_{2} ,t)/g} \right)\sin \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right) + \left\{ {a_{{{\text{i}}_{{\text{h}}} }} (h_{2} ,t)/g} \right\}\tan \phi _{2} \cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} } \right)}}{{\cos \left( {\alpha _{{{\text{A1}}}} - \phi _{1} - \delta _{1} } \right)}}} \right\} + \left\{ {\frac{{\left( {1 - \frac{{h_{1} }}{{B_{0} }}\cot \alpha _{{{\text{A1}}}} } \right)}}{{1 + \frac{{h_{1} }}{{B_{0} }}}}} \right\} \\ & \quad \left\{ {\frac{{\left( {1 \pm a_{{{\text{t}}_{{\text{v}}} }} (h_{1} ,t)/g} \right)\sin \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right) + {\text{ }}\left\{ {a_{{{\text{t}}_{{\text{h}}} }} (h_{1} ,t)/g} \right\}\tan \phi _{1} \cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} } \right)}}{{\cos \left( {\alpha _{{{\text{A2}}}} - \phi _{2} - \delta _{2} } \right)}}} \right\} \\ \end{aligned}$$