Introduction

For decades, researchers have been studying liquid stream in porous media. The study of uniform flow past an impervious bodies embedded in porous media have numerous applications in environmental, manufacturing, and life science procedures. Some of these instances are as follows: the filtration of solids from liquids, underground spreading of chemical waste, oil reservoir recovery, flow of blood through arteries and lungs, drug permeation through human skin, energy extraction from geothermal zones, flow of liquids through ion exchange beds, chemical catalytic reactors, the study of dispersion of cholesterol and other fat substances from arteries to endothelium, and others. Aside from the aforementioned, fluid flows through porous media has been successfully employed to forecast flow behavior in a variety of physical applications. Numerous conceptual models for explaining fluid flow through porous media have been evolved due to the wide range of applications.

Due to the various applications of these studies, many conceptual models for describing liquid motion through porous media have been established. Darcy [1] introduced the 1st mathematical model for fluid motion in porous medium. On the other hand, Darcy’s law tends to be insufficient for streaming with high porosity and high shear rates, as well as for flows close to the surface of a surrounded porous medium. Brinkman [2] suggested an amendment to Darcy's law to model such flows. Further, Tam [3] and Lundgren [4] both theoretically explained the significance of Brinkman equation. Moreover, Yu and Kaloni [5] have considered a Cartesian tensor solution of Brinkman’s equations influenced by porous medium and calculated drag force on the sphere. In addition, Padmavathi et al. [6] used Brinkman's model in a general non-axisymmetric creeping motion to determine the resistance and torque for the porous sphere. Barman [7] published an empirical analysis of viscous liquid motion through an impermeable sphere immersed in a porous media of continuous porosity using the Brinkman model. Furthermore, using Brinkman model, Pop and Ingham [8] have determined the flow over a sphere embedded in a porous medium, and they found this flow configuration does not have any flow separation. Srinivasacharya and Murthy [9] studied the motion of viscous liquid over an impervious sphere immersed in a porous media using Brinkman’s model and extracted a general formula for the drag and calculated the drag for the slightly deformed sphere. The Stokes motion passing through a swarm of porous spherical particles with solid core was investigated by Yadav et al. [10] using the stress-jump condition at a fluid–porous interface. Deo and Gupta [11] examined viscous incompressible liquid motion past a porous sphere enclosed in another porous medium and calculated the drag force past an oblate spheroid. After that, in the case of spheroid the same problem was investigated by Yadav and Deo [12]. The slow viscous flow over a porous spheroid with solid core was analyzed by Srinivasacharya and Madasu [13] using no-slip condition. Jaiswal and Gupta [14] have treated the Stokes flow of a Reiner-Rivlin fluid spheroid in a spherical container. The Forchheimer–Brinkman–Darcy extended model was applied by Juncu [15] to study the creeping motion over an impervious sphere immersed in a porous medium. The Stokes flow of viscous liquid over a micropolar liquid spheroid was reported by Madasu and Kaur [16]. Yadav et al. [17] investigated the problem of Stokes flow past a porous membrane consisting of solid spheroidal particles coated with a porous layer and after that, they calculated the expression for the hydrodynamic permeability acting on the membrane. Tiwari et al. [18] studied the Stokes flow problem past swarm of non-homogeneous porous cylindrical particles using Darcy's law. They studied the influences of different parameters on hydrodynamic permeability of membrane. Madasu and Bucha [19] studied the steady viscous flow around a permeable spheroidal particle using Beavers–Joseph–Saffman–Jones condition and evaluated the hydrodynamic drag force acting on the permeable spheroidal particle. Jaiswal [20] investigated the problem of creeping motion of a non-Newtonian Reiner-Rivlin liquid motion past a slightly deformed fluid spheroid.

A diverse number of problems involving flow past various particles are solved, yielding significant results. Many researchers have been focused to determine the significant and beneficial areas of MHD in the last few years. The effect of applied magnetic field on the flow of fluid through various bodies is being studied by researchers. Magneto-hydrodynamics has a wide range of uses in everyday life, including biological science, astrophysics, geophysics, metallurgy, planetary atmospheres, and so on. During our review of the literature, we discovered that Stewartson [21] studied the steady motion of a perfect sphere in an inviscid conducting liquid in the presence of MHD impact. Devi and Raghavachar [22] studied the MHD stratified motion over a sphere. The book [23] provides a basic introduction of magnetohydrodynamic flow. The problem of magneto-hydrodynamics streaming through porous medium was examined by Geindreau and Auriaultthe [24]. Jayalakshmamma et al. [25] scrutinized the creeping motion over a rigid core surrounded by porous medium under magnetic field. Using cell model technique, Tiwari et al. [26] discussed the impact of magnetic field on the hydrodynamic permeability of a membrane of solid cylindrical particles made up by a porous layer. They have discussed the influence of the Hartmann number on the membrane's hydrodynamic permeability. Further, Srivastava et al. [27] have investigated the creeping motion of an electrically conducting liquid past a porous sphere under MHD effect using cell model technique. Moreover, Iyengar and Radhika [28] have examined the slow viscous flow over a porous spheroid. The Magnetohydrodynamic influence on the hydrodynamic permeability of a membrane coated by porous spherical particles was examined by Yadav et al. [29]. Applying the cell model procedure, the problem of a swarm of spherical particles was described, and the influences of several significant flow parameters were investigated, and streamline patterns were also presented. Using the Brinkman equation, Ansari and Deo [30] scrutinized the MHD effect over a porous sphere immersed in another porous medium. Saad [31] investigated the quasisteady flow past an assemblage of porous spheres using transverse magnetic field. Prasad et al. [32] adopted the Darcy’s law for the streaming over an electrically conducting fluid inside the semipermeable sphere.

Recently, using a cell model technique, Yadav [33] studied the impact of MHD on the Stokes flow past a porous spheroid: hydrodynamic permeability of a membrane. Madasu and Bucha [34] studied the magnetic influence on the creeping motion over a porous spheroidal particle using Brinkman's model. Namdeo and Gupta [35] investigated the problem of slow viscous flow past a spherical particle covered by semipermeable shell in the presence of magnetic field. Saini et al. [36] studied the effect of variable viscosity on the slow viscous flow of Jeffrey fluid through a swarm of porous cylindrical particles using Brinkman-Forchheimer model. Sapa and Alsudais [37] investigated the impact of magnetic field on the creeping flow of two impermeable spheres of dissimilar shapes with slip surfaces, immersed in a porous medium. Namdeo and Gupta [38] discussed the problem of slow viscous flow past a slightly deformed sphere in the presence of magnetic using slip boundary condition. They evaluated the hydrodynamic drag force exerted by the fluid on the spheroid. Further, Namdeo and Gupta [39] have discussed the magnetohydrodynamic influence on the Stokes motion over an approximate semipermeable sphere and calculating the resistance past an oblate spheroid. All foregoing analysis highlights the effect of magnetohydrodynamic to be altering with varying geometry of the particles.

Motivated from the foregoing analysis and gaps, we have discussed the magnetic effect on the creeping motion around a solid spheroid implanted in a porous medium with the Brinkman model. As a particular case, we used the oblate spheroid and obtained the drag on the surface of the spheroid and its graphical results are obtained and discussed for different fluid parameters. Also, we derive some distinctive and well-known outcomes and compared with some previous work whenever possible. Our major goal is to show the impact of the involved physical parameters like, permeability, deformation parameter and Hartmann number on the drag coefficient and shearing stress.

Problem Formulation and Solution

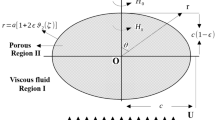
Figure 1 demonstrates the steady, axisymmetric, Stokes motion of an electrically conducting liquid with uniform velocity \({U}_{\infty }\) through a rigid spheroid immersed in a porous media in the presence of magnetic impact in transverse direction. For outside the impervious spheroid, we assume well-known Brinkman equation [2]. In addition, we supposed that the magnetic Reynolds number \(R{e}_{m}=Ua{\mu }_{h}\sigma \) is exceedingly small, where \({\mu }_{h}\) and \(\sigma \) are the magnetic permeability and electric conductivity respectively. Also, we assumed that any applied outer electric field is neglected, hence the induced current is extremely minute and therefore, it can be ignored.

Fig. 1
figure 1

Geometrical sketch of the problem

Full size image

The force F applied by a magnetic field on a streaming electrical current is called a Lorentz force is defined as \(\mathbf{F}=\mathbf{J}\times \mathbf{H}\) or \(\mathbf{F}={\mu }_{h}^{2}\sigma \left(\mathbf{q}\times \mathbf{H}\right)\times \mathbf{H}\). Where \(\mathbf{J}\) and \(\mathbf{H}\) denotes the electric current density and magnetic field intensity respectively. So, equation for motion outside the impermeable spheroid under magnetohydrodynamic impact is expressed by modified Brinkman equation with continuity condition:

$$\nabla .\mathbf{q}=0,$$
(1)
$$\nabla p+\frac{\mu }{k}\mathbf{q}+\mu \nabla \times \nabla \times \mathbf{q}-{\mu }_{h}^{2}\sigma (\mathbf{q}\times \mathbf{H})\times \mathbf{H}=0,$$
(2)

where \(\mathbf{q}\) denotes the velocity vector of the fluid; \(p\), \(\mu \) and \(k\) are the pressure, viscosity and permeability of the fluid respectively.

To express the governing equation in non-dimensional form, the following dimensionless variables are used

$$r=a\tilde{r },\mathbf{q}=U\stackrel{\sim }{\mathbf{q}},\nabla =\frac{\stackrel{\sim }{\nabla }}{a},p= \frac{\mu U}{a}\stackrel{\sim }{p,} \mathbf{H}={H}_{0}\stackrel{\sim }{\mathbf{H}},\psi =U{a}^{2}\stackrel{\sim }{\psi }.$$
(3)

Putting the above values in Eqs. (1) and (2), and eliminating the tildes above the non—dimensional variables, we get the following equations

$$\nabla .\mathbf{q}=0,$$
(4)
$$\nabla p+{\xi }_{1}^{2}\mathbf{q}+\nabla \times \nabla \times \mathbf{q}-{\xi }_{2}^{2}(\mathbf{q}\times \mathbf{H})\times \mathbf{H}=0,$$
(5)

where \({\xi }_{1}^{2}=\frac{{a}^{2}}{k}\) is the permeability parameter, and \({\xi }_{2}=\sqrt{\frac{{\mu }_{h}^{2}{H}_{0}^{2}\sigma {a}^{2}}{\mu }}\) is the Hartmann number.

Here,\((r\), \(\theta \), \(\phi )\) indicate spherical polar coordinate system. All quantities are independent of \(\phi \) because the flow is generated in the meridian plane and is axis-symmetric. Thus, the azimuthal component of velocity \({q}_{\phi }=0\) for axisymmetric Stokes flow and component of velocity can be written as

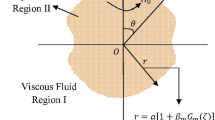
$$\mathbf{q}={q}_{r}\left(r,\theta \right){\mathbf{e}}_{r}+{q}_{\theta }\left(r,\theta \right){\mathbf{e}}_{\theta }.$$
(6)

Let \(r=a[1+\chi \left(\theta \right)]\) be the equation of surface of the approximate sphere that differs from perfect sphere \(r=a\). The orthogonality of Gegenbauer polynomials \({G}_{m}\left(\zeta \right)\),\(\zeta =\mathrm{cos}\theta \) ordinarily permits us to write \(\chi \left(\theta \right)\) as the under mentioned way \(\chi \left(\theta \right)=\sum_{m=2}^{\infty }\alpha {}_{m}{G}_{m}\left(\zeta \right)\), and relation between Gegenbauer polynomial \({G}_{n}\left(\zeta \right)\) and Legendre polynomial \({P}_{n}\left(\zeta \right)\) as

$${G}_{n}\left(\zeta \right)=\frac{\left[{P}_{n-2}\left(\zeta \right)-{P}_{n}\left(\zeta \right)\right]}{\left(2n-1\right)},n\ge 2.$$
(7)

Thus, the surface of the slightly deformed sphere can be selected as \(r=1+{\alpha }_{m}{\mathrm{G}}_{\mathrm{m}}\left(\upzeta \right)\). We assume the coefficient \({\alpha }_{m}\) is extremely minute therefore \(O({\epsilon }^{2})\) and its higher powers can be overlooked i.e., \({r}^{y}\approx 1+y{\alpha }_{m}{G}_{m}\left(\zeta \right)\) where, \(y\) may be positive or negative integer. The following are the velocity components associated with stream function \(\psi \):

$${q}_{r}=-\frac{1}{{r}^{2}\mathrm{sin}\theta }\frac{\partial \psi }{\partial \theta }, {q}_{\theta }=\frac{1}{r\mathrm{sin}\theta }\frac{\partial \psi }{\partial r}.$$
(8)

Further, eliminating the pressure term in Eq. (5) and substituted velocity components from Eq. (8), we get

$${E}^{2}\left({E}^{2}-{\beta }^{2}\right)\psi =0,$$
(9)

here, \({E}^{2}=\frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{(1-{\zeta }^{2})}{{r}^{2}}\frac{{\partial }^{2}}{\partial {\zeta }^{2}}\) is the Stokes stream function operator and \({\beta }^{2}={\xi }_{1}^{2}+{\xi }_{2}^{2}\). Furthermore, the expression for tangential stress \({T}_{r\zeta }\) and normal stress \({T}_{rr}\) are given by

$${T}_{r\zeta }=\frac{\mu }{r\mathrm{sin}\theta }\left[\frac{{\partial }^{2}\psi }{\partial {r}^{2}}-\frac{2}{r}\frac{\partial \psi }{\partial r}-\frac{\left(1-{\zeta }^{2}\right)}{{r}^{2}}\frac{{\partial }^{2}\psi }{\partial {\zeta }^{2}}\right],$$
(10)
$${T}_{rr}=-p-\frac{2\mu }{{r}^{2}}\left[\frac{2}{r}\frac{\partial \psi }{\partial \zeta }-\frac{{\partial }^{2}\psi }{\partial r\partial \zeta }\right].$$
(11)

As we know, the Eq. (9) is completely separable; therefore, the regular solution outside the solid spheroid in spherical polar coordinate system is easily obtained using the regularity condition at infinity (i.e. \(\psi \to \frac{1}{2}U{r}^{2}{\mathrm{sin}}^{2}\theta \) as \(r\to \infty \)) and can be written as

$$\psi =\left[{r}^{2}+{a}_{2}{r}^{-1}+{b}_{2}\sqrt{r}{K}_{\frac{3}{2}}\left(\beta r\right)\right]{G}_{2}\left(\zeta \right)+\sum_{n=3}^{\infty }\left[{A}_{n}{r}^{-n+1}+{B}_{n}\sqrt{r}{K}_{n-\frac{1}{2}}\left(\beta r\right)\right]{G}_{n}\left(\zeta \right),$$
(12)

and the pressure term is

$$p={\beta }^{2}\left[\left(r-\frac{{a}_{2}}{2{r}^{2}}\right){P}_{1}\left(\zeta \right)-\sum_{n=3}^{\infty }\frac{{A}_{n}{r}^{n}}{n}{P}_{n-1}\left(\zeta \right)\right],$$
(13)

where \({K}_{n-\frac{1}{2}}\left(\beta r\right)\) is the modified Bessel function and \({a}_{2}\),\({b}_{2}\),\({A}_{n}\) and \({B}_{n}\) are the unknowable constants to be calculated by applying different boundary conditions.

The boundary conditions are used at the surface \(r=a\left[1+{\alpha }_{m}{\mathrm{G}}_{\mathrm{m}}\left(\upzeta \right)\right]\) of impervious spheroid.

$$\psi (r, \theta )={\psi }_{r}(r,\theta )=0,$$
(14)

Initially, the solutions corresponding to the boundary \(r=1+{\alpha }_{m}{\mathrm{G}}_{\mathrm{m}}\left(\upzeta \right)\) are developed. If the body is sphere, then the stream function \(\psi \) can be expressed as

$$\psi =\left[{r}^{2}+{a}_{2}{r}^{-1}+{b}_{2}\sqrt{r}{K}_{\frac{3}{2}}\left(\beta r\right)\right]{G}_{2}\left(\zeta \right).$$
(15)

Comparing (12) with the above equation, we find that the terms involving \({A}_{n}\) and \({B}_{n}\) for \(n>2\) are additional terms which don't occur for the case of perfect sphere. In the current problem, we assume that the body is slightly deformed and the flow not too far deviates from the sphere's shape. The entire coefficient \({A}_{n}\) and \({B}_{n}\) for \(n>2\) will be of order \({\alpha }_{m}\). As a result, motion over an impervious spheroidal particles embedded in porous region will differ a bit from streaming past a impermeable sphere surrounded in a porous media. We have considered \(r=1+\sum_{m=2}^{\infty }{\alpha }_{m}{G}_{m}\left(\zeta \right)\) when solving a problem of this kind.

Now, applying the boundary conditions from Eq. (14) in Eq. (12), we get

$$\left[1+{a}_{2}+{b}_{2}{K}_{\frac{3}{2}}\left(\beta \right)\right]{G}_{2}\left(\zeta \right)+\left[2-{a}_{2}-{b}_{2}\left({K}_{\frac{3}{2}}\left(\beta \right)+\beta {K}_{\frac{1}{2}}\left(\beta \right)\right)\right]{G}_{2}\left(\zeta \right){G}_{m}\left(\zeta \right)\alpha {}_{m}+\sum_{n=3}^{\infty }\left[{A}_{n}+{B}_{n}{K}_{n-\frac{1}{2}}\left(\beta \right)\right]{G}_{n}(\zeta )=0,$$
(16)
$$\left[2-{a}_{2}-{b}_{2}\left({K}_{\frac{3}{2}}\left(\beta \right)+\beta {K}_{\frac{1}{2}}\left(\beta \right)\right)\right]{G}_{2}\left(\zeta \right)+\left[2+2{a}_{2}+{b}_{2}({\beta }^{2}+2){K}_{\frac{3}{2}}\left(\beta \right)\right]{G}_{2}\left(\zeta \right){G}_{m}\left(\zeta \right)\alpha {}_{m}+\sum_{n=3}^{\infty }\left[\left(1-n\right){A}_{n}-{B}_{n}\left({(n-1)K}_{n-\frac{1}{2}}\left(\beta \right)+\beta {K}_{n-\frac{3}{2}}\left(\beta \right)\right)\right]{G}_{n}(\zeta )=0.$$
(17)

The aforementioned equations' leading terms are equal to 0, and we get

$${a}_{2}=-1-\frac{3{K}_{\frac{3}{2}}\left(\beta \right)}{\beta {K}_{\frac{1}{2}}\left(\beta \right)},{b}_{2}=\frac{3}{\beta {K}_{\frac{1}{2}}\left(\beta \right)}.$$
(18)

Substituting the values of \({a}_{2} \;\mathrm{and} \;{b}_{2}\) from Eq. (18) to Eqs. (16) and (17), and we use the following identity

$${G}_{m}\left(\zeta \right){G}_{2}\left(\zeta \right)=\frac{-\left(m-2\right)(m-3)}{2\left(2m-1\right)(2m-3)}{G}_{m-2}\left(\zeta \right)+\frac{m(m-1)}{\left(2m+1\right)(2m-3)}{G}_{m}\left(\zeta \right)-\frac{\left(m+1\right)\left(m+2\right)}{2\left(2m-1\right)\left(2m+1\right)}{G}_{m+2}\left(\zeta \right).$$
(19)

We get on simplification the following equation

$$\sum_{n=3}^{\infty }\left[{A}_{n}+{B}_{n}{K}_{n-\frac{1}{2}}\left(\beta \right)\right]{G}_{n}(\zeta )=0,$$
(20)
$$\left[-\frac{3\beta {K}_{\frac{3}{2}}\left(\beta \right)}{{K}_{\frac{1}{2}}\left(\beta \right)}\right]{G}_{2}\left(\zeta \right){G}_{m}\left(\zeta \right)\alpha {}_{m}+\sum_{n=3}^{\infty }\left[\left(1-n\right){A}_{n}-{B}_{n}\left({(n-1)K}_{n-\frac{1}{2}}\left(\beta \right)+\beta {K}_{n-\frac{3}{2}}\left(\beta \right)\right)\right]{G}_{n}(\zeta )=0.$$
(21)

By solving Eq. (20) and (21) we get, \({A}_{n}={B}_{n}=0\) for \(n\ne m-2\), \(m\), \(m+2\) and another system of equations in \({A}_{n} \mathrm{and} {B}_{n}\), when \(n=m-2\), \(m\), \(m+2\), we get

$${A}_{n}+{B}_{n}{K}_{n-\frac{1}{2}}\left(\beta \right)=0,$$
(22)
$$\left(1-n\right){A}_{n}-{B}_{n}\left({\left(n-1\right)K}_{n-\frac{1}{2}}\left(\beta \right)+\beta {K}_{n-\frac{3}{2}}\left(\beta \right)\right)=-\overline{b} {\omega }_{1},$$
(23)

where \(\overline{b }=\frac{n(n-1)\alpha {}_{m}}{\left(2n+1\right)(2n-3)}\), \({\omega }_{1}=\frac{3\beta {K}_{\frac{3}{2}}\left(\beta \right)}{{K}_{\frac{1}{2}}\left(\beta \right)}\).

Solving Eq. (22) and (23) we get the expressions \({A}_{n}\) and \({B}_{n}\) for \(n=m-2\), \(m\), \(m+2\) So, we have established the apparent manifestation for the stream function \(\psi \) for the flow region of the impermeable spheroidal surface as

$$\psi =\left[{r}^{2}+{a}_{2}{r}^{-1}+{b}_{2}\sqrt{r}{K}_{\frac{3}{2}}\left(\beta r\right)\right]{G}_{2}\left(\zeta \right)+\left[{A}_{m-2}{r}^{-m+3}+{B}_{m-2}\sqrt{r}{K}_{m-\frac{5}{2}}\left(\beta r\right)\right]{G}_{m-2}\left(\zeta \right)+\left[{A}_{m}{r}^{-m+1}+{B}_{m}\sqrt{r}{K}_{m-\frac{1}{2}}\left(\beta r\right)\right]{G}_{m}\left(\zeta \right)+\left[{A}_{m+2}{r}^{-m-1}+{B}_{m+2}\sqrt{r}{K}_{m+\frac{3}{2}}\left(\beta r\right)\right]{G}_{m+2}\left(\zeta \right),$$
(24)

where the entire constants have been determined. Under the boundary conditions described above, the Eq. (24) is a new result of the Brinkman equation.

Application to Spheroid

We investigate the flow past a prolate and oblate spheroid as one of the examples of the described flow. In the Cartesian coordinate system \((x; y; z)\), the equation characterizing the spheroid's surface is

$$\frac{{x}^{2}+{y}^{2}}{{d}^{2}}+\frac{{z}^{2}}{{d}^{2}{\left(1-\epsilon \right)}^{2}}=1,$$
(25)

where the equatorial radius is \(d\). Furthermore, the deformation parameter \(\epsilon \) is considered to be extremely minute hence its quadratic and higher powers are overlooked. Polar form of Eq. (25) can be written as

$$r=a\left[1+2\epsilon {G}_{2}(\zeta )\right],$$
(26)

where \(a=d(1-\epsilon )\). Comparing Eq. (26) of spheroid with \(r=1+{\alpha }_{m}{\mathrm{G}}_{\mathrm{m}}\left(\upzeta \right)\) of approximate sphere, we find that \({\alpha }_{2}=2\epsilon \) and \({\alpha }_{m}=0\) when \(m\ne 2\). Using Eq. (26) in Eq. (24) we get the stream function around the oblate spheroid as

$$\psi =\left({r}^{2}+\left({a}_{2}+{A}_{2}\right){r}^{-1}+\left({b}_{2}+{B}_{2}\right)\sqrt{r}{ K}_{\frac{3}{2}}\left(\alpha r\right)\right){G}_{2}\left(\zeta \right)+\left({A}_{4}{r}^{-3}+{B}_{4}\sqrt{r}{ K}_{\frac{7}{2}}\left(\alpha r\right)\right){G}_{4}\left(\zeta \right).$$
(27)

Drag on a Spheroid

The flow resistance to the stream direction is generated by the magnetohydrodynamic creeping motion over a rigid spheroid surrounded by a porous material, which is recognized as a drag force. Using the formula proposed by Saad [26], the resistance force can be calculated.

$${F}_{D}=\pi \mu Ua\int_0^\pi{\left[{r}^{4}{\mathrm{sin}}^{3}\theta \frac{\partial }{\partial r}\left(\frac{{E}^{2}\psi }{{r}^{2}{\mathrm{sin}}^{2}\theta }\right)-{\alpha }^{2}{r}^{2}\mathrm{sin}\theta \frac{\partial \psi }{\partial r}\right]}_{r=\left[1+{\alpha }_{2}{G}_{2}\left(\zeta \right)\right]}\mathrm{d}\theta .$$
(28)

Inserting the value of \(\psi \) from Eq. (27) in Eq. (28) and integrating with respect to \(\theta \), we obtain

$${F}_{D}=\frac{2}{3}\pi \mu Ua{\beta }^{2}\left[-2+{a}_{2}+{A}_{2}-2\left({b}_{2}+{B}_{2}\right){K}_{\frac{3}{2}}\left(\beta \right)+\frac{4}{5}\beta \alpha {}_{2}{b}_{2}{K}_{\frac{1}{2}}\left(\beta \right)-\frac{12}{5}{\alpha }_{2}\right].$$
(29)

Substituting the values of \({a}_{2}\), \({b}_{2}\), \({A}_{2}\), \({B}_{2}\) and further substituting \(a=d\left(1-\epsilon \right)\), \({\xi }_{1}={\chi }_{1}\left(1-\epsilon \right)\), \({\xi }_{2}={\chi }_{2}\left(1-\epsilon \right)\), leading to \(\beta ={\beta }_{1}\left(1-\epsilon \right)\) with \({\beta }_{1}^{2}={\chi }_{1}^{2}+{\chi }_{2}^{2}\) in Eq. (29), we obtain

$${F}_{D}=-2\pi \mu Ud\left[3+3{\beta }_{1}+3{\beta }_{1}^{2}-\frac{1}{5}\epsilon \left(3+6{\beta }_{1}+3{\beta }_{1}^{2}\right)\right],$$
(30)

where \({\chi }_{1}^{2}=\frac{{d}^{2}}{k}\), \({\chi }_{2}=\sqrt{\frac{{\mu }_{h}^{2}{H}_{0}^{2}\sigma {d}^{2}}{\mu }}\).

At any point of the oblate spheroid, the non-dimensional shearing stress can be described as

$$\frac{{T}_{r\theta }}{\left(\frac{\mu U}{a}\right)\mathrm{sin}\theta } \mathrm{at}\, r=a[1+{\alpha }_{2}{G}_{2}\left(\zeta \right)]$$
$$=\left[3\left({a}_{2}+{A}_{2}\right)+\left\{\frac{1}{2}\left({\beta }^{2}+6\right){K}_{\frac{3}{2}}\left(\beta \right)+\beta {K}_{\frac{1}{2}}\left(\beta \right)\right\}\left({b}_{2}+{B}_{2}\right)\right]-2\epsilon \left[6{a}_{2}+\left\{\left({\beta }^{2}+6\right){K}_{\frac{3}{2}}\left(\beta \right)+\left(2\beta +\frac{1}{4}{\beta }^{3}\right){K}_{\frac{1}{2}}\left(\beta \right)\right\}{b}_{2}\right]\left(1-{\mathrm{cos}}^{2}\uptheta \right).$$
(31)

Special Cases

With Magnetic Effect

Case I: If \(k\to \infty \) then \({\chi }_{1}\to 0\) i.e., the porous medium change the clear fluid in Eq. (30), then the drag force will become

$${F}_{D}=-2\pi \mu Ud\left[{\chi }_{2}^{2}+3{\chi }_{2}+3-\frac{\epsilon }{5}\left({\chi }_{2}^{2}+6{\chi }_{2}+3\right)\right],$$
(32)

the above equation coincides with the work derived previously by Prasad and Bucha [34].

Case II: When \(\epsilon \to 0\) and \(k\to \infty \), that is the rigid oblate spheroid embedded in porous region transforms into perfect rigid sphere in a clear fluid and the expression for resistance force from Eq. (30) becomes

$${F}_{D}=-2\pi \mu Ud\left[{\chi }_{2}^{2}+3{\chi }_{2}+3\right],$$
(33)

this drag expression is comparable to Prasad and Bucha's result [32].

Case III: If \(\epsilon =0\) in Eq. (30), then the oblate spheroid becomes a rigid sphere and drag force will becomes

$${F}_{D}=-2\pi \mu Ud\left[3+3{\beta }_{1}+3{\beta }_{1}^{2}\right].$$
(34)

Without Magnetic Effect

Case IV: If \({\chi }_{2}\to 0\), in Eq. (30), then the drag force become

$${F}_{D}=-2\pi \mu Ud\left[3+\frac{1}{k}+3\sqrt{\frac{1}{k}} -\frac{\epsilon }{5}\left(3+\frac{1}{k}+6\sqrt{\frac{1}{k}} \right)\right].$$
(35)

Case V: If \({\chi }_{2}\to 0\) and \(k\to \infty \), that is, the porous medium transforms into a clear fluid and the expression for drag force reduced to

$${F}_{D}=-6 \pi \mu U d\left[1-\frac{\epsilon }{5}\right],$$
(36)

this result agrees with the famous Stokes formula [40].

Results and Discussion

In this section, an endeavor is made to find the influence of a variety of physical parameters such as permeability, Hartmann number, and deformation parameter on the non-dimensional drag and shearing stress. The ratio of \({F}_{D}\) to \({F}_{st}\) be defined as non-dimensional drag \({D}_{N}\):

$${D}_{N}=\frac{{F}_{D}}{-6 \pi \mu U d}$$
(37)

We show in Fig. 2 the dependences of \({D}_{N}\) for diverse values of Hartmann number \({\chi }_{2}\) with permeability parameter \(k\), when (a) \(\epsilon =0.03\), (b) \(\epsilon =-0.03\). Figure 2 demonstrates that the non-dimensional drag rises when increasing the values of \({\chi }_{2}\). This is because of the Lorentz force's presence in the magnetic field. However, the drag coefficient decreases when the value of permeability parameter \(k\) increases. As can be seen in Fig. 2, the resistance force of an oblate spheroid is less than that of a prolate spheroid.

Fig. 2
figure 2

Dependences of \({D}_{N}\) against \(k\) for diverse values of \({\chi }_{2}\) for a \(\epsilon =0.03\), b \(\epsilon =-0.03\)

Full size image

Further, Dependences of \({D}_{N}\) against parameter \(k\) for diverse values of \(\epsilon \) is illustrated in Fig. 3. This graph shows that the drag of the perfect sphere \(\left(\epsilon =0\right)\) is higher than that of the oblate spheroid \(\left(\epsilon >0\right)\) and that the resistance is fewer than that of the prolate spheroid \((\epsilon <0)\). When we analyze both graphs, we can see that the resistance force on the oblate spheroid under magnetic effect is greater than the curve without the magnetic impact.

Fig. 3
figure 3

Dependences of \({D}_{N}\) against \(k\) for various values of \(\epsilon \) for a \({\chi }_{2}=5\), b \({\chi }_{2}=0\)

Full size image

On the other hand, the profile of dimensionless shearing stress \({T}_{r\theta }\) verses permeability parameter \(k\) for enhancing deformation parameter \(\epsilon \) is demonstrated in Fig. 4. This finding reveals that the shearing stress is higher in the perfect sphere than in the prolate spheroid but lower in the oblate spheroid. Here we noted that the shearing stress increases in the case of prolate spheroid when the value of permeability \(k\approx 0.02\) and after that it is decreases. For both of the plots in Fig. 4, we observed that the curves for the shearing stress are higher under the MHD effect than the absence of the magnetic field.

Fig. 4
figure 4

Dependences of dimensionless shearing stress \({T}_{r\theta }\) against parameter \(k\) for various values of \(\epsilon \) when \(\theta =\frac{\pi }{4}\) and a \({\chi }_{2}=5\), b \({\chi }_{2}=0\)

Full size image

Moreover, the depiction of the dimensionless shearing stress \({T}_{r\theta }\) with respect to \(k\) for numerous values of Hartmann number \({\chi }_{2}\) at (a) \(\epsilon =0.3\), (b) \(\epsilon =0\), and \(\theta =\frac{\pi }{4}\) is presented in Fig. 5. This graph shows how the shearing stress decreases rapidly as the permeability parameter k increases. Also, this diagram demonstrates that as the Hartman number rises, dimensionless shearing stress increases. This observation indicates that the shearing stress is diminishing rapidly when \(0\le k\le 0.1\) and it decreases gradually for \(k\ge 0.1\).

Fig. 5
figure 5

Dependences of \({T}_{r\theta }\) against \(k\) for numerous values of \({\chi }_{2}\) when \(\theta =\frac{\pi }{4}\), and a \(\epsilon =0.3\), b \(\epsilon =0\)

Full size image

Stream-line patterns of the flow around a spheroid for different values of Hartmann number \({\chi }_{2} ({\chi }_{2}=0.75\) and \({\chi }_{2}=7)\), permeability parameter \(k=0.25\) are sketched in Fig. 6. From this figure, we noticed that the Hartmann numbers strength is increased, the streamlines are moving closer to the impermeable surface of a spheroid.

Fig. 6
figure 6

Stream-line patterns for fixed parameter \(k=0.25\) and various value of Hartmann number \({\chi }_{2}\). a \({\chi }_{2}=0.75\), b \({\chi }_{2}=7\)

Full size image

Conclusions

The motion of a viscous fluid past an approximate spheroidal particle embedded in a porous region has been investigated under transverse magnetic field. The Brinkman equation is used for studying the flow in porous medium. The mathematical expression for the flow field is calculated in terms of stream function. Also, we have calculated the drag coefficient and its variations have been plotted for different fluid parameters. The present analysis is summarized as follows:

  • Some special cases of drag forces are obtained and compared to previous literature, which validates our present work.

  • It is found that the drag coefficient and shearing stress \({T}_{r\theta }\) decreases with permeability \(k\) increases and increases with increasing the values of Hartman number \({\chi }_{2}\).

  • We discovered that drag is greater in the presence of magnetohydrodynamic impact than in the absence of a magnetohydrodynamic impact.

  • The drag of a prolate spheroid is discovered to be higher than that of an oblate spheroid.

  • The magnetic field is seen to have a vital role in the flow of fluids past porous media and has a major impact on the non-dimensional drag.