Stokes flow past a porous spheroid embedded in another porous medium

Abstract

A study is made with an analysis of an incompressible viscous fluid flow past a slightly deformed porous sphere embedded in another porous medium. The Brinkman equations for the flow inside and outside the deformed porous sphere in their stream function formulations are used. Explicit expressions are investigated for both the inside and outside flow fields to the first order in small parameter characterizing the deformation. The flow through the porous oblate spheroid embedded in another porous medium is considered as the particular example of the deformed porous sphere embedded in another porous medium. The drag experienced by porous oblate spheroid in another porous medium is also evaluated. The dependence of drag coefficient and dimensionless shearing stress on the permeability parameter, viscosity ratio and deformation parameter for the porous oblate spheroid is presented graphically and discussed. Previous well-known results are then also deduced from the present analysis.

1 Introduction

The flow through porous media has attracted considerable practical and theoretical interest in science, engineering and technology. The flow through porous media occurs commonly in geophysical and biomechanical problems and also has many engineering applications, such as, flow in fixed beds, petroleum industry, hydrology, lubrication problems, etc. [1]. Engineering system based on fluidized bed combustion, enhance oil reservoir recovery, underground spreading of chemical waste and chemical catalytic reactors, the movement of water and other fluids in the sandy or the earthen soil, the flow of water through the porous bank of rivers, intrusion of sea water to coastal area, the flow of blood through lungs and arteries are just a few examples of applications of the study of flow through porous media. The most practical example of physical process of viscous flow inside a porous spherical region is the structure of the earth. In the engineering practice, porous particles often have geometrical shape, which differ significantly from spherical. The simplest possible geometry to study the effect shape of the permeable particle on the drag force is spheroid.

Due to its broad areas of applications in science, engineering and industries; several conceptual models have been developed for describing fluid flow in porous media. There are many different theoretical and experimental models that have been used for the analysis of the fluid flow in a porous medium. The Darcy’s law as proposed by Henri Darcy [2] states that the rate of flow is proportional to pressure drop through a densely packed bed of fine particles, is one of the basic model that has been used extensively in the literature. In a densely packed porous medium saturated with turbulent flow, the curvature of the flow due to meandering of flow gives raise to quadratic drag of the form $\rho C_{b}|\mathbf{v} |\mathbf{v} / \sqrt{k}$, in addition to the linear drag μ v/k. In that case momentum equation is called Darcy-Forchheimer’s equation

$$\nabla p = - \frac{\mu}{k}\mathbf{v} - \frac{\rho C_{b}}{\sqrt{k}} |\mathbf{v} |\mathbf{v} . $$

(1)

In sparsely packed porous medium of porosity ϕ the Darcy-Forchheimer’s equation is no longer valid and in that case one has to take into account of boundary layer effect. The modified form of (1) which involve the boundary layer effect called as Darcy-Lapwood-Forchheimer-Brinkaman equation (Nield and Bejan [3]) as

(2)

Joseph and Tao [4] examined the flow of a viscous incompressible fluid past a porous spherical particle by using Darcy’s law in the porous region. They found that the drag on the porous sphere is same as that of solid sphere with reduced radius. However, this law appears to be inadequate for the flows with high porosity, large shear rates and for flows near the surface of the bounded porous medium. Many early authors on convection in porous media used various types of extended Darcy models e.g. Boutros et al. [5], were discussed Lie-group method of solution for steady two dimensional boundary-layer stagnation-point flow towards a heated stretching sheet placed in a porous medium, Radiation effect on forced convective flow and heat transfer over a porous plate in a porous medium was studied by Mukhopadhyay and Layek [6]. During nineteenth century after the Darcy’s work, flow through porous media has been simulated by questions arising in practical problems. Brinkman [7] proposed a modification of the Darcy’s law for a porous medium which was assumed to be governed by a swarm of homogeneous spherical particles and provides an expression like

$$ \tilde{\mu} \nabla^{2}\mathbf{v} - \frac{\mu}{k}\mathbf{v} = \nabla p,$$

(3)

where, $\tilde{\mu}$ denotes the effective viscosity of porous medium, k being the permeability of a swarm, μ is the viscosity of fluid and v being the velocity of fluid. However, for steady Stokes flow through porous medium, (3) can also be obtained by neglecting convective inertia and form drag terms in (2). This equation reduces to Stokes equation for large permeability k $(\tilde{\mu} \nabla^{2}\mathbf{v} = \nabla p)$, whereas, for low permeability medium this equation resembles with Darcy empirical equation $(- \frac{\mu}{k}\mathbf{v} = \nabla p)$. The no-slip boundary condition has been found to be inapplicable, when a viscous fluid flows over a permeable surface. William [8] has suggested the following matching conditions at the interface:

(4)

where, ϕ is the porosity of porous medium, n is the direction of normal to the interface and λ being the ratio of viscosities of fluid in the porous medium to that in the clear fluid region.

The problem of creeping flow relative to permeable spheres was solved by Neale et al. [9]. Higdon and Kojima [10] have studied the Stokes flow past porous particles using the Brinkman’s equations for the flow inside. They derived some asymptotic results for small and large permeability by using Green’s function formulation of the Brinkman’s equation. A Cartesian-tensor solution of the Brinkman’s equation governed by the porous media was investigated by Qin and Kaloni [11] and using this solution they also evaluated the hydrodynamic force experienced by a porous sphere. Pop and Cheng [12] have considered the problem of an incompressible steady viscous flow past a circular cylinder embedded in a constant porosity medium based on the Brinkman model and they obtained a closed form exact solution of stream function of Brinkman equation. Bhatt and Sacheti [13] have studied the problem of viscous flow past a porous spherical shell using the Brinkman model and they evaluated the drag force experienced by the shell. Barman [14] has studied the problem of a Newtonian fluid past an impervious sphere embedded in a constant porous medium. Using Brinkman model, he reported an exact solution of the stream function to the governing equation specifying constant velocity away from the sphere. Pop and Ingham [15] have also discussed the flow past a sphere embedded in a porous medium based on the Brinkman model. The problem of an incompressible steady flow past a porous impervious sphere embedded in a constant and high porosity porous medium using Brinkman model has been studied by Rudraiah et al. [16]. They had obtained an exact solution for the governing equation specifying a constant shear away from the sphere. Creeping flow about a slightly deformed sphere was studied by Palaniappan [17] and Ramkissoon [18] by using slip boundary condition at the porous surface. Pal and Mondal were discussed Radiation effects on combined convection over a vertical flat plate embedded in a porous medium of variable porosity [19].

Zlatanovski [20] has considered the axi-symmetric Stokes flow of an incompressible viscous fluid past a porous prolate spheroidal particle using the Brinkman model for the flow inside the spheroidal particle. Slip flow past a prolate spheroid was investigated by Deo and Datta [21] and evaluated the drag force experienced by it. The Stokes flow past a fluid prolate spheroid is also studied by Deo and Datta [22]. Creeping flow past a porous approximate sphere has been discussed by Srinivascharya [23]. The drag force experienced by a swarm of porous deformed oblate spheroidal particles was evaluated by Deo and Yadav [24]. The variation of drag coefficient with permeability and solid volume fraction was also discussed by them. Deo [25] has solved the problem of Stokes flow past a swarm of deformed porous spheroidal particles with Happel boundary condition. Recently, Deo and Gupta [26] have evaluated the drag force on a porous sphere embedded in another porous medium. Yadav et al. [27] have evaluated the hydrodynamic permeability of membranes built up by spherical particles covered by porous shells. These above investigations, motivate us to discuss the slow viscous flow past and through a porous deformed sphere embedded in another porous medium which included these above mentioned few cases of a porous sphere or a porous spheroid.

This paper concerns the solution of the problem of slow viscous flow past and through a porous deformed spheroid embedded in another porous medium. The Brinkman equations for the flow inside and outside the porous spheroid, whose shape deviates slightly from that of sphere, in their stream function formulations are used. Explicit expressions for the stream function are investigated for both the inside and outside flow fields to the first order in small parameter characterizing the deformation. A new result for the drag on a porous deformed sphere embedded in another porous medium has been reported. As a particular case, slow viscous flow through a porous oblate spheroid embedded in another porous medium is considered and the drag experienced by it is evaluated. The dependence of the drag coefficient on permeability for a porous oblate/prolate spheroid is presented graphically and discussed. It is seen that effect of permeability is to reduce the drag force. An expression for the shearing stress at the porous spheroid has been also reported. The results reported earlier by Qin and Kaloni [11] for a perfect porous sphere, Deo [25] for a porous oblate spheroid, Ramkissoon [18] for a rigid spheroid in an unbounded medium and Deo and Gupta [26] for a porous sphere embedded in another porous medium are then deduced as special cases of the present analysis.

2 Statement and mathematical formulation of the problem

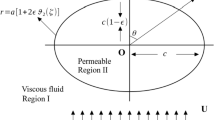
The model employed here is that of a porous spheroidal particle of permeability k ₁, whose shape deviates slightly from that of sphere, embedded in another porous medium of permeability k ₂. The porosities of inside and outside porous media are ϕ ₁ and ϕ ₂, respectively.

We shall consider a uniform, axi-symmetric, slow viscous flow of a Newtonian fluid past and through a porous spheroidal particle. For convenience, we consider the porous spheroid to be stationary having its center at the origin with the fluid approaching in the positive z-direction with uniform velocity U, as illustrated in Fig. 1. Let the surface S of a spheroid which departs but a little in shape from a sphere r=a be

$$r = a\bigl(1 + \beta_{m} G_{m} (\zeta)\bigr). $$

(5)

Further, assuming that the coefficients β _m is sufficiently small so that squares and higher powers may be neglected, i.e.

$$\biggl( \frac{r}{a} \biggr)^{n} \approx 1 + n\beta_{m}G_{m}(\zeta), $$

(6)

where, n may be positive or negative.

Fig. 1

Co-ordinate system for axi-symmetric flow past a porous spheroid

The inside and outside regions of the porous deformed sphere are fully saturated with the viscous fluid. We shall denote i=1 in an entity for inside and i=2 for outside regions of the porous deformed sphere, respectively. The governing Brinkman equations for the both regions can be expressed as

$$\nabla^{2}\mathbf{v}^{(i)} - \frac{\sigma ^{2}}{a^{2}}\mathbf{v}^{(i)}= \frac{1}{\tilde{\mu} _{i}}\nabla p^{(i)},\quad i = 1,2. $$

(7)

Here, $\sigma_{i}^{2}=\frac{\mu _{i}a^{2}}{\tilde{\mu} _{i}k_{i}} =\frac{\beta a^{2}}{k_{i}}$, $\beta = \frac{\mu _{i}}{\tilde{\mu}_{i}}$, μ _i are the viscosities of fluids, $\tilde{\mu} _{i}$ denotes the effective viscosity of porous media and k _i being the permeability in both regions. Since, σ _i are dimensionless quantities related inversely with the permeability, therefore, we named σ _i as the dimensionless permeability parameter. In addition, the equations of continuity for incompressible fluids must be satisfied in both regions:

$$\operatorname{div}\mathbf{v}^{(i)} = 0,\quad i = 1,2. $$

(8)

These equations of continuity for axi-symmetric, incompressible viscous fluid in the spherical polar coordinates (r,θ,φ) for both regions can also be expressed as (Happel and Brenner [30])

$$ \frac{\partial}{\partial r}(r^{2}v_{r}^{(i)}) + \frac{r}{\operatorname{sin} \theta}\frac{\partial}{\partial \theta} (v_{\theta} ^{(i)}\operatorname{sin}\theta) = 0,$$

(9)

where, $v_{r}^{(i)}$ and $v_{\theta} ^{(i)}$, are components of velocities in the direction of r and θ, respectively. The Stokes stream functions ψ ⁽ⁱ⁾(r,θ) in both regions satisfying equations of continuity (9) can be defined as

$$v_{r}^{(i)} = - \frac{1}{r^{2}\operatorname{sin} \theta} \frac{\partial \psi ^{(i)}}{\partial \theta} ; \qquad v_{\theta} ^{(i)} = \frac{1}{r\operatorname{sin} \theta}\frac{\partial \psi ^{(i)}}{\partial r}. $$

(10)

Therefore, on elimination of pressures from the Brinkman’s equations and using (10), we get the following fourth order partial differential equations

$$E^{2}\biggl(E^{2} - \frac{\sigma _{i}^{2}}{a^{2}}\biggr)\psi^{(i)} = 0, $$

(11)

where, the operator

$$E^{2} = \frac{\partial ^{2}}{\partial r^{2}} + \frac{(1 - \zeta ^{2})}{r^{2}}\frac{\partial ^{2}}{\partial \zeta ^{2}},\qquad \zeta =\operatorname{cos}\theta. $$

(12)

Furthermore, the expressions for tangential and normal stresses for both regions $T_{r\zeta} ^{(i)}$ and $T_{rr}^{(i)}$, i=1,2 are given by

(13)

(14)

Also, the pressures in both regions may be obtained by integrating the following relations respectively for both regions as

$$\left. \begin{array}{l}\frac{\partial p^{(i)}}{\partial r} = -\frac{\tilde{\mu} _{i}}{r^{2}\operatorname{sin} \theta} \frac{\partial}{\partial \theta} \{ (E^{2} - (\frac{\sigma _{i}}{a})^{2})\psi^{(i)}\} \\\noalign{\vspace*{6pt}}\frac{\partial p^{(i)}}{\partial \theta} = \frac{\tilde{\mu} _{i}}{\operatorname{sin}\theta} \frac{\partial}{\partial r}\{ (E^{2} - (\frac{\sigma _{i}}{a})^{2})\psi^{(i)}\} \\ \end{array} \right\}. $$

(15)

A regular solution on the symmetry axis-z of the Brinkman’s equation (7) in the spherical polar coordinates can be taken (Zlatanovski [20]) as

(16)

Here, $I_{\nu} (\frac{\sigma _{i}r}{a})$ and $K_{\nu} (\frac{\sigma _{i}r}{a})$ are modified Bessel functions of order ν of first and second kind, respectively as defined in Abramowitz and Stegun [28] and A _n , B _n , C _n & D _n are constants of integration. The function G _n (ζ) is the Gegenbauer function of first kind of order n and related to Legendre function P _n (ζ) of first kind by the relation

$$G_{n}(\zeta) = \frac{P_{n - 2}(\zeta ) - P_{n}(\zeta )}{(2n - 1)},\quad n\geq 2. $$

(17)

3 Solution of the problem

The solution given by (16) provides the flow in both regions with proper choice of these constants. For the flow inside the porous deformed sphere (r=a(1+β _m G _m (ζ))) where origin occurs the constants B _n , C _n should be zero [25]. Therefore, we assume that the regular solution inside the porous spheroid in non-dimensional form with the help of uniform stream function as

(18)

For the flow in the region outside the porous spheroid which satisfies the uniform condition, the constant D _n will be zero [26]. Therefore, the regular solution outside the porous spheroid in non-dimensional form can be taken as

(19)

The only coefficients which contribute to the flow past a porous sphere are a ₂, d ₂, $a_{2}^{*}$, $c_{2}^{*}$ and consequently, we may expect that all other coefficients in (18) and (19) are of order β _m . Therefore, except where these coefficients enter, we may take the surface to be r=a instead of the exact form of the spheroid.

Boundary Conditions: The boundary conditions those are physically realistic and mathematically consistent for this proposed problem can be taken as:

On the porous surface: r=a(1+β _m G _m (ζ))

(20)

(21)

The condition at infinity

(22)

for a uniform stream flowing with velocity U in the direction of positive z-axis. By using condition (22), we get $a_{2}^{*} = - 1$.

Applying the boundary conditions (20)–(21) and using the perturbation method, we have the following equations:

(23)

(24)

(25)

(26)

where, $\lambda = \frac{\mu _{2}}{\mu 1}$ and porosity ratio $\varphi =\frac{\phi _{2}}{\phi _{1}}$.

Solving the leading terms in (23)–(26), we can obtained the values of a ₂, d ₂, $b_{2}^{*}$ and $c_{2}^{*}$. Here, it is noted that these values corresponds to the flow past a porous sphere embedded in another porous medium which were evaluated by Deo and Gupta [26].

Substituting the values of a ₂, d ₂, $b_{2}^{*}$ and $c_{2}^{*}$ into (23)–(26) and using the following identities:

(27)

(28)

we get on simplification the following equations

(29)

(30)

(31)

(32)

where,

(33)

(34)

(35)

(36)

(37)

By solving (29)–(32), we can obtain the non-vanishing coefficients which correspond to n=m−2, m, m+2.

Therefore, we have determined the explicit expression for the stream functions for the flow inside and outside of the porous deformed sphere S as

(38)

(39)

where, all the constants have been determined. These above expressions (38) and (39) are the new solutions of the Brinkman equation under the above mentioned boundary conditions.

4 Application to a porous oblate spheroid

We consider an approximate porous oblate spheroid as an application of the above analysis. Let us consider that porous oblate spheroid is stationary and the steady axi-symmetric flow has been established around its symmetry axis z by a uniform velocity U. Let the Cartesian equation of an oblate spheroid be

$$\frac{x^{2} + y^{2}}{d^{2}} + \frac{z^{2}}{d^{2}(1 - \varepsilon )^{2}}= 1, $$

(40)

whose equatorial radius is d, in which ε is so small that squares and higher powers of it may be neglected. Its polar equation can be written in the form

$$r = a(1 + 2\varepsilon G_{2}(\zeta)), $$

(41)

where, a=d(1−ε). Here, it may be mentioned that for the case of 0<ε≤1, the shape of spheroid will be oblate, whereas, for ε<0 the shape will become prolate spheroid. Clearly, when ε=0, (40) represents a sphere of radius d. Upon comparison with (5), we are led to the values m=2, β _m =2ε. Since A ₀, D ₀, $B_{0}^{*}$, $C_{0}^{*}$ are all become zero and further using (41), we find from (38) and (39) that the stream functions around and through the porous oblate spheroid are

(42)

(43)

Thus the flow fields around and through the porous oblate spheroid are also completely determined.

5 Results and discussion

The drag force F experienced by a porous oblate spheroid embedded in another porous medium can be evaluated by integrating the stresses over the porous oblate spheroid as:

(44)

On evaluation of stress-components, we get

(45)

(46)

Therefore, inserting these values of (45) and (46) in (44) and integrating, we find that

(47)

This is the new result for the drag experienced by a porous oblate spheroid embedded in another porous medium, where the values of constants $b_{2}^{*}$, $c_{2}^{*}$, $B_{2}^{*}$ and $C_{2}^{*}$ are given in Appendix A.

Also, the drag coefficient C _D can be found as

(48)

where, $\mathrm{Re} = \frac{2dU}{\nu _{2}}$ and $v_{2} =\frac{\mu _{2}}{\rho}$ being the Reynolds number and kinematic viscosity of fluid, respectively.

Figure 2 represents the variation of Re C _D for various values of σ ₂ with σ ₁, when viscosity ratio λ=0.5, porosity ratio φ=5 and deformation parameter ε=0.05. This shows that the Re C _D increases on the porous oblate spheroid with the increase of permeability parameter σ ₁. The variation of Re C _D is almost same for different values of σ ₂ when σ ₁<1 and then increases rapidly for 1<σ ₁<10 and after this it become almost constant (Table 1).

Fig. 2

Variation of the drag coefficient C _D with permeability parameter σ ₁ for a porous oblate spheroid for various values of σ ₂ when viscosity ratio λ=0.5, porosity ratio φ=5 and ε=0.05

Table 1 Quantitative values of Re C _D for different values of σ ₁ and σ ₂ for porous oblate spheroid and porous prolate spheroid and porous sphere

For porous oblate spheroid, the value of Re C _D decreases with increase of σ ₂, when σ ₁<0.4 and then increases with increases of σ ₂ but for porous prolate spheroid the value of Re C _D increases with increases of σ ₂ for all values of σ ₁ (Table 1).

The value of Re C _D decreases on the porous oblate spheroid embedded in another porous medium with the increase of viscosity ratio λ and inside permeability k ₁, when σ ₂=0.1, porosity ratio φ=5 and ε=0.05 (Fig. 3).

Fig. 3

Variation of drag coefficient C _D with permeability parameter σ ₁ for a porous oblate spheroid for various values of viscosity ratio λ when σ ₂=0.1, φ=5 and ε=0.05

Figure 4 shows that the value of Re C _D increases on the porous oblate spheroid with the increase of ε and for a permeability parameter σ ₁<7 and it becomes constant for all values of ε, when 7<σ ₁<8 but the value of Re C _D increases with decrease of ε, when permeability parameter σ ₁≥8. Similar, above variations in the value of Re C _D will take place for the case of a porous prolate spheroid as it can be observed from Table 1.

Fig. 4

Variation of the drag coefficient Re C _D for a porous oblate spheroid on permeability parameter σ ₁ for various values of ε when viscosity ratio λ=1, porosity ratio φ=5 and σ ₂=0.1

The dimensionless shearing stress at any point on the porous oblate spheroid can be defined as

$$ \begin{array}{l} = \frac{T_{r\theta} ^{(2)}}{(\frac{\mu _{2}U}{a})\operatorname{sin}\theta} \quad \mbox{at}\ r = a \\= [3 (b_{2}^{*} + B_{2}^{*}) + \biggl\{\frac{1}{2}(\sigma_{2}^{2} + 6)K_{3/2}(\sigma_{2}) +\sigma_{2}K_{1/2}(\sigma_{2})\biggr\} (c_{2}^{*} + C_{2}^{*})] \\{}- 2\varepsilon [6b_{2}^{*} + \{ (\sigma_{2}^{2} + 6)K_{3/2}(\sigma_{2}) +\biggl(2\sigma_{2} + \frac{1}{4}\sigma_{2}^{3}\biggr)K_{1/2}(\sigma_{2})\}c_{2}^{*}] (1 - \operatorname{cos}^{2}\theta) \\{}+ [30B_{4}^{*} + \{ (\sigma_{2}^{2} +30)K_{7/2}(\sigma_{2}) + 2\sigma_{2}K_{5/2}(\sigma_{2})\}C_{4}^{*}]\frac{(5\operatorname{cos} ^{2}\theta - 1)}{8}. \\ \end{array}$$

(49)

where the values of constants $b_{2}^{*}$, $c_{2}^{*}$, $B_{2}^{*}$, $C_{2}^{*}$, $B_{4}^{*}$ and $C_{4}^{*}$ are given in Appendix A.

The effect of deformation parameter ε and permeability parameters σ ₁ & σ ₂ on the dimensionless shearing stress of porous oblate spheroid is shown in Figs. 5 and 6. Figure 5 shows that the dimensionless shearing stress increases with increase of ε but it is almost same for all values of ε (for σ ₁≤4), when φ=5, λ=1, θ=π/4 and σ ₂=0.1. The dimensionless shearing stress increases slowly with decrease of σ ₁>20 and increases rapidly with decrease of σ ₁≤20. Figure 6 shows that the dimensionless shearing stress decreases with increase of σ ₂ and almost same for σ ₂≈2 when φ=5, λ=1, θ=π/4 and σ ₂=0.1. The dimensionless shearing stress increases slowly with decrease of σ ₁>20 and increases rapidly with decrease of σ ₁≤20. Similar, above variations in the value of T _rθ will take place for the case of a porous prolate spheroid as it can be observed from Table 2. For limiting case ε=0, our results agree with those of Deo and Gupta [26]. These calculations and graphs made here are evaluated by using Mathematica software.

Fig. 5

Variation of the dimensionless shearing stress T _rθ for porous oblate spheroid on permeability parameter σ ₁ for various values of ε when φ=5, λ=1, θ=π/4 and σ ₂=0.1

Fig. 6

Variation of the dimensionless shearing stress T _rθ for porous oblate spheroid on permeability parameter σ ₁ for various values of, σ ₂ when φ=5, λ=1, θ=π/4 and ε=0.01

Table 2 Quantitative values of T _rθ for different values of σ ₁ and σ ₂ for porous oblate spheroid and porous prolate spheroid and porous sphere

6 Deductions of some special known results

6.1 Porous oblate spheroid in an unbounded fluid

If k ₂→∞, then σ ₂→0, i.e., porous region will be clear fluid and hence the value of the drag force on the porous oblate spheroid in an unbounded clear fluid, for the case when λ=1 and φ=1, will be

(50)

and drag coefficient C _D comes out as

(51)

These results agree with the previously established similar results by Deo [25] for the drag force experienced by a porous oblate spheroid in an unbounded fluid medium.

6.2 Rigid oblate spheroid in an unbounded fluid medium

If σ ₁→∞ i.e., k ₁→0 and k ₂→∞ i.e., σ ₂→0, then the porous oblate spheroid embedded in another porous medium reduces to the rigid oblate spheroid in an unbounded clear fluid. In this case, the value of drag force F experienced by the rigid oblate spheroid will be

$$F = 6\pi d\mu_{2}U\biggl(1 - \frac{1}{5}\varepsilon\biggr). $$

(52)

This result agrees with a well-known result reported earlier by Palaniappan [17] and Ramkissoon [18] for the flow past a rigid spheroid in an unbounded fluid medium.

6.3 Porous sphere embedded in another porous medium (ε=0)

In this case, the value of drag force F experienced by a porous sphere of radius a embedded in another porous media will become as

$$F = \frac{2}{3} \pi\tilde{\mu} _{2} a U\sigma_{2}^{2}[2 + b_{2}^{*} -2K_{3/2}(\sigma_{2})c_{2}^{*}], $$

(53)

and the drag coefficient C _D comes out as

$$C_{D} = \frac{\frac{8}{3} \sigma _{2}^{2}[2 + b_{2}^{*} -2K_{3/2}(\sigma _{2})c_{2}^{*}]}{\mathrm{Re}} . $$

(54)

These results and Figs. 7, 8 and 9 agree with the previously established results by Deo and Gupta [26] for the drag force experienced by a porous sphere embedded in another porous medium.

Fig. 7

Variation of drag coefficient Re C _D with permeability parameter σ ₁ for a porous sphere for various values of viscosity ratio λ, when σ ₂=0.1

Fig. 8

Variation of the drag coefficient C _D with permeability parameter σ ₁ for a porous sphere for various values of σ ₂ when viscosity ratio λ=1

Fig. 9

Variation of the dimensionless shearing stress T _rθ for porous sphere on permeability parameter σ ₁ for various values of σ ₂ when λ=1

The quantitatively comparison in the values of Re C _D and −T _rθ for porous oblate spheroid, porous prolate spheroid and porous sphere are shown in Table 1 and in Table 2 respectively for particular values of permeability parameters σ ₁ and σ ₂ at λ=0.5, φ=5 (for Table 1); and λ=0.5, $\theta = \frac{\pi}{4}$ (for Table 2). It is observed from Table 1 that for small values of permeability parameter σ ₂(≈0.1) and σ ₁>1 the value of Re C _D for porous prolate spheroid is higher than the value of Re C _D for porous sphere and the value of Re C _D for porous sphere is higher than the value of Re C _D for porous oblate spheroid but for large values of permeability parameter σ ₂(≥0.4) and σ ₁>4 the value of Re C _D for porous oblate spheroid is higher than the value of Re C _D for porous sphere and the value of Re C _D for porous sphere is higher than the value of Re C _D for porous prolate spheroid. From Table 2 it is seen that for σ ₁ (≥1) the value of T _rθ for porous oblate spheroid is higher than the value of T _rθ for porous sphere and the value of T _rθ for porous sphere is higher than the value of T _rθ for porous prolate spheroid.

6.4 Porous sphere in an unbounded fluid medium

If k ₂→∞ i.e., σ ₂→0 and ε=0, then the porous oblate spheroid embedded in another porous medium reduces to the porous sphere in an unbounded clear fluid. In this case, the value of drag force F experienced by the porous sphere of radius a, for the case λ=1 will be

$$F = 12 \pi\mu_{2} a U\biggl[\frac{\sigma _{1}^{2}(\sigma _{1}\cosh \sigma _{1} - \sinh \sigma _{1})}{\sigma _{1}(3 + 2\sigma _{1}^{2})\cosh \sigma _{1} - 3\sinh \sigma _{1}}\biggr]. $$

(55)

This result agrees with a well-known result reported earlier by Qin and Kaloni [11] for the drag force experienced by a porous sphere in an unbounded clear fluid.

6.5 Solid sphere in an unbounded clear fluid

If σ ₁→∞, i.e., k ₁→0, σ ₂→0, i.e., k ₂→∞ and ε=0, then the porous oblate spheroid embedded in another porous medium reduces to a solid sphere in an unbounded clear fluid. In this case, the value of drag force F experienced by the solid sphere of radius a, for the case λ=1 comes out as

$$F = 6\pi\mu_{1}Ua. $$

(56)

This result agrees with a well-known result for the drag reported earlier by Stokes [29] for flow past a solid sphere in unbounded fluid medium.

7 Conclusion

There are many physical situations in which the flow of a viscous fluid in porous medium occurs in which the porous spheroidal particles are embedded. Hence the results of this paper are applicable to study the flow of porous fluids past porous rocks of spheroidal shape, aloxite materials, earthen soil, etc. Bear [31]. Here, authors would like to study the case in which porosity of the material inside the spheroid is less than that of the outside one. Such situations occur when the water or other fluid flows past a porous spheroidal object or porous rocks of spheroidal shape embedded in sand or earthen soil of more porosity. Expressions for stream functions and a new result for the drag on a porous spheroid embedded in another porous medium have been registered. It is seen that effect of permeability is to reduce the drag force.

Appendix A

Where, a ₁=I _1/2(σ ₁), a ₂=I _3/2(σ ₁), b ₁=K _1/2(σ ₂), b ₂=K _3/2(σ ₂), c ₁=I _7/2(σ ₁), c ₂=I _5/2(σ ₁), d ₁=K _7/2(σ ₂), d ₂=K _5/2(σ ₂).