Effect of magnetic field on the slow motion of a porous spheroid: Brinkman’s model

Abstract

The major goal of this work is to analyze the magnetic effect on the creeping viscous flow past a porous spheroidal particle, a particle of slightly deformed spherical shape. Brinkman’s model is proposed to govern the flow in the porous media. Boundary value problem considers the conditions of continuity of velocity components, continuity of normal stresses, and stress jump boundary condition for tangential stress. A transverse magnetic field of uniform nature is applied to the flow. An expression for the drag force acting on the spheroidal particle is derived analytically. The effects of the physical parameters involved in the flow like permeability, deformation, Hartmann number’s, viscosity ratio, and stress jump coefficient parameters are visualized through graphs and tables. The applied magnetic field seems to suppress the flow of fluid that leads to the increase in the drag experienced on the porous spheroid. It is also observed that the increase in the deformation, stress jump, and permeability decreases the drag coefficient. Our results without magnetic effect match with the results reported earlier in the literature.

1 Introduction

In the era of modern science, the area concerned about the study of the interaction between an electrically conducting fluid and magnetic field, generally known as magnetohydrodynamics, has been found to be of keen interest. The presence of the magnetic field produces an electromagnetic force called Lorentz force which acts on the fluid and has the tendency to alter the behavior of the flow. Due to its relation with various applications of science and engineering, it has been in the limelight among many researchers. Some important areas of its application are in the fields of biological science, astrophysics, geophysics, metallurgy, and many more. It is also applied in generating hydrodynamic generator, micro-electronic devices, pumps, purifying molten metals, meters, bearings, etc. The study of magnetohydrodynamic behavior of the boundary layers towards rigid or moving surface under the action of the transverse magnetic field is one of the basic and important problems in this area of fluid mechanics.

The class of problems concerned about convection in porous media is treated as an important area of research over the centuries, notably due to its easy presence in natural and man-made flows. Instantly, such flow can be found in flow through a sponge, the flow of oil through porous rocks, extraction of crude oils from earth’s surfaces, sedimentation of the particles, the filtration of solids from liquids, permeation of drugs through human skin, transport of nutrients from synovial fluid to cartilages in synovial joints, and many more. In view of its vast application, many investigations have been done by various authors. The pioneering work of Stokes [1] provided knowledge on the drag force experienced by a moving or rigid particle of considerable range. In view of modeling flow in porous media, Darcy’s law [2] provides an empirical formula in which the viscous stress tensors are neglected. Importantly, this law is fruitful for the flow in porous media bearing low permeability. However, this law is found to be inadequate for media with higher permeability. To overcome this situation, Brinkman [3] introduced one additional effective viscosity term in Darcy’s equation and obtained the relation between particle size density and permeability. Concentrating on the discrepancies in terms of choosing boundary conditions while studying motion in porous media, we come across the following conditions. At the porous fluid interface, the traditional no-slip condition which was used extensively earlier is later found to not always hold true in real circumstances. Therefore, some slip may be experienced at the interface. Important fluid-porous boundary conditions are proposed by Beavers-Joseph et al. [4,5,6,7].

The literature based on the motion of Newtonian flow past porous spherical or cylindrical particles is found to be very rich and significant. On the contrary, under nature and engineering practices, porous particles are found to be of shapes differing from that of spherical geometry, and the spheroidal-shaped particles are of the simplest configuration allowing to explore the effect of geometrical shapes on the drag resistance and their settling velocity. Despite the complex geometry, flow past spheroidal shape has gained the attention of researchers over the last few centuries. However, some of the important works most relevant to our study are pointed out. Zlatanovski [8] illustrated the axisymmetric flow of fluid past a porous prolate spheroid by using Brinkman’s media. This analysis further took into consideration the eigenvalues and eigen functions of the stream function for the porous medium. The translational and the rotational movement of porous spheroid enclosed within a spheroidal cell was studied by Saad [9]. In this study, the small departure from a spherical shape is considered for the spheroidal particles, and the expressions for the flow fields are presented to the first order of the deformation parameter. Additionally, Saad [10] investigated the Stokes flow past a porous spheroidal particle confined in a spheroidal container using cell models. He evaluated the analytical expressions for the drag for all the chosen cell models. Srinivasacharya and Krishna Prasad [11,12,13] studied the Newtonian fluid flow past and through porous approximate sphere, porous approximate sphere with deformed solid core, and porous approximate spherical shell, respectively. In the article by Sherief et al. [14], the problem dealing with the oscillating spheroidal particle in the micropolar fluid was reported, considering the slip condition. The drag and the couple exerted on the particle are evaluated and expressed in terms of the prolate and oblate spheroids. A steady rotation of a porous approximate sphere contained inside an approximate spherical vessel using stress jump condition was handled by Srinivasacharya and Krishna Prasad [15]. The expression for the torque on the porous approximate particle was also calculated. Krishna Prasad and Kaur [16] explored the problem of a viscous fluid past a spheroid filled with micropolar fluid by using an analytical method. They evaluated the hydrodynamic drag force experienced by the fluid spheroid. Recently, using the Beavers–Joseph–Saffman–Jones condition, Krishna Prasad and Bucha [17] examined the problem of flow past a permeable spheroidal particle. In their work, an analytical expression of drag force acting on the particle is derived.

Numerous early works contributing to the area of magnetohydrodynamics explained well its importance in science and engineering. A basic review of this type of flow can be found in the following books [18, 19]. Earlier, magnetohydrodynamic flow through a circular channel filled with a saturated porous medium was investigated by Verma and Singh [20]. The expression of the velocity, average velocity, rate of volume flow, and shear stress is obtained. Yadav et al. [21] found the dominating effect of Hartmann’s number on the hydrodynamic permeability of membrane containing porous spherical shell. The problem through the swarm of spherical particles was modeled by using the cell model method, and the effect of several important flow parameters was studied. Saad [22] made a study to explore the effect of the magnetic field on the motion of suspension of the porous particles of different geometry (sphere and cylinder) bounded by a cell. While making a comparison, he found the value of the Kozeny constant which was derived during the study, to be smaller for a sphere as compared to the parallel and perpendicular cylindrical flows in the voidage range. Nasir et al. [23] worked on the natural convection flow of micropolar fluid inside a porous square conduit and studied the effects of the magnetic field, heat generation/absorption, and thermal radiation on the flow. In the current scenario, varieties of problems handling the vast range of fluids with magnetic influence and different particle geometries have been studied [24,25,26,27,28,29,30,31,32]. Effects of velocity second slip model and induced magnetic field on peristaltic transport of non-Newtonian fluid in the presence of double-diffusivity convection in nanofluids were carried out by Akram et al. [33]. Bilal and Nazeer [34] analyzed the motion of non-Newtonian fluid over a stratified stretching/shrinking inclined sheet with the aligned magnetic field and nonlinear convection. Nabil et al. [35] tackled the MHD peristaltic flow of power-law nanofluid passing through a non-Darcy porous medium inside a non-uniform inclined channel.

In the series of investigations made by Krishna Prasad and Bucha [36,37,38,39,40,41], the influence of magnetic field on the flow through particles with different geometrical shapes has been carried out in detail. The influence of imposed transverse magnetic field on the volumetric flow past a porous cylindrical shell is deeply studied by using both analytical and numerical approaches [36]. At the interface of the fluid-porous region, the continuity of velocity components, a stress jump condition for tangential stresses, and the Happel and Kuwabara cell model are used. The volumetric flow rate of the fluid is also calculated. Moreover, the impact of MHD on the drag force exerted on the semipermeable sphere due to the viscous flow has been discussed [37]. The explicit expression for the drag on the semipermeable sphere is derived which shows the enhancement in the drag force on the application of the magnetic field. The motion of fluid past bounded fluid sphere with a fluid of different viscosity has been studied under the impact of the transverse magnetic field using Kuwabara cell model [38]. The drag acting on the inner fluid sphere is also derived. Thereafter, the MHD effect on the Stokes flow past a weakly permeable sphere enclosed by a spherical cell using Happel and Kuwabara cell models together with Saffman boundary condition is carried out [39]. The expressions for drag force, hydrodynamic permeability, and Kozeny constant for the bounded spherical particle are found. The flow of magnetic fluid through the porous cylindrical shell with a liquid core has been investigated, employing the unit cell models [40]. An expression for the Kozeny constant on the cylindrical shell is presented. The flow dealing with magnetic fluid past a weakly permeable cylindrical particle is studied [41]. Applying the Saffman’s slip condition, the drag, hydrodynamic permeability, and Kozeny constant for the permeable cylinder are evaluated. All the mentioned works emphasize the impact of MHD to be changing with altering shapes of the particle. Therefore, it is significant to study the MHD effect on varying particle geometry.

The above-discussed literature survey indicates that the MHD effect on flow past a porous spheroidal geometry has yet not been investigated. Several works have been carried out by researchers to predict the parameters which are highly influencing the flows. The nature of fluid and the size, shape, and type of particles are among the important factor involved in characterizing the amount of flow. Applying a magnetic field on such flow produces a suppressive force which in turn reduces the flow velocity by increasing the resisting force acting on the particle. To the best of our knowledge, magnetic influence on the low Reynolds flow past a porous particle of deformed spherical shape is not been studied earlier, despite its application in different fields of sciences. To address this scientific gap, we considered modeling the flow past a Brinkman governed porous spheroid under the MHD effect. An expression for the drag acting on the spheroidal particle, to the first order in a small parameter characterizing the deformation of the spheroidal surface from the spherical shape, has been derived analytically. The influence of several dimensionless parameters that arises while pursuing the analysis like permeability, stress jump coefficient, deformation, Hartmann number, and viscosity ratio on the nature of the drag coefficient is discussed using graphs and tables. The obtained drag result without the magnetic field and in the absence of stress jump is found in agreement with that of Saad’s result [9]. Also, various other results produced in reduction cases are found to be agreeing with those available in the literature.

2 Modeling the problem

2.1 Physical and mathematical description

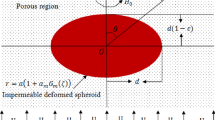
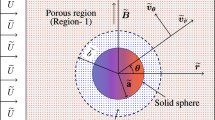
The geometry of the steady, axisymmetric flow of conducting fluid past a porous spheroid under the execution of a transverse uniform magnetic field is illustrated in Fig. 1. During this investigation, we assume the magnetic Reynold’s number as $Re_m={U\ a}\mu _h\sigma _i$ to be extremely small where $\sigma _i$ denotes the electric conductivity of the fluid and $\mu _h$ the magnetic permeability of the fluid. Also, $\mu _h$ is supposed to be similar for both the fluid and porous regions and any applied external electric field is ignored. Also, the induced magnetic field is neglected.

Now, the magnetic force called Lorentz force, denoted as $\mathbf {F}$, comes into play while dealing with the magnetohydrodynamic flow and is given as

$$\begin{aligned} \mathbf {F}=\mu _h\mathbf {J}\times \mathbf {H}. \end{aligned}$$

(1)

where $\mathbf {J}$ and $\mathbf {H}$ are the electric current density and the magnetic field intensity.

Therefore,

$$\begin{aligned} \mathbf {F}=\mu _h^{2}\sigma _i\left( \mathbf {q}\times \mathbf {H}\right) \times \mathbf {H}. \end{aligned}$$

(2)

Obtained magnetic forces balance the pressure and the viscous stresses, in order to produce the modified Stokes and modified Brinkman’s equation, respectively. Therefore, the modified Stokes equation [22, 37, 38, 43] governs the flow in region I, and the modified Brinkman’s equation [3, 36] governs the flow in region II.

The viscous fluid region I and porous region II are specified using i, where $i=1, 2$ respectively. Further, the transverse magnetic field is represented as $\mathbf {H}^{(i)}=H_o\mathbf {e_r}, i=1,\ 2$.

Fig. 1

Visualization of MHD flow past a porous spheroid

2.2 Basic flow equations

The present flow is supposed to be of low Reynolds number, and therefore, Stokes equation is considered to be the flow governing equation in the fluid region, and Brinkman’s equation is used for the flow in the porous region.

The equations for movement of a viscous fluid in the region I under MHD effect governed by modified Stokes equation are given by

$$\begin{aligned}&\nabla \cdot \mathbf {q}^{\ (1)}=0, \end{aligned}$$

(3)

$$\begin{aligned}&{\nabla }p^{(1)}+\mu \nabla \times \nabla \times \mathbf {q}^{(1)}-\mu ^{2}_h\sigma _i\left( \mathbf {q}^{\ (1)}\times \mathbf {H}^{\ (1)}\right) \times \mathbf {H}^{\ (1)}=0, \end{aligned}$$

(4)

Equations for motion in region II under MHD effect are defined by modified Brinkman’s equation

$$\begin{aligned}&\nabla \cdot {\mathbf {q}^{\ (2)}}=0, \end{aligned}$$

(5)

$$\begin{aligned}&{\nabla }{p^{\ (2)}}+\mu _e{\nabla }\times {\nabla }\times \mathbf {q}^{\ (2)}+\frac{\mu }{k}\mathbf {q}^{\ (2)}\nonumber \\&-\,\frac{\mu ^{2}_h\sigma _e}{\epsilon }\left( \mathbf {q}^{\ (2)}\times \mathbf {H}^{\ (2)}\right) \times \mathbf {H}^{\ (2)}=0, \end{aligned}$$

(6)

where $\mathbf {q}^{\ (i)}$, ${p^{\ (i)}}$ are velocity vector and pressure, $\sigma _i$ and $\sigma _e$ the electric conductivity and effective electric conductivity, and $\mu$ and $\mu _e$ the viscosity and the effective viscosity with k and $\epsilon$ to be the permeability and porosity of porous region, respectively. The effective viscosity theoretically takes into account the stress within the fluid when it passes through a porous medium. Basically, the viscosity $\mu$ and effective viscosity $\mu _e$ are distinct [42]. Although at the macrolevel it can be treated as equal, it does not hold true at microlevel. Furthermore, the electric conductivity of clear fluid and porous region is distinct [22, 44].

To transform the flow equations into dimensionless form, the following non-dimensional variables come into play

$$\begin{aligned} {r}=a\tilde{r},\ \mathbf {q}^{(i)}=U\tilde{\mathbf {q}}^{(i)},\ {\nabla }=\frac{\tilde{{\nabla }}}{a},\ p^{(i)}=\frac{\mu U}{a}\tilde{p}^{(i)},\ \mathbf {H}^{\ (i)}=H_o\ \tilde{\mathbf {H}}^{\ (i)}. \end{aligned}$$

(7)

Utilizing the above values in Eqs. (3)–(6) and then ignoring the tildes, we obtain the final equations as

$$\begin{aligned}&{\nabla }\cdot {\mathbf {q}^{(1)}}=0, \end{aligned}$$

(8)

$$\begin{aligned}&{\nabla }p^{(1)}+\nabla \times \nabla \times \mathbf {q}^{(1)}-\alpha ^{2}\left( \mathbf {q}^{\ (1)}\times \mathbf {H}^{\ (1)}\right) \times \mathbf {H}^{\ (1)}=0, \end{aligned}$$

(9)

$$\begin{aligned}&{\nabla }\cdot \mathbf {q}^{(2)}=0, \end{aligned}$$

(10)

$$\begin{aligned}&{\nabla }p^{(2)}+\gamma ^{2}\xi _{1}^{2}\mathbf {q}^{\ (2)}+\gamma ^{2}\nabla \times \nabla \times \mathbf {q}^{\ (2)}-\gamma ^{2}\xi _2^{2}\left( \mathbf {q}^{\ (2)}\times \mathbf {H}^{\ (2)}\right) \times \mathbf {H}^{\ (2)}=0, \end{aligned}$$

(11)

where the symbols represent the following

• 1. $\displaystyle {\alpha =\sqrt{\frac{\mu ^{2}_hH_o^{2}\sigma _i a^{2}}{\mu _{1}}}}$, the Hartmann number for viscous fluid region I.

• 2. $\displaystyle {\gamma ^{2}=\frac{\mu _2}{\mu _{1}}}$, the viscosity ratio between the inner fluid in porous media and outer viscous fluid.

• 3. $\displaystyle {\xi _{1}^{2}=\frac{a^{2}}{k}\frac{1}{\gamma ^{2}}}$, the permeability parameter.

• 4. $\displaystyle {\xi _2=\sqrt{\frac{\mu ^{2}_hH_o^{2}\sigma _e a^{2}}{\epsilon \mu _2}}}$, the Hartmann number for Brinkman porous region II.

• 5. $\displaystyle {\beta ^{2}=\xi _{1}^{2}+\xi _2^{2}}$.

Here, $(r,\theta ,\phi )$ denote spherical coordinate system. The flow is axially symmetric, which further indicates the flow quantities are independence of $\phi$. Thus, we assume velocity vectors as

$$\begin{aligned} \mathbf {q}^{(i)}=q_{r}^{(i)}(r,\theta )\mathbf {e}_{r}+q_{\theta }^{(i)}(r,\theta )\mathbf {e}_{\theta },\ \ i=1,2. \end{aligned}$$

(12)

The spheroidal surface is supposed to be of the form $r=a\left[ 1+f(\theta )\right]$ [43], and its shape is slightly deviated from that of the spherical surface $r=a$. Now, in general situation, the orthogonality relations of Gegenbauer functions $\vartheta _{m}(\zeta )$, $\zeta =\cos \theta$ permit us to consider the expansion $f{(\theta )} =\sum _{m=2}^{\infty }\alpha _{m}\vartheta _m{(\zeta )}$. In the above equation, the Gegenbauer function in relation to Legendre function $P_{n}{(\zeta )}$ is given as

$$\begin{aligned} \vartheta _{n}{(\zeta )} = \frac{P_{n-2}{(\zeta )}-P_{n}{(\zeta )}}{2n-1},\quad n\ge {2}. \end{aligned}$$

(13)

Therefore, the surface of the spheroid can be chosen as $r= a[1+\alpha _{m}\vartheta _m{(\zeta )}]$. The coefficient $\alpha _{m}$ is assumed to be very small so that their squares and higher powers can be ignored [43]. Subsequently, we have $(r/a)^y\approx {1+y\alpha _{m}\vartheta _m{(\zeta )}}$, where y is positive or negative.

Let us suppose $\psi ^{(i)}$ to be the stream functions for fluid and porous regions, respectively, with $i=1,2$.

Considering the stream function, the velocity components are

$$\begin{aligned} q_{r}^{(i)}=\frac{1}{r^{2}}\frac{\partial {\psi ^{(i)}}}{\partial \zeta }, q_{\theta }^{(i)}=\frac{1}{r\sqrt{1-\zeta ^{2}}}\frac{\partial \psi ^{(i)}}{\partial {r}};\ \ i=1,2. \end{aligned}$$

(14)

After the elimination of pressure terms $p^{(1)}$ and $p^{(2)}$ from Eqs. (9) and (11), we finally obtain

$$\begin{aligned} E^{2}(E^{2}-\alpha ^{2})\psi ^{(1)}= & {} 0, \end{aligned}$$

(15)

$$\begin{aligned} E^{2}(E^{2}-\beta ^{2})\psi ^{(2)}= & {} 0, \end{aligned}$$

(16)

where $\displaystyle {E^{2}=\frac{\partial ^{2}}{\partial {r^{2}}}+\frac{1-\zeta ^{2}}{r^{2}}\frac{\partial ^{2}}{\partial {\zeta ^{2}}}}$ is the Stokes operator.

3 Boundary conditions

The requirement of finding the closed-form solution of the boundary value problem arises the need for interface conditions, which validate the problem both physically and mathematically. While dealing with flow past Brinkman media, it was conveyed that the frequently considered continuity of stresses may not always be appropriate; therefore, the discontinuity condition for shearing stresses was proposed by Ochoa-Tapia and Whitaker [6, 7]. Thus, continuity of the velocity components, continuity of the normal stresses, and stress jump condition for the tangential stress components [22, 36] are chosen to be applicable to the present problem. Mathematically, at the spheroidal surface, we have the following boundary conditions

$$\begin{aligned} (\mathbf {q}^{(1)}-\mathbf {q}^{(2)})\cdot \mathbf {n}= & {} 0 , \end{aligned}$$

(17)

$$\begin{aligned} (\mathbf {q}^{(1)}-\mathbf {q}^{(2)})\cdot \mathbf {s}= & {} 0 , \end{aligned}$$

(18)

$$\begin{aligned} \mathbf {n}\cdot (\tau ^{\ (2)}-\tau ^{\ (1)})\cdot \mathbf {n}= & {} 0, \end{aligned}$$

(19)

$$\begin{aligned} \mathbf {n}\cdot (\tau ^{\ (2)}-\tau ^{\ (1)})\cdot \mathbf {s}= & {} \frac{\sigma \mu _{1}}{\sqrt{k}}(\mathbf {q}^{(2)}\cdot \mathbf {s}). \end{aligned}$$

(20)

where $\sigma$ is the stress jump coefficient.

Moreover, $\mathbf {n}=\mathbf {e}_r-\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}\mathbf {e}_\theta ,$ and $\mathbf {s}=-\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}\mathbf {e}_r-\mathbf {e}_\theta ,$ are the unit normal vector and an arbitrary tangential vector at the spheroidal surface $r=a[1+\alpha _{m}\vartheta _m{(\zeta )}]$.

Boundary conditions at infinity ($r\rightarrow \infty$) for the external flow are written as $q_{r}^{(1)}=-U\cos \theta$ and $q_{\theta }^{(1)}=U\sin \theta$.

Substituting the above values of $\mathbf {n}$ and $\mathbf {s}$ in Eqs. (17)–(20), we get the boundary conditions in non-dimensional form as

$$\begin{aligned} {q}_r^{(1)}-{q}_r^{(2)}= & {} ({q}_\theta ^{(1)}-{q}_\theta ^{(2)})\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}, \end{aligned}$$

(21)

$$\begin{aligned} {q}_{\theta }^{(1)}-{q}_{\theta }^{(2)}= & {} 0, \end{aligned}$$

(22)

$$\begin{aligned} \tau _{rr}^{\ (1)}-\tau _{rr}^{\ (2)}= & {} 2\alpha _{m}\left( \tau _{r\theta }^{\ (1)}-\tau _{r\theta }^{\ (2)}\right) \sqrt{1-\zeta ^{2}} P_{m-1}{(\zeta )}, \end{aligned}$$

(23)

$$\begin{aligned}&\tau _{r\theta }^{\ (2)}-\tau _{r\theta }^{\ (1)}+\alpha _{m}\left[ \left( \tau _{rr}^{\ (2)}-\tau _{\theta \theta }^{\ (2)}\right) -\left( \tau _{rr}^{\ (1)}-\tau _{\theta \theta }^{\ (1)}\right) \right] \nonumber \\ \sqrt{1-\zeta ^{2}} P_{m-1}{(\zeta )}= & {} \sigma \xi _{1}\gamma \left( {q}_\theta ^{(2)}+{q}_r^{(2)}\alpha _{m}\sqrt{1-\zeta ^{2}}P_{m-1}{(\zeta )}\right) . \end{aligned}$$

(24)

In terms of stream functions $\psi ^{(i)}$; $i=1,2$, we have the expressions below

$$\begin{aligned}&\left( \frac{\partial \psi ^{(1)}}{\partial \zeta } -\frac{\partial \psi ^{(2)}}{\partial \zeta }\right) =r\alpha _{m}P_{m-1}{(\zeta )}\left( \frac{\partial \psi ^{(1)}}{\partial {r}} -\frac{\partial \psi ^{(2)}}{\partial {r}}\right) , \end{aligned}$$

(25)

$$\begin{aligned}&\frac{\partial \psi ^{(1)}}{\partial r}-\frac{\partial \psi ^{(2)}}{\partial r}=0, \end{aligned}$$

(26)

$$\begin{aligned}&{p}^{(2)}-{p}^{(1)}-\frac{2}{r^{2}}\left[ \frac{2}{r}\left( \frac{\partial \psi ^{(1)}}{\partial \zeta }-\gamma ^{2}\frac{\partial \psi ^{(2)}}{\partial \zeta }\right) -\left( \frac{\partial ^{2}\psi ^{(1)}}{\partial r\partial \zeta }-\gamma ^{2}\frac{\partial ^{2}\psi ^{(2)}}{\partial r\partial \zeta }\right) \right] \nonumber \\&-\,\frac{2\alpha _{m}P_{m-1}{(\zeta )}}{r}\left[ 2r\frac{\partial }{\partial {r}}\left\{ \frac{1}{r}\left( \frac{\partial \psi ^{(1)}}{\partial r}-\gamma ^{2}\frac{\partial \psi ^{(2)}}{\partial r}\right) \right\} +E^{2}\left( \gamma ^{2}\psi ^{\ (2)}-\psi ^{\ (1)}\right) \right] =0, \end{aligned}$$

(27)

$$\begin{aligned}&2r\frac{\partial }{\partial {r}}\left[ \frac{1}{r}\left( \gamma ^{2}\frac{\partial \psi ^{(2)}}{\partial {r}}-\frac{\partial \psi ^{(1)}}{\partial {r}}\right) \right] +E^{2}\left( \psi ^{\ (1)}-\gamma ^{2}\psi ^{\ (2)}\right) \nonumber \\&+\,2\alpha _{m}\vartheta _2{(\zeta )}P_{m-1}{(\zeta )}\left[ \frac{4}{r}\left( \gamma ^{2}\frac{\partial ^{2}\psi ^{(2)}}{\partial r\partial \zeta }-\frac{\partial ^{2}\psi ^{(1)}}{\partial r\partial \zeta }\right) -\frac{6}{r^{2}}\left( \gamma ^{2}\frac{\partial \psi ^{(2)}}{\partial \zeta }-\frac{\partial \psi ^{(1)}}{\partial \zeta }\right) \right. \nonumber \\&+\,\left. \frac{P_{1}{(\zeta )}}{r\vartheta _2{(\zeta )} }\left( \gamma ^{2}\frac{\partial \psi ^{(2)}}{\partial {r}}-\frac{\partial \psi ^{(1)}}{\partial {r}}\right) \right] =\sigma \xi _{1}\gamma \left( \frac{\partial \psi ^{(2)}}{\partial {r}}+\frac{2}{r}\alpha _{m}\frac{\partial \psi ^{(2)}}{\partial \zeta }\vartheta _2{(\zeta )}P_{m-1}{(\zeta )}\right) . \end{aligned}$$

(28)

4 Mathematical solution

The stream functions for the flow in region I and II are

$$\begin{aligned} \psi ^{(1)}= & {} \left[ r^{2}+\frac{a_2}{r}+b_2\sqrt{r} K_{{3}/{2}}(\alpha r)\right] \vartheta _2{(\zeta )}\nonumber \\&+\,\sum _{n=3}^\infty \left[ A_nr^{-n+1}+B_n\sqrt{r}K_{n-{1}/{2}}(\alpha r)\right] \vartheta _n{(\zeta )} \end{aligned}$$

(29)

$$\begin{aligned} \psi ^{(2)}= & {} \left[ c_2r^{2}+d_2\sqrt{r} I_{{3}/{2}}(\beta r)\right] \vartheta _2{(\zeta )}\nonumber \\&+\,\sum _{n=3}^\infty \left[ C_nr^{n}+D_n\sqrt{r}I_{n-{1}/{2}}(\beta r)\right] \vartheta _n{(\zeta )} \end{aligned}$$

(30)

The expression of the pressure terms is

$$\begin{aligned} p^{(1)}= & {} \alpha ^{2}\left[ \left( r-\frac{a_2}{2r^{2}}\right) P_{1}{(\zeta )} -\sum _{n=3}^\infty \frac{A_nr^{-n}}{n}P_{n-1}{(\zeta )}\right] \end{aligned}$$

(31)

$$\begin{aligned} p^{(2)}= & {} \gamma ^{2}\beta ^{2}\left[ c_2r P_{1}{(\zeta )} +\sum _{n=3}^\infty C_n\frac{r^{n-1}}{n-1}P_{n-1}{(\zeta )}\right] \end{aligned}$$

(32)

Initially, the results corresponding to the boundary $r=1+\alpha _{m}\vartheta _{m}{(\zeta )}$ are evaluated. The comparison of Eqs. (29) and (30) with the expression that are generated, while studying the flow of viscous fluid past a porous sphere, shows that the quantities containing $A_n$, $B_n$, $C_n$ and $D_n$ for the case $n>2$ are extra terms which are not present for the flow of porous sphere. Presently, we suppose the motion of fluid through a particle of spheroidal shape which it is not much deviates from the shape of sphere. Therefore, flow through the spheroidal particle is expected to be slightly varying from the case of flow through a porous sphere. While solving problem of this kind, we consider

$$\begin{aligned} r=1+\sum _{m=2}^{\infty }\alpha _{m}\vartheta _{m}{(\zeta )}. \end{aligned}$$

(33)

Thereafter, using a similar technique for each m, the expressions for stream functions of the problem are obtained.

5 Specific case of porous spheroid

As one of the cases of the mentioned flow, we examine the flow through a porous prolate and oblate spheroid. The equation of the spheroidal surface in terms of a Cartesian coordinate system is

$$\begin{aligned} \frac{x^{2}+y^{2}}{c^{2}}+\frac{z^{2}}{c^{2}{(1-\epsilon )^{2}}}=1 \end{aligned}$$

(34)

where c and $\epsilon$ are the radius of the equator and the deformation parameter, respectively. The $\epsilon$ is assumed so small that its squares and higher powers can be neglected. In terms of polar coordinate, Eq. (34) is expressed as

$$\begin{aligned} r=a[1+2\epsilon \vartheta _{2}{(\zeta )}] \end{aligned}$$

(35)

where $a=c(1-\epsilon )$.

The surface given by Eq. (35) is an oblate spheroid for $0<\epsilon \le 1$, and it represents a prolate spheroid for $\epsilon <0$. Moreover, $\epsilon =0$, it is identical with the equation of the sphere having radius c.

By applying the above analysis, one has to choose $m=2$; $\alpha _{m}=2\epsilon$. Thus, the expression for stream functions are

$$\begin{aligned} \psi ^{(1)}= & {} \left[ r^{2}+(a_2+A_2)r^{-1}+(b_2+B_2)\sqrt{r}K_{3/2}(\alpha r)\right] \vartheta _2{(\zeta )}+\left[ A_4{r^{-3}}+{B_4}\sqrt{r}K_{{7}/{2}}\right] \vartheta _4{(\zeta )}, \end{aligned}$$

(36)

$$\begin{aligned} \psi ^{(2)}= & {} \left[ (c_2+C_2)r^{2}+(d_2+D_2)\sqrt{r}I_{3/2}(\alpha r)\right] \vartheta _2{(\zeta )}+\left[ C_4r^{4}+{D_4}\sqrt{r}I_{{7}/{2}}\right] \vartheta _4{(\zeta )}. \end{aligned}$$

(37)

6 Hydrodynamic drag acting on porous spheriod

The flow of magnetoviscous fluid past a porous spheroidal particle generates a force opposite to the flow direction known as drag force. It can be calculated by the formula below [10, 14, 22, 43]

$$\begin{aligned} F_D=\int _{S}{(\mathbf {n}\cdot \tau ^{(1)})\cdot \mathbf {k}}{\mathrm{d}}S \end{aligned}$$

(38)

where $\mathbf {n}=\mathbf {e}_r-\epsilon \sin {2\theta } \mathbf {e}_{\theta }$; ${\mathrm{d}}S=2\pi a^{2}(1+2\epsilon \sin ^{2}\theta )\sin \theta {\mathrm{d}}\theta$; $\mathbf {k}$ is the unit vector acting in the z direction and integrating over the surface of the body $r=1+\epsilon \sin ^{2}\theta$. we have

$$\begin{aligned} F_D=2\pi a^{2}\int _{0}^{\pi } r^{2}[\left( \tau _{rr}-\epsilon \tau _{\theta r}\sin 2\theta \right) \cos \theta -\left( \tau _{r\theta }-\epsilon \tau _{\theta \theta }\sin 2\theta \right) \sin \theta ]|_{r=1+\epsilon \sin ^{2}\theta }\sin \theta {\mathrm{d}}\theta . \end{aligned}$$

(39)

Simplifying it, by using stress components and stream function given in Eq. (36), we have

$$\begin{aligned} F_D= & {} \frac{2}{3}\pi \mu Ua \alpha ^{2}\nonumber \\&\times \,\left[ a_2+A_2-2-2(b_2+B_2) K_{3/2}(\alpha ) +\frac{4\epsilon }{5}\left( -5+a_2+\frac{b_2}{\alpha +1}\left( 2\alpha ^{2}+\alpha +1 \right) K_{3/2}(\alpha )\right) \right] \end{aligned}$$

(40)

The values of $a_2$, $b_2$, $A_2$, and $B_2$ are found by solving the system of equations obtained from boundary conditions (Eqs. 25–28). As the expressions are too lengthy, we are not presenting it here.

By making use of these values and further substituting $a=c(1-\epsilon )$, $\alpha =\alpha _{1}(1-\epsilon )$, $\xi _{1}=\chi _{1}(1-\epsilon )$, $\xi _2=\chi _2(1-\epsilon )$, leading to $\beta =\beta _{1}(1-\epsilon )$ with $\beta _{1}^{2}=\chi _{1}^{2}+\chi _2^{2}$ , we obtain the expression for the drag acting on porous spheroid under MHD effect.

Where $\displaystyle {\alpha _{1}=\sqrt{\frac{\mu ^{2}_hH_o^{2}\sigma _i c^{2}}{\mu _{1}}}}$, $\displaystyle {\chi _{1}^{2}=\frac{c^{2}}{k}\frac{1}{\gamma ^{2}}}$ and $\displaystyle {\chi _2=\sqrt{\frac{\mu ^{2}_hH_o^{2}\sigma _e c^{2}}{\epsilon \mu _2}}}$.

6.1 Some special results

Several results for drag in reduction cases as well as some new results are given below which validated our work.

6.1.1 Magnetic effect

The following are the results in the presence of MHD effect:

• Case 1: For deformation parameter $\epsilon =0$ in the results obtained after solving Eq. (40), the problem reduces to flow past a porous sphere with stress jump and the drag is

  $$\begin{aligned} F_D=-\,4\pi \mu _{1}Uc\left[ \frac{ \Delta _{1} \gamma \ \delta _{1} \sigma \ \chi _{1}+\beta _{1}^{2} \left( \Delta _2\ \delta _{1}-\Delta _3\ \gamma ^{2}\ \delta _6\right) }{\left( \Delta _3\gamma \delta _4+2 \Delta _4 \right) \sigma \ \chi _{1}-\Delta _3\delta _7+\Delta _5 \gamma ^{2}+2 \Delta _2\ \beta _{1}^{2}}\right] \end{aligned}$$

  (41)

• Case 2: For $\sigma =0$ in Eq. (41), the problem reduces to that of flow past porous sphere with continuity of stress jump condition and the drag is given as

  $$\begin{aligned} F_D=-\,4\pi \mu _{1}Uc\left[ \frac{\beta _{1}^{2} \left( \Delta _2\ \delta _{1}-\Delta _3\ \gamma ^{2}\ \delta _6\right) }{\Delta _5 \gamma ^{2}+2 \Delta _2\ \beta _{1}^{2}-\Delta _3\delta _7}\right] \end{aligned}$$

  (42)

• Case 3: If $\chi _{1}\rightarrow \infty$ leading $\beta _{1}\rightarrow \infty$ in the simplified result of Eq. (40), the problem of flow past a solid spheroid is obtained and the drag force is

  $$\begin{aligned} F_D=-\,2\pi \mu _{1} U c\left[ \left( {{{\alpha _{1}}}^{2}}+3{\alpha _{1}}+3\right) - \epsilon \frac{\left( 3 {{{\alpha _{1}}}^{2}}+6 {\alpha _{1}}+3\right) }{5}\right] \end{aligned}$$

  (43)

• Case 4: Substituting $\epsilon =0$ in Eq. (43), it resembles the case of flow past a solid sphere and the drag force is

  $$\begin{aligned} F_D= -2\pi \mu _{1} U c({{\alpha _{1} }^{2}}+3 \alpha _{1} +3) \end{aligned}$$

  (44)

  which supports the work of Krishna Prasad and Bucha given in [37, 39].

6.1.2 Absence of magnetic effect

The following are the results in the absence of MHD effect:

• Case 1: If $\alpha _{1}\rightarrow 0$ and $\chi _2=0$ (i.e., $\beta _{1}=\chi _{1}$) with $\sigma =0$ and $\gamma =1$ in Eq. (40), we get the drag acting on the porous spheroid with continuity of tangential stress is

  $$\begin{aligned} F_D=-\,\frac{12\pi \mu _{1}Uc\chi _{1}^{2}}{3\tanh \chi _{1}-2 {{\chi _{1}}^{3}}-3\chi _{1}}\left[ \tanh \chi _{1} -\chi _{1}+\frac{\epsilon }{5}\frac{(54\chi _{1}\tanh \chi _{1}-(2\chi _{1}^4+27)\tanh ^{2} \chi _{1}-27\chi _{1}^{2})}{(3\tanh \chi _{1}-2 {{\chi _{1}}^{3}}-3\chi _{1})}\right] \end{aligned}$$

  (45)

  which agree with the results of Saad [9, 10] for the drag on porous spheroid in unbounded medium.

• Case 2: If the deformation $\epsilon =0$ together with $\alpha _{1}\rightarrow 0$ and $\chi _2=0$ in Eq. (40), flow past a perfect porous sphere with the effect of stress is obtained as

  $$\begin{aligned} F_D=-\,12\pi \mu _{1}Uc\left[ \frac{\chi _{1}\gamma \left( \gamma \chi _{1}\left( \gamma ^{2}\nu _3-2 \nu _2\right) +\left( 4 \nu _2+\gamma ^{2}\nu _{1}\right) \sigma \right) }{\gamma ^{2}\left( 2\gamma ^{2}\nu _3\chi _{1}^{2}-3\nu _4\right) +\gamma \left( 9\nu _2+2\gamma ^{2}\nu _{1}\right) \sigma \chi _{1}-18\nu _2} \right] \end{aligned}$$

  (46)

• Case 3: From Equation (45) along with $\varepsilon =0$, the flow past a porous sphere with continuity of tangential stress is obtained. The evaluated drag is

  $$\begin{aligned} F_D=-12\pi \mu _{1}Uc\chi _{1}^{2}\left[ \frac{ \tanh \chi _{1} -\chi _{1}}{3\tanh \chi _{1}-2 {{\chi _{1}}^{3}}-3\chi _{1}}\right] \end{aligned}$$

  (47)

  This drag expression is similar to the renowned results by Brinkman [3] and Neale et al. [45].

• Case 4: Considering $\chi _{1}\rightarrow \infty$ (permeability $k=0$) in Eq. (45), the drag expression gives the renowned Stokes flow past a solid spheroid [43]

  $$\begin{aligned} F_D=-6\pi \mu _{1} U c\left[ 1-\frac{\epsilon }{5}\right] \end{aligned}$$

  (48)

• Case 5: If $\epsilon =0$ in Eq.(48), the classical Stokes drag for viscous flow past a solid sphere [43] is obtained

  $$\begin{aligned} F_D=-6\pi \mu _{1} Uc \end{aligned}$$

  (49)

  All the expressions introduced are given in “Appendix B”.

7 Numerical representation and discussion

In this section, an effort is made to visualize the effect of several flow parameters, namely Hartmann number’s $\alpha _{1}$, $\chi _2$ for fluid and porous region, stress jump coefficient $\sigma$, deformation parameter $\epsilon$, non-dimensional permeability parameter $\displaystyle {k_{1}=\frac{c^{2}}{\gamma ^{2}\chi _{1}^{2}}}$, viscosity ratio $\gamma$ on the drag force acting on the porous spheroid. The drag force in the normalized form known as drag coefficient or the coefficient of drag is the ratio of the drag on the porous spheroidal particle to that of the drag acting on a solid sphere in an unbounded medium. Mathematically, it is expressed as

$$\begin{aligned} D_N=\frac{F_D}{-6\pi \mu _{1} Uc} \end{aligned}$$

(50)

The graphical description of the drag coefficient versus permeability parameter showing the influence of several pertinent parameters is plotted in Figs. 2,  3, 4, 5 and 6. In Figs. 2 and 3, the plots relating to the variation of the drag coefficient for a prolate ($\epsilon =-\,0.3$) and an oblate ($\epsilon =0.3$) porous spheroid are shown for increasing values of Hartmann numbers $\alpha _{1}$ and $\chi _2$ acting on the fluid and porous region, respectively.

Examination of these plots shows that $D_N$ is affected by the magnetic field and is a monotonically increasing function of the magnetic parameters or Hartmann number’s $\alpha _{1}$ and $\chi _2$, keeping the other dimensionless parameters fixed. This clearly explains that the flow is restricted due to the applied transverse magnetic field which generates a resisting force called Lorentz force. This force possesses a property to decrease the velocity of the fluid flow. It is interesting to note that the drag is lower for the case of an oblate porous spheroid as compared to the prolate spheroid case. The drag is stronger when the permeability $k_{1}$ of Brinkman’s media is smaller.

Fig. 2

Drag coefficient with permeability $k_{1}$ and Hartmann number $\alpha _{1}$ with $\chi _2=3$, $\sigma =0.3$ and $\gamma =0.5$ for a $\epsilon =-\,0.3$, b $\epsilon =0.3$

Fig. 3

Drag coefficient with permeability $k_{1}$ and Hartmann number $\chi _2$ with $\alpha _{1}=2$, $\sigma =0.1$ and $\gamma =1.5$ for a $\epsilon =-\,0.3$, b $\epsilon =0.3$

The depiction of the drag coefficient for enhancing viscosity ratio $\gamma$ for the case with and without the MHD effect for different deformation values is presented in Fig. 4. It is observed that with increasing values of $\gamma$, the drag coefficient increases. The curves indicating $\alpha _{1}\rightarrow 0$ and $\chi _2\rightarrow 0$ demonstrates the situation when there is no magnetic effect in both fluid and porous regions. The position of without magnetic effect curves is lower to the curves having a magnetic effect. So, it shows that there is an increase in the drag coefficient for increasing $\gamma$ and is higher in the presence of the MHD effect. Moreover, the curve with $\gamma =1$ represents the case when the dynamic viscosity of the fluid region and effective viscosity of the porous region are equal.

Fig. 4

Drag coefficient with permeability $k_{1}$ and viscosity ratio $\gamma$ both in the presence of magnetic effect ($\alpha =3$, $\chi _2=2$) and absence of magnetic effect ($\alpha \rightarrow 0$, $\chi _2\rightarrow 0$) with $\sigma =0.3$ for a $\epsilon =-\,0.3$, b $\epsilon =0.3$

The profile of drag coefficient versus permeability for varying deformation is visualized in Fig. 5. This observation indicates that the resistance to the flow is decreased by increasing deformation parameters. The curve for $\epsilon =0$ represents the flow past a perfectly spherical particle, and it signifies that the drag acting on a porous spherical particle is higher than the drag on an oblate spheroid but comparatively lower than the drag on the prolate spheroidal particle. Comparing both the plots of this figure, we arrive at the conclusion that the curves for the drag force on the porous spheroidal particle under the magnetic force are situated higher than the curve without magnetic force.

Fig. 5

Drag coefficient with permeability $k_{1}$ and deformation $\epsilon$ with $\sigma =0.1$ and $\gamma =1.5$ for a $\alpha _{1}=3$, $\chi _2=3$, b $\alpha _{1}\rightarrow 0$, $\chi _2=0$

Figure 6 presents the behavior of $D_N$ for altering values of stress jump coefficient $\sigma$ corresponding to the porous prolate and oblate spheroid. As proposed by Ochoa-Tapia and Whitaker [6, 7], we have chosen the range of $\sigma$ between $-1$ and 1. For the increase in the stress jump $\sigma$, the drag coefficient noted to be decreasing for considered values of $\alpha _{1}$, $\chi _2$, and $\gamma$. Besides, it is worth paying attention to both the curves of this figure which represents oblate and prolate spheroids. This observation shows the drag forces to be higher on prolate spheroid in relation to that of an oblate spheroid. The discussed figures indicate the decrease in drag with the enhancing permeability.

The numerical results of the altering values of $D_N$ are listed in Tables 1 and 2 for varying range of parameters. In Table 1 the magnitude of drag coefficient for varying deformity in relation to permeability is shown for the flow with and without the MHD effect. It prevails that the resistance to flow is higher for flow under magnetic effect. Further, this resistance is found to be lower for the increasing $\epsilon$.

Table 2 addresses the value of $D_N$ for increasing Hartmann numbers $\alpha _{1}$ and $\chi _2$. It indicates that the higher the effect of magnetic parameters acting on the flow regime, the higher is the drag force acting on the particle with constant values of the rest of the effective parameters. It’s value increases as the permeability parameter increases.

By studying above numerical results, the concept of introducing the magnetic field in the motion of a particle is found to have a dominant effect. Intensifying the magnetic forces leads to magnification in the drag force.

Fig. 6

Drag coefficient with permeability $k_{1}$ and stress jump $\sigma$ with $\alpha _{1}=3$,$\chi _2=3$, $\gamma =1.5$ for a $\epsilon =-\,0.3$, b $\epsilon =0.3$

Table 1 Drag coefficient for flow past porous spheroid with varying deformation for the case with ($\alpha _{1}=3$, $\chi _2=2$) and without ($\alpha _{1}\rightarrow 0$, $\chi _2=0$) MHD effect against permeability keeping other parameters as $\gamma =1.5$, $\sigma =0.1$

Table 2 Drag coefficient for flow past a porous spheroid with varying magnetic effect $\alpha _{1}$ (with $\chi _2=2$) and $\chi _2$ (with $\alpha _{1}=3$) against permeability keeping other parameters as $\epsilon =0.3$, $\gamma =1.5$, $\sigma =0.1$

8 Conclusions

The problem under consideration studies the motion of the conducting viscous fluid past a porous particle of deformed spherical geometry, i.e., spheroidal particle under the transverse external magnetic field. In the Stokes flow regime, Stokes and Brinkman’s equations are used for studying the flow in fluid and porous regions, respectively. With the adequate knowledge of boundary conditions, i.e., continuity of velocities, continuity of normal stress, and the stress jump condition for the tangential stresses, the analytical solution of the problem is presented. The effect of different significant parameters on the dynamics of fluid flow is studied through graphs and tables.

The present analysis is summarized as follows:

• An explicit expression for drag is derived by adopting an analytical approach. The drag expressions for several cases in reduction form are computed, which validates our work.

• The imposed uniform magnetic field acting on the viscous fluid possesses the tendency to retard the fluid velocity leading to an increase in the drag forces. It clearly signifies that the transverse magnetic field has a property to opposes the transport phenomena.

• It is remarkably noticed that the drag coefficient is an increasing function of magnetic parameters $\alpha _{1}, \chi _2$ and a decreasing function of deformation $\epsilon$, stress jump $\sigma$, and permeability $k_{1}$.

• Therefore, we state that on the porous spheroid, the drag is higher for the flow under the magnetic effect.

• The results emphasize that the magnetic field plays an important role in determining the characteristic of fluid flow and the imposed external magnetic field permits to explain more accurately the impact of magnetic forces on the motion of fluid in porous particles.

The flexibility of the presented model permits its application for a varying range of fluids. The current work can be further carried out by using different non-Newtonian fluid flows [16] passing through a homogenous or heterogeneous [46] porous media. The current work deals with the steady flow of fluid, and the unsteady flow problems can also be studied. Thus, there is a vast scope of future investigation, through which significant effects on the fluid flow can be observed.

Appendices

Appendix A

On applying Eqs. (25) to (28) up to first order of $\alpha _{m}$, we obtain the following equations

$$\begin{aligned}&\left[ -1-a_2-S_{2}\ b_2+c_2+T_{2}\ d_2\right] P_{1}(\zeta ) +\alpha _{m}\omega _{1}\left[ \vartheta _{m}{(\zeta )}P_{1}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ -A_n-S_{7}\ B_n+C_n+T_{7}\ D_n\right] P_{n-1}(\zeta )=0 \end{aligned}$$

(A.1)

$$\begin{aligned}&\left[ 2-a_2-S_{3}\ b_2-2\ c_2+T_{3}\ d_2\right] \vartheta _{2}(\zeta )+\alpha _{m}\omega _2\vartheta _{m}{(\zeta )}\vartheta _{2}(\zeta ) \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ (1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n\right] \vartheta _{n}(\zeta )=0 \end{aligned}$$

(A.2)

$$\begin{aligned}&\left[ -\alpha ^{2}+(6+\alpha ^{2}/2)\ a_2+2\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2-2\gamma ^{2}\ T_{4}\ d_2\right] P_{1}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _3\vartheta _{m}(\zeta )P_{1}(\zeta ) +\alpha _{m}\omega _4\left[ P_{1}(\zeta )\vartheta _{m}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] \nonumber \\&\quad +\,\sum _{n=3}^{\infty }\left[ \left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\right] P_{n-1}(\zeta )=0 \end{aligned}$$

(A.3)

$$\begin{aligned}&[-6a_2-S_{5}\ b_2-2\sigma \xi _{1}\gamma \ c_2+\left( \gamma ^{2}\ T_{5}+\sigma \xi _{1}\gamma \ T_{3}\right) \ d_2]\vartheta _{2}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _5\vartheta _2(\zeta )\vartheta _m(\zeta ) +2\alpha _m\omega _6\ P_{1}(\zeta )\vartheta _2(\zeta )P_{m-1}(\zeta )\nonumber \\&\quad +\,\sum _{n=3}^{\infty }[2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n]\vartheta _{n}(\zeta )=0\nonumber \\ \end{aligned}$$

(A.4)

where

$$\begin{aligned} S_{1}= & {} K_{1/2}(\alpha ),\qquad T_{1}=I_{1/2}(\beta ),\\ S_{2}= & {} K_{3/2}(\alpha ),\qquad T_{2}=I_{3/2}(\beta ),\\ S_{3}= & {} S_{2}+\alpha \ S_{1}, \qquad T_{3}=T_{2}-\beta \ T_{1},\\ S_{4}= & {} 3\ S_{2}+\alpha \ S_{1},\qquad T_{4}=3\ T_{2}-\beta \ T_{1},\\ S_{5}= & {} (6+\alpha ^{2})\ S_{2}+2\ \alpha \ S_{1},\qquad T_{5}=(6+\beta ^{2})\ T_{2}-2\ \beta \ T_{1},\\ S_{6}= & {} K_{n-3/2}(\alpha ), \qquad T_{6}=I_{n-3/2}(\beta ),\\ S_{7}= & {} K_{n-1/2}(\alpha ), \qquad T_{7}=I_{n-1/2}(\beta ),\\ S_{8}= & {} (n-1)\ S_{7}+\alpha \ S_{6}, \qquad T_{8}=(n-1)\ T_{7}-\beta \ T_{6},\\ S_{9}= & {} (n+1)\ S_{7}+\alpha \ S_{6}, \qquad T_{9}=(n+1)\ T_{7}-\beta \ T_{6},\\ S_{10}= & {} (2(n^{2}-1)+\alpha ^{2})\ S_{7}+2\ \alpha \ S_{6}, \qquad T_{10}=(2(n^{2}-1)+\beta ^{2})\ T_{10}-2\ \beta \ T_{9},\\ \omega _{1}= & {} -2+a_2+S_{3}\ b_2+2\ c_2-T_{3}\ d_2, \\ \omega _{2}= & {} 2+2\ a_2+\left( 2+\alpha ^{2}\right) \ S_{2}\ b_2-2c_2-\left( 2+\beta ^{2}\right) T_{2}\ d_2, \\ \omega _{3}= & {} -\alpha ^{2}-(\alpha ^{2}+12)\ a_2-4\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2+4\gamma ^{2}\ T_{4}\ d_2, \\ \omega _{4}= & {} -12\ a_2-2\ S_{5}\ b_2+2\gamma ^{2}\ T_{5}\ d_2, \\ \omega _{5}= & {} 18a_2+(6+\alpha ^{2})\ S_{4}\ b_2-2\sigma \xi _{1}\gamma \ c_2-\left( \gamma ^{2}(6+\beta ^{2})\ T_{4}+\sigma \xi _{1}\gamma (2+\beta ^{2})\ T_{2}\right) \ d_2,\\ \omega _{6}= & {} -9a_2- 3\ S_{4}\ b_2+\sigma \xi _{1}\gamma c_2+\left( 3\gamma ^{2}\ T_{4}\ +\sigma \xi _{1}\gamma \ T_{2}\right) \ d_2, \end{aligned}$$

The leading terms of Eqs. (A.1)–(A.4) are equated to zero, and we get

$$\begin{aligned}&-1-a_2-S_{2}\ b_2+c_2+T_{2}\ d_2=0 \end{aligned}$$

(A.5)

$$\begin{aligned}&2-a_2-S_{3}\ b_2-2\ c_2+T_{3}\ d_2=0 \end{aligned}$$

(A.6)

$$\begin{aligned}&-\alpha ^{2}+(6+\alpha ^{2}/2)\ a_2+2\ S_{4}\ b_2+\gamma ^{2}\beta ^{2}\ c_2-2\gamma ^{2}\ T_{4}\ d_2=0 \end{aligned}$$

(A.7)

$$\begin{aligned}&-6a_2-S_{5}\ b_2-2\sigma \xi _{1}\gamma \ c_2+\left( \gamma ^{2}\ T_{5}+\sigma \xi _{1}\gamma \ T_{3}\right) \ d_2=0 \end{aligned}$$

(A.8)

Solving this system of Eqs. (A.5)–(A.8), the values of $a_2$, $b_2$, $c_2$, and $d_2$ are obtained. Now, Eqs. (A.1)–(A.4) are

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ -A_n-S_{7}\ B_n+C_n+T_{7}\ D_n\right] P_{n-1}(\zeta )+\alpha _{m}\omega _{1}\left[ \vartheta _{m}{(\zeta )}P_{1}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] =0 \end{aligned}$$

(A.9)

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ (1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n\right] \vartheta _{n}(\zeta )+\alpha _{m}\omega _2\vartheta _{m}{(\zeta )}\vartheta _{2}(\zeta )=0 \end{aligned}$$

(A.10)

$$\begin{aligned}&\sum _{n=3}^{\infty }\left[ \left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\right] P_{n-1}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _3\vartheta _{m}(\zeta )P_{1}(\zeta ) +\alpha _{m}\omega _4\left[ P_{1}(\zeta )\vartheta _{m}(\zeta )+\vartheta _{2}(\zeta )P_{m-1}(\zeta )\right] =0 \end{aligned}$$

(A.11)

$$\begin{aligned}&\sum _{n=3}^{\infty }[2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n]\vartheta _{n}(\zeta )\nonumber \\&\quad +\,\alpha _{m}\omega _5\vartheta _2(\zeta )\vartheta _m(\zeta ) +2\alpha _m\omega _6\ P_{1}(\zeta )\vartheta _2(\zeta )P_{m-1}(\zeta )=0 \end{aligned}$$

(A.12)

To find the arbitrary constants $A_n$, $B_n$, $C_n$, and $D_n$, we use the following identities

$$\begin{aligned}&\vartheta _{m}{(\zeta )}\vartheta _{2}{(\zeta )}=-\,\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}+\frac{m(m-1)}{(2m+1)(2m-3)}\vartheta _{m}{(\zeta )} -\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(A.13)

$$\begin{aligned}&\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}+P_{m-1}{(\zeta )}\vartheta _{2}{(\zeta )}=-\frac{(m-2)(m-3)}{2(2m-1)(2m-3)}P_{m-3}{(\zeta )}\nonumber \\&\quad +\,\frac{m(m-1)}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}-\frac{(m+1)(m+2)}{2(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(A.14)

$$\begin{aligned}&P_{1}{(\zeta )}\vartheta _{2}{(\zeta )}P_{m-1}{(\zeta )}=-\frac{(m-1)(m-2)(m-3)}{2(2m-1)(2m-3)}\vartheta _{m-2}{(\zeta )}+\frac{m(m-1)}{2(2m+1)(2m-3)}\vartheta _{m}{(\zeta )}+\frac{m(m+1)(m+2)}{2(2m-1)(2m+1)}\vartheta _{m+2}{(\zeta )} \end{aligned}$$

(A.15)

$$\begin{aligned}&\vartheta _{m}{(\zeta )}P_{1}{(\zeta )}=\frac{(m-2)}{(2m-1)(2m-3)}P_{m-3}{(\zeta )}+\frac{1}{(2m+1)(2m-3)}P_{m-1}{(\zeta )}-\frac{(m+1)}{(2m-1)(2m+1)}P_{m+1}{(\zeta )} \end{aligned}$$

(A.16)

In solving Eqs. (A.9)–(A.12), it is observed that

$$\begin{aligned} A_n=B_n=C_n=D_n=0 \quad \text{ for } \quad n\ne m-2,m,m+2 \end{aligned}$$

(A.17)

For $n=m-2,m,m+2$, we have the following system of equations

$$\begin{aligned}&-\,A_n-S_{7}\ B_n+C_n+T_{7}\ D_n+\omega _{1} \overline{a}_n=0 \end{aligned}$$

(A.18)

$$\begin{aligned}&(1-n)A_n-S_{8}\ B_n-n\ C_n+T_{8}\ D_n+\omega _2 \overline{a}_n=0 \end{aligned}$$

(A.19)

$$\begin{aligned}&\left( 2(n+1)+{\alpha ^{2}}/n\right) \ A_n+2\ S_{9}\ B_n+\left( 2\gamma ^{2}(n-2)+\frac{\gamma ^{2}\beta ^{2}}{(n-1)}\right) \ C_n -2\gamma ^{2}\ T_{9}\ D_n\nonumber \\&\quad +\,\omega _3 \overline{c}_n+\omega _4 \overline{a}_n=0 \end{aligned}$$

(A.20)

$$\begin{aligned}&2(1-n^{2})A_n-S_{10}\ B_n+\left( n\gamma (2\gamma (n-2)-\sigma \xi _{1})\right) C_n+ \left( \gamma ^{2}\ T_{10}+\sigma \xi _{1}\gamma \ T_{8}\right) D_n\nonumber \\&\quad +\,\omega _5 \overline{a}_n+2\omega _6 \overline{b}_n=0 \end{aligned}$$

(A.21)

where

$$\begin{aligned} \overline{a}_{n}= & {} \frac{n(n-1)\alpha _{n}}{(2n+1)(2n-3)}, \end{aligned}$$

(A.22)

$$\begin{aligned} \overline{b}_{n}= & {} \frac{n(n-1)\alpha _{n}}{2(2n+1)(2n-3)}, \end{aligned}$$

(A.23)

$$\begin{aligned} \overline{c}_{n}= & {} \frac{\alpha _{n}}{(2n+1)(2n-3)}. \end{aligned}$$

(A.24)

Solving Eqs. (A.18)–(A.21) gives the expressions for $A_n$, $B_n$, $C_n$, and $D_n$ when $n=m-2,m,m+2$.

Appendix B

The symbols present in Eqs. (41)–(47) are defined by

$$\begin{aligned} \delta _{1}= & {} \alpha _{1}^{2}+3\alpha _{1}+3, \\ \delta _2= & {} {\alpha _{1}}^{2}+3\alpha _{1}-9, \\ \delta _3= & {} \alpha _{1}^{2}+9\alpha _{1}+9, \\ \delta _4= & {} \alpha _{1}^{2}+\alpha _{1}+9, \\ \delta _5= & {} {\alpha _{1}}^{2}+7 \alpha _{1}+3, \\ \delta _6= & {} {\alpha _{1}}^{3}+3 \alpha _{1}^{2}+6{\alpha _{1}}+6, \\ \delta _7= & {} {\alpha _{1}}^{3}+3 \alpha _{1}^{2}+18{\alpha _{1}}+18, \\ \delta _8= & {} \beta _{1}^4-3\beta _{1}^{2}-12, \\ \delta _9= & {} \beta _{1}^{2}+3, \\ \delta _{10}= & {} \beta _{1}^{2}+2, \\ \Delta _{1}= & {} 4 \left( \sinh \beta _{1} \ \delta _9-3 {\beta _{1}}\ \cosh \beta _{1}\right) +\gamma ^{2} \left( \sinh \beta _{1} \ \delta _8-{\beta _{1}}\ \left( \beta _{1}^{2}-12\right) \ \cosh \beta _{1}\right) , \\ \Delta _2= & {} \gamma ^{4} \left( 3 \sinh \beta _{1}\delta _{10}-\beta _{1}\ \left( \beta _{1}^{2}+6\right) \ \cosh {\beta _{1}}\right) , \\ \Delta _3= & {} \sinh \beta _{1}\delta _9-3 \beta _{1} \cos \beta _{1} \\ \Delta _4= & {} \gamma ^{3}\left( \sinh \beta _{1}\delta _8-{\beta _{1}}\left( \beta _{1}^{2}-12 \right) \cosh {\beta 1}\right) , \\ \Delta _5= & {} \sinh {\beta _{1}}\ \left( 3 {\beta 1}^{2}{\delta _5}+6{\delta _3}-2 \left( {\alpha _{1}}+3\right) \ {\beta _{1}}^{4}\right) -\cosh {\beta _{1}}\ \left( 6{\delta _3}+{\beta _{1}}^{2}{\delta _2}\right) {\beta _{1}}, \\ \nu _{1}= & {} \left( \chi _{1}^4-3 {\chi _{1}}^{2}-12\right) \sinh \chi _{1} -{\chi _{1}}\ \left( \chi _{1}^{2}-12\right) \ \cosh \chi _{1}, \\ \nu _2= & {} \left( \chi _{1}^{2}+3\right) \sinh \chi _{1} -3{\chi _{1}} \cosh \chi _{1}, \\ \nu _3= & {} 3\left( \chi _{1}^{2}+2\right) \ \sinh \chi _{1} -{\chi _{1}}\ \left( \chi _{1}^{2}+6\right) \ \cosh \chi _{1}, \\ \nu _4= & {} \left( 2 \chi _{1}^4-3 {\chi _{1}}^{2}-18\right) \ \sinh \chi _{1} -3{\chi _{1}}\ \left( \chi _{1}^{2}-6\right) \ \cosh \chi _{1}. \end{aligned}$$