Introduction

The study of heat transfer fascinates the researchers to emphasize several engineering domains, especially in fluid flow. For example, better plastic and polymer want a higher rate of heat transfer. They are using nanofluids as an advanced method for developing heat transfer. These fluids are engineered colloidal suspensions of nanoparticles in a base fluid. In the novel, nanofluids are formed by different kinds of nanoparticles. The representation of nano liquids regarding heat transport improvement over reduced particles of nanometer was conveyed through Choi [1]. Hsiao [2] studied the MHD stagnation-point flow of nano liquid through slip boundary conditions on the stretched sheet. Unsteady boundary layer movement of Maxell nanofluid flow in heat source or sink act reported in Ahmed et al. [3]. This study exposed that heat source and radiation enhances the temperature field. Acharya [4] implement a model this studies the result of Brownian movement, thermophoresis, and convective flow of nanofluids. More studies are in [5,6,7,8,9,10,11,12,13,14,15,16,17,18].

Nowadays, nanofluids are notorious for quickly engineer fluids accomplished with regular fluid and nanomaterials (1–100 nm). This type of fluids has more excellent thermal conductivity and heat transfer coefficients than a single chapter associated with conventional fluids. An innovative kind of nanofluid made by mixing two different types of nanomaterials called composite or hybrid particles in the regular fluid is known as hybrid or composite nanofluid. Hybrid nanofluid combines the physical and chemical properties of changed nanofluids instantaneously and offers similar stage properties. These fluids are realistically a new nanofluid class with several potential applications in entirely heat transport fields, i.e., acoustics, manufacturing, defense, microfluidics, transportation, naval structures, etc. Enhancement of hybrid-nanofluid with relative stability and thermal conductivity increased. It is noteworthy and guides sustainability and minimization/maximization of energy, increasing efficiency (Das [19]). Sarkar et al. [20] and Sidik et al. [21] have summarized the previous and present study and enrichment related to the preparation of hybrid nanofluids, the effects of thermophysical of hybrid liquids, recent applications of hybrid-nanofluid. With the impacts of viscous dissipation and Joule heat, Khan et al. [22] revealed thermal properties of (ethylene glycol-based) \(Si{O}_{2}-Mo{S}_{2}\) hybrid nanofluid. Influence of water-based hybrid nanofluid through mixing nanoparticles \((Mo{S}_{2}\) and \(Si{O}_{2})\) with thermal radiation was estimated by Khan et al. [23]. Nadeem et al. [24] conducted a numerical treatment of the hybrid nanofluid over a curved surface with suction/injection. Hanif et al. [25] accomplished a test on thermal performance and heat transfer in magnetic impact on hybrid nanofluid flow in a porous cone. This experiment's duration detected an augmentation in thermal efficiency and the heat transfer rate of hybrid nanofluid via growing the radiation impact. The related literature can be found in [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47].

Magnetohydrodynamics (MHD) allows describing the fluid flow and electro-magnetism characteristics. Precisely this is a proper technique to appropriating fluid flow significances which electrically conducted by the magnetic field. Flow and heat transport procedure for a viscous fluid in the occurrence of the magnetic field takes massive proposal in various engineering and high-tech domains like MHD power generators, petroleum industries, noteworthy responses in nuclear reactors cooling, the area of plasma, extractions of energy in the geothermal area, acclimatization the structure of boundary layer. Several artificial techniques have been established and affirmed to control the layout of the boundary layer structure. Yet, out of that, the applicable code of MHD is an effective method for flow transfer in the required path by changing the boundary layer's shape. In light of the flow entity and heat transfer process, MHD flow's characteristic features attracted several scientists and more general engineers in the last few decades. Kotha et al. [48] studied the impact of bioconvection on MHD nanofluid flow with gyrotactic microorganisms. The studies related to the flow features in a magnetic field could be seen in [49,50,51,52].

Literature review approves the study of fluid flow on the curved surface have been hardly evaluated. Models of 2D fluid working on the curved surface are the fluid boundary, similar to aerosol droplets, foam bubbles, or molecular films. Similarly, a real-life situation fluid flow on the bent surface is the soap films are widely applied to inspect traditional two-dimensional hydro-dynamic augmentation. Additional scientific application of coiled body discovered over the bent jaw of stretchy accumulating apparatus in industries. A microbiological example is found over the fluid motion done lipid bilayer films over a prominent cell member. Lipid bilayers disclose hydromagnetic features dispersion and viscosity, and random examinations affirm such outcomes—viscous fluid flow overstretched bent sheet studied by Sajid et al. [53]. The problem of MHD on heat transfer over a bent surface was examined by Abbas et al. [54]. Entropy analysis for copper—alumina hybrid nanofluid over curved texture was carried out by Afridi et al. [55].

Original fluids, including two dense ingredients distributed in a convectional fluid, were developed and intensely have been widely used in recent years. These fluids are called hybrid nanofluids, tend to increase thermal conductivity and lead to heat transport augmentation in heat exchangers. Therefore, the present work aims to analyze the magnetic field on \(Cu-{Fe}_{3}{O}_{4}\)/water hybrid nanofluid over a curved surface, but it has not been reported yet. Furthermore, heat transfer is discussed in the existence of viscous dissipation. Curvilinear coordinates are chosen for the mathematical formulation, and parallel study is working to facilitate the governing equations. Computational evaluation executed on a summarized system utilizing the fourth-fifth order R-K-F method in software MATLAB. We, too, emphasized the effects of injection/suction parameters, Curvilinear parameter, magnetic parameter, and Eckert number on the hybrid nanofluid over tables and graphs. Expressions of the friction and Nusselt numbers were demonstrated to interpret the properties of the flow. The new outputs of present scrutiny might be significant in enlightening exploration and plastic, ceramic, and polymer industries.

Mathematical Formulation

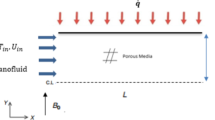
A curved surface is predicted, which is overflown by a viscous, incompressible, steady hybrid nanofluid. The surface radius \({R}_{1}\), curvilinear composition \({r}_{1}\) and \({s}_{1}\). Which is supposed to be in a curved manner within the spiral configuration. The curved texture stretching speed is \({u}_{w}=a{s}_{1}\) in \({s}_{1}\)—direction; so, the stream formulates boundary layer over \({r}_{1}\)—direction. Here, \({R}_{1}\) shows radius of stretched surface, furthermore, expresses the surface profile; i.e., raised values of \({R}_{1}\) the surface changed to flat. The geometrical representation of our recent study is disclosed in Fig. 1. Now, hybrid nanofluid is a small configuration of copper \((Cu)\) and Ferrous \(\left({Fe}_{3}{O}_{4}\right)\) including water. Uniform magnetic field (\({B}_{0}\)) generally working to the surface.

Fig. 1
figure 1

Physical model and coordinate system

Full size image

We depended on certain suppositions all over the investigation, like the nonappearance of Joule heating and heat radiation. Additionally, the slip mechanism and nanoparticles chemical reactions are overlooked. Nanofluids are in the equilibrium position. In light of the above concept, the necessary driving conditions of an appropriate framework are organized as follows ((Abbas et al. [54] and Nadeem et al. [24]):

$$ \frac{\partial }{{\partial r_{1} }}\left\{ {\left( {r_{1} + R_{1} } \right)v} \right\} + R_{1} \frac{{\partial u_{1} }}{{\partial s_{1} }} = 0, $$
(1)
$$ \frac{{u_{1}^{2} }}{{r_{1} + R_{1} }} = \frac{1}{{\rho_{hnf} }}\frac{\partial p}{{\partial r_{1} }}, $$
(2)
$$ \begin{aligned} &v_{1} \frac{{\partial u_{1} }}{{\partial r_{1} }} + \frac{{R_{1} }}{{r_{1} + R_{1} }}\left( {u_{1} \frac{{\partial u_{1} }}{{\partial s_{1} }}} \right) + \frac{1}{{r_{1} + R_{1} }}\left( {u_{1} v_{1} } \right) \\ & = - \frac{1}{{\rho_{hnf} }}\frac{{R_{1} }}{{r_{1} + R_{1} }}\frac{\partial p}{{\partial s_{1} }} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ & \quad + \frac{{\mu_{hnf} }}{{\rho_{hnf} }}\left( {\frac{{\partial^{2} u_{1} }}{{\partial r_{1}^{2} }} + \frac{1}{{r_{1} + R_{1} }}\frac{{\partial u_{1} }}{{\partial r_{1} }} - \frac{{u_{1} }}{{\left( {r_{1} + R_{1} } \right)^{2} }}} \right) - \frac{{\sigma_{hnf} B_{0}^{2} }}{{\rho_{hnf} }}u_{1} , \\ \end{aligned} $$
(3)
$$ v_{1} \frac{{\partial T_{1} }}{{\partial r_{1} }} + \frac{{R_{1} }}{{r_{1} + R_{1} }}\left( {u_{1} \frac{{\partial T_{1} }}{{\partial s_{1} }}} \right) = \frac{{\kappa_{hnf} }}{{\left( {\rho C_{p} } \right)_{hnf} }}\left( {\frac{{\partial^{2} T_{1} }}{{\partial r_{1}^{2} }} + \frac{1}{{r_{1} + R_{1} }}\frac{{\partial T_{1} }}{{\partial r_{1} }}} \right) + \mu_{hnf} \left( {\frac{{\partial u_{1} }}{{\partial r_{1} }} - \frac{{u_{1} }}{{r_{1} + R_{1} }}} \right)^{2} , $$
(4)

Relevant boundary conditions are

$$ u_{1} = as_{1} ,\,v = - v_{w} ,\,\,T_{1} = T_{w} ,\;\;{\text{at}}\;\;r_{1} = 0, $$
(5)
$$ u_{1} \to 0,\,\,\frac{{\partial u_{1} }}{{\partial r_{1} }} \to 0,\,\,T_{1} \to T_{\infty } ,\;{\text{as}}\;r_{1} \to \infty , $$
(6)

where \({u}_{1}\) and \({v}_{1}\) represents Velocities in the direction of \({s}_{1}\), and \({r}_{1}\). \(p\) designates nanofluid pressure, \({v}_{w}>0\) and \({v}_{w}<0\) represents suction and injection velocity, respectively.

In this present problem, we continued jointly for hybrid nanofluid and usual nanofluid. namely \(Cu\) and \({Fe}_{3}{O}_{4}\).\(Cu\) for usual nanofluid and \({Fe}_{3}{O}_{4} for\) hybrid nanofluid. Table 1 shows the hydrothermal relations perfectly. We have gathered the principal equations using the thermo-physical model hybrid nanofluid discovered through Takabi et al. [31]. It's far essential to cope with that introducing \({\phi }_{2}=0.01 l\) eads to the nanofluid model conveyed by, Oztop and Abu-Nada [17] and Maxwell [18]. These equations are as follows

$$ \begin{aligned} \mu_{hnf} & = \frac{{\mu_{f} }}{{\left( {1 - \varphi_{1} } \right)^{2.5} \left( {1 - \varphi_{2} } \right)^{2.5} }}, \\ \rho_{hnf} & = \left( {1 - \varphi_{2} } \right)\left[ {\left( {1 - \varphi_{1} } \right)\rho_{f} + \varphi_{1} \rho_{s1} } \right] + \varphi_{2} \rho_{s2} , \\ \frac{{\sigma_{hnf} }}{{\sigma_{nf} }} & = \frac{{\sigma_{s2} + 2\sigma_{nf} - 2\varphi_{2} \left( {\sigma_{nf} - \sigma_{s2} } \right)}}{{\sigma_{s2} + 2\sigma_{nf} + \varphi_{2} \left( {\sigma_{nf} - \sigma_{s2} } \right)}}, \\ {\text{where}}\;\frac{{\sigma_{nf} }}{{\sigma_{f} }} & = \frac{{\sigma_{s1} + 2\sigma_{f} - 2\varphi_{1} \left( {\sigma_{f} - \sigma_{s1} } \right)}}{{\sigma_{s1} + 2\sigma_{f} + \varphi_{1} \left( {\sigma_{f} - \sigma_{s1} } \right)}}, \\ \frac{{\kappa_{hnf} }}{{\kappa_{nf} }} & = \frac{{\kappa_{s2} + (n - 1)\kappa_{nf} - \left( {n - 1} \right)\varphi_{2} \left( {\kappa_{nf} - \kappa_{s2} } \right)}}{{\kappa_{s2} + (n - 1)\kappa_{nf} + \varphi_{2} \left( {\kappa_{nf} - \kappa_{s2} } \right)}} \\ {\text{where}}\;\frac{{\kappa_{nf} }}{{\kappa_{f} }} & = \frac{{\kappa_{s1} + (n - 1)\kappa_{f} - \left( {n - 1} \right)\varphi_{1} \left( {\kappa_{f} - \kappa_{s1} } \right)}}{{\kappa_{s1} + (n - 1)\kappa_{f} + \varphi_{1} \left( {\kappa_{f} - \kappa_{s1} } \right)}}, \\ \left( {\rho C_{p} } \right)_{hnf} & = \left( {1 - \varphi_{2} } \right)\left( {\rho C_{p} } \right)_{nf} + \varphi_{2} \left( {\rho C_{p} } \right)_{s2} , \\ {\text{where}}\;\left( {\rho C_{p} } \right)_{nf} & = \left( {1 - \varphi_{1} } \right)\left( {\rho C_{p} } \right)_{f} + \varphi_{1} \left( {\rho C_{p} } \right)_{s1} . \\ \end{aligned} $$
(7)
Table 1 Thermal and mechanical properties of water and nanoparticles (Hanif et al. [32])
Full size table

By using transformations, the governing momentum and energy equations changed into the coupled nonlinear equations (Sajid et al. [53], Acharya [4]):

$$ \begin{aligned} \eta & = \sqrt {\frac{a}{{\nu_{f} }}} r_{1} ,\,u_{1} = as_{1} \tilde{f}^{\prime}(\eta ),\,\,v = - \frac{{R_{1} }}{{r_{1} + R_{1} }}\sqrt {a\nu_{f} } \tilde{f}(\eta ),\,\, \\ \tilde{\theta }(\eta ) & = \frac{{T_{1} - T_{\infty } }}{{T_{w} - T_{\infty } }},\,p = \rho_{f} \left( {as_{1} } \right)^{2} \tilde{P}(\eta ), \\ \end{aligned} $$
(8)

Here \(\eta \) directs as similarity variable.

Using the change in (8), governing Eqs. (1)–(4) along the boundary conditions in (5)-(6) are converted into the form as follows.

$$ \tilde{P^{\prime}} = \frac{{\tilde{f^{\prime}}^{2} }}{\eta + K}, $$
(9)
$$ \begin{aligned} \frac{2K}{{\eta + K}}\tilde{P} & = \frac{{A_{1} }}{{A_{2} }}\left[ {\tilde{f^{\prime \prime \prime}} + \frac{{\tilde{f^{\prime\prime}}}}{\eta + K} - \frac{{\tilde{f^{\prime}}}}{{\left( {\eta + K} \right)^{2} }}} \right] - \frac{K}{\eta + K}\tilde{f}^{\prime 2} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \quad + \frac{K}{\eta + K}\tilde{f^{\prime}}\,\tilde{f^{\prime\prime}} + \frac{K}{{\left( {\eta + K} \right)^{2} }}\tilde{f}\,\tilde{f^{\prime}} - \frac{{A_{3} }}{{A_{2} }}M\,\tilde{f^{\prime}}, \\ \end{aligned} $$
(10)
$$ \frac{1}{\Pr }\frac{{A_{4} }}{{A_{5} }}\left( {\tilde{\theta^{\prime\prime}} + \frac{1}{\eta + K}\tilde{\theta^{\prime}}} \right) + \frac{K}{\eta + K}\tilde{f}\,\tilde{\theta^{\prime}} + A_{1} \Pr Ec\left( {\tilde{f^{\prime\prime}} - \frac{{\tilde{f^{\prime}}}}{\eta + K}} \right)^{2} = 0. $$
(11)

Prime reflects the differentiation w. r. t. \({\varvec{\eta}}\) and

$$ A_{1} = \frac{{\mu_{hnf} }}{{\mu_{f} }},\,\,A_{2} = \frac{{\rho_{hnf} }}{{\rho_{f} }},\,\,A_{3} = \frac{{\sigma_{hnf} }}{{\sigma_{f} }},\,\,A_{4} = \frac{{\kappa_{hnf} }}{{\kappa_{f} }},\,\,A_{5} = \frac{{\left( {\rho C_{p} } \right)_{hnf} }}{{\left( {\rho C_{p} } \right)_{f} }}. $$

Corresponding boundary conditions are transformed as:

$$ f(0) = S,\,f^{\prime}(0) = 1,\,\,\theta (0) = 1,\;\;{\text{at}}\;\;\eta = 0, $$
(12)
$$ f^{\prime} \to 0,\,\,f^\prime\prime \to 0,\,\,\theta \to 0,\;\;{\text{as}}\;\;\eta \to \infty , $$
(13)

where \(=-{v}_{w}\sqrt{a{\nu }_{f}}\), \(S>0\) indicates suction and \(S<0\) injections, \(M=\frac{{\sigma }_{f}{B}_{0}^{2}}{{\rho }_{f}a}\) is the magnetic parameter, \(Pr=\frac{{\mu }_{f}{C}_{p}}{{\kappa }_{f}}\) is the Prandtl number and \(Ec=\frac{{u}_{w}^{2}}{{C}_{p}({T}_{w}-{T}_{\infty })}\) is the Eckert number.

Eliminating the pressure term form (9) and (10), we have

$$ \begin{aligned} & f^{iv} + \frac{2}{\eta + K}\tilde{f^{\prime\prime\prime}} - \frac{1}{{\left( {\eta + K} \right)^{2} }}\tilde{f^{{\prime\prime}}} + \frac{1}{{\left( {\eta + K} \right)^{3} }}\tilde{f^{\prime}} \\ & \quad + \frac{{A_{2} }}{{A_{1} }}\left[ \begin{aligned} \frac{K}{\eta + K}\left( {\tilde{f}\,\tilde{f^{\prime\prime\prime}} - \tilde{f^{\prime}}\,\tilde{f^{\prime\prime}}} \right) - \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {\tilde{f^{\prime}}^{2} - \tilde{f}\,\tilde{f^{\prime\prime}}} \right) \hfill \\ - \frac{K}{{\left( {\eta + K} \right)^{3} }}\tilde{f}\,\tilde{f^{\prime}} - \frac{{A_{3} }}{{A_{2} }}M\left( {\tilde{f^{\prime\prime}} + \frac{{\tilde{f^{\prime}}}}{\eta + K}} \right) \hfill \\ \end{aligned} \right] = 0, \\ \end{aligned} $$
(14)

The physical quantities of interest are the frictional coefficient, and Nusselt number are defined as:

$$ C_{f} = \frac{{\tau_{w} }}{{\rho_{hnf} \left( {as_{1} } \right)^{2} }},\,\,Nu = \frac{{s_{1} q_{w} }}{{\kappa_{f} (T_{w} - T_{\infty } )}}, $$
(15)

Here \(\tau_{w} = \mu_{hnf} \left( {\frac{{\partial u_{1} }}{{\partial r_{1} }} - \frac{{u_{1} }}{{r_{1} + R_{1} }}} \right)_{{r_{1} = 0}} ,\) and \(q_{w} = - \kappa_{hnf} \left( {\frac{{\partial T_{1} }}{{\partial r_{1} }}} \right)_{{r_{1} = 0}} .\)

Introducing the dimensionless variables as in (8), we obtain the reduced frictional coefficient and Nusselt number as follows:

$$ \begin{aligned} Cf_{{r_{1} }} & = \sqrt {{\text{Re}}_{{s_{1} }} } C_{f} = A_{1} \left( {\tilde{f^{\prime\prime}}(0) - \frac{1}{K}\tilde{f^{\prime}}(0)} \right), \\ Nu_{{r_{1} }} & = \frac{Nu}{{\sqrt {{\text{Re}}_{{s_{1} }} } }} = - \frac{{\kappa_{hnf} }}{{\kappa_{f} }}\tilde{\theta^{\prime}}(0), \\ \end{aligned} $$
(16)

where \({Re}_{{s}_{1}}=\frac{a{s}_{1}^{2}}{{\nu }_{f}}\) is the local Reynold number.

Computational Procedure

The nonlinear coupled compact system of Eqs. (14)–(11) go together with boundary conditions (12)–(13) is distributed using the steady and recognized process of shooting technique rooted with R-K-F method. Initially, the higher-order differential equations were reduced into first-order differential equations by presenting the following variables:

$$ \left( {\begin{array}{*{20}c} f \\ {f^{\prime}} \\ {f^{\prime\prime}} \\ {f^{\prime \prime \prime}} \\ \theta \\ {\theta^{\prime}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\Psi_{1} } \\ {\Psi^{\prime}_{1} = \Psi_{2} } \\ {\Psi^{\prime}_{2} = \Psi_{3} } \\ {\Psi^{\prime}_{3} = \Psi_{4} } \\ {\Psi_{5} } \\ {\Psi^{\prime}_{5} = \Psi_{6} } \\ \end{array} } \right), $$
(17)

BVP is changed into IVP by familiarizing initial conditions in terms of unknown named as shooting parameters:

$$ \left( {\begin{array}{*{20}c} {\Psi_{1} (0)} \\ {\Psi_{2} (0)} \\ {\Psi_{3} (0)} \\ {\Psi_{4} (0)} \\ {\Psi_{5} (0)} \\ {\Psi_{6} (0)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} S \\ 1 \\ {C_{1} } \\ {C_{2} } \\ 1 \\ {C_{3} } \\ \end{array} } \right). $$
(18)

first-order differential equation expressed in the reduced form as:

$$ \left( {\begin{array}{*{20}c} {\Psi^{\prime}_{1} } \\ {\Psi^{\prime}_{2} } \\ {\Psi^{\prime}_{3} } \\ {\Psi^{\prime}_{4} } \\ {\Psi^{\prime}_{5} } \\ {\Psi^{\prime}_{6} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\Psi_{2} } \\ {\Psi_{3} } \\ {\Psi_{4} } \\ { - \frac{2}{\eta + K}\Psi_{4} + \frac{1}{{\left( {\eta + K} \right)^{2} }}\Psi_{3} - \frac{1}{{\left( {\eta + K} \right)^{3} }}\Psi_{2} - \frac{{A_{2} }}{{A_{1} }}\left[ \begin{gathered} \frac{K}{\eta + K}\left( {\Psi_{1} \Psi_{4} - \Psi_{2} \Psi_{3} } \right) \hfill \\ + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {\Psi_{1} \Psi_{3} - \Psi_{2}^{2} } \right) \hfill \\ - \frac{K}{{\left( {\eta + K} \right)^{3} }}\Psi_{1} \Psi_{2} \hfill \\ - \frac{{A_{3} }}{{A_{2} }}M\left( {\Psi_{3} + \frac{{\Psi_{2} }}{\eta + K}} \right) \hfill \\ \end{gathered} \right]} \\ {\Psi_{6} } \\ { - \Pr \frac{{A_{5} }}{{A_{4} }}\left[ {\left( {\frac{K}{\eta + K}} \right)\Psi_{1} \Psi_{6} + A_{1} Ec\left( {\Psi_{3} - \frac{{\Psi_{2} }}{\eta + K}} \right)^{2} } \right] - \frac{1}{\eta + K}\Psi_{6} } \\ \end{array} } \right) $$
(19)

Shooting parameters \({C}_{1}, {C}_{2}\) and \({C}_{3}\) are calculated by employing the Newton technique until boundary conditions, i.e., \({f}^{{\prime}}\left(\eta \right)\to 0,{f}^{{{\prime\prime}}}\left(\eta \right)\to 0, \theta (\eta )\to 0,\) as \(\eta \to \infty \) are reached against each group of parameters up to the sixth decimal place. A computational study is accomplished in MATLAB.

Code of Authentication

Prevent the accuracy of our current study, and we have calculated the values of skin friction coefficient \(({Cf}_{r})\) for several values of curvature factor \(K\) and suction/injection in usual fluids. Employed values in Table 2 and associated those values with Mehmood et al. [14] and Abbas et al. [54]. It approves our desired accuracy. Thus, the code of authentication is acceptable.

Table 2 The comparative numerical values of skin friction coefficient \(({C}_{f})\) for regular fluids with our present results when \(M=0\)
Full size table

Results and Discussion

A numerical analysis has been performed in this work to investigate the impact of dynamic parameters on both hybrid nanofluid and usual nanofluid hydrothermal behavior. Needful graphs and tables are disclosing the same. Frictional factor, heat transfer numerical results are computed and studied. An elaborated comparative study between usual nanofluid and hybrid nanofluid focuses on investigating the above fluids' hydrothermal variations. \(K=5.0, M=2.0, Ec=0.1 ,\mathrm{Pr}=6.2, {\phi }_{1}={\phi }_{2}=0.1\) are few parametric values that are used in the problem. To study the variations of engineering quantities more realistically, many have applied the regression slope method\(({{\varvec{S}}{\varvec{l}}}_{{\varvec{p}}})\). According to Koriko et al. [15], Afridi et al. [33], and Acharya [4], this method is used to determine the discrimination between the impact of various parameters.

The parametric analysis about the transference of fluid mixture (a mixture of biofluid, \(Cu\) and \({Fe}_{3}{O}_{4}\)) is investigated, and outputs are exhibited in Figs. 2, 3, 4, 5, 6, 7, 8 and 9. Biofluid copper mixture is eventually known as nanofluid, whereas a combination of \(Cu, {Fe}_{3}{O}_{4},\) and biofluid is called hybrid nanofluid. The curvature parameter's impact on the velocity of nanofluid and hybrid nanofluid is shown in Fig. 2. Figure 2a. These show the suction values, and Fig. 2b shows the injection values for different parameters. Solid and dashed curves define the velocity profile of nanofluid and hybrid nanofluid. For higher values of K, both convection and hybrid nanofluid flow velocity are enhanced, and the velocity of hybrid nanofluid is higher than the usual nanofluid. Physically, the dimensionless definition of \(K=R\sqrt{\frac{a}{{\nu }_{f}}}\) permit us to predict that hardly any kinematic viscosity will be experienced for increased curvature factor due to which the fluid flows without much effort. (The deviation of the curves in each curve of injection is much less when noticed.

Fig. 2
figure 2

a Effect of \(K\) on velocity for suction. b Effect of \(K\) on velocity for injection

Full size image
Fig. 3
figure 3

a Effect of \(M\) on velocity for suction. b Effect of \(M\) on velocity for injection

Full size image
Fig. 4
figure 4

Effect of \({\phi }_{2}\) on velocity for suction and injection

Full size image
Fig. 5
figure 5

a Effect of \(K\) on pressure for suction. b Effect of \(K\) on pressure for injection

Full size image
Fig. 6
figure 6

a Effect of \(M\) on pressure for suction. b Effect of \(M\) on pressure for injection

Full size image
Fig. 7
figure 7

a Effect of \(K\) on temperature for suction. b Effect of \(K\) on temperature for injection

Full size image
Fig. 8
figure 8

a Effect of \(M\) on temperature for suction. b Effect of \(M\) on temperature for injection

Full size image
Fig. 9
figure 9

Effect of \({\phi }_{2}\) on temperature for suction and injection

Full size image

Figure 3a represents the magnetic effect on the hydrothermal variation of condensed nanofluid and hybrid nanofluid for suction. Figure 3b shows the same for injection. In the presence of a magnetic field, the fluid velocity is noted to be declined in both cases. This phenomenon is due to Lorentz pressure, which emerges from the collaboration of electric and magnetic fields during a fluid flow, which is conducted electrically. The produced Lorentz force controls the fluid's motion in the boundary layer and reduces the momentum's thickness in the boundary layer. Hence, the rise in M diminishes the velocity of nanofluid and hybrid nanofluids. Figure 4 shows the impact of different values of nanoparticles, volume fraction \({\phi }_{2}\) on hybrid nanofluid velocity profiles. In both, we noticed that suction and injection hybrid nanofluid velocity is enhanced for greater values of nanosized solid particles. Physically, the nanoparticle volume fractions were added to reduce the viscosity of a convectional regular fluid (water in the present investigation). Hence, the boundary layer velocity is enhanced.

The non-dimensional curvature radius \(K\) on the pressure \(P\) is seen in Fig. 5a in nanofluid and hybrid nanofluids for suction and Fig. 5b for injection. Previous studies of [Sajid et al. [39], Ahmed and Khan [16]] got the same effect. This figure shows a decrease in \(K\) causes an increase in the pressure magnitude inside the boundary layer for convectional nanofluid and hybrid nanofluids. The pressure profile becomes zero when the curved surface in this figure is decreased to the planner surface for greater values of \(K,\) we conclude that the smaller values of \(K\), the more curves of the surface. The curvature of the surface causes secondary flow due to the fluid flow's curvilinear nature under the act of centrifugal force as the fluid particles cross the curved track along the sheet's surface. The secondary flow is hence superimposed on the primary flow due to the increase in the velocity field. Though the pressure variation is remarkably noticed inside the boundary layer, changes in pressure cannot be neglected in a curved surface as frequently done for the flat stretching sheet. Figure 6 shows a decreasing behavior in the magnitude of pressure profile inside the boundary and associated boundary layer for the higher values of the magnetic parameter for suction and injection cases. A similar effect was observed by Abbas et al. [40]. Furthermore, the magnitude in pressure for hybrid nanofluid rises more than in convectional nanofluid.

Figure 7a demonstrates the curvature impact on the temperature in both usual nanofluid and hybrid nanofluid for suction; Fig. 7b gives similar outputs for the case of injection. Solid curves represent the temperature profiles of usual nanofluid, and temperature profiles of hybrid nanofluid are illustrated in dashed curves. For amplifying the curvature factor, the temperature is minimized. Hybrid nanofluid shows high thermal behavior. Double metallic nanoparticles within the host fluid are absorbed by hybrid nanofluid as expected. Figure 7b shows that more liquid entry inside the boundary layer shows more different temperature outlines than suction. Thus, thermal performance becomes more noticeable.

Figure 8a, 8 b shows the temperature in linear association with \(M\). Interruption in viscosity caused due to \(M\) produces friction between fluid molecules and the surface, converting frictional energy into thermal energy. Impact of \({Fe}_{3}{O}_{4}\) volumetric fraction \({\phi }_{2}\) on temperature, diffusion is found in Fig. 9 for both suction and injection. This figure represents the presence of \({\phi }_{2}\) has a substantial role in heat transfer within the fluid, increasing fluid temperature. The changes in temperature profile for different values of the Eckert number \(Ec\) is given in Fig. 10. It is noticed that the temperature distribution and thermal boundary layer thickness are augmented by enhancing the values of \(Ec\) in both cases of suction and injection, it may be since the temperature at the surface is higher \(({T}_{w}>{T}_{\infty })\) when compared to that of fluid temperature.

Fig. 10
figure 10

a Effect of \(Ec\) on temperature for suction. b Effect of \(Ec\) on temperature for injection

Full size image

The dynamics of wall shear stress against curvature and magnetic properties are studied by conducting different numerical experiments, and the observations are displayed in Table 3. It is noticed that a significant rise in wall shear stress of nanofluid is increased when the magnetic parameter is increased and vice versa with an increase in values of curvature factor for hybrid nanofluid. High wall shear stress is found in hybrid nanofluid, and the strength of the slender body is also found to increase while using hybrid nanofluid than nanofluid. On observation from the slope analysis, the rate of increase in skin friction dominates for suction. From the linear regression slope obtained in Table 3, it is evident that the increment for injection in the hybrid nanofluid case is at the rate \(0.446801\), while it is \(0.445751\) in a nanofluid. Subsequently, the slope rates for suction and injection are \(0.612459\) and \(0.610378\) in the case of hybrid nanofluid. The slope analysis decreases at the rate of 0.001485 for suction and 0.001702 for injection for usual nanofluids in the curvature factor. In contrast, for hybrid nanofluid, the regression slope is \(0.00198\) and \(0.00225\) for suction and injection, respectively. We notice a change in the texture of the curved surface as furthermore dragged for suction.

Table 3 Variation in skin friction coefficients
Full size table

In Table 4, several numerical methods are used to calculate the wall heat transfer rate. With the increase in values of \(K\), the wall heat transfer rate for nanofluid and hybrid nanofluid is noticeably increased, and the opposite results were found for rising values of \(M\) and \(Ec\). It is observed that the wall heat transfer rate in hybrid nanofluid is greater than that of the nanofluid. Suction consumes higher thermal significances in comparison to injection. Table 4 illustrates an increase at the rate \(0.000361\) for suction, while \(0.000253\) has been valued by the slope method for injection in \(Cu\)/water nanofluid. Hence, for suction, efficient heat transfer is possible. In the case of \(Cu-{Fe}_{3}{O}_{4}\)/water hybrid nanofluid, the slope rate is \(0.000312\) for suction and \(0.000212\) for injection. -ve values of slope in Table 4 conformed diminishing in heat transfer. The rate of exhaustion seems to be more significant for injection than suction. With an increment in \(M\) and \(Ec\), the reduction rate is \(0.175521, 4.109375\) for suction and \(0.197243, 3.153297\) for injection in case of \(Cu\)/water nanofluid. In the case of \(Cu-{Fe}_{3}{O}_{4}\)/water hybrid nanofluid, the slope rate is \(0.20034, 3.97506\) for suction, and \(0.22855, 3.13484\) for injection.

Table 4 Variation in Nusselt numbers
Full size table

Finally, Table 5 presents that the skin friction coefficient increases with the rise in \({\phi }_{1}\) and \({\phi }_{2}\) at the linear regression slope values are \(0.069275, 0.054585\) for suction, and \(0.058161, 0.049023\) for injection. The rate of heat transfer decreased with \({\phi }_{1}\). Declining suction is \(0.00661,\) and it is \(0.00341\) for injection; positive values of linear regression slope affirm that heat transfer is an increasing function of \({\phi }_{2}\) in Table 5. Injection exhibits \(0.015286\) rates of increment and \(0.013493\) for suction.

Table 5 Variation in skin friction coefficients and Nusselt numbers in a hybrid nanofluid
Full size table

Conclusion

The present work investigates the hydrothermal variations of magnetized hybrid nanofluid transport over a permeable curved surface. Copper and Ferrous nano components, including water, constitute the base medium as host fluid. Magnetic field and viscosity have been fused in this study. Moreover, the presence of suction/injection is also hypothesized in the processes. Shooting based RKF-45 scheme was applied to disclose the hydrothermal results. During numerical experiments, the following novel observations are noted.

  1. 1.

    Progressive curvature parameter values are registered for nanofluid and hybrid nanofluids, while regressive values are recorded for the magnetic parameter. The high-velocity profiles of injection and suction very incredible. Similarly, Cu-Fe3O4/water hybrid nanofluid gains a high-velocity profile over Cu/water nanofluid.

  2. 2.

    Skin friction increases for the magnetic parameter, though the maximum impact is brought by injection. Hybrid nanofluid conveys high skin friction as compared to conventional nanofluid.

  3. 3.

    Curvature parameter temperature is recorded to be inversely proportional to the magnetic parameter and Eckert number. Acute thermal outcomes are noticed in injection, unlike in suction. Maximum temperature occurs in Cu-Fe3O4/water hybrid nanofluid compared to Cu/water nanofluid

  4. 4.

    Magnetic parameters and Eckert number show augmentation in heat transfer. The curvature parameter is contrary to this. Hybrid nanofluid gets a high heat transfer rate as compared to usual nanofluid

  5. 5.

    The conclusions are authenticated by referring to the published results. There is a good correlation between the published and the present work.

The current research focuses on steady-state flow. Further research can be conducted on time-dependent flows in porous media and will be communicated imminently. The updated results of the present study may be valuable in enriching the research and in the ceramic, plastic, and polymer industry.