Numerical simulation for MHD flow of Sisko nanofluid over a moving curved surface: A revised model

Abstract

An analysis regarding diverse features of Sisko fluid flow over a curved stretching surface in the presence of magneto-nanoparticles is presented. For larger value of the curvature parameter, the curved surface reduces into the planner sheet. The governing equations are modeled in curvilinear coordinate system and transformed into system of nonlinear ordinary differential equations. The obtained equations are solved numerically by employing the boundary value solver (bvp4c) in Matlab as well as bvp traprich in Maple. From the obtained results, we observed a decline in the magnitued of velocity field as well as pressure inside the boundary layer with increasing values of magnetic parameter. On the other hand, the temperature of fluid is noticed in enhancing trend with growing values of Brownian motion and thermophoresis parameters. Moreover, concentration is also to be growing with augmented values of the Schmidt number. A comparison for validation of the present results is performed between the bvp4c function in Matlab and Richardson extrapolation method in Maple with an excellent agreement. The results are also verified with previous works.

1 Introduction

Recently attention towards fluid flow with nanotechnology is playing a significant role in the development of nano-divices. Meanwhile, introduction of nanofluids for heat transfer in base fluid is a new door towards the arena of engineering and technology. In order to improve effectiveness of many processes, the characteristics of heat transfer must be improved with some new agents. Therefore, nanometer size particles namely nanoparticles are responsible for enhancing heat transfer. Thus nanofluids have many applications in industry such as heat exchangers, microchannel heat sinks and lubricants, cancer therapy and coolants etc. In like manner, in late decades, several examiners have been occupied with considering nanofluids applications in different fields. Choi (1995), for instance, built up the idea of nanofluids in cooling advances. Such regular fluids as water, oil and ethylene glycol in nature are poor in thermal conductivity, which restrains the heat transfer execution. Because of development in innovation by means of scaling down of an electronic gadget requires the further progress of heat transfer from vitality sparing. To triumph over this demanding situation leads to a new elegance of fluid called nanofluid. Since nanofluids have a higher thermal conductivity when contrasted with regular fluids and they have high potential to upgrade heat transfer rate in building frameworks particularly for cooling of electronic gadgets. In this regard, Hayat et al. (2016) discussed water–carbon nanofluid flow with variable heat flux by a thin needle. Ahmed and Akbar (2017) addressed numerical simulation of the forced convective nanofluid flow through an annulus sector duct. At present a few hundred gatherings around the globe chip away at nanofluids (Beck et al. 2007; Das et al. 2007; Lee and Mudawar 2007; Turkyilmazoglu 2017a; Akbar et al. 2018).

Buongiorno (2006) demonstrated that the single phase model is conflict with the experimental perception and unadulterated liquid relationships, (for example, Dittus–Boelter’s) under predict the nanoliquid heat transfer coefficient. At that point an alternate model that wipes out the deficiencies of the single phase or scattering models (DPM models) was created. He thought about seven slip instruments, at that point presumed that exclusive Brownian diffusion and thermophoresis are the overwhelming slip mechanisms in nanoliquids. With these findings as a premise, he proposed a non-homogeneous two phase equilibrium model for convective transport in nanoliquids. One of the upsides of this new model is that the impact of the relative velocity amongst nanoparticles and base fluid is depicted more mechanistically than in the scattering models. Kuznetsov and Nield (2010) illustrated convective boundary layer flow of nanofluid due to vertical plate. Akbar (2013) presented numerical study of Williamson nanofluid fluid flow in an asymmetric channel. Radiative flow of micropolar nanofluid accounting thermophoresis and Brownian moment is reported by Hayat et al. (2017a). Nadeem et al. (2014) elucidated numerically MHD boundary layer flow of non-Newtonian Maxwell fluid over a stretching sheet in the companying nanoparticles. Due to a wide range of applications of such types of nanoparticles in the flow which many researchers (Khan et al. 2017a; Hayat et al. 2017b, c; Turkyilmazoglu 2018; Nabil et al. 2018) paved attention to improve the thermal conductivity of different types of fluids.

The liquid flow because of continuous stretching of surface is considered in numerous mechanical procedure. For instance, polymer handling, expulsion process, wire and fiber covering, sustenance stuff preparing, outline of different heat transfer and substance preparing hardware, and so on. In a dissolve turning process, the extruder from bite the dust is by and large drawn and all the while extended into a fiber or sheet, at that point it hardens through fast. In this regard, Crane (1970) was the first who discussed the fluid flow due to a linear stretching sheet. His work has been reached out from multiple points of view alongside expected physical highlights including heat and mass transfer along flat plate, impact of suction and injection, magnetic field etc. Stretching flow subject to suction and injection was scrutinized by Gupta and Gupta (1977). Ahmad and Asghar (2012) found the analytical and numerical solutions for flow and heat transfer for hyperbolic stretching surface. Turkyilmazoglu (2015) investigated the exact solutions of MHD flow and heat transfer over two–three dimensional deforming bodies. Equivalences and correspondences between the deforming body induced flow and heat in two–three dimensions was deliberated by Turkyilmazoglu (2016). The effects of radiation with magnetic field on stretching surface were studied by Turkyilmazoglu (2017b). Furthermore, Mat Yasin (2016) reported the solution of MHD two-phase dusty fluid flow and heat model over deforming isothermal surfaces. Recently, Turkyilmazoglu (2017c) discussed mathematically the existence for MHD mixed convection flow of a micropolar fluid past a cooled or heated in the presence of heat generation/absorption effects on the stretching surface.

Rather than planner boundary, there is a developing interest for studying of the effects of curvature by a few examiners recently. Very few papers have been examined on this theme and found that its essence inside the boundary layer is not any more insignificant as on account of a stretching sheet. Sajid et al. (2010) considered curved stretching surface of viscous fluid flow and found that the boundary layer thickness increments for a curved surface contrasted with flat surface. Rosca and Pop (2015) examined the boundary layer flow over an unsteady permeable stretching/shrinking sheet. Furthermore, it is also strongly observed that in case of curved surface as compared to flat surface the drag force is smaller. The preceeding work was then extended by Sajid et al. (2011). Moreover, Abbas et al. (2016) addressed slip effect with heat generation and thermally radiated boundary layer flow on curved surface.

The Sisko liquid model is of much significance because of its satisfactory portrayal of numerous non-Newtonian liquids over the most imperative scope of shear rates. This model is a three parameter experimental model, which is suitable in describing flow in the power-law and upper Newtonian regions. Informative results about this fluid model are presented in the form of shear-thinning and shear-thickening characteristics. Specifically, the pseudo plastic or shear thinning fluids are those in which for decreasing shea rate, the viscosity of such fluids increases. This importance is one of the attentions towards the rheological study of one of the example of shear thinning fluids like blood, ketchup, whipped cream etc. Particularly bio rheology speaks to the examination experienced on the flow and distortion of biological systems and materials got from living life forms. The objective of biorheology is to relate the rheological properties of frameworks/materials to their molecular, cell and auxiliary properties. Blood rheology is profoundly important for both scholarly and down to practical purposes. The flow properties of blood directly affect human wellbeing, from stenosis or hemolysis up to cardiovascular medical procedure. From the rheological perspective, blood is essentially a complex liquid framework, deformable particles (mostly red cells) suspended in plasma. The investigation of flow conduct of blood, focuses particularly on the current connection between its micro structural changes and rheology. During the flow of blood being a pseudo plastic or shear thinning fluid characteristics of Sisko fluid model can be studied. For the reason of their excellent combined dampening and dispersing nature, Sisko (1958) introduced this phenomenon for the first time in 1958. The basic boundary layer flow equations due to stretching velocity in two dimensional Cartesian geometry was first time formulated and then solved analytically for integral values by Khan and Shahzad (2013). Malik et al. (2014) demonstrated the effects of convective boundary conditions and non isothermal nonlinear stretching sheet with vertical magnetic field in the Sisko fluid flow. Khan et al. (2017b) studied the influence of Cattaneo–Christove heat flux model with homogeneous–heterogeneous reactions in the flow of Sisko fluid for the bidirectional stretching geometry. Moreover, a lot of works in this regard are illustrated in references (Khan et al. 2017; Ahmad et al. 2017; Khan et al. 2018a, b, c).

Keeping all above in the view, the motivation behind present paper is to study the impact of nanoparticles and magnetic field in the boundary layer flow with heat and mass transfer characteristics of Sisko fluid over a curved stretching sheet. The curvilinear coordinates system is utilized to formulate the momentum equations for the Sisko fluid flow in two dimensional geometry. Overseeing the transformed ODEs arising due to the new geometry are then considered for solution while using the Matlab built in function namely bvp4c. The flow pattern is displayed in the form of streamlines and the related velocity, temperature and concentration profiles of the fluid and are presented through several graphs. Another important concern in this regard is displayed in the form of tabular values of the local skin friction, Nusselt and Sherwood numbers. To verify the problem formulation, a comparison is performed with the previous published data. Additionally, a comparison of the present method is performed with Richardson extrapolation method in Maple with an excellent agreement.

2 Configuration of the problem

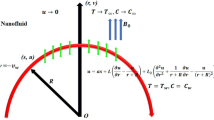
The effect of Brownian motion and thermophoresis parameters in an incompressible steady flow of Sisko fluid due to curved stretching sheet in the presence of magnetic field is considered. Flow configuration presented is modeled in curvilinear coordinated and is shown in Fig. 1. The curved surface coiled in a circle of radius R about the curvilinear coordinates (r, s) and is stretched kinematically along the axial direction s with velocity $U_{w}=cs$. The distance of surface from the origin R defines the shape of curved geometry of the problem. So that larger values of R goes to slightly curved sheet. The temperature and concentration of fluid at surface are T_w and $C_{w}$, respectively, while the ambient temperature and concentration of the fluid are T$_{\infty }$ and C$_{\infty }$, respectively. Under the aforementioned assumptions, the basic equations for the Sisko nanofluid flow in the form of continuity, momentum along with Boussinesq approximation, heat and concentration are developed as follows

Fig. 1

Physical model and coordinates system

$$\begin{aligned} \frac{\partial }{\partial r}\left\{ (r+R)v\right\} +R\frac{\partial u}{ \partial s}=0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{u^{2}}{r+R}=\frac{1}{\rho_f}\frac{\partial p}{\partial r}, \end{aligned}$$

(2)

$$\begin{aligned} v\frac{\partial u}{\partial r}+\frac{Ru}{r+R}\frac{\partial u}{\partial s}+ \frac{uv}{r+R}= & {} -\frac{1}{\rho_f }\frac{R}{r+R}\frac{\partial p}{\partial s}+ \frac{a}{\rho_f (r+R)^{2}}\frac{\partial }{\partial r}\left[ (r+R)^{2}\left( \frac{\partial u}{\partial r}-\frac{u}{r+R}\right) \right] \nonumber \\&+\frac{b}{\rho_f (r+R)^{2}}\frac{\partial }{\partial r}\left[ (r+R)^{2}\left( \frac{\partial u}{\partial r}-\frac{u}{r+R}\right) ^{n} \right] -\frac{\sigma B_{0}^{2}}{\rho_f }u, \end{aligned}$$

(3)

$$\begin{aligned} v\frac{\partial T}{\partial r}+\frac{Ru}{r+R}\frac{\partial T}{\partial s} =\alpha _{1}\left( \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r+R}\frac{ \partial T}{\partial r}\right) +\frac{\left( \rho c\right) _{p}}{\left( \rho c\right) _{f}}\left[ D_{B}\left( \frac{\partial T}{\partial r}\frac{\partial C}{\partial r}\right) +\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{ \partial r}\right) ^{2}\right] , \end{aligned}$$

(4)

$$\begin{aligned} v\frac{\partial C}{\partial r}+\frac{Ru}{r+R}\frac{\partial C}{\partial s} =D_{B}\left( \frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r+R}\frac{ \partial C}{\partial r}\right) +\frac{D_{T}}{T_{\infty }}\left( \frac{ \partial ^{2}T}{\partial r^{2}}+\frac{1}{r+R}\frac{\partial T}{\partial r} \right) . \end{aligned}$$

(5)

The associated boundary conditions are as follows:

$$\begin{aligned} u=U_{w}(s)=cs,\quad v=0,\quad T=T_{w},\quad C=C_{w}\quad \text { at } \quad r=0, \end{aligned}$$

(6)

$$\begin{aligned} u\rightarrow 0,\quad \frac{\partial u}{\partial r}\rightarrow 0,\quad T\rightarrow T_{\infty },\quad C\rightarrow C_{\infty }\quad \text { as } \quad r\rightarrow \infty . \end{aligned}$$

(7)

The governing momentum, energy and concentration equations can be transformed into the coupled nonlinear ordinary equations by using the following suitable transformations

$$\begin{aligned} u= & {} U_{w}f^{\prime }\left( \eta \right) ,\quad v=\frac{-U_{w}R}{r+R}{Re} _{b}^{-\frac{1}{n+1}}\left[ \frac{2n}{n+1}f\left( \eta \right) +\frac{1-n}{ 1+n}\eta f^{\prime }\left( \eta \right) \right] , \quad \psi =sU_{w}{Re }_{b}^{-\frac{1}{n+1}}f(\eta ),\nonumber \\ \theta \left( \eta \right)= & {} \frac{T-T_{\infty }}{T_w-T_{\infty }},\quad \phi \left( \eta \right) =\frac{C-C_{\infty }}{C_w-C_{\infty }},\ p=\rho a^{2}s^{2}P(\eta ),\quad \eta =\frac{r}{s}{Re} _{b}^{\frac{1}{n+1}}. \end{aligned}$$

(8)

Upon making use of transformations (8), Eq. (1) is identically satisfied and Eqs. (2) and (3) are reduced in the following form

$$\begin{aligned} \frac{\partial P}{\partial \eta }=\frac{f^{\prime 2}}{\eta +K}, \end{aligned}$$

(9)

$$\begin{aligned} \frac{2K}{\eta +K}P= & {} \frac{K}{\eta +K}\left( \frac{2n}{n+1}\right) \left( ff^{\prime \prime }+\frac{1}{\eta +K}ff^{\prime }\right) -\frac{K}{\eta +K} f^{\prime 2}\nonumber \\&+A\left[ f^{\prime \prime \prime }+\frac{1}{\eta +K}f^{\prime \prime }-\frac{1}{\left( \eta +K\right) ^{2}}f^{\prime }\right] +n\left( f^{\prime \prime }-\frac{1}{\eta +K}f^{\prime }\right) ^{n-1}\left( f^{\prime \prime \prime }-\frac{1}{\eta +K}f^{\prime \prime }+\frac{1}{ \left( \eta +K\right) ^{2}}f^{\prime }\right) \nonumber \\&+\frac{2}{\eta +K}\left( f^{\prime \prime }-\frac{1}{\eta +K}f^{\prime }\right) ^{n}-Mf^{\prime }. \end{aligned}$$

(10)

Eliminating the pressure term between Eqs. (9) and (10) in combination with Eq. (8), then Eqs. (4) to (7) reduces in the following form

$$\begin{aligned}& A\left[ f^{\prime \prime \prime \prime }+\frac{2}{\eta +K}f^{\prime \prime \prime }-\frac{1}{\left( \eta +K\right) ^{2}}f^{\prime \prime }+\frac{1}{ \left( \eta +K\right) ^{3}}f^{\prime }\right] \nonumber \\& \quad +\left( \frac{2n}{n+1}\right) \left[ \frac{K}{\eta +K}\left( ff^{\prime \prime \prime }+f^{\prime }f^{\prime \prime }\right) \right. \nonumber \\& \quad \left. + \frac{K}{\left( \eta +K\right) ^{2}}\left( ff^{\prime \prime }+f^{\prime 2}\right) -\frac{K}{\left( \eta +K\right) ^{3}}ff^{\prime } \right] \\ & \quad -\frac{2K}{\eta +K}f^{\prime }f^{\prime \prime }-\frac{2K}{\left( \eta +K\right) ^{2}}f^{\prime 2}+n\left( f^{\prime \prime }-\frac{1}{\eta +K} f^{\prime }\right) ^{n-1}\left( f^{\prime \prime \prime \prime }+\frac{2}{ \eta +K}f^{\prime \prime \prime }-\frac{1}{\left( \eta +K\right) ^{2}} f^{\prime \prime }+\frac{1}{\left( \eta +K\right) ^{3}}f^{\prime }\right) \nonumber \\& \quad +n(n-1)\left( f^{\prime \prime }-\frac{1}{\eta +K}f^{\prime }\right) ^{n-2}\left( f^{\prime \prime \prime }-\frac{1}{\eta +K}f^{\prime \prime }+ \frac{1}{\left( \eta +K\right) ^{2}}f^{\prime }\right) ^{2}\nonumber \\&\quad +2n\left( f^{\prime \prime }-\frac{1}{\eta +K}f^{\prime }\right) ^{n-1}\left( \frac{1}{\eta +K}f^{\prime \prime \prime \prime }-\frac{1}{ \left( \eta +K\right) ^{2}}f^{\prime \prime }+\frac{1}{\left( \eta +K\right) ^{3}}f^{\prime }\right) -M\left( f^{\prime \prime }-\frac{1}{\eta +K} f^{\prime }\right) =0, \end{aligned}$$

(11)

$$\begin{aligned} \theta ^{\prime \prime }+\frac{\Pr K}{\eta +K}\left( \frac{2n}{n+1}\right) f\theta ^{\prime }+\frac{1}{\eta +K}\theta ^{\prime }+\Pr \left( N_{b}\theta ^{\prime }\phi ^{\prime }+N_{t}\left( \theta ^{\prime }\right) ^{2}\right) =0, \end{aligned}$$

(12)

$$\begin{aligned} \phi ^{\prime \prime }+\frac{ScK}{\eta +K}\left( \frac{2n}{n+1}\right) f\phi ^{\prime }+\frac{1}{\eta +K}\theta ^{\prime }+\frac{N_{t}}{N_{b}}\left( \theta ^{\prime \prime }+\frac{1}{\eta +K}\theta ^{\prime }\right) =0, \end{aligned}$$

(13)

$$\begin{aligned} f(0)=0, \quad f^{\prime }(0)=1,\quad \theta (0)=1,\quad \phi (0)=1, \end{aligned}$$

(14)

$$\begin{aligned} f^{\prime }\rightarrow 0,\quad f^{\prime \prime }\rightarrow 0,\quad \theta \rightarrow 0, \quad\phi \rightarrow 0 \quad \text {as } \quad \eta \rightarrow \infty , \end{aligned}$$

(15)

where all the physical parameters which governs the flow are listed below:

${Re}_{a}$ $=\frac{U_{w}s\rho_f }{a},$	$\alpha _{1}=\frac{k}{(\rho c_{p})_f}$
${Re}_{b}$ $=\frac{U_{w}^{2-n}s^{n}\rho_f}{b}$	$\Pr$ $=\frac{sU_{w}}{ \alpha _{1}}{Re}_{b}^{-\frac{2}{n+1}}$
A $=\frac{{Re}_{b}^{\frac{2}{n+1}}}{{Re}_{a}}$	Sc $=\frac{sU_{w}}{D_{B}}{Re}_{b}^{-\frac{2}{n+1}}$
$M=\frac{\sigma B_{0}^{2}}{\rho_f c}$	$N_{b}=\frac{\left( \rho c\right) _{p}D_{B}(C_w-C_{\infty })}{\left( \rho c\right) _{f}\alpha _{1}}$
K $=\frac{R}{s}{Re}_{b}^{\frac{1}{n+1}}$	$N_{t}=\frac{\left( \rho c\right) _{p}D_{T}\left( T_{w}-T_{\infty }\right) }{\left( \rho c\right) _{f}\alpha _{1}T_{\infty }}$

The important physical quantities of interest namely the local skin-friction coefficient, Nusselt and Sherwood numbers are defined by

$$\begin{aligned} C_{f}=\frac{\tau _{w}}{\frac{1}{2}\rho_f U_{w}^{2}},\quad Nu_{s}=\frac{q_{m}s}{ k\left( T_w-T_{\infty }\right) },\quad Sh_{s}=\frac{q_{m}s}{D_{B}\left( C_w-C_{\infty }\right) }. \end{aligned}$$

(16)

Using the transformations defined through Eq. (8), we finally obtain the reduced form of the local skin friction, Nusselt and Sherwood numbers as follows:

$$\begin{aligned} \frac{1}{2}{Re}_{b}^{\frac{1}{n+1}}C_{f}=A\left( f^{\prime \prime }(0)- \frac{1}{K}f^{\prime }(0)\right) +\left( f^{\prime \prime }(0)-\frac{1}{K} f^{\prime }(0)\right) ^{n}, \end{aligned}$$

(17)

$$\begin{aligned} {Re}_{b}^{-\frac{1}{n+1}}Nu_{s}=-\theta ^{\prime }(0), \end{aligned}$$

(18)

$$\begin{aligned} {Re}_{b}^{-\frac{1}{n+1}}Sh_{s}=-\phi ^{\prime }(0). \end{aligned}$$

(19)

3 Results validation

The governing nonlinear ODEs (11)–(13) are considered for the numerical solution. The results obtained with the implementation of bvp4c method are given through Table 1 and are compared with bvp traprich in Maple which uses Richardson extrapolation method. An excellent agreement is found between these two numerical methods. Numerical outcomes produced in the limiting cases are compared with published work by Mabood and Das (2016) and Imtiaz et al. (2016). The results found in present study are in excellent correlation with the earlier works and presented in Table 2.

4 Numerical outcomes and discussion

Numerical simulation of the Sisko magneto-nanofluid flow due to curved stretching surface is performed. The Buongiorno nanofluid model is considered to study heat and mass transfer phenomena in flow of Sisko fluid. Highly nonlinear Eqs. (11) to (13) with the boundary conditions (14) and (15) are modeled in curvilinear coordinates. All governing parameters like material parameter A, magnetic field parameter M, power-law parameter n, radius of curvature K, generalized Prandtl number $\Pr$, Brownian motion parameter $N_{b}$, therrmophoresis parameter $N_{t}$ and generalized Schmidt number Sc are used to demonstrate the flow, heat as well as mass transfer characteristics of Sisko nanofluid.

4.1 Flow pattern

To show the flow pattern in the form of streamlines with the influence of different flow parameters like material parameter A and power-law parameter n. While the remaining flow parameters are fixed, i.e., $Re_{b}=1000$, $c=1$ and $M=2.0$. Streamlines in Fig. 2a are plotted for the Newtonian fluid, $(n=1$ and $A=0)$. The flow pattern subjected to this case exhibits a non-symmetric reduction behavior near the curved surface, while on other hand through Fig. 2b, the behavior of the flow near the stretching surface is prominent for shear thinning fluid and the flow in this case reduces symmetrically about the horizontal axis. In both Figs., the effect of A and n causes the flow being drag into the center and this is due to the equal forces of buoyant flow. The flow pattern of Sisko fluid is plotted through Fig. 3a, where the fluid flow is stretched toward the curved surface symmetrically about the horizontal axis and flow of Sisko fluid is reduced near the curved stretching surface for $n>1$. Another flow pattern is plotted through Fig. 3b for $A=2.5$ and $n=1$. A symmetric conduct about the horizontal axis away from the curved stretching surface is observed and fluid flow is reduced near the stretching curved surface, where the fluid flow is found in non-uniform pattern. The flow pattern produced for shear-thinning and shear-thickening fluids in Fig. 4a, b, where the fluid flow is stretched near the curved stretching surface for both cases, i.e., $0<n<1$ and $n>1$.

Fig. 2

Streamlines pattern for A = 0. a n = 1.0 and b n = 0.5

Fig. 3

Streamlines pattern for A = 2.5. a n = 1.5 and b n = 1.0

Fig. 4

Streamlines pattern for A = 0. a n = 0.5 and b n = 1.5

Fig. 5

Effect of A on velocity $f^{\prime }(\eta)$

Fig. 6

Effect of K on velocity $f^{\prime }(\eta)$

Fig. 7

Effect of M on velocity $f^{\prime }(\eta)$

Fig. 8

Effect of n and A on pressure $P(\eta)$

4.2 Velocity profile

A considerable growing effect of increasing values of A is noticed during plotting the velocity profile and related momentum boundary layer thickness of Sisko fluid flow over a curved stretching surface as shown in Fig. 5a, b. The result for the shear thinning fluid is more effective as compared to shear thickening fluid. This physical enhancement conduct with the variation of material parameter causes low shear rate with higher viscosity and high shear rate for low viscosity regarding Sisko nanofluid flow. The influence of uplifting values of K on velocity profile for shear-thinning as well as shear-thickening fluids is found in the increasing order along with associated momentum boundary layer thickness as demonstrated through Fig. 6a, b. Here the result is more acceptable in the case of shear thinning fluid. It has been examined that the radius of curved surface increases for augmented values of curvature parameter K due to which motion of the fluid rises. A very significant reduction behavior through Fig. 7a, b is observed for higher values of M, when n is fixed for shear-thinning and shear-thickening fluids and relevant momentum boundary layer thickness is perceived in reduction conduct. The physical reasoning concerning to this conduct is due to the enhancment of Lorentz forces which reduces the velocity of the fluid.

4.3 Pressure profile

Figure 8a establishes a decreasing conduct in the magnitude of the pressure for larger values of n. On other hand, the effect of higher values of material parameter on magnitude of pressure inside boundary layer is observed in the form of declining behavior and is shown through Fig. 8b. In both cases the associated boundary layer thickness is detected in enrichment demeanor. Furthermore, the decreasing values of curvature parameter cause an escalating behavior in the magnitude of pressure profile inside the boundary layer and is shown in Fig. 9a. Wherein a curved surface is reduced in the planner surface for higher value of K and the pressure profile becomes zero. For smaller values of K, the curved surface will be more curved. It can be explained on the basis that the curvature of the surface give rises to a secondary flow due to the curvilinear nature of the fluid flow under the accomplishment of centrifugal force as the fluid particles navigate the curved track along the surface of the sheet. The secondary flow is therefore superimposed on the primary flow due to augment the velocity field. Though, in the situation of a curved surface the variation of pressure is significant inside the boundary layer and therefore the pressure discrepancy cannot be neglected as is frequently done for a flat stretching sheet. Fig. 9b exhibits a declining conduct in the magnitude of pressure profile inside the boundary and associated boundary layer for the larger values of magnetic parameter.

Fig. 9

Effect of K and M on pressure $P(\eta)$

4.4 Temperature profile

Figure 10a, b demonstrate a diminishing behavior for the increasing values of A. Whereas the temperature profiles of fluid and relevant boundary layer thickness also reduce for shear-thinning and shear-thickening fluids. Physically this is due to fact that the increasing values of A enhance the shear rate and as a result the viscosity of the fluid shall be reduced. The impact of the several increasing values of K enriche the temperature field and thermal boundary layer thickness in both cases, i.e., shear-thinning and shear-thickening fluids. This significant behavior is presented in Fig. 11a, b. Through Fig. 12a, b, an enhancement behavior is perceived while plotting the temperature profile of the liquid flow. Figure 13a, b showing a diminishing conduct of temperature profiles with increasing values of $\Pr$ for shear thinning fluid as well as shear thickening fluid. The associated thermal boundary layer is reduced in this case. Enhancment of Brownian motion parameter results in growing the temperature field and related boundary layer thickness is also increases for shear-thinning fluid as well as shear-thickening fluid as shown through Fig. 14a, b. From Fig. 15a, b, it is concluded that whenever the therrmophoresis parameter is considered in the increasing order the temperature profile and the associated thermal boundary layer will be enhanced while testing both the cases, i.e., shear thinning and shear thickening fluids.

Fig. 10

Effect of A on temperature $\theta (\eta)$

Fig. 11

Effect of K on temperature $\theta (\eta)$

Fig. 12

Effect of M on temperature $\theta (\eta)$

Fig. 13

Effect of $\Pr$ on temperature $\theta (\eta)$

Fig. 14

Effect of $N_{b}$ on temperature $\theta (\eta)$

Fig. 15

Effect of $N_{t}$ on temperature $\theta (\eta)$

4.5 Concentration profile

In Figure 16a, b we have investigated the variation of A while plotting the nanoparticle concentration profile. Wherein a reduction is found for both shear-thinning and shear-thickening fluids. The associated layer thickness is also diminshed. A remarkable increasing nanoparticle concentration with the several values of M is plotted through Fig. 17a, b, where both cases are considered namely shear-thinning and shear-thickening fluids. The result is very significant in case of shear thinning fluid. Figure 18a, b illustrate the influence of K on the nanoparticle concentration. It is noted that for the growing values of K the concentration profile and the associated boundary layer is diminishing for both situations, i.e., shear-thinning as well as shear-thickening fluids. From Fig. 19a, b it is observed that by varying $N_{b}$, a deteriorating behavior is demonstrated while plotting the nanoparticle concentration for shear-thinning fluid as well as shear-thickening fluid. In this regard the boundary layer thickness is also reduced. In Fig. 20a, b the increasing values of $N_{t}$ cause a reduction in nanoparticle concentration profile and associated boundary layer thickness. Shear thinning and shear thickening fluids properties are also utilized but the result are more acceptable in case of shear thinning fluid. Figure 21a, b depict a diminishing behavior of nanoparticle concentration for growing values of Sc and related layer thickness is also reduced in both shear-thinning as well as shear-thickening fluids.

Fig. 16

Effect of A on concentration $\phi (\eta)$

Fig. 17

Effect of M on concentration $\phi (\eta)$

Fig. 18

Effect of K on concentration $\phi (\eta)$

Fig. 19

Effect of $N_{b}$ on concentration $\phi (\eta)$

Fig. 20

Effect of $N_{t}$ on concentration $\phi (\eta)$

Fig. 21

Effect of Sc on concentration $\phi (\eta)$

4.6 Local skin friction, Nusselt and Sherwood number

Behavior of the material parameter A on the local-skin friction is observed in the increasing order for shear-thinning fluid case as well as shear-thickening fluid and is shown in Fig. 22a, b. Diminishing behavior is illustrated during plotting of local Nusselt number in both situations of power-law fluids, i.e., shear-thinning and shear-thickening fluids and is presented in Fig. 23a, b. Through Fig. 24a, b, the effect of increasing values of Sc on the local Sherwood number is found in the augmented conduct while testing both cases of shear-thinning as well shear-thickening fluids. The effect of A, M and K are utilized to demonstrate the impact of resistive forces. In this regard the tabular values as shown in Table 3 are computed to depict the effect of frictional forces during fluid flow. Local skin friction increases, whereas the magnetic parameter is taking in increasing order while on the other hand enhancing values of curvature parameter causes a reduction. In preceding table three constraints are imposed on the power-law index n, i.e., for $n=1$ (non-Newtonain fluid), $n=0.5$ (shear-thinning fluids) and $n=1.5$ (shear-thickening fluid). The impacts of different governing flow parameters on the local Nusselt number is depicted in Table 4. The rate of heat transfer is reducing while increasing magnetic parameter M and rate of heat transfer is increasing function of curvature parameter K for three cases, i.e., non-Newtonian, shear-thinning and shear-thickening fluids. A decreasing behavior is noticed for the rate of heat transfer when the Brownian motion and therrmophoresis parameters are varying in increasing order. Table 5 is presented to show the rate of mass transfer with the influence of different flow parameters like A, M, K, $\Pr$, $N_{b}$, $N_{t}$ and Sc. The rate of mass transfer is diminishing whenever the curvature parameter K increases for the same restrictions on the power-law index n as presented in the previous table. Enhancement in rate of the mass transfer is perceived for numerous values of Brownian motion parameter $N_{b}$ and an opposite trend is noted for different growing values of therrmophoresis parameter $N_{t}$. Rate of mass transfer also increases when the Schmidt number rises for all three restrictions on the power-law index n.

Fig. 22

Local skin friction via K for different values of A

Fig. 23

Local Nusselt number via $N_{b}$ for different values of $N_{t}$

Fig. 24

Local Sherwood number via $N_{t}$ for different values of Sc

Table 1 Comparison of bvp4c with Richardson extrapolation method, when $n=3,\ A=3.5$ and$\ K=1$

Table 2 Comparison of the present work with previous results when $n=1,\ A=0$and$\ K\rightarrow \infty$

Table 3 Variation of the local-skin friction for varying values of A, M and K

Table 4 Variation of the local Nusselt number for varying values of $A,\ M,\ K,\ \Pr ,\ N_{b}$ and $N_{t}$

Table 5 Variation of local Sherwood number for varying values of $A,\ M,\ K,\ \Pr ,\ N_{b},\ N_{t}$ and Sc

5 Concluding remarks

The Sisko nanofluid flow over a curved stretching surface accompanying magnetic field was analyzed in this work. The modeled governing equations are considered for the numerical computations. All outcomes are presented in the form of graphs and tabular values. A comparison with previous data and another built in method in Maple namely bvp traprich which uses Richardson extrapolation is carried out to validate the computational results.

The velocity profile was noticed in increasing trend for higher values of dimensionless radius of curvature K and a reverse behavior have been observed with increasing values of magnetic parameter for both shear-thinning and shear-thickening fluids. With decreasing values of the curvature parameter K,  the magnitude of pressure profile was exhibited in an increasing order inside boundary layer. However, outside boundary layer it becomes zero. The magnitude of pressure profile was also zero when K goes to infinity. The magnitude of pressure was noticed in declining conduct while increasing the magnetic field. Enhancement in the temperature profile of non-Newtonian Sisko nanofluid flow was noticed with growing values of curvature parameter K, Brownian motion parameter $N_{b}$ and thermophoresis parameter $N_{t}$. Concentration profile was also reduced with various increasing values of K when $n=0.8$ and $n=1.8$. An important diminishing trend due to the increasing values of $N_{t}$ was perceived and a reverse conduct was observed during increasing values of $N_{t}$. Additionally, rates of heat and mass transfer were decreasing with growing values of curvature parameter K.