Joint Effect of Magnetic Field and Heat Transfer on Particulate Fluid Suspension in a Catheterized Wavy Tube

Abstract

The effect of wall slip conditions, porous media, and heat transfer on peristaltic inflow of MHD Newtonian fluid with suspended particles in a catheterized tube has been studied with long-wavelength and low-Reynolds number approximations. The analytical solution has been derived for velocity and temperature. The amplitude ratio, particle concentration, catheter size, and the dimensionless flow rate were used to discuss the pressure gradient. The solutions for velocity and temperature derived in the analysis have been computed numerically and investigated. The tube surface is maintained at a fixed temperature. The variations of physical variables with the pertinent parameters were discussed graphically. The mathematical model presented corresponds to the flow in the annular space between two concentric tubes. It has been deduced that the thermal energy is reduced with particles’ concentration and with slip condition through the catheterized tube. The flow accelerates with the magnetic field and slip condition at the wall, whereas it decreases at the catheter. The catheter size has a different effect on both pressure drop and friction force.

1 Introduction

The peristaltic flows of fluids through conduits have attracted great attention due to their tremendous applications in physiological and medical engineering sciences, some of which, urine flow from kidney to bladder, motion of ova in the fallopian tubes, transport of food through esophagus, and through any other glandular duct. In manufacturing firms, these flows occur in blood pumping machines, in hygienic fluid transport, and in the transport of erosive fluids. It is clear the peristaltic transport of two immiscible viscous fluids in circular tube which has been investigated by Ramachandra and Usha [1]. Takabatake et al. [2] have investigated peristaltic pumping in circular tubes with numerical study of fluid transport and its efficiency. Abdelmaboud et al. [3] investigated the peristaltic motion via a conduit of finite length with varying the fluid viscosity. They later discussed the peristaltically induced motion of a couple stress fluid with rotation and concluded that the couple stress strongly reduces the pressure gradient [4]. Abdelsalam and Bhatti [5] investigated the effect of peristaltic blood flow along with ion slip and Hall effects on a nanofluid and came to a conclusion that both the temperature and concentration profiles are reduced under the effect of chemical reaction. For more work concerning peristalsis in different flow fields, the reader may be referred to refs. [6,7,8,9,10] and to the references therein. The theory of fluid suspension is very important in various situations such as sedimentation, dust filtration, ignition, argentine ash flow, ecological pollution, fluidization, and atmospheric collapse. Lately, the attention has developed in applying the theory of particle-fluid suspension to include biological flows such as the transport of blood through arterioles and veins [11, 12].

Ever since the pristine work of Latham [13] and Shapiro et al. [14] had come into sight, plentiful amount of applications about the peristaltic flows have developed. The study of slip flow via porous media has attracted much interest recently. It is widely known that transport through a porous media has important feasible implementations especially in seismic fluid dynamics. For instance, coast sand, sedimentary rocks, lumber, human bellows, gallstones, and in small blood arteries are some forms of natural porous media. In clinical pathology, the allocation of cholesterol and blood agglomeration that clogs the arteries in the hollow organs is analogous to a porous medium. Many researchers carried out several investigations through porous media such as that work that studies the effect of compliant walls on peristaltic motion through a 2D channel which was investigated by Abd Elnaby and Haroun [15]. Muthu et al. [16] discussed the peristalsis of a micropolar fluid and elastic properties of walls in circular cylindrical conduits. El Shehawey et al. [17] investigated the peristaltic fluid flow through a porous medium. Srinivas et al. [18] discussed the influence of slip conditions and porous medium on a peristaltic fluid flow. Hayat et al. [19] studied the magnetohydrodynamic (MHD) peristaltic flow of a non-Newtonian fluid through a channel of porous medium with compliant walls. In addition, slip flow was experimentally investigated by Derek et al. [20]. Hron et al. [21] obtained the analytical solutions of a generalized fluid flow taking into account that the slip conditions at the walls affect the flow. The boundary conditions of Newtonian fluid on peristaltic motion have been considered by Kwang and Fang [22]. For more work concerning slip boundary conditions in different flow fields, the reader may be referred to refs. [23,24,25,26,27,28,29] and to the references therein.

The MHD fluid flow in a tube with peristaltic motion has caught great attention in connection with specific problems that constitutes the motion of conductive organic fluids through glandular ducts, motion of the blood via pump machines, etc. And with the need for heretical research that runs through the operation of MHD peristaltic motion, some researchers, such as Sud et al. [30], discussed the influence of magnetic field on blood flow where it was observed that the effect of proper moving magnetic field accelerates the blood flow. Ebaid [31], on the other hand, investigated the impact of wall slip along with magnetic field on the peristalsis of a Newtonian fluid via and asymmetric conduit. The interaction of peristaltic motion with heat transfer plays a very important role as well in our life. Radhakrishnamacharya et al. [32] studied the effect of heat transfer and wall effects on the transport of an incompressible viscous fluid through a channel. Nadeem and Akbar [33] analyzed the effect thermal conductivity and variable viscosity along with magnetohydrodynamic peristaltic transport of a Newtonian incompressible fluid in a uniform conduit. Kothandapani and Srinivas [34] discussed the elasticity effect of flexible walls and thermal conductivity on the peristalsis of a magnetohydrodynamic fluid flow via a permeable medium. Radhakrishnamacharya and Srinisvasulu [35] showed the effect of wall properties accompanied with thermal conduction on the peristaltic motion. Taneja and Jain [36] investigated the impact of MHD on free convective flow with the existence of a heat source not depending on the temperature for an incompressible fluid via vertical wavy and parallel flat walls. For more applications about incorporating magnetic fields and heat transfer in different types of flows, the reader may be referred to refs. [37,38,39,40,41,42,43,44,45,46].

Since the discovery of the real reasons of diseases in the human body has greatly depended upon the use of endoscope theory, the catheter has played an important role in the modification of pressure gradient and in the exploration of small hollow ducts such as small intestines and stomach. It has turned into an essential tool for examining and curing of many cardiovascular diseases in modern medicine. Vajravelu et al. [47] studied the peristaltic motion with heat conduction through a vertical porous annulus with lubrication approach. Mekheimer and Abdelmaboud [48] investigated the impact of magnetic field and heat transfer on the peristalsis of a Newtonian fluid through an annulus as an application of endoscope. For more similar work incorporating particulate suspension through annular regions, the reader is referred to refs. [49, 50] and to the references therein. With the above discussion in mind, the purpose of the present work is to provide such an attempt for studying the MHD Newtonian fluid through porous catheterized tube. The characteristics of the flow are featured by the presented graphs. The paper has been organized as follows. In Section 1, the problem is modeled and the non-dimensional governing equations are formulated. Section 2 includes the solution of the problem under a low-Reynolds number and long-wavelength approximations. Numerical results and discussion are presented in Section 3. The conclusions have been summarized in Section 4.

2 Mathematical Formulation

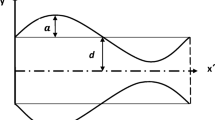
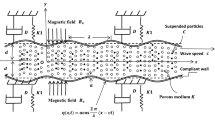
Suppose the flow of a viscous Newtonian fluid through a 2D symmetrical circular tube of radius a . The walls of the tube are considered flexible and are taken as a stretched membrane on which traveling sinusoidal waves of moderate amplitude is imposed (Fig. 1). A rigid catheter of radius a₁ is symmetrically implemented. The flow is caused by the imposed sinusoidal wave on the compliant wall of tube. The wave shape can be written as

$$ H\left({z}^{\prime },{t}^{\prime}\right)=a+b\sin \left(\frac{2\pi }{\lambda}\left({z}^{\prime }-{c}_w{t}^{\prime}\right)\right), $$

(1)

Fig. 1

Geometry of the problem

where b (0 ≤ b ≤ (a-a₁)) is the wave amplitude, λ (≤ is the length of the considered tube L) is the wavelength, c_w is the wave speed of propagation, t^′ is the time, and z^′ is the axial coordinate. The momentum, continuity, and energy equations for both the fluid and particle phases are applied on the mathematical model as expressed in [36, 44]. Neglecting the inertia forces of the particles, the governing equations can be written as

Axial momentum (fluid)

$$ \left(1-C\right){\rho}_f\left[\frac{\partial {u}_f^{\prime }}{\partial {t}^{\prime }}+{u}_f^{\prime}\frac{\partial {u}_f^{\prime }}{\partial {z}^{\prime }}+{v}_f^{\prime}\frac{\partial {u}_f^{\prime }}{\partial {r}^{\prime }}\right]=-\left(1-C\right)\frac{\partial {p}^{\prime }}{\partial {z}^{\prime }}-\sigma {\beta}_o^2{u}_f^{\prime }-\frac{\mu_o}{K}{u}_f^{\prime }+\left(1-C\right){\mu}_s(C)\left(\frac{1}{r^{\prime }}\frac{\partial }{\partial {r}^{\prime }}\left({r}^{\prime}\frac{\partial {u}_f^{\prime }}{\partial {r}^{\prime }}\right)+\frac{\partial }{\partial {z}^{\prime }}\left(\frac{\partial {u}_f^{\prime }}{\partial {z}^{\prime }}\right)\right)+C{S}^{\prime}\left({u}_p^{\prime }-{u}_f^{\prime}\right), $$

(2)

Radial momentum (fluid)

$$ \left(1-C\right){\rho}_f\left[\frac{\partial {v}_f^{\prime }}{\partial {t}^{\prime }}+{u}_f^{\prime}\frac{\partial {v}_f^{\prime }}{\partial {z}^{\prime }}+{v}_f^{\prime}\frac{\partial {v}_f^{\prime }}{\partial {r}^{\prime }}\right]=-\left(1-C\right)\frac{\partial {p}^{\prime }}{\partial {r}^{\prime }}+\left(1-C\right){\mu}_s(C)\left(\frac{1}{r^{\prime }}\frac{\partial }{\partial {r}^{\prime }}\left({r}^{\prime}\frac{\partial {v}_f^{\prime }}{\partial {r}^{\prime }}\right)-\frac{v_f^{\prime }}{{r^{\prime}}^2}+\frac{\partial }{\partial {z}^{\prime }}\left(\frac{\partial {v}_f^{\prime }}{\partial {z}^{\prime }}\right)\right)+C{S}^{\prime}\left({v}_p^{\prime }-{v}_f^{\prime}\right), $$

(3)

Mass equation (fluid)

$$ \frac{1}{r^{\prime }}\frac{\partial }{\partial {r}^{\prime }}\left({r}^{\prime}\left(1-C\right){v}_f^{\prime}\right)+\frac{\partial }{\partial {z}^{\prime }}\left(\left(1-C\right){u}_f^{\prime}\right)=0, $$

(4)

Axial momentum (particle)

$$ C{\rho}_p\left[\frac{\partial {u}_p^{\prime }}{\partial {t}^{\prime }}+{u}_p^{\prime}\frac{\partial {u}_p^{\prime }}{\partial {z}^{\prime }}+{v}_p^{\prime}\frac{\partial {u}_p^{\prime }}{\partial {r}^{\prime }}\right]=-C\frac{\partial {p}^{\prime }}{\partial {z}^{\prime }}+C{S}^{\prime}\left({u}_f^{\prime }-{u}_p^{\prime}\right), $$

(5)

Radial momentum (particle)

$$ C{\rho}_p\left[\frac{\partial {v}_p^{\prime }}{\partial {t}^{\prime }}+{u}_p^{\prime}\frac{\partial {v}_p^{\prime }}{\partial {z}^{\prime }}+{v}_p^{\prime}\frac{\partial {v}_p^{\prime }}{\partial {r}^{\prime }}\right]=-C\frac{\partial {p}^{\prime }}{\partial {r}^{\prime }}+C{S}^{\prime}\left({v}_f^{\prime }-{v}_p^{\prime}\right), $$

(6)

Mass equation (particle)

$$ \frac{1}{r^{\prime }}\frac{\partial }{\partial {r}^{\prime }}\left({r}^{\prime }C{v}_p^{\prime}\right)+\frac{\partial }{\partial {z}^{\prime }}\left(C{u}_p^{\prime}\right)=0, $$

(7)

The energy equation can be expressed as

$$ \left(1-C\right){c}_p\left[\frac{\partial T}{\partial {t}^{\prime }}+{v}_r^{\prime}\frac{\partial T}{\partial {r}^{\prime }}+{v}_z^{\prime}\frac{\partial T}{\partial {z}^{\prime }}\right]=\frac{K}{\rho}\left[\frac{\partial^2T}{\partial {r^{\prime}}^2}+\frac{1}{r^{\prime }}\frac{\partial T}{\partial {r}^{\prime }}+\frac{\partial^2T}{\partial {z^{\prime}}^2}\right]+\left(1-C\right)\frac{\mu_s}{\rho}\left(2\left({\left(\frac{\partial {v}_r^{\prime }}{\partial {r}^{\prime }}\right)}^2+{\left(\frac{\partial {v}_z^{\prime }}{\partial {z}^{\prime }}\right)}^2+{\left(\frac{v_r^{\prime }}{r^{\prime }}\right)}^2\right)+{\left(\frac{\partial {v}_r^{\prime }}{\partial {z}^{\prime }}+\frac{\partial {v}_z^{\prime }}{\partial {r}^{\prime }}\right)}^2\right), $$

(8)

where u^′ and v^′ are the velocity components, μ is the coefficient of dynamic viscosity, T is the temperature, K is the thermal conductivity, c_p is the specific heat at constant pressure, and z^′ is the axial coordinate.

The boundary conditions that must be satisfied by the fluid on the wall of the catheter are the slip conditions suggested by Kwang and Fang [22] and can be written as

$$ {u}_w^{\prime }=\pm A\frac{\partial {u}_w^{\prime }}{\partial {r}^{\prime }}-1,\mathrm{at}\ {r}^{\prime }={a}_1\mathrm{and}\ r\hbox{'}=a+b\ \sin \left(\frac{2\pi }{\lambda}\left(z\hbox{'}{c}_wt\hbox{'}\right)\right), $$

(9)

$$ {v}_w^{\prime }=\pm \frac{\partial \eta }{\partial {t}^{\prime }},\kern0.5em \mathrm{at}\kern0.5em r\hbox{'}=a+b\ \sin \left(\frac{2\pi }{\lambda}\left(z\hbox{'}{c}_wt\hbox{'}\right)\right), $$

(10)

where ${u}_w^{\prime }$ and ${v}_w^{\prime }$ are the fluid or particle velocities in the streamwise and radial directions, respectively.

$$ T={T}_1,\mathrm{at}\kern0.5em r\hbox{'}=a+b\ \sin \left(\frac{2\pi }{\lambda}\left(z\hbox{'}{c}_wt\hbox{'}\right)\right),\kern0.5em \left(\mathrm{isothermal}\ \mathrm{condition}\right) $$

(11)

$$ \frac{\partial T}{\partial {r}^{\prime }}=0,\mathrm{at}\ r\hbox{'}=a1\ \left(\mathrm{adiabatic}\ \mathrm{condition}\right) $$

(12)

where A is the mean free path (it ranges from 0.05 to 0.15 for liquids), $\eta \left({z}^{\prime },{t}^{\prime}\right)=b\sin \left(\frac{2\pi }{\lambda}\left({z}^{\prime }-{c}_w{t}^{\prime}\right)\right),{r}^{\prime }$ is the radial coordinate, $\left({u}_f^{\prime },v{\hbox{'}}_f\right)$ and $\left({u}_p^{\prime },v{\hbox{'}}_p\right)$ denote the velocity components of the fluid and particle phase along (z^′, r') directions, respectively. C is the volume fraction of particulate phase that is chosen to be constant and whish was found to be a good approximation for low concentration of small particles, p^′ is the pressure, ρ_f and ρ_p are the actual densities of the material comprising fluid and particle phases, respectively. S^′ is the drag coefficient of interaction, and μ_s(C) is the mixture viscosity.

The empirical formulae for the suspension viscosity (μ_s) has been chosen for the present problem as [51]:

$$ {\mu}_S(C)=\frac{\mu_o}{1- mC}, $$

(13)

where$m=0.07\exp \left[2.49C+\left(\frac{1107}{T}\right)\exp \left(-1.69C\right)\right]$, T is the temperature of the mixture measured in absolute scale (K), and μ_ois the carrier fluid viscosity. The viscosity of the mixture expressed by Eq. (13) is found to be reasonably precise up to C = 0.59 (i.e., 59% particle concentration) [52].

The formulae for the drag coefficient of interaction S^′ is selected from Tam [53] as

$$ {S}^{\prime }=\frac{9}{2}\frac{\mu_o}{a_o^2}D,\mathrm{where}\kern0.5em D=\left[\frac{4+3{\left[8\ C-3\ {C}^2\right]}^{1/2}+3\ C}{{\left[2-3\ C\right]}^2}\right], $$

(14)

with a_o as the radius of a particle.

We introduce the following dimensionless variables $r=\frac{r^{\prime }}{a},z=\frac{z^{\prime }}{\lambda },{u}_f=\frac{u_f^{\prime }}{c_w},{v}_f=\frac{\lambda {v}_f^{\prime }}{a\ {c}_w},{u}_p=\frac{u_p^{\prime }}{c_w},{v}_p=\frac{\lambda {v}_p^{\prime }}{a{c}_w},S=\frac{S^{\prime }{a}^2}{\mu_o},\mu =\frac{\mu_s}{\mu_o},t=\frac{c_w{t}^{\prime }}{\lambda },P=\frac{a^2{P}^{\prime }}{\lambda {c}_w{\mu}_o},k=\frac{K}{a^2},\theta =\frac{\left(T-{T}_o\right)}{T_o}$, $and\kern0.50em Kn=\frac{A}{a},$ such that Kn is knudsen number, θ is the dimensionless temperature, and k is the dimensionless thermal conductivity.

Substituting the dimensionless parameters into the governing Eqs. (2)–(12) yields the followings:

$$ {\displaystyle \begin{array}{c}\left(1-C\right)\delta \operatorname{Re}\left(\frac{\partial {u}_f}{\partial t}+{u}_f\frac{\partial {u}_f}{\partial z}+{v}_f\frac{\partial {u}_f}{\partial r}\right)=-\left(1-C\right)\frac{\partial p}{\partial z}-\left(\frac{\sigma {\beta}_o^2{a}^2}{\mu_o}+\frac{1}{k}\right){u}_f\\ {}\left(1-C\right)\mu \left(\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial {u}_f}{\partial r}\right)+{\delta}^2\frac{\partial }{\partial z}\left(\frac{\partial {u}_f}{\partial z}\right)\right)+ CS\left({u}_p-{u}_f\right),\end{array}} $$

(15)

$$ \left(1-C\right)\delta \operatorname{Re}\left(\frac{\partial {v}_f}{\partial t}+{u}_f\frac{\partial {v}_f}{\partial z}+{v}_f\frac{\partial {v}_f}{\partial r}\right)=-\left(1-C\right)\frac{\partial p}{\partial r}+\left(1-C\right)\mu\ {\delta}^2\left(\frac{\partial }{\partial r}\frac{1}{r}\left(\frac{\partial \left(r\ {v}_f\right)}{\partial r}\right)-\frac{1}{r^2}+{\delta}^2\frac{\partial }{\partial z}\left(\frac{\partial {v}_f}{\partial z}\right)\right)+ CS\left({v}_p-{v}_f\right), $$

(16)

$$ \frac{1}{r}\frac{\partial }{\partial r}\left(r\left(1-C\right){v}_f\right)+\frac{\partial }{\partial z}\left(\left(1-C\right){u}_f\right)=0, $$

(17)

$$ C\frac{\rho_p}{\rho_f}\operatorname{Re}\delta \left(\frac{\partial {u}_p}{\partial t}+{u}_p\frac{\partial {u}_p}{\partial z}+{v}_p\frac{\partial {u}_p}{\partial r}\right)=-C\frac{\partial p}{\partial z}+ CS\left({u}_f-{u}_p\right), $$

(18)

$$ C\frac{\rho_p}{\rho_f}\operatorname{Re}\delta \left(\frac{\partial {v}_p}{\partial t}+{u}_p\frac{\partial {v}_p}{\partial z}+{v}_p\frac{\partial {v}_p}{\partial r}\right)=-C\frac{\partial p}{\partial r}+ CS{\delta}^2\left({v}_f-{v}_p\right), $$

(19)

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( rC{v}_p\right)+\frac{\partial }{\partial z}\left(C{u}_p\right)=0, $$

(20)

$$ \left(1-C\right)\delta \operatorname{Re}\left(\frac{\partial \theta }{\partial t}+{v}_r\frac{\partial \theta }{\partial r}+{v}_z\frac{\partial \theta }{\partial z}\right)=\frac{k}{c_p{\mu}_0}\left(\frac{\partial^2\theta }{\partial {r}^2}+\frac{1}{r}\frac{\partial \theta }{\partial r}+{\delta}^2\frac{\partial^2\theta }{\partial {z}^2}\right)+\left(1-C\right)\frac{\mu {c}^2}{c_p{T}_o}\left(2{\delta}^2{\left(\frac{\partial {v}_r}{\partial r}\right)}^2+2{\delta}^2{\left(\frac{\partial {v}_z}{\partial z}\right)}^2+2{\delta}^2{\left(\frac{v_r}{r}\right)}^2+{\delta}^4{\left(\frac{\partial {v}_r}{\partial z}\right)}^2+{\left(\frac{\partial {v}_z}{\partial r}\right)}^2+2{\delta}^2\frac{\partial {v}_r}{\partial z}\frac{\partial {v}_z}{\partial r}\right), $$

(21)

The amplitude equation will be dimensionalized to become h = 1 + ϕ sin(2πz).

The dimensionless parameters in the previous equations are Re = ρ_fc_wa/μ_o, δ = a/λ and ϕ = $\frac{b}{a}$, ε = a₁/a, $M=\sqrt{\sigma /{\mu}_o}{\beta}_oa$, where Re is the Reynolds number, δ is the wave number, ϕ is the amplitude ratio, ε is the catheter size, and M is the magnetic parameter, respectively.

With the aid of the long-wavelength approximation (i.e., δ < < 1) as considered by Shapiro et al. [14], the equations describing the flow in the wave frame can be reduced to

Reduced radial momentum equation of particle

$$ \frac{dp}{dr}=0, $$

(22)

Reduced radial momentum equation of fluid

$$ \left(1-C\right)\frac{dp}{dr}= CS\left({v}_p-{v}_f\right), $$

(23)

$$ {v}_p={v}_f=0\kern0.50em at\ \ r=\varepsilon, $$

$$ {v}_p={v}_f\ne 0\kern0.50em at\ \ r=h. $$

Reduced axial momentum equation of fluid

$$ \left(1-C\right)\frac{dp}{dz}=\left(1-C\right)\frac{\mu }{r}\frac{\partial }{\partial r}\left(r\frac{\partial {u}_f}{\partial r}\right)-\left({M}^2+\frac{1}{k}\right){u}_f+ CS\left({u}_p-{u}_f\right). $$

(24)

Reduced axial momentum equation of particle

$$ C\frac{dp}{dz}= CS\left({u}_f-{u}_p\right). $$

(25)

Reduced energy equation

$$ -\frac{k}{c_p{\mu}_o}\left(\frac{\partial^2\theta }{\partial {r}^2}+\frac{1}{r}\frac{\partial \theta }{\partial r}\right)=\left(1-C\right)\frac{\mu {c}_w^2}{c_p{T}_o}{\left(\frac{\partial {v}_z}{\partial r}\right)}^2. $$

(26)

The non-dimensional slip and temperature conditions are

$$ {\mathrm{u}}_f=\pm Kn\frac{\partial {\mathrm{u}}_f}{\partial r}-1\mathrm{at}\kern0.5em r=\varepsilon, $$

(27)

$$ {\displaystyle \begin{array}{l}{\mathrm{u}}_f=\pm Kn\frac{\partial {\mathrm{u}}_f}{\partial r}-1\kern0.5em \mathrm{at}\kern0.5em r=h=1+\phi \sin \left(2\pi z\right),\\ {}\ \end{array}} $$

(28)

$$ {\displaystyle \begin{array}{l}{\theta}_f={\theta}_1=1,\kern0.5em \mathrm{at}\kern0.75em r=h=1+\phi \sin \left(2\pi z\right),\\ {}\ \end{array}} $$

(29)

$$ \frac{\partial\ \theta }{\partial\ r}=0,\mathrm{at}\kern0.5em r=\varepsilon . $$

(30)

The expressions for the velocity distributions, u_f and u_p, can be obtained by solving Eqs. (24) and (25) subject to the boundary conditions (27) and (28) as follows:

$$ {u}_f=\frac{\frac{\left( dp/ dz\right)}{\left(1-C\right)\mu }}{-\left({M}^2+\frac{1}{k}\right)}+{n}_1b{r}_1+{m}_1b{r}_2,{\psi}_f=\underset{\varepsilon }{\overset{h}{\int }}r.{u}_f\; dr $$

(31)

$$ {u}_p={u}_f-\frac{1}{S}\frac{dp}{dz}, $$

(32)

$$ \frac{dp}{dz}=\frac{-8\mu \left(1-C\right)\left(Q-1-\frac{\phi^2}{2}+{h}^2\right)}{\left({h}^2-{\varepsilon}^2\right){X}_z} $$

(33)

where n₁,m₁, d, X_z, β are given by

$$ {\displaystyle \begin{array}{c}{n}_1=\frac{d\left(b{\varepsilon}_2-{k}_n{q}_6\right)-d\left(b{h}_2-{k}_n{q}_4\right)}{\left(b{h}_1-{k}_n{q}_3\right)\left(b{\varepsilon}_2-{k}_n{q}_6\right)-\left(b{h}_2-{k}_n{q}_4\right)\left(b{\varepsilon}_1-{k}_n{q}_5\right)},\\ {}{m}_1=\frac{d\left(b{h}_1-{k}_n{q}_3\right)-d\left(b{\varepsilon}_1-{k}_n{q}_5\right)}{\left(b{h}_1-{k}_n{q}_3\right)\left(b{\varepsilon}_2-{k}_n{q}_6\right)-\left(b{h}_2-{k}_n{q}_4\right)\left(b{\varepsilon}_1-{k}_n{q}_5\right)},\\ {}d=-1+\frac{\frac{\left( dp/ dz\right)}{\left(1-C\right)\mu }}{M^2+\frac{1}{k}},{X}_z={h}^2+{\varepsilon}^2+\beta -\frac{\left({h}^2-{\varepsilon}^2\right)}{\ln \left(\frac{h}{\varepsilon}\right)},\beta =\frac{8\mu\ C\left(1-C\right)}{S},\end{array}} $$

such that

$$ {\displaystyle \begin{array}{c}b{r}_1={I}_0(r)=1+\frac{g^2{r}^2}{4}+\frac{g^4{r}^4}{64},\\ {}b{r}_2={K}_0(r)=-\ln \left(\frac{g.r}{2}\right)-\frac{g^2{r}^2\ln \left(\frac{g.r}{2}\right)}{4}+\frac{\left(2-2\gamma \right){g}^2{r}^2}{8}-\gamma, \\ {}b{h}_1={I}_0(h),b{h}_2={K}_0(h),b{\varepsilon}_1={I}_0\left(\varepsilon \right),b{\varepsilon}_2={K}_0\left(\varepsilon \right),\\ {}{q}_3=\frac{\partial b{h}_1}{\partial h},{q}_4=\frac{\partial b{h}_2}{\partial h},{q}_5=\frac{\partial b{\varepsilon}_1}{\partial \varepsilon },{q}_6=\frac{\partial b{\varepsilon}_1}{\partial \varepsilon },g=\sqrt{\left({M}^2+\frac{1}{k}\right)},\end{array}} $$

such that I₀ is the modified Bessel function at zero order of the first kind, and K₀ is the modified Bessel function at zero order of the second kind.

It is worth noting that Eq. (31) represents the same formula obtained by Medhavi [54] with neglecting the effect of magnetic field, porous media, and slip condition from the current flow field.

The expression of the temperature profile θ obtained as a solution of Eq. (26) with introducing the temperature conditions (29) and (30), the pressure drop, and the friction force are given by:

$$ \theta ={C}_1+{C}_2\ln (r)-\left(1-C\right)\mu\ {B}_r\ {T}_p, $$

(34)

$$ \varDelta P=2\mu \left(1-C\right)\left(\left(Q-1-\frac{\phi^2}{2}\right){I}_1+{I}_2\right), $$

(35)

$$ F=2\mu \left(1-C\right)\left(\left(Q-1-\frac{\phi^2}{2}\right){I}_2+{I}_3\right), $$

(36)

$$ {I}_1=4\underset{0}{\overset{1}{\int }}\frac{dz}{\left({h}^2-{\varepsilon}^2\right)\chi (z)},{I}_2=4\underset{0}{\overset{1}{\int }}\frac{dz}{\left(1-\frac{\varepsilon^2}{h^2}\right)\chi (z)},{I}_3=4\underset{0}{\overset{1}{\int }}\frac{h^2 dz}{\left(1-\frac{\varepsilon^2}{h^2}\right)\chi (z)}. $$

where

$$ {\displaystyle \begin{array}{c}\begin{array}{l}{T}_p=a\Big[b\left(\frac{g^4{r}^3}{36}+\frac{g^8{r}^7}{16^2.49}+\frac{g^6{r}^5}{16.25}\right)+\frac{1}{r}+\frac{g^4{r}^3}{16.9}+\frac{g^4{r}^3}{36}{\left(\ln \frac{g}{2}\right)}^2+\frac{g^4{r}^3}{36}\left({\left(\ln r\right)}^2-\frac{4r}{3}\ln r+\frac{2}{3}\right)\\ {}+\frac{g^4{r}^3}{18}\ln \left(\frac{g}{2}\right)\left(\ln r-\frac{2}{3}\right)+\frac{g^4{r}^3}{16.9}\left(2-2\gamma \right)-\frac{g^4{r}^3}{36}\left(\left(2-2\gamma \right)+1\right)\left(\ln \frac{g}{2}+\ln r-\frac{2}{3}\right)-\frac{g^4{r}^3}{8.9}\left(2-2\gamma \right),\\ {}+{g}^2r\left(\ln \frac{g}{2}+\ln r-2\right)+\frac{g^2r}{2}\left(1-\left(2-2\gamma \right)\right)-2\sqrt{b}\Big(-\frac{g^2r}{2}-\frac{g^4{r}^3}{16.9}-\frac{g^4{r}^3}{8.9}+\frac{g^6{r}^5}{64.25}-\\ {}\frac{g^4{r}^3}{36}\left(\ln \frac{g}{2}+\ln r-\frac{2}{3}\right)-\frac{g^6{r}^5}{32.25}\left(\ln \frac{g}{2}+\ln r-\frac{2}{3}\right)+\frac{g^4{r}^3}{8.9}\left(2-2\gamma \right)+\frac{g^6{r}^5}{64.25}\left(2-2\gamma \right)\left)\right)\end{array}\\ {}\begin{array}{l}{C}_1={\theta}_1-{C}_2\ln h+\left(1-C\right)\mu {B}_ra\Big[b\left(\frac{g^4{h}^3}{36}+\frac{g^8{h}^7}{16^2.49}+\frac{g^6{h}^5}{16.25}\right)+\frac{1}{h}+\frac{g^4{h}^3}{16.9}+\frac{g^4{h}^3}{36}{\left(\ln \frac{g}{2}\right)}^2+\frac{g^4{h}^3}{36}\left({\left(\ln h\right)}^2-\frac{4h}{3}\ln h+\frac{2}{3}\right)\\ {}+\frac{g^4{h}^3}{18}\ln \left(\frac{g}{2}\right)\left(\ln h-\frac{2}{3}\right)+\frac{g^4{h}^3}{16.9}\left(2-2\gamma \right)-\frac{g^4{h}^3}{36}\left(\left(2-2\gamma \right)+1\right)\left(\ln \frac{g}{2}+\ln h-\frac{2}{3}\right)-\frac{g^4{h}^3}{8.9}\left(2-2\gamma \right)\\ {}+{g}^2h\left(\ln \frac{g}{2}+\ln h-2\right)+\frac{g^2h}{2}\left(1-\left(2-2\gamma \right)\right)-2\sqrt{b}\Big(-\frac{g^2h}{2}-\frac{g^4{h}^3}{16.9}-\frac{g^4{h}^3}{8.9}+\frac{g^6{h}^5}{64.25}-\\ {}\kern0.50em \ \kern0.50em \ \kern0.50em \ \frac{g^4{h}^3}{36}\left(\ln \frac{g}{2}+\ln h-\frac{2}{3}\right)-\frac{g^6{h}^5}{32.25}\left(\ln \frac{g}{2}+\ln h-\frac{2}{3}\right)+\frac{g^4{h}^3}{8.9}\left(2-2\gamma \right)+\frac{g^6{h}^5}{64.25}\left(2-2\gamma \right)\left)\right),\end{array}\\ {}\begin{array}{l}{C}_2=\left(1-C\right)\mu {B}_r\varepsilon a\left[b\left(\frac{g^4{r}^2}{12}+\frac{g^8{r}^6}{16^2.7}+\frac{g^6{r}^4}{16.5}\right)-\frac{1}{r^2}+\frac{g^4{r}^2}{16.3}+\frac{g^4{r}^2}{12}{\left(\ln \frac{g}{2}\right)}^2+\frac{g^4}{36}{\left(2{r}^2\ln r+\left(\ln r\right)\right)}^23{r}^2-\frac{4}{3}\left({r}^2+3{r}^2\ln r\right)+2{r}^2\right)\\ {}+\frac{g^4}{18}\ln \left(\frac{g}{2}\right)\left({r}^2+3{r}^2\ln r-2{r}^2\right)+\frac{g^4{r}^2}{16.3}{\left(2-2\gamma \right)}^2-\frac{g^4}{4}\left(\left(2-2\gamma +1\right)\right)\left(\frac{r^2}{3}\ln \frac{g}{2}+\frac{1}{9}\left({r}^2+3{r}^2\ln r-2{r}^2\right)\right)-\frac{g^4{r}^2}{8.3}\left(2-2\gamma \right)\\ {}+{g}^2\left(\ln \frac{g}{2}+\ln r-1\right)+\frac{g^2}{2}\left(1-\left(2-2\gamma \right)\right)-2\sqrt{b}\Big(-\frac{g^2}{2}-\frac{g^4{r}^2}{16.3}-\frac{g^4{r}^2}{8.3}+\frac{g^6{r}^4}{64.5}-\\ {}\ \frac{g^4}{4}\left(\frac{r^2}{3}\ln \frac{g}{2}+\frac{1}{9}\left({r}^2+3{r}^2\ln r-2{r}^2\right)\right)-\frac{g^6}{32}\left(\frac{r^4}{5}\ln \frac{g}{2}+\frac{1}{25}\left({r}^4+5{r}^4\ln r-2{r}^4\right)\right)+\left(2-2\gamma \right)\left(\frac{g^4{r}^2}{8.3}+\frac{g^6{r}^4}{64.5}\right)\left)\right),\end{array}\end{array}} $$

where

$$ a={\left({m}_1\right)}^2,b={\left(\frac{n_1}{m_1}\right)}^2,\Pr ={\mu}_o{c}_p/k,E={c}^2/{c}_p{T}_o, Br=E\ \Pr . $$

in which Pr is the Prandtl number, E is the Eckert number, and Br is the Brinkman number.

3 Numerical Results and Discussion

The impact of the diverse parameters including the particle concentration, C, the catheter size, ε, and the amplitude ratio, ϕ, is going to be discussed in this section. The analytical outcomes derived in the study are considered at a reference temperature of 298 K. The parameters values are selected as a (tube radius) = 1.25 cm; C = 0, 0.2, 0.4, and 0.59; ϕ = 0, 0.2, 0.4, and 0.6; ε = 0, 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6; a_o (radius of a particle) = 0.1 cm and Q = 0, 0.4, 0.6, 0.8, and 1.0. The present study includes different cases for C = 0 (absence of concentration) and C ≠ 0 (presence of concentration). On the other hand, the variation of amplitude ratio is taken into consideration. Also, the results of the thermal study have been investigated under different values of flow rate (Q = 0, 0.2, 0.4), catheter size (ε = 0.1, 0.2, 0.3), amplitude ratio (ϕ = 0, 0.2, 0.4), and fluid suspension (C = 0, 0.2, 0.4, 0.59).

Figure 2 shows the axial velocity profiles at different locations at z = 0.75. It is seen that the velocity increases due to the reduced flow area, whereas at z = 0.25, the velocity decreases due to the enlarged cross section.

Fig. 2

Velocity profiles at different values of z for (a) Kn = 0 and (b) Kn = 0.1 at (ε = 0.2, M = 2, k = 5, ϕ = 0.2, Q = 0.2)

Figure 3 represents the velocity profiles of the fluid at different flow rates. It is observed that with the absence of catheter, the velocity profiles are identical with increase in the central velocity with the flow rate. It is also seen that the tube wall velocity increases with an increase in the flow rate in the case of catheterized tube (Kn = 0.1), alternatively, a deceleration in the behavior of the catheter wall velocity with r is noticed.

Fig. 3

Velocity profiles at different flow rates for (a) Kn = 0 and (b) Kn = 0.1 at (ε = 0.2, M = 2, k = 5, ϕ = 0.2, Q = 0.2)

The effects of particles’ concentration on the velocity distribution at ϕ = 0.2, ε = 0.2, and Q = 0.2 are seen in Fig. 4. For both non-slip condition and slip condition, it is noticed that different suspensions have no effect on the velocity distribution.

Fig. 4

Velocity profiles at different concentrations for (a) Kn = 0 and (b) Kn = 0.1 at (ε = 0.2, M = 2, k = 5, ϕ = 0.2, Q = 0.2)

Figure 5 represents the velocity profiles of the fluid with slip condition at different Knudsen number. It is observed that slip conditions on the tube wall enhances the near-wall velocity, while slip conditions at the catheter reduces the near-wall velocity.

Fig. 5

Velocity profiles at different values of Kn at (ε = 0.2, M = 2, k = 5, ϕ = 0.2, Q = 0.2)

Figure 6 shows the velocity profiles of the fluid at different values of the magnetic parameter. It is noticed that the magnetic parameter on the tube wall enhances the near-wall velocity, while the near-wall velocity of the catheter decreases with magnetic parameter.

Fig. 6

Velocity profiles at different values of M for (a) Kn = 0 and (b) Kn = 0.1 at (ε = 0.2, C = 0.2, k = 5, ϕ = 0.2, Q = 0.2)

Figure 7 represents the effect of porous medium on the velocity distributions for ϕ = 0.2, ε = 0.2, and Q = 0.2. It is observed the effect of porosity is insignificant on the velocity distribution.

Fig. 7

Velocity profiles at different porous media for (a) Kn = 0 and (b) Kn = 0.1 at (ε = 0.2, C = 0.2, M = 2, ϕ = 0.2, Q = 0.2)

Figure 8 elucidates the behavior of velocity profile that is plotted versus different values of the amplitude ratio, with the slip parameter. It is observed that in either cases (no-slip or slip conditions), the flow accelerates with the catheter.

Fig. 8

Velocity profiles at different catheter sizes for (a) Kn = 0 and (b) Kn = 0.1 at (k = 5, C = 0.2, M = 2, ϕ = 0.2, Q = 0.2)

The effect of amplitude ratio (ϕ) on the velocity distribution is shown in Fig. 9 where it is seen that the velocity decreases with an increase in ϕ.

Fig. 9

Velocity profiles at different amplitude ratios for (a) Kn = 0 and (b) Kn = 0.1 at (k = 5, C = 0.2, M = 2, ε = 0.2, Q = 0.2)

Figure 10 shows the relation between the temperature and the radius at different locations where it is seen that at both the expansion (z = 0.25) and the contraction (z = 0.75), the temperature increases.

Fig. 10

Temperature profiles at different values of z for (a) Kn = 0 and (b) Kn = 0.1 at (k = 5, C = 0.2, M = 2, ε = 0.2, Q = 0.2, ϕ = 0.2)

Since the flow rate plays an important role in enhancing the temperature (θ), it is observed from Fig. 11 that with increasing the flow rate, the thermal energy increases with/without slipping.

Fig. 11

Variation of θ with the flow rate for (a) Kn = 0 and (b) Kn = 0.1 at (k = 5, C = 0.2, M = 2, ε = 0.2, ϕ = 0.2)

It is seen that temperature (θ) decreases with an increase in the suspension (C), as shown in Fig. 12, for both slip and non-slip flows.

Fig. 12

Variation of θ with suspension for (a) Kn = 0 and (b) Kn = 0.1 at (k = 5, C = 0.2, M = 2, ε = 0.2, ϕ = 0.2)

Figure 13 shows the relation between the temperature and the slip parameter at the wall and catheter where it is seen that the temperature decreases when Knudsen number increases.

Fig. 13

Temperature profiles at different values of Kn

Figure 14 elucidates that the temperature increases with the increase in the magnetic parameter (M) since the enhanced thermal energy accompanies the magnetic field.

Fig. 14

Variation of θ with the magnetic field for (a) Kn = 0 and (b) Kn = 0.1 at (K = 5, C = 0.2, C = 0.2, ε = 0.2, ϕ = 0.2)

It is observed that there is no variation in the temperature distribution under the effect of porous medium parameter as seen in Fig. 15.

Fig. 15

Variation of θ with the porous media for (a) Kn = 0 and (b) Kn = 0.1 at (M = 2, C = 0.2, C = 0.2, ε = 0.2, ϕ = 0.2)

For both slip and non-slip conditions, it is observed that the temperature is seen to increase with Brinkman number (Br) as observed in Fig. 16. Also, the temperature is seen to increase with the presence of catheter as described in Fig. 17. The effect of amplitude ratio (ϕ) on the temperature distribution is shown in Fig. 18 where it is noticed that the temperature increases when (ϕ) increases.

Fig. 16

Variation of θ with the Brinkman number for (a) Kn = 0 and (b) Kn = 0.1 at (M = 2, C = 0.2, C = 0.2, ε = 0.2, ϕ = 0.2, k = 5)

Fig. 17

Variation of θ with the catheter size for (a) Kn = 0 and (b) Kn = 0.1 at (M = 2, C = 0.2, Q = 0.2, ϕ = 0.2, k = 5)

Fig. 18

Variation of θ with the amplitude ratio for (a) Kn = 0 and (b) Kn = 0.1 at (M = 2, C = 0.2, Q = 0.2, ε = 0.2, k = 5)

For any given set of parameters, a linear relationship between the pressure difference and the flow is shown in Figs. 19, 20, and 21. The pressure drop (Δp) increases with flow rate (Q) for other parameters given which in turn implies that an increase in the flow rate reduces the pressure rise (-Δp); thus, the maximum flow rate is achieved at zero pressure rise and the maximum pressure occurs at zero flow rate. It is seen that Δp increases with particle concentration for any given flow rate in both catheterized and uncatheterized tubes as shown in Fig. 19. One also observes that the pressure drop decreases indefinitely with increasing the amplitude ratio for any given set of other parameters as analyzed in Fig. 20. Figure 21 shows that Δp assumes higher magnitudes for larger flow rate with small values of the amplitude ratio, but the property reverses for large values of ϕ. It is further shown in Fig. 22 that ε has a decreasing effect on Δp.

Fig. 19

Variation of ΔP with the flow rate at different values of suspended paricle concentration at (ϕ = 0, ε = 0.2)

Fig. 20

Variation of ΔP with the flow rate at different values of amplitude ratio at (C = 0.2, ε = 0.2)

Fig. 21

Variation of ΔP with the amplitude ratio at different values of flow rate at (C = 0.2, ε = 0.2)

Fig. 22

Variation of ΔP with the particle concentration at different values of catheter size at (Q = 0.2, ϕ = 0.2)

It is seen fom Fig. 23 that the friction force at the tube wall (F) is seen to increase with the particle concentration (C) for any given values of Q, ϕ, and ε. Figure 24 shows that F decreases indefinitely with increasing amplitude ratio (ϕ). The flow characteristic F is also seen to increase with increasing the flow rate and with increasing the catheter size as seen in Figs. 25 and 26. The streamlines are further presented in Figs. 27, 28, and 29 for various value of the pertinent parameters. Our investigation represents a general model to the cases studied by the authors in refs. [48,49,50].

Fig. 23

Variation of F with the flow rate at different values of suspended paricle concentration at (ϕ = 0.2, ε = 0.2)

Fig. 24

Variation of F with the flow rate at different values of amplitude ratio at (C = 0.2, ε = 0.2)

Fig. 25

Variation of F with the amplitude ratio at different values of flow rate at (C = 0.2, ε = 0.2)

Fig. 26

Variation of F with the suspended particle concentration at different values of catheter size at (Q = 0.2, ϕ = 0.2)

Fig. 27

Streamlines with Knudsen number at (Q = 0.2, ϕ = 0.4, C = 0.2, ε = 0.2)

Fig. 28

Streamlines with flow rate at (Kn = 0.1, ϕ = 0.4, C = 0.2, ε = 0.2)

Fig. 29

Streamlines with flow rate at (Kn = 0.1, Q = 0.2, C = 0.2, ε = 0.2)

4 Conclusions

This study investigates the combined effect of slip condition and heat transfer on particulate-fluid suspension with peristaltic transport in a catheterized tube under the influence of a magnetic field and porosity. The analytical solution has been developed and used for extracting, the velocity, and temperature of fluid via uniform tube under a long-wave length and low-Reynolds number approximations. The features of the flow characteristics are presented using graphs for both slipping and no slipping cases. The main points obtained from the present study are as follows:

• 1- Unlike the velocity behavior at the contracted flow field, it decreases at the expanded part.

• 2- The flow rate enhances the velocity at the wall and reduces the velocity at the catheter.

• 3- The particle concentration and porous media have insignificant effect on the velocity.

• 4- The flow accelerates with the magnetic field and slip condition at the wall, whereas it decreases at the catheter.

• 5- The temperature decreases at the contracted region, while increases at the expanded one.

• 6- The flow rate, magnetic field, and the presence of catheter enhance the thermal energy of the fluid.

• 7- The particle concentration and slip condition reduce the thermal energy, whereas the porosity has no effect on the temperature.

• 8- The Brinkman number enhances the temperature.

• 9- The catheter size has a different effect on both pressure drop and friction force.

• 10- This model is more general than other models, where the study of Mekheimer and Abdelmaboud [50] was recovered by neglecting the heat transfere (transfer not transfere), slip boundary conditions, and porous media ("porosity parameter" instead of "porous media"). Also, the results of Medhavi’s study [54] are recovered by neglecting the effects of slip condition, porous media, heat transfer, and the magnetic field in our study.