Thermal analysis in unsteady radiative Maxwell nanofluid flow subject to heat source/sink

Abstract

Currently, various researchers achieved theoretical and experimental works to scrutinize the influence of nanofluid in diverse forms of heat exchangers. In any engineering applications heat exchangers are critical components. Nanofluids are colloidal assortment of non-metallic or metallic particles suspended in base liquid. This study communicates a critical analysis of heat transport application of nanofluid. We established a model for unsteady flow of Maxwell nanofluid with the aspect of thermal radiation due to stretched cylinder. Moreover, heat source/sink is considered. Appropriate conversions yield the ordinary differential equations (ODEs) and then solved via homotopic methodology. Graphical outcomes of the velocity, temperature and concentration fields for influential parameters are plotted and discussed physically. The achieved outcomes specify that the temperature and concentration distribution increases for the higher unsteadiness parameter, curvature parameter and Maxwell parameter. Moreover, both thermophoresis and Brownian motion parameters enhances the thermal energy transport in flow.

Introduction

The subject of the heat transfer analysis attract the researchers now a days due its importance in the many engineering areas specially the heat transport in the fluid flow. Such as production of plastic and polymers needs the higher rate of heat transport for the better quality of the product. To replace the working liquids with nanoparticles as a innovative approach to enhance the heat transport phenomena in liquid. Nanofluid is a colloidal fusion where the possession of both nanomaterials and base liquids provide the change in the transport and thermal aspects of base liquids. In recent, diverse sorts of nanoparticles, for the instance, metallic and ceramic nanoparticles, have been utilized for formation of nanofluids. The notion of nanofluids concerning heat transport enhancement through dense particles of nano-meter was reported by Choi (1995). Hsiao (2016) analyzed the mixed convective stagnation point flow of nanofluid with the slip boundary condition on the stretching sheet. Magnetohydrodynamics flow of micropolar nanofluid over stretching sheet under the impact of viscous dissipation was reported by Hsiao (2017). This study revealed that both magnetic parameter and Eckert number enhance the temperature field. By utilizing FEM scheme, Haq and Aman (2019) investigated the performance of CuO nanoparticles with inner heated obstacle, in partially heated trapezoidal cavity. Xu et al. (2019) studied the phenomena of thermal radiation, heat convection/conduction and phase change heat transport to nanofluid. The properties of radiation and chemical reaction in Maxwell nanofluid were addressed by Hayat et al. (2019). Impacts of activation energy and chemical reaction in peristaltic blood flow with nanoparticles was explored by Ellahi et al. (2019). They noted that the gold particles condenses large particles to transport important drugs powerfully to the effected portion of the organ. Additionally, relevant works dealing with nanofluid were reported in see Refs. Irfan et al. (2019), Mahanthesh and Joseph (2019), Khan et al. (2019), Turkyilmazoglu (2019a), Turkyilmazoglu (2019b) and Turkyilmazoglu (2020).

Recently, the study of non-linear fluids have noteworthy consideration due to their practical applications in engineering and trade. For instance, piping, extrusion methodology in metallurgy, in large scale cooling/heating structures, and oil recovery etc includes the flow of non-linear liquids. To increase the efficiency in thermal extrusion manufacturing Hsiao (2017a), Hsiao (2017b) studied the flow of non-Newtonian nanofluid with impact of thermal radiation, magnetic field and viscous dissipation. One important aspect of these fluids is their advanced apparent viscosity. Additionally, various researchers have reported their investigations for the flow of non-linear fluids with diverse aspects (see Refs Malik and Khan 2018; Bai et al. 2019; Moshkin et al. 2019; Khan and Nadeem 2019; Hamid et al. 2018). The considered Maxwell fluid model is the special type of non-Newtonian fluid in which the characteristics of both elastic and viscous forces are described. This model is good for viscoelastic fluids because it can described the stress relaxation phenomenon accurately in these types of fluid. Ahmed et al. (2019) analyzed thin film flow Maxwell fluid with heat transport in the presence of non-linear radiation. The convective phenomena on Maxwell fluid utilizing Brownian and thermophrotic forces for nanofluid was studied by Khan et al. (2019).

In view of the above studies, we noted that no study has been made to report the unsteady flow of Maxwell nanofluid towards stretched cylinder. Thus, the present analysis is reported to investigate the flow and heat transport of Maxwell nanofluid with impact of heat source/sink and thermal radiation. Additionally, the Brownian and thermophoretic forces are taken in account to study the convective heat transport enhancement. The well known homotopic approach (Turkyilmazoglu 2011, 2012, 2018) is employed for solutions of the governing problem. The results are presented graphically and validated through tabular data.

Fig. 1

Physical sketch of the problem

Mathematical formulation

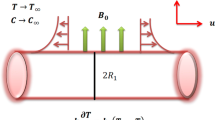
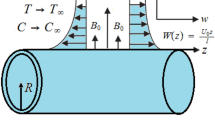
Consider 2D unsteady flow of Maxwell nanofluid induced by stretching cylinder of radius $R_{1}.$ The cylinder is stretched with velocity $u(t,z)= \frac{az}{1-\gamma t}$ along $z-$direction, where $a=\frac{U_{0}}{L}$ is the stretching rate, $\gamma$ the positive constant with property $\gamma t\le 1.$ Let the cylindrical polar coordinates (z, r) are taken to be in such approach that $z-axis$ runs along the axis of the cylinder and $r-axis$ is restrained perpendicular to it as exposed in blow (Fig. 1). Additionally, heat sink/source aspects are considered. Under above consideration the governing boundary layer equations (Moshkin et al. 2019; Khan et al. 2019) for Maxwell nanofluid model are specified as follows.

$$\begin{aligned}&\frac{\partial (ru)}{\partial z}+\frac{\partial \left( rw\right) }{\partial r }=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial z}+w\frac{ \partial u}{\partial r}=\nu \left[ \frac{\partial ^{2}u}{\partial r^{2}}+ \frac{1}{r}\frac{\partial u}{\partial r}\right] \nonumber \\&\quad -\lambda _{1}\left[ \frac{\partial ^{2}u}{\partial t^{2}}+2u\frac{\partial ^{2}u}{\partial t\partial z}+2w\frac{\partial ^{2}u}{\partial r\partial t}\right. \nonumber \\&\quad \left. +2uw\frac{\partial ^{2}u}{\partial r\partial z}+w^{2}\frac{\partial ^{2}u}{ \partial r^{2}}+u^{2}\frac{\partial ^{2}u}{\partial z^{2}}\right] , \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial z}+w\frac{ \partial T}{\partial r}=\alpha _{1}\left[ \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}\right] \nonumber \\&\quad -\frac{1}{(\rho c)_{f} }\left[ \frac{1}{r}\frac{\partial }{\partial r}\left( rq_{r}\right) \right] \nonumber \\&\quad +\tau \left[ D_{B}\frac{\partial C}{\partial r}\frac{\partial T}{\partial r} +\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{\partial r}\right) ^{2} \right] +Q_{\circ }\left( \frac{T-T_{\infty }}{(\rho c)_{f}}\right) , \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial z}+w\frac{\partial C}{\partial r}=D_{B}\frac{1}{r}\frac{\partial }{\partial r}\left[ \left( r \frac{\partial C}{\partial r}\right) \right] \nonumber \\&\quad +\frac{D_{T}}{T_{\infty }}\frac{ 1}{r}\frac{\partial }{\partial r}\left[ \left( r\frac{\partial T}{\partial r} \right) \right] , \end{aligned}$$

(4)

with boundary conditions

$$\begin{aligned}&u(t,z,r) =u(t,z)=\frac{az}{1-\gamma t},\ w(t,z,r)=0,\nonumber \\&\quad T=T_{w},\ C=C_{w}\text { at }r=R_{1}, \end{aligned}$$

(5)

$$\begin{aligned}&u \rightarrow 0,\ T\rightarrow T_{\infty },\ C\rightarrow C_{\infty }\text { as } r\rightarrow \infty . \end{aligned}$$

(6)

Here (u, w) are the velocity components in the $z-$ and $r-$directions, respectively, $\nu$ the kinematic viscosity, $\lambda _{1}$ the relaxation time, $\alpha _{1}$ the thermal diffusivity, (T, C) the temperature and concentration of fluid, $\tau$ the heat capacity ratio of nanoparticles to base fluid and $Q_{0}$ the source/sink, $T_{w}$ and $C_{w}$ the wall temperature and concentration, respectively, $T_{\infty }$ and $C_{\infty }$ the ambient temperature and concentration of fluid, respectively, $(D_{B },D_{T})$ the Brownian and thermophoresis diffusion coefficients, respectively. $q_{r}$ the radiative heat flux which defined as

$q_{r}=\frac{-16\sigma ^{*}}{3k*}T_{\infty }^{3}\frac{\partial T}{ \partial r}$ where ($\sigma ^{*},k*$) the Stefan -Boltzmann constant and mean absorption coefficient, respectively.

Introducing the following conversions

$$\begin{aligned}&u=\frac{az}{1-\gamma t}f^{\prime }(\eta ),\ w=-\frac{R_{1}}{r}\sqrt{\frac{a\nu }{(1-\gamma t)}}f(\eta ),\ \theta (\eta )\nonumber \\&\quad =\frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \nonumber \\&\phi (\eta )=\frac{C-C_{\infty }}{C_{w}-C_{\infty }},\ \eta = \sqrt{\frac{a}{\nu (1-\gamma t)}}\left( \frac{r^{2}-R_{1}^{2}}{2R_{1}} \right) . \end{aligned}$$

(7)

Above conversions yield the following ODEs of Maxwell nanofluid flow with energy transport:

$$\begin{aligned}&(1+2\alpha \eta )f^{\prime \prime \prime }+2\alpha ff^{\prime \prime }- \frac{S}{2}\eta f^{\prime \prime }-Sf^{\prime }\nonumber \\&\quad -f^{\prime 2}+ff^{\prime \prime }-\frac{7}{4}\beta _{1}S^{2}\eta f^{\prime \prime }\nonumber \\&\quad -\frac{\beta _{1}}{4}\eta ^{2}S^{2}f^{\prime \prime \prime }-2\beta _{1}S^{2}f^{\prime }-2S\beta _{1}f^{\prime 2}\nonumber \\&\quad -\beta _{1}\eta Sf^{\prime }f^{\prime \prime }+3S\beta _{1}ff^{\prime \prime }\nonumber \\&\quad +S\beta _{1}\eta ff^{\prime \prime \prime }+2\beta _{1}ff^{\prime }f^{\prime \prime }\nonumber \\&\quad -\frac{\alpha \beta _{1}}{1+2\alpha \eta }f^{2}f^{\prime \prime }-\beta _{1}f^{2}f^{\prime \prime \prime }=0, \end{aligned}$$

(8)

$$\begin{aligned}&(1+\frac{4}{3}R_{d})(1+2\alpha \eta )\theta ^{\prime \prime }+2\alpha \theta ^{\prime }+\Pr f\theta ^{\prime }-\Pr \frac{S}{2}\eta \theta ^{\prime }\nonumber \\&\quad +(1+2\alpha \eta )\Pr N_{b}\theta ^{\prime }\phi ^{\prime }+(1+2\alpha \eta )\Pr N_{t}\theta ^{\prime 2}+\Pr \delta \theta =0, \end{aligned}$$

(9)

$$\begin{aligned}&(1+2\alpha \eta )\phi ^{\prime \prime }+2\alpha \phi ^{\prime }+Le\Pr f\phi ^{\prime }-Le\Pr \frac{S}{2}\eta \phi ^{\prime }\nonumber \\&\quad +(1+2\alpha \eta )\left( \frac{N_{t}}{N_{b}}\right) \theta ^{\prime \prime }+2\alpha \left( \frac{N_{t}}{N_{b}}\right) \theta ^{\prime }=0, \end{aligned}$$

(10)

with boundary conditions

$$\begin{aligned}&f(0)=0,\ f^{\prime }(0)=1,\ \theta \left( 0\right) =1,\ \phi (0)=1, \end{aligned}$$

(11)

$$\begin{aligned}&f^{\prime }(\infty )=0,\ \theta (\infty )=0,\ \phi (\infty )=0. \end{aligned}$$

(12)

Where S $\left( =\frac{\gamma }{a}\right)$ is the unsteadiness parameter, $\alpha \left( =\frac{1}{R_{1}}\sqrt{\frac{\nu (1-\gamma t)}{a}}\right)$ the curvature parameter, $\beta _{1}$ $\left( =\frac{\lambda _{1}a}{ 1-\gamma t}\right)$ the Maxwell parameter, $\Pr \left( =\frac{\nu }{ \alpha _{1}}\right)$ the Prandtl number, $N_{b}$ $\left( =\frac{\tau D_{B}(C_{w}-C_{\infty })}{\nu }\right)$ the Brownian motion parameter, $N_{t}$ $\left( =\frac{\tau D_{T}(T_{w}-T_{\infty })}{\nu T_{\infty }}\right)$ the thermophoresis parameter, Le $\left( =\frac{\alpha _{1}}{D_{B}} \right)$ the Lewis number, $R_{d}$ $\left( =\frac{4\sigma ^{*}T_{\infty }^{3}}{kk^{*}}\right)$ radiation parameter and $\delta$ $\left( =\frac{ Q_{0}(1-\gamma t)}{a(\rho c)_{f}}\right)$ the heat source/sink parameter.

Physical quantities

Expressions for the local Nusselt $(Nu_{z})$ and local Sherwood $(Sh_{z})$ numbers are

$$\begin{aligned} Nu_{z}=\frac{zq_{s}}{k(T_{w}-T_{\infty })},\ \ Sh_{z}=\frac{ zj_{s}}{D_{B}(C_{w}-C_{\infty })}, \end{aligned}$$

(13)

where $q_{s}$ and $\ j_{s}$ are the heat and mass fluxes, respectively,

$$\begin{aligned} q_{s}= & {} -k\left( \frac{\partial T}{\partial r}\right) _{r=R_{1}}- \frac{4\sigma ^{*}T_{\infty }^{3}}{3k^{*}}\left( \frac{\partial T}{ \partial r}\right) _{r=R_{1}},\nonumber \\ j_{s}= & {} -D_{B}\left( \frac{ \partial C}{\partial r}\right) _{r=R_{1}}, \end{aligned}$$

(14)

in dimensionless forms these are given by

$$\begin{aligned} Nu_{z}\hbox {Re}_{z}^{-\frac{1}{2}}=-\left( 1+\frac{4R_{d}}{3}\right) \theta ^{\prime }(0), \ \ Sh_{z}\hbox {Re}_{z}^{-\frac{1}{2}}=-\phi ^{\prime }\left( 0\right) , \end{aligned}$$

(15)

where $\hbox {Re}_{z}=\frac{u(t,z)z}{\nu }$ signifies the Reynolds number.

Fig. 2

Impact of curvature parameter $\alpha$ on $\theta (\eta )$ and $\phi (\eta )$

Solution scheme

To achieve the series solutions of Eqs. (8)–(10) along the boundary conditions given in Eqs. (11, 12) the well known homotopy analysis method for the highly non-linear ordinary differential system has been utilized. The following initial estimates $(f_{0},\theta _{0},\phi _{0})$ and linear operators $\left( \pounds _{f},\pounds _{\theta },\pounds _{\phi }\right)$ are selected for the governing problem as

$$\begin{aligned} f_{0}(\eta )= & {} 1-e^{-\eta },\ \theta _{0}(\eta )=e^{-\eta },\ \phi _{0}(\eta )=e^{-\eta }, \end{aligned}$$

(16)

$$\begin{aligned} \pounds _{f}[f(\eta )]= & {} f^{\prime \prime \prime }-f^{\prime }, \pounds _{\theta }[\theta (\eta )]=\theta ^{\prime \prime }-\theta ,\pounds _{\phi }[\phi (\eta )]\nonumber \\= & {} \phi ^{\prime \prime }-\phi . \end{aligned}$$

(17)

Fig. 3

Impact of Maxwell parameter $\beta _{1}$ on $\theta (\eta )$ and $\phi (\eta )$

Fig. 4

Impact of thermophoresis $N_{t}$ and Brownian motion parameters $N_{b}$ on $\theta (\eta )$

Fig. 5

Impact of thermophoresis $N_{t}$ and Brownian motion parameter $N_{b}$ on $\phi (\eta )$

Fig. 6

Impact of unsteadiness parameter S on $\theta (\eta )$ and $\phi (\eta )$

Fig. 7

Impact of Prandtl number $\Pr$ and Lewis number Le on $\theta (\eta )$ and $\phi (\eta ),$ respectively

Fig. 8

Impact of heat sink $\delta <0$ and heat source $\delta >0$ on $\theta (\eta )$

Fig. 9

Impact of radiation parameter $R_{d}$ on $\theta (\eta )$

Results and discussion

This section discusses the aspects of influential parameters on the velocity, temperature and concentration fields via homotopic scheme. The outcomes for scheming parameters are graphed and discussed in detail with physical arguments. The value of physical parameters are taken to be fixed as $S=\beta _{1}=\alpha =R_{d}=0.5,$ $\delta =0.2,$ $N_{t}=N_{b}=0.4$ and $Le=\Pr =7.$ Figure 2 illustrate the effect of curvature parameter $\alpha$ on nanoliquid temperature and concentration fields. We observed that the temperature, and concentration fields of Maxwell nanoliquid are increasing function of $\alpha$. Physically, rise in the curvature parameter $\alpha$ declines the radius of cylinder due to which the interaction region of the cylinder with the liquid is diminished. Hence, fluid influenced in stretching cylinder is less. Furthermore, we noted that the higher values of $\alpha$ enhance both the temperature and its allied thermal thickness of boundary layer. The impact of $\alpha$ on temperature field is more prominent than the concentration field. The temperature and concentration fields for Maxwell parameter are portrayed in Fig. 3. From these interpretation, it is observed that the intensification in $\beta _{1}$ enhances both the temperature and concentration distribution in Maxwell liquid. As $\beta _{1}$ is the ratio of relaxation time to observation time and rise in $\beta _{1}$ means there is higher the relaxation time in the fluid. Due to which the fluid becomes solid like and consequently, the conduction of thermal and solutal energy increases in the fluid motion. Figures 4 and 5 are represented to envision the impact of thermophoresis $N_{t}$ and Brownian motion $N_{b}$ parameters on nanoliquid temperature and concentration fields. Here, we reported that a rise in the value of $N_{t}$ enhances both the temperature and concentration fields. Physically, higher value of $N_{t}$ enhances the temperature difference between wall and free stream. Hence, the heat transfer rate is enhanced which enhances the temperature field. Furthermore, rise in Brownian motion parameter $N_{b}$ causes the enhance of temperature field. Because for higher value of $N_{b}$ the collision of nanoparticles boost up which intensify the temperature field. On the other hand, concentration field declines with higher values of $N_{b}$. Physically, for higher values of $N_{b}$ the particles collision provides the disturbance for mass transfer and thus, as a result the declines in concentration field is noted. To picture the impact of unsteadiness parameter S on nanoliquid temperature and concentration of Maxwell fluid Fig. 6 are delineated. We observed that enhancement in the value of S rises the temperature and concentration fields. The impact of Prandtl number $\Pr$ and Lewis number Le on temperature and concentration fields, respectively, are visualized in Fig. 7. We noted that the increase in $\Pr$ and Le result in decreases the thermal and mass diffusivity of naoliquid which declines the temperature and concentration in the Maxwell fluid flow. The temperature field for the effects of heat source/sink $\delta$ is illustrated in Fig. 8. The temperature field increases for higher values of heat source and it declines for increasing heat sink parameter. Physically, the heat source provides the additional heat to the liquid which enhances the temperature field and converse behavior is true for heat sink parameter. Moreover, for $\delta <0$ much heat is absorbed which declines temperature field. The effect of radiation parameter $R_{d}$ on temperature field is illustrated in Fig. 9. We noted that the increase in values of $R_{d}$ results in an enhancement in the heat transfer rate. Physically, the increase in $R_{d}$ rises the ambient temperature of nanofluid and declines the mean absorption coefficient. Hence, the heat transfer rate increases which enhances the temperature field.

Tabular comparisons

Tables 1 and 2 are assessment tables of $-f^{\prime \prime }(0)$ for different values of $\beta _{1}$ and S for Newtonian case. Table 3 is a comparison of $-\theta ^{\prime }(0)$ in limiting case for various values of $\Pr .$ From these tables, we noted that the current outcomes are appropriate which assured the validation of our scheme. Table 4 is also established for the Numerical values of Nusselt and Sherwood numbers for various values of $N_{t},$ $N_{b},$ $R_{d}$ and M. These numerical values of Nusselt and Sherwood number are obtained by utilizing the built in MATLAB scheme namely as bvp4c. From these results we conclude that the higher value of both thermophoretic and Brownian forces decline the thermal gradient at the surface of cylinder.

Table 1 A comparison of $-f^{\prime \prime }(0)$ for $\beta _{1}$ when $\alpha =S=0$

Table 2 A comparison of $\ f^{\prime \prime }(0)$ for S when $\alpha =\beta _{1}=0$

Table 3 A comparison of $-\theta ^{\prime }(0)$ for $\Pr$ when $\alpha =S=\beta _{1}=N_{t}=R_{d}=\delta =0,$ and $N_{b}\rightarrow 0$

Table 4 Numerical values of Nusselt number and Sherwood number for various values of $N_{t},$ $N_{b},$ $R_{d}$ and with fixed $S=\alpha =\beta _{1}=0.5$ and $\delta =0.2$

Concluding remarks

A mathematical analysis for unsteady 2D flow of radiative Maxwell nanofluid with heat and mass transport in presence of heat source/sink has been achieved. Homotopy approach (HAM) has been utilized for the solutions of ODEs. The final conclusions of our study are given below:

• The unsteadiness parameter S enhanced both the temperature and concentration distributions.

• Both temperature and concentration fields enhanced for higher values of curvature parameter $\alpha .$

• An increase in the value of Maxwell parameter $\beta _{1}$ augmented both the temperature and concentration fields.

• Temperature of Maxwell fluid intensified for increasing Brownian motion parameter $N_{b}$ whereas, conflicted behavior was noted on concentration field.

• The temperature fields declined for higher value of Prandtl number $\Pr$.

• Increase in radiation parameter $R_{d}$ boost up the temperature profile.