Clustering Validity Function Fusion Method of FCM Clustering Algorithm Based on Dempster–Shafer Evidence Theory

Abstract

With the deepening of the research on clustering algorithm, clustering validity has become an indispensable part of cluster analysis. However, due to the complexity of data structure and different attributes, any clustering validity function cannot be applied to all datasets, so clustering validity function has been bringing forth new ones. Therefore, this paper proposes a clustering validity function fusion model based on D–S evidence theory (DS-CVFFM), which adopts FCM clustering algorithm as the base algorithm, calculates the values of different validity functions, and then uses the values of different clustering validity functions as the evidence source to construct the basic probability assignment function (BPA). Finally, it integrates with the fusion rules of D–S evidence theory, and outputs the optimal clustering number according to the decision conditions. DS-CVFFM uses the information fusion of multiple clustering validity functions to judge the number of optimal clusters without the need to propose complex validity functions, and avoid the influence of expert factors in the weighted combination clustering validity evaluation method. Finally, 4 sets of artificial datasets and 14 sets of UCI datasets are selected to verify the effectiveness of the proposed model. The experimental results show that compared with the traditional clustering validity evaluation methods, the proposed fusion model has a significant improvement in the accuracy of judging the optimal number of clusters, and the stability is improved under different values of fuzzy exponent, which can overcome the shortcomings of traditional clustering validity evaluation methods.

1 Introduction

Cluster analysis is an important research topic in the field of machine learning and pattern recognition. As an unsupervised learning method, cluster analysis is to divide similar samples into one category and dissimilar samples into different categories for data without prior knowledge, so that the samples of the same category are as similar as possible and the samples of different categories are as different as possible [1]. Clustering methods are mainly divided into hierarchy-based clustering, partition-based clustering, density-based clustering, model-based clustering and more [2,3,4,5]. FCM clustering algorithm [6], as one of the algorithms for partition clustering, introduces the concept of fuzzy set [8] into K-means clustering algorithm [7], so that hard clustering can be extended to fuzzy clustering. In this way, data samples that are similar between classes have a better basis for division, and the clustering results become better and more closer to the practical needs [9]. FCM clustering algorithm has become one of the most widely used clustering algorithms by virtue of its simple principle, fast calculation speed and wide range of problem solving [10]. However, FCM clustering algorithm needs to verify the effectiveness of clustering, so as to determine the optimal number of clusters and judge the quality of clustering results. From the current research point of view, the research of clustering validity can be roughly divided into the research of clustering validity function and the research of combined clustering validity evaluation method.

The research on clustering validity function mainly focuses on the following two aspects: (1) Fuzzy clustering validity function based on membership degree only. For example, Bezdek proposed the partition coefficient [11], which was the first index to describe the validity of fuzzy clustering by the coincidence degree of data objects. Referring to the partition coefficient and Shannon's information theory [12], the partition entropy [13] was proposed. Dave proposed the modified partition coefficient [14] to suppress the monotonous change of the partition entropy and partition coefficient with the number of clusters, and the P index [15] proposed by Chen and Links in 2004. (2) Fuzzy clustering validity function based on membership degree and geometric structure of data set. For example, Xie-Beni validity function [16], Fakuyame-Sugeno validity function proposed in 1989 [17], clustering validity function proposed by Knows [18], the clustering validity function proposed by Wang [19], the clustering validity function [20] proposed by Zhu and more. However, due to the complexity of data structure and different attributes, any clustering validity function cannot be applied to all datasets. Because of this, the validity function of fuzzy clustering has been bringing forth new ideas, which also leads to the more and more complex structure design of the fuzzy clustering validity function.

The research on the validity evaluation method of combinatorial clustering mainly focuses on the weighted combination method. Weighted sum validity function (WSVF) proposed by Sheng in 2005 is a combination of hard clustering validity functions [21]. Xu also studied the combination method of hard clustering validity function [22]. Dong proposed the fuzzy weighted sum validity function (FWSVF) based on the idea of Sheng [23]. After that, Wu changed the weighted method of FWSVF and proposed a dynamic weighted sum validity function (DWSVF) [24]. Li extended the index of FWSVF to the combination of 10 validity functions and proposed weighted sum type of cluster validity index (WSCVI) [25]. Wang proposed a hybrid weighted method combining subjective weighted and objective weighted, which balanced the influence of subjectivity and objectivity on the results, which is named as the hybrid weighted clustering validity function (HWCVF) [26]. Compared with the clustering validity functions, the combined clustering validity method only needs the weighted combination of the existing validity functions. Its form is simple and easy to understand, but the weighted factor is often difficult to determine.

Since the cluster analysis is to cluster the data set without labels, after clustering the data set using the FCM clustering algorithm, it is necessary to evaluate the validity of the final result to obtain the best number of clusters and then judge the clustering results are good or bad. Single clustering validity function will fail with the number of data samples, the change of dimensions, and the influence of noise data and overlapping data, meanwhile, the clustering validity function will become more and more complex with the advent of the era of big data. Combined clustering validity evaluation method will be difficult to select the weighting method, and prone to over fitting problems. In order to improve the accuracy of the clustering results of the FCM clustering algorithm and the judgment of the optimal number of clusters, it is not feasible to rely only on a single validity function and a combined validity evaluation method. It is necessary to find a method that can be applied to a large amount of data which can be used to judge the final clustering result. For this reason, this paper starts from the perspective of fusing multiple validity functions to determine the optimal number of clusters and improving the stability and accuracy of cluster validity evaluation. A fusion model (DS-CVFFM) based on D–S evidence theory [27,28,29] is proposed to integrate the information of multiple clustering validity functions.

Based on the idea of D–S evidence theory, this paper proposes a fusion model (DS-CVFFM) based on the information of clustering validity functions. The main idea of DS-CVFFM is to fuse multiple validity functions using D–S evidence theory. Firstly, FCM clustering algorithm is used to cluster the data set, and then several validity functions are used to judge the validity of the clustering results. There are some differences in the optimal cluster number of the same data set by different validity functions, and then normalize the values of different validity functions. The normalized values are used as propositions to construct the basic probability assignment function (BPA) of the validity function. Finally, the BPA value of the validity functions is taken as the input, and the D–S evidence theory is used to judge the confidence. The number of clusters corresponding to the maximum confidence value is the optimal number of clusters.

Finally, the feasibility of DS-CVFFM is verified by experimental simulation. The artificial data sets and UCI data sets are selected for experiments, and the proposed fusion model DS-CVFFM is compared with the traditional validity evaluation methods. The experimental results show that the accuracy of DS-CVFFM is significantly better than the traditional validity evaluation methods under the same data sets and experimental parameters. The experimental results show that DS-CVFFM has best stability under different values of fuzzy weighted. Therefore, DS-CVFFM can effectively avoid the influence of human factors caused by subjective weighting and the problem of objective weighting selection. It can also avoid the problem that a single cluster validity function is easy to fail in the face of datasets with different structures. At the same time, it does not need to design a complex structure validity function, while taking into account the advantages of multiple validity functions, which provides a new solution for the research of fuzzy clustering effectiveness evaluation method.

2 FCM Clustering Algorithm and Clustering Validity Functions

2.1 FCM Clustering Algorithm

The fuzzy C-means (FCM) clustering algorithm proposed by Bezdek is the most representative one of the fuzzy clustering methods, and is also the most widely used one of the clustering algorithms. FCM clustering algorithm divides $n$ objects $x_{1}$, $x_{2} , \ldots ,x_{n}$ of data ${ }X$ into $c$ fuzzy clusters by finding the minimum objective function, which is defined as follows [30]:

$$J_{m} \left( {U,V} \right) = \mathop \sum \limits_{i = 1}^{c} \mathop \sum \limits_{j = 1}^{n} \left( {u_{ij} } \right)^{m} \left\| x_{j} - v_{i}^{2}\right\|$$

(1)

where ${ }J_{m} \left( {U,V} \right)$ is the square error clustering criterion and the minimum value of ${ }J_{m} \left( {U,V} \right)$ is called the minimum square error stationary point, V = {$v_{1} ,v_{2} , \ldots ,v_{n}$} is the corresponding cluster center divided on the data set $X$, parameter $c$ represents the number of clusters. The parameter $m$ is the fuzzy weighted, which is used to control the degree of fuzziness within the scope $m \epsilon$ (1, $\infty$), $x_{j} - v_{i}$ represents the European distance between the data object $x_{j}$ and cluster center $v_{i}$, $u_{ij}$ (0 ≤ $u_{ij}$ ≤ 1) is the membership degree of data object $x_{j}$ of cluster center $v_{i}$. In Eq. (1), $u_{ij} \in$ U, where in $U$ is a membership matrix with fuzzy division of $c \times n$ that must satisfy the following conditions, and $U_{0}$ is called the initial membership matrix: $\mathop \sum \limits_{i = 1}^{c} u_{ij} = 1$(j = 1, 2,…, ${ }n$) and $0 < \mathop \sum \limits_{j = 1}^{c} u_{ij} < n$(i = 1, 2, …, $c$).

The clustering validity is a problem of finding the optimal solution of $c$ under the condition of $J_{m}$ minimization. In fact, more attention must be paid to the clustering validity if cluster analysis is to make a great contribution to engineering applications. Since $J_{m}$ decreases monotonically with the decrease of $c$, an effective partition evaluation criterion is needed. The process of FCM clustering algorithm is described as follows [31]:

Step 1::

Fix the cluster parameter $c$ and fuzzy weighted $m$ (usually between 1.5 and 2.5). When $m$ = 1, FCM clustering algorithm is equivalent to K-means clustering algorithm, when $m$ approaches 1 indefinitely, FCM tends to be more and more clustering algorithm of hardening fraction. On the contrary, when $m$ tends to be infinite, all data objects $x_{j}$ and cluster center $v_{i}$ will coincide, while data object $x_{j}$ belongs to each cluster will have the same membership degree, with the value of 1/$c$.

Step 2::

Initialize fuzzy division membership matrix.

Step 3::

According to Eq. (2), update the cluster centers $V = \left\{ {v_{1} ,v_{2} , \ldots ,v_{c} } \right\}$.

$$v_{i} = \frac{{\mathop \sum \nolimits_{{j = 1}}^{n} u_{{ij}}^{{\left( t \right)m}}\,\cdot\,x_{i} }}{{\mathop \sum \nolimits_{{j = 1}}^{n} u_{{ij}}^{{\left( t \right)m}} }}$$

(2)

Step 4::

According to Eq. (3), update the fuzzy partition matrix $U = \left( {u_{ij} } \right)_{c \times n} ;$

$$u_{ij} = \left[ {\mathop \sum \limits_{k = 1}^{c} \left( {\frac{{x_{j} - v_{i}^{2} }}{{x_{j} - v_{k}^{2} }}} \right)^{{2/\left( {m - 1} \right)}} } \right]^{ - 1}$$

(3)

For $i = 1,2,\ldots,\,c{\text{ and }} j = 1,2,\ldots ,n.$

Step 5::

Calculate e = $V_{t + 1} - V_{t}$. If $e$ ≤ $\varepsilon { }$($\varepsilon$ is a threshold value usually from 0.001 to 0.01), the algorithm is stopped and the final clustering result is calculated, otherwise t = t + 1 and repeat Step 2.

FCM clustering algorithm has been widely concerned by scholars since it came out, and now it has formed a very mature theory. However, it also has many defects, such as the complex calculation process, the need to calculate all the samples in the data set, and facing the complex datasets easy to fail and so on. Therefore, scholars improve and optimize FCM clustering algorithm from different perspectives. In 1994, Park combined gradient descent with FCM and proposed a Gradient based fuzzy c-means (GBFCM) algorithm (GBFCM) [32], which can speed up the convergence of the algorithm. Wu proposed a new FCM clustering algorithm based on Mercer kernel function (FKCM) [33], which improved the stability of FCM algorithm. Sanchez proposed the Fuzzy Granular Gravitational Clustering Algorithm (FGGCA) in 2014 [34], which uses Newtonian gravity and granular computing to analyze the similarity of data set samples. Based on Wu's idea, Ding proposed Gauss kernel based FCM (KFCM) [35] in 2016 using Gauss kernel function and genetic algorithm to update membership and optimize FCM. Rubio used type-2 fuzzy logic techniques to optimize fuzzy Possibilistic C-means (FPCM) algorithm [36] in 2017 to improve the accuracy of PFCM. Kuo proposed a new clustering algorithm by combining heuristic algorithm with kernel function [37]. A design methodology for a Mamdani based Interval Type-2 Fuzzy Logic System (MAM-IT2FLS) with Center-Of-Sets defuzzification was proposed by Moreno in 2020[38], which adopts the descriptive statistics and granular computing theory to better define the limits of uncertainty within the Interval Type-2 Membership Functions (IT2MF) as extracted from available data.

2.2 Clustering Validity Functions

The clustering validity functions can be roughly divided into two categories. One is based on membership degree only and the other is based on membership degree and geometric structure of data set. The clustering validity functions based on membership degree lack the connection with the geometric structure of the data set, so the final results are often one-sided and the accuracy needs to be improved. At present, clustering validity functions based on membership degree and geometric structure is a popular research direction. This paper lists some of the more common clustering validity functions (the name of the function, the definition formula, and the criteria to determine the optimal number of $c$) as shown in Tables 1 and 2.

Table 1 Cluster validity function based on membership degree

Table 2 Clustering validity function based on geometric structure and membership degree

For the clustering validity functions shown in Tables 1 and 2, $u_{ij}$ indicates the fuzzy membership matrix, $n$ indicates the number of data samples, $c$ indicates clustering number, $m$ indicates fuzzy index, $x_{j}$ indicates data samples, $v_{i}$ indicates the clustering center, $v_{i} - x_{j}$ indicates the distance between clustering center and the sample data, $\overline{v} = \mathop \sum \limits_{i = 1}^{c} v_{i} /c$, $u_{mj} = \mathop {\min }\limits_{1 \le i \le c} \mathop \sum \limits_{j = 1}^{n} u_{ij}^{2}$, $\beta_{T} = \frac{1}{c}\mathop \sum \limits_{i = 1}^{c} v_{i} - \overline{v}^{2}$, $medianv_{i} - v_{k}^{2}$ represents the median of the distance between two cluster centers.

In addition to the clustering validity function listed above, the validity function of fuzzy clustering has always been a hot topic in the study of cluster validity evaluation. For example, Feng proposed a validity function based on compactness and overlap degree in 2016 [43]. The HF validity function proposed by Haouas in 2017 [44] with the improvement of $V_{WL}$. Geng also defined the overlap degree in 2019, and proposed a new validity function for three variables of compactness and variability [45]. Ouchica proposed an ECS validity function to standardize separation and compactness in 2020 [46]. Liu proposed a new validity function, which is the combination of $V_{WL}$ and HF combination [47]. From the above study of validity function, the single validity function is more and more complex because of the different data set structure. Most of the validity functions are based on compactness, separation degree and overlap degree, but only different calculation methods. Because of the diversity of datasets, there is no one validity function that can be used for all datasets, which is also the reason why fuzzy clustering validity functions emerge endlessly.

2.3 Combination Clustering Validity Evaluation Methods

Sheng proposed WSVF [21] composite clustering effectiveness evaluation method for hard clustering algorithm is defined as follows Eq. (4).

$$\max WSVF = \mathop \sum \limits_{i = 1}^{m} w_{i} f_{i} \left( x \right)$$

(4)

where $m$ = 6, $\mathop \sum \limits_{i = 1}^{m} w_{i} = 1, w_{1} = w_{2} = w_{3} = w_{4} = w_{5} = w_{6} = \frac{1}{6}$, $f_{i} \left( x \right)$ is consist of 1/$V_{DB}$, ${ }V_{SIL}$, $V_{D}$, $V_{33}$, ${ }V_{CH}$ and $V_{PBM} .$

Dong proposed FWSVF by introducing the Sheng's WSVF into the fuzzy clustering. The definition is described as Eq. (5).

$$max FWSVF = \mathop \sum \limits_{i = 1}^{r} w_{i} f_{i} \left( x \right)$$

(5)

where ${ }r$ = 4, $f_{i} \left( x \right)$ is consist of 1/$V_{XB}$, 1/$V_{PE}$, $V_{PC}$ and $V_{PBMF}$, and $w_{i}$ is consisted of different options based on different datasets.

WSCVI proposed by Li [25] is defined as Eq. (6).

$$\min WSCVI = \mathop \sum\nolimits_{i = 1}^{N} w_{i} CVI_{i}$$

(6)

where $N$ = 10 and $\mathop \sum \limits_{i = 1}^{N} w_{i} = 1, 0 \le w \le 1$, where $CVI_{i}$ is consisted of 1/$V_{PC}$, 1/$V_{NPC}$, $V_{PE}$, $V_{NPE}$, $V_{XB}$, $V_{K}$, 1/$V_{PBMF}$, $V_{FS}$, $V_{T}$ and $V_{SC}$.

DWSVF proposed by Wu can be defined as Eq. (7).

$$\min DWSVF = \mathop \sum \limits_{i = 1}^{m} w_{i} f_{i} \left( x \right)$$

(7)

where $w_{i} = \frac{{sum f_{i} - f_{i} }}{{sum f_{i} }}$, $w_{i}$ is a dynamic weighting that can be weighted based on the values of different indicators, and $f_{i} \left( x \right)$ is composed of 1/$V_{MPC}$,${ }V_{XB}$ and ${ }V_{PBMF}$.

Wang et al. proposed a hybrid weighted combination method HWCVF [26]. The definition of HWCVF is shown in Eq. (8).

$$\min HWCVF = \mathop \sum \limits_{i = 1}^{m} w_{hybrid} F_{i} \left( x \right)$$

(8)

where expert weighted and information entropy weighted are combined, that is to say that $w_{hybrid} = \theta w_{object} + \left( {1 - \theta } \right)w_{subject}$, where $w_{object}$ is the expert weighted [48], $w_{subject}$ is information entropy weighted [49], $\theta$ is balance factor, and $F_{i} \left( x \right)$ are the clustering validity functions after standardization. The evaluation method is based on the idea of linear superposition of combined function with the $V_{MPC}$, $V_{XB}$,${ }V_{K}$,${ }V_{P}$,$V_{PBMF}$,${ }V_{WL}$,${ }V_{Z}$ and ${ }V_{HY}$.

At present, the research based on combinatorial validity function is not very deep, but from the above research status, most of the research on combinatorial validity function is based on weighted combination. Weighted is also a method of information fusion of validity functions, but the weighted factors are often difficult to determine. For example, the selection of subjective weighted is easily affected by the factors of decision-makers, and the objective weighted will ignore the accuracy of each validity function. Therefore, it is difficult to choose an appropriate weighting factor.

3 FCM Clustering Validity Function Fusion Based on D–S Evidence Theory

3.1 Basic Concepts and Combination Rules of D–S Evidence Theory

Dempster used the upper and lower limit probability to solve the problem of multi valued mapping at first [50]. After that, Shafer introduced the concept of trust function to further develop evidence theory, and formed a set of mathematical methods to deal with uncertain reasoning problems, which also marks that evidence theory has officially become a complete theory to deal with uncertain problems. Then Yager proposed an improved evidence theory [51] by considering the problem of evidence conflict. Nowadays, evidence theory has been widely used in the field of information fusion [52,53,54,55]. This section will introduce the basic concepts and combination rules of D–S evidence theory [56]. In D–S evidence theory, set is used to represent proposition. If $\Theta { }$ is a finite set, then $\Theta$ is called the recognition framework, which contains $c$ mutually exclusive elements. $2^{\Theta }$ is the power set of $\Theta$, which is defined as Eq. (9)

$$\left\{ {\begin{array}{*{20}c} {2^{\Theta } = \left\{ {A|A \subseteq \Theta } \right\}} \\ {\Theta = \left\{ {\theta_{1} ,\theta_{2} , \ldots ,\theta_{c} } \right\}} \\ \end{array} } \right.$$

(9)

The basic probability assignment function (BPA) on the recognition framework is a function $m$ that maps from $2^{\Theta }$ to [0, 1]. Under the condition of Eq. (10), $m$ is called the mass function of the recognition framework.

$$\left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{A \subseteq \Theta } m\left( A \right) = 1} \\ {m\left( \emptyset \right) = 0} \\ \end{array} } \right.$$

(10)

where $m\left( A \right)$ indicates the degree to which a subset belongs to a set $A$. If $m\left( A \right) > 0$, the set $A$ is called focus element, and specially $m\left( \emptyset \right) = 0$ indicates that the truth value does not belong to the trust degree of the recognition framework $\Theta$. The $m\left( \Theta \right)$ indicates the degree of trust that truth value belongs to $\Theta$, but it can't determine which element it is. Given the mass function $m$, the corresponding belief function (Bel) and plausibility function (PL) can be obtained. Bel and PL definitions are respectively shown as Eq. (11 and 12):

$$Bel\left( A \right) = \mathop \sum \limits_{B \subset A} m\left( B \right)$$

(11)

$$Pl\left( A \right) = \mathop \sum \limits_{B \cap A \ne \emptyset } m\left( B \right)$$

(12)

$\left[ {Bel\left( A \right),Pl\left( A \right)} \right]$ indicate the belief interval and the degree of trust in each hypothesis. There are one-to-one correspondence among the $m$, Bel and Pl. For $\forall A \subseteq \Theta$ and $n$ numbers of $m$ ($m_{1} ,m_{2} , \ldots ,m_{n}$) on $\Theta$, the D–S fusion rule is shown in Eq. (13).

$$\left( {m_{1} \oplus m_{2} \oplus \ldots \oplus m_{n} } \right)\left( A \right) = \frac{1}{k}\mathop \sum \limits_{{A_{1} \cap A_{2} \cap \ldots \cap A_{n} = A}} m_{1} \left( {A_{1} } \right) \cdot m_{2} \left( {A_{2} } \right) \cdot \ldots \cdot m_{n} \left( {A_{n} } \right)$$

(13)

where $A_{1} ,A_{2} , \ldots ,A_{n} \subseteq \Theta$, and $k$ is a probability of conflict, which is defined as Eq. (14).

$$k = \left( {m_{1} \oplus m_{2} \oplus \ldots \oplus m_{n} } \right)\left( \emptyset \right)\; = \;\mathop \sum \limits_{{A_{1} \cap A_{2} \cap \ldots \cap A_{n} = \emptyset }} m_{1} \left( {A_{1} } \right) \cdot m_{2} \left( {A_{2} } \right) \cdot \ldots \cdot m_{n} \left( {A_{n} } \right)$$

(14)

D–S evidence theory can be widely concerned and applied, which is inseparable from the advantages of data analysis. Its main advantages include the ability to deal with uncertain and incomplete information efficiently. The information of the target and the subset of the recognition framework is corresponding and transformed into a mathematical model, which is convenient for data fusion. The support of evidence can be described by the evidence interval, and the unclear problems can be well expressed. When the evidence data are fused, the target prior knowledge is not needed. With the continuous expansion of the application of D–S evidence theory, it is found that the evidence theory also has some shortcomings that cannot be ignored. For example, the problem of information source independence, the problem of calculation explosion, the method of obtaining basic probability and the inability to deal with evidence conflict [57].

3.2 Construction of BPA Matrix of Clustering Validity Function

In the process of cluster validity fusion, for the judgment of the best cluster number of the same data set under $m$ cluster validity functions, there are $m$ results, that is to say that there are $m$ possible types of targets. The value of $c$ is generally $\left[ {2,\sqrt {nmax} } \right]$, where $nmax$ is the number of samples in the data set, so let $n = \sqrt {nmax}$, the validity function is set up for this purpose, and the BPA matrix is defined as $M_{n \times m}$, as shown in Eq. (15).

$$M = \left[ {\begin{array}{*{20}c} {M_{1} } \\ {M_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {M_{n} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } & {\begin{array}{*{20}c} \cdots & {m_{1m} } \\ \end{array} } \\ {m_{21} } & {m_{22} } & {\begin{array}{*{20}c} \cdots & {m_{2m} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {m_{n1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {m_{n2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & \vdots \\ \cdots & {m_{nm} } \\ \end{array} } \\ \end{array} } \right]$$

(15)

where $m_{11}$ is the confidence degree of the first cluster validity function to $c = 2$, when $n = 1$. And so on, $m_{nm}$ is the confidence degree of the $m$-th cluster validity function for $c = n$ when $n = \sqrt {nmax}$. The sum of the confidence degree of the identification result of the number of clusters by the same cluster validity function should be 1, that is $\mathop \sum \limits_{i = 2}^{n} m_{ij}$ = 1, where $j = 1,2, \ldots ,m.$..

Different cluster validity functions vary greatly in the range of judging the number of clusters. Therefore, the cluster validity functions should be normalized and standardized to make the interval fall into [0, 1], which is realized by Eq. (16).

$$f_{i} = \frac{{F_{i} - F_{i}^{min} \left( x \right)}}{{F_{i}^{max} \left( x \right) - F_{i}^{min} \left( x \right)}}.$$

(16)

where $F_{i}$ is the value of validity function, $F_{i}^{min} \left( x \right)$ is the minimum value of the validity function, $F_{i}^{max} \left( x \right)$ is the maximum value of the validity function, $f_{i}$ is the value of validity function after normalization.

wever, directly inputting the value of the normalized validity function into the confidence matrix cannot satisfy the $\mathop \sum \limits_{i = 1}^{n} m_{ij}$ = 1, and clustering validity functions are maximum efficiency and some are minimum efficiency. When the cluster validity function takes the maximum value of $c$, the BPA function is $m_{ij} = \frac{{f_{i} }}{{sum\,f_{i}}}$. When the cluster validity function takes the minimum value of $c$ as efficient, the minimum value of $c$ should be transformed into the maximum validity, so the BPA function is $m_{ij} = \frac{{1 - f_{i} }}{{sum\,1 - f_{i}}}$. After the transformation, the sum of confidence degree results is 1.

A new matrix $A_{m \times m}$ can be obtained by multiplying one row of $M$ with another row, ant the definition of $A_{m \times m}$ is shown in Eq. (17).

$$A = M_{i}^{T} \times M_{j} = \left[ {\begin{array}{*{20}c} {m_{i1} \times m_{j1} } & {\begin{array}{*{20}c} {m_{i1} \times m_{j2} } & \ldots & {m_{i1} \times m_{jm} } \\ \end{array} } \\ {\begin{array}{*{20}c} {m_{i2} \times m_{j1} } \\ \vdots \\ {m_{im} \times m_{j1} } \\ \end{array} } & {\begin{array}{*{20}c} {m_{i2} \times m_{j2} } & \ldots & {m_{i2} \times m_{jm} } \\ {\begin{array}{*{20}c} \vdots \\ {m_{im} \times m_{j2} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ \ldots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {m_{im} \times m_{jm} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$

(17)

where the main diagonal element is the cumulative confidence of the $i$-th and $j$-th clustering validity function for target recognition with the best number of clusters, which defined as $Z = m_{ip} \times m_{jq } \left( {p = q} \right)$, the sum of non-principal diagonals constitutes the normalization factor $k$ of evidence, which is defined as Eq. (18).

$$k = \mathop \sum \limits_{p \ne q} m_{ip} \times m_{jq } p,q = \left( {1,2,3, \ldots ,m} \right)$$

(18)

3.3 Clustering Validity Function Ensemble Model and Algorithm Flowchart

As shown in Fig. 1, DS-CVFFM is a fusion model of clustering validity functions proposed in this paper. In the research process of clustering validity, the clustering validity functions are independent of each other, and they have their own advantages and disadvantages for different types of datasets. In order to apply the clustering validity method to more datasets as much as possible, DS-CVFFM regards each clustering validity function as an independent evidence. Firstly, the clustering data set are input, and the value of clustering validity function is obtained by FCM clustering algorithm. Then the values of cluster validity functions are normalized, and the BPA is constructed by the results of cluster validity functions. Finally, the information from different cluster validity functions is fused using D–S evidence theory and the optimal number of clusters $c$ is given using decision module. On the basis of FCM clustering algorithm, considering the advantages of adapting to different data, the fusion strategy of multiple clustering validity functions can better adapt to different types of data.

Fig. 1

D–S evidence theory-based clustering validity function fusion model (DS-CVFFM)

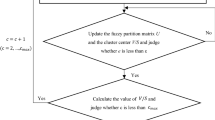
When designing the decision module for DS-CVFFM, set $A_{i} \left( {i = 1,2, \ldots ,n} \right)$ is the number of clusters, $A_{\omega }$ is the target type, and after get the $m_{ij} \left( \theta \right)$ about $A_{i}$ that in $\Theta$, the design of decision module should comply with the following rules: (1) $m\left( {A_{\omega } } \right) = {\text{max}}\left( {m\left( {A_{i} } \right)} \right)$, that is, the target type (the best number of clusters) with maximum confidence. (2) $m\left( {A_{\omega } } \right) - m\left( {A_{i} } \right) > \varepsilon ,(\varepsilon > 0)$, that is, the reliability difference between the target class and other classes must be greater than a set threshold. The flowchart of DS-CVFFM is shown in Fig. 2.

Fig. 2

Algorithm flowchart of DS-CVFFM

It can be seen from Fig. 2 that DS-CVFFM uses FCM algorithm as the base algorithm to judge the clustering center $V$ and membership matrix ${ }U$, and then calculates multiple fuzzy clustering validity functions $F_{i}$ under different clustering number $c$ value conditions. By calculating different $F_{i}$, in this case, $F_{i}$ has judged the validity of FCM clustering results, but the value of the best cluster number is different. Therefore, BPA function is constructed and different $F_{i}$ is normalized so that the optimal number of clusters corresponding to $F_{i}$ is the maximum effective, that is, the maximum probability of BPA function corresponds to the optimal $c$. At this time, DS-CVFFM has judged the probability of the optimal $c$ for $F_{i}$ under different number of clusters. However, when judging the optimal $c$, it is often based on the change trend and peak value of the validity function.

Sometimes the local minimum or maximum value corresponds to the optimal $c$, so that the next highest probability value corresponds to the optimal $c$. Therefore, the D–S evidence theory is used to fuse the probabilities of different $F_{i}$ under different cluster numbers. In this way, even if the individual validity function is second maximum validity, it will be determine the optimal number of clusters because other validity functions are modified at the maximum validity. In the Sect. 4, the paper will carry out simulation experiments on DS-CVFFM to prove the feasibility of the scheme.

4 Experimental Simulation and Result Analysis

4.1 Selection of Datasets and Experimental Parameters

In order to verify the effectiveness of DS-CVFFM, this paper selects 4 sets of artificial datasets and 14 sets of UCI datasets for experiments. The number of clusters selected in the experiment is $2 \le c \le 14$, and the value of fuzzy weighted $m$ is different according to different designs. The threshold of D–S decision module is $\varepsilon = 0.1$. The experimental environment is Windows 10 operating system and the experimental platform is Matlab 2018a. The artificial datasets are shown in Fig. 3a–d, where data_2_3 is a set of 2-D and 3-class data set which obey Uniform distribution, data_2_5 is a set of 2-D and 5-class data set which obey Gaussian distribution, data_3_3 is a set of 3-D and 3-class data set which obey Gaussian distribution, and data_3_6 is a set of 3-D and 6-class data set with Uniform distribution. UCI datasets are shown in Table 3. The first list shows the name of the data set, the second list shows the number of samples of the data set, the third list shows the attributes of the data set, the fourth list shows the number of classification of the data, and the fifth list shows the source of the data set.

Fig. 3

Scatter plot of artificial datasets

Table 3 Information introduction of UCI data set

4.2 Verify the feasibility of DS-CVFFM

In this section, 4 artificial datasets and 2 UCI datasets (iris and seeds) are selected to test the feasibility of DS-CVFFM. The structure and attributes of artificial data set are relatively simple, and it is easy to identify the best number of clusters. Iris and seeds datasets are the most frequently used datasets to verify the effectiveness of clustering. Four clustering validity functions ($V_{MPC} , V_{P} , V_{Z} , V_{HY}$) are selected to fusion. The fuzzy weighted $m = 2.0$ is selected, and the simulation results are shown in Table 4 and Fig. 4.

Table 4 Feasibility of DS-CVFFM under different datasets

Fig. 4

Feasibility of DS-CVFFM verified by different datasets

It can be found in Table 4 that the confidence degree is the highest for data_2_3 when $c = 3$, the confidence degree is the highest for data_2_3 when $c = 5$, the confidence degree is the highest for data_3_6 when $c = 6$, and the confidence degree is the highest for iris and seeds when $c = 3$. The confidence of the six selected datasets is the highest when the number of clusters is the optimal, the results show that DS-CVFFM is feasible and can find the correct number of clusters. In order to intuitively see the confidence change of each data set to $c$ under the judgment of DS-CVFFM, the data in Table 4 is plotted as a scatter diagram, as shown in Fig. 4.

4.3 Influence of Different Number of Clustering Validity Functions on DS-CVFFM

DS-CVFFM can obtain the final number of clusters by fusion multiple cluster validity functions. Therefore, the selection of the number of cluster validity functions will affect the final clustering results. For this reason, this section selects 4, 6, 8, 10 cluster validity functions for experiments to observe the influence on the final clustering results when selecting different number of cluster validity functions. Because the structure of artificial datasets are simple, only 8 sets of UCI datasets are used in this experiment, and the fuzzy weighted $m = 2$. The experimental results are shown in Tables 5, 6, 7, and 8.

Table 5 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${\varvec{V}} = 4$

Table 6 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${\varvec{V}} = 6$

Table 7 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${\varvec{V}} = 8$

Table 8 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${\varvec{V}} = 10$

Table 5 shows that when the number of cluster validity functions is 4 ($V_{PC} ,V_{PE} ,V_{MPC} ,V_{P}$), the confidence result of $c$. The results show that DS-CVFFM cannot judge the correct number of clusters for balance and sonar when $V = 4$. For sonar, although the maximum confidence value is found at $c = 2$ which is in line with the selection of the best number of clusters, the difference between the confidence value and the maximum confidence value at $c = 3$ is less than the threshold value, so the correct number of clusters cannot be output. Therefore, under the condition of $V = 4$, DS-CVFFM can find the optimal number of clusters for 6 datasets. Table 6 shows that when the number of cluster validity functions is 6 ($V_{PC} ,V_{PE} ,V_{MPC} ,V_{P} ,V_{XB} ,V_{FS}$), the confidence result of $c$. The results show that DS-CVFFM cannot judge the correct number of clusters for bupa and breast under the condition of $V = 6$. Therefore, under the condition of $V = 6$, DS-CVFFM can find the optimal number of clusters for 6 datasets. Table 7 shows that when the number of cluster validity functions is 8 ($V_{PC} ,V_{PE} ,V_{MPC} ,V_{P} ,V_{XB} ,V_{FS} ,V_{Z} ,V_{HY}$), the confidence result of $c$. The results show that DS-CVFFM cannot judge the correct number of clusters for bupa only under the condition of $V = 8$, so DS-CVFFM can find the best number of clusters for 7 datasets under the condition of $V = 8$. Table 8 shows that when the number of cluster validity functions is 10 ($V_{PC} ,V_{PE} ,V_{MPC} ,V_{P} ,V_{XB} ,V_{FS} ,V_{Z} ,V_{HY} ,V_{WL} ,V_{PCAES}$), the confidence result of $c$. The results show that DS-CVFFM cannot judge the correct number of clusters for breast, bupa and sonar under the condition of $V = 10$, so DS-CVFFM can find the best number of clusters for 5 datasets under the condition of $V = 10$.

According to the experimental results listed in Tables 5, 6, 7, and 8, it can be found that DS-CVFFM has the highest accuracy in judging the optimal number of clusters for different datasets under the condition of $V = 8$, with only one error, and the lowest accuracy under the condition of $V = 10$. Under the condition of $V = 4$ and $V = 6$, there are two errors. Compared with $V = 8$, the variety of the correct rate of judging the optimal number of clusters is not very significant. In order to distinguish the influence of $V = 4$, $V = 6$ and $V = 8$ on DS-CVFFM, the number of $V$ is determined by judging the difference between the maximum and the second largest value of $c$. when the difference between the maximum and the second largest value is larger, the value of $c$ corresponding to the maximum confidence of $c$ can be regarded as the optimal number of clusters. For this reason, 4 experimental datasets (iris, seeds, heart, german) which can still obtain the optimal number of clusters after fusing the clustering validity functions with different numbers are selected from the above four groups of experiments for comparison, as shown in Figs. 5, 6, 7, and 8a–d.

Fig. 5

Confidence values of ${\varvec{c}}$ with the increase of the number of validity functions for iris data set

Fig. 6

Confidence values of ${\varvec{c}}$ with the increase of the number of validity functions for seeds data set

Fig. 7

Confidence values of ${\varvec{c}}$ with the increase of the number of validity functions for heart data set

Fig. 8

Confidence values of ${\varvec{c}}$ with the increase of the number of validity functions for german data set

As shown in Fig. 5a–d, the selected experimental data set is iris. When $V = 4$, the difference between the maximum and the second largest value of $c$ confidence is 0.2799 (approximate to four decimal places). Similarly, when $V = 6$, the difference between the maximum and the second largest value of $c$ confidence is 0.6231, $V = 8$ is 0.5664, and $V = 10$ is 0.5881. When the selected data set is seeds, the experimental results are shown in Fig. 6a–d. When $V$ is 4, 6, 8 and 10, respectively, the corresponding differences are 0.2944, 0.3747, 0.5295 and 0.5916. When the selected data set is heart, the experimental results are shown in Fig. 7a–d. When $V$ is 4, 6, 8 and 10, respectively, the corresponding differences are 0.3404, 0.2251, 0.2696 and 0.2917. When the selected data set is german, the experimental results are shown in Fig. 8a–d. When $V$ is 4, 6, 8 and 10, the corresponding differences are 0.2814, 0.2690, 0.4108 and 0.6130. The difference summary is shown in Table 9. When $V = 10$, there are three datasets with the largest difference, and $V = 6$ has 1 data set with the largest difference. However, when $V = 8$, although there is no maximum difference, the difference is second only to $V = 10$. According to the comprehensive experimental results in Tables 5, 6, 7, 8, and 9, $V = 8$ is the most appropriate number of clustering effectiveness functions.

Table 9 Difference between maximum value and second maximum value of the confidence for different ${\varvec{c}}$ when selecting different numbers of cluster validity functions

4.4 Influence of Fuzzy Weighted on DS-CVFFM

The selection of fuzzy weighted $m$ has a certain impact on the final clustering results. In the past research process, $m$ is usually taken as $m = 2$, but it is not suitable for all datasets and clustering algorithms. In order to improve the ability of DS-CVFFM to find the optimal number of clusters, select multiple $m$ for the same group of cluster validity functions, and then fusion the values of the final validity functions to make the final results more reliable. Therefore, different values of $m$ are changed to observe the fusion results of DS-CVFFM on different datasets. The experimental results are shown in Tables 10, 11, and 12.

Table 10 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${{m}} = 2.0$

Table 11 Confidence values of ${\varvec{c}}$ for DS-CVFFM under different datasets and ${{m}} = 1.5, 2.0\,{{and}}\,3.0$

Table 12 Confidence values of $c$ for DS-CVFFM under different datasets and $m = 1.5, 1.75,2.0, 2.5 and 3.0$

As shown in Table 10, When $m = 2.0$, set the fusion period $T = 1$, and select the number of clustering validity functions $V = 8$. DS-CVFFM cannot get the correct number of clusters for haberman and sonar datasets and the correct number of clusters can be obtained for the other 6 datasets. When $m = 1.5, 2.0\,{\text{and}}\, 3.0$, as shown in Table 11, set the fusion period $T = 3$, and select the number of clustering validity functions $V = 8$. DS-CVFFM cannot get the correct number of clusters for haberman, blast, bupa and sonar datasets and the correct number of clusters can be obtained for the other 4 datasets. When $m = 1.5, 1.75,2.0, 2.5\,{\text{and}}\, 3.0$, as shown in Table 12, set the fusion period $T = 5$ and select the number of clustering validity functions $V = 8$. DS-CVFFM can get the correct number of clusters for 8 datasets.

According to Tables 10, 11, and 12, it can be found that when $m = 2.0$ is indeed the most appropriate value of fuzzy weighted. When $m = 1.5$, $m = 3.0$, there will be some interference to the final fusion results, resulting in some data cannot find the correct number of clusters. However, when we continue to expand the value condition of $m$, it can find that taking $m = 1.75$ and $m = 2.5$ in the left and right fluctuation of $m = 2$ can improve the accuracy of the final clustering results. And when $m = 1.5, 1.75,2.0, 2.5\,{\text{and}}\,3.0$, DS-CVFFM gets the highest number of datasets. In order to better observe the change of confidence of DS-CVFFM under different $m$ values, Tables 10, 11, and 12 can also be shown in the form of Figs. 9, 10, and 11.

Fig. 9

Confidence values of $c$ for DS-CVFFM under different datasets and $m\,=\,2.0$

Fig. 10

Confidence values of $c$ for DS-CVFFM under different datasets and ${{m}} = 1.5, 2.0\,{\text{and}}\,3.0$

Fig. 11

Confidence values of ${{c}}$ for DS-CVFFM under different datasets and ${{m}} = 1.5, 1.75, 2.0, 2.5\,{{and}}\,3.0$

4.5 Comparison of DS-CVFFM and Traditional Clustering Validity Evaluation Methods

In order to verify that the result of DS-CVFFM is more accurate than that of clustering validity functions and combined validity evaluation methods in judging the optimal number of clusters of data set, DS-CVFFM is selected to compare with clustering validity functions ($V_{MPC}$, $V_{XB}$, $V_{K}$, $V_{P}$, $V_{WL}$, $V_{Z}$, $V_{HY}$) and combined clustering validity evaluation methods (DWSVF, FWSVF, WSCVI, HWCVF). The comparative experimental results of DS-CVFFM and clustering validity functions are shown in Tables 13 and 14, and the comparative experimental results of DS-CVFFM and combined clustering validity evaluation methods are shown in Figs. 12 and 13.

Table 13 Comparison between DS-CVFFM and single cluster validity function, when the selected data set cluster is ${\varvec{c}}$ < 5

Table 14 Comparison between DS-CVFFM and single cluster validity function, when the selected data set cluster is 5 < ${\varvec{c}}$ < 10

Fig. 12

Comparison between DS-CVFFM and combined validity evaluation methods, when the selected data set cluster is ${\varvec{c}}$ < 5

Fig. 13

Comparison between DS-CVFFM and combined validity evaluation methods, when the selected data set cluster is 5 < ${\varvec{c}}$ < 10

Select DS-CVFFM and $V_{MPC}$, $V_{XB}$, $V_{K}$, $V_{P}$, $V_{WL}$, $V_{Z}$, $V_{HY}$ was compared in 14 UCI datasets, and the experimental results are shown in Tables 13 and 14. Table 13 shows the experiment of selecting the data set with the best number of clusters $c$ < 5, and Table 14 shows the experiment of selecting the data set with the best number of clusters 5 < $c$ < 10. The table only intercepts the value of $c$, and reserves the data results that provide comparison for the experiment. As shown in Table 13 (a–j), for iris data set, DS-CVFFM and $V_{HY}$ can judge the optimal number of clusters. For seeds data set, DS-CVFFM, $V_{MPC}$, $V_{P}$ and $V_{HY}$ can judge the optimal number of clusters. For heart, ionosphere, wpbc, bupa 4 data set, only $V_{MPC}$ cannot judge the optimal number of clusters. For balance data set, DS-CVFFM and $V_{MPC}$ can judge the optimal number of clusters. For sonar data set, DS-CVFFM, $V_{XB}$, $V_{K}$, $V_{Z}$ and $V_{HY}$ can judge the optimal number of clusters. For hfcr data set, DS-CVFFM, $V_{XB}$ and $V_{Z}$ can judge the optimal number of clusters. As shown in Table 14 (a–d), satimage and Led7 datasets can be found the correct clustering number by DS-CVFFM, $V_{WL}$ and $V_{HY}$. For segment dataset $V_{XB}$, $V_{K}$, $V_{WL}$ and DS-CVFFM can judge the correct number of clusters. For the pageblocks dataset, $V_{XB}$, $V_{K}$, $V_{Z}$ and DS-CVFFM can judge the correct number of clusters. According to the experimental results in Tables 13 and 14. The results show that DS-CVFFM can find the correct number of clusters for all 14 datasets, $V_{HY}$ and $V_{XB}$ can find 8 datasets, $V_{Z}$, $V_{K}$ and $V_{WL}$ can find 7 datasets, $V_{P}$ can find 5 datasets, $V_{MPC}$ can find 2 datasets. Thus, the performance of DS-CVFFM is significantly better than that of single clustering validity function.

DS-CVFFM is selected to compare with DWSVF, FWSCF, WSCVI, HWCVF in 15 UCI datasets, and the results are shown in Figs. 12 and 13. Figure 12 shows the experiment of selecting the data set with the best number of clusters $c$ < 5, and Fig. 13 shows the experiment of selecting the data set with the best number of clusters 5 < $c$ < 10. The abscissa is the number of clusters, and the ordinate is the value of each method. For iris, seeds and balance data set, only FWSCF cannot find the correct optimal number of clusters. For heart, ionosphere and sonar datasets, only DWSVF cannot find the correct optimal number of clusters. For wpbc and bupa datasets, DWSVF and WSCVI cannot find the correct number of clusters. For hfcr dataset, DWSVF and FWSCF cannot find the correct optimal number of clusters. For the german dataset, all methods can determine the optimal number of clusters. As shown in Fig. 13, only DS-CVFFM can find the correct optimal cluster number for the data set of satimage and led7. DWSVF, WSCVI and DS-CVFFM can judge the optimal clustering number for pageblocks dataset. HWCVF, WSCVI and DS-CVFFM can judge the optimal clustering number for segment data set. From Figs. 12 and 13, it can be seen that DS-CVFFM is more accurate than the weighted cluster validity evaluation method.

5 Conclusions

In this paper, a novel clustering validity evaluation method is proposed, which combines D–S evidence theory with multiple clustering validity functions. By standardizing the values of clustering validity functions, the basic probability assignment function (BPA) is constructed, the integration is carried out according to the fusion rules of D–S evidence theory, and the optimal number of clusters is output by decision module. Finally, the validity of the proposed model (DS-CVFFM) is verified by artificial data set and UCI data set. The accuracy of DS-CVFFM is judged by comparing DS-CVFFM with traditional validity evaluation methods, and then the stability of DS-CVFFM is judged by changing the fuzzy weight. The experimental results show that DS-CVFFM has better stability and accuracy than the traditional clustering validity evaluation methods under different datasets.

However, D–S evidence theory has some limitations, such as large amount of calculation, easy failure and evidence conflict in the face of independent information sources, which makes it impossible to determine the optimal number of clusters. Therefore, other optimization techniques can be used to replace D–S evidence theory to avoid the above problems. Some clustering validity functions are only suitable for datasets with a small number of clusters. This also causes DS-CVFFM to fail to obtain the optimal number of clusters for datasets with a high number of clusters. We can preprocess the data set and then improve the accuracy of the final model. FCM algorithm also has some defects in updating the membership and clustering center. Therefore, in the future work, we will also consider using multiple FCM clustering algorithms combined with multiple validity functions to obtain the final optimal number of clusters, so as to optimize the DS-CVFFM model and improve the stability and accuracy of the model.