Exponent and Logarithm Component-Wise Construction Method of FCM Clustering Validity Function Based on Subjective and Objective Weighting

Abstract

The cluster validity function is used to evaluate the quality of the cluster results, and giving the exact number of initial cluster categories will rationalize the cluster results. Most single cluster validity functions and combined cluster validity functions generally have strong subjective problems, which also increases the burden on decision analysts and have great limitations in applications. To overcome the shortcomings of these clustering validity functions and improve the accuracy of the optimal cluster category classification for the datasets, based on the clustering performance evaluation components, a validity functional component construction method based on the exponential and log form was proposed. The weighting method adopts the combination of expert empowerment and standard separation method to combine the five weights so as to obtain 52 different fuzzy clustering validity functions. Then, based on the fuzzy C-mean (FCM) clustering algorithm, the performance analysis are carried out by using multiple data sets. Experimental simulation of these functions are proceeded on six commonly used UCI datasets. A clustering validity function with the simplest structure and the best classification effect was selected by comparison. Finally, this function is compared with 8 typical single clustering validity functions and four common clustering validity combination evaluation methods on 8 UCI data sets. Through experimental simulation, the proposed validity function is compared in processing data sets, but also has strong scientific theoretical basis. Thus, the feasibility and effectiveness of the proposed clustering validity function construction method are proved.

1 Introduction

Clustering is accompanied by the emergence and development of human society. People in the process of understanding and mastering objective things, always distinguish different things and recognize the similarity between things. Therefore, the research of cluster analysis is not only of great theoretical significance, but also has important engineering application and humanistic values. With its theory development, clustering has been widely used in many fields, such as speech recognition, face recognition, radar target recognition, biological information analysis [1, 2], image segmentation [3,4,5,6], edge detection [7], image compression [8], curve fitting, target detection and tracking, mobile robot positioning, traffic flow video detection [9, 10], and model identification and fuzzy rule establishment [11, 12]. Clustering learning is one of the earliest methods used in pattern recognition and data mining tasks, and is used to study large databases in various applications. Therefore, the clustering algorithm for big data has attracted more and more attention.

In recent years, with the development of computing theory and technology, many clustering methods have been proposed. According to the implementation ideas of clustering algorithms, they can be divided into hierarchical clustering algorithm, partitioned clustering algorithm, density based clustering algorithm, grid based clustering algorithm, and model-based clustering algorithm. Goldberger et al. Proposed a hierarchical clustering algorithm based on classical Hungarian method [13]. Typical clustering methods include k-means algorithm, k-medoids algorithm, and fuzzy c-means algorithm [14]. Macqueen proposed K-means clustering algorithm [15] in 1967, which has become one of the most classic clustering algorithms. Yodern et al. proposed a semi-supervised K-means clustering algorithm in 2017 [16]. Gengzhang et al. proposed a DC k-means algorithm in 2018 [17]. Hiep proposed a differential privacy preserving K-Modes algorithm in 2018 [18]. So far, many clustering algorithms have been put forward for different types of clustering, which can meet the different clustering requirements. However, many existing clustering algorithms need to specify the number of clusters in order to obtain the optimal clustering partition of the target datasets before performing the clustering task. The clustering validity index is used to evaluate the partition result of clustering algorithm, which are modeled by mathematical knowledge and can evaluate the effectiveness of clustering partition results. Through the mathematical evaluation of the clustering results for datasets, the clustering algorithm can also obtain the best clustering results under the premise of unable to achieve the given optimal number of clusters. From the present point of view, the research on clustering validity can be roughly divided into the study of single cluster validity function and the research of combined clustering validity evaluation method. The research on single clustering validity function focuses on the following two aspects.

• (1) The fuzzy clustering validity function based on membership degree. Partition coefficient $(V_{PC} )$ defined by Bezdek is used to measure the overlap between clusters [19]. Bezdek will also proposed partition entropy $(V_{PE} )$ used to measure the fuzziness of clustering partition [20]. This index is similar to $V_{PC}$. Bezdek proved that for all probabilistic cluster partitions, the structure of $V_{PC}$ and $V_{PE}$ is simple and the amount of calculation is small, but they will change monotonously with the number of clusters. An improved partition coefficient $(V_{MPC} )$ is revised on $V_{PC}$ about the existed monotone decreasing trend problem, but other aspects of the defects have not been improved [21]. In 2004, Chen and links proposed an effective index in the form of subtraction $(V_{P} )$, which is an effective function that only focuses on membership [22]. In 2013, Jiashun proposed a clustering validity function $(V_{CS} )$, which can effectively suppress noise data [23]. Joopudi used the maximum membership degree and the minimum membership degree to measure the data overlap and proposed a clustering validity function $(V_{GD} )$ [24].

• (2) The fuzzy clustering validity function based on geometric structure. Xie and Beni proposed a clustering validity function $(V_{XB} )$ based on proportion operation in 1991 [25], which is the first clustering validity function which takes into account the structure of the data set. It is the ratio of the compactness within the cluster and the separation between the clusters. $V_{K}$ is an validity index proposed by Kwon. The method of adding penalty items to the numerator of the index effectively restrained the trend of decreasing monotonously of $V_{XB}$. $V_{PCAES}$ index is a clustering validity index proposed by Wu and Yang in 2005. It describes the compactness and separation of clustering by fuzzy membership function and the relative value of the center distance of an exponential type structure [26]. Chi-Hung Wu proposed a clustering validity function $(V_{WL} )$ in 2015 [27]. It considers all clusters and the overall compactness separation ratio of each cluster. Chi Yun proposed a validity function $(V_{FM} )$ in 2007 [28], which takes the partition entropy and fuzzy partition factor into account, and defines the compactness and separation of clustering, but its performance on noisy data sets is poor. Zhu proposed a new clustering validity function $(V_{ZLF} )$ in 2019 [29], which can divide high-dimensional data sets accurately. In 2021, Wang used the definition of compactness, separation, and overlap as reference, introduced a new concept to enhance the adaptability of the validity function, and thus proposed a clustering validity function $(V_{HY} )$ [30]. Wang proposed a new clustering validity function $(V_{WG} )$ in 2021, which can find the best clustering number of the noise, overlapping, and high-dimensional datasets [31].

The final clustering results will be directly affected by the performance of the clustering validity functions. Aiming at the shortcomings of the existing fuzzy clustering validity functions, this paper proposes a new fuzzy c-means clustering validity function based on multi clustering performance evaluation components by combining the subjective weighting method and standard deviation method. Two kinds of combination weighting methods in exponential and logarithmic forms are proposed, and then five FCM clustering performance evaluation components are continuously arranged and combined in weighted form. Several clustering validity functions based on combination weighting strategy are tested on UCI datasets. The experimental results show that the two validity functions can obtain the correct clustering results on UCI datasets, which can overcome the defects of other clustering validity functions, and become a new direction to solve the problem of fuzzy clustering validity problem, and expand the theoretical system of constructing clustering validity functions based on components.

2 FCM Clustering Algorithm and Combined Clustering Validity Evaluation Method

2.1 FCM Clustering Algorithm

Fuzzy C-means (FCM) algorithm is a common soft clustering algorithm, and it is also the most representative fuzzy clustering algorithm. It is widely used in pattern recognition and clustering analysis. Set the target data set $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ composed of $n$ samples, the sample data $x_{j} = [x_{1j} ,x_{2j} , \ldots ,x_{sj} ]^{T}$, where $x_{kj}$ is the the $k$ property value of $x_{j}$. For a given sample set $X$_, the cluster analysis of $X$ is divided into the $c$ clusters. The minimum objective function is found by iteration, which is defined in Eq. (1).

$$J_{FCM} (U,V) = \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {(u_{ij} )^{m} } } \left\| {x_{j} - v_{i} } \right\|^{2}$$

(1)

where $J_{FCM} (U,V)$ represents the square error clustering criterion, and its minimum value is called as the stationary point of least square error. $V = \left\{ {v_{1} ,v_{2} , \ldots ,v_{n} } \right\}$ represents the set of clustering centers, whose definition is shown in Eq. (2).

$$v_{i} = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} \cdot x_{i} } } }}{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} } }}$$

(2)

where, c represents the number of clusters; $m \in (1,\infty )$ is the fuzzy coefficient to control the fuzziness of membership degree of each group data the range; $v_{i}$ is on behalf of the i-th clustering centers; $\left\| {x_{j} - v_{i} } \right\|$ represents the distance between the objects $x_{j}$ to the cluster center $v_{i}$, which usually adopts the euclidean distance; $u_{ij} (0 \le u_{ij} \le 1)$ represents the membership degree of the data objects $x_{j}$ belonging to the cluster center $v_{i}$; $u_{ij} \in U$ and U is the membership matrix of fuzzy partition and meet the following conditions.

$$u_{ij} = \left[ {\sum\nolimits_{k = 1}^{c} {\left( {\frac{{\left\| {x_{j} - v_{i} } \right\|^{2} }}{{\left\| {x_{j} - v_{k} } \right\|^{2} }}} \right)}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {m - 1}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${m - 1}$}}}} } \right]^{ - 1} ,\sum\nolimits_{i = 1}^{c} {u_{ij} = 1} ,0 \le \sum\nolimits_{j = 1}^{n} {u_{ij} \le n}$$

(3)

where, $1 \le j \le n$, $1 \le i \le c$.

The FCM clustering algorithm process is described as follows:

Step 1: Set the clustering parameter $c$, fuzzy factor $m$, and convergence threshold $\varepsilon$_.

Step 2: Initialize the clustering center matrix $V$ and membership matrix $U$, and obtain $U_{0}$ and $V_{0}$.

Step 3: Update the fuzzy partition matrix $U={({u}_{ij})}_{c\times n}$ according to Eq. (3).

Step 4: Update the clustering center $V = \left\{ {v_{1} ,v_{2} , \ldots ,v_{c} } \right\}$ according to Eq. (2).

Step 5: Calculate $e = \left\| {u_{t + 1} - u_{t} } \right\|$. If $e \le \varepsilon$ ($\varepsilon$ is a threshold from 0.001 to 0.01), the algorithm stops and the final clustering result is calculated. Otherwise, $U_{t} = U_{t + 1}$ and repeat from Step 2.

2.2 Combined Clustering Validity Evaluation Method

The clustering validity problem mainly lies in how to select a clustering validity function to determine the optimal number of clusters in datasets. The clustering validity functions can be roughly divided into external validity function, internal validity function, and relative validity function. Both the internal fuzzy clustering validity function and the relative fuzzy clustering validity function have developed very mature and the system is more and more perfect. At present, the fusion of clustering validity functions mostly uses the weighted combination. The typical weighted combination clustering validity evaluation methods are listed in Table 1.

Table 1 Weighted combination clustering validity evaluation methods

3 Exponent and Logarithm Component-wise Construction Method of FCM Clustering Validity Function

3.1 Clustering Validity Evaluation Components

Based on the characteristics of FCM clustering algorithm and typical clustering validity functions, five clustering validity evaluation components (CP) are defined in this paper. These components are used to represent the compactness, similarity, variability within the datasets, and the degree of separation and overlap between datasets, which are shown in Table 2.

Table 2 Clustering validity evaluation components

3.2 Exponent and Logarithm Component-Wise Construction Method

In order to explore the combinatorial weighting component construction method of clustering validity evaluation, the above five components are normalized and standardized to make them in the same dimension range. Then, these components are arranged and combined in the form of combination weight. The new exponential and logarithmic clustering validity functions are constructed. Their construction rules are shown in Eq. (4) and (5).

$$\min V = \sum\limits_{i = 1}^{m} {w_{hybrid} e^{{CP_{i} }} }$$

(4)

$$\min S = \sum\limits_{j = 1}^{n} {w_{hybrid} \ln (1 + CP_{j} )}$$

(5)

where, m, i, n, and j are random positive integers from 1 to 5.

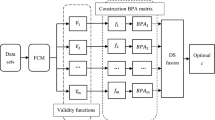
This paper proposed a clustering validity function constructed in the form of logarithm and exponent. The exponential function $y = e^{x}$ and the logarithm function $y = \ln x$ are monotonically increasing functions. In the interval $0 + \infty$, the ordinate value of the exponential function is always greater than 0, while the value of the logarithmic function is less than 0 in the interval, and it needs to be greater than 0 in the constructor. Therefore, this problem can be solved by expressing it with the logarithmic form $y = \ln (1 + x)$. Then $V$ and $S$ are applied to the FCM clustering algorithm, and the algorithm flowchart for obtaining the optimal number of clusters is shown in Fig. 1. The flowchart of the FCM clustering algorithm based on $V$ and $S$ are described as follows.

Fig. 1

Flowchart of FCM clustering algorithm based on the proposed validity function

The design method draws lessons from the linear superposition idea and the characteristics of exponential and logarithmic functions based on the previous combined clustering validity methods. However, the components selected in this paper have the problem that they are effective under different extreme conditions. Therefore, the components with the maximum effective value in Eq. (4) is used as ($1 - CP_{i}$). In Eq. (5), the component is dealt with ($1 + CP_{j}$) so as to obtain $CP_{j} = \{ (1 + CP_{1} ),(1 + CP_{2} ),(1 + CP_{3} ),(1 + CP_{4} ),(1 + CP_{5} ),(1 + CP_{6} )\}$. In this way, the format of each validity function can be guaranteed to be unified. In addition, for different components, the amount of information is different, but a component corresponds to a weight, which is independent of the position of the component in the clustering validity function. So $w_{hybrid}$ based on five components can be expressed as $w_{hybrid} = \{ w_{1} ,w_{2} ,w_{3} ,w_{4} ,w_{5} ,w_{6} \}$. In this way, the clustering validity function is constructed as $V$ and $S$. It is more convenient to carry out the simulation and contrast tests in the following paper by using similar structure mode and all the minimum values are effective.

3.3 Subjective and Objective Weighting Strategy

The selection of weight is very important in the combination evaluation process of clustering validity function. Different weight will bring different influence. The weight types can be mainly divided into the following two types.

• (1) Subjective weighting method. It is a method to determine the attribute weight according to the subjective attention of decision makers (experts). Common methods include Delphi method, analytic hierarchy process (AHP), fuzzy analysis method, linked ratio method, correlation tree method, set-valued iteration method, and eigenvalue method. The subjective weighting method is that the experts reasonably determine the weight of each attribute according to the actual decision-making problems and their own knowledge and experience. The determination of the weight is generally in line with the reality, so it is highly explanatory. But the decision-making and evaluation results have strong subjectivity and randomness, so its objectivity is weak and has great limitations in application.

• (2) Objective weighting method. It is mainly based on the degree of connection between indicators, the amount of information provided by each index, and the impact on other indicators. Therefore, the obtained weight is observable and does not increase the burden of decision makers. This method has strong mathematical theoretical basis. Common objective weighting methods include the principal component analysis method, multi-objective programming method, entropy weight method, CRITIC method, and standard deviation method.

In this paper, the hybrid weighting method of subjective and objective combination is used to eliminate subjective deviation and objective one-sided, and show the subjective and objective information while determining the weight so that it can truly and objectively reflect the actual situation of single cluster validity function. The hybrid weighting method can be defined as follows:

$$w_{hybrid} = \delta w_{object} + (1 - \delta )w_{subject}$$

(6)

where, $w_{object}$ is the subjective empowerment, $w_{subject}$ is the objective empowerment, $w_{hybrid}$ is the hybrid empowerment, and $\delta$ is the adjustment coefficient ($\delta \in [0,1][0,1]$).

When $\delta = 0$, $w_{hybrid} = w_{object}$ becomes the subjective weight. When $\delta = 1$, $w_{hybrid} = w_{subject}$ and the hybrid weight becomes the objective weight. When $\delta = 0.5$, we can conclude the objective index $w_{object}$ and the subjective index $w_{subject}$ have the same influence on $w_{hybrid}$. $\delta$ may be revised according to the importance of the index and the characteristics of the data set so as to improve the classification accuracy. The value of $w_{object}$ is determined by the decision maker and is taken as $w_{object} = 1/n$ without special instructions, where $n$ is the number of clustering validity functions. $w_{subject}$ is determined by information entropy weighting.

The standard deviation method is used to determine the index weight. First, the standard deviation of the index is calculated, and then the weight is determined based on the mean square deviation of the index. In the multi-index comprehensive evaluation, because the dimension of the index or the quantity of the datasets may be different, there is no comparability between the indicators. So the first step is to process the data and make the indexes comparable. There are many ways to deal with it, such as normalization, standardization, and some other dimensionless methods.

For the convenience of the following description, it is advisable to set the index set as $G = \{ G_{1} G_{2} \ldots G_{m} \}$, the sample set (or scheme set) is $A = \{ A_{1} A_{2} \ldots A_{n} \}$, and the corresponding sample point is $X_{ij}$($i = 1,2 \ldots n$ and $j = 12 \ldots ,m$). The weight vector of evaluation index is $W = (w_{1} w_{2} \ldots w_{m} )^{T}$, which satisfies $\sum {w_{i} = 1}$. After dimensionless or standardized treatment, the matrix $X = (X_{ij} )$ is changed to the matrix $Z = (Z_{ij} )$. The standard deviation determines the weight of the index. The principle is that if the standard deviation of an index is smaller, the variation degree of the index is smaller, the amount of information provided is smaller, and the role played in the comprehensive evaluation is smaller, so the weight of the index is smaller. On the contrary, the greater the weight. The characteristic of standard deviation weighting method is that the index weight reflects the amount of data information or the change of index data.

The specific calculation steps of subjective and objective weighting are described as follows.

Step 1: The original data matrix $X_{ij} (i = 1,2, \ldots ,n;j = 1,2, \ldots ,m)$ is carried out the dimensionless treatment. The extreme method is generally used for dimensionless treatment. The positive indices are $Z_{ij} = (X_{ij} - \min_{j} \{ X_{ij} \} )/(\max_{j} \{ X_{ij} \} - \min_{j} \{ X_{ij} \} )$. For the inverse index $Z_{ij} = (X_{ij} - \max_{j} \{ X_{ij} \} - X_{ij} )/(\max_{j} \{ X_{ij} \} - \min_{j} \{ X_{ij} \} )$, obtain the matrix $Z_{ij}^{\prime }$.

Step 2: Calculate the mean value of random variables by $\overline{{Z_{j} }} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {Z_{ij} }$;

Step 3: Calculate the mean square error of index j by $\sigma_{j} = \sqrt {\sum\nolimits_{i = 1}^{n} {(Z_{ij} - \overline{{Z_{j} }} )^{2} } }$;

Step 4: Calculate the weight of index j by $w_{j} = \sigma_{j} /\sum\nolimits_{j = 1}^{p} {\sigma_{j} }$;

Step 5: According to the multi-index weighted comprehensive evaluation model $D_{i} = \sum\nolimits_{j = 1}^{m} {W_{j} } \cdot Z_{ij} (i = 1,2, \ldots ,n;j = 1,2, \ldots m)$, calculate the comprehensive evaluation value, where $W_{i}$ is the weight of the $j$ the index.

4 Simulation Experiment and Result Analysis

According to the composition rules shown in Eq. (4) and Eq. (5), 52 different clustering validity functions can be formed by permutation and combination of five components in the form of exponent and logarithm. In order to facilitate the experiment, these 52 validity functions were divided into six groups (eight in four groups and nine in two groups), which are listed in Tables 3, 4, 5, 6, 7, and 8, respectively. These tables show the names and the simplified function form of the 52 validity functions. According to the prior knowledge, the fuzzy index can be determined as $1.5 \le m \le 2.5$ and the number of clusters is selected as $2 \le c \le \sqrt n$. This paper chooses $m = 2$ and $2 \le c \le 14$. Then whether the classification by using each clustering validity function is accurate is judged on different data sets. In this paper, we select the UCI datasets to carry out simulation experiments, such as Iris, Seeds, Balance, Hfcr, Glass, and Cooking. The amount of data, categories, and attributes of the adopted UCI datasets are listed in Table 9. In order to better observe the changing trend of six groups of clustering validity functions in the face of UCI datasets, the function values of their experimental results are placed in the normalized coordinate system, as shown in Figs. 1, 2, 3, 4, 5, and 6. In this way, the clustering effect of each validity function can be compared more intuitively. Finally, for different UCI datasets, the optimal number of clusters for each cluster validity function is listed. The results are listed in Tables 10, 11, 12, 13, 14, and 15.

Table 3 Exponent clustering validity functions (Group 1)

Table 4 Exponent clustering validity functions (Group 2)

Table 5 Exponent clustering validity functions (Group 3)

Table 6 Logarithmic clustering validity functions (Group 1)

Table 7 Logarithmic clustering validity functions (Group 2)

Table 8 Logarithmic clustering validity functions (Group 3)

Table 9 UCI data sets (component experiments)

Table 10 The best cluster number of the exponential validity functions for UCI datasets (Group 1)

Table 11 The best cluster number of the exponential validity functions for UCI datasets (Group 2)

Table 12 The best cluster number of the exponential validity functions for UCI datasets (Group 3)

Table 13 The best cluster number of the logarithmic validity functions for UCI datasets (Group 1)

Table 14 The best cluster number of the logarithmic validity functions for UCI datasets (Group 2)

Table 15 The best cluster number of the logarithmic validity functions for UCI datasets (Group 3)

5 Simulation Results and Analysis on Exponent Validity Functions (Group 1)

As can be seen from Fig. 2a–f, the six clustering validity functions of the first group of indices are defined as $V_{1}$, $V_{5}$, $V_{6}$, $V_{7}$, $V_{8}$, and $V_{9}$, which cannot classify any group of UCI datasets. Each group of data in UCI data set can be classified by $V_{2}$. It can be seen from Fig. 2a–c that Iris, Seeds and Balance data sets can be correctly divided into three categories by $V_{3},$ and the other data sets are classified incorrectly. Finally, it can be seen from Fig. 2b and d, $V_{3}$ only can the optimal number of clusters for the Seeds and Hfcr datasets. It can be found in the comparison experiment of the first group of exponent clustering validity functions. Three UCI datasets can be distinguished correctly by $V_{3}$; Only two sets of real datasets can be correctly divided by $V_{4}$; $V_{1}$, $V_{5}$, $V_{6}$, $V_{7}$, $V_{8}$, and $V_{9}$ unable to accurately cluster any set of UCI datasets. The validity function $V_{2}$ has the best clustering performance, which can be achieved by dividing all UCI datasets.

Fig. 2

Variation trend of normalized exponential clustering validity functions (Group 1)

6 Simulation Results and Analysis on Exponent Validity Functions (Group 2)

From the experimental results in Fig. 3a–d, it can be concluded that when processing Glass and Cooking datasets, the second group of clustering validity function cannot correctly classify them. It can be seen from Fig. 3a–b that the samples in Iris and Seeds datasets can be accurately divided into three categories by $V_{11}$, $V_{12}$, and $V_{14}$. It can be found from Fig. 3b and d that Seeds and Hfcr datasets can be effectively classified by $V_{13}$. As shown in Fig. 3c, Balance can be accurately divided into three categories by $V_{12}.$ Through the comparative experiments on the second group of exponential validity functions, it can be found that, $V_{10}$, $V_{15}$, $V_{16}$, $V_{17}$, and $V_{18}$ are unable to successfully distinguish any of the selected UCI datasets. Two UCI datasets can be distinguished successfully by $V_{11}$, $V_{13}$, and $V_{14}$. The best clustering number of three UCI datasets can be obtained by $V_{12}$.

Fig. 3

Variation trend of normalized exponential clustering validity functions (Group 2)

7 Simulation Results and Analysis on Exponent Validity Functions (Group 3)

In Fig. 4d-f, it can be found that none of the eight validity functions can classify Hfcr, Glass, and Cooking data sets. As can be seen from Fig. 4c, in addition to the validity function $V_{21}$, the other seven validity functions can classify the Balance data set into three categories and the classification performance is excellent. Finally, according to Fig. 4a and b, Iris and Seeds datasets can be correctly divided into three categories by $V_{21},$ while other seven validity functions cannot effectively classify these two datasets. Based on the comparative experiment results by adopting the third group of exponential validity functions, we can draw the conclusion that $V_{21}$ can successfully separate two datasets, while the other seven validity functions cannot classify the other datasets except the Balance data set. The classification performance of the eight clustering validity functions is relatively poor and is excluded from the selection range.

Fig. 4

Variation trend of normalized exponential clustering validity functions (Group 3)

8 Simulation Results and Analysis on Logarithm Validity Functions (Group 1)

According to Fig. 5a–f, the six datasets in UCI datasets can be classified successfully by $S_{2}$. Seen from Fig. 5c, Balance can be divided into three categories by $S_{5},$ and the optimal cluster number of Balance is c = 3. However, the rest of the log validity functions in the first group cannot distinguish any selected UCI datasets correctly. The experimental results are similar to those of the first exponential group. According to the contrast experiment results on the first group of logarithmic validity functions, it can be concluded that $S_{5}$ can obtain the perfect clustering number of data sets accurately. The clustering performance of $S_{2}$ is very good and it can accurately and effectively classify all adopted UCI datasets, so it is included in our selection range.

Fig. 5

Variation trend of normalized logarithmic clustering validity functions (Group 1)

9 Simulation Results and Analysis on Logarithm Validity Functions (Group 2)

From Fig. 6a–f, it can be observed that the performance of the nine logarithmic validity functions in the clustering and classification process on UCI data sets is very poor, and it is impossible to classify any datasets successfully. Therefore, it shows that the nine logarithmic validity functions in the simulation experiments cannot be used to classify UCI data sets, it is necessary to select and compare other logarithmic validity functions composed of components.

Fig. 6

Variation trend of normalized logarithmic clustering validity functions (Group 2)

10 Simulation Results and Analysis on Logarithm Validity Functions (Group 3)

It can be observed from Fig. 7a–f that the simulation results of this group are similar to those of the second group of logarithmic clustering functions. These eight logarithmic validity functions also have no way to distinguish UCI datasets effectively. As can be seen from Fig. 7e, Glass dataset can only be divided into three categories by $S_{22}$, but it is still not the optimal number of clusters. The other validity functions in this group can only divide each data set into two categories, and none of them can be classified successfully. Therefore, the performance of these eight logarithmic validity functions in this group is still very poor and is not in the selected range.

Fig. 7

Variation trend of normalized logarithmic clustering validity functions (Group 3)

The validity functions $V$ and $S$ are the best clustering validity evaluation criteria when both the minimum value $c$ is taken. From Fig. 2 to Fig. 7, 52 validity functions constructed in this paper can clustering the selected data sets into several categories, which is the improved quantitative result. In practice, if a data is given, in the cluster number $2 \le c \le \sqrt n$, the two optimal validity functions $V_{2}$ and $S_{2}$ compared with the 52 validity functions are used to determine how much is the optimal cluster number.

11 Simulation Comparison with Single Clustering Validity Functions and Combined Clustering Validity Methods

11.1 Simulation Comparison with Single Clustering Validity Functions

Through the simulation comparison on the above six groups of clustering validity functions, six UCI datasets can only be divided successfully by the exponential validity function $V_{2}$ and the logarithmic validity function $S_{2}$. In order to fully reflect the clustering performance of the validity function $V_{2}$ and $S_{2}$, this paper selected the eight common clustering validity functions ($V_{MPC}$, $V_{XB}$, $V_{PCAES}$, $V_{WL}$, $V_{FM}$, $V_{ZLF}$, $V_{HY}$, and $V_{WG}$) and 8 kinds of commonly used UCI datasets to carry out the comparative experiments with $V_{2}$ and $S_{2}$. The function description and optimal cluster number of the eight typical clustering validity functions are listed in Table 16, where $\overline{v} = \sum\nolimits_{i = 1}^{c} {v_{i} } /c$ represents the mean value of the cluster centers. The geometric meaning of $u_{mj} = \mathop {\min }\nolimits_{1 \le i \le c} \sum\nolimits_{j = 1}^{n} {(u_{ij} )^{2} }$ can refer to the component $CP_{4}$ shown in Sect. 3. l and $median\left\| {v_{i} - v_{k} } \right\|^{2}$ represents the median distance between two cluster centers.

Table 16 Typical clustering validity functions

Table 17 lists the number of samples, attributes, and categories of UCI datasets selected in this experiment. Vehicle and Led7 datasets are added in the comparison process to improve the experiment integrity by adopting the 10 normalized fuzzy validity functions ($V_{MPC}$, $V_{XB}$, $V_{PCAES}$, $V_{WL}$, $V_{FM}$, $V_{ZLF}$, $V_{HY}$, $V_{WG}$, $V_{2}$, and $S_{2}$) in the same coordinate system. The simulation results are shown in Fig. 7a–h. Finally, for different UCI datasets, the optimal number of clusters for each cluster validity function is listed in Table 18.

Table 17 UCI datasets (comparative experiments)

Table 18 The best cluster number of the different validity functions for UCI datasets

As can be seen from Fig. 8a, b, Iris and Seeds data sets can be successfully divided into three categories by the four validity functions ($V_{HY}$, $V_{WG}$, $V_{2}$, $S_{2}$), while other six validity functions could not get the correct cluster number. This shows that when dealing with Iris and Seeds datasets with complex structures, $V_{2}$ and $S_{2}$ have the better performance compared with some other typical clustering validity functions. As shown in Fig. 8e-h, only $V_{2}$ and $S_{2}$ can accurately distinguish Glass, Cooking, Vehicle and Led7 datasets. It can be observed from Fig. 8c and d, except that $V_{2}$ and $S_{2}$, there are other validity functions that distinguish individual datasets from UCI datasets, such as $V_{WL}$ can get the correct number of clusters in the Balance data set. The optimal clustering number of Hfcr data set can be correctly divided by $V_{ZLF}$, whose the best cluster number can be divided into four. As shown in Fig. 8a–h. The best classification number of all UCI datasets can only be found by $V_{2}$ and $S_{2}$, which indicates that when faced with data sets with overlapping samples, noise data and higher dimensions, the classification number of UCI datasets can be found. The clustering result of $V_{2}$ and $S_{2}$ is better than other clustering validity functions.

Fig. 8

Variation trend of normalized clustering validity functions

This paper constructs 52 validity functions. The computational complexity of simulating these 52 validity function experiments is the same as the calculation complexity of a single validity function. The single validity function calculation complexity takes time, and the time complexity is positively proportional to the number of validity function so that the time complexity is a positive linear relationship with the constructed validity function. The selected eight common clustering validity functions ($V_{MPC}$, $V_{XB}$, $V_{PCAES}$, $V_{WL}$, $V_{FM}$, $V_{ZLF}$, $V_{HY}$, and $V_{WG}$) are designed through subjective experience based on the basic concepts of FCM clustering algorithm and validity evaluation criteria. The improved partition coefficients $V_{MPC}$ correct the $V_{PC}$ existing monotonic reduction problem, but still lack a direct connection to the geometry of the data set. $V_{XB}$ is the structure of the data set clustering validity function, but this calculation method often ignore the noise data. $V_{PCAES}$ is a function of exponential operation proposed by Wu and Yang et al. $V_{WL}$ has best classification effect among these eight validity functions. $V_{FM}$ has poor performance on the data set with noise. On the other hand, the exponential validity function $V_{2}$ and the log validity function $S_{2}$ used for comparison are the two best clustering validity functions by the objective combination and then performance comparison. These two validity functions proposed in this paper not only avoid the strong subjective randomness of the subjective experience in designing the validity function, but also greatly reduce the limitations in real applications.

11.2 Simulation Comparison with Combined Clustering Validity Methods

In order to better highlight the advantages of the weighting method and validity function proposed in this paper compared with other traditional methods, so as to enhance its persuasiveness, four combined clustering validity methods introduced in Sect. 2.2 (DWSVF, FWSVF, WSCVI, and HWCVF) and 8 UCI datasets are selected to carry out the simulation experiments. They are compared with $V_{2}$ and $S_{2}$ through simulation experiments. Then the six clustering validity evaluation methods (DWSVF, FWSVF, WSCVI, HWCVF, $V_{2}$, and $S_{2}$) are placed in the normalized coordinate system, and the experimental results are shown in Fig. 9a–h. Finally, Table 19 lists the optimal number of clusters for each clustering validity evaluation method for different UCI datasets.

Fig. 9

Variation trend of normalized clustering combination evaluation methods

Table 19 The best cluster number of different clustering combination evaluation methods for UCI datasets

As can be seen from Fig. 8a–c, the Iris, Seeds and Balance datasets can be accurately classified into three subsets by DWSVF, WSCVI, $V_{2}$, and $S_{2}$. In Fig. 9d and h, it can be found that when processing Hfcr, Glass, Cooking, Vehicle, and Led7 datasets, only $V_{2}$ and $S_{2}$ can obtain the best cluster number of these six datasets. None of the other clustering combination evaluation methods can accurately divide these six datasets. Obviously, $V_{2}$ and $S_{2}$ are much better than other classical clustering combination evaluation methods. From the experimental results shown in Fig. 8a–h, the following conclusions can be drawn. For the above 8 commonly used UCI data sets, the classification performance of $V_{2}$ and $S_{2}$ is also better.

12 Conclusion

In this paper, a new combination empowerment method is defined through subjective empowerment and standard separation method empowerment, and a component construction method of FCM clustering validity function based on five cluster performance evaluation components was proposed. By using the UCI data sets, the best clustering validity function was selected by carrying out the simulation comparison. Finally, the eight commonly used single clustering validity functions and four typical combined clustering validity evaluation methods were simulated and verified on 8 UCI datasets. The simulation results prove that the proposed validity function based on this construction method is more complex in the data structure. The datasets with noise and overlapping data interference is better than other single or combination clustering validity functions. The screening and comparison of many experiments prove the proposed constructor more objective. With a strong scientific theoretical basis, it can reduce the one-sided aspect of proposing the validity function based on the subjective intention and improve the research depth of the clustering validity function. However, the construction method also has its own limitations, so some constructed superior validity functions will be selected to integrate the method, and comprehensively use multiple validity functions for evaluation. Therefore, the component integration for the clustering validity function is put into further study.