1 Introduction

As an important research content in the field of data mining, clustering is an unsupervised pattern recognition method, which is to cluster data sets under the guidance of no prior knowledge, so that the data in the same category is as similar as possible, and the greater the difference between different categories, the better [1]. Clustering is mainly divided into two directions: hard clustering and fuzzy clustering. Hard clustering, for example, k-means clustering algorithm [2] performs clustering according to the idea of “non-0 equals 1”, which requires that each sample must be clearly divided into different sub-categories, only belonging and not belonging two situations. But in fact, most data are uncertain, and a data sample will belong to multiple categories to varying degrees [3]. This hard clustering method ignores the existence of overlapping data samples between the two classes, which is often not logical in application. As Ruspini [4] introduced the concept of fuzzy division on the basis of hard clustering, fuzzy clustering came into being. It can allocate each element in the data set proportionally according to the size of different membership degrees, so that the element belongs to multiple classes. Among them, fuzzy C-means (FCM) clustering algorithm is the most commonly used clustering method in fuzzy clustering, which is more consistent with the actual sample situation, convenient operation, wide application range and other characteristics [5]. In recent years, FCM algorithm and fuzzy logic have been continuously improved, and their application fields are more and more extensive. For example, in 2014, M. A. Sanchez et al. [6] proposed a new fuzzy grain-size gravity clustering algorithm for multi-variable data. Ari et al. [7] proposed generalized Possibilistic Fuzzy C-means with Novel Cluster Validity Indices for Clustering noisy data in 2017. In the same year, Elid Rubio et al. [8] extended the fuzzy possibility C-Means (FPCM) algorithm of Type-2 fuzzy logic technology and improved the efficiency of FPCM algorithm. In 2018, F. V. Farahani et al. [9] proposed an intelligent approach based on spatially focused FCM and ensemble learning for the diagnosis of pulmonary nodules. To solve the extended target tracking problem in PHD filter, Bo Yan et al. [10] proposed an improved segmentation algorithm based on FCM algorithm in 2019. In 2020, Haibo Liang et al. [11] proposed the improved SVM-FCM algorithm for rock image segmentation. However, FCM algorithm needs to pass clustering validity verification to judge the optimal partition result of data samples, so finding an appropriate clustering validity function is an important research direction in the field of FCM clustering algorithm [12].

At present, many scholars have proposed various cluster validity functions. However, due to the large differences in the structure and attributes of the data sets, it is impossible for any cluster validity functions to correctly divide all data sets, and no one validity function is always better than others. It is precisely because of this status quo that new clustering validity functions continue to appear. The current research directions of fuzzy clustering validity functions are mainly concentrated in the following two categories:

  1. (1)

    Fuzzy clustering validity functions based only on membership degree. In 1974, Bezdek et al. firstly proposed the validity function for fuzzy clustering, namely the partition coefficient \((V_{PC} )\) [13]. Subsequently, Bezdek et al. proposed the partition entropy \((V_{PE} )\) based on \(V_{PC}\) and Shannon's theorem in Shannon's information theory [14]. Dave et al. proposed an improved partition coefficient \((V_{MPC} )\) in 1996 [15]. In 1999, Fan et al. proposed an improved fuzzy entropy clustering validity function \((V_{MPE} )\) [16], which can suppress the monotonic change of \(V_{PC}\) and \(V_{PE}\) as the number of clusters increases. Gai-yun Gong et al. redefines the fuzzy partition matrix based on data information in 2004 and proposed a clustering validity function \((V_{PF} )\) based on the partition ambiguity [17]. Zalik et al. proposed a clustering validity function \((V_{CO} )\) that adopts the membership to define overlap and compactness in 2010 [1]. In 2019, Yong-li Liu et al. added the degree of separation module in \(V_{CO}\) and proposed a novel clustering validity function [18], which can improve the stability of \(V_{CO}\). Jiashun et al. proposed a clustering validity function \((V_{CS} )\) that can effectively suppress noise data in 2013 [19]. Joopudi et al. used the largest membership degree and the second largest membership degree to measure the overlap of data in the same year, and proposed the clustering validity function \((V_{GD} )\) [20]. In 2014, Zhang et al. proposed a membership validity function based on two-part modularization [21].

  2. (2)

    Fuzzy clustering validity functions based on membership degree and geometric structure of data sets. In 1991, Xie and Beni et al. proposed \(V_{XB}\) [22] as the first clustering validity function that considered the geometric structure of the data set. In 1996, Bensaid et al. also proposed the clustering validity function \((V_{SC} )\) using the ratio of the degree of compactness within a class and the degree of separation between classes [23]. In 1998, Know et al. introduced a penalty term on the basis of \(V_{XB}\) and proposed the clustering effectiveness function \((V_{K} )\) [24]. In 2005, Kuo-Lung Wu et al. proposed a PCAES clustering validity function \((V_{PCAES} )\) based on exponential operation [25]. In 2019, Zhu et al. proposed a clustering validity function \((V_{ZLF} )\) in the form of a ratio [26]. Ouchicha et al. proposed a standardized superimposed clustering validity function \((V_{ECS} )\) in 2020 [27]. Liu et al. proposed an IMI clustering validity function \((V_{IMI} )\) in 2021 [28]. In 2021, Hong-Yu Wang et al. proposed a clustering validity function \((V_{HY} )\) based on intra-class compactness and inter-class separation [29]. In the same year, Wang et al. proposed a hybrid weighted combination method (HWCVF) [30].

Any clustering validity function is composed of several sub-parts representing different geometric meanings, namely components. Although the excellent performance of clustering validity function emerge in endlessly, but there is no scholar from the view of the components of a validity function for further study. Therefore, this paper puts forward six components (the compactness, similarity, variation degree, the degree of separation between data sets and the overlap degree of clustering to realize the performance evaluation. At the same time, the theoretical basis of these six components is explained in details. Finally, these six components constitute a new validity function of fuzzy C-means clustering. This function can suppress the influence of noise data and divide high-dimensional data and overlapping data accurately. Simulation results show that the proposed validity function can obtain correct clustering results on both artificial and UCI data sets.

In the second section, this article will explain the basic theory and algorithm process of the FCM algorithm, and finally introduce the advantages and disadvantages of traditional cluster effectiveness functions.

2 FCM Clustering Algorithm and Cluster Validity Functions

2.1 FCM Clustering Algorithm

FCM clustering algorithm is based on the fuzzy C-partition of the objective function. Through iteration, the objective function is minimized and optimized to obtain c fuzzy subsets [31]. Suppose there are n samples in the data set, and each sample is p-dimensional, \(X = \left\{ {x_{1} ,x_{2} , \cdots ,x_{n} } \right\}\), \(X \in R^{p}\). \(V = \left\{ {v_{1} ,v_{2} , \cdots ,v_{n} } \right\}\) is the collection of cluster centers in the data set X, which is a matrix of \(c \times p\). The objective function of FCM clustering algorithm was defined as:

$$J_{m} (U,V) = \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {(u_{ij} )^{m} \left\| {x_{j} - v_{i} } \right\|} }^{2}$$
(1)

where, \(J_{m} (U,V)\) is the square error criterion function, and the minimum value of \(J_{m} (U,V)\) is called the minimum error balance point. In Eq. (1), \(m \in (1,\infty )\) represents the fuzzy weighted index to control the degree of fuzzy membership of each group of data. When m infinity approaches 1, FCM clustering algorithm will increasingly tend to the hard clustering algorithm. When m = 1, FCM clustering algorithm is equivalent to the K-means clustering algorithm. On the contrary, when m tends to infinity, all data objects \(x_{j}\) and the cluster centers \(v_{i}\) will overlap, and the membership degree of the data objects \(x_{j}\) belonging to each cluster will be the same, whose value is 1/\(C\). The parameter c is the number of divisions of the fuzzy subset. \(\left\| {x_{j} - v_{i} } \right\|\) is the Euclidean distance between the cluster center \(v_{i}\) and the data point \(x_{j}\). \(u_{ij}\)\((0 \le u_{ij} \le 1)\) is the membership degree of the data point \(x_{j}\) to the cluster center \(v_{i}\), where \(u_{ij} \in U\) and \(U\) is a \(c \times n\) membership matrix that satisfies \(\sum\nolimits_{i = 1}^{c} {u_{ij} = 1}\) and \(0 \le \sum\nolimits_{j = 1}^{n} {u_{ij} \le n}\), where \(1 \le j \le n\), \(1 \le i \le c\).

FCM clustering algorithm minimizes the objective function by constantly and iteratively updating the cluster centers and the membership matrix to find the optimal solution for c. The steps of FCM clustering algorithm are described as follows.

Step 1: Given the number of clusters c and the fuzzy index m.

Step 2: Initialize the cluster center \(V\) and the membership matrix \(U\), and then obtain \(U_{0}\) and \(V_{0}\).

Step 3: Update the fuzzy cluster center \(V\) by Eq. (2)

$$v^{(t + 1)} = \frac{{\sum\nolimits_{j = 1}^{n} {(u_{ij}^{(t)} )^{m} x_{i} } }}{{\sum\nolimits_{j = 1}^{n} {(u_{ij}^{(t)} )^{m} } }}\;among\,them\,1 \le i \le c$$
(2)

Step 4: Update the fuzzy partition matrix \(U = (u_{ij}^{(t + 1)} )_{c \times n}\) by Eq. (3).

$$u_{ij}^{(t + 1)} = \left[ {\sum\limits_{k = 1}^{c} {\left( {\frac{{\left\| {x_{j} - v_{i} } \right\|}}{{\left\| {x_{j} - v_{k} } \right\|}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {(m - 1)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${(m - 1)}$}}}} } } \right]^{ - 1}$$
(3)

where, \(1 \le i \le c\), \(1 \le j \le n\).

Step 5: Calculate the error \(e = \left\| {v_{t + 1} - v_{t} } \right\|\). If \(e\) ≤ ε (ε is a threshold from 0.001 to 0.01), the loop ends and the final clustering result is obtained, otherwise go to Step 2.

2.2 Clustering Validity Functions

2.2.1 Partition Coefficient \((V_{PC} )\) and Partition Entropy \((V_{PE} )\)

Bezdek first proposed the partition coefficient \(V_{PC}\) and partition entropy \(V_{PE}\) for fuzzy clustering as shown in Eq. (4) and Eq. (5), respectively.

$$V_{PC} = \frac{1}{n}\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {(u_{ij} )^{2} } }$$
(4)
$$V_{PE} = - \frac{1}{n}\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {[u_{ij} \log_{a} (u_{ij} )]} }$$
(5)

The principle of partition coefficient and partition entropy is simple, and the amount of calculation is small. But they only consider the similarity within the data set, and lack the connection with the geometric structure of the data set. As the number of clusters increases, \(V_{PC}\) and \(V_{PE}\) will show a monotonic trend, which makes it impossible to divide the data set correctly. \(V_{PC}\) and \(V_{PE}\) take the minimum and maximum c, respectively, as the optimal number of clusters.

2.2.2 Improved Partition Coefficient \((V_{MPC} )\)

The improved partition coefficient \(V_{MPC}\) corrects the existing monotonic reduction problem of \(V_{PC}\), but still lacks a direct connection with the geometric structure of the data set. c with the maximum value of \(V_{MPC}\) is the best clustering result, and \(V_{MPC}\) can be calculated by:

$$V_{MPC} = 1 - \frac{c}{c - 1}(1 - V_{PC} )$$
(6)

2.2.3 Xie-Beni Clustering Validity Function \((V_{XB} )\)

The calculation of \(V_{XB}\) can be realized by:

$$V_{XB} = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {(u_{ij} )^{m} \left\| {x_{j} - v_{i} } \right\|} }^{2} }}{{n\mathop {\min }\limits_{i \ne j} \left\| {v_{i} - v_{j} } \right\|^{2} }}$$
(7)

The numerator of \(V_{XB}\) represents the tightness, and the smaller the numerator, the tighter the data within the class. The denominator of \(V_{XB}\) is used to define the degree of separation. The larger the denominator, the more separated the data between classes. Therefore, when \(V_{XB}\) takes the minimum value, c is the optimal number of clusters. However, this clustering validity function has two shortcomings. (1) When \(c \to n\), \(V_{XB}\) will tend to zero. (2) When \(m \to \infty\), \(V_{XB}\) will become infinite.

2.2.4 Knows Clustering Validity Function (\(V_{K}\))

Know et al. introduced a penalty term \(\frac{1}{c}\sum\nolimits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|}^{2}\) on the basis of \(V_{XB}\), which successfully suppressed the monotonically decreasing trend of \(V_{XB}\) when \(c \to n\). But when \(m \to \infty\), \(V_{XB}\) will become infinite. \(V_{K}\) is also valid to take the minimum value, and calculated by Eq. (8).

$$V_{K} = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {(u_{ij} )^{2} \left\| {x_{j} - v_{i} } \right\|} }^{2} + \frac{1}{c}\sum\nolimits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|}^{2} }}{{\mathop {\min }\limits_{i \ne j} \left\| {v_{i} - v_{j} } \right\|^{2} }}$$
(8)

2.2.5 PCAES Clustering Validity Function \((V_{PCAES} )\)

\(V_{PCAES}\) is a clustering validity function with an exponential operation method shown in Eq. (9). The first part of \(V_{PCAES}\) is the ratio of the sum of the squares of the degree of membership and the minimum degree of membership. The second part of \(V_{PCAES}\) represents the relative distance between the cluster centers, and the adoption of exponential operation can suppress the monotonic trend of \(( - \mathop {\min }\limits_{k \ne i} \left\| {v_{i} - v_{j} } \right\|^{2} )/\beta_{T}\).

$$V_{PCAES} = \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {\frac{{u_{ij}^{2} }}{{u_{M} }} - \sum\limits_{i = 1}^{c} {\exp \left( {\frac{{ - \mathop {\min }\limits_{k \ne i} \left\| {v_{i} - v_{k} } \right\|^{2} }}{{\beta_{T} }}} \right)} } }$$
(9)

where, \(u_{M} = \mathop {\min }\limits_{1 \le i \le c} \sum\limits_{j = 1}^{n} {u_{ij}^{2} }\), \(\beta_{T} = \frac{1}{c}\sum\limits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|}^{2}\), \(\overline{v} = \frac{1}{c}\sum\limits_{i = 1}^{c} {v_{i} }\). The maximum value of \(V_{PCAES}\) is valid.

2.2.6 Tang Clustering Validity Function \((V_{T} )\)[32]

\(V_{T}\) is a new fuzzy clustering validity function proposed by Tang et al. which is based on \(V_{K}\) [23]. The second term in its numerator is a penalty term, which represents the distance between any two different cluster centers. It can also suppress the problem of monotonically decreasing of \(V_{XB}\) when \(c \to n\). But unlike \(V_{K}\), the penalty term \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}\) in the denominator of \(V_{T}\) can solve this problem that \(V_{XB}\) will become infinite when \(m \to \infty\). This validity function can be defined as:

$$V_{T} = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} \left\| {x_{j} - v_{i} } \right\|^{2} + \frac{1}{c(c + 1)}\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{k = 1;k \ne i}^{c} {\left\| {v_{i} - v_{k} } \right\|^{2} } } } } }}{{\mathop {\min }\nolimits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2} + \frac{1}{c}}}$$
(10)

2.2.7 P clustering Validity Function \((V_{P} )\)[33]

Chen and Links proposed a clustering validity function \(V_{P}\) based only on membership degree in 2004, as shown in Eq. (11). The first half of \(V_{P}\) represents the sum of the maximum values of the data in each category. The larger the value, the better the tightness of the data within the category. The second part of \(V_{P}\) represents the degree of similarity between classes, and is used to judge the membership degree of the intersection between \(v_{i}\) and \(v_{j}\). The smaller the value, the more separation between classes. When taking the maximum value of \(V_{P}\), c is the optimal number of clusters.

$$V_{P} = \frac{1}{n}\sum\nolimits_{j = 1}^{n} {\mathop {\max }\nolimits_{i} } (u_{ij} ) - \frac{1}{k}\sum\nolimits_{i = 1}^{c - 1} {\sum\nolimits_{j = i + 1}^{c} {\left[ {\frac{1}{n}\sum\nolimits_{k = 1}^{n} {\min (u_{ik} ,u_{ik} )} } \right]} }$$
(11)

2.2.8 WL Clustering Validity Function \((V_{WL} )\)[34]

\(V_{WL}\) is a cluster validity function proposed by Chih-Hung Wu et al., as shown in Eq. (12). The numerator of \(V_{WL}\) adopts the sum of the average Euclidean distances from the data points to all cluster centers to define the compactness. The first term of the denominator represents the compactness between clusters, and the second term is the median distance between all cluster centers. For a uniformly distributed data set, it has a better classification performance.

$$V_{WL} = \frac{{\sum\nolimits_{i = 1}^{c} {\left( {\frac{{\sum\nolimits_{j = 1}^{n} {u_{ij}^{2} \left\| {x_{j} - v_{i} } \right\|^{2} } }}{{\sum\nolimits_{j = 1}^{n} {u_{ij} } }}} \right)} }}{{\mathop {\min }\nolimits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2} + median\left\| {v_{i} - v_{k} } \right\|^{2} }}$$
(12)

2.2.9 FM Clustering Validity Function \((V_{FM} )\)[35]

Taking the partition entropy \((V_{PE} )\) and the fuzzy partition factor \((\alpha_{f} )\) into consideration, the compactness and separation of clustering are defined, as shown in Eq. (13). However, this clustering validity function does not perform well on noisy data sets.

$$V_{FM} = \alpha_{f} \times \left\{ { - \frac{1}{n}\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {\left[ {u_{ij} \log_{a} (u_{ij} )} \right]} } } \right\}$$
(13)

where, \(\alpha_{f} = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {(u_{ij} - \frac{1}{c})^{2} \left\| {x_{j} - v_{i} } \right\|^{2} } } }}{{n\mathop {\min }\nolimits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2} }}\). \(V_{FM}\) is valid with the minimum value.

2.2.10 PBMF Clustering Validity Function \((V_{PBMF} )\)[36]

In 2005, Pakhiar et al. proposed a cluster validity function in the form of a product, as shown in Eq. (14). The first item of the product is the reciprocal of the number of clusters, and the second item of the product is used to measure the intra-class compactness, which represents the ratio of the intra-class distance when the entire data set is divided into one category and classified into c. The last item of \(V_{PBMF}\) indicates the maximum separation. When \(V_{PBMF}\) takes the maximum value, c is the optimal number of clusters.

$$V_{PBMF} = \left( {\frac{1}{c} \times \frac{{\sum\nolimits_{j = 1}^{n} {\left\| {x_{j} - v_{i} } \right\|} }}{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {u_{ij}^{m} \left\| {x_{j} - v_{i} } \right\|^{2} } } }} \times \mathop {\max }\nolimits_{i,j = 1}^{c} \left\| {v_{i} - v_{j} } \right\|} \right)^{2}$$
(14)

2.2.11 Clustering Validity Function Proposed by Zhu \((V_{ZLF} )\)

\(V_{ZLF}\) is composed of the ratio of compactness and separation, which is shown in Eq. (15).

$$V_{ZLF} = \frac{comp}{{sep}} = \frac{{\sum\nolimits_{j = 1}^{n} {\frac{{1 - \mathop {\max }\limits_{i} u{}_{ij}}}{{\sum\nolimits_{i = 1}^{c} {\left\| {x_{j} - v{}_{i}} \right\|} }}} }}{{\sum\nolimits_{k = 1}^{c} {\sum\nolimits_{i = 1;i \ne k}^{c} {{\raise0.7ex\hbox{${\left\| {v_{i} - v_{k} } \right\|}$} \!\mathord{\left/ {\vphantom {{\left\| {v_{i} - v_{k} } \right\|} {\frac{c(c - 1)}{2}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\frac{c(c - 1)}{2}}$}}} } }}$$
(15)

where, \(\mathop {\max }\limits_{i} u_{ij}\) is the maximum membership degree of all samples in a certain class. If the data in the class is more compact, \(\mathop {\max }\limits_{i} u_{ij} \to 1\) and \((1 - \mathop {\max }\limits_{i} u_{ij} ) \to 0\). The smaller the value, the better the clustering performance. \(\left\| {x_{j} - v_{i} } \right\|\) in the numerator is the compactness within the class. The denominator of \(V_{ZLF}\) is the average of the sum of the distances between cluster centers, which defines the degree of separation between clusters. \(\left\| {v_{i} - v_{k} } \right\|\) is the distance between cluster centers, and \(c(c - 1)/2\) is the number of distances between cluster centers. When \(V_{ZLF}\) takes the minimum value, c is the optimal number of clusters.

2.2.12 ECS Clustering Validity Function \((V_{ECS} )\)

The \(V_{ECS}\) is proposed by Ouchicha in 2020, which is defined in Eq. (16).

$$V_{ECS} = \frac{{SC - SC_{\min } }}{{SC_{\max } - SC_{\min } }} + \frac{{PEC - PEC_{\min } }}{{PEC_{\max } - PEC_{\min } }}$$
(16)

where, the SC was defined as \((\frac{1}{n}\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {u_{ij} \left\| {x_{j} - v_{i} } \right\|}^{2} } )/\frac{1}{c}\sum\limits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|^{2} }\), and the PEC was defined as \((\frac{1}{n(1 - m)}\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {\log (u_{ij}^{m} + (1 - u_{ij} )^{m} )} } )/V_{PC}\). \(V_{ECS}\) was the normalized of SC and PEC. The minimum value of \(V_{ECS}\) corresponds to the optimal number of clusters.

In the next section, six multiple clustering performance evaluation components are introduced in details so as to form a new fuzzy cluster effectiveness function \(V_{WG}\).

3 FCM Clustering Validity Function Based on Multiple Clustering Performance Evaluation Components

3.1 Clustering Performance Evaluation Components

Based on the FCM clustering algorithm, fuzzy membership and the geometric structure of the data set, this paper defines six clustering performance evaluation components, including compactness, variation, overlap, similarity, and separation.

3.1.1 Compactness (\(comp\))

Equation (17) is the criterion function of the FCM clustering algorithm, which represents the sum of the distance between the cluster center \(v_{i}\) and the data sample \(x_{j}\). The smaller the value, the higher the similarity of the data within the class, and the closer the data within the class.

$$comp = \sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{n} {(u_{ij} } } )^{2} \left\| {x_{j} - v_{i} } \right\|^{2}$$
(17)

3.1.2 Variation (\({\text{var}}\)) [37]

Equation (18) adopts the exponential function to suppress the characteristics of noise data interference, which is used to measure the compactness of the data within the class. Similarly, the smaller the value, the more compact the data in the class.

$${\text{var}} = \frac{1}{n}\sum\limits_{{i = 1}}^{c} {\sum\limits_{{j = 1}}^{n} {\left( {\exp - \frac{{\left\| {x_{j} - v_{i} } \right\|^{2} }}{\varepsilon }} \right)} }$$
(18)

where, \(\varepsilon = \frac{1}{n}\sum\limits_{j = 1}^{n} {\left\| {x_{j} - \overline{x}} \right\|^{2} }\) (\(\overline{x} = \frac{1}{n}\sum\nolimits_{j = 1}^{n} {x_{j} }\) is the mean value of the data samples) represents the average sum of the distance between the data within the class and the mean value of the data samples. Equation (18) is used to measure the degree of variation of the data within the class. The smaller the calculated value, the more stable the data within the class.

3.1.3 Overlap (\(overlap\))

Equation (19) is based on the degree of membership to express the degree of overlap between data sets. If the data point \(x_{k}\) in the overlapping part belongs to the i-th cluster, then the membership degree \(u_{ik}\) will be close to 1, and if the data point \(x_{k}\) belongs to the j-th cluster, the degree of membership \(u_{jk}\) will be close to 0. If the data in the overlapping part are separated better, the difference of \(\left| {u_{ik} - u_{jk} } \right|\) will be closer to 1, and the value of \(1 - \left| {u_{ik} - u_{jk} } \right|\) will be smaller. Therefore, a small value for this item indicates a better classification effect.

$$overlap = \mathop {\min }\nolimits_{{i \ne j}} \left( {\frac{1}{n}\sum\nolimits_{{j = 1}}^{n} {\left( {1 - \left| {u_{{ik}} - u_{{jk}} } \right|} \right)} } \right)$$
(19)

3.1.4 Similarity (\(sim\))

Equation (20) represents the sum of the squares of the membership degrees of the data point \(x_{j}\) belonging to the cluster center \(v_{i}\). The larger the value of this term, the more similar the data within the cluster.

$$sim = \mathop {\min }\limits_{1 \le i \le c} \sum\limits_{j = 1}^{n} {(u_{ij} )^{2} }$$
(20)

3.1.5 Separation (\(sep\))

Equation (21) and Eq. (22) are two clustering performance evaluation components used to define the degree of overlap between clusters. \(sep_{1} = \mathop {\min }\limits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2}\) indicates the minimum distance between any two clusters. The larger the value, the better the separation between classes. \(sep_{2} = \frac{1}{c}\sum\nolimits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|^{2} }\)(\(\overline{v} = \frac{1}{c}\sum\nolimits_{i = 1}^{c} {v_{i} }\) is the average of all cluster centers) represents the sum of the average distances from all cluster centers to the balance point of the cluster centers. The larger the value, the more separated the classes are from each other.

$$sep_{1} = \mathop {\min }\limits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2}$$
(21)
$$sep_{2} = \frac{1}{c}\sum\limits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|^{2} }$$
(22)

3.2 FCM Clustering Validity Function Based on Multiple Clustering Performance Evaluation Components

Based on the six clustering performance evaluation components (compactness, variability, overlap, similarity, and separation), a ratio type of clustering validity function was constituted, which is defined as follows:

$$\begin{gathered} V_{WG} = \frac{{comp + {\text{var}} + overlap}}{{sim + sep_{1} + sep_{2} }} \\ = \frac{{\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {(u_{ij} )^{2} \left\| {x_{j} - v_{i} } \right\|^{2} + \frac{1}{n}\sum\nolimits_{i = 1}^{c} {\sum\nolimits_{j = 1}^{n} {\exp ( - \frac{{\left\| {x_{j} - v_{i} } \right\|^{2} }}{\varepsilon }) + \mathop {\min }\nolimits_{i \ne j} (\frac{1}{n}\sum\nolimits_{j = 1}^{n} {(1 - \left| {u_{ik} - u_{jk} } \right|))} } } } } }}{{\mathop {\min }\nolimits_{1 \le i \le c} \sum\nolimits_{j = 1}^{n} {(u_{ij} )^{2} + \mathop {\min }\nolimits_{i \ne k} \left\| {v_{i} - v_{k} } \right\|^{2} + \frac{1}{c}\sum\nolimits_{i = 1}^{c} {\left\| {v_{i} - \overline{v}} \right\|^{2} } } }} \\ \end{gathered}$$
(23)

where, \(\varepsilon = \frac{1}{n}\sum\limits_{j = 1}^{n} {\left\| {x_{j} - \overline{x}} \right\|^{2} }\), \(\overline{x} = \frac{1}{n}\sum\limits_{j = 1}^{n} {x_{j} }\), \(\overline{v} = \frac{1}{c}\sum\limits_{i = 1}^{c} {v_{i} }\).

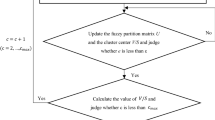
Then \(V_{WG}\) is applied to the FCM clustering algorithm, and the algorithm flowchart for obtaining the optimal number of clusters is shown in Fig. 1. The flow of the FCM clustering algorithm based on \(V_{WG}\) is described as follows.

Fig. 1
figure 1

Flowchart of FCM clustering algorithm based on \(V_{WG}\)

Full size image

Step 1: Given the maximum number of clusters \(c_{\max } (c_{\max } \le \sqrt n )\), the maximum number of iterations \(I_{\max }\), the fuzzy index m \((1.5 \le m \le 2.5)\) and the termination threshold \(\varepsilon\).

Step 2: Initialize the membership matrix U, the cluster center V and the number of clusters c.

Step 3: Update the fuzzy partition matrix \(U^{(t + 1)}\) and cluster center \(V^{(t + 1)}\) and judge whether \(e = \left\| {v_{t + 1} - v_{t} } \right\|\) is less than \(\varepsilon\). If \(e < \varepsilon\), go to Step 4. Otherwise, if \(e \ge \varepsilon\), then go to Step 2.

Step 4: Let \(c = c + 1\), use FCM clustering algorithm to calculate the minimum value of \(V_{WG}\), and obtain the optimal solution of c. If \(c < c_{\max }\), repeat Step 2. If \(c \ge c_{\max }\), go to Step 5.

Step 5: Select the number of clusters \(\min \left\{ {V_{WG} (U,V,c_{o} )} \right\}\) corresponding to \(c_{o}\) as the optimal number of clusters, and finally output the value of \(V_{WG}\).

Next, the proposed validity function and eight typical validity functions are compared with five artificial data sets and eight UCI data sets to verify the effectiveness of the proposed \(V_{WG}\).

4 Simulation Experiments and Results Analysis

4.1 Testing Artificial Data Sets

In order to verify the validity of the proposed validity function \((V_{WG} )\), this paper selects 8 typical cluster validity functions (\(V_{MPC}\), \(V_{XB}\), \(V_{T}\), \(V_{P}\), \(V_{PCAES}\), \(V_{FM}\), \(V_{WL}\) and \(V_{ZLF}\)) for comparison experiments. According to the prior knowledge [38], the fuzzy index \(1.5 \le m \le 2.5\) and the number of clusters \(2 \le c \le \sqrt n\) can be determined. This paper chooses \(m = 2\), \(2 \le c \le 14\) to conduct simulation experiments, and then judge whether the classification of each clustering validity function is accurate when using different data sets. Four artificial data sets selected to carry out the simulation experiments are listed in Table 1. Among them, Data_2_3 (noise) in the artificial data set is a Gaussian 2-dimensional 3-category data set with 100 noise data added, Data_2_3 (overlap) is a Gaussian 2-dimensional 3-category data set with overlapping data between classes, Data_3_3 is a 3-dimensional 3-type data set that obeys Gaussian distribution, Data_3_6 is a 3-dimensional 6-type data set that obeys a uniform distribution. Data_2_5 is a 2-dimensional 5-type data set that obeys a uniform distribution. The samples distributions of these four artificial data sets are shown in Fig. 2a–e.

Table 1 Artificial data sets
Full size table
Fig. 2
figure 2

Artificial data sets

Full size image

4.2 Simulation Experiments and Results Analysis on Artificial Data Sets

The experimental results on the artificial data sets (Data_2_3 with noise, Data_2_3 with overlap, Data_3_3, Data_3_6 and Data_2_5) are shown in Fig. 3a–i to Fig. 7a–i. It can be seen from Fig. 3 that when classifying the noise data set Data_2_3(noise), except for \(V_{PCAES}\) and \(V_{FM}\), all other clustering validity functions can find the optimal number of clusters. Figure 4 shows that for the overlapping data set Data_2_3(overlap), only \(V_{WG}\) can get the optimal number of clusters c = 3. Figure 5 shows that when the dimension of the data set is increased to 3, \(V_{XB}\),\(V_{P}\), \(V_{ZLF}\), \(V_{WG}\) can still determine the optimal number of clusters c = 3. As can be seen in Fig. 6, only \(V_{WG}\) can be classified into 6 categories. Finally, as shown in Fig. 7, only \(V_{MPC}\), \(V_{P}\) and \(V_{WG}\) can find the optimal clustering number c = 5. The simulation results on five artificial data sets show that only \(V_{WG}\) can obtain the optimal number of clusters for the five sets of artificial data sets. Among them, \(V_{XB}\), \(V_{WL}\), and \(V_{MPC}\) can distinguish the optimal number of clusters for 2 sets of data sets, \(V_{P}\) can divide 3 groups of data sets, \(V_{T}\) and \(V_{ZLF}\) can only divide 1 group of data sets, but for 5 sets of artificial data sets, \(V_{PCAES}\) and \(V_{FM}\) cannot get the correct number of clusters. The above experiment shows that \(V_{WG}\) is better than these typical clustering validity functions. This is because when the data set is affected by noisy data, overlapping data and high-dimensional data, \(V_{WG}\) is less disturbed.

Fig. 3
figure 3

Change trend of clustering validity functions under Data_2_3 (noise) data set

Full size image
Fig. 4
figure 4

Change trend of clustering validity functions under Data_2_3 (overlap) data set

Full size image
Fig. 5
figure 5

Change trend of clustering validity functions under Data_3_3 data set

Full size image
Fig. 6
figure 6

Change trend of clustering validity functions under Data_3_6 data set

Full size image
Fig. 7
figure 7

Change trend of clustering validity functions under Data_2_5 data set

Full size image

In order to better observe the changing trend of each clustering performance evaluation component of \(V_{WG}\) on the artificial data sets, six clustering performance evaluation components of \(V_{WG}\) are normalized and placed in the same coordinate system, which is shown in Fig. 8a–e. Next, The function values of \(V_{MPC}\), \(V_{XB}\), \(V_{T}\), \(V_{P}\), \(V_{PCAES}\), \(V_{FM}\), \(V_{WL}\), \(V_{ZLF}\) and \(V_{WG}\) on the artificial data sets are placed in the normalized coordinate system, which are shown in Fig. 9a–e. In this way, the clustering effect of \(V_{WG}\) and other validity functions can be compared more intuitively. Finally, for different artificial data sets, the optimal number of clusters of each clustering validity are listed in Table 2.

Fig. 8
figure 8

Changing trend of each component in \(V_{WG}\) under artificial data sets

Full size image
Fig. 9
figure 9

Changing trend of normalized clustering validity functions under artificial data sets

Full size image
Table 2 Optimal number of clusters under different validity functions for artificial data sets
Full size table

4.3 Simulation Experiments and Results Analysis on UCI Data Sets

Due to the simple structure of the artificial data sets and the small number of samples, in order to verify the effectiveness of \(V_{WG}\) clustering on the complex data sets, the following simulation experiments will be carried out using UCI data sets. The real data sets selected in the experiment are Iris, Seeds, Phoneme, Haberman, HTUR2, Hfcr, Segment and Heart in the UCI database. The data volume, category and attributes of each UCI data set are listed in Table 3. The experimental results on UCI data sets are shown in Fig. 10–Fig. 17a–i. It can be seen from Fig. 10 that only \(V_{WG}\) can get the optimal number of clusters c = 3. Figure 11 shows that \(V_{P}\) and \(V_{WG}\) can determine the best clustering result c = 3. It can be seen from the experimental results in Fig. 10 and Fig. 11 that when processing data sets with higher dimension such as Iris and Seeds, the optimal number of clusters can be obtained by \(V_{WG}\). This shows that the number of clusters is relatively high in the data set. In this case, the classification ability of \(V_{WG}\) is better than other typical clustering validity functions. It can be seen from Fig. 12 that only \(V_{FM}\) and \(V_{WG}\) can divide two categories. In Fig. 13, \(V_{MPC}\), \(V_{T}\), \(V_{FM}\), \(V_{WL}\) and \(V_{WG}\) can determine the best clustering result c = 2. Figure 14 shows that except for \(V_{PCAES}\), other validity functions can classify correctly. Figure 15 shows that only \(V_{ZLF}\) and \(V_{WG}\) can obtain the best cluster number c = 4. Finally, in Fig. 16, still only \(V_{WG}\) can accurately classify 7 categories. Figures 15 and 16 are simulations for Hfcr and Segment data sets, and only \(V_{WG}\) can correctly classify them. This means that when the number of samples and complexity of the data set are relatively higher, the clustering effect of \(V_{WG}\) is significantly better than other validity functions. Finally, it can be seen from the experimental results in Fig. 17 that \(V_{XB}\), \(V_{T}\), \(V_{FM}\), \(V_{WL}\),\(V_{ZLF}\) and \(V_{WG}\) can be divided into two categories. From the experimental results in Fig. 10 to Fig. 17, it can be seen that only \(V_{WG}\) can find the best classification number of all UCI data sets, and when there are data sets with overlapping samples, noisy data, high dimensions and a large number of samples, the ideal number of clusters can still be found.

Table 3 UCI data sets
Full size table
Fig. 10
figure 10

Change trend of clustering validity functions under Iris data set

Full size image
Fig. 11
figure 11

Change trend of clustering validity functions under Seeds data set

Full size image
Fig. 12
figure 12

Change trend of clustering validity functions under Phoneme data set

Full size image
Fig. 13
figure 13

Change trend of clustering validity functions under Haberman data set

Full size image
Fig. 14
figure 14

Change trend of clustering validity functions under HTUR2 data set

Full size image
Fig. 15
figure 15

Change trend of clustering validity functions under Hfcr data set

Full size image
Fig. 16
figure 16

Change trend of clustering validity functions under Segment data set

Full size image
Fig. 17
figure 17

Change trend of clustering validity functions under Heart data set

Full size image

Similarly, in order to better observe the changing trend of each clustering performance evaluation component of \(V_{WG}\) when UCI data sets are adopted, six clustering performance evaluation components of \(V_{WG}\) are normalized and placed in the same coordinate system, which are shown in Fig. 18a-h. Then the function values of \(V_{MPC}\), \(V_{XB}\), \(V_{T}\), \(V_{P}\), \(V_{PCAES}\), \(V_{FM}\), \(V_{WL}\), \(V_{ZLF}\) and \(V_{WG}\) on UCI data sets are put in the normalized coordinate system, which are shown in Fig. 19a–h. In this way, the clustering effect of \(V_{WG}\) and other clustering validity functions can be compared more intuitively. Finally, for different UCI data sets, the optimal number of clusters of each cluster validity function are listed in Table 4.

Fig. 18
figure 18figure 18

Changing trend of each component in \(V_{WG}\) under UCI data sets

Full size image
Fig. 19
figure 19

Changing trend of normalized clustering validity functions under UCI data sets

Full size image
Table 4 Optimal number of clusters under different validity functions for UCI data sets
Full size table

5 Conclusions

In this paper, six evaluation components of clustering performance are defined based on compactness, variation, overlap, similarity and separation. After combining the six components, a new fuzzy clustering validity function \(V_{WG}\) is proposed, which is simulated on artificial data set and UCI data set. The experimental results show that \(V_{WG}\) can get accurate clustering number in Data_2_3(noise), Data_2_3(overlap), Data_2_5, Data_3_3, Data_3_6 and other manual data sets. \(V_{WG}\) for UCI data sets such as Iris, Seeds, Phoneme, Haberman, HTUR2, Hfcr, Segment and Heart can also be accurately divided. By comparison, it can be seen that the classification effect of \(V_{WG}\) is better than other traditional validity functions in data sets with noise data, overlapping data and high-dimensional data. Each clustering validity function is composed of various components, and different components play different roles in dividing a data set. Therefore, in the future work, we will analyze the rule of component synthesis of clustering validity function, and discuss the function and influence of different components through comparative experiments. At the same time, the idea of clustering validity function components can also be extended to the weighting and information integration among components to divide data sets.