Stability analysis and constrained fuzzy tracking control of positive nonlinear systems

Abstract

This paper is concerned with stability and tracking control of positive nonlinear systems via Takagi–Sugeno (T–S) fuzzy modeling. Firstly, some less conservative stability conditions for positive nonlinear systems that can be represented by a class of positive T–S fuzzy model with only nonnegative state variables are derived by proposing the so-called quadratic copositive Lyapunov functions. Secondly, a constrained control via the parallel distributed compensation scheme is designed to stabilize a positive nonlinear system, while imposing positivity in closed loop, upon which a constrained fuzzy tracking controller is also given to guarantee the tracking performance and positivity in closed loop. Finally, a numerical example is provided to show the advantages of the proposed methods, and an example of a real plant is presented to demonstrate the controller design scheme.

1 Introduction

Many physical systems involve variables that are always confined to the positive orthant [1, 2]. For example, absolute temperatures, levels of liquids in tanks, and concentrations of substances in chemical processes are always positive. Such systems are generally termed as positive systems [1]. The positivity can yield some interesting and special properties to positive systems [3]. For instance, it is widely known that time delay may cause instability to a general linear system, but for a positive system, the system stability is independent of delays [4]. More typical phenomena are described in [5] and the references therein.

In recent years, considerable attention has been paid to positive systems due to their extensive applications in areas such as economics, biology, and communication networks. Major efforts have been devoted to properties such as realizability [6], reachability/controllability [7], and particularly stability [8, 9]. For positive systems, Lyapunov functions for general systems may result in conservative conditions. Meanwhile, the existence of a linear copositive Lyapunov function (LCLF) is necessary and sufficient for stability of a positive linear system [1].

For positive systems, relatively fewer attempts have been put on control synthesis [10–14]. Control of positive systems must take the positivity constraint into account. Otherwise, the mathematical model of such systems can move into infeasible regions, causing loss of stability or performance. Because of the positivity, some traditional techniques, such as linear transformation and variable elimination, may not be applicable, which makes control synthesis more difficult. By proposing some effective methodologies, the output-feedback control was solved in [15]; the observer was designed in [16]; the problem of model reduction was presented in [17], to list a few.

However, the aforementioned works are all focused on positive linear systems, and few results have been reported for positive nonlinear systems. Yet positive nonlinear systems have a notably wide range of practical applications such as gas-lifted oil wells [18], synchronized communication networks [8], energy markets [19]. Therefore, it is of fundamental importance to numerous applications and theoretically challenging to carry out studies of positive nonlinear systems.

During the past years, the fuzzy control [20–22], in particular, Takagi–Sugeno (T–S) fuzzy model-based control has been considered in the development of analysis and synthesis of nonlinear systems? [23, 24]. It has been proved that T–S fuzzy models can approximate any smooth nonlinear system to any accuracy on a compact set [25]. The main idea of the T–S fuzzy modeling is to obtain linear time-invariant models close to the nonlinear system in some regions of the state space and then combine these linear models using nonlinear fuzzy membership functions. Such a “blending” makes T–S fuzzy systems similar to linear system, and thus, some analysis and synthesis techniques developed for linear systems can be used for T–S fuzzy systems. For the stability analysis of T–S fuzzy control systems, many researchers have presented the conventional quadratic Lyapunov function approaches to find a constant positive definite matrix of a quadratic Lyapunov function satisfying the stability conditions of all subsystems, since the quadratic stability conditions are likely generalized to tackle the problems of control synthesis [26, 27]. If the obtained conditions are formulated in terms of linear matrix inequalities (LMIs) [28], the problem can be efficiently solved by recently developed convex optimization techniques. So far, many control issues for nonlinear systems have been investigated based on the T–S fuzzy model [29]. To list a few, the problems of stability analysis and stabilization were studied in [30]; $H_{\infty }$ control designs were reported in [31]; estimation and filtering were addressed in [32]; output regulation was investigated in [33]; fault detection was considered in [34]; and adaptive sliding-mode control was designed in [35].

Given are the widespread applications of T–S fuzzy control [36, 37]. Recently, some efforts have been put on the T–S fuzzy modeling, analysis, and synthesis of positive nonlinear systems. Using the common quadratic Lyapunov function approach, the authors in [38] presented the process control of four linked tanks on the basis of continuous-time T–S fuzzy modeling. Then, by adopting similar techniques, the delay-dependent stabilization of controlled positive T–S fuzzy systems with time-varying delay was investigated in [39]. Exploring the fuzzy Lyapunov function method, the authors in [40] established improved results. Meanwhile, the problems of stability analysis and constrained control of positive nonlinear systems based on discrete-time T–S fuzzy models have also been considered in [19]. Note that the Lyapunov functions employed in the above-mentioned works are introduced from those applicable for general T–S fuzzy systems. However, as mentioned above that the states of a positive system are always restricted in the first quadrant, those Lyapunov functions defined in the whole state space will obviously lead to conservative results. Considering the positivity, improved results on stability and constrained control of positive T–S fuzzy systems have been obtained in [41] by utilizing the LCLF approach that has been proved efficient for positive linear systems. However, although the existence of an LCLF is sufficient and necessary for the stability of a given positive linear system, the existence of a common LCLF for all linear subsystems is only sufficient for a positive T–S fuzzy system [42].

The above observations motivate us to carry out the present study: proposing the so-called quadratic copositive Lyapunov function (QCLF) that generalizes the linear copositive Lyapunov function and the quadratic Lyapunov function to improve some existing results on fuzzy control of positive nonlinear systems based on T–S fuzzy model.

The first contribution of this paper lies in that the so-called quadratic copositive Lyapunov function is proposed to establish improved and numerically easily verified stability conditions for positive T–S fuzzy systems. In addition, our approach admits further relaxations in the obtained stability conditions. Besides, a constrained fuzzy tracking controller is designed such that the state of the resulting closed-loop system can track a given reference input with a prescribed performance index while preserving positivity. The remainder of the paper is organized as follows. Section 2 reviews necessary definitions and lemmas. In Sect. 3, some existence conditions of the QCLF ensuring the stability of a given positive T–S fuzzy system are derived, where relationships among these conditions are also discussed. Then, the problems of controlled stabilization and constrained tracking control are also presented. Section 4 provides a numerical example and an example of a real plant to verify the theoretical findings, and Sect. 5 concludes the paper.

Notations: In this paper, the notations used are fairly standard. $A\succ 0$ and $x\succ 0$ (or $A\succeq 0$, $x\succeq 0$) mean that all elements of matrix A and x are positive (or nonnegative); $\mathbb {R}$, $\mathbb {R}^{n}$ and $\mathbb {R}^{n\times n}$ denote the field of real numbers, n-dimensional Euclidean space, and the space of $n\times n$ matrices with real entries, respectively, and $\mathbb {R}_{0}^{n}$ denotes $\mathbb {R}^{n}\backslash \{0^{n}\}$; $\mathbb {R}_{+}^{n}$ stands for the nonnegative orthant in $\mathbb {R}_{0}^{n}$; $\mathbb {N}_{+}$ is the set of positive natural numbers and integers; $y^{[m]}:=\left[ \begin{array}{cccc} y_{1}^{m}&y_{2}^{m}&\ldots&y_{n}^{m} \end{array} \right] ^{T},\forall y\in \mathbb {R}^{n}$; $y^{\{m\}}$ is a base vector containing all homogeneous monomials of degree m in y; the script $\mathcal {I}_{m}=[0_{(n-m+1)\times (m-1)} |I_{n-m+1}]\in \mathbb {R}^{(n-m+1)\times n}$; $A\equiv [a_{ij}]_{n\times n}$; $\vartheta (n,m)\equiv (n+m-1)!/((n-1)!m!)$; $A\otimes B$ denotes the Kronecker product of matrices A and B; in addition, the notation $P>0(\ge$0) means that P is a real symmetric and positive definite (semi-positive definite) matrix.

2 Problem formulation and preliminaries

This paper considers the following positive nonlinear system

$$\begin{aligned} \dot{x}(t)=f(x(t),u(t),t), \quad x(t_{0})=x_{0}\succeq 0 \end{aligned}$$

(1)

can be represented as follows:

$\blacklozenge$ Model rule i: IF $\theta _{1}(t)$ is $M_{1}^{i}$ and $\cdots \, \theta _{p}(t)$ is $M_{p}^{i}$, THEN

$$\begin{aligned} \dot{x}(t)=A_{i}x(t)+B_{i}u(t), \quad i\in R=\{1,2,\ldots , r\} \end{aligned}$$

(2)

where $x(t)\in \mathbb {R}^{n}$ is the state vector; $u(t)\in \mathbb {R}^{m}$ is the control input; $M_{j}^{i}$ is the fuzzy set, and r denotes the number of IF-THEN rules; $\theta (t)=\big [\theta _{1}(t),\theta _{2}(t), \ldots , \theta _{p}(t)\big ]^{T}$ is the premise variable vector assumed independent of input u(t); in addition, $A_{i}$, $B_{i}$, $i\in R$, are real matrices with appropriate dimensions. A more compact presentation of the continuous-time T–S fuzzy model can be given by

$$\begin{aligned} \dot{x}(t)= & {} A(h(t))x(t)+B(h(t))u(t) \nonumber \\= & {} \sum \limits _{i=1}^{r}h_{i}( \theta (t))(A_{i}x(t)+B_{i}u(t)) \end{aligned}$$

(3)

where $h_{i}(\theta (t))$ are the normalized membership functions:

$$\begin{aligned} h_{i}(\theta (t))= & {} \displaystyle \frac{\prod _{j=1}^{p}M_{j}^{i}(\theta _{j}(t)) }{\sum \nolimits _{i=1}^{r}\prod _{j=1}^{p}M_{j}^{i}(\theta _{j}(t))}\ge 0, \\&\sum \limits _{i=1}^{r}h_{i}(\theta (t))=1 \end{aligned}$$

with $M_{j}^{i}(\theta _{j}(t))$ representing the grade of membership of premise variable $\theta _{j}(t)$ in $M_{j}^{i}$.

Definition 1

System (1) is said to be positive if for any initial condition $x(0)\in \mathbb {R}_{+}^{n}$ and any input function u(t), the corresponding state trajectory $x(t)\in \mathbb {R}_{+}^{n}$, $\forall t >0$.

Definition 2

A linear system $\dot{x}(t)=Ax(t)+Br(t)$ is positive, if for any initial condition $x(0)\in \mathbb {R}_{+}^{n}$ and $r(t)\in \mathbb {R}_{+}^{n}$, the corresponding state trajectory $x(t)\in \mathbb {R}_{+}^{n}$.

Lemma 1

A linear system $\dot{x}(t)=Ax(t)+Br(t)$ is positive for any r(t) $\in \,\mathbb {R}_{+}^{n}$, if and only if A is a Metzler matrix and B is a nonnegative matrix.

Lemma 2

System (3) is positive when u(t) $\in \, \mathbb {R}_{+}^{n}$, if $A_{i},\, i\in R$, are Metzler matrices and $B_{i},\, i\in R$ are nonnegative matrices.

Remark 1

Due to the fact that $0\le h_{i}(\theta (t))\le 1$, Lemma 2 can be easily obtained by Lemma 1.

Definition 3

Positive T–S fuzzy system (3) is said to be controlled positive relative to an initial state $x(0)\in \mathbb {R}_{+}^{n}$ if there exists a control input u(t) such that the corresponding state trajectory $x(t)\in \mathbb {R}_{+}^{n}$, $\forall t>0$.

Remark 2

Definition 2, Lemmas 1 and 2 mean that a fuzzy system is positive if each of its local linear systems is positive. The stability of each local system is equivalent to the existence of a linear copositive Lyapunov function (LCLF) $V(x(t))=x^{T}(t)v,v\in \mathbb {R}_{+}^{n}$. However, the existence of an LCLF is only sufficient but not necessary for the stability of positive T–S fuzzy system (3). On the other hand, when we design a controller for T–S fuzzy system (3), the positivity of the closed-loop system should be considered for correct approximation. Therefore, it is of importance to introduce the concept of constrained positive control.

In this paper, we establish less conservative stability conditions for positive nonlinear system (1) based on T–S fuzzy model (3), upon which a control input u(t) is designed such that the resulting closed-loop system (3) is controlled positive, and the state x(t) tracks a given reference input $x_{r}(t)$ in the positive orthant.

3 Main results

3.1 Stability analysis

When $u(t)=0$, we consider the positive nonlinear system (1) which can be approximated by positive T–S fuzzy system (3). In this subsection, we shall focus on deriving improved global stability criteria for positive T–S fuzzy system (3) by exploring a new Lyapunov function. Before proceeding, the following remark is presented for the subsequent derivations.

Remark 3

For a polynomial p(x) with any order in $x\in \mathbb {R}_{0}^{n}$, it can be easily verified that$\ p(x)>0,\ \forall x\in \mathbb {R} _{+}^{n}\Leftrightarrow p\left( x^{[2]}\right) >0,\quad \forall x\in \mathbb { R}_{0}^{n}$.

Now, we are in a position to provide the first version of the stability conditions for positive T–S fuzzy system (3) in the following theorem by QCLF approach.

Theorem 1

Consider positive T–S fuzzy system (3) with $u(t)=0$, if there exist real matrices $P\in \mathbb {R}^{n\times n}$, ${\varPhi } =\left[ \phi _{pq}\right] _{(p,\,q)\in n\times n}$ and ${\varTheta }_{i}=\left[ \theta _{pq}^{i} \right] _{(p,\,q)\in n\times n}$, $i\in R$, such that $\forall i\in R$,

$$\begin{aligned}&-{\varPhi } +\mathrm{diag}\{\phi _{11},\phi _{22},\ldots ,\phi _{nn}\}-P < 0 \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{diag}\{\bar{\phi }_{1},\ldots ,\bar{\phi }_{n-1}\} <0 \end{aligned}$$

(5)

$$\begin{aligned}&A_{i}^{T}P + PA_{i}+\mathrm{diag}\{\theta _{11}^{i},\theta _{22}^{i},\ldots ,\theta _{nn}^{i}\}-{\varTheta }_{i} <0 \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{diag}\{\bar{\theta }_{1}^{^{i}},\ldots ,\bar{\theta }_{n-1}^{i}\} <0 \end{aligned}$$

(7)

where

$$\begin{aligned} \bar{\phi }_{k}\triangleq & {} \mathrm {diag} \left\{ \phi _{k(k+1)}+\phi _{(k+1)k},\ldots ,\phi _{kn}+\phi _{nk}\right\} \\ \bar{\theta }_{k}^{i}\triangleq & {} \,\mathrm {diag}\left\{ \theta _{k(k+1)}^{i}+\theta _{(k+1)k}^{i},\ldots ,\theta _{kn}^{i}+\theta _{nk}^{i}\right\} \\&k\in \{1,2,\ldots ,n-1\}, \end{aligned}$$

then $V(x(t))=x^{T}(t)Px(t)$ is a QCLF that ensures the underlying system to be asymptotically stable in $\mathbb {R}_{+}^{n}$.

Proof

Here, we choose a QCLF candidate for positive T–S fuzzy system (3) as follows:

$$\begin{aligned} V(x(t)) = x^{T}(t)Px(t),\quad x(t)\in \mathbb {R}_{+}^{n} \end{aligned}$$

(8)

where $P=[p_{pq}]_{(p,q)\in n\times n}$ is a real matrix satisfying (4) and (6). Then, one has from Remark 3 that $V(x(t))>0,$ $\forall x(t)\in \mathbb {R }_{+}^{n}$, is equivalent to, $\forall x(t)\in \mathbb {R}_{0}^{n}$

$$\begin{aligned} V\left( x^{[2]}(t)\right) = \sum _{p=1}^{n}\sum _{q=1}^{n}p_{pq}x_{p}^{2}(t)x_{q}^{2}(t)>0 \end{aligned}$$

(9)

Define $\tilde{x}(t)\triangleq [ (x_{1}(t)\mathcal {I}_{2}x(t))^{T},(x_{2}(t)\mathcal {I}_{3}x(t))^{T},\, \ldots ,(x_{n-1}(t)\mathcal {I}_{n}x(t))^{T} ]^{T}$. One can get that

$$\begin{aligned} \left( x^{[2]}(t)\right) ^{T}{\varPhi } x^{[2]}(t)= & {} \sum _{p=1}^{n}\sum _{q=1,q\ne p}^{n}\phi _{pq}x_{p}^{2}(t)x_{q}^{2}(t) \nonumber \\&+\sum _{p=1}^{n}\phi _{pp}x_{p}^{4}(t) \nonumber \\= & {} \sum _{p=1}^{n-1}\sum _{q=p+1}^{n}(\phi _{pq}+\phi _{qp})x_{p}^{2}(t) \nonumber \\&x_{q}^{2}(t) +\sum _{p=1}^{n}\phi _{pp}x_{p}^{4}(t) \nonumber \\= & {} \tilde{x}^{T}(t)\mathrm {diag}\{\bar{\phi }_{1},\cdots ,\bar{\phi }_{n-1}\}\tilde{x}(t) \nonumber \\&+\left( x^{[2]}(t)\right) ^{T} \mathrm {diag}\{\phi _{11},\phi _{22}, \nonumber \\&\cdots ,\phi _{nn}\} x^{[2]}(t) \end{aligned}$$

(10)

Set $\hat{x}(t)\triangleq \left[ \left( x^{[2]}(t)\right) ^{T},\tilde{x}^{T}(t)\right] ^{T}\in \mathbb {R}^{\vartheta (n,2)}$. This together with (4), (5), and (10) yields that

$$\begin{aligned}&\left( x^{[2]}(t)\right) ^{T}Px^{[2]}(t)\nonumber \\&\quad =-\tilde{x}^{T}(t)\mathrm {diag}\{ \bar{\phi }_{1},\ldots ,\bar{\phi }_{n-1}\}\tilde{x}(t) \nonumber \\&\qquad +\left( x^{[2]}(t)\right) ^{T}\left[ p_{pq}+\phi _{pq}\right] _{(p,q)\in n\times n} \nonumber \\&\qquad \times \, x^{[2]}(t) -\left( x^{[2]}(t)\right) ^{T}\mathrm {diag}\{\phi _{11},\phi _{22}, \nonumber \\&\qquad \cdots ,\phi _{nn}\}x^{[2]}(t) \nonumber \\&\quad =\hat{x}^{T}(t)\mathrm {diag}\{P+{\varPhi } - \mathrm {diag}\{\phi _{11},\phi _{22}, \nonumber \\&\qquad \quad \cdots ,\phi _{nn}\}, -\mathrm {diag}\{\bar{\phi }_{1}, \ldots ,\bar{\phi }_{n-1}\}\} \nonumber \\&\qquad \times \, \hat{x}(t) \nonumber \\&\quad >0 \end{aligned}$$

(11)

In the sequel, one can obtain from (8) and (9) that $\forall x(t)\in \mathbb { R}_{+}^{n}$,

$$\begin{aligned} V(x(t))>0 \end{aligned}$$

(12)

Moreover, it can be derived from (8) that $\forall x(t)\in \mathbb {R}_{+}^{n}$,

$$\begin{aligned} \dot{V}(x(t))= & {} x^{T}(t)\left( \sum \limits _{i=1}^{r}h_{i}(\theta (t))A_{i}^{T}P+P\sum \limits _{i=1}^{r}h_{i}(\theta (t))A_{i}\right) \nonumber \\&\times x(t) \nonumber \\= & {} \sum \limits _{i=1}^{r}h_{i}(\theta (t))x^{T}(t)[\bar{v}_{pq}^{i}]_{(p,q)\in n\times n}x(t) \nonumber \\= & {} \sum \limits _{i=1}^{r}\sum _{p=1}^{n} \sum _{q=1}^{n}h_{i}(\theta (t))\bar{v}_{pq}^{i}x_{p}(t)x_{q}(t) \end{aligned}$$

(13)

where $[\bar{v}_{pq}^{i}]_{(p,q)\in n\times n}=A_{i}^{T}P+PA_{i}$. Likewise, we can get from Remark 3 and (13) that $\dot{V}(x(t))<0,\forall x(t)\in \mathbb {R}_{+}^{n},$ is equivalent to, $\forall x(t)\in \mathbb {R}_{0}^{n}$

$$\begin{aligned} \dot{V}\left( x^{[2]}(t)\right) = \sum \limits _{i=1}^{r}\sum _{p=1}^{n}\sum _{q=1}^{n}h_{i}(\theta (t))\bar{v}_{pq}^{i}x_{p}^{2}(t)x_{q}^{2}(t) < 0 \end{aligned}$$

(14)

Note that $1\ge h_{i}(\theta (t))\ge 0$. Thus, it can be seen from (14) that $\dot{V}(x^{[2]}(t))<0,\forall x(t)\in \mathbb {R}_{0}^{n}$, if $\forall i\in R,x(t)\in \mathbb {R}_{0}^{n}$,

$$\begin{aligned} \sum _{p=1}^{n}\sum _{q=1}^{n}\bar{v}_{pq}^{i}x_{p}^{2}(t)x_{q}^{2}(t)<0 \end{aligned}$$

(15)

Then, according to the similar developments in (10)–(12), it can be obtained from (15) that (6)–(7) imply $\forall x(t)\in \mathbb {R}_{+}^{n}$,

$$\begin{aligned} \dot{V}(x(t))<0 \end{aligned}$$

(16)

Finally, we can conclude from (12) and (16) that if (4)–(7) hold, $V(x(t))=x^{T}(t)Px(t)$ is a QCLF that guarantees the positive T–S fuzzy system (3) to be asymptotically stable in $\mathbb {R}_{+}^{n}$. This completes the proof. $\square$

Remark 4

In Theorem 1, QCLF is essentially a quadratic Lyapunov function that satisfies the following two inequalities:

$$\begin{aligned} V(x(t))= & {} x^{T}(t)Px(t)>0,\quad \forall x(t)\in \mathbb {R}_{+}^{n} \\ \dot{V}(x(t))= & {} x^{T}(t)\left( \sum \limits _{i=1}^{r}h_{i}(\theta (t))A_{i}^{T}P\right. \\&\left. +\sum \limits _{i=1}^{r}h_{i}(\theta (t))PA_{i}\right) \\&\times x(t)<0,\quad \forall x(t)\in \mathbb {R}_{+}^{n} \end{aligned}$$

Note that we do not require $P>0$ and $A_{i}^{T}P+PA_{i}<0,\forall i\in R$. Besides, another merit of our proposed QCLF lies in that the obtained stability conditions in Theorem 1 can be further improved via high-order relaxations in the QCLF and its time derivative.

Note the fact that $x(t)\in \mathbb {R}_{+}^{n}$. Hence, $\left( \sum \nolimits _{j=1}^{n}x_{j}(k)\right) ^{l} >0$ for any integer $l\in \mathbb { N}_{+}$. Then, for positive fuzzy system (3), we define $V^{l}(x(t))$ and $U_{i}^{l}(x(t)),i\in R$, as follows

$$\begin{aligned} V^{l}(x(t))= & {} \left( \sum \limits _{j=1}^{n}x_{j}(t)\right) ^{l}V(x(t)) \end{aligned}$$

(17)

$$\begin{aligned} U^{l}(x(t))= & {} \left( \sum \limits _{j=1}^{n}x_{j}(t)\right) ^{l}\dot{V}(x(t)) \end{aligned}$$

(18)

where V(x(t)) is the QCLF defined in (8). It is immediately clear that $V^{l}(x(t))>0$ and $U^{l}(x(t))<0,$ if and only if $V(x(t))>0$ and $\dot{V} (x(t))<0$ since $x(t)\in \mathbb {R}_{+}^{n}$. Considering (8) and (17), we have,

$$\begin{aligned} V^{l}(x(t)) = \left( \sum \limits _{j=1}^{n}x_{j}(t)\right) ^{l}\sum _{p=1}^{n}\sum _{q=1}^{n}p_{pq}x_{p}(t)x_{q}(t) \end{aligned}$$

(19)

Subsequently, we can get from Remark 3 that $V^{l}(x(t))>0,\forall x(t)\in \mathbb {R}_{+}^{n}$, is equivalent to $\forall x(t)\in \mathbb {R}_{0}^{n}$,

$$\begin{aligned}&V^{l}\left( x^{[2]}(t)\right) \nonumber \\&\quad =\left( \sum \limits _{j=1}^{n}x_{j}^{2}(t)\right) ^{l}\sum _{p=1}^{n}\sum _{q=1}^{n}p_{pq}x_{p}^{2}(k)x_{q}^{2}(k)>0 \end{aligned}$$

(20)

Note that $V^{l}(x^{[2]}(t))$ is a polynomial with degree $2l+4$ in x(t). Thus, a sufficient condition for (20) is the existence of appropriately defined sum of squares decomposition which can be understood as the existence of a matrix V (often called the Gram matrix) such that

$$\begin{aligned} V^{l}(x^{[2]}(t))=\left( x^{\{l+2\}}(t)\right) ^{T}Vx^{\{l+2\}}(t) \end{aligned}$$

(21)

where

$$\begin{aligned} x^{\{l+2\}}(k)= & {} \left[ \left( x_{1}(t)x^{\{l+1\}}(t)\right) ^{T},\left( x_{2}(t)(\mathcal {I}_{2}x(t))^{\{l+1\}}\right) ^{T}, \right. \nonumber \\&\left. \cdots ,\left( x_{n-1}(t)(\mathcal {I}_{n-1}x(t))^{\{l+1\}}\right) ^{T},x_{n}^{l+2}(t)\right] ^{T} \nonumber \\\in & {} \mathbb {R}^{\vartheta (n,l+2)}. \end{aligned}$$

(22)

The representation of matrices describing $V^{l}(x^{[2]}(t))$ is not unique. Let V be a symmetric matrix variable, then, by expanding the right-hand side of (21) and matching the corresponding coefficients, we get $\vartheta (n,2(l+2))$ independent linear constraints on the entries of V in a linear system. Accordingly, a linear parameterization expression for the family of matrices representing $V^{l}(x^{[2]}(t))$ is obtained,

$$\begin{aligned} V^{^{\prime }}(z)=V+V(z) \end{aligned}$$

(23)

where $z\in \mathbb {R}^{\vartheta (n,l+2)(\vartheta (n,l+2)+1)/2-\vartheta (n,2(l+2))}$ is a vector of free parameters. Followed by (23), (21) can be rewritten as

$$\begin{aligned} V^{l}\left( x^{[2]}(t)\right)= & {} \left( x^{\{l+2\}}(t)\right) ^{T}V^{^{\prime }}(z)x^{\{l+2\}}(t) \nonumber \\= & {} \left( x^{\{l+2\}}(t)\right) ^{T}(V+V(z))x^{\{l+2\}}(t) \nonumber \\ \end{aligned}$$

(24)

On the other hand, it is obvious from (13) and (18) that

$$\begin{aligned} U^{l}(x(t))= & {} \left( \sum \limits _{j=1}^{n}x_{j}(t)\right) ^{l}\sum \limits _{i=1}^{r}\sum _{p=1}^{n}\sum _{q=1}^{n}h_{i}(\theta (t))\bar{v}_{pq}^{i} \nonumber \\&x_{p}(t)x_{q}(t) \end{aligned}$$

(25)

It is immediate from $1\ge h_{i}(\theta (t))\ge 0$ and (25) that $U^{l}(x(t))<0$, $\forall x(t)\in \mathbb {R}_{+}^{n},$ if $\forall x(t)\in \mathbb {R}_{+}^{n}$,

$$\begin{aligned} U_{i}^{l}(x(t))=\left( \sum \limits _{j=1}^{n}x_{j}(t)\right) ^{l}\sum _{p=1}^{n}\sum _{q=1}^{n}\bar{v}_{pq}^{i}x_{p}(t)x_{q}(t)<0 \end{aligned}$$

(26)

Then, similar to the derivations in (20)–(24), we can also find a linear parameterization $U_{i}^{^{\prime }}(w_{i})=U_{i}+U_{i}(w_{i})\in \mathbb {R}^{\vartheta (n,l+2)\times \vartheta (n,l+2)}$, $i\in R$, fulfilling

$$\begin{aligned} U_{i}^{l}\left( x^{[2]}(t)\right) = \left( x^{\{l+2\}}(t)\right) ^{T}(U_{i}+U_{i}(w_{i}))x^{\{l+2\}}(t) \end{aligned}$$

(27)

So far, the following improved stability conditions for positive T–S fuzzy system (3) can be given on the basis of the above discussions.

Theorem 2

Consider positive T–S fuzzy system (3), if there exist a scalar $l\in \mathbb {N}_{+}$ and parameter vectors z, $w_{i}\in \mathbb {R}^{\vartheta (n,l+2)(\vartheta (n,l+2)+1)/2-\vartheta (n,2(l+2))}$, $i\in R$, such that, $\forall i\in R$,

$$\begin{aligned}&V+V(z)>0 \end{aligned}$$

(28)

$$\begin{aligned}&U_{i}+U_{i}(w_{i}) <0 \end{aligned}$$

(29)

where $V,V(z),U_{i},U_{i}(w_{i})\in \mathbb {R}^{\vartheta (n,l+2)\times \vartheta (n,l+2)}$ are symmetric matrices defined in (24) and (27), and then, system (3) has a QCLF in the form of (8) which guarantees that system (3) is asymptotically stable in $\mathbb {R}_{+}^{n}$.

Proof

By the discussions in (17)–(27), it is immediately clear that if (28)–(29) hold, then $\forall x(t)\in \mathbb {R}_{+}^{n}$,

$$\begin{aligned} V^{l}(x(t))> & {} 0 \end{aligned}$$

(30)

$$\begin{aligned} U^{l}(x(t))< & {} 0 \end{aligned}$$

(31)

This together with (17) and (18) implies that $V(x(t))>0$ and $\dot{V} (x(t))<0,\forall x(t)\in \mathbb {R}_{+}^{n}$. This completes the proof. $\square$

Remark 5

In Theorem 2, an improved stability result is derived by performing high-order relaxations in the QCLF and its time derivative by the positive states. In the case of $n=1$, (20) and (26) are equivalent to (21) and (27), respectively. Thus, the stability conditions of Theorem 2 are equivalent for all $l \in \mathbb {N}_{+}$. Then, a question naturally arises: Is there a relation between the conditions of l and $l+1$ for other n. The following theorem answers the question.

Theorem 3

For a given scalar $l\in \mathbb {N}_{+}$, if there exist parameter vectors $z,w_{i}\in \mathbb {R}^{\vartheta (n,l+2)(\vartheta (n,l+2)+1)/2 -\vartheta (n,2(l+2))}$, $i\in R$ such that (28)–(29) hold, then there also exist parameter vectors $\bar{z}$, $\bar{w}_{i}\in \mathbb {R} ^{\vartheta (n,l+3)(\vartheta (n,l+3)+1)/2-\vartheta (n,2(l+3))}$ such that $\forall i\in R$,

$$\begin{aligned}&\bar{V}+\bar{V}(\bar{z})>0 \end{aligned}$$

(32)

$$\begin{aligned}&\bar{U}_{i}+\bar{U}_{i}(\bar{w}_{i})<0 \end{aligned}$$

(33)

where $\bar{V}+\bar{V}(\bar{z})$, $\bar{U}_{i}+\bar{U}_{i}(\bar{w}_{i})\in \mathbb {R}^{\vartheta (n,l+3)\times \vartheta (n,l+3)}$ are linear parameterization expressions of the matrices representing $V^{l+1}(x^{[2]}(t))$ and $U_{i}^{l+1}(x^{[2]}(t))$ which are defined in (20) and (26), respectively.

Proof

It is true that

$$\begin{aligned} V^{l+1}\left( x^{[2]}(t)\right)= & {} \left( x^{\{l+3\}}(t)\right) ^{T} \nonumber \\&(\bar{V}+\bar{V}(\bar{z}))x^{\{l+3\}}(t) \end{aligned}$$

(34)

where $x^{\{l+3\}}(t)=[\left( x_{1}(t)x^{\{l+2\}}(t)\right) ^{T},\ldots ,\, \big (x_{n-1}(t)(\mathcal {I}_{n-1}x(t))^{\{l+2\}}\big )^{T}, x_{n}^{l+3}(t) ]^{T}\in \mathbb {R}^{\vartheta (n,l+3)}$. It is also clear:

$$\begin{aligned}&V^{l+1}\left( x^{[2]}(t)\right) \nonumber \\&\quad = \left( \sum \limits _{j=1}^{n}x_{j}^{2}(t)\right) V^{l}(x^{[2]}(t)) \nonumber \\&\quad =\left( \sum \limits _{j=1}^{n}x_{j}^{2}(t) \right) \left( x^{\{l+2\}}(t)\right) ^{T}(V+V(z)) \nonumber \\&\qquad \;\times \,x^{\{l+2\}}(t) \nonumber \\&\quad = x^{T}(t)x(t)\left( x^{\{l+2\}}(t) \right) ^{T}(V+V(z)) \nonumber \\&\qquad \; \times \,x^{\{l+2\}}(t) \nonumber \\&\quad =\left( x(t)\otimes x^{\{l+2\}}(t)\right) ^{T}\left( I_{n}\otimes (V+V(z))\right) \nonumber \\&\qquad \;\times \left( x(t)\otimes x^{\{l+2\}}(t)\right) \nonumber \\&\quad =\left( x^{\{l+3\}}(t)\right) ^{T}\bigg [Y_{l+3}^{T}(I_{n}\otimes (V \nonumber \\&\qquad \; +V(z)))Y_{l+3}\bigg ]x^{\{l+3\}}(t) \end{aligned}$$

(35)

where $Y_{l+3}$ is a full column rank matrix such that $x(t)\otimes x^{\{l+2\}}(t)=Y_{l+3}x^{\{l+3\}}(t), \forall l\in \mathbb {N}_{+},x(t)\in \mathbb {R}_{0}^{n}$. On the other hand, it is noted that $V+V(z)>0$. Therefore, there exists a parameter vector

$\bar{z}\in \mathbb {R}^{\vartheta (n,\gamma +3)(\vartheta (n,\gamma +3)+1)/2-\vartheta (n,2(\gamma +3))}$ such that

$$\begin{aligned} Y_{l+3}^{T}\left[ I_{n}\otimes (V+V(z))\right] Y_{l+3}=\bar{V}+\bar{V}(\bar{z} )>0 \end{aligned}$$

Furthermore, in accordance with the similar processes above, we can conclude that if there exist parameter vectors $w_{i}$, $i\in R$ such that (29) holds, then we can also find $\bar{w}_{i}$ such that (33) is satisfied, which completes the proof. $\square$

Remark 6

We can see from Theorem 3 that if (28) and (29) have feasible solutions for a given $l \in \mathbb {N}_{+}$, then for scalar $l+1$, we can also find a QCLF ensuring the stability of system (3). Yet, the converse is not true.

3.2 Constrained fuzzy controller design

In this subsection, the problem of constrained tracking control for positive nonlinear system (1) is presented based on T–S fuzzy modeling. Our objective is to design a controller to ensure the positivity of the system (3) and the state x(t) can track a given reference input $x_{r}(t)$ in the positive orthant. Before designing the tracking controller, we first establish the constrained stabilization conditions for system (3). Here, the well-known PDC technique is employed to design the fuzzy controller, and the PDC fuzzy controller is defined as follows:

$\blacklozenge$ Model rule i: IF $\theta _{1}(t)$ is $M_{1}^{i}$ and $\cdots$ $\theta _{p}(t)$ is $M_{p}^{i}$, THEN

$$\begin{aligned} u(t)=K_{i}x(t),\quad i\in R=\{1,2,\ldots ,r\} \end{aligned}$$

(36)

Then, the closed-loop system (3) can be rewritten as follows:

$$\begin{aligned} \dot{x}(t)= & {} A(h(\theta ))x(t)+B(h(\theta ))K(h(\theta ))x(t) \nonumber \\= & {} \bar{A}(h(\theta ))x(t) \end{aligned}$$

(37)

Theorem 4

Considering the closed-loop T–S fuzzy system in (37), if there exist symmetric matrices $V\in \mathbb {R}^{n\times n}$, ${\varPsi } =\left[ \psi _{pq} \right] _{(p,\,q)\in n\times n}$, ${\varPi }_{ij}=\left[ \pi _{pq}^{ij} \right] _{(p,\,q)\in n\times n}$, $(i,j) \, \in R\times R$, such that $\forall (i,j)\in R\times R$,

$$\begin{aligned}&-{\varPsi } +Q_{1}-V < 0 \end{aligned}$$

(38)

$$\begin{aligned}&\mathrm{diag}\{\bar{\psi }_{1},\ldots ,\bar{\psi }_{n-1}\} < 0 \end{aligned}$$

(39)

$$\begin{aligned}&(A_{i}+B_{i}K_{j})^{T}V+V(A_{i}+B_{i}K_{j}) \nonumber \\&+Q_{2}-{\varPi }_{ij} < 0 \end{aligned}$$

(40)

$$\begin{aligned}&\mathrm{diag}\left\{ \bar{\pi }_{1}^{ij},\ldots ,\bar{\pi }_{n-1}^{ij}\right\} < 0 \end{aligned}$$

(41)

$$\begin{aligned}&-e_{p}(A_{i}+B_{i}K_{j})e_{q}^{T} \le 0, \nonumber \\&(p,\, q) \in \Bbbk \times \Bbbk =\{1,2,\ldots ,n\},\, p\ne q \end{aligned}$$

(42)

where $Q_{1}=\mathrm{diag}\{\psi _{11},\psi _{22},\ldots ,\psi _{nn}\}$,

$Q_{2}=\mathrm{diag}\{\pi _{11}^{ij},\pi _{22}^{ij},\ldots ,\pi _{nn}^{ij}\}$,

$\bar{\psi }_{k}\triangleq \mathrm {diag}\{2\psi _{k(k+1)},\ldots ,2\psi _{kn}\}$,

and $\bar{\pi }_{k}^{ij}\triangleq \mathrm {diag}\{2\pi _{k(k+1)}^{ij},\ldots ,2\pi _{kn}^{ij}\}$, $k\in \{1,2,\ldots ,n-1\}$, then there exists a stabilizing controller in the form of (36) with gains $K_{i}$ such that system (37) is controlled positive and asymptotically stable.

Proof

It can be derived from (42) that $A_{i}+B_{i}K_{j},\, \forall (i,j)\in R\times R$, are Metzler matrices. Also note that $1\ge h_{i}(\theta (t))\ge 0,\forall i\in R$. Therefore, it is seen that

$$\begin{aligned} \bar{A}(h(t))=\sum \limits _{i=1}^{r}h_{i}(\theta (t))\sum \limits _{j=1}^{r}h_{j}(\theta (t))(A_{i}+B_{i}K_{j}) \end{aligned}$$

are Metzler matrices, $\forall t>0.$ One can conclude by Lemma 2 and Definition 3 that system (37) is controlled positive.

On the other hand, we substitute the Lyapunov matrix P in Theorem 1 by a symmetric matrix V. Then, by similar derivations in Theorem 1, the closed-loop system (37) can be proved to be asymptotically stable if the conditions (38)–(41) are satisfied. We omit the proof here. $\square$

Next, we design a constrained fuzzy tracking controller. Here, we suppose that the reference signal $x_{r}(t)\in \mathbb {R}_{+}^{n}$ is generated by:

$$\begin{aligned} \dot{x}_{r}(t) = A_{r}x_{r}(t)+r(t) \end{aligned}$$

where $A_{r}$ is a specific Hurwitz Metzler matrix, and $r(t)\in \mathbb {R}_{+}^{n}$ is a bounded input. To achieve our main aim, we now propose the following fuzzy tracking controller which shares the same fuzzy rules as (2):

$\blacklozenge$ Model rule i: IF $\theta _{1}(t)$ is $M_{1}^{i}$ and $\cdots \,\theta _{p}(t)$ is $M_{p}^{i}$, THEN

$$\begin{aligned} u(t)=K_{1i}x(t)+K_{2i}x_{r}(t),\quad i\in R=\{1,2,\ldots ,r\} \end{aligned}$$

(43)

Then, the closed-loop system can be represented by

$$\begin{aligned} \dot{x}(t)= & {} A(h(\theta ))x(t)+B(h(\theta ))K_{1}(h(\theta ))x(t) \nonumber \\&+B(h(\theta ))K_{2}(h(\theta ))x_{r}(t) \nonumber \\= & {} \sum \limits _{i=1}^{r}h_{i}(\theta (t))\sum \limits _{j=1}^{r}h_{j}(\theta (t))(A_{i}+B_{i}K_{1j})x(t) \nonumber \\&+\sum \limits _{i=1}^{r}h_{i}(\theta (t))\sum \limits _{j=1}^{r}h_{j}(\theta (t))B_{i}K_{2j}x_{r}(t) \end{aligned}$$

(44)

Based on the above stabilization criterion, the objective is that the state x(t) of (44) tracks a given reference $x_{r}(t)$ as $t\rightarrow \infty$. In order to do so, the following augmented system is first defined:

$$\begin{aligned} \dot{X}(t)=\tilde{A}(h(\theta ))X(t)+\tilde{B}(h(\theta ))u(t)+\tilde{D} (h(\theta ))r(t) \end{aligned}$$

(45)

where

$$\begin{aligned}&\tilde{A}(h(\theta )) = \sum \limits _{i=1}^{r}h_{i}(\theta (t))\left[ \begin{array}{cc} A_{i} &{} 0 \\ 0 &{} A_{r} \end{array} \right] =\sum \limits _{i=1}^{r}h_{i}(\theta (t))\tilde{A}_{i} \\&\tilde{B}(h(\theta )) =\sum \limits _{i=1}^{r}h_{i}(\theta (t))\left[ \begin{array}{c} B_{i} \\ 0 \end{array} \right] =\sum \limits _{i=1}^{r}h_{i}(\theta (t))\tilde{B}_{i} \\&\tilde{D}(h(\theta )) = \sum \limits _{i = 1}^r {{h_i}} (\theta (t))\left[ {\begin{array}{c} 0\\ I \end{array}} \right] = \sum \limits _{i = 1}^r {{h_i}} (\theta (t)){\tilde{D}_i} \\&X(t) = \left[ {\begin{array}{c} {x(t)}\\ {{x_r}(t)} \end{array}} \right] \end{aligned}$$

and

$$\begin{aligned} u(t)= & {} \sum \limits _{i=1}^{r}h_{i}(\theta (t))K_{1i}x(t)+\sum \limits _{i=1}^{r}h_{i}(\theta (t))K_{2i}x_{r}(t) \nonumber \\= & {} K_{1i}(h(\theta ))x(t)+K_{2i}(h(\theta ))x_{r}(t). \end{aligned}$$

Theorem 5

Consider the closed-loop T–S fuzzy system in (44). For given scalars $\epsilon _{ij}>0,$ $\gamma >0$ and a semi-definite matrix $Q\in \mathbb {R}^{n\times n},$ if there exist a symmetric nonsingular matrix $\tilde{V}\in \mathbb {R}^{2n\times 2n},$ and symmetric matrices $\tilde{{\varPsi }} =[\tilde{\psi }_{pq}]_{(p,q)\in 2n\times 2n}$, $\tilde{{\varPi }}_{ij}=[\tilde{\pi }_{pq}^{ij}]_{(p,q)\in 3n\times 3n}$, $(i,j)\in R\times R$, such that $\forall (i,j)\in R\times R$,

$$\begin{aligned}&\left[ \begin{array}{ccc} T_{1} &{}\quad \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} &{}\quad T_{2} \\ \tilde{D}_{i}^{T}\tilde{V}-\tilde{{\varPi }}_{ij}^{21} &{}\quad T_{3} &{}\quad 0 \\ T_{4} &{}\quad 0 &{}\quad -\epsilon _{ij}\tilde{V}^{-1} \end{array} \right] <0 \end{aligned}$$

(46)

$$\begin{aligned}&\quad -\tilde{{\varPsi }}+\mathrm{diag}\left\{ \tilde{\psi }_{11},\tilde{\psi }_{22},\cdots ,\tilde{\psi }_{(2n)(2n)}\right\} -\tilde{V} <0 \end{aligned}$$

(47)

$$\begin{aligned}&\quad \mathrm {diag}\left\{ \tilde{\psi }_{1}^{^{\prime }},\ldots ,\tilde{\psi }_{2n-1}^{^{\prime }}\right\} < 0 \end{aligned}$$

(48)

$$\begin{aligned}&\quad \mathrm {diag}\left\{ \tilde{\pi }_{1}^{ij},\ldots ,\tilde{\pi }_{3n-1}^{ij}\right\} <0 \end{aligned}$$

(49)

$$\begin{aligned}&\quad -e_{p}(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j})e_{q}^{T} \le 0, \end{aligned}$$

(50)

$$\begin{aligned} (p,q)\in \tilde{\Bbbk }\times \tilde{\Bbbk }=\{1,2,\ldots ,2n\},\, p\ne q \end{aligned}$$

where $T_{1}=-2\tilde{V}-\tilde{{\varPi }}_{ij}^{11}-\epsilon _{ij}\tilde{V}+\tilde{Q}+\bar{{\varPi }} _{ij}^{11}$,

$T_{2}=\epsilon _{ij}I+(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I)^{T}$,

$T_{3}=-\gamma ^{2}I-\tilde{{\varPi }}_{ij}^{22}+\bar{{\varPi }}_{ij}^{22}$,

$T_{4}=\epsilon _{ij}I+\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I$,

$\tilde{{\varPi }}_{ij}=[\tilde{{\varPi }}_{ij}^{11},\,\tilde{{\varPi }}_{ij}^{12}; \, \tilde{{\varPi }}_{ij}^{21}$, $\tilde{{\varPi }}_{ij}^{22}],\, \tilde{Q} =[Q,\,-Q; -Q, Q], \bar{{\varPi }}_{ij}^{11}=\mathrm{diag}\{\tilde{\pi }_{11}^{ij}, \ldots ,\, \tilde{\pi }_{(2n)(2n)}^{ij}\},\, \bar{{\varPi }}_{ij}^{22}=\mathrm{diag}\{\tilde{\pi }_{(2n+1)(2n+1)}^{ij},\, \ldots , \tilde{\pi }_{(3n)(3n)}^{ij}\}$, $\tilde{\psi }_{k}^{^{\prime }}\triangleq \mathrm {diag}\{2\tilde{\psi }_{k(k+1)},\ldots ,2\tilde{\psi }_{k(2n)}\}$, $k\in \left\{ 1,2,\ldots ,\right.$ $\left. 2n-1\right\} ,$ $\tilde{\pi }_{k}^{ij}\triangleq \,\mathrm {diag}\{2\tilde{\pi }_{k(k+1)}^{ij},\ldots ,2\tilde{\pi }_{k(2n)}^{ij}\}$,

$k\in \left\{ 1,2,\ldots ,\right.$ $\left. 3n-1\right\}$, $\tilde{K}_{i}\triangleq \left[ K_{1i},K_{2i}\right]$, then there exists a constrained fuzzy state-feedback controller in the form of (43) with gains $\tilde{K}_{i}$ such that system (44) is controlled positive and the states x(t) can track a given reference $x_{r}(t)$ with attenuation performance $\gamma$.

Proof

First, define a QCLF candidate for system (45) as:

$$\begin{aligned} V(X(t))=X^{T}(t)\tilde{V}X(t) \end{aligned}$$

Then, by the above discussions, Schur complement, and Theorem 4, the following result can be trivially derived: If (46)–(50) have feasible solutions, then there exists a constrained fuzzy state-feedback controller in the form of (43) with gains $\tilde{K}_{i},$ such that the closed-loop augmented system (45) with $r(t)=0$ is controlled positive and asymptotically stable. This implies that system (44) is controlled positive and asymptotically stable. Furthermore, when $r(t)\ne 0,$ one has

$$\begin{aligned}&\dot{V}(X(t))+(x(t)-x_{r}(t))^{T}Q(x(t)-x_{r}(t)) \nonumber \\&\quad -\gamma ^{2}r^{T}(t)r(t) \nonumber \\&\quad =\sum \limits _{i=1}^{r}h_{i}(\theta (t))\sum \limits _{j=1}^{r}h_{j}(\theta (t))\left[ \begin{array}{c} X(t) \\ r(t) \end{array} \right] ^{T} \nonumber \\&\qquad \quad \left[ \begin{array}{cc} F_{1}&{}\quad \tilde{V }\tilde{D}_{i} \\ (\tilde{V}\tilde{D}_{i})^{T} &{}\quad -\gamma ^{2}I \end{array} \right] \nonumber \\&\quad \quad \times \left[ \begin{array}{c} X(t) \\ r(t) \end{array} \right] \end{aligned}$$

(51)

where $F_{1}=\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) ^{T}\tilde{V}+\tilde{V }\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) +\tilde{Q}$.

Since $1\ge h_{i}(\theta (t))\ge 0$ and $[X^{T}(t)$ $r^{T}(t)]\succeq 0$, $\dot{V}(X(t))+(x(t)-x_{r}(t))^{T}Q(x(t)-x_{r}(t))-\gamma ^{2}r^{T}(t)r(t)<0$, if $\forall (i,j)\in R\times R$, (49) holds and

$$\begin{aligned} \left[ \begin{array}{cc} F_{2} &{} \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} \\ (\tilde{V}\tilde{D}_{i})^{T}-\tilde{{\varPi }}_{ij}^{21} &{} -\gamma ^{2}I-\tilde{{\varPi }}_{ij}^{22}+\bar{{\varPi }}_{ij}^{22} \end{array} \right] <0 \end{aligned}$$

(52)

where $F_{2}=\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) ^{T}\tilde{V}+\tilde{V }\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) +\tilde{Q}-\tilde{{\varPi } }_{ij}^{11}+\bar{{\varPi }}_{ij}^{11}$.

It is true that

$$\begin{aligned}&\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) ^{T}\tilde{V} + \tilde{V}\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}\right) + \tilde{Q} -\tilde{{\varPi }}_{ij}^{11}+\bar{{\varPi }}_{ij}^{11} \nonumber \\&\quad = \left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\right) ^{T}\tilde{V}+\tilde{V} \left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\right) \nonumber \\&\quad -2\tilde{V}+\tilde{Q}-\tilde{{\varPi }}_{ij}^{11}+\bar{{\varPi }}_{ij}^{11} \end{aligned}$$

(53)

Therefore, (52) holds if and only if there exist sufficiently small scalars $\varepsilon _{ij}>0,\forall (i,j)\in R\times R$, such that

$$\begin{aligned} \left[ \begin{array}{cc} \begin{array}{c} F_{3} \end{array} &{} \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} \\ (\tilde{V}\tilde{D}_{i})^{T}-\tilde{{\varPi }}_{ij}^{21} &{} -\gamma ^{2}I-\tilde{{\varPi } }_{ij}^{22}+\bar{{\varPi }}_{ij}^{22} \end{array} \right] <0 \end{aligned}$$

where $F_{3}=\left( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\right) ^{T} \tilde{V}+\tilde{V}\big ( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\big ) -2\tilde{V}+\tilde{Q}-\tilde{{\varPi }}_{ij}^{11} +\varepsilon _{ij}^{T}\big ( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\big ) V\big ( \tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I\big ) + \bar{{\varPi }}_{ij}^{11}$, which is equivalent to $\forall (i,j)\in R\times R$,

$$\begin{aligned} \left[ \begin{array}{cc} \begin{array}{c} F_{4} \end{array} &{} \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} \\ (\tilde{V}\tilde{D}_{i})^{T}-\tilde{{\varPi }}_{ij}^{21} &{} -\gamma ^{2}I-\tilde{{\varPi } }_{ij}^{22}+\bar{{\varPi }}_{ij}^{22} \end{array} \right] <0 \end{aligned}$$

(54)

where $F_{4}=\left[ I+\varepsilon _{ij}(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I)\right] ^{T}\varepsilon _{ij}^{-1}\tilde{V}$

$\left[ I+\varepsilon _{ij}(\tilde{A}_{i}+ \tilde{B}_{i}\tilde{K}_{j}+I)\right] -2\tilde{V}+\tilde{Q}-\tilde{{\varPi }}_{ij}^{11}-\varepsilon _{ij}^{-1}\tilde{V}+ \bar{{\varPi }}_{ij}^{11}$. It then follows by Schur complement that (54) holds, if and only if $\forall (i,j)\in R\times R$,

$$\begin{aligned} \left[ \begin{array}{ccc} F_{5} &{} \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} &{} F_{6} \\ \tilde{D}_{i}^{T}\tilde{V}-\tilde{{\varPi }}_{ij}^{21} &{} -\gamma ^{2}I-\tilde{{\varPi }}_{ij}^{22}+\bar{{\varPi }}_{ij}^{22} &{} 0 \\ F_{7} &{} 0 &{} -\varepsilon _{ij}\tilde{V}^{-1} \end{array} \right] <0 \end{aligned}$$

(55)

where $F_{5}=-2\tilde{V}-\tilde{{\varPi }}_{ij}^{11}-\varepsilon _{ij}^{-1}\tilde{V}+\tilde{Q}+ \bar{{\varPi }}_{ij}^{11}$, $F_{6}=I+\varepsilon _{ij}(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I)^{T}$, $F_{7}=I+\varepsilon _{ij}(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I)$. Next, by setting $\varepsilon _{ij}=\epsilon _{ij}^{-1}$ and performing a congruence transformation to (55) via $\mathrm {diag}\left( I,I,\epsilon _{ij}I\right)$, we can obtain that (46) and (55) are equivalent. Noting that $V(X(t))>0,\forall X(t)\in \mathbb {R}_{+}^{2n},t>0,$ and $V(X(0))=0$ for $X(0)=0,$ it is clear that

$$\begin{aligned}&\int \nolimits _{0}^{t}[\dot{V}(X(s))+(x(s)-x_{r}(s))^{T}Q(x(s)-x_{r}(s)) \nonumber \\&\quad -\gamma ^{2}r^{T}(s)r(s)]\mathrm{d}s \nonumber \\&\quad > \int \nolimits _{0}^{t}[(x(s)-x_{r}(s))^{T}Q(x(s)-x_{r}(s)) \nonumber \\&\quad \quad -\gamma ^{2}r^{T}(s)r(s)]\mathrm{d}s \end{aligned}$$

(56)

Thus, it yields from (51)–(56) that if (46) and (49) are satisfied, then, for a finite time $t>0,$

$$\begin{aligned}&\int \nolimits _{0}^{t}(x(s)-x_{r}(s))^{T}Q(x(s)-x_{r}(s))\mathrm{d}s \nonumber \\&\quad < \gamma ^{2}\int \nolimits _{0}^{t}r^{T}(s)r(s)\mathrm{d}s \end{aligned}$$

(57)

which implies that the effect of input r(t) on the tracking error $x(t)-x_{r}(t)$ is attenuated with a prescribed performance $\gamma$.

Finally, we conclude that if (46)–(50) are feasible, then the closed-loop system (44) is controlled positive, and the state x(t) can track the reference $x_{r}(t),$ which completes the proof. $\square$

The conditions of Theorem 5 are nonconvex. However, such a problem can be solved by using the cone complementarity linearization (CCL). Next, the following algorithm solves the nonconvex problem formulated in Theorem 5.

Algorithm 1 (solving controller gain for system (44)):

• [Step 1.] For given scalars $\epsilon _{ij}>0$, $(i,j)\in R\times R$, $\gamma >0$ and a semi-definite matrix $Q\in R^{n\times n}$, find a feasible solution denoted as $(\tilde{K}_{i}^{0}, \tilde{{\varPi }}_{ij}^{0},\tilde{{\varPsi }}^{0},\tilde{V}^{0},\tilde{U}^{0})$ for the linear matrix inequalities (47)–(50) and, $\forall (i,j)\in R\times R$,

  $$\begin{aligned}&\left[ \begin{array}{ccc} M_{1} &{} \quad \tilde{V}\tilde{D}_{i}-\tilde{{\varPi }}_{ij}^{12} &{} \quad M_{2} \\ \tilde{D}_{i}^{T}\tilde{V}-\tilde{{\varPi }}_{ij}^{21} &{} \quad M_{3} &{} \quad 0 \\ M_{4} &{} \quad 0 &{} \quad -\epsilon _{ij}\tilde{U} \end{array} \right] < 0 \nonumber \\\end{aligned}$$

  (58)
  $$\begin{aligned}&\left[ \begin{array}{cc} \tilde{V} &{} I \\ I &{} \tilde{U} \end{array} \right] \ge 0 \end{aligned}$$

  (59)

  where $M_{1}=-2\tilde{V}-\tilde{{\varPi }}_{ij}^{11}-\epsilon _{ij}\tilde{V}+\tilde{Q}+\bar{{\varPi }}_{ij}^{11}$, $M_{2}=\epsilon _{ij}I+(\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I)^{T}$, $M_{3}=-\gamma ^{2}I-\tilde{{\varPi }}_{ij}^{22}+\bar{{\varPi }}_{ij}^{22}$, $M_{4}=\epsilon _{ij}I+\tilde{A}_{i}+\tilde{B}_{i}\tilde{K}_{j}+I$. Then, set $k=0$, $\tilde{V}^{0}$, and $\tilde{U}^{0}$ as the iterative initial values.

• [Step 2.] Find a feasible solution with respect to the convex minimization problem:

  $$\begin{aligned}&\min _{\left( \tilde{K}_{i}^{p+1},\tilde{{\varPi }}_{ij}^{p+1},\tilde{{\varPsi }}^{p+1},\tilde{V }^{p+1},\tilde{U}^{p+1}\right) }\mathrm{trace}\{\tilde{V}^{p+1}\tilde{U}^{p}\\&\quad +\tilde{U}^{p+1} \tilde{V}^{p}\} \end{aligned}$$

  s.t. (47)–(50) and (58)–(59)

• [Step 3.] If (46)–(50) are satisfied for $(K_{i}, \tilde{{\varPi }}_{ij},\tilde{{\varPsi }},\tilde{V},\tilde{U})=(\tilde{K}_{i}^{k+1}, \tilde{{\varPi }}_{ij}^{k+1},\tilde{{\varPsi }}^{k+1},\tilde{V}^{k+1},\tilde{U}^{k+1})$, then $\tilde{K}_{i}$ is a set of stabilizing controllers, EXIT.

• [Step 4.] If $k>N_{0}$ ($N_{0}$ is the prescribed iteration number), EXIT. Otherwise, $k=k+1$, and go to Step 2.

Examples in the next section demonstrate the validity of our obtained criteria, as well as the less conservativeness than some existing ones.

4 Numerical examples

We provide the following two examples in this section to verify the developed results.

Example 1

Consider the following autonomous continuous-time nonlinear positive system described by

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}_{1}(t) &{}=&{} -(1+9\sin ^{2}(x_{1}(t)))x_{1}(t)\\ &{}&{}+(a-a\sin ^{2}(x_{1}(t))+10\sin ^{2}(x_{1}(t)))x_{3}(t) \\ \dot{x}_{2}(t) &{} = &{} (b-b\sin ^{2}(x_{1}(t)))x_{1}(t)\\ &{}&{}-(1+9\sin ^{2}(x_{1}(t)))x_{2}(t) \\ \dot{x}_{3}(t) &{} = &{} 10\sin ^{2}(x_{1}(t))x_{2}(t)\\ &{}&{}-(10-9\sin ^{2}(x_{1}(t)))x_{3}(t) \end{array} \right. \end{aligned}$$

(60)

with $a>0$ and $b>0$.

Now, we formulate the T–S fuzzy model of positive nonlinear system (60) as follows: Let $\theta (t)=\sin ^{2}(x_{1}(t))$ with two fuzzy rules:

$$\begin{aligned}&\mathbf{Model rule} \, 1 : {\mathbf{IF}} \,\theta (t)\text { is }0, \mathbf{THEN} \\&\quad \dot{x}(t) = A_{1}x(t) \\&\quad {\mathbf{Model rule}}\, 2 : {\mathbf{IF}}\, \theta (t)\text { is }1, {\mathbf{THEN}} \\&\quad \dot{x}(t) = A_{2}x(t) \end{aligned}$$

where the normalized membership functions are $h_{1}(\theta )=1- \sin ^{2}(x_{1}(t)),h_{2}(\theta )=\sin ^{2}(x_{1}(t))$, and

$$\begin{aligned} A_{1}=\left[ \begin{array}{ccc} -1 &{} \quad 0 &{} \quad a \\ b &{} \quad -1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad -10 \end{array} \right] , \quad A_{2}=\left[ \begin{array}{ccc} -10 &{} \quad 0 &{} \quad 10 \\ 0 &{} \quad -10 &{} \quad 0 \\ 0 &{} \quad 10 &{} \quad -1 \end{array} \right] . \end{aligned}$$

Note that both $A_{1}$ and $A_{2}$ are Metzler matrices. Therefore, the positive nonlinear system (60) has been described by a positive T–S fuzzy model, which means that both Theorem 1 and Theorem 2 can be applied for the system. Next, we identify the region of the plane $a\times b\in [0,10]\times [0,5]$ such that global asymptotic stability of the system with $x(t)\in \mathbb {R}_{+}^{n}$ is preserved. We can obtain the regions of the plane $a\times b$ by some existing results including Proposition 1 of [43], Theorem 3.1 of [39], Theorem 3 of [42], Theorems 1 and 2 of this paper, respectively, and the comparison results are depicted in Fig. 1. We can see that the results in our paper yield larger regions than the other ones. Taking $a=2$ and $b=2$ for instance, it can be seen from Fig. 2 that the corresponding system is stable, which cannot be checked out by existing methods other than Theorems 1 and 2 ($l=1$) in our paper. In this case, we can obtain a QCLF ensuring the stability of the above system by Theorem 1 with the following parameters (note that the matrix P is not symmetric positive definite):

$$\begin{aligned} P=10^{5}\times \left[ \begin{array}{ccc} 0.0008 &{} \quad 0.8692 &{} \quad 1.1196 \\ -0.8695 &{} \quad 0.0007 &{} \quad -0.2359 \\ -1.1203 &{} \quad 0.2373 &{} \quad 0.0009 \end{array} \right] \end{aligned}$$

Example 2

[41] Consider the process composed of two linked tanks of both 22 l capacity, which can be described by:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}(t)=u_{1}(t)-Q_{12}(t)-Q_{1}(t) \\ \dot{x}_{2}(t)=u_{2}(t)+Q_{12}(t)-Q_{2}(t) \end{array} \right. \end{aligned}$$

(61)

where $x_{i}(t)$ stands for the level of tank i in liter; $u_{i}(t)$ represents the flow of pump i in liter/min; $Q_{12}(t)$ is the variation of the flow between the two tanks; $Q_{i}(t)$ denotes the loss flow of tank $i,i\in \{1,2\}$.

By Torricelli law [38], we can obtain

$$\begin{aligned}&Q_{1}(t) =\gamma _{1}S_{1}\sqrt{2gx_{1}(t)} \\&Q_{2}(t) =\gamma _{1}S_{2}\sqrt{2gx_{2}(t)} \\&Q_{12}(t)=\gamma _{12}S_{1}\sqrt{2g\left| x_{1}(t)-x_{2}(t)\right| } \mathrm {sign}\left( x_{1}(t)-x_{2}(t)\right) \end{aligned}$$

where $\gamma _{1}$ and $\gamma _{12}$ are physical constants, $S_{i}$ is the ith tank sectional area, and g represents the gravity acceleration. The process (61) is then described by:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1}(t) = {u_1}(t) - {R_1}\sqrt{{x_1}(t)} \\ \qquad \qquad - {R_{12}}\sqrt{\left| {{x_1}(t) - {x_2}(t)} \right| } \mathrm{{sign}}({x_1}(t) - {x_2}(t)) \\ \begin{array}{l} {{\dot{x}}_2}(t) = {u_2}(t) - {R_2}\sqrt{{x_2}(t)} \\ \qquad \qquad + {R_{12}}\sqrt{\left| {{x_1}(t) - {x_2}(t)} \right| } \mathrm{{sign}}({x_1}(t) - {x_2}(t)) \end{array} \end{array} \right. \end{aligned}$$

(62)

where $R_{1}=\gamma _{1}S_{1}\sqrt{2g},R_{2}=\gamma _{1}S_{2}\sqrt{2g}$ and $R_{12}=\gamma _{12}S_{1}\sqrt{2g}$. We use the parameter values $R_{1}=R_{2}=0.9$ and $R_{12}=0.5$. It should be pointed out that model (62) is a positive nonlinear system since $x_{i}(t)$ must be positive. Then, by setting $\theta _{i}(t)=\frac{1}{\sqrt{x_{i}(t)}}>0$, we have $\sqrt{ \left| x_{1}(t)-x_{2}(t)\right| }=\sqrt{\left| \theta _{1}^{2}(t)-\theta _{2}^{2}(t)\right| }/\theta _{1}(t)\theta _{2}(t).$ Thus, system (62) is rewritten as $\dot{x}(t)=A(t)x(t)+Bu(t)$, where

$$\begin{aligned} A(t)=\left[ \begin{array}{cc} a_{11}&{} a_{12} \\ a_{21} &{} a_{22} \end{array} \right] , B=I \end{aligned}$$

with $a_{11}=-R_{1}\theta _{1}(t)-\displaystyle \frac{R_{12}\theta _{1}(t)\theta _{2}(t)}{ \sqrt{\left| \theta _{1}^{2}(t)-\theta _{2}^{2}(t)\right| }}$,

$a_{12}=\displaystyle \frac{R_{12}\theta _{1}(t)\theta _{2}(t)}{\sqrt{\left| \theta _{1}^{2}(t)-\theta _{2}^{2}(t)\right| }}$,

$a_{21}=-\displaystyle \frac{R_{12}\theta _{1}(t)\theta _{2}(t)}{\sqrt{\left| \theta _{1}^{2}(t)-\theta _{2}^{2}(t)\right| }}$,

$a_{22}=-R_{2}\theta _{2}(t)+ \displaystyle \frac{R_{12}\theta _{1}(t)\theta _{2}(t)}{\sqrt{\left| \theta _{1}^{2}(t)-\theta _{2}^{2}(t)\right| }}$.

Fig. 1

Comparison of the regions with respect to (a, b) obtained by different stability criteria

Fig. 2

State trajectory of positive nonlinear system (60)

Suppose that $\theta _{i}(t)\in \left[ a_{i},b_{i}\right] ,$ and consider the following 4 fuzzy rules:

$$\begin{aligned}&\mathbf{Model rule}\, 1: \mathbf{IF}\, \theta _{1}(t) \text { is about }a_{1}\text {, and }\theta _{2}(t) \text { is about }a_{2}, \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\mathbf{THEN} \, A(t)=A_{1}. \\&\mathbf{Model rule} \,2:\mathbf{IF}\, \theta _{1}(t) \text { is about }a_{1}\text {, and }\theta _{2}(t)\text { is about }b_{2}, \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \, \mathbf{THEN}\, A(t)=A_{2}. \\&\mathbf{Model rule}\, 3:\mathbf{IF}\, \theta _{1}(t) \text { is about }b_{1}\text {, and }\theta _{2}(t)\text { is about }a_{2}, \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \, \mathbf{THEN} \, A(t)=A_{3}. \\&\mathbf{Model rule} \, 4:\mathbf{IF}\, \theta _{1}(t) \text { is about }b_{1}\text {, and }\theta _{2}(t)\text { is about }b_{2}, \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \, \mathbf{THEN} \, A(t)=A_{4}. \end{aligned}$$

The membership functions are chosen as: $h_{1}(\theta )=f_{11}(\theta )f_{21}(\theta )$, $h_{2}(\theta )=f_{11}(\theta )f_{22}(t)$, $h_{3}(\theta )=f_{12}(\theta )f_{21}(\theta )$, $h_{4}(\theta )=f_{12}(\theta )f_{22}(\theta ),$ with $f_{i1}(\theta )=(\theta _{i}(t)-b_{i})/(a_{i}-b_{i}),f_{i2}(\theta )=1-f_{i1}(\theta )$. Thus, the obtained matrices $A_{i}$ are:

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{cc} -R_{1}a_{1}-\displaystyle \frac{R_{12}a_{1}a_{2}}{\sqrt{\left| a_{1}^{2}-a_{2}^{2}\right| }} &{} \displaystyle \frac{R_{12}a_{1}a_{2}}{ \sqrt{\left| a_{1}^{2}-a_{2}^{2}\right| }} \\ -\displaystyle \frac{R_{12}a_{1}a_{2}}{\sqrt{\left| a_{1}^{2}-a_{2}^{2}\right| }} &{} -R_{2}a_{2}+\displaystyle \frac{ R_{12}a_{1}a_{2}}{\sqrt{\left| a_{1}^{2}-a_{2}^{2}\right| }} \end{array} \right] \nonumber \\ A_{2}= & {} \left[ \begin{array}{cc} -R_{1}a_{1}-\displaystyle \frac{R_{12}a_{1}b_{2}}{\sqrt{\left| a_{1}^{2}-b_{2}^{2}\right| }} &{} \displaystyle \frac{ R_{12}a_{1}b_{2}}{\sqrt{\left| a_{1}^{2}-b_{2}^{2}\right| }}\\ -\displaystyle \frac{R_{12}a_{1}b_{2}}{\sqrt{\left| a_{1}^{2}-b_{2}^{2}\right| }} &{} -R_{2}b_{2}+\displaystyle \frac{R_{12}a_{1}b_{2}}{\sqrt{\left| a_{1}^{2}-b_{2}^{2}\right| }} \end{array} \right] \nonumber \\ \end{aligned}$$

(63)

$$\begin{aligned} A_{3}= & {} \left[ \begin{array}{cc} -R_{1}b_{1}-\displaystyle \frac{R_{12}b_{1}a_{2}}{\sqrt{\left| b_{1}^{2}-a_{2}^{2}\right| }} &{}\displaystyle \frac{ R_{12}b_{1}a_{2}}{\sqrt{\left| b_{1}^{2}-a_{2}^{2}\right| }} \\ -\displaystyle \frac{R_{12}b_{1}a_{2}}{\sqrt{\left| b_{1}^{2}-a_{2}^{2}\right| }} &{}-R_{2}a_{2}+\displaystyle \frac{R_{12}b_{1}a_{2}}{\sqrt{\left| b_{1}^{2}-a_{2}^{2}\right| }} \end{array} \right] \nonumber \\ A_{4}= & {} \left[ \begin{array}{cc} -R_{1}b_{1}-\displaystyle \frac{R_{12}b_{1}b_{2}}{\sqrt{\left| b_{1}^{2}-b_{2}^{2}\right| }} &{} \displaystyle \frac{ R_{12}b_{1}b_{2}}{\sqrt{\left| b_{1}^{2}-b_{2}^{2}\right| }} \\ -\displaystyle \frac{R_{12}b_{1}b_{2}}{\sqrt{\left| b_{1}^{2}-b_{2}^{2}\right| }} &{} -R_{2}b_{2}+\displaystyle \frac{R_{12}b_{1}b_{2}}{\sqrt{\left| b_{1}^{2}-b_{2}^{2}\right| }} \end{array} \right] \nonumber \\ \end{aligned}$$

(64)

Next, we are interested in designing a controller in the form of (43) such that the resulting closed-loop system is positive, and x(t) can track a given reference $x_{r}(t)=\left[ 9+2\sin (t);6+\sin (0.7t)\right]$. Assume that the level of tank 1 is between 6 and 20 l, while the level of tank 2 is between 5 and 15 l. Then, $a_{1}=0.26,$ $b_{1}=0.45,$ $a_{2}=0.22$, and $b_{2}=0.41$. To meet the target, we set $\gamma =0.67,\, Q=I,\,A_{r}=-I,\, r(t)=\left[ 9+2\sin (t);6+\sin (0.7t)\right]$. Applying Algorithm 1 to the obtained T–S fuzzy system, we can get the following solutions after 11 iterations:

$$\begin{aligned} K_{11}= & {} \left[ \begin{array}{cc} -1.6117 &{} -0.1369 \\ 0.2757 &{} -2.0603 \end{array} \right] ,\quad K_{21}=\left[ \begin{array}{cc} 2.0070 &{} 0.0462 \\ 0.0462 &{} 2.0069 \end{array} \right] \\ K_{12}= & {} \left[ \begin{array}{cc} -1.7004 &{} -0.1006 \\ 0.2356 &{} -1.9016 \end{array} \right] ,\quad K_{22}=\left[ \begin{array}{rr} 2.0590 &{} 0.0473 \\ 0.0473 &{} 2.0590 \end{array} \right] \\ K_{13}= & {} \left[ \begin{array}{cc} -1.5388 &{} -0.0572 \\ 0.1950 &{} -1.9980 \end{array} \right] ,\quad K_{23}=\left[ \begin{array}{cc} 2.0265 &{} 0.0449 \\ 0.0448 &{} 2.0264 \end{array} \right] \\ K_{14}= & {} \left[ \begin{array}{cc} -1.1852 &{} -0.4297 \\ 0.5654 &{} -2.2161 \end{array} \right] ,\quad K_{24}=\left[ \begin{array}{rr} 2.0450 &{} 0.0462 \\ 0.0462 &{} 2.0447 \end{array} \right] \end{aligned}$$

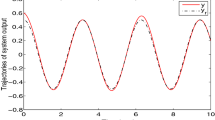
Finally, the corresponding state responses of the system under initial state condition $x(0)=\left[ \begin{array}{cc} 10&10 \end{array} \right] ^{T}$ and $x_{r}(0)=\left[ \begin{array}{cc} 0&0 \end{array} \right] ^{T}$ are shown in Fig. 3, from which one can see that the obtained controller achieves the tracking purpose as t increases, while imposing the positivity in closed loop.

Fig. 3

State responses of the corresponding closed-loop system

5 Conclusions

The problems of stability and control for a class of positive nonlinear systems are investigated in this paper based on T–S fuzzy modeling. By proposing a quadratic copositive Lyapunov function approach, improved stability conditions are first established for positive nonlinear systems that can be represented by positive T–S fuzzy systems. Then, the concept of “controlled positive” is introduced for a given positive nonlinear system, based on which, the problem of constrained stabilization is solved. Furthermore, a constrained fuzzy controller ensuring the tracking performance and positivity in closed loop is also designed for the underlying systems by defining an augmented system. Finally, two examples are provided to verify the advantages and applicability of our proposed results by comparing with the existing ones. By our proposed idea, extending the results of this paper to positive nonlinear systems with time delay or to membership-dependent conditions will be considered in our future work.