1 Introduction

Ball screw feed system is widely used in CNC machine tool, aerospace and many other situations due to its high positioning accuracy, high axial stiffness, efficient, and long service life. The dynamic characteristics and positioning accuracy of the feed system are closely related to thermal deformation [1], preload [2], machining force, and the condition of each kinematic joints. The health condition of each component, such as double row angular contact ball bearing (DRACBB), screw shaft, and screw nut, plays an important role during the positioning process, respectively. The dynamic response of each component has been widely discussed in detail.

The dynamic behavior of the ball screw feed system has been studied using different analytical models [3,4,5,6,7]. Rafsanjani et al. [8] developed a two-degrees-of-freedom analytical model considering the radial clearance and unbalance force to study the effect of the local defect on the stability and dynamic characteristics of a rolling bearing. Liu et al. [9] proposed a force deflection model to describe the time-varying contact force between the ball and the raceway of rolling bearing, and discussed the effect of the local defect, it found that the root mean square value increased with the defect size. Liu et al. [10] discussed the effects of rotor eccentricity, preload, internal, and external waviness on the system nonlinear dynamics response, and compared the steady-state response between linear model, nonlinear model, and displacement coordinate model. Considering the contact deformation at the edge of local defect, Liu and Shao [11] proposed a piecewise function to describe the local defect of rolling bearing, the vibration response with different defect shapes is discussed, and the results showed that the waveform was greatly influenced by defect parameters. Liu and Shao [12] discussed the vibration response generated by a local defect with different sizes, and take the deformation at the sharp edges into consideration. Liu et al. [13] considered the offset and bias of local defect in the outer race of ball bearing, and discussed the effect of bias angle and offset distance on the vibration response. For angular contact ball bearing, the contact angle changes with the axial deformation. Therefore, the calculation process would be time-consuming. Liao and Lin [14] used Newton's method to calculate the contact angle of angular contact ball bearings. Although the Hertzian contact constant between ball and raceway varies individually upon the contact angle, Jones [15] found that their sum was nearly a constant for any given contact angle when calculating the relationship between axial load and deformation of angular contact ball bearings. Gunduz et al. [16] developed an analytical model to investigate the effect of preload on the modal characteristics of a shaft-bearing system assembly with a DRACBB. Moreover, a modal experimental measurement was used to validate the proposed model. To investigate the relationship between load and axial displacements of bearing ring, Yang et al. [17] introduced a three-dimensional mode and investigated the effect of the variation of several parameters, such as the raceway curvature radius, the load magnitude, and the thickness of bearing ring. Mcfadden and Smith [18] developed a model to describe the vibration response produced by a single and multiple local defects on the raceway of rolling bearing, the model took the effects of the speed, the transfer function, the bearing geometry, the decay of vibration, and the load distribution of the system into consideration.

Many scholars have discussed the dynamic characteristics of the ball screw feed system under different condition. In order to achieve the dynamic behavior of ball screw drive system, Ansoategui and Campa [19] integrated the proposed dynamic model of ball screw feed drive into a mechatronic model of the actuator. Including motor velocity, the whole mechatronic system, the table position, and motor velocity were considered in the proposed 7-DOF dynamic model. To analyze the vibration response of a coupled feed system, Wang et al. [20] established a seven-degrees-of-freedom dynamics model and introduced the restoring force of nonlinear kinematic joints into the model. In addition, the effect of screw nut position on the positioning accuracy was studied in detail. Xu [21] using the finite element method (FEM) and a modified lumped capacitance method (MLCM) to estimate the thermal error of the ball screw feed system. To evaluate the dynamic characteristic of the ball screw-driven system, Chen et al. [22] introduced friction models that combined two significant characteristics of static friction: the hysteresis and the plasticity. Zou et al. [23] developed a variable-coefficient lumped parameter model considering the stiffness of screw nut to be position-dependent, and investigated the effect on dynamic characteristics of the system. To calculate the contact stress and fatigue life of the ball screw system, Zhen and An [24] proposed a model of ball screw feed system considering dimension errors of balls. Moreover, the axial and lateral load of the ball screw had been taken into consideration throughout the calculation process. Considering axis coupling effects, Wang et al. [25] proposed a three-axis gantry milling machine tool model, and analyzed the influence of the stiffness of kinematic joints. Besides, Wang et al. found that the natural frequency is closely related to the center position. The preload of the ball screw has a great influence on the dynamic stiffness of machine tool structure. Mi et al. [26] studied the effects of different preloads on the whole machine tool structure and found that it could enhance the natural frequency.

The above papers discussed the dynamic response of the ball screw feed system and gave methods of modeling. However, the amplitude–frequency characteristic of the feed system is rarely studied. Yang et al. [27] used the harmonic balance method with alternating frequency and time-domain technique (HB-AFT) to obtain the dynamic response of a rigid-rotor ball bearing system. Hou and Chen [28] indicated that super-harmonic resonance could be regarded as the identification signal of the rotor system with a crack failure, the super-harmonic signals had a close connection with the stiffness of the system, and the system will resonance at some specific frequencies. Gao et al. [29] used the amplitude–frequency curve to discuss the dynamic characteristics of the aerospace dual rotor system. The dual rotor system could exhibit abnormal resonance when there exists a local defect on the inter shaft bearing. The resonance frequency was strongly influenced by the roller number and the rotation speed of inner shaft bearing. Moreover, the linear stiffness and the damping of the system can have an influence on the abnormal resonant frequency and the vibration amplitude. To study the characteristics of ball bearing subharmonic resonance, Bai et al. [30] built a six-degrees-of-freedom force model. By comparing the numerical and experimental results, it revealed that the bearing internal clearance and nonlinear Hertz contact force jointly caused the subharmonic resonance.

In the previous papers, the effect of various system parameters on vibration response and abnormal resonance had been studied in detail. However, the effect of local defect on the dynamic response of the feed system is rarely studied. This paper aims to establish a three-degrees-of-freedom force model considering the exciting force with different frequencies, based on which, the dynamic characteristics of the feed system effected by the local defect are analyzed. The local defects have been modeled into three shapes: the rectangular shape, the triangular shape, and the half-sine shape. With consideration of the preload, two kinds of piecewise functions are given to build the relationship between restoring force and axial displacement for the screw nut and DRACBB. The axial displacement of DRACBB will change when the ball falls into the defect area. This paper compares the dynamic responses with different defect depths, defect lengths, defect shapes, and motor speeds. The results show that the feed system will resonance at some specific excitation frequency when there exists a local defect on DRACBB, and the system may exhibit different dynamic responses at different motor speeds. The amplitude of the abnormal resonance is closely related to the parameters of the defect, such as length, depth, and geometric shape. The waveform and spectrum are used to analyze the frequency components of vibration response. As the abnormal resonance adversely affect the positioning accuracy of the system, the results of this paper can be helpful for the diagnosis of the ball screw feed system.

2 Dynamic model and governing equations of motion

2.1 Ball screw feed system

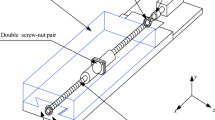
As shown in Fig. 1, the ball screw feed system consists of a motor, a coupling, a pair of DRACBB, a screw shaft, a screw nut, and a worktable. The motor is connected to the screw shaft through a coupling. The left end of the screw shaft is fixed on the DRACBB, and the other side is supported by a deep groove ball bearing. The arrangement of DRACBB is face to face. At the right end, the deep groove ball bearing can move along the axial direction to offset the deformation error of the screw shaft. The worktable moves to the right at speed v as the motor rotates at a constant speed ωn. The harmonic excitation F(t) is applied to the mass center of the worktable to simulate the cutting force along the axial direction at different excitation frequencies. In order to study the dynamic response of DRACBB, screw shaft, and screw nut is considered as mass spring damper system, respectively.

Fig. 1
figure 1

a Schematic of ball screw feed system. b 3-DOF dynamic model

Full size image

2.2 Restoring force of components

2.2.1 Restoring force of DRACBB

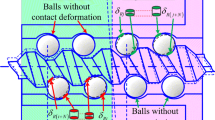
As shown in Fig. 2, DRACBB consists of balls, inner raceway, and outer raceway. ωc is the angular velocity of the cage, ωn is the angular velocity of the inner raceway. Oo and Oi are the curvature center of the outer and inner raceway. The contact deformation of the ith ball will reduce when it falls into the defect region.

Fig. 2
figure 2

Schematic of DRACBB with a local defect

Full size image

Figure 3 shows the relationship between ball deformation, contact angle, and axial displacement of the inner race when the preload and load are applied to DRACBB. The elastic deformation of balls causes the axial displacement of inner raceway xb, xb0 is the axial displacement caused by preload applied on the left and right bearings, α0 is the initial contact angle of the right and left bearing. The contact angle and deformation of the left bearing are αl and δbl, and for the right bearing are αr and δbr. Ab is the initial distance between the curvature center of the inner and outer raceway.

Fig. 3
figure 3

Relationship between deformation and axial displacement under preload: a left bearing b right bearing

Full size image

The distance between the curvature center of the inner and outer raceway is

$$ A_{b} = r_{{\text{o}}} + r_{{\text{i}}} - 2r_{b} $$
(1)

where ri is the curvature radius of the inner raceway, and ro is the curvature radius of the outer raceway. The contact angles of the left and right bearings which are under load can be formulated as

$$ \sin \alpha_{{\text{l}}} = \frac{{A_{b} \sin \alpha_{0} + x_{b0} + x_{b} }}{{\sqrt {\left( {A_{b}^{2} \cos^{2} \alpha_{0} + \left( {A_{b} \sin \alpha_{0} + x_{b0} + x_{b} } \right)^{2} } \right)} }} $$
(2)
$$ \sin \alpha_{{\text{r}}} = \frac{{A_{b} \sin \alpha_{0} + x_{b0} - x_{b} }}{{\sqrt {\left( {A_{b}^{2} \cos^{2} \alpha_{0} + \left( {A_{b} \sin \alpha_{0} + x_{b0} - x_{b} } \right)^{2} } \right)} }} $$
(3)

In this paper, a local defect is set on the outer race of the left bearing. Therefore, according to the geometric relationship shown in Fig. 3, the deformation of balls of left and right bearing δbr and δbl can be obtained as follows:

$$ \delta_{{{\text{bl}}}} = \sqrt {\left( {A_{b}^{2} \cos^{2} \alpha_{0} + \left( {A_{b} \sin \alpha_{0} + x_{b0} + x_{b} } \right)^{2} } \right)} - A_{b} - H\left( t \right) $$
(4)
$$ \delta_{{{\text{br}}}} = \sqrt {\left( {A_{b}^{2} \cos^{2} \alpha_{0} + \left( {A_{b} \sin \alpha_{0} + x_{b0} - x_{b} } \right)^{2} } \right)} - A_{b} $$
(5)

where H(t) is the defect function of time t and the expression can be derived from Eqs. (6)–(11) according to Ref. [11]

$$ \theta_{j} \left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{2\pi }{Z}\left( {j - 1} \right) + \omega_{c} t} \hfill & {\text{defect on outer race }} \hfill \\ {\frac{2\pi }{Z}\left( {j - 1} \right) + \left( {\omega_{n} - \omega_{c} } \right)t} \hfill & {\text{defect on inner race}} \hfill \\ \end{array} } \right. $$
(6)

where θj is the position angle of the jth ball at time t, ωn is the angular velocity of the inner raceway, and the expression of the angular velocity of cage ωc can be given by

$$ \omega_{{\text{c}}} = \frac{1}{2}\omega_{n} \left( {1 - \frac{{d_{b} }}{{d_{bm} }}\cos \alpha_{l} } \right) $$
(7)

where db is the diameter of ball, and dbm is the diameter of the pitch circle. In this paper, the default function of the local defect is assumed to be half-sine piecewise function, which is shown in Fig. 2. As the width of defect is limited, the descending distance of the ball cannot equal to the depth of the defect, and according to Ref. [13], the descending distance equation in relation to B and L can be given by

$$ H\left( {B,L} \right) = \min (H_{d} ,0.5d_{b} - \sqrt {\left( {0.5d_{b} } \right)^{2} - \left( {0.5 * \min (B,L)} \right)^{2} } ) $$
(8)

Therefore, the half-sine piecewise defect function can be given by

$$ H_{{{\text{sin}}}} \left( t \right) = \left\{ {\begin{array}{*{20}l} {H\left( {B,L} \right)\sin \left( {\frac{{\pi \left( {\theta_{j} - \theta_{0} } \right)}}{\Delta t}} \right)} \hfill & {\theta_{0} \le \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) \le \theta_{0} + \Delta t} \hfill \\ {H\left( {B,L} \right)} \hfill & {\theta_{0} + \Delta t < \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) < \theta_{0} + \Delta t + \Delta T} \hfill \\ {H\left( {B,L} \right)\sin \left( {\frac{{\pi \left( {\theta_{j} - \theta_{0} - \Delta T} \right)}}{\Delta t}} \right)} \hfill & {\theta_{0} + \Delta t + \Delta T \le \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) \le \theta_{3} } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(9)

Moreover, to study the effect of defect shape, the defect function of triangle is given by:

$$ H_{{{\text{triangle}}}} \left( t \right) = \left\{ {\begin{array}{*{20}l} {H\left( {B,L} \right)\frac{{\theta_{j} - \theta_{0} }}{0.5\Delta T}} \hfill & {\theta_{0} \le \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) \le \frac{{\theta_{3} - \theta_{0} }}{2}} \hfill \\ {H\left( {B,L} \right)\frac{{0.5\Delta T - \theta_{j} + \theta_{1} }}{0.5\Delta T}} \hfill & {\frac{{\theta_{3} - \theta_{0} }}{2} < \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) < \theta_{3} } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(10)

and the defect function of rectangle is

$$ H_{{{\text{ranctangle}}}} \left( t \right) = \left\{ {\begin{array}{*{20}c} {H\left( {B,L} \right)} & {\theta_{0} \le \bmod \left( {\theta_{j} \left( t \right),2\pi } \right) \le \theta_{3} } \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. $$
(11)

As shown in Fig. 2, Hd is the depth of the defect, θ0 is the starting position angle of the defect, and θ1 = θ0 + Δt, θ2 = θ1 + ΔT, θ3 = θ2 + Δt, Δt is the angle experienced that the ball goes from the edge to the bottom, ΔT is the angle experienced when the descending distance of ball reaches the maximum, and the expression of Δt and ΔT can be written as

$$ \Delta t = \left\{ {\begin{array}{*{20}c} {arcsin\left( {\min \left( {\text{L,B}} \right)/d_{b0} } \right)} & {\text{defect on outer race}} \\ {arcsin\left( {\min \left( {\text{L,B}} \right)/d_{bi} } \right)} & {\text{defect on inner race}} \\ \end{array} } \right. $$
(12)
$$ \Delta T = \left\{ {\begin{array}{*{20}c} {\arcsin \left( {\frac{L}{{d_{bo} }}} \right) - 2\Delta t} & {\text{defect on outer race}} \\ {\arcsin \left( {\frac{L}{{d_{bi} }}} \right) - 2\Delta t} & {\text{defect on inner race}} \\ \end{array} } \right. $$
(13)

where L is the length of the defect. According to Hertzian contact theory in Ref. [32, 33] and the geometric relationship, the contact force of the jth and ith ball in the left and right bearing along axial direction can be given by

$$ F_{{{\text{br}}}} = K_{{\text{b}}} \delta_{{{\text{br}}}}^{1.5} \sin \alpha_{{\text{r}}} $$
(14)
$$ F_{{{\text{bl}}}} = K_{{\text{b}}} \lambda \left( {\delta_{{{\text{bl}}}} } \right)\delta_{{{\text{bl}}}}^{1.5} \sin \alpha_{{\text{l}}} $$
(15)

where Kb is the Hertzian contact stiffness between the ball and the raceway, the expression and calculation process can be obtained in Ref. [33, 34] and λ can be defined in Ref. [11]

$$ \lambda \left( \delta \right) = \left\{ {\begin{array}{*{20}c} 1 & {\delta > 0} \\ 0 & {\delta \le 0} \\ \end{array} } \right. $$
(16)

Therefore, when considering the effects of axial loads, preload, and local defect, the piecewise function of restoring force of DRACBB Fb(x1, t) can be given by

$$ F_{b} \left( {x_{1} ,t} \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{j = 1}^{{N_{b} }} {F_{br} } - \sum\limits_{i = 1}^{{N_{b} }} {F_{bl} } } \hfill & { - x_{0} \le x_{b} \le x_{0} } \hfill \\ {\sum\limits_{j = 1}^{{N_{b} }} {F_{br} } } \hfill & {x_{b} > x_{0} } \hfill \\ { - \sum\limits_{i = 1}^{{N_{b} }} {F_{bl} } } \hfill & {x_{b} < - x_{0} } \hfill \\ \end{array} } \right. $$
(17)

where x1 is the absolute axial displacement of DRACBB inner race, and satisfy x1 = xb. x0 is the initial axial displacement of the inner race caused by preload. Fbr is the contact force of jth ball of left bearing, Fbl is the contact force of ith ball of right bearing, and Nb is the number of balls.

2.2.2 Restoring force of ball screw

As shown in Fig. 4, a single-nut ball screw consists of balls, screw shaft, and ball nut. The preload is created by a variable lead.

Fig. 4
figure 4

Schematic of single-nut ball screw under preload

Full size image

F(t) is the excitation force acting on the worktable. Fnl and Fnr are the contact force of balls in the left and right section.

Figure 5 shows the relationship between axial displacement xn and ball deformation δnl, δnr when F(t) is applying on the worktable. Furthermore, the contact angle of the left section of screw nut changed from γ0 to γl, and the right section changed from γ0 to γr. \({O}_{iL}^{^{\prime}}\) and \({O}_{oL}^{^{\prime}}\) are the curvature center of the screw shaft and screw nut in the left section, similarly \({O}_{iR}^{^{\prime}}\) and \({O}_{oR}^{^{\prime}}\) are the curvature center for the right section. An0 is the initial distance between the curvature center of the screw shaft and screw nut, and the expression can be given by

$$ A_{n0} = r_{s} + r_{n} - 2r_{w} $$
(18)

where rs and rn are the curvature radius of the screw shaft raceway and ball nut raceway, rw represents the radius of the ball. According to the geometric relationship shown in Fig. 5, the deformation of balls in the left and right section of screw nut can be formulated as

$$ \delta_{nr} = \sqrt {\left( {A_{n}^{2} \cos^{2} \gamma_{0} + \left( {A_{n} \sin \gamma_{0} + x_{n0} + x_{n} } \right)^{2} } \right)} - A_{n} $$
(19)
$$ \delta_{nl} = \sqrt {\left( {A_{n}^{2} \cos^{2} \gamma_{0} + \left( {A_{n} \sin \gamma_{0} + x_{n0} - x_{n} } \right)^{2} } \right)} - A_{n} $$
(20)

where γ0 is the initial contact angle, γl and γr represent the contact angle in the left and right section. The expression of contact angle γl and γr can be calculated by

$$ \sin \gamma_{r} = \frac{{A_{n} \sin \gamma_{0} + x_{n0} + x_{n} }}{{\sqrt {\left( {A_{n}^{2} \cos^{2} \gamma_{0} + \left( {A_{n} \sin \gamma_{0} + x_{n0} + x_{n} } \right)^{2} } \right)} }} $$
(21)
$$ \sin \gamma_{l} = \frac{{A_{n} \sin \gamma_{0} + x_{n0} - x_{n} }}{{\sqrt {\left( {A_{n}^{2} \cos^{2} \gamma_{0} + \left( {A_{n} \sin \gamma_{0} + x_{n0} - x_{n} } \right)^{2} } \right)} }} $$
(22)

where xn is the relative displacement between the screw nut and the screw shaft when exciting force F(t) is acting on the worktable, and xn0 is the initial displacement caused by preload. Therefore, the contact force of balls in the left and right section along axial direction can be formulated as

$$ F_{nr} = K_{n} \delta_{nr}^{1.5} \sin \gamma_{r} $$
(23)
$$ F_{nl} = K_{n} \delta_{nl}^{1.5} \sin \gamma_{l} $$
(24)

where Knr and Knl are the Hertzian contact stiffness between ball and raceway, and the expression can be obtained in Ref. [33, 34]. Therefore, according to the formulas proposed above, the piecewise function of the ball nut restoring force can be determined by

$$ F_{n} \left( {x_{1} ,x_{2} ,x_{3} ,t} \right) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{j = 1}^{{N_{S} }} {F_{nr} } - \sum\limits_{i = 1}^{{N_{S} }} {F_{nl} } } \hfill & { - x_{n0} \le x_{n} \le x_{n0} } \hfill \\ {\sum\limits_{j = 1}^{{N_{S} }} {F_{nr} } } \hfill & {x_{n} > x_{n0} } \hfill \\ { - \sum\limits_{i = 1}^{{N_{S} }} {F_{nl} } } \hfill & {x_{n} < - x_{n0} } \hfill \\ \end{array} } \right. $$
(25)

where xn is the deformation of the rolling element in screw nut along the axial direction, and satisfy xn = x3–x2.

Fig. 5
figure 5

Deformation and axial displacement of the ball screw. a Left section. b Right section

Full size image

2.2.3 Restoring force of screw shaft

The stiffness of the screw shaft can be given by Ref. [23]

$$ K_{s} \left( t \right) = 1/\left( {1/\frac{{4GE\pi^{3} d_{n}^{4} }}{{16G\pi^{2} d_{n}^{2} \left( {X_{0} + \frac{\omega t}{{2\pi }}P} \right) + 32P^{2} E\left( {X_{0} + \frac{\omega t}{{2\pi }}P} \right)}} + 1/\frac{{\pi Ed_{n}^{2} }}{{4\left( {X_{0} + \frac{\omega t}{{2\pi }}P} \right)}}} \right) $$
(26)

where X0 is the initial distance between screw nut and DRACBB, P is the lead of screw shaft, G and E represent the shear modulus and elastic modulus, dn represents the diameter of the pitch circle of the ball screw. As the screw nut moves to the right end of screw shaft, the distance between screw nut and DRACBB changes over time, and the stiffness of the screw shaft can be considered as time-varying. Therefore, the deformation of screw shaft δs can be expressed by

$$ \delta_{s} = x_{2} - x_{1} - \frac{\omega t}{{2\pi }}P $$
(27)

the restoring force of the screw shaft can be given by

$$ F_{s} \left( {x_{1} ,x_{2} ,t} \right) = K_{s} \left( t \right)\left( {x_{2} - x_{1} - \frac{\omega t}{{2\pi }}P} \right) $$
(28)

where x1 is the absolute displacement of DRACBB inner race, x2 represents the absolute displacement of the screw shaft, and x3 represents the absolute displacement of the screw nut, all of them are along axis direction.

2.3 Governing equations of motion

In this section, components such as DRACBB, screw shaft, and screw nut are modeled as mass spring damper system, which is shown in Fig. 6.

Fig. 6
figure 6

Mechanical relationship of three-degrees-of-freedom dynamic model

Full size image

According to the analysis in Fig. 6, the governing equations of motion for three-degrees-of-freedom ball screw feed system can be represented by

$$ \left\{ {\begin{array}{*{20}l} {m_{b} \ddot{x}_{1} + c_{S} \left( {\dot{x}_{1} - \dot{x}_{2} + \omega_{n} P/2\pi } \right) + c_{B} \dot{x}_{1} + F_{b} \left( {x_{1} ,t} \right) = F_{s} \left( {X_{l} } \right)} \hfill \\ {m_{s} \ddot{x}_{2} + c_{S} \left( {\dot{x}_{2} - \dot{x}_{1} - \omega_{n} P/2\pi } \right) + c_{N} \left( {\dot{x}_{2} - \dot{x}_{3} } \right) + F_{s} \left( {x_{1} ,x_{2} ,t} \right) = F_{n} \left( {x_{1} ,x_{2} ,x_{3} ,t} \right)} \hfill \\ {m_{n} \ddot{x}_{3} + c_{N} \left( {\dot{x}_{3} - \dot{x}_{2} } \right) + F_{n} \left( {x_{1} ,x_{2} ,x_{3} ,t} \right) = F\left( t \right)} \hfill \\ \end{array} } \right. $$
(29)

where x1, x2, and x3 represented the absolute displacement of the inner race of DRACBB, screw shaft, and screw nut. \(\dot{{\text{x}}_{1}}\), \(\dot{{\text{x}}_{2}}\), and \(\dot{{\text{x}}_{3}}\) are the velocity, respectively. ωn is the angular velocity of the motor. mb, ms, and mn represent the mass of DRACBB, the screw shaft and the screw nut. Fb(x1, t), Fs(x1, x2, t) and Fn(x1, x2, x3, t) are the restoring force of DRACBB, screw shaft and screw nut. F(t) is the excitation force which is a sinusoidal force applied on the worktable, the expression is F(t) = F0sinωt, ω is the excitation frequency which satisfy ω = 2πf and F0 is the excitation amplitude.

3 Discussion and experimental verification

3.1 System parameter estimation and experimental verification

3.1.1 System parameter estimation

To validate the proposed dynamic model and estimate the system damping, two experiments are conducted in this section. The parameters of the feed system are listed in Tables 1 and 2. In order to obtain the system damping and validate the primary resonance frequency of simulation, an impact test is conducted. As shown in Fig. 7, an accelerometer(Micro-epsilon optoNCDT2300-20) is mounted on the left side of screw nut to measure the vibration response of the system. The impact hammer (Sinocera LC-01A) with a force transducer is used to determine the impacts of varying amplitude and duration. The schematic of the test can be shown in Fig. 7. The waveform of the input force, the vibration response of the feed system, and the frequency response curve are shown in Fig. 8a–c. In this study, a half-power band width method is employed to estimate the damping ratios of the feed system by using the obtained frequency response curve. According to Ref. [35], the expression of damping ratio can be expressed by

$$ \zeta = \frac{{\omega_{2} - \omega_{1} }}{{2\omega_{dm} }} $$
(30)

where ωdm represents the nature frequency of the system, ω1 and ω2 are the half-power frequency when the amplitude satisfy A = 0.707Amax. Amax is the corresponding amplitude of ωdm. As shown in Fig. 8c, ω1 = 255.31 Hz, ω2 = 282.5 Hz, ωdm = 272.7 Hz. Based on the experiment results, the damping ratio of the system can be obtained ζ = 0.0997. Hence, the viscous damping coefficient c can be estimated by c = 4πζω0m, where ω0 represents the corresponding nature frequency, and m is the mass of each governing equation. Furthermore, the nature frequencies of the feed system from experiment and simulation are shown in Fig. 8c, d, the difference is 2.02% which validate the proposed model (Table 3).

Table 1 Parameters for DRACBB
Full size table
Table 2 Parameters for ball screw
Full size table
Table 3 Specification of experimental test rig
Full size table
Fig. 7
figure 7

Schematic of hammer excitation test

Full size image
Fig. 8
figure 8

a Input force. b Vibration response of the feed system. c Measured frequency response function of the feed system. d Simulated frequency amplitude curve

Full size image

3.1.2 Experimental verification

In this subsection, an experiment is conducted to validate the proposed model, and the experiment results are compared with the simulation results. As shown in Fig. 9, the ball screw feed system consists of a worktable, a screw shaft (THK SBN4016), DRACBB (NTN 7206BDB), and a motor control system (Siemens Sinumerik 828D). The vibration response is acquired by a data collection system (DH5956), a PC, a charge amplifier (Sinocera YE5874A), a power amplifier (YE5874A), a force censor (CL-YD-331A), and an accelerometer (Micro-epsilon optoNCDT2300-20). The accelerometer is installed on the right end surface of the screw nut to measure the dynamic response of the feed system. As shown in Fig. 9, the harmonic excitation is generated by an electromagnetic shaker (Sinocera JZK-50) which is applied on the feed system. The vibration response and excitation amplitude are measured by the force censor and the accelerometer. The mounting type of DRACBB is face to face. The local defect is set on the outer race of the left bearing of DRACBB using a method of electrical spark machining. The length, width, and depth of the defect are set to 4 mm, 3 mm, and 0.5 mm, respectively. Moreover, the worktable moves from the midpoint to the right end of screw shaft at a constant feed rate ωnP/2π. The comparison of vibration response between experiment and simulation with different excitation frequencies and feed rates are shown in Fig. 10, where ωnP/2π represents the feed rate. In the vibration test, the external load F0 applied on the worktable and the feed speed of the system ωnP/2π can be seen in the caption of Fig. 10. The sampling frequency of the test is 10 kHz. The mounting method can be seen in Figs. 7 and 9. In order to link the electromagnetic shaker to the screw nut, a worktable is added in the vibration validation test. In this subsection, the vibration response between simulation and experiment is compared when the mass of screw nut changed from mn to mn + mw. As shown in Fig. 10, the results from experiment are slightly larger than the simulation results which is caused by the machine body deformation, and the error is in an acceptable range (Fig. 11).

Fig. 9
figure 9

Schematic of experiment setup for vibration response measurement

Full size image
Fig. 10
figure 10

Comparison of vibration response between experiment and simulation with different feed rate Vf and excitation frequency ω/2π. a Vf = 100 mm/min, ω/2π = 100 Hz, F0 = 50 N. b Vf = 100 mm/min, ω/2π = 300 Hz, F0 = 50 N. c Vf = 200 mm/min, ω/2π = 100 Hz, F0 = 50 N. d Vf = 200 mm/min, ω/2π = 300 Hz, F0 = 50 N. e Vf = 300 mm/min, ω/2π = 100 Hz, F0 = 50 N. f Vf = 300 mm/min, ω/2π = 300 Hz, F0 = 50 N

Full size image
Fig. 11
figure 11

Flow chart of numerical simulation

Full size image

3.2 Simulation and discussion

A fourth-order Runge–Kutta method is used to solve the three-degrees-of-freedom governing equations of motion. The calculation process of the proposed method can be shown in Fig. 7. The preload of DRACBB and screw nut are 290N and 1690N [20]. The detailed geometric parameters of them are shown in Tables 1 and 2. The default defect geometry is L = 5 mm, B = 3 mm, and Hd = 1 mm, where L, B, and Hd represent the length, width, and depth of the defect. The movement of screw nut is linear from the midpoint of screw shaft to the right end of screw shaft. The angular velocity of motor ωn is 16 rad/s.

In this paper, the root mean square value (RMS) is used to replace the traditional amplitude to describe the characteristics of the vibration signal. The value of RMS is directly related to the energy of the vibration signal and often used to extract features from the vibration signal for prognosis [29]. The definition of RMS can be given by Ref. [37]

$$ {\text{RMS}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {x_{i} - \overline{x}} \right)^{2} } }}{N}} $$
(31)

where xi is the value of ith data point, \(\overline{\text{x}}\) is the average value of data points, and N is the length of the data. The peak to peak (PtP) value is introduced to compare the effects of different defect parameters at the specific excitation frequency. The PtP value can directly reflect the positioning accuracy of the feed system. The definition of PtP can be given by

$$ {\text{PTP}} = \left| {\max \left( x \right) - \min \left( x \right)} \right| $$
(32)

where x represents the worktable displacement solution vector. The displacement used in the vibration response analysis in this paper can be given by

$$ x = x_{3} - \frac{\omega t}{{2\pi }}P $$
(33)

x equals to the absolute displacement of the screw nut minus the displacement caused by the screw helix angle. In other words, x is the sum of the deformation of DRACBB, screw shaft, and screw nut. Therefore, x can directly reflect the positioning accuracy of the feed system.

As shown in Fig. 12, there exist two abnormal resonance B, and C. Abnormal resonance B is caused by the exciting frequency coinciding with the natural frequency of the feed system. Abnormal resonance C is closely related to the motor speed, and the relationship between them will be discussed in Sect. 3.2.3. As shown in Fig. 13, apart from B, and C, there exist fault induced resonance A. It can be observed that the amplitude–frequency curve shows typical hardening type nonlinearity at abnormal resonance A, and there exist jumping discontinuous phenomena at B, and C.

Fig. 12
figure 12

Amplitude–frequency curve with excitation frequency ω/2π as control parameter at ωn = 16 rad/s, L = 0 mm, and B = 0 mm, and Hd = 0 mm

Full size image
Fig. 13
figure 13

Amplitude–frequency curve with excitation frequency ω/2π as control parameter at ωn = 16 rad/s, L = 10 mm, and B = 3 mm, and Hd = 1 mm

Full size image

Figures 14 and 15 are used to analyze the vibration response of abnormal resonance A, and C (fA and fC represent the excitation frequency at A, and C). The waveform and spectrum are used to analyze the frequency components of vibration response. The definition of BPFO (Ball Pass Frequency Outer) can be given by:

$$ {\text{BPFO}} = f\frac{{N_{b} }}{2}\left( {1 - \frac{{d_{b} }}{{d_{bm} }}\cos \alpha_{0} } \right) $$
(34)

where f represents the rotation speed of the screw shaft. The defect is on the outer race of the left bearing of DRACBB. As shown in Figs. 14 and 15, the main frequency of the system is the excitation frequency, and the BPFO (14.13 Hz) can be observed in the enlarged drawing of Figs. 14 and 15.

Fig. 14
figure 14

Vibration response for abnormal resonance peak A at fA = ω/2π = 83.91 Hz, L = 10 mm, and B = 3 mm, and Hd = 1 mm. a Waveform, b Spectrum

Full size image
Fig. 15
figure 15

Vibration response for abnormal resonance peak C fC = ω/2π = 666 Hz, L = 10 mm, and B = 3 mm, and Hd = 1 mm. a Waveform, b Spectrum

Full size image

3.2.1 Effect of defect depth

In this section, the effect of the local defect with different values will be discussed in detail. The defect depths are Hd = 0.001 mm, Hd = 0.01 mm, Hd = 0.015 mm, Hd = 0.02 mm, and Hd = 1 mm, the default defect width is B = 3 mm, the defect length is L = 5 mm. In addition, the defect shape is half-sine.

Figure 16 shows the amplitude–frequency curves of the feed system with excitation frequency as control parameters for different defect depths. As the increase in the defect depth from 0.001 to 1 mm, the bearing fault induced abnormal resonance become more obvious. The corresponding amplitude become larger, and the abnormal resonance region broadens. Except abnormal resonance region, the influence of defect depth is limited.

Fig. 16
figure 16

Amplitude–frequency curve with excitation frequency ω/2π as control parameter at ωn = 16 rad/s, L = 5 mm, and B = 3 mm for different defect depth

Full size image

As shown in Fig. 16, the variation of A is obvious, while abnormal resonance C change slightly. The influenced frequency range at A becomes wider, and the corresponding amplitude becomes larger as the depth of the defect increases. In the enlarge drawing of B, it can be shown in the figure, the amplitude increases from 0.05264 to 0.06983 at ω/2π = 115.4 Hz with the variation of defect depth from 0.01 mm to 1 m.

As shown in Fig. 17, different feature values of displacement response from simulation are compared to characterize the vibration of the system. The expression of the features can be found in [38]. According to (a) and (c), the value of crest factor and kurtosis decrease with the excitation force. For (d) and (e), both PtP and RMS value increase with the excitation force. Especially when the excitation force equals to 5000N, the values of PtP and RMS increase with the defect depth. As shown in Fig. 17b, f, when the excitation forces are 5000N and 8000N, the defect depth equals to 5 μm, the values of impulse factor and shape factor are larger.

Fig. 17
figure 17

The effect of excitation force and defect depth on signal features at ω/2π = 120.6 Hz, ωn = 16 rad/s, L = 5 mm, and B = 3 mm. a Crest factor, b Impulse factor, c Kurtosis, d Peak to Peak value, e Root mean square, f Shape factor

Full size image

3.2.2 Effect of defect length

In this section, the effect of defect length on abnormal resonance will be discussed. The values of defect length are L = 1 mm, L = 2 mm, L = 3 mm, L = 4 mm, L = 5 mm, and L = 8 mm. The default defect geometry is defect width B = 3 mm, and defect depth Hd = 0.05 mm. The amplitude–frequency curve with excitation frequency as control parameter for different defect length are shown in Fig. 18. It can be observed in the enlarged drawing, the value of fault induced abnormal resonance become larger as the defect length increase. In contrast, the effect of defect length on other excitation frequencies is limited.

Fig. 18
figure 18

Amplitude–frequency curve with excitation frequency ω/2π as control parameter at ωn = 16 rad/s, B = 3 mm, and Hd = 1 mm for different defect length L

Full size image

As shown in Fig. 19, for (a) and (c), crest factor and kurtosis value decrease with excitation force. For (d) and (e), PtP and RMS values both increase with the excitation force. Furthermore, the values of PtP and RMS increase more significantly when the excitation force is 5000N and the defect length is larger than 3 mm. For (b) and (f), the values of impulse factor and shape factor are bigger than the surrounding data point when the excitation force is 5000N and the defect length is relatively small (0.5–2 mm).

Fig. 19
figure 19

The effect of excitation force and defect length on signal features. a Crest factor, b Impulse factor, c Kurtosis, d Peak to Peak value, e Root mean square, f Shape factor

Full size image

3.2.3 Effect of motor speed

In this section, the effect of motor speed will be discussed. The value of motor speeds is ωn = 1–20 rad/s. The default defect geometry is L = 5 mm, B = 3 mm, and Hd = 1 mm. In addition, the default defect shape is half-sine.

Figure 20 shows the 3D amplitude–frequency curves of fault free feed system with different values of motor speed. Apart from the primary resonance and motor speed induced resonance, there exists no obvious abnormal resonance. As shown in Fig. 21, the abnormal resonance caused by local defect get obvious at some specific motor speeds such as ωn = 8 rad/s, and ωn = 16 rad/s, which is most obvious at ωn = 16 rad/s. It indicates that the existence of abnormal resonance induced by a local defect is closely related to the excitation frequency, the parameters of the defect, and motor speed.

Fig. 20
figure 20

3-D Amplitude–frequency curve with excitation frequency ω as control parameter at L = 0, B = 0 mm, and Hd = 0 mm for different motor speed ωn

Full size image
Fig. 21
figure 21

3-D Amplitude–frequency curve with excitation frequency ω/2π as control parameter at L = 5 mm, B = 3 mm, and Hd = 1 mm for different motor speed ωn

Full size image

3.2.4 Effect of defect shape

Amplitude–frequency curves and PtP values are used to investigate the effect of different defect shapes. The shapes of defect are rectangle, half-sine, and triangle, which can be shown in Fig. 22, and the corresponding function of each shape can be found in Eqs. (9)–(11). The default defect geometry is L = 5 mm, B = 3 mm, and Hd = 1 mm, where L, B, and Hd represent the length, width, and depth of the defect. Furthermore, the depth and length of them are same. As shown in Fig. 20, by contrast with the scope of the influence of abnormal resonance A, the rectangle is slightly larger than the others. The enlarge drawing of abnormal resonance B shows that the rectangular defect has the largest RMS amplitude. In Fig. 21, for the rectangle case, the PtP value is 0.2924, for the half-sine is 0.2915, for the triangle is 0.2880 (Fig. 23).

Fig. 22
figure 22

Amplitude–frequency curve with excitation frequency ω/2π as control parameter at L = 5 mm, B = 3 mm, and Hd = 1 mm for different defect shape

Full size image
Fig. 23
figure 23

a Schematic of different defect shapes. b Peak to Peak value of different defect shapes when ω/2π = 125.9 Hz

Full size image

4 Conclusion

In this study, with consideration of the motion characteristic of the feed system, the axial stiffness of screw shaft is modeled as time-varying, except the external harmonic excitation applied on the screw nut, the excitation caused by the local defect of support bearing has also been taken into consideration, and then a three-degrees-of-freedom force model is developed to study the dynamic behavior of the feed system. The simulation is conducted under the corresponding two kind of external excitation, based on which, the effects of defect depth, defect length, motor speed, and defect shape on the vibration response of the feed system are discussed. The results show that the modeling method can provide a way to study the fault induced abnormal resonance of the ball screw feed system. The main conclusions are shown as follows:

  1. 1.

    Apart from the primary resonance, the harmonic excitation and bearing fault excitation act synergistically in affecting the abnormal resonance by analyzing the vibration response at the resonance frequency, the system exhibits two frequency components: excitation frequency component and defect frequency component.

  2. 2.

    The depth and length of a defect on DRACBB can increase the amplitude of abnormal resonance A, and the region of fault induced resonance broadens. The length of defect can produce fluctuation of the amplitude–frequency curve near the abnormal resonance point.

  3. 3.

    The speed of the motor plays a key role in affecting the dynamic characteristics and determines the existence of fault induced abnormal resonance. Furthermore, the motor speed can influence the amplitude of abnormal resonance C.