1 Introduction

Ball screws have been used in missiles and aircraft to move control surface [1]. It is also used in machine tools, robots, and many other precision assembly equipment pieces due to its high efficiency, great stiffness, and long service life [2]. The positioning accuracy of ball screw feed system is usually influenced by preload [3], thermal deformation [4], and health condition of each kinematic joint [5]. During the positioning process, the precision of the feed system can be strongly affected by working condition, manufacturing accuracy, and assembly quality. Due to the nonlinear Hertzian contact stress, piecewise restoring force, and deflection angle, the system can exhibit a wide variety of nonlinear dynamics. However, the influence of assembly error on nonlinear dynamic characteristic has been discussed by few papers. In addition, the preload can be changed with the increase in service life. Therefore, it is necessary to study the nonlinear behavior of ball screw feed system to avoid the reduction in positioning accuracy under the complex working conditions. The dynamic characteristics of ball screw have been studied by many researchers under different conditions.

Liu et al. [6] proposed a nine-degree-of-freedom dynamic model of ball screw feed system, the effect of assembly error on the nonlinear dynamics of the system was discussed, and the screw nut in the proposed model had three degrees of freedom. However, the screw nut was also subjected to torsional moment, and the moment should not be ignored. Guo and Yi [7] investigated the relationship between the detected vibration signals and the variation of preload and developed a lumped dynamic model to study the preload variation of the ball screw feed system. Bo et al. [8] developed a mathematical model to predict the structural nature frequency influenced by moving component. Considering the influences of dimension errors of balls in screw nut, Ni and Qi [9] proposed a calculation model to analyze the effect of ball’s dimension error on mechanical properties of a ball screw drive system, and the fatigue life influenced by ball’s machining accuracy was studied. Chen and Tang [10] found that the force of each ball was not same and developed stiffness transition matrices for the ball screw mechanism to study the influence of the contact stiffness. Due to the large friction force, the contact state of each component could change and hence influenced the dynamic characteristics of the ball screw feed system. Using hybrid element method, Zhang et al. [11] theoretically investigated the relationship between ball screw feed system natural frequency and feed rates and pointed out that the resonance may occur when the natural frequency of the feed system was near the torque ripple harmonic frequency of the motor. Dong and Tang [12] established a hybrid model to study the structural dynamics of the ball screw drive and analyzed the axial, torsional, and flexural dynamic behaviors of ball screw feed system by using the method of continuous beam. Wang et al. [13] developed a time-varying dynamic model to investigate the vibration characteristics of multi-degree-of-freedom feed system, the restoring force of screw nut was considered as a piecewise function, and the coupling effects of screw nut position and excitation amplitude were investigated by simulation. Xu et al. [14] presented an analytical restoring force function to study the effect of sliding platform position, external excitation, and nominal contact angles. Moreover, the dynamic response of the system is discussed. High acceleration could cause the large inertial force of the moving components, which lead to the change of the contact stiffness, and bring influence to the dynamic behaviors of the ball screw feed system. Considering the effect of acceleration, Zhang et al. [15] proposed an equivalent dynamic model using lumped parameter method and derived the equivalent axial stiffness of screw nut based on the contact state which is influenced by the variation of inertial force. Moreover, it pointed out that the return tube of a ball screw-driven mechanism has been designed to provide the path for balls rolling in screw nut grooves. Due to the complexity of working environment, the return tube might damage which is caused by high excitation frequency and excitation amplitude. Huang et al. [16] developed an impact–contact formula for the feed system and investigated the transient behavior using finite element method. Due to the complexity of working condition, the contact angle of angular contact ball bearing was not a constant value. Liao and Lin [17] established a three-dimensional expression of balls based on the geometry parameters at different position angles and discussed the effect of radial and axial deformation on the contact deformation, normal force, and contact angle. Due to the machining error, assembly error, and complicated working condition, the distribution of the load distribution of ball screws was unbalanced. Liu et al. [18] established an appropriate transformation coordinate system to analyze the static load distribution of ball nut. Moreover, the effect of initial contact angle and axial load was discussed in detail. In order to analyze the contact load of balls in screw nut when there exists a turning torque caused by an assembly error, Zhao et al. [19] establish a load distribution model. Furthermore, the effect of the elastic creep on transmission accuracy was studied. As the sliding wear of ball nut was the main reason which caused the decrease in preload. Wei et al. [20] proposed a two-body abrasion model to study the variations of wear depths in the axial direction which are directly related to the preload of screw nut. Okwudire and Altintas [21] analytically and experimentally proved that the lateral dynamics of the ball screw feed system could affect the positioning accuracy under the condition of high acceleration. Considering the influence of the deformation of the screw nut and geometry error, Zhou et al. [22] proposed a modified load distribution model. In addition, an experiment was conducted to validate the proposed model. As the increase in velocity and acceleration of the ball screw drives the system, the resonant of the system may degrade the positioning accuracy. Diego et al. [23] developed a high-frequency dynamic model of a ball screw drive feed system. Simultaneously, the frequency variation with different worktable position was studied. Kolar et al. [24] investigated the effect of frame properties on the dynamic characteristics and conducted a cutting experiment to validate the simulation result. To reduce the impact of thermal error and control vibration, lots of theoretical analysis and experimental research had been done by many researchers [25,26,27,28]. Wang et al. [29] established a quasi-static model with consideration of thermal effect and proposed a calculation strategy considering the variation of boundary conditions. Using the proposed method, the temperature field and thermal error were predicted accurately. To obtain the key point transient temperatures, Li et al. [30] presented a random thermal network model. Based on the proposed model, the positioning accuracy could be accurately predicted. Beyond that, using a finite element model, Mi et al. [31] study the dynamic characteristics of the spindle nose of a horizontal machining center during the cutting process.

From literature reviews, the physical model-based methods could obtain the vibration response of the system with consideration of different working parameters. The effect of deflect angle has been rarely studied. Due to the incipient fault and periodic maintenance, the working parameters of screw nut such as geometric error and preload can be changed over time. Furthermore, due to the complexity of working condition, the system can be sensitive to the changed parameters. This can lead to the occurrence of unstable vibration and decrease the stability of the system. However, few papers pay attention to the influence of the variation of working parameters on dynamic characteristics of single nut ball screw with five degrees of freedom. The outline of this paper is as follows: Sect. 2 proposes the five-degree-of-freedom nonlinear dynamic model and introduced the relationship between defection angle and contact deformation. Section 3 reveals the effect of excitation amplitude, deflection angle, the number of balls, and preload by the bifurcation diagram and 3-D frequency spectrum. Section 4 measures the dynamic parameters of system and validated the proposed model by vibration response and amplitude frequency curve. Section 5 lists the conclusions.

2 Dynamic model and governing equations of motion

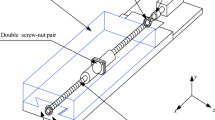
As shown in Fig. 1, the single nut consists of ball nut, balls, and screw shaft. The single nut is preloaded by variable lead; the value of preload force is given in Table 1. Due to the existence of preload and the difference of contact force, the balls in screw nut can be divided into two parts: left section and right section. Therefore, the axial restoring force of a single nut can be deduced into a piecewise function which can be seen in Eq. 15. In this paper, the feed rate is set to 0. Due to the existence of the initial deflection angle, the deformation of each ball in the screw nut can be different, it depends on the deflection angle φ, the distance Li and Lj, which is shown in Fig. 1. Therefore, some balls in screw nut can be deformed due to the unique stress condition, and some balls are not. Because of the nonlinear Hertzian contact force and piecewise restoring function, the vibration system can exhibit a wide variety of dynamics.

Fig. 1
figure 1

Schematic of screw nut

Full size image
Table 1 Parameters for ball screw
Full size table

According to Ref. [32], the expression of the position angle of ith ball in the left section of ball nut and the position angle of the jth ball in the right section of ball nut can be given by

$$ \theta_{i} = \frac{2\pi }{N}\left( {i - 1} \right) $$
(1)
$$ \theta_{j} = \frac{2\pi }{N}\left( {j - 1} \right) $$
(2)

where N is the number of balls per circle in ball nut. As shown in Fig. 1, Li is the axial distance between ith ball and the center of screw nut in the left section, and Lj is the axial distance between jth ball and the center of screw nut in the right section. The expression of Li and Lj can be given by

$$ L_{i} = \left( {N_{c} - \frac{{\theta_{i} }}{2\pi }} \right)P $$
(3)
$$ L_{j} = \frac{{\theta_{j} }}{2\pi }P $$
(4)

P is the lead of screw shaft, and Nc represents the number of loaded circles. According to Refs. [33,34,35], the elastic deformation along the radial direction of ith ball for the left section of ball nut can be formulated as

$$ \delta_{rLi} = \left( {x + u_{i} L_{i} \varphi_{y} } \right)\cos \theta_{i} + \left( {y - u_{i} L_{i} \varphi_{x} } \right)\sin \theta_{i} $$
(5)

and for the right section, the elastic deformation along the radial direction of jth ball of ball nut can be formulated as

$$ \delta_{rRj} = \left( {x + u_{i} L_{j} \varphi_{y} } \right)\cos \theta_{j} + \left( {y - u_{i} L_{j} \varphi_{x} } \right)\sin \theta_{j} $$
(6)

where x and y represent the displacement of screw shaft, and φx and φy are the rocking motions about x- and y-axes Coefficient ui is a dimensionless constant which can be determined by [33]

$$ u_{i} = \left\{ {\begin{array}{*{20}c} { - 1} & {\text{left section}} \\ 1 & {\text{right section}} \\ \end{array} } \right. $$
(7)

The elastic deformation along the axial direction of ith ball for the left section of ball nut can be formulated as [33]

$$ \delta_{zLi} = z + \frac{{d_{m} }}{2}\left( {\varphi_{x} \sin \theta_{i} - \varphi_{y} \cos \theta_{i} } \right) + v_{i} \left( {A\sin \alpha_{0} + z_{p} } \right) $$
(8)

Similarly, the elastic deformation along the axial direction of jth ball for the right section of ball nut can be formulated as [33]

$$ \delta_{zRj} = z + \frac{{d_{m} }}{2}\left( {\varphi_{x} \sin \theta_{j} - \varphi_{y} \cos \theta_{j} } \right) + v_{i} \left( {A\sin \alpha_{0} + z_{p} } \right) $$
(9)

where dm represents the pitch circle diameter. The dimensionless constant vi is dominated on the configuration of rolling elements which can be expressed as follows [33]:

$$ v_{i} = \left\{ {\begin{array}{*{20}c} 1 & {\text{left section}} \\ { - 1} & {\text{right section}} \\ \end{array} } \right. $$
(10)

Therefore, the total contact deformation along the contact angle direction of the ball in the left section of screw nut can be formulated as

$$ \delta_{Li} = \sqrt {\delta_{rLi}^{2} + \delta_{zLi}^{2} } - A $$
(11)

A is the distance between screw shaft raceway curvature center and screw nut raceway curvature center. The total contact deformation along the contact angle direction of the ball in the right section of screw nut can be formulated as

$$ \delta_{Rj} = \sqrt {\delta_{rRj}^{2} + \delta_{zRj}^{2} } - A $$
(12)

In addition, for the left section of screw nut, the contact angle of the ith ball can be written as

$$ \alpha_{Li} = \arctan \left( {{\raise0.7ex\hbox{${\delta_{zLi} }$} \!\mathord{\left/ {\vphantom {{\delta_{zLi} } {\delta_{rLi} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\delta_{rLi} }$}}} \right) $$
(13)

and for the right section of screw nut, the contact angle of the jth ball in the right section of screw nut can be written as

$$ \alpha_{Rj} = \arctan \left( {{\raise0.7ex\hbox{${\delta_{zRj} }$} \!\mathord{\left/ {\vphantom {{\delta_{zRj} } {\delta_{rRj} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\delta_{rRj} }$}}} \right) $$
(14)

According to Refs. [13, 36, 37], the axial piecewise restoring force function can be formulated as

$$ F_{NZ} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = \left\{ {\begin{array}{*{20}c} {K\sum\limits_{i = 1}^{N} {\delta_{iL}^{3/2} \sin \alpha_{Li} } - K\sum\limits_{j = 1}^{N} {\delta_{jR}^{3/2} \sin \alpha_{Rj} } } & { - z_{p} \le z \le z_{p} } \\ {K\sum\limits_{i = 1}^{N} {\delta_{Li}^{3/2} \sin \alpha_{Li} } } & {z > z_{p} } \\ { - K\sum\limits_{j = 1}^{N} {\delta_{Rj}^{3/2} \sin \alpha_{Rj} } } & {z < - z_{p} } \\ \end{array} } \right. $$
(15)

where K is the Hertzian contact stiffness between balls and races, which can be calculated by the method according to Ref. [38]. Furthermore, the restoring force along x- and y-axis can be formulated as

$$ F_{Nx} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = K\sum\limits_{i = 1}^{N} {\delta_{Li}^{3/2} } cos\alpha_{Li} \cos \theta_{i} + K\sum\limits_{j = 1}^{N} {\delta_{Rj}^{3/2} } cos\alpha_{Rj} \cos \theta_{j} $$
(16)
$$ F_{Ny} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = K\sum\limits_{i = 1}^{N} {\delta_{Li}^{3/2} } \cos \alpha_{Li} \sin \theta_{i} + K\sum\limits_{j = 1}^{N} {\delta_{Rj}^{3/2} } \cos \alpha_{Rj} \sin \theta_{j} $$
(17)

The restoring moments about x- and y-axis caused by the deformation of balls in screw nut can be expressed as follows:

$$ \begin{aligned} &M_{Nx} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) \hfill \\ &= K\sum\limits_{i = 1}^{N} {\delta_{Li}^{3/2} \left( {\frac{{d_{m} }}{2}\sin \alpha_{Li} + L_{i} \cos \alpha_{Li} } \right)} \sin \theta_{i} \hfill \\ & \quad + K\sum\limits_{j = 1}^{N} {\delta_{Rj}^{3/2} \left( {\frac{{d_{m} }}{2}\sin \alpha_{Rj} - L_{j} \cos \alpha_{Rj} } \right)} \sin \theta_{j} \hfill \\ \end{aligned} $$
(18)
$$ \begin{aligned} &M_{Ny} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) \hfill \\ & = K\sum\limits_{i = 1}^{N} {\delta_{Li}^{3/2} \left( { - \frac{{d_{m} }}{2}\sin \alpha_{Li} - L_{i} \cos \alpha_{Li} } \right)} \cos \theta_{i} \hfill \\ &\quad + K\sum\limits_{j = 1}^{N} {\delta_{Rj}^{3/2} \left( { - \frac{{d_{m} }}{2}\sin \alpha_{Rj} + L_{j} \cos \alpha_{Rj} } \right)} \cos \theta_{j} \hfill \\ \end{aligned} $$
(19)

Considering the nonlinear contact restoring force and piecewise restoring force, the equivalent dynamic model of screw nut can be simplified as a five-degree-of-freedom mass–spring–damping model which is shown in Fig. 2. According to the analysis of restoring force and restoring moment along x, y, z, φx, and φy directions, the governing equations of motion for screw nut with five degrees of freedom can be written as follows:

$$ m\ddot{x} + c_{y} \dot{x} + F_{Nx} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = mg + F_{x} \left( t \right) $$
(20)
$$ m\ddot{y} + c_{y} \dot{y} + F_{Ny} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = F_{y} \left( t \right) $$
(21)
$$ m\ddot{z} + c_{z} \dot{z} + F_{NZ} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = F_{z} \left( t \right) $$
(22)
$$ I_{x} \ddot{\varphi }_{x} + c_{y} \dot{\varphi }_{x} + M_{Nx} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = M_{x} $$
(23)
$$ I_{y} \ddot{\varphi }_{y} + c_{y} \dot{\varphi }_{y} + M_{Ny} \left( {x,y,z,\varphi_{x} ,\varphi_{y} ,t} \right) = M_{y} $$
(24)
Fig. 2
figure 2

A lumped spring mass model schematic of ball screw

Full size image

where an overdot describes time differentiation; m represents the mass of screw shaft; cy and cz represent the viscous damping coefficient along the radial and axial directions. The influence of damping originated from the viscous damping is suitable for the structural characteristics of the proposed model [39]; the value of cy and cz can be identified by the test of vibration response, which is shown in Sect. 4. Fx, Fy, and Fz represent the external load. In this study, the expression of external force satisfies Fx = Fy = Fz = F0sinωt, where F0 is the excitation amplitude and ω represents the excitation frequency. Mx and My are the external moment and satisfy Mx = My = lF0sinωt, where l is the arm of force and satisfies l = 0.5L.

3 Results and discussion

In this section, the numerical solution to the governing equations of the proposed dynamic model is archived by fourth-order Runge–Kutta method. The parameters of the studied ball screw are listed in Table.1. In order to accelerate the convergence of calculation, the initial condition for the differential equations is set to [\(\dot{\text{x}}\), x,\(\dot{\text{y}}\), y,\(\dot{\text{z}}\), z, φx, φy] = [− 3.5741 × 10−4 mm, − 3.4863 × 10−4 mm/s, − 9.6292 × 10−4 mm, − 3.5542 × 10-4 mm/s, − 2.0984 × 10−4 mm, − 1.0713 × 10−4 mm/s, − 3.8483 × 10−4 mm, − 8.5445 × 10−4 mm/s, 4.5331 × 10−4 mm, 1.9655 × 10−4 mm/s]; the values are determined by the mean value of the steady-state solution. In this study, a steady state for a differential equation is a solution where the nature of the motion does not change over time. Considering the time consumption and the required computational accuracy, the time step is set to 5 × 10−6 s, and the absolute tolerance and the relative tolerance are set to 10–5[mm, mm, mm, rad/s, rad/s] and 10–5, respectively. In order to reflect the energy of vibration signal, the root-mean-square value (RMS) is employed to express the amplitude instead of conventional amplitude in amplitude frequency curve (only in Fig. 15). For a vibration response of N values {x1, x2,…,xN}, the RMS value is [40, 41]

$$ {\text{RMS}} = \sqrt {\frac{1}{N}\left( {\left( {x_{1} - \overline{x}} \right)^{2} + \left( {x_{2} - \overline{x}} \right)^{2} + \cdots + \left( {x_{N} - \overline{x}} \right)^{2} } \right)} $$
(25)

where \(\stackrel{\mathrm{-}}{\text{x}}\) represents the mean value of {x1, x2,…,xn}. The RMS value is only used in the amplitude frequency curve, the amplitudes are presented in the bifurcation diagram, and 3-D spectrum has a conventional amplitude which can be defined by Poincaré section and fast Fourier transform.

3.1 Effect of excitation amplitude

Excitation amplitude is one of the most significant parameters that influence the dynamic behavior of vibration system. In this subsection, the dynamic behaviors are investigated by bifurcation diagram and 3-D spectrum with excitation amplitude and excitation frequency as control parameters. The waveform, spectrum, phase diagram and Poincaré section are used to analyze the complex dynamic behavior at some specific points.

The corresponding bifurcation diagrams of the vibration system with excitation frequency as control parameter under different excitation amplitude (F0 = 3000 N, F0 = 6000 N, F0 = 9000 N, F0 = 12000 N, F0 = 15000 N) are shown in Fig. 3. With the increase in excitation amplitude, the vibration system exhibits a wide variety of dynamic behaviors including chaotic motion, quasiperiodic motion, and period-n motion. In the range of ω ∈ [100, 610]rad/s, with the increase in excitation amplitude, more jump discontinuous phenomena appear, and the system exhibits chaotic motion in this interval. In the range of [610, 760]rad/s which is near resonance frequency, the extent of chaotic motion increases markedly, and the chaotic characteristics strengthen. This indicates that the excitation amplitude has impacts on the dynamic behavior of vibration system. Increasing the excitation amplitude, in the range of [960, 1210]rad/s, the influence range of chaotic motion relative to the whole excitation frequency broadens. With a further increase in the excitation frequency, the motion of the system changed from simple period-1 motion to quasiperiodic motion and chaotic motion in the range of [1350, 1730]rad/s.

Fig. 3
figure 3

Bifurcation diagrams with excitation frequency ω as the control parameter at φ = 0°, N = 23, and preload = Fp for different excitation amplitudes F0

Full size image

The bifurcation diagram of the system at F0 = 15000 N is exhibited in Fig. 4. The system jumps from one to the other at relatively lower excitation frequency of interval T1. In the range of T1, the system exhibits a narrow quasiperiodic motion and chaotic motion. As excitation frequency is increased, the system shows chaotic motion in the range of T2. Increasing the excitation frequency, the system exhibits period-n and chaotic motion in the interval T3. By increasing excitation frequency further, after experiencing chaotic motion in the range of T4, the motion of the system from simple period-1 motion in the interval T5 enters period-n and quasiperiodic motion in the range of T6, although at some region the system exhibits chaotic motion, finally to period-1 motion at T7.

Fig. 4
figure 4

Bifurcation diagrams with excitation frequency ω as the control parameter at φ = 0°, N = 23, and preload = Fp for F0 = 15000 N

Full size image

The 3-D frequency spectrum with respect to excitation frequency for different excitation amplitude is illustrated in Fig. 5. At low excitation amplitude, the fundamental frequency f is the dominant frequency component. As the excitation amplitude is increased, the continuous frequency component appears in the interval [610, 760]rad/s and frequency multiplication (2f,3f) becomes more obvious. Furthermore, frequency demultiplication (4f/5) appears when F0 = 9000 N, and the main frequency changes from the fundamental frequency f to frequency demultiplication (4f/5) in the range of [1350, 1700]rad/s when F0 > 9000 N.

Fig. 5
figure 5

3-D frequency spectrums for different excitation amplitudes with excitation frequency ω as the control parameter at φ = 0°, N = 23 and preload = Fp for a F0 = 3000 N, b F0 = 6000 N, c F0 = 9000 N, d F0 = 12000 N, e F0 = 15000 N

Full size image

To further investigate the effect of excitation amplitude on dynamic behavior of the system, the dynamic response is illustrated with excitation amplitude F0 as control parameter for different excitation amplitudes in Fig. 6. In Fig. 6a1, the motion of the system exhibits simple period-1 and period-3 motion in interval T1, and the main frequency is the fundamental frequency f in Fig. 6b1. With the increase in excitation amplitude, the system shows quasiperiodic and chaotic motion in the range of T2, and the vibration system shows continuous frequency component. As shown in Fig. 6a2 and a3, the system exhibits simple period-1 motion at T1 and quasiperiodic motion in interval T2. Beyond that, as shown in Fig. 6b3, 3f/10 becomes the main frequency as an excitation amplitude is F0 > 8600 N.

Fig. 6
figure 6

Dynamic responses of the system with excitation amplitude F0 as control parameter at φ = 0°, N = 23 and preload = Fp for ω = 360 rad/s, ω = 1000 rad/s and ω = 1460 rad/s. a Bifurcation diagram; b 3-D frequency spectrum

Full size image

Figure 7 shows the corresponding vibration response at F0 = 3000 N and F0 = 15000 N when ω = 1000 rad/s. In Fig. 7c1, the Poincaré section shows only one point and the phase diagram shows a closed circle, which further proves that the system exhibits a simple period-1 motion. In Fig. 7c2, there exist finite points in the Poincaré section and the phase diagram is regular, where the system exhibits quasiperiodic motion. The comparison of vibration response between F0 = 9000 N and F0 = 15000 N at ω = 1460 rad/s is shown in Fig. 8, where the system presents quasiperiodic motion at F0 = 15000 N. However, the 2-frequency quasiperiodic motions are rare and interesting observations in mechanical system. The similar phenomena in machine tool vibrations can be observed in Ref. [42] and Ref. [43]. Figure 9 shows the comparison between F0 = 12000 N and F0 = 15000 N at ω = 1590 rad/s. When F0 = 15000 N, the waveform loses the periodicity in Fig. 9a2, and the continuous spectral appears in Fig. 9b2. As can be seen in Fig. 9c2, there exists infinite point in the Poincaré section, and the phase diagram is irregular and loses periodicity, which illustrates that the system presents chaotic motion at this point.

Fig. 7
figure 7

Vibration responses at φ = 0°, N = 23, ω = 1000 rad/s and Preload = Fp for F0 = 3000 N and F0 = 15000 N. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image
Fig. 8
figure 8

Vibration responses at φ = 0°, N = 23, and ω = 1460 rad/s and Preload = Fp for F0 = 9000 N and F0 = 15000 N. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image
Fig. 9
figure 9

Vibration responses at φ = 0°, N = 23, ω = 1590 rad/s and Preload = Fp for F0 = 12000 N and F0 = 15000 N. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image

Therefore, at relative low excitation amplitude, the vibration system exhibits less nonlinear dynamic properties. In addition, except the region near resonance frequency, the motion of the system exhibits simple period-1 motion. When the excitation amplitude becomes higher, the system presents a wide variety of dynamic behaviors. These further proved that the excitation amplitude has a considerable impact on the dynamic characteristic of the system.

3.2 Effect of deflection angle

In the previous studies, the deflection angle of ball screw is often ignored. However, due to human error and assembly error the deflection angle is inevitable to some extent. Considering the complex working conditions, the investigation of defection angle on nonlinear dynamic characteristics is crucial. In this subsection, the nonlinear dynamics of the system with deflection angle and excitation frequency as control parameter are examined.

The comparison of dynamic response between φ = 0° and φ = 0.5° is shown in Fig. 10. As shown in Fig. 10a1, the vibration system exhibits simple period-1 motion in the interval T1, and in Fig. 10b1 the main frequency is the fundamental frequency f. As the excitation frequency is increased, the system exhibits quasiperiodic motion in the range of T2, and frequency demultiplication (f/5, 2f/5, 3f/5) is shown in Fig. 10b1. Increasing the deflection angle from 0° to 0.5°, the nonlinear characteristics strengthen. As seen in Fig. 10a2, the system shows period-1 motion in the range of T1, experiencing period-1 and period-5 motion in the range of T2, to quasiperiodic motion in the interval T3. It can be seen in Fig. 10b2 that the fundamental frequency is the dominant frequency component, and the frequency demultiplication (f/5, 2f/5, 3f/5, 4f/5) is lower than f. With the increase in excitation amplitude, the motion of system enters quasiperiodic motion in the interval [1047, 1090]rad/s. Furthermore, no complicated chaotic motion appears.

Fig. 10
figure 10

Dynamic responses of the system with excitation frequency ω as control parameter at F0 = 6000 N, N = 23 and preload = Fp for φ = 0° and φ = 0.5°. a Bifurcation diagram; b 3-D frequency spectrum

Full size image

In order to further study the effect of deflection angle on dynamic response, Figure 11 shows the corresponding bifurcation diagram and 3-D frequency spectrum with deflection angle as control parameter at ω = 1008 rad/s and ω = 1050 rad/s. It can be seen in Fig. 11a1 and b1, after experiencing a short period-1 motion at relatively small deflection, the system enters quasiperiodic motion in the interval T1, the main frequency is demultiplication frequency 3f/5, and the fundamental frequency f is the second largest. Increasing the deflection angle, the motion of the system presents period-1 motion again in the range of T2, and the fundamental frequency f becomes the largest frequency component. By increasing the deflection angle further, the system enters quasiperiodic motion, and demultiplication frequency 3f/5 becomes the dominant frequency in the interval T3. Similarly, as shown in Fig. 11a2, the system exhibits simple period-1 motion in the interval T1, and the system presents two types of motion state at T2, i.e., period-1 motion and period-5 motion. Moreover, the fundamental frequency f is the dominant frequency component and the demultiplication frequency component 2f/5 is the second largest which is shown in Fig. 11b2. The comparison of vibration response between φ = 0° and φ = 0.02° at ω = 1050 rad/s is shown in Fig. 12. As seen in the figure, with the increase in deflection angle, the motion of the system changed from simple period-1 motion to quasiperiodic motion. Moreover, the comparison of vibration response between φ = 0° and φ = 0.5° at ω = 1008 rad/s is shown in Fig. 13 which indicates that the increase in deflection leads the motion of the system to change from period-1 motion to quasiperiodic motion.

Fig. 11
figure 11

Dynamic responses of the system with deflection angle φ as control parameter at F0 = 6000 N, N = 23 and Preload = Fp for ω = 1008 rad/s and ω = 1050 rad/s. a Bifurcation diagram; b 3-D frequency spectrum

Full size image
Fig. 12
figure 12

Vibration responses at N = 23, F0 = 6000 N ω = 1050 rad/s and preload = Fp for φ = 0° and φ = 0.02°. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image
Fig. 13
figure 13

Vibration responses at N = 23, F0 = 6000 N ω = 1008 rad/s and preload = Fp for φ = 0° and φ = 0.5°. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image

3.3 Effect of the number of balls

The number of balls is closely corresponding to the required rigid and the lead of screw shaft and then significantly changes the dynamic characteristics of ball screw. Because the range of working frequency is fixed, it is important to determine a suitable number to guarantee the dynamic performance of the system. In this subsection, the dynamic responses are exhibited with respect to excitation frequency. To further study the effect of the number of balls on the dynamic characteristic, the bifurcation diagrams with different numbers of balls (N = 10, N = 23, N = 36) are shown in Fig. 14. It can be seen in the figure that chaotic motion, quasiperiodic motion, and period-n motion can make a distinction between each other, and the critical transformation frequency among different kinds of motions can be identified. As the decrease in the number of balls, all three cases present chaotic motion near the resonance frequency, and the corresponding resonance frequency is reduced. Moreover, at the excitation frequency which is lower than resonance frequency, jump discontinuous phenomena can be observed repeatedly.

Fig. 14
figure 14

Bifurcation diagrams with excitation frequency ω as the control parameter at, F0 = 6000 N, φ = 0°, and preload = Fp for N = 10, N = 23 and N = 36

Full size image

Depending on the variation of stiffness caused by different numbers of balls, the resonance frequency increases with the number of balls. As shown in Fig. 15, the resonance frequency and sub-harmonic resonance frequency increase, and the peak value of amplitude frequency curves enhances. In order to further illustrate the influence of the number of balls, Fig. 16 presents the corresponding bifurcation diagrams at relative low excitation frequency ω ∈ [100, 500]rad/s. In Fig. 16a, in the interval T1, the response repeatedly shows jump discontinuous phenomenon, and the system exhibits period-1 and period-2 motion. Increasing the excitation frequency further, the system exhibits period-n and chaotic motion in the range of T2. As seen in Fig. 16b, when the number of balls decreases from N = 36 to N = 10, the system exhibits a wide variety of dynamic behaviors in the range of ω ∈ [100, 500]rad/s. In the interval T1, the motion of the system is period-1. As the increase in excitation frequency, different motion states can be observed, such as period-n, quasiperiodic, and chaotic motion in the range of T2. After experiencing chaotic motion in interval T3, the motion of the system enters period-1 and chaotic motion in the range of T4. The corresponding 3-D frequency spectrums are shown in Fig. 17, and the continuous frequency components can be distinguished from other discrete frequency components, as shown in Fig. 17b.

Fig. 15
figure 15

Amplitude frequency curve at N = 23, F0 = 6000 N, φ = 0°, and preload = Fp for the number of balls N = 10, N = 23 and N = 36

Full size image
Fig. 16
figure 16

Bifurcation diagrams with excitation frequency ω as the control parameter at φ = 0°, F0 = 6000 N, and preload = Fp for different numbers of balls. a N = 36, b N = 10

Full size image
Fig. 17
figure 17

3-D frequency spectrums with excitation frequency ω as the control parameter at φ = 0°, F0 = 6000 N, and preload = Fp for different numbers of balls. a N = 36, b N = 10

Full size image

3.4 Effect of preload

By creating a load between screw shaft and ball nut, a preload can bring greater stiffness to ball screw. Therefore, the displacement of structure can be reduced when the system is under external force. In this subsection, to investigate the influence of preload on the dynamic behaviors, the preload Fp and excitation frequency ω are chosen as control parameter. The corresponding 3-D bifurcation diagrams with respect to excitation frequency are shown in Fig. 18; five different values of the preload, i.e., preload = Fp, preload = 1.2Fp, preload = 1.4Fp, preload = 1.6Fp, and preload = 1.8Fp, are studied. With the decrease in preload, the system exhibits different kinds of motion states. The system only exhibits simple period-1 motion and quasiperiodic motion when the preload ≥ 1.6Fp, and the main frequency in Fig. 19d and e is the fundamental frequency f. Decreasing the preload from 1.4Fp to 1.2Fp, as shown in Fig. 18, the interval of quasiperiodic and chaotic motion relative to the whole excitation frequency broadens, and frequency demultiplication (4f/13) appears as shown in Fig. 19b and c. By further decreasing the preload from 1.2Fp to Fp, the region of period-n, quasiperiodic, and chaotic motion continuously broadens, and continuous spectrum appears as shown in Fig. 19a. This indicates that lower preload can degrade the dynamic performance of ball screw in some specific excitation frequency range.

Fig. 18
figure 18

Bifurcation diagrams with excitation frequency ω as the control parameter at N = 23, F0 = 15000 N and φ = 0° for different preload. a Preload = Fp, b preload = 1.2Fp, c preload = 1.4Fp, d preload = 1.6Fp, e preload = 1.8Fp

Full size image
Fig. 19
figure 19

3-D frequency spectrum with excitation frequency ω as control parameter at N = 23, F0 = 15000 N and φ = 0° for different preload. a Preload = Fp, b preload = 1.2Fp, c preload = 1.4Fp, d preload = 1.6Fp, e preload = 1.8Fp

Full size image

As shown in Fig. 20, in order to further investigate the influence of preload, the dynamic response at ω = 1585 rad/s and ω = 1585 rad/s is exhibited with preload as control parameter. It can be seen from Fig. 20a1 and Fig. 20b1 that the system exhibits chaotic motion in the range of T1. The corresponding 3-D frequency spectrum shows that the fundamental frequency component f is the second largest, and continuous frequency component appears in the interval T1. As the increase in preload, the system enters quasiperiodic motion in the range of T2, except at some points where the motion of the system is period-1, the continuous frequency component disappeared, and 3f/10 becomes the dominant frequency component. Increasing the preload further, the system presents simple period-1 motion in the range of T3, and the main frequency in 3-D spectrum is the fundamental frequency f. Similarly in Fig. 20a2 and b2, after experiencing quasiperiodic motion in the range of T1, the system enters period-1 motion in the interval T2, and the main frequency changed from frequency demultiplication (6f/25 and 7f/25) in the range of T1 to fundamental frequency f in the range of T2. The dynamic behavior of quasiperiodic motion at ω = 1680 rad/s and preload = Fp is exhibited in Fig. 21, which presents that the system exhibits quasiperiodic motion at this point.

Fig. 20
figure 20

Dynamic responses of the system with deflection angle preload as control parameter at F0 = 15000 N, and N = 23 for ω = 1585 rad/s, and ω = 1680 rad/s. a Bifurcation diagram; b 3-D frequency spectrum

Full size image
Fig. 21
figure 21

Vibration responses at preload = Fp, N = 23, F0 = 15000 N and φ = 0° for ω = 1680 rad/s. a Waveform, b frequency, c phase diagram and Poincaré section

Full size image

4 Experimental verification

To validate the proposed dynamic model and obtain the dynamic parameters used in the previous section, an experiment is set up in this section. The top view schematic of experiment setup is shown in Fig. 22. As seen in the figure, the ball screw (THK SBN4016) is fixed on a test rig. The parameters of ball screw are listed in Table 1. In the experiment, the deflection angle of screw shaft is generated by a hydraulic jack acting on the right end of screw shaft, and the dial gauge is used to measure the static displacement in the circumferential direction. The vibration response is measured by the accelerometer (Sinocera CA-YD-189) mounted on the right end of screw shaft. Using an electromagnetic shaker (Sinocera JZK-50) to generate harmonic excitation, a piezoelectric force senor (Sinocera CL-YD-331A) is used to measure the excitation amplitude acting on screw shaft along z-axis. As shown in the figure, the signal collection and generating system consist of a power amplifier (YE5874A), a signal generator (Sinocera YE1311), a charge amplifier (Sinocera YE5874A), a data collection system (DH5956), and a PC.

Fig. 22
figure 22

Experimental setup

Full size image

In this study, the half-power bandwidth method is employed to extract damping ratios from the frequency response function. The frequency response function along y and z directions can be obtained by impact test, and the result is shown in Fig. 23. According to the equation in Ref. [44], the expression of damping ratio ζ can be given by

$$ \zeta = \frac{{\omega_{2} - \omega_{1} }}{{2\omega_{dm} }} $$
(26)
Fig. 23
figure 23

Frequency response function obtained from impact test in two directions; a x-axis. b z-axis

Full size image

where ωdm represents the nature frequency of screw nut, ω1 and ω2 are the half-power frequency when the corresponding amplitude A = 0.707Amax, where Amax represents the corresponding amplitude of ωdm. Therefore, the results are shown in Fig. 23, ωy1 = 65.3 Hz, ωy2 = 66.935 Hz, ωydm = 65.9 Hz, ωz1 = 96.85 Hz, ωz2 = 101.2 Hz, ωzdm = 102 Hz. Based on the measurement results above, the dimensionless damping ratio along y-axis ζy = 0.0124 and z-axis ζz = 0.0213 can be estimated. The viscous damping coefficient c used in the previous section can be calculated by c = 4πζω0m; hence, the value of cy and cz can be evaluated. Furthermore, the amplitude frequency curve of screw nut from simulation and experiment is compared in Fig. 24. The difference of the nature frequency from experiment and simulation is 1.6%, which validates the proposed model. In order to verify the proposed method with the consideration of deflection angle, two values of excitation frequency, i.e., ω/2π = 74 Hz and ω/2π = 126 Hz, are selected to compare the vibration response between experiment and simulation, which is seen in Fig. 25. According to the measuring result of dial gauge, the deflection angle equals 0.7162°. The comparison of vibration response between the selected two points is shown in Fig. 25.

Fig. 24
figure 24

Amplitude frequency curve obtained from impact test at F0 = 50 N. a Experimental result. b Simulation result

Full size image
Fig. 25
figure 25

Vibration response between simulation and experiment. a ω/2π = 74 Hz, F0 = 50 N. b ω/2π = 126 Hz, F0 = 50 N

Full size image

5 Conclusion

In this paper, a five-degree-of-freedom dynamic model of variable lead preloaded single nut ball screw considering the effect of deflection angle is proposed; the proposed model is investigated by the numerical method. The relationship between the deflection angle and the contact deformation of each ball is given. The effects of different system parameters, i.e., excitation amplitude, deflection angle, the number of balls, and preload, are quantitatively studied. Bifurcation diagram, 3-D frequency spectrum, and RMS value amplitude frequency curves with respect to different parameters are used to study the influence on dynamic behaviors. To validate the proposed dynamic model and estimate the dynamic parameters, a series of experiments are conducted. The main conclusions of this study are listed as follows:

  1. (1)

    Based on different system parameters, the system presents various nonlinear dynamics, namely period-n motion, quasiperiodic motion, chaotic motion, and jump discontinuity phenomenon.

  2. (2)

    In the whole range of excitation frequency, the excitation amplitude has impacts on system dynamic response. In contrast, for other system parameters, i.e., preload and the number of balls, the influenced range of excitation frequency is relatively limited.

  3. (3)

    The system parameters can affect the dynamic characteristic by different ways. Excitation amplitude and deflection angle can enhance the nonlinear properties of the system. In contrast, the preload can improve dynamics. Furthermore, the number of balls can change the resonance frequency of the system.