1 Introduction

The ball screw feed system (BSFS), as an important functional component, has been widely used to improve the machining accuracy and efficiency of Computer Numerical Control (CNC) machine tools [1,2,3]. The dynamic characteristics of the BSFS have an important influence on the machining stability of a machine tool [2] and subsequently affect good surface finish and high-dimensional accuracy of components [4,5,6].Therefore, it is significant to research the dynamic characteristics of the BSFS.

Many scholars have carried out dynamic modeling and dynamic characteristic analysis on the feed system in recent years. Zhang [7] used the energy method to establish the dynamic model and dynamic equation of the BSFS and discussed the influence of contact stiffness, lead, speed and table mass on the vibration amplitude of the machine tool. Bertolino et al. [8, 9] established a simplified dynamic model with lumped parameters based on the BSFS in electro-mechanical actuators (EMA). The influence of clearance and preload on the performance of the ball screw can be considered by this dynamic model, so as to realize the fault diagnosis based on the dynamic model. Poignet et al. [10] simplified the BSFS into a series–parallel system of 8 masses and 7 springs, thereby analyzing the dynamic characteristics of the feed system. Shiau [11] derived the dynamic equation of the BSFS during the machining process from Lagrange's equation and analyzed the influence of nut feed speed, ball rotation speed, and grinding feed depth on the surface roughness of the workpiece. Feng and Pan [12] analyzed the elastic force of the ball screw nut and the ball based on the Hertz contact theory and established the dynamic model of the BSFS by using the lumped parameter method. Gu and Cheng [13] established the dynamic model of the CNC machine tool feed system, and obtained the dynamic response of the ball screw by the Runge–Kutta method. The inertia effect of the high-speed moving nut has been mainly studied on the dynamic response of the ball screw feed system. Moreover, some researchers [14,15,16,17] also considered the contact stiffness of the ball screw pair; the vibration characteristics of the feed system are studied based on the lumped mass parameter method.

The frictional heat of the ball screw will cause thermal deformation, which will directly affect the motion performance of the ball screw. Therefore, the friction between the ball and the track is also the research focus of the BSFS [18,19,20]. Gupta [21] first derived the dynamic model of the rolling bearing system under sliding, and studied the transient motion of the rolling bearing under the condition of elastic lubrication. Murase [22] studied the static friction force of the ball screw pair under different axial loads and obtained the static friction coefficient of the ball screw under the condition of oil lubrication. Xu et al. [23] introduced a creep analysis model to predict the friction of ball screws based on roll contact theory and provided a theoretical basis for reducing the friction between the balls. Yung and Yan [24] derived a new set of expressions for the rolling friction of a viscoelastic sphere rolling on a hard plane. Bowen et al. [25] presented a method of identifying the friction parameters in a ball-screw energy-harvesting shock absorber system for subsequent computational simulation, but the influence of frictional heat on the system is ignored.

Furthermore, there are also many research on the thermal model of the BSFS. Week and Zangs [26] used the finite element method-possibilities and limitations to compute the thermal of machine tools. Xu et al. [27] used the finite element method to estimate the thermal error of the ball screw system and effectiveness of the air cooling system. Li et al. [28] provided a comprehensive error compensation method for the time-varying positioning error of machine tools based on simulation and experimental analysis. Han et al. [29] presented a new approach for building an effective mathematical thermal error for machine tools which is capable of improving the accuracy of the machine tool effectively. Huang et al. [30] studied further the relationship between thermal deformation and heat quantity through modeling the thermal deformations of stretching bar and bending beam using heat quantity as the independent variable, and the stretching model is verified based on finite element method. Zhang et al. [31] presented different prediction models for positioning error of ball screw feed drive system based on the mounting condition.

However, there are very little researchers to perform the dynamic analysis of the BSFS based on thermal deformation. Xu et al. [32] proposed a novel lumped dynamic model accounting for the analytical piecewise restoring force function involving the overall axial deformation. Then, a comprehensive dynamic model of a BSFS considering nonlinear kinematic joints is introduced to investigate the varying dynamic characteristics when the worktable is subjected to combined load from six directions. The model is promising for comprehension of machine dynamic behavior and for the development of sophisticated control strategies through experiments [33]. These two articles study screw dynamics, but neither consider the effect of thermal deformation. Liu et al. [34] proposed the optimization method of the thermal boundary conditions, including the thermal loads, the convective heat transfer coefficient, and the thermal contact resistance to improve the simulation accuracy of the traditional transient thermal characteristics analysis model of the ball screw feed drive system. Li et al. [35] presented an improved random thermal network model subjected to dynamic thermal excitation for calculating real-time transient temperatures of ball-screw systems. These two articles studied the thermal deformation of the ball screw but did not study the dynamics of the ball screw. Liu et al. [36] proposed a comprehensive coupled CNC lathe spindle-bearing model considering the thermal effect to predict the dynamic characteristics of the system. Although Liu studies thermodynamics, it studies the spindle rather than the ball screw. Therefore, we study the thermodynamics of the ball screw. In this paper, the dynamic model of the BSFS considering thermal deformation as shown in Fig. 1 is established, and the dynamic characteristics of the BSFS under thermal deformation are studied. The novel dynamic model of the BSFS including bearing joints, screw-nut joints and screw shaft is developed under time varying loads. Through the Hertz contact theory, the relationship between elastic restoring force and axial deformation of bearing joints, screw-nut joints and screw is established, respectively. Moreover, the influence of different system parameters on the BSFS’s dynamic characteristics is discussed.

Fig. 1
figure 1

Ball screw feed system

Full size image

2 Dynamic modeling under thermal deformation

2.1 Analysis for thermal expansion

2.1.1 Heat generation

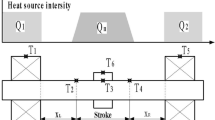
When the BSFS is in the transmission work, the heat is generated from friction heat, and the friction heat is mainly caused by the friction between the ball and the raceway or groove during the working process of the bearing and nut. Therefore, the main heat sources include the front and rear bearings and nut pairs, and the heat generation principle diagram is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of heat generation of ball screw feed system

Full size image

During the working of the ball screw, friction and heat are generated between the bearing balls and the inner and outer rings of the bearing. The friction loss of the bearing is almost entirely converted into heat inside the bearing, which causes the temperature of the bearing to rise. The calorific value of the bearing can be calculated by the following empirical formula [37]:

$$ Q_{{\text{b}}} = 1.047 \times 10^{ - 4} nM_{1} $$
(1)

where Qb is the calorific value of the bearing; n is the speed of the ball screw; M1 is the total friction torque of the bearing.

The preload of the ball screw nut pair will cause friction and heat generation of the nut pair. During the movement of the nut pair on the screw, the ball, the nut and the groove of the screw will rub against each other and produce frictional heat. Then the heat will be transferred to the screw, which causes the temperature of the screw to rise. According to the empirical formula, the friction heat of the nut pair can be obtained by the following formula [38, 39]:

$$ Q_{{\text{n}}} = 0.12\pi nf_{0} v_{0} M_{2} $$
(2)

where Qn is the calorific value of the nut; f0 is the coefficient related to the nut type and lubrication method; ν0 is the kinematic viscosity of the lubricating fluid; M2 is the total friction torque of the nut.

2.1.2 Thermal deformation analysis

From a macro-perspective, the thermal effect of the screw shaft of the BSFS is axial elongation. For the screw shaft, the principle can be shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of thermal expansion analysis of ball screw

Full size image

We consider a very small part of ΔL0 for analysis (ΔL0 is small enough). At time t, the temperature increases from T0 to T(x, t), the length extends to ΔL(x), and the point x moves to x(t). The axial deformation at position x can be obtained by Eq. (3) [40].

$$ x\left( t \right) - x = \int\limits_{0}^{x} {\gamma \left( {T\left( {x,t} \right) - T_{0} } \right){\text{d}}\delta } $$
(3)

where γ is the thermal expansion coefficient.

So the thermal expansion deformation of a ball screw with a length of L can be expressed as:

$$ \Delta L = L\left( t \right) - L = \int\limits_{0}^{L} {\gamma \left( {T\left( {x,t} \right) - T_{0} } \right){\text{d}}x} $$
(4)

2.2 Equivalent mechanical model of the kinematic joints

Research shows that frictional heat is the main heat source of the ball screw feed system and thermal deformation has a greater impact on the contact stiffness; this paper considers the effect of thermal deformation and force deformation on the stiffness of the joint surface, and establishes a more accurate stiffness theoretical model.

2.2.1 The elastic restoring force of double screw-nut joints

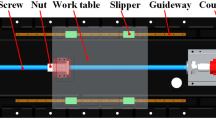
As shown in Fig. 1, when the worktable is subjected to axial load, the axial force is transmitted to the ball screw through the double screw-nut joints. The worktable is directly connected with the nut through the flange, and then the nut transmits the load to the screw through the ball. The balls will produce contact deformation when subjected to axial load, which will directly affect the axial stiffness of the BSFS that requires precision transmission. In the actual machining process of a CNC machine tool, the friction heat generated during the operation of the machine tool will also cause thermal deformation of the nut and then change the dynamic characteristics of the BSFS. This section takes the CJK6130 CNC machine tool as the research object, which is a double screw-nut joints with initial preload. Figure 4 shows the locations of the ball centers and groove curvature centers of the screw-nut joint.

Fig. 4
figure 4

Location changes of the groove curvature centers of the screw-nut joint

Full size image

A preload can eliminate the axial clearance and improve the stiffness of the BSFS. According to Hertz contact theory [41], the relationship between initial deformation δ0n and initial preload Fpn can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\delta_{{0{\text{n}}}} = K_{{\text{n}}} Q_{{0{\text{n}}}}^{2/3} } \\ {Q_{{0{\text{n}}}} = \frac{{F_{{{\text{pn}}}} }}{Z\sin \beta \cos \lambda }} \\ \end{array} } \right. $$
(5)

where Kn denotes the contact deformation coefficient of the double screw-nut joint [42]; Z denotes the number of screw-nut balls;

In Fig. 4, Fa is the axial load, and Qn is the normal load under the axial load; λ is the helix angle of the screw; rn and rs are the curvature radius of the screw-nut and screw, respectively; OnL, OnR and OsL, OsR are the left and right initial groove curvature centers of the screw-nut and screw, respectively; OsL1, and OsR1 are the left and right groove curvature centers of the screw-nut and screw, respectively, when the screw-nut joint bears axial load Fa; OnL2, OnR2 and OsL2, OsR2 are the left and right groove curvature centers of the screw-nut and screw, respectively, when the screw-nut joint occurs thermal deformation; β is the initial contact angle of the screw-nut joint, and ignores the influence of the initial preload on the contact angle; β1L and β1R are the contact angle when the screw-nut joint bears axial load; β2L and β2R are the contact angle when the screw-nut joint occurs thermal deformation. A is the center distance of curvature between nut and screw groove under preload.

According to the geometric relationship, the normal force Qn1 and deformation δnL1 derived from the axial loads of each left ball can be obtained as [43]:

$$ \left\{ {\begin{array}{*{20}c} {F_{{\text{a}}} = Q_{{{\text{n}}1}} Z\sin \beta_{{1{\text{L}}}} \cos \lambda } \\ {\delta_{{{\text{nL}}1}} = A_{{1{\text{L}}}} - A_{0} } \\ {A_{{1{\text{L}}}} = \sqrt {(A\cos \beta )^{2} + (A\sin \beta + \delta_{{x1{\text{L}}}} /\cos \lambda )^{2} } } \\ {\sin \beta_{{1{\text{L}}}} = \frac{{A\sin \beta + \delta_{{x1{\text{L}}}} /\cos \lambda }}{{\sqrt {(A\cos \beta )^{2} + (A\sin \beta + \delta_{{x1{\text{L}}}} /\cos \lambda )^{2} } }}} \\ \end{array} } \right. $$
(6)

where A0 denotes the distance between the center of curvature of the nut and the screw groove in the initial state; A1L denotes the distance between the center of curvature of the left nut and the screw groove when the screw-nut joint bearing an axial load; δx1L denotes the axial deformation of the left screw-nut ball.

Through the Hertz contact theory, the relationship between the elastic restoring force and the axial displacement of left nut under axial load can be expressed as:

$$ F_{{{\text{nL}}1}} = ZK_{{\text{n}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{nL}}1}}^{3/2} \sin \beta_{{1{\text{L}}}} \cos \lambda $$
(7)

Similarly, according to the geometric relationship, the normal force Qn1 and deformation δnR1 of each right ball can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{\text{a}}} = Q_{{{\text{n}}1}} Z\sin \beta_{{1{\text{R}}}} \cos \lambda } \\ {\delta_{{{\text{nR}}1}} = A_{{1{\text{R}}}} - A_{0} } \\ {A_{{1{\text{R}}}} = \sqrt {(A\cos \beta )^{2} + (A\sin \beta - \delta_{{x1{\text{R}}}} /\cos \lambda )^{2} } } \\ {\sin \beta_{{1{\text{R}}}} = \frac{{A\sin \beta - \delta_{{x1{\text{R}}}} /\cos \lambda }}{{\sqrt {(A\cos \beta )^{2} + (A\sin \beta - \delta_{{x1{\text{R}}}} /\cos \lambda )^{2} } }}} \\ \end{array} } \right. $$
(8)

where A1R the distance between the center of curvature of the right nut and the screw groove when the screw-nut joint bearing an axial load; δx1R denotes the axial deformation of the right screw-nut ball. The relationship between the elastic restoring force FnR1 and the axial displacement of right bearing under axial load can be expressed as:

$$ F_{{{\text{nR}}1}} = ZK_{{\text{n}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{nR}}1}}^{3/2} \sin \beta_{{1{\text{R}}}} \cos \lambda $$
(9)

When the machine tool is operating, friction occurs between the nut ball and the screw-nut groove. The friction will generate frictional heat, which will cause thermal deformation of the nut. The locations change of the ball centers and groove curvature centers of the bearing joint as shown in Fig. 4. On the basis of the geometric relationship, the elastic restoring force FnL2 and deformation δnL2 of each right ball after thermal deformation can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{{\text{nL}}2}} = Q_{{{\text{n}}2}} Z\sin \beta_{{2{\text{L}}}} \cos \lambda } \\ {A_{{2{\text{L}}}} = A_{{1{\text{L}}}} - \delta_{{{\text{nb}}}} } \\ {\delta_{{{\text{nL}}2}} = A_{{2{\text{L}}}} - A_{0} } \\ {\sin \beta_{{2{\text{L}}}} = \frac{{A\sin \beta + \delta_{{x{\text{L}}}} /\cos \lambda }}{{A_{{2{\text{L}}}} }}} \\ \end{array} } \right. $$
(10)

where A2L denotes the distance between the center of curvature of the left nut and the screw groove when the screw-nut joint occurring thermal deformation; δxL denotes the axial deformation of the left screw-nut ball under thermal deformation; δnb is the thermal deformation of the nut ball, which can be obtained by Eq. (11):

$$ \delta_{{{\text{nb}}}} = \gamma \int_{0}^{{d_{{\text{b}}} }} {\left( {T_{{\text{n}}} - T_{0} } \right)} {\text{d}}x $$
(11)

where db denotes the diameter of the nut ball; Tn denotes the temperature of the screw -nut during thermal equilibrium; T0 denotes the ambient temperature.

During the operation of the machine tool, the bearings and nuts are heated and deformed. The center of curvature of the inner and outer rings of the bearing and the groove curvature centers of the screw-nut and screw also changes accordingly. In fact, the contact angles of bearings and nuts also will change, but the inner and outer rings and the center of curvature of the bearing and the groove curvature centers of the screw-nut and screw don’t change geometrically. This leads to a lot of unknown angle variables when establishing the relationship of the contact angle, and the equation does not have enough constraints. So the equation about contact angle cannot be solved. Therefore, we simplified the model and assumed that the initial contact angle after thermal deformation is equal to the initial contact angle when thermal deformation is not considered. In Xu's paper [3], regardless of the influence of thermal deformation, their work also didn’t consider the change of contact angle.

Assuming that the contact angle is approximately constant after thermal deformation, that is, β1L is equal to β2L. Through calculation, it is found that δx1L and δxL are linear, so the relationship between δx1L and δxL can be expressed as:

$$ \delta_{{x1{\text{L}}}} = \delta_{{x{\text{L}}}} + 0.3671 \times 10^{ - 6} $$
(12)

According to Hertz contact theory, the relationship between the elastic restoring force FnL2 and the axial displacement of left nut after thermal deforming can be expressed as:

$$ F_{{{\text{nL}}2}} = ZK_{{\text{n}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{nL}}2}}^{3/2} \sin \beta_{{2{\text{L}}}} \cos \lambda $$
(13)

Similarly, the elastic restoring force FnR2 and deformation δnR2 of each right ball after thermal deformation can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{{\text{nR}}2}} = Q_{{{\text{n}}2}} Z\sin \beta_{{2{\text{R}}}} \cos \lambda } \\ {A_{{2{\text{R}}}} = A_{{1{\text{R}}}} - \delta_{{{\text{nb}}}} } \\ {\delta_{{{\text{nR}}2}} = A_{{2{\text{R}}}} - A_{0} } \\ {\sin \beta_{{2{\text{R}}}} = \frac{{A\sin \beta - \delta_{{x{\text{R}}}} /\cos \lambda }}{{A_{{2{\text{R}}}} }}} \\ \end{array} } \right. $$
(14)

where A2R denotes the distance between the center of curvature of the right nut and the screw groove when the screw-nut joint occurring thermal deformation; δxLR denotes the axial deformation of the right screw-nut ball under thermal deformation.

Similarly, the relationship between δx1R and δxR can be expressed as:

$$ \delta_{{x1{\text{R}}}} = \frac{{\left( {\delta_{{x{\text{R}}}} - 0.3671 \times 10^{ - 6} } \right)}}{0.9999} $$
(15)

The relationship between the elastic restoring force FnR2 and the axial displacement of right nut after occurring thermal deformation can be expressed as:

$$ F_{{{\text{nR}}2}} = ZK_{{\text{n}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{nR}}2}}^{3/2} \sin \beta_{{2{\text{R}}}} \cos \lambda $$
(16)

2.2.2 The elastic restoring force of the bearing joints

As shown in Fig. 5, the front bearing of the screw is a pair of angular contact bearings installed back to back, and the rear bearing is a deep groove ball bearing. As we know from the previous article, deep groove ball bearing only bear radial load, so only the angular contact bearings needs to be considered. Angular contact ball bearings feature a preload when installed.

Fig. 5
figure 5

Angular contact support bearing

Full size image

According to Hertz contact theory, the relationship between initial deformation δ0b and initial preload Fpb can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\delta_{{0{\text{b}}}} = K_{{\text{b}}} Q_{{0{\text{b}}}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} } \\ {Q_{{0{\text{b}}}} = \frac{{F_{{{\text{pb}}}} }}{m\sin \alpha }} \\ \end{array} } \right. $$
(17)

where Kb is the contact deformation coefficient of bear; m is number of bearing balls.

Because the bearing has strict symmetry, the upper bearing is selected for analysis. In Fig. 6, Qb is the normal load under axial load; ri and ro are the curvature radius of the bearing inner and outer ring, respectively; OiL, OiR and OoL, OoR are the left and right initial groove curvature centers of the bearing inner and outer ring, respectively; OsL1 and OsR1 are the left and right groove curvature centers of the bearing inner and outer ring, respectively, when the bearing joint bears axial load Fa; OnL2, OnR2 and OsL2, OsR2 are the left and right groove curvature centers of bearing inner and outer ring, respectively, when the bearing joint occurs thermal deformation; α is the initial contact angle of the bearing joint, and ignores the influence of the initial preload on the contact angle; α1L and α1R are the contact angle when the bearing joint bears axial load Fa; α2L and α2R are the contact angle when the bearing joint occurs thermal deformation. B is the center distance of curvature between nut and screw groove under preload.

Fig. 6
figure 6

Location changes of the groove curvature centers of the bearing joint

Full size image

Based on the geometric relationship, the normal force Qb1L and deformation δbL1 of each left ball can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{\text{a}}} = Q_{{{\text{b1L}}}} m\sin \alpha_{{1{\text{L}}}} } \\ {\delta_{{{\text{bL1}}}} = B_{{1{\text{L}}}} - B_{0} } \\ {B_{{1{\text{L}}}} = \sqrt {(B\cos \alpha )^{2} + (B\sin \alpha + \delta_{{x1{\text{L}}}} )^{2} } } \\ {\sin \alpha_{{1{\text{L}}}} = \frac{{B\sin \alpha + \delta_{{x1{\text{L}}}} }}{{\sqrt {(B\cos \alpha )^{2} + (B\sin \alpha + \delta_{{x1{\text{L}}}} )^{2} } }}} \\ \end{array} } \right. $$
(18)

where B0 denotes the distance between the center of curvature of the bearing inner and outer ring in the initial state; B1L denotes the distance between the center of curvature of the left bearing inner and outer ring when the bearing joint bearing an axial load; δx1L denotes the axial deformation of the left bearing ball. The relationship between the elastic restoring force and the axial displacement of left bear under axial load can be expressed as:

$$ F_{{{\text{bL}}1}} = mK_{{\text{b}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{bL}}1}}^{3/2} \sin \alpha_{{1{\text{L}}}} $$
(19)

Similarly, the normal force Qb1R and deformation δnR1 of each right ball can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{\text{a}}} = Q_{{{\text{b1R}}}} m\sin \alpha_{{1{\text{R}}}} } \\ {\delta_{{{\text{bR}}1}} = B_{{1{\text{R}}}} - B_{0} } \\ {B_{{1{\text{R}}}} = \sqrt {(B\cos \alpha )^{2} + (B\sin \alpha - \delta_{{x1{\text{R}}}} )^{2} } } \\ {\sin \alpha_{{1{\text{R}}}} = \frac{{B\sin \alpha + \delta_{{x1{\text{R}}}} }}{{\sqrt {(B\cos \alpha )^{2} + (B\sin \alpha - \delta_{{x1{\text{R}}}} )^{2} } }}} \\ \end{array} } \right. $$
(20)

where B1R denotes the distance between the center of curvature of the right bearing inner and outer ring when the bearing joint bearing an axial load; δx1R denotes the axial deformation of the right bearing ball.

The relationship between the elastic restoring force FbR1 and the axial displacement of right bearing under axial load can be expressed as:

$$ F_{{{\text{bR}}1}} = mK_{{\text{b}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{bR}}1}}^{3/2} \sin \alpha_{{1{\text{R}}}} $$
(21)

The bearing will also undergo thermal deformation under heated. The locations change of the ball centers and groove curvature centers of the bearing joint as shown in Fig. 6. According to the geometric relationship, the elastic restoring force FbL2 and deformation δbL2 of each left ball after thermal deformation can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{{\text{bL}}2}} = Q_{{{\text{b2L}}}} m\sin \alpha_{{2{\text{L}}}} } \\ {B_{{2{\text{L}}}} = B_{{1{\text{L}}}} - \delta_{{{\text{bb}}}} } \\ {\delta_{{{\text{bL}}2}} = B_{{2{\text{L}}}} - B_{0} } \\ {\sin \alpha_{{2{\text{L}}}} = \frac{{B\sin \alpha + \delta_{{x{\text{L}}}} }}{{B_{{2{\text{L}}}} }}} \\ \end{array} } \right. $$
(22)

where B2L denotes the distance between the center of curvature of the right bearing inner and outer ring when the bearing joint occurring thermal deformation; δxL denotes the axial deformation of the left joint ball under thermal deformation; δbb is the thermal deformation of the bearing ball, which can be obtained by Eq. (23):

$$ \delta_{{{\text{bb}}}} = \gamma \int_{0}^{{D_{{\text{b}}} }} {\left( {T_{{\text{b}}} - T_{0} } \right)} {\text{d}}x $$
(23)

where Db denotes the diameter of the bearing ball; Tb denotes the temperature of the bear during thermal equilibrium.

Similar to screw-nut processing method, the relationship between δx1L and δxL can be expressed as:

$$ \delta_{{x1{\text{L}}}} = \frac{{\delta_{{x{\text{L}}}} + 0.69 \times 10^{ - 7} }}{0.9998} $$
(24)

The relationship between the elastic restoring force FbL2 and the axial displacement of left bear after occurring thermal deformation can be expressed as:

$$ F_{{{\text{bL}}2}} = mK_{{\text{b}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{bL}}2}}^{3/2} \sin \alpha_{{2{\text{L}}}} $$
(25)

The elastic restoring force FbR2 and deformation δbR2 of each right ball after thermal deformation can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {F_{{{\text{bR2}}}} = Q_{{{\text{b2R}}}} m\sin \alpha_{{{\text{2R}}}} } \\ {B_{{{\text{2R}}}} = B_{{{\text{1R}}}} - \delta_{{{\text{bb}}}} } \\ {\delta_{{{\text{bR2}}}} = B_{{{\text{2R}}}} - B_{0} } \\ {\sin \alpha_{{{\text{2R}}}} = \frac{{B\sin \alpha + \delta_{{x{\text{R}}}} }}{{B_{{2{\text{R}}}} }}} \\ \end{array} } \right. $$
(26)

where B2R denotes the distance between the center of curvature of the right nut and the screw groove when the screw-nut joint occurring thermal deformation; δxR denotes the axial deformation of the right screw-nut ball under thermal deformation.

Similarly, the relationship between δx1R and δxR can be expressed as:

$$ \delta_{{x1{\text{R}}}} = \frac{{\delta_{{x{\text{R}}}} - 0.6903 \times 10^{ - 7} }}{0.9998} $$
(27)

The relationship between the elastic restoring force FbR2 and the axial displacement of right nut after occurring thermal deformation can be expressed as:

$$ F_{{{\text{bR2}}}} = mK_{{\text{b}}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-\nulldelimiterspace} 2}}} \delta_{{{\text{bR2}}}}^{3/2} \sin \alpha_{{2{\text{R}}}} $$
(28)

2.2.3 The elastic restoring force of the screw shaft

The screw shaft also produces the elastic deformation under the axial load. The deformation occurs at the right side of nut, which is the length from the BSFS end supported by the angular contact ball bearings to the sliding platform as shown in Fig. 1. The relationship between the elastic restoring force and the axial displacement of screw shaft may be expressed as Eq. (29):

$$ F_{{\text{s}}} = \frac{{\pi E\left( {d_{{{\text{s}}0}} - d_{{{\text{sb}}}} \cos \alpha } \right)^{2} }}{{4l_{0} }}\delta_{{{\text{s}}x}} $$
(29)

where E denotes the elastic modulus of the screw material; ds0 denotes nominal diameter of ball screw; dsb denotes nut ball diameter; l0 denotes the distance from the nut to the fixed end of the ball screw.

When the machine tool is running, the feed system causes the temperature of the ball screw to increase under the influence of frictional heat, which causes the ball screw to undergo thermal expansion and deformation. According to the empirical formula of thermal deformation, the axial thermal deformation of the screw δs can be expressed as

$$ \delta_{{\text{s}}} = \int_{0}^{{l_{0} }} {\gamma \left( {T_{{\text{s}}} - T_{0} } \right){\text{d}}x} $$
(30)

where γ denotes thermal expansion coefficient; Ts denotes screw temperature.

2.3 Equivalent dynamic model

At present, the BSFS is commonly used on CNC machine tools. A double nut BSFS is shown in Fig. 1. It consists of servo motor, coupling, support bearing units, screw-nut pairs, screw shaft and dovetail groove rail. The lead screw is connected to the servo motor through a coupling, and one end close to the servo motor is supported by a pair of angular contact bearings mounted “back-to-back”. The other end is supported by a deep groove ball bearing, which is mainly subjected to radial load. The positioning accuracy in the x direction directly affects the processing quality of the workpiece. It is highly vital to analyze the dynamic characteristics of the BSFS in the x-axis.

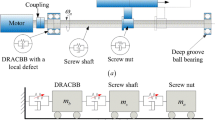
The equivalent dynamic model of the BSFS in the x-axis under thermal deformation is established using the lumped mass method as shown in Fig. 7.

Fig. 7
figure 7

Spring-damped vibrator model of ball screw feed system

Full size image

2.4 Dynamic equation

In Fig. 7, mb, ms and mn denote the equivalent mass of the bearing joints, screw shaft, and screw-nut joints, respectively; kb, cb, ks, cs, kn, and cn are the axial stiffness and damping coefficient of the bearing joints, screw shaft, and screw-nut joints, respectively; the equivalent dynamic model shown in Fig. 1 can be simplified as a three degrees of freedom coupling mass-spring-damping system. The differential equation of motion with restoring force under harmonic excitation can be written as follows:

$$ \left\{ {\begin{array}{*{20}c} {m_{{\text{b}}} \ddot{x}_{{\text{b}}} + c_{{\text{b}}} \dot{x}_{{\text{b}}} + F_{{\text{b}}} \left( {x_{{\text{b}}} } \right) - c_{{\text{s}}} \left( {\dot{x}_{{\text{s}}} - \dot{x}_{{\text{b}}} } \right) - F_{{\text{s}}} \left( {x_{{\text{s}}} - x_{{\text{b}}} } \right) = 0} \\ {m_{{\text{s}}} \ddot{x}_{{\text{s}}} + c_{{\text{s}}} \left( {\dot{x}_{{\text{s}}} - \dot{x}_{{\text{b}}} } \right) + F_{{\text{s}}} \left( {x_{{\text{s}}} - x_{{\text{b}}} } \right) - c_{{\text{n}}} \left( {\dot{x}_{{\text{n}}} - \dot{x}_{{\text{s}}} } \right) - F_{{\text{n}}} \left( {x_{{\text{n}}} - x_{{\text{s}}} } \right) = 0} \\ {m_{{\text{n}}} \ddot{x}_{{\text{n}}} + c_{{\text{n}}} \left( {\dot{x}_{{\text{n}}} - \dot{x}_{{\text{s}}} } \right) + F_{{\text{n}}} \left( {x_{{\text{n}}} - x_{{\text{s}}} } \right) = P\sin \omega t} \\ \end{array} } \right. $$
(31)

where x, \(\dot{x}\) and \(\ddot{x}\) are the displacement, velocity, and acceleration of the system, respectively; Fb, Fs, Fn are the restoring force of the bearing joints, screw shaft, and screw-nut joints, respectively.

2.5 Experimental verification of the dynamic model

To ensure the accuracy of the dynamic model, an experimental on the x-feed system is carried out and the acceleration response of the worktable is collected and compared with the numerical simulation result. As shown in Fig. 8, the sinusoidal excitation is applied to the workbench of the lathe through a vibration exciter (JZK-50), and the vibration exciter is suspended by an overhead frame to apply horizontal excitation to the workbench. The exciter is connected with the force sensor, and the other side of the force sensor is connected with the worktable as shown in Fig. 9. The acceleration response of the worktable are measured by the acceleration sensors (B&K 4524-B-001) and collected by the signal test and analysis system (DH5956).

Fig. 8
figure 8

Ball screw feed system response measurement test bench

Full size image
Fig. 9
figure 9

Sinusoidal excitation applying device

Full size image

During the experiment, set the magnitude of the external excitation F = 100 N, and select the frequency of 100 Hz, 120 Hz and 150 Hz to apply the excitation. It can be seen in Figs. 10, 11 and 12 that the acceleration result obtained from the experiment is accordance with the numerical simulation result in a whole, which proves the validity of the present study.

Fig. 10
figure 10

Acceleration responses of the system obtained from the experiment and from the numerical simulation (F = 100 N, f = 100 Hz)

Full size image
Fig. 11
figure 11

Acceleration responses of the system obtained from the experiment and from the numerical simulation (F = 100 N, f = 120 Hz)

Full size image
Fig. 12
figure 12

Acceleration responses of the system obtained from the experiment and from the numerical simulation (F = 100 N, f = 150 Hz)

Full size image

3 Simulation results and discussion

Based on the numerical solution obtained by Runge–Kutta method, the nonlinear dynamic characteristics of the system are mainly discussed, so as to obtain a system with better performance. Ding and Cheng [44] identified the nonlinear dynamical behaviors by using the Poincare map and the phase portrait to indicate periodic motions or chaotic motions occurring in the transverse motion of the axially accelerating viscoelastic beam. Yan et al. [45] focused on the nonlinear dynamic behaviors in the transverse vibration of an axially accelerating viscoelastic Timoshenko beam with the external harmonic excitation and identified the motion form of the nonlinear vibration by using the time history, the Poincare map, and the sensitivity to initial conditions. The Poincare map is obtained by sampling the time domain of the system at specified time intervals. When there is only one fixed point and a few discrete points on the Poincare map, it can be judged that the movement is periodic; when the Poincare map is a closed curve, it can be judged that the movement is quasi-periodic; when the Poincare map is a patch of dense points, and when there is a hierarchical structure, it can be judged that the motion is in a state of chaos. So it can be used to judge the movement state of the system. Ding et al. [46] focused on the natural frequencies of nonlinear free transverse oscillations of transporting tensioned beams via FFT with the time responses histories. The FFT plots the graph of the relationship between amplitude and frequency. In the FFT plots, we can see that the system has several frequency components, which are not shown in the time domain diagram, and when the multiple frequency components appear in the FFT plots, it indicates that the system has a nonlinear motion phenomenon. Meanwhile, the nonlinear dynamic responses of the system were analyzed by using time domain diagrams, waterfall plots, Poincare maps, and bifurcation diagrams [47, 48].

3.1 Effect of thermal deformation on dynamic response

Figure 13 shows the displacement–time diagram and velocity-displacement phase diagram of the feed system that ignores thermal deformation and the feed system that considers thermal deformation. It can be seen that under the influence of thermal deformation, the amplitude of the vibration response of the feed system increases significantly.

Fig. 13
figure 13

Time domain diagram of the system

Full size image

3.1.1 Effect of different speed on dynamic response

Figure 14 shows the time history diagram of the feed system under the speed of n = 1000 r/min, n = 2000 r/min and n = 3000 r/min. We can see that the vibration amplitude of the feed system is 37.04 μm, 41.84 μm and 60.48 μm when the speed is 1000 r/min, 2000 r/min and 3000 r/min, respectively. From the phase diagram in Fig. 15, it can also be seen that the vibration amplitude of the system increases with the increase in speed. Therefore, in the case of meeting the processing conditions, we try to choose a low speed to reduce the impact of thermal deformation on the vibration response of the BSFS, thereby improving the motion stability of the feed system and the machining accuracy of the machine tool.

Fig. 14
figure 14

Time history diagram of different speed

Full size image
Fig. 15
figure 15

Phase diagram of different speed

Full size image

3.1.2 Effect of different preload on dynamic response

Figure 16 shows the time history diagram of the feed system under the preload of Fp = 1000 N, Fp = 1500 N and Fp = 2000 N. We can see that the vibration amplitude of the feed system is 51.40 μm, 41.80 μm and 51.82 μm when the preload is 1000 N, 1500 N and 2000 N, respectively. From the phase diagram in Fig. 17, it can also be seen that the vibration amplitude of the system is greater than the preload of 1500 N when the preload is 1000 N and 2000 N. Therefore, within the temperature rise of the system, proper application of a certain preload can improve the motion stability and cutting accuracy of the system.

Fig. 16
figure 16

Time history diagram of different preload

Full size image
Fig. 17
figure 17

Phase diagram of different preload

Full size image

3.2 Effect of different frequencies on dynamic response

Figure 18 shows the state of motion when the excitation frequency of the BSFS is 500 Hz. It can be seen from the displacement–time history graph that the displacement response state of the system is in the form of a standard sine function, and its vibration amplitude is 250 μm. The displacement-speed phase diagram image is a closed curve, and the Poincare surface of section corresponds to an isolated point. According to the identification characteristics of nonlinear motion, the motion state of the system is a single-period motion when the excitation frequency is 500 Hz.

Fig. 18
figure 18

Vibration response of the feed system (f = 500 Hz, F = 5000 N)

Full size image

Figure 19 shows the vibration response characteristic curve of the feed system when the selected excitation frequency is 1082 Hz. It can be seen from the displacement–time history graph that the maximum amplitude of vibration is about 85.12 μm. The phase diagram is a closed curve, and the Poincare cross-section image contains seven points. According to the identification characteristics of nonlinear motion, it can be known that when the excitation frequency is 1082 Hz, the motion state of the feeding system is a sevenfold periodic motion.

Fig. 19
figure 19

Vibration response of the feed system (f = 1082 Hz, F = 5000 N)

Full size image

Figure 20 shows the vibration response characteristic curve of the feed system when the selected excitation frequency is 382 Hz. It can be seen from the displacement–time history graph that the maximum amplitude of vibration is about 226 μm. The phase diagram appears as a curve with a certain width, and the Poincare cross-section image appears as a closed curve. According to the identification characteristics of nonlinear motion, it can be known that when the excitation frequency is 382 Hz, the motion state of the feeding system is a quasi-periodic motion.

Fig. 20
figure 20

Vibration response of the feed system (f = 382 Hz, F = 5000 N)

Full size image

Figure 21 shows the vibration response characteristic curve of the feed system when the selected excitation frequency is 636.6 Hz. It can be seen from the displacement–time history graph that the maximum amplitude of vibration is about 544.5 μm. The Poincare cross-section image contains an infinite number of points, which are distributed in a certain area. According to the characteristics of nonlinear motion recognition, it can be known that the motion state of the feed system is chaotic motion when the excitation frequency is 636.6 Hz.

Fig. 21
figure 21

Vibration response of the feed system (f = 636.6 Hz, F = 5000 N)

Full size image

Figures 18, 19, 20 and 21 describe the motion state of the system under different excitation frequencies. When the excitation frequency is in the resonance zone of the system, the motion state of the system is not stable. So we selected the above four special excitation frequencies for discussion and described the motion state of the system at each frequency. For theoretical analysis and scientific research, the simulation analysis under extreme conditions is carried out. The proposed general model and simulation within a wide range of parameters could provide the theoretical basis for dynamic structural optimization design, and expand the application range of ball screw feed systems,

3.3 Effect of the basic parameters of the system on dynamic response

In order to investigate the effect of the basic parameters of the BSFS on the vibration characteristics of the system, some parameters of the bearing and the nut are mainly discussed. The dynamic characteristics of the feed system under the influence of different ball diameters, different numbers of rolling elements, and different initial contact angles of bearings and nuts are analyzed, respectively.

3.3.1 Effect of different ball diameters on dynamic response

Figure 22 shows the three-dimensional waterfall plot of the bearing ball diameter as the control parameter when the external excitation amplitude is 5000 N. It can be found that there is a phenomenon of frequency doubling in the spectrogram of the system. As the diameter of the ball increases, the amplitude of the dominant frequency and each frequency multiplier response increases, too.

Fig. 22
figure 22

3D spectrogram of different bearing ball diameters

Full size image

Figure 23 shows the three-dimensional waterfall plot of the nut ball diameter as the control parameter when the external excitation amplitude is 5000 N. It can be found that there is a phenomenon of frequency doubling in the spectrogram of the system. As the diameter of the ball increases, the amplitude of the dominant frequency and each frequency multiplier response increases, too.

Fig. 23
figure 23

3D spectrogram of different nut ball diameters

Full size image

3.3.2 Effect of the number of balls on dynamic response

Figure 24 shows the bifurcation diagram of the BSFS when the number of bearing balls is 13, 16, and 20, respectively. It can be found that as the number of bearing balls changes, the movement status of the system has also changed. The system with different numbers of balls all have chaotic motions in the resonance zone. When the number of bearing balls is 13, there are twofold periodic motion and threefold periodic motion. When the number of bearing balls is increased to 20, the motion state of the BSFS at the frequency of 3342 Hz is quasi-periodic motion.

Fig. 24
figure 24

The bifurcation graph of the number of different bearing balls

Full size image

Figure 25 shows the bifurcation diagram of the BSFS when the number of nut balls is 40, 50 and 60, respectively. It can be found that as the number of bearing balls changes, the movement status of the system has also changed. When the number of nut balls is 40 and 50, it can be found that the system has chaotic motion in the main resonance area, and when the number of balls is 60, there is no chaotic motion. When the number of nut balls is 50, the motion state of the system between 1560  and 1719 Hz also shows the phenomenon of three times periodic motion. When the number of balls is 60, the system will appear twice-period motion, triple-period motion, triple-period motion, and quintuple-period motion at frequencies 986.8 Hz, 1401 Hz, 1432 Hz, and 2196 Hz in sequence.

Fig. 25
figure 25

The bifurcation graph of the number of different nut balls

Full size image

3.3.3 Effect of different initial contact angles on dynamic response

Figure 26 shows the frequency response curves of the BSFS when the initial contact angles of the bearings are 30°, 40°, and 50°. It can be found that as the initial contact angle increases, the resonant frequency of the feed system continues to increase. As the frequency increases, the vibration amplitude of the feed system continues to increase and reach a peak, and there is a jump phenomenon at the peak, showing a hard nonlinear characteristic. When the initial contact angle is 30°, a secondary jump occurs around the frequency of 1200 Hz, and when the initial contact angle is increased to 40°, the vibration amplitude of the system has a secondary jump around the frequency of 1500 Hz. It can also be found that the frequency response curves of the feed system still has a soft nonlinear phenomenon near the frequency of 200 Hz.

Fig. 26
figure 26

Frequency response curve of the number of different initial contact angles of bearings

Full size image

Figure 27 shows the frequency response curves of the BSFS when the initial contact angle of the nut are 30°, 40°, and 50°. It can be found that as the frequency becomes larger, the vibration amplitude of the feed system continues to increase and reach a peak, and there is a jump phenomenon at the peak, showing a hard nonlinear characteristic. When the initial contact angle of the nut increases to 50°, the frequency response curve of the feed system has a secondary jump around 1460 Hz. It can also be found that the frequency response curves of the feed system still has a soft nonlinear phenomenon near the frequency of 200 Hz.

Fig. 27
figure 27

Frequency response curve of the number of different initial contact angles of nut

Full size image

4 Conclusion

The present study investigates nonlinear dynamic characteristics of BSFS considering thermal deformation. Theoretical analysis, numerical simulation and the experimental study can draw the following conclusions.

  1. 1.

    The amplitude of the vibration response of the feed system has increased significantly under the influence of thermal deformation. Therefore, based on meeting the processing requirements, the generation of thermal deformation is reduced. For example, when the machining accuracy is satisfied, the speed should be as small as possible.

  2. 2.

    The excitation frequency will not only affect the amplitude of the system vibration but also change the motion state of the system vibration response, resulting in the phenomenon of period-doubling motion, quasi-periodic motion, and chaotic motion. Therefore, we should avoid the rotation speed corresponding to the frequency that causes the unstable motion of the system, and reduce the system vibration.

  3. 3.

    As the number of balls increases, the resonance frequency of the system gradually increases, and the motion state of the system becomes more and more stable. With the increase of the initial contact angle, the motion state of the system becomes more and more unstable, and the phenomenon of period-doubling motion and quasi-periodic motion will also appear. Therefore, we should choose bearings and nuts with a large number of balls and a small initial contact angle.