Study for ball bearing outer race characteristic defect frequency based on nonlinear dynamics analysis

Abstract

The characteristic defect frequencies are widely used for diagnosing the local defect of the ball bearing. The varying compliance (VC) frequency of a fault-free rotor–bearing system equals to the BPFO (ball bearing outer race defect frequency) due to the internal kinematic relationship of a bearing assembly. In order to indicate this issue, a semi-analytical method—the harmonic balance method with alternating frequency/time domain technique—is exploited to obtain the solutions of rotor–ball bearing systems with /without an outer race defect. The solutions and the features of a rotor–ball bearing system with essentially nonlinear parametric excitation are analyzed. We prove the VC frequency equals the BPFO and explain the reasons that the harmonics of the characteristic defect frequency generally appear in the frequency domain. The VC, BPFO as well as their harmonics affected by the primary and super-harmonic resonance of the system are found out. Finally, a test rig of a rigid rotor–bearing system is established to verify the theoretical analysis qualitatively by presenting the performance of VC, BPFO and their harmonics in the frequency domain. In addition, the tests are accomplished in a cycle of running up and down to reveal the primary and super-harmonic resonance characteristics. On the basis of the theoretical and experimental results, the basic BPFO is not enough to judge an outer race defect. The discussion on frequency spectrum, the primary and super-harmonic resonance provides a more reliable way to elucidate the characteristic defect frequencies.

1 Introduction

A rolling bearing failure is one of the most common causes for breakdowns of a rotating machine. The local defects have become one central issue of concerns in the usual types, e.g., a pit or spall on the raceway, ball, attracting the attention of researchers in many areas. A localized defect is usually initiated by subsurface fatigue cracks that appear during the operation. Even the bearing is in good operating condition, the subsurface cracks will grow and break through to the surface to cause a spall or crack as the service time increases [1].

In recent years, a great many researchers worked on local defect of rolling bearings. McFadden and Smith [2] modeled the short-time impact produced by a local defect as a pulse and calculated the frequency spectrum of the inner race defect. Tandon and Choudhury [3, 4] thought the impact as an impulse because of the short duration of the striking process, and they utilized the mode harmonic superposition method to acquire the frequency spectrum of ball bearings with different local defects. Choudhury and Tandon [5] employed the pulse model to establish an analytical formulation for a defective bearing test rig to show the frequency performance of a defective bearing system. Rafsanjani et al. [6] employed the pulse model to set up a dynamic equation of a rigid rotor–bearing system with various local defects. Some complex behaviors such as quasi-periodic and chaotic motions were reported in the paper. Feng et al. [7] modeled the local defect with an angle span and a depth to illustrate the vibration behavior. Sopanen and Mikola [8, 9] embedded a rectangle shaped local defect into a bearing model to exhibit the vibration behavior. Sawalhi and Randall [10, 11] presented a combined dynamic model for gears and bearings containing a local and an extended fault in the inner/outer race of rolling element bearings under gear interaction. Sassi et al. [12] modeled the vibration generated by a point defect as a function of the operational and structural parameters of a rolling bearing system. Cao and Xiao [13] investigated the effects of localized surface defects on vibration responses of a double-row spherical roller bearing system. Arslan and Aktürk [14] established a dynamic model of a bearing–rotor system where the shaft, balls and raceways were treated as contact springs, and the vibrations of the system with/without defects were studied in both time and frequency domains. Nakhaeinejad and Bryant [15] developed a dynamic model of rolling element bearing in vector bond graphs, in which each component has rotation DOF and translation DOF. Patil et al. [16] presented an analytical model for predicting the effect such as the size and location of a localized defect on the ball bearing vibrations. Patel et al. [17] studied the dynamic characteristics of a deep groove ball bearing system, single and multiple surface defects were explored, and some frequency characteristics were concluded. Tadina and Boltežar [18] modeled the outer raceway using finite element method to simulate its flexible deformations, and various surface defects due to local deformations were introduced into the developed model. Kankar et al. [19] set up a dynamic equation of a rigid rotor–bearing system with various defects to reveal complex dynamic behaviors. Pandya et al. [20] proposed a dynamic rotor–bearing model containing combined local defects to explore the dynamic behaviors, and the results show the motion of the system is quite unstable and quasi-periodic and chaotic trends to appear in the entire speed range. Bogdevicius and Skrickij [21] investigated five cases of various defects on different components based on a dynamic model established by Lagrange equation. Wang et al. [22] established 5-DOF roller bearing model, and the effects of time-varying surface models, different defect types and defect sizes on system dynamic responses were studied. Liu et al. [23,24,25,26] proposed piecewise function models to describe different local defect types and the edge effect based on Hertizian contact mechanism, and the ratio of the ball size to the defect size was considered. Ahmadi et al. [27] thought of the edge effect of a local defect on the contact deformation to stress the importance of modeling the finite size of rolling elements. Niu et al. [28, 29] established comprehensive dynamic models based on the Gupta’s model to explore the high-speed vibration response and ball passing frequencies of a defective bearing system. Among them, a few scholars modeled pedestal freedoms to simulate resonance of some components of a bearing assembly or model vibrations of the bearing housing [7, 10, 11, 28,29,30]. Besides, some scholars analyzed the multi events in the time domain responses based on the geometric model to judge a local defect or estimate the size or severity of the defect [31,32,33,34].

Recently, Singh et al. [35] and El-Thalji and Jantunen [36] reviewed the current literatures on modeling and dynamic behaviors of the local defect of rolling bearings, in which Singh et al. laid particular emphasis on the dynamic modeling and the dynamic phenomena, while El-Thalji et al. emphasized the signals analysis and features extraction methods. Compared to other criterion [36, 37], the characteristic defect frequencies [38] which can give a direct insight into the defective bearing system are widely used for the judgement of a local defect [3,4,5,6, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25, 27,28,29, 35, 37, 39, 40]. Some signal processing methods such as the envelope analysis [2, 7, 10, 11, 28,29,30, 41] and time–frequency analysis methods [42,43,44] are usually used to obtain the defect characteristic frequency. In addition, many other mathematical theories and techniques are also employed to enhance the useful information to match the characteristic defect frequency for diagnosis [36, 37, 45, 46].Therefore, the characteristic defect frequency plays an important role for judgment of defective rolling bearing.

The number of rolling elements and their position in the load zone change with shaft rotation, which leads to a periodical variation in the total stiffness of the rolling bearing, known as varying compliance (VC) vibration [47]. The nature of the VC vibration is not changed when a local defect exists, so the VC frequency equals to the BPFO in frequency domain. However, few scholars pay attention to the relationship between VC and BPFO in the frequency domain (see Appendix). In addition, few scholars highlight the fact that a rotor–ball bearing system is an essentially nonlinear parametric excitation, the solution of which usually contains the basic excitation and the harmonics. Furthermore, they are influenced by the resonance characteristic, which in turn affects the frequency spectrum of a rotor–bearing system with an outer race defect. Therefore, the motivation of this paper is to stress the issue that the VC frequency equals to the BPFO and study the frequency spectrum performance based on nonlinear dynamics.

The rest of the paper is organized as follows. Section 2 briefly introduces the modeling process. Section 3 contains establishment of experiment system and dynamic parameters estimation. The numerical analysis is carried out in Sect. 4. The experimental results are presented and analyzed in Sect. 5. The discussions and conclusion lie in Sect. 6.

2 System modeling

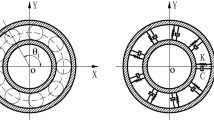
The 2-DOF mass–spring rotor–bearing system model used in this paper was developed by Sunnersjö [47]. The rotor is simplified as a lumped mass point in the center with two same bearings at ends (Fig. 1a). The ball bearing is simplified as a spring and damping system based on the Hertzian contact (Fig. 1b). The outer race and the inner race are assumed to be, respectively, fixed rigidly by an interference fit in a rigid support and with the shaft. Because we focus on a fundamental and qualitative research, some factors such as the gyroscopic moment, centrifugal force and lubrication traction/slip between bearing components are neglected [34]. The equation of motion for a rotor–bearing system can be established as

$$\begin{aligned} m\left[ {{\begin{array}{l} {\ddot{x}} \\ {\ddot{y}} \\ \end{array} }} \right] +c\left[ {{\begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ \end{array} }} \right] +\left[ {{\begin{array}{l} {f_x } \\ {f_y } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} 0 \\ {-W} \\ \end{array} }} \right] , \end{aligned}$$

(1)

where m is half mass of the rotor, $f_{x }$and $f_{y}$ are the restoring forces, W is half the gravity of the shaft, c is the damping coefficient and the rotor is assumed to be balanced.

2.1 Restoring forces

Based on the Hertzian point contact theory [39], the force between rolling element and raceway is modeled as

$$\begin{aligned} Q_j =K_\mathrm{c} \delta _j^{{3/2}} , \end{aligned}$$

(2)

where $K_\mathrm{c}$ is contact stiffness and $\delta _{j }$ is the contact deformation of the $j\hbox {th}$ rolling element, and it is given by

$$\begin{aligned} \delta _j =x\hbox {cos}\theta _j +y\hbox {sin}\theta _j -\delta _0, \end{aligned}$$

(3)

where $2\delta _{0}$ is the radial clearance and $\theta _{j}$ is angular position of the $j\hbox {th}$ rolling element.

$$\begin{aligned} \theta _j =2\pi (j-1)/{N_\mathrm{b} }+\omega _\mathrm{c} t, \end{aligned}$$

(4)

where $\omega _\mathrm{c}$ is the cage speed and $N_\mathrm{b}$is the number of the rolling elements. The cage speed has a relationship with the rotor speed $\omega _\mathrm{s}$, which is determined by the structure of a bearing assembly.

$$\begin{aligned} \omega _\mathrm{c} =B\omega _\mathrm{s} , \end{aligned}$$

(5)

where $B=D_\mathrm{i}/(D_\mathrm{i}+D_\mathrm{o})$ for a deep groove ball bearing $D_\mathrm{i}$ is the diameter of the inner raceway and $D_\mathrm{o}$ is the diameter of the outer raceway. Referring to the coordinate system in Fig. 1b, the restoring forces are accumulated over each rolling element to give overall forces on the shaft and housing into x and y directions.

$$\begin{aligned} f_x= & {} \sum _{j=1}^{N_\mathrm{b}}{G(\delta _j )}Q_j\hbox {cos}\theta _j , \end{aligned}$$

(6)

$$\begin{aligned} f_y= & {} \sum _{j=1}^{N_\mathrm{b}}{G(\delta _j )}Q_j\hbox {sin}\theta _j , \end{aligned}$$

(7)

where $G(\cdot )$ is the Heavisde function, obtaining the value 1 for positive arguments and the value 0 for negative or zero arguments. The parametric excitation VC is determined by the number of the rolling elements and the cage rotation speed.

$$\begin{aligned} \omega _{\mathrm{vc}} =N_{\mathrm{b}}\omega _\mathrm{c}. \end{aligned}$$

(8)

2.2 Defect model

The pits or spalls affect the deformation relation of each ball and race, and additional deformation is introduced into Eq. (3) when a ball runs over the defect zone as shown in Fig. 1b. This kind of modeling tries to directly depict the physical boundaries of a local defect, which is essentially the change of the clearance [7]. The contact deformation of $j\hbox {th}$ element in Eq. (1) changes when the ball runs across the defect

$$\begin{aligned} \delta _j =\left\{ {\begin{array}{cc} \delta _j -\delta _\mathrm{d} &{} {|}\theta _{{\mathrm{bd}}j} {|<}\quad {{\theta }_\mathrm{e} }/{2} \\ \delta _j &{} {|}\theta _{{\mathrm{bd}}j} {|>}\quad {{\theta }_{\mathrm{e}} }/{2} \\ \end{array} } \right. , \end{aligned}$$

(9)

where $\theta _\mathrm{e}$ is the span of the defect (see Fig. 1b), $\delta _\mathrm{d}$ is the depth of the defect, $\theta _{\mathrm{bd}j}$ is the angular difference between $j\hbox {th}$ rolling element and the local defect, denoted as

$$\begin{aligned} \theta _{\mathrm{bd}j} =mod (\theta _j ,2\pi )-\varphi , \end{aligned}$$

(10)

where $mod(\cdot )$ is the function calculating the remainder after division and $\varphi$ is the defect angle (Fig. 1b). To avoid the stiff problem during the calculation, a dimensionless equation is implemented. Introducing a nondimensional time $\tau = \omega _\mathrm{c}t$, differentiation with t being changed with $\tau$, the governing equation is transformed into the following equation. Letting $X=x/\delta _{0}$, $Y=y/\delta _{0}$, the governing equation of the defective bearing rotor system can be expressed as follows

$$\begin{aligned}&\left[ {{\begin{array}{l} {X^{{\prime }{\prime }}} \\ {Y^{{\prime }{\prime }}} \\ \end{array} }} \right] +\frac{c}{m{{\varOmega }}}\left[ {{\begin{array}{l} {X^{{\prime }}} \\ {Y^{{\prime }}} \\ \end{array} }} \right] +\frac{1}{m{{\varOmega }}^{2}}\left[ {{\begin{array}{l} {F_x } \\ {F_y } \\ \end{array} }} \right] \nonumber \\&\quad =\left[ {{\begin{array}{c} 0 \\ {-\frac{W}{m\delta _0 {{\varOmega }}^{2}}} \\ \end{array} }} \right] ; \end{aligned}$$

(11)

the restoring force is expressed as

Fig. 1

Schematic map of a defective bearing–rotor system. a Bearing–rotor system and b defective bearing

$$\begin{aligned}&\left[ {{\begin{array}{l} {F_x } \\ {F_y } \\ \end{array}}} \right] =K_\mathrm{c} \delta _0^{0.5} \sum _{j=1}^{N_\mathrm{b} } {\left( {\delta _j^*{G}\left( \delta _j^*\right) } \right) } ^{1.5}\left[ {{\begin{array}{l} {\cos \theta _j^*} \\ {\sin \theta _j^*} \\ \end{array} }} \right] , \end{aligned}$$

(12)

$$\begin{aligned}&\delta _j^*=\left\{ {{\begin{array}{ll} {X\hbox {cos}\theta _j^*+Y\hbox {sin}\theta _j^*-1-{\delta _\mathrm{d}}/{\delta _{0}}} &{} {{|}\theta _{\mathrm{bd}j} {|<}\quad {\theta _\mathrm{e} }/{2}} \\ {X\hbox {cos}\theta _j^*+Y\hbox {sin}\theta _j^*-{1}} &{} {{|}\theta _{\mathrm{bd}j} {|>}\quad {\theta _\mathrm{e} }/{2}} \\ \end{array} }} \right. , \end{aligned}$$

(13)

where $\theta _j^*=2\pi (j-1)/N_\mathrm{b} +\tau$ and ${\varOmega }$ is taken instead of $\omega _\mathrm{c}$ in the dimensionless process. Then, the nondimensional VC frequency of Eq. (11) is $N_\mathrm{b}$.

2.3 Methodology

The harmonic balance (HB) method can obtain a solution expression to reflect the relationship between the excitation and its response. Moreover, the HB is a suitable numerical method to solve a nonlinear system [48,49,50,51]. Thus, this HB method will elucidate the topics of this paper. The solution of Eq. (11) can be expressed by Eq. (14) through Fourier series, and the restoring force of Eq. (12) is replaced by Eq. (15) identically.

$$\begin{aligned}&\left[ {{\begin{array}{l} X \\ Y \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {a_{X0} } \\ {a_{Y0} } \\ \end{array} }} \right] \nonumber \\&\quad +\sum _{k=1}^K \left( \left[ {{\begin{array}{l} {a_{Xk} } \\ {a_{Yk} } \\ \end{array} }} \right] \cos (k\tau ) -\left[ {{\begin{array}{l} {b_{Xk} } \\ {b_{Yk} } \\ \end{array} }} \right] \sin (k\tau )\right) , \end{aligned}$$

(14)

$$\begin{aligned}&\left[ {{\begin{array}{l} {F_X } \\ {F_Y } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {c_{X0} } \\ {c_{Y0} } \\ \end{array} }} \right] \nonumber \\&\quad +\sum _{k=1}^K {\left( \left[ {{\begin{array}{l} {c_{Xk} } \\ {c_{Yk} } \\ \end{array} }} \right] \cos (k\tau )-\left[ {{\begin{array}{l} {d_{Xk} } \\ {d_{Yk} } \\ \end{array} }} \right] \sin (k\tau )\right) } , \end{aligned}$$

(15)

where k is the order of the harmonic terms.

Substituting these two equations into the governing Eq. (11), the algebraic equations about coefficient $a_{Xk,} \quad a_{Yk,}{\ldots }, c_{Xk}$ and $c_{Yk}$ can be obtained according to the different orders of harmonic terms. The coefficients of the displacement and restoring force can be expressed as a vector [49].

$$\begin{aligned} \left[ {{\begin{array}{l} U \\ V \\ \end{array} }} \right] \!=\! \left[ {{\begin{array}{lllllllllll} {a_{X0} }&{} {a_{Y0} }&{} {a_{X1} }&{} {a_{Y1} }&{} {b_{X1} }&{} {b_{Y1} }&{} {,\ldots ,}&{} {a_{XK} }&{} {a_{YK} }&{} {b_{XK} }&{} {b_{YK} } \\ {c_{X0} }&{} {c_{Y0} }&{} {c_{X1} }&{} {c_{Y1} }&{} {d_{X1} }&{} {d_{X2} }&{} {,\ldots ,}&{} {c_{XK} }&{} {c_{YK} }&{} {d_{XK} }&{} {d_{YK} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$

(16)

The number of the algebraic equations is less than that of the harmonic coefficients. The AFT procedure can be a bridge for $a_{Xk}$,$c_{Xk}$,$a_{Yk}$ and $c_{Yk}$ [48, 49].

$$\begin{aligned}&\left[ {{\begin{array}{l} {c_{X0} } \\ {c_{Y0} } \\ \end{array} }} \right] =\frac{1}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_X } \\ {F_Y } \\ \end{array}}} \right] } , \end{aligned}$$

(17)

$$\begin{aligned}&\left[ {{\begin{array}{l} {c_{Xk} } \\ {c_{Yk} } \\ \end{array} }} \right] =\frac{2}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_X } \\ {F_Y } \\ \end{array} }} \right] \cos \left( \frac{2\pi kn}{N}\right) } , \end{aligned}$$

(18)

$$\begin{aligned}&\left[ {{\begin{array}{l} {d_{Xk} } \\ {d_{Yk} } \\ \end{array} }} \right] =\frac{2}{N}\sum _{n=0}^{N-1} {\left[ {{\begin{array}{l} {F_X } \\ {F_Y } \\ \end{array} }} \right] \sin \left( \frac{2\pi kn}{N}\right) } , \end{aligned}$$

(19)

where N is the discrete point number in time domain. After the AFT procedure, the numbers of the unknowns and the algebraic equations are equal. The Newton–Raphson iteration procedure is used to obtain harmonic coefficients of the solutions of Eq. (14). A brief flowchart of the HB-AFT is displayed in Fig. 2. The details can refer the reference [48,49,50,51].

Fig. 2

Flowchart of the HB-AFT

Fig. 3

Experiment system of bearing–rotor system. a Test rig of ball bearing, b systems of signal acquisition and motor controlling and c sensors

3 Experiment system

This section contains the brief introduction of the test rig, estimation of contact stiffness and damping efficient.

3.1 Brief introduction of test rig

The system consists of three parts: (a) the test rig of a rotor bearing system; (b) the signal acquisition and motor controlling system; (c) the eddy current displacement sensors. In Fig. 3a, the right end of the rig is the tested rolling bearing, and the fault-free bearing and outer raceway defective bearing can be installed there. The real bearings used in this paper are displayed in Fig. 4, and they are 6312 deep groove bearing. The loading equipment lies in the middle of the rig which can supply the vertical force on the shaft; the left end of the bearing rig is the accompanying bearing; the drive end is a servo motor; and the motor and shaft are connected through a coupling and a soft rope to reduce the disturbance from the motor. The signal acquisition and motor controlling system are displayed in Fig. 3b. Figure. 3c shows the eddy current sensors installation, and sensors are mounted to measure the vertical and horizontal displacements of shaft and bearing pedestal in the right end. The eddy current sensors are fixed to the ground through a magnet base, and the eddy sensors can acquire the direct displacement responses of the rotor. The parameters of the test bearing and rotor are listed in Table 1.

3.2 Contact stiffness and damping estimation

The contact stiffness $K_\mathrm{c}$ in Eq. (2) can be calculated or estimated [39]; however, some parameters are changed after installation. The estimation of contact stiffness of rolling bearing is measured by a test in the paper, and the schematic diagram and measuring schematic are illustrated in Fig. 5. The deformation and radial load has a relationship when one rolling element is adjusted in the vertical direction [39], in which the space angle $\theta _\mathrm{s}$ is $\pi$/4 due to three rolling elements in the load zone (Fig. 5a).

$$\begin{aligned}&2K_\mathrm{c} (\delta _\mathrm{s} \cos \theta _\mathrm{s} -{P_\mathrm{d} }/2)^{1.5}\cos \theta _\mathrm{s} +K_\mathrm{c} (\delta _\mathrm{r} -\delta _0 )^{1.5} \nonumber \\&\quad ={F_\mathrm{r} }/2+W/2, \end{aligned}$$

(20)

Fig. 4

6312 deep groove ball bearing used in this paper. a Fault-free bearing and b outer raceway defect

Table 1 Parameters for numerical analysis and experiment

Fig. 5

Schematic diagram of stiffness measuring. a Schematic of bearing under load and b measuring schematic

where $K_\mathrm{c}$ is the contact stiffness, $\delta _\mathrm{s}$ is the projection of $\delta _\mathrm{r}$ along $\theta _\mathrm{s}$, $\delta _\mathrm{r}$ is the vertical displacement of the rotor,$F_\mathrm{r}$ is the vertical load force, Wis the weight of the rotor (Fig. 5a). The two eddy current sensors are mounted in the vertical direction to measure the displacement of the loaded rotor (Fig. 5b). Thus, $K_\mathrm{c}$ can be gained through Eq. (20). The displacement and the load are plotted in Fig. 6 marked as blue circle. The displacement and Load can be fitted by Hertzian point contact via the least squares fit method marked as the red star. Furthermore, according to an aeroengine design manual [52], the radial stiffness estimation can be calculated as follows.

$$\begin{aligned} K_{rr} =0.117\times 10^{4}\root 3 \of {F_\mathrm{r} Z^{2}d\cos ^{5}\beta }, \end{aligned}$$

(21)

Fig. 6

Relationship between radial load and deformation

where d is the diameter of a rolling element (mm), Z is the number of rolling elements in contact which is three for 6312 deep groove ball bearing, $\beta$ is the contact angle (zero for deep groove ball bearing), $F_\mathrm{r}$ is the radial load force (N). The approximate formula results via Eq. (21) are displayed in green plus. It shows the approximate stiffness is a little larger than the test data and Hertzian fitting results. The contact stiffness $K_\mathrm{c}$ from experiment is 7.26$\times 10^{9}$ (N/m$^{1.5}$) and is listed in Table 1.

Fig. 7

Orbit results contract between the RK method and the HB-AFT method (4055 rpm). a Healthy system and b defective system

For the damping coefficient, Krämer [53] provided an estimation of the bearing damping, and Wang et al. put up an identification method for damping ratio in rotor systems [54]. We estimate the damping by the free attenuation vibration method [55].

$$\begin{aligned} c=\frac{M\omega }{n\pi }\mathrm{In}\frac{A_i }{A_{i+n} } \end{aligned}$$

(22)

where $A_{i}$ is the amplitude of the $i\hbox {th}$ free periodic vibration, n is the periodic interval, M is the mass of the rotor, $\omega$ is the linearized resonance frequency. The estimated damping is about 142 Ns/ml; thus, a linearized damping of 200 Ns/m is used in this paper. In addition, the first-order natural resonance of the rotor is 808 Hz through a theoretical analysis. It is noted all the structure parameters in the operation state are different from those measured in a static status.

4 Numerical analysis

$$\begin{aligned}&X_\mathrm{fault-free}^1 (t)=0.004+0.031\cos (\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.846\sin (\omega _\mathrm{vc} t) \nonumber \\&\quad -\, 0.001\cos (2\omega _\mathrm{vc} t)-0.025\sin (2\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.001\sin (3\omega _\mathrm{vc} t), \end{aligned}$$

(23)

$$\begin{aligned}&Y_\mathrm{fault-free}^1 (t)=-7.593+0.126\cos (\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.003\sin (\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.012\cos (2\omega _\mathrm{vc} t)-0.001\sin (2\omega _\mathrm{vc} t), \end{aligned}$$

(24)

$$\begin{aligned}&X_\mathrm{od}^1 (t)=0.001+0.033\cos (\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.941\sin (\omega _\mathrm{BPFO} t)\nonumber \\&\quad -\, 0.001\cos (2\omega _\mathrm{BPFO} t)-0.007\sin (2\omega _\mathrm{BPFO} t), \end{aligned}$$

(25)

$$\begin{aligned}&Y_\mathrm{od}^1 (t)=-7.746-0.954\cos (\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.014\sin (\omega _\mathrm{BPFO} t)\nonumber \\&\quad -\, 0.213\cos (2\omega _\mathrm{BPFO} t)+0.002\sin (2\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.070\cos (3\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.004\cos (4\omega _\mathrm{BPFO} t) \nonumber \\&\quad +\, 0.019\cos (5\omega _\mathrm{BPFO} t)+0.012\cos (6\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.008\cos (7\omega _\mathrm{BPFO} t)+0.005\cos (8\omega _\mathrm{BPFO} t) \end{aligned}$$

(26)

A rectangular defect is adopted in this paper, and the defect parameters are listed in Table 1. The solution of the rotor–bearing system at shaft speed 4055 rpm is first calculated by the HB-AFT method. The iteration error set as $1\times 10^{-12}$ and the item less $1\times 10^{-3}$ are ignored. The orbits comparison based on different methods for fault-free and defective system is illustrated in Fig. 7, where the Runge–Kutta (RK) and the HB method match well for each other. The solution expressions obtained by HB-AFT method are listed in Eqs. (23)–(26). It is clear that the expressions contain the excitation frequency and its harmonics for both fault-free and defective systems, this is due to nonlinearity of Hertzian contact and the radial clearance, and it is one feature that distinguishes the nonlinear dynamic system from the linear dynamics system [56]. As the defect locates in vertical direction and the impact energy concentrates, the harmonic terms of rotor response of Eq. (26) are increased. The FFT maps of the response solutions are illustrated in Fig. 8 to make it clear. Their frequencies are equal as is mentioned in Introduction; besides, the frequency difference in Fig. 8b is tiny and the basic VC frequency and BPFO are evident.

Fig. 8

Frequency spectrums contract of two directions (4055 rpm). a Horizontal direction and b vertical direction

Fig. 9

Orbit results contract between the RK method and the HB method (2345 rpm). a Healthy system and b defective system

Fig. 10

Frequency spectrums contract of two directions (2345 rpm). a Horizontal direction and b vertical direction

Another case is carried out at rotor speed 2345 rpm. The orbit contrast for fault-free and defective system obtained by different methods is illustrated in Fig. 9. The Runge–Kutta and the HB method match well for a fault-free system, while there are some errors for the defective system, and this is because of the weakness of the HB-AFT. The solution expressions are listed in Eqs. (27)–(30), in which every solution has the basic and harmonics of the excitation frequency. The FFT maps of the response solutions are illustrated in Fig.10 as well. In Fig. 10a, the basic and the harmonics are similar. In Fig. 10b, the difference for the basic frequency is tiny, while the imparity for the second harmonic is obvious. It is clear the basic characteristic defect frequency is not enough to judge an outer race defect from the results comparison at rotor speed 4055 and 2345 rpm.

$$\begin{aligned}&X_\mathrm{fault-free}^2 (t)=0.011+0.019\cos (\omega _\mathrm{vc} t)\nonumber \\&\quad -\,0.349\sin (\omega _\mathrm{vc} t) -0.003\cos (2\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.064\sin (2\omega _\mathrm{vc}t)\nonumber \\&\quad +\, 0.002\sin (3\omega _\mathrm{vc} t) - 0.002\cos (3\omega _\mathrm{vc} t)\nonumber \\&\quad +\, 0.002\sin (4\omega _\mathrm{vc} t) \nonumber \\&\quad - 0.001\cos \cos (4\omega _\mathrm{vc} t)+0.003\sin (5\omega _\mathrm{vc} t), \end{aligned}$$

(27)

$$\begin{aligned}&Y_\mathrm{fault-free}^2 (t)=-7.600+0.054\cos (\omega _\mathrm{vc} t)\nonumber \\&\quad -\, 0.001\sin (\omega _\mathrm{vc} t)\nonumber \\&\quad -\, 0.018\cos (2\omega _\mathrm{vc} t)+0.969\sin (2\omega _\mathrm{vc} t)\nonumber \\&\quad -\, 0.001\cos (3\omega _\mathrm{vc} t)+0.001\sin (3\omega _\mathrm{vc} t) \nonumber \\&\quad +\, 0.006\cos (4\omega _\mathrm{vc} t) \end{aligned}$$

(28)

$$\begin{aligned}&X_\mathrm{od}^2 (t)=-0.007-0.004\cos (\omega _\mathrm{BPFO} t)\nonumber \\&\quad -\, 0.379\sin (\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.005\cos (2\omega _\mathrm{BPFO} t)+0.064\sin (2\omega _\mathrm{BPFO} t) \nonumber \\&\quad -\, 0.002\cos (3\omega _\mathrm{BPFO} t)-0.005\sin (3\omega _\mathrm{BPFO} t)\nonumber \\&\quad -\, 0.002\sin (4\omega _\mathrm{BPFO} t)-0.006\cos (4\omega _\mathrm{BPFO} t) \end{aligned}$$

(29)

$$\begin{aligned}&Y_\mathrm{od}^2 (t)=-7.403-0.098\cos (\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.009\sin (\omega _\mathrm{BPFO} t)+3.501\cos (2\omega _\mathrm{BPFO} t) \nonumber \\&\quad -\, 0.889\sin (2\omega _\mathrm{BPFO} t)+0.089\cos (3\omega _\mathrm{BPFO} t)\nonumber \\&\quad -\, 0.005\sin (3\omega _\mathrm{BPFO} t)-0.048\cos (4\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.043\sin (4\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.013\cos (5\omega _\mathrm{BPFO} t)+0.001\sin (5\omega _\mathrm{BPFO} t) \nonumber \\&\quad +\, 0.009\cos (6\omega _\mathrm{BPFO} t)+0.001\sin (6\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.006\cos (7\omega _\mathrm{BPFO} t)+0.001\sin (7\omega _\mathrm{BPFO} t)\nonumber \\&\quad +\, 0.004\cos (8\omega _\mathrm{BPFO} t) \end{aligned}$$

(30)

From the results of the two cases above, the difference for the solution responses is large. In fact, the response is affected by the resonance characteristics. It is noted the resonance concept in the rotor–bearing system is different from the bearing component resonance or the pedestal resonance in the bearing fault diagnosis [7, 10, 12, 37, 40]. The resonance characteristics of the rotor–bearing system can be estimated by the linearized stiffness [57, 58]; in addition, the relationship between the single rolling element as well as total bearing stiffness and externally applied load agrees with Hertzian contact theory and is nonlinear [39], written as

$$\begin{aligned} \left[ {{\begin{array}{l} {k_x (t)} \\ {k_y (t)} \\ \end{array}}} \right] =\left[ {{\begin{array}{l} {{\partial F_x }/{\partial x}} \\ {{\partial F_y }/{\partial y}} \\ \end{array} }} \right] , \end{aligned}$$

(31)

where $F_{x}$ and $F_{y}$ are the restoring forces in Eq. (11). The coupling stiffness $k_{xy}$ is nearly null on average [57]. Then, the time-varying resonance frequencies of the rotor–bearing system are

$$\begin{aligned} \left[ {{\begin{array}{l} {{\omega }_{x} (t)} \\ {{\omega }_{y} (t)} \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\sqrt{{k_{x} (t)}/{m}}} \\ {\sqrt{{k_{y} (t)}/{m}}} \\ \end{array} }} \right] , \end{aligned}$$

(32)

where m is the mass of the rotor. These frequencies are changing with the rotation of the rotor, $\omega _{x}$ and $\omega _{y}$ can be averaged and then resonance frequencies can also be calculated.

$$\begin{aligned} \left[ {{\begin{array}{l} {n_\mathrm{X} } \\ {n_\mathrm{Y} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} \hbox {mean}(\omega _{x} (t)) \\ \hbox {mean}(\omega _{y} (t)) \\ \end{array} }} \right] . \end{aligned}$$

(33)

Fig. 11

Experiment frequency spectrums and time response for the fault-free system at different rotation speeds, X stands for shaft frequency. a Horizontal direction (3600 rpm) and b vertical direction (2800 rpm)

Generally, resonances are aroused when the parametric frequencies or combination of them run near the estimated ones. For example, the resonance frequency caused by BPFO or VC is expressed as follows.

$$\begin{aligned} \left[ {{\begin{array}{l} {{n_\mathrm{XVC}}} \\ {{n_\mathrm{YVC}}} \\ \end{array}}} \right] =\left[ {{\begin{array}{l} n_\mathrm{X} /N_\mathrm{b} \\ n_\mathrm{Y} /N_\mathrm{b} \\ \end{array}}} \right] . \end{aligned}$$

(34)

The estimation resonance of vertical direction is 4750 rpm for fault-free system and 4870 rpm for the defective system, the rotor speed 2345 rpm for the second case is about half of the resonance frequency, and this is the twice super-harmonic resonance, which is a unique phenomenon for a nonlinear system. The similar results appeared in the similar dynamic system for a cracked rotor–ball bearing system during flight maneuvers [59]. The theoretical calculations show VC frequency equals to the BPFO and the frequency performance is affected by resonance characteristics of the rotor system. The mechanism of producing the harmonics is also explained in the view of nonlinear dynamics.

5 Experiment results

The experimental results in this section are to verify the theoretical calculations and the topics of this paper qualitatively. As the VC and the BPFO convey the information for rotor–bearing system, the VC, BPFO, and their harmonics are paid attention during the tests, and the sample rate is set as 16384 Hz. The change of rotor rotation speed is in a cycle of running up and down, the step of which is 30–200 rpm (a small step in resonance zone or a big step in nonresonance zone). It maintains 10–15 s for every speed step. The values are averaged during running up and down in the nonresonance zone while the higher values retain in resonance zone. The local defect locates in the center of the bearing load zone.

The horizontal direction and vertical direction frequency spectrums and time response of the fault-free system at rotation speed 3600 and 2800 rpm are displayed in Fig. 11a, b, respectively. The VC frequency is shown in Fig. 11a, b, while the 2VC is relatively weak in Fig. 11a, b. Because the eccentricity of the rotor cannot be eliminated, the basic shaft frequency (X) and its harmonics appear in the frequency spectrums maps. As the 3X and VC frequency are close and dominated, the time response reveals beat phenomenon in time response map (see Fig.  11a). The results in Fig. 11a, b can be affirmed faulty depending on the basic BPFO; therefore, the basic BPFO is not enough for judging an outer race defect.

Fig. 12

Frequency–amplitude curves of VC and 2VC for two directions. a Horizontal direction and b vertical direction

Fig. 13

Frequency–amplitude curves of BPFO and 2BPFO for two directions. a Horizontal direction and b vertical direction

Fig. 14

Comparison of the harmonics of the fault-free system and defective system. a Horizontal direction and b vertical direction

The VC and 2VC frequency–amplitude values for two directions at different rotation speeds are extracted to form the frequency–amplitude curves in Fig. 12. There exist obvious peaks around 3600 rpm for horizontal direction and 2800 rpm for vertical direction, while peaks on the 2VC curves are not distinct. By analyzing the frequency–amplitude curves in Fig. 12a, b and the FFT maps in Fig. 11, the obvious peak are actually the resonance peak of the rotor–bearing system, the resonance characteristics of which have been studied by Zhang [58, 60] and Jin et al. [61]. The frequency–amplitude curves of BPFO and 2BPFO for two directions are illustrated in Fig. 13, in which the resonance characteristic is more complicated compared to the results in Fig. 12. One obvious difference is the occurrence of the super-harmonic resonance for two directions. The vibration level for the basic excitation frequency (VC and BPFO) is similar; however, the vibration level for the second harmonic 2BPFO and 2VC is different. The comparisons for the second harmonic are illustrated in Fig. 14, in which the vibration level of the 2BPFO is much larger than the 2VC for the vertical direction in the whole speed range, while the 2BPFO is larger than the 2VC only in the super-harmonic and the primary regions for vertical direction. The static clearance of the fault-free bearing is much larger than that of the defective bearing (the static clearance is measured by a dial indicator, and the difference is apposed to be more obvious if the two tested bearings are with the same radial clearance [62, 63]).

The frequency spectrums and time response for both directions in the super-harmonic resonance region are displayed in Fig. 15. That the 2BPFO is larger than the basic BPFO is clearly seen in Fig. 15, which can be a sign for the twice super-harmonic resonance of defective bearing–rotor system and in accordance with the results in Fig. 10b. Furthermore, the cage frequency appears evidently in Fig. 15a, b, which is different from the results in Fig. 11, and the similar results are reported in Pandya’s paper [20]. Based on the current experiment results, the VC and the BPFO are clearly presented in the frequency spectrum, which is in agreement with the theoretical analysis. The experiment results show the basic BPFO is not enough to judge an outer race local defect and the harmonic of the BPFO is more reliable to judge a local defect.

Some unusual phenomena, such as the resonance point for the vertical direction and horizontal direction, are further explained. The effect of the load device needs to be mentioned here (Fig. 16). The slide bar, acting as a guide rail, leads the vertical load on the shaft in the vertical direction. However, the friction force between the bar and the sliding block can decrease vertical displacement of the rotor. This is why the resonance amplitude value of the vertical direction is smaller than that of the horizontal direction, which is different from the theoretical results [58, 60]. In addition, the loading device constrains the horizontal displacement of the rotor, and it can be depicted as a resilience force. The bar can be regarded as a beam with two ends restrained, the effect of which on the rotor can be expressed as simple linear spring.

$$\begin{aligned} F_{x\_extra} ={k}_\mathrm{bar} x, \end{aligned}$$

(35)

Fig. 15

FFT maps and time responses in resonance regions, X stands for the shaft frequency. a Horizontal (2300 rpm) and b vertical (1650 rpm)

Considering linearized stiffness Eq. (31), the general stiffness can be depicted as

$$\begin{aligned}&\left[ {{\begin{array}{l} {{\partial F}/{\partial x}} \\ {{\partial F}/{\partial y}} \\ \end{array} }} \right] \nonumber \\&\quad =\left\{ {{\begin{array}{l} {1.5K_\mathrm{c} \sum \limits _{j=1}^{N_\mathrm{b}} {(\delta _j H(\delta _j ))^{0.5}} \cos ^{2}\theta _j +{{k}}_\mathrm{bar}} \\ {1.5K_\mathrm{c} \sum \limits _{j=1}^{N_\mathrm{b}} {(\delta _j H(\delta _j ))^{0.5}} \sin ^{2}\theta _j} \\ \end{array}}} \right. . \end{aligned}$$

(36)

It can be concluded from Eq. (36) the restraint from the slide bars can increase the equivalent stiffness of the horizontal direction. Generally, the resonance point of the vertical direction is higher than that of the horizontal direction because of the gravity action [57]. However, the additional stiffness in bold form in Eq. (36) will enlarge the resonance point. This is why the resonance point of vertical direction is lower than that of the horizontal for the experiment results. In addition, the experimental resonance points of two systems (fault-free and defective) are different that is mainly because of the radial clearance. The static radial clearances of two tested bearing are different, about 4um for the defective bearing and about 30um for the fault-free bearing. Generally, the resonance point decreases with the increase in the radial clearance [58, 63], that is why that the resonance points of the two directions of the fault-free system are lower than those of the defective system in experiment.

Fig. 16

Enlarged view of the loading device

6 Discussions and conclusions

In view of a direct problem, the frequency performance of rigid rotor–bearing systems with/without an outer race defect is studied because the VC frequency equals to the BPFO due to the internal kinematics property of a rolling bearing. A rotor–ball bearing system is an essentially nonlinear parametric excitation system affected by the varying compliance characteristic, Hertizian contact nonlinearities and clearance. The fundamental excitation for a balanced rotor–bearing system is the varying compliance excitation, so the response solution contains the basic excitation and harmonics whatever a local defect exists. The semi-analytical HB-AFT is exploited to analyze the relationship between the excitation and response. The basic excitation and their harmonics are demonstrated in the analytical solutions of the fault-free and defective system, and they are equal in frequency domain. Thus, only the basic BPFO is not reliable to judge an outer race local defect. In addition, the results show that the super-harmonic and sub-harmonic resonance tend to occur in a parametric excitation system and the resonance characteristics are revealed. Then, an experiment system is established to verify the topics of this paper from the qualitative aspect. The basic VC frequency and the BPFO are clearly exhibited in the frequency spectrums of the rotor response, which agree well with the theoretical analysis. The experiment results prove the basic BPFO is not sufficient to judge an outer race local defect, while the results show the 2BPFO is more reliable. The primary and super-harmonic resonance produced by an outer race local defect is illustrated via measuring the vibration signal in a cycle of running up and down. Therefore, the conclusions can be drawn as follows:

• (1) The BPFO equals to the VC in frequency domain, the basic BPFO is not sufficient to judge the outer race defect, while the harmonic frequency is more reliable;

• (2) The harmonics of BPFO and VC take place because of nonlinear characteristics of the rotor–bearing system;

• (3) The super-harmonic resonance occurs in a rotor–ball bearing system with an out race defect.

The results obtained in this paper will help elucidate the dynamic behaviors of rotor–ball bearing systems with an outer race defect and may make an improvement for the diagnosis of the rolling bearing.

Appendix

When the outer race is fixed, the characteristic defect frequencies for outer race are as follows [39]:

Cage rotation frequency

$$\begin{aligned} \omega _\mathrm{c} =\frac{\omega _\mathrm{s} }{2}\left( 1-\frac{d}{D}\cos \alpha \right) \end{aligned}$$

(A.1)

VC frequency

$$\begin{aligned} \omega _\mathrm{vc} =N_\mathrm{b} \omega _\mathrm{c} =\frac{N_\mathrm{b} \omega _\mathrm{s} }{2}\left( 1-\frac{d}{D}\cos \alpha \right) \end{aligned}$$

(A.2)

Outer raceway defect (BPFO)

$$\begin{aligned} \omega _{\mathrm{BPFO}} =N_\mathrm{b} \omega _\mathrm{c} =\frac{N_\mathrm{b} \omega _\mathrm{s} }{2}\left( 1-\frac{d}{D}\cos \alpha \right) \end{aligned}$$

(A.3)

where $\omega _\mathrm{s }$is the shaft rotation speed, d is the diameter of the ball, D is the pitch diameter,$\alpha$ is contact angle, $N_\mathrm{b }$is the number of the rolling element.