Introduction

Among the intensifying challenges of current world, the effectiveness and efficiency of engineering applications are becoming more prominent. Energy depletion is one of the essential concerns in the modern word. To avoid the energy loss in transportation phenomena’s, it is highly required to use efficient medium. Modern methodologies have paved the way to manufacture materials at nanoscale. Nanotechnology is the most dynamic area that fascinates the research community owing to their significant features and enabling the substantial enhancement in the performance of devices. Furthermore, outstanding characteristics of nanomaterials have contributed significantly in numerous industrial thermal exchange liquid improvements. Recently, meaningful work has been performed to produce innovative heat transfer liquid termed as nanoliquid. Nanoliquids possess higher thermal properties in comparison with base liquids. Choi (1995) was the first who established nanoliquids. Such liquids have the capability to enhance thermal conductivity and thermal performance of carrier liquids. Heat transfer improvement can be modified by type of number of submerged nanoparticles, material and shape of particle. Nanoliquids have large-scale utilization in industrial and technological processes such as nuclear reactor cooling, power generator, micro-reactors, melt-spinning, drying and cooling of papers, air planes and glass fiber technology. Nanoliquid mechanism includes numerous factors such as thermophoretic force, thermal diffusion, micro-convection, particle to particle coupling, Brownian movement and conduction which were investigated recently by several scientists. These scientists proved that nanoparticle Brownian movement is the leading factor that improves thermal characteristics and energy productivity of liquids. Some literature regarding nanoliquid flow has been studied. Sheikholeslami et al. (2014) studied the flow of \({\text{CuO}}\) water nanofluid and transfer of heat considering the aspects of Lorentz forces. Khan and Khan (2014) reported heat sink–source aspects for 3D non-Newtonian nanofluid. Ellahi et al. (2015) examined the effect of nanosize particle for CO–H2O over inverted vertical cone. Khan et al. (2016), Khan and Khan (2015, 2016) described properties of nanofluid by considering different non-Newtonian fluid models. Waqas et al. (2016) investigated the flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Khan and Khan (2016) presented characteristics of Burgers fluid by considering features of nanomaterials. Sulochana et al. (2017) analyzed the consequences of thin din needle with joule heating. Hayat et al. (2017) worked on the effects of applied magnetic field on nanofluid flow due to exponential stretching sheet with effect of thermal radiation. Sheikholeslami and Shehzad (2017) explored properties of nanofluid by considering characteristics of Lorentz force. Some recent developments on nanofluid have been discussed in Refs. (Sheikholeslami and Shamlooei 2017; Sheikholeslami and Rokni 2017; Irfan et al. 2018; Hayat et al. 2018; Sheikholeslami et al. 2018; Gireesha et al. 2018; Mahanthesh et al. 2018; Sheikholeslami 2018a, b; Akbar and Khan 2016; Sheikholeslami and Shehzad 2018a, b; Sheikholeslami and Sadoughi 2018; Sheikholeslami and Seyednezhad 2018; Irfan et al. 2018, 2019; Khan et al. 2018; Sheikholeslami and Rokni 2018; ; 2019; Sheikholeslami et al. Sheikholeslami 2019a, b; Khan et al. 2019; Sheikholeslami et al. 2019; Sheikholeslami and Mahian 2019; Nematpour Keshteli and Sheikholeslami 2019).

A chemical reaction is a process (reversible/irreversible) that generates entropy. Many chemical reaction systems, homogeneous and heterogeneous, catalytic and non-catalytic, and single and multiple, are categorized with respect to their chemical and physical properties. The homogeneous reactions are uniform consisting a single phase space; it may be gas, liquid or solid. Unlike homogeneous reactions, the heterogeneous reactions are not uniform in nature. The homogeneous reaction can be the component of heterogeneous reaction. The homogeneous/heterogeneous mixture of chemical reaction system has received much attention from researchers due to its widespread applications in industrial process, biochemical system and catalysis. Khan et al. (2016, 2017) examined feature chemical process for non-Newtonian fluids. Mahanthesh et al. (2017) revealed properties of nanofluid for vertical plate. Impact of chemical processes and modified heat flux relation was studied by Sohail et al. (2017). Ramesh et al. (2018) considered chemical processes and zero mass flux relation for Maxwell nanoliquid. Irfan et al. (2018) studied aspects of chemical processes for Carreau fluid with heat sink–source and variable conductivity. Non-Newtonian nanofluid with aspects of activation and chemical processes was investigated by Khan et al. (2018). Irfan et al. (2019) discussed the heterogeneous–homogeneous reactions for Oldroyd-B fluid.

Keeping in prospect of beforehand mentioned published works, it is detected that entropy generation aspects for Cross fluid have not yet been examined. Therefore, the main theme of existing consideration is to colloidal and entropy generation aspects for Cross material. Transportation of heat is examined through heat sink–source aspects. Effects of viscous dissipation and thermal radiation are also taken into account. Physical interpretation of involved parameters in modeled problem is inspected via graphs.

Formulation

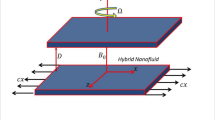
Here aspects of activation energy and entropy generation minimization for radiative flow of Cross nanomaterial in the presence of Lorentzís forces are considered. Mathematical formulation is based on thermophoresis and Brownian motion. Moreover, viscous dissipation and radiation features in energy expression are taken into account. Arrhenius activation energy is also a part of discussion. Governing problem for the present situation is listed as

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} & = \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] +\upsilon \left( {1 - \beta^{ * } } \right)\,\frac{\partial u}{\partial y}\frac{\partial }{\partial y}\left[ {\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right]\, \\ & - \frac{{\sigma^{ * } B_{0}^{2} }}{{\rho_{\text{f}} }}u + g\left[ {A_{1} \left( {T - T_{\infty } } \right) + A_{2} \left( {C - C_{\infty } } \right)} \right], \\ \end{aligned}$$
(2)
$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} & = \frac{v}{{c_{\text{p}} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] + \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} \\ & + \tau D_{\text{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} - \frac{1}{{(\rho c)_{\text{f}} }}\frac{{\partial q_{\text{w}} }}{\partial y}, \\ \end{aligned}$$
(3)
$$\begin{aligned} u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} & = \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} \\ & - k_{\text{r}}^{2} \left( {C - C_{\infty } } \right)\,\left( {\frac{T}{{T_{\infty } }}} \right)^{m} \exp \left( { - \frac{{E_{\text{a}} }}{\kappa T}} \right), \\ \end{aligned}$$
(4)

with

$$u = U_{\text{w}} = cx,\;v = 0,\;T = T_{\text{w}} ,\;D_{\text{B}} \frac{\partial C}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{\partial y} = 0\;{\text{at}}\;{\text{y = 0,}}$$
(5)
$$u \to 0, \, T \to T_{\infty } ,\,\;C \to C_{\infty } \;{\text{as }}y \to \infty .$$
(6)

Considering

$$\begin{aligned}& \eta = y\sqrt {\frac{c}{v},} \;v = - \sqrt {cv} f(\eta ),\,u = cxf^{{^{\prime } }} (\eta ) \\ &\theta (\eta ) = \frac{{T_{\infty } - T}}{{T_{\infty } - T_{\text{w}} }},\, \, \varphi (\eta ) = \frac{ C-{C_{\infty }}}{{C_{\infty } }}. \, \\ \end{aligned}$$
(7)

One has

$$\begin{aligned} \left[ {\beta^{ * } \left\{ {1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} } \right\}^{2} + \left( {1 - \beta^{ * } } \right)\,\left\{ {1 + \left( {1 - n} \right)\,\left( {Wef^{{^{\prime \prime } }} } \right)^{n} } \right\}} \right]f^{{^{\prime \prime \prime } }} \hfill \\ -\left[ {1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} } \right]^{2} \left[ {f^{{^{\prime } 2}} + ff^{{^{\prime \prime } }} + \lambda \left( {\theta + Nr\phi } \right)} \right] = 0, \hfill \\ \end{aligned}$$
(8)
$$\left( {1 + \frac{4}{3}R} \right)\,\theta^{{^{\prime \prime } }} + \mathop {\Pr }\limits \left[ {f\theta^{{^{\prime } }} + Nb\theta^{{^{\prime } }} \phi^{{^{\prime } }} +\, Nt\theta^{{^{\prime } 2}} + Ecf^{{^{\prime \prime } 2}} \beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{{Ecf^{{^{\prime \prime } 2}} }}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right] = 0$$
(9)
$$\phi^{{^{\prime \prime } }} + Sc\left[ {f\phi^{{^{\prime } }} + \frac{Nt}{Nb}\theta^{{^{\prime \prime } }} - \sigma \left( {1 + \delta \theta } \right)^{m} \phi \exp \left( { - \frac{E}{1 + \delta \theta }} \right)} \right] = 0$$
(10)
$$f\left( 0 \right) = 0,\, \, \;f^{{^{\prime } }} \left( 0 \right) - 1 = 0,\,\; \, f^{{^{\prime } }} \left( \infty \right) \to 0,$$
(11)
$$\theta \left( 0 \right) = 1,\, \, \theta \left( \infty \right) \to 0$$
(12)
$$Nb\phi^{{^{\prime } }} \left( 0 \right) = - Nt\theta^{{^{\prime } }} \left( 0 \right),\,\phi \left( \infty \right) \to 0.$$
(13)

Non-dimensional form of variables occurring in Eqs. (8)–(13) is given below:

$$\begin{aligned} M = & \frac{{\sigma^{ * } B_{0}^{2} }}{{\rho_{\text{f}} c_{\text{f}}}},\mathop {Pr}\limits = \frac{\nu }{\alpha },\,R = \frac{{4\sigma^{ * * } T_{\infty }^{3} }}{{k^{\text{*}} k }},\,Nb = \frac{{\tau D_{\text{B}} \left({C_{\infty } } \right)}}{\upsilon },\,Nt = \frac{{\tau D_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\nu T_{\infty } }},\,\sigma = \frac{{kr^{2} }}{c},\, \\ Ec = & \frac{{c^{2} x^{2} }}{{c_{\text{p}} \left( {T_{\text{w}} - T_{\infty } } \right)}},\,We =\sqrt{ \frac{\varGamma^{ 2 } c^{3}x^{2}}{\nu }},\,Sc = \frac{\nu }{{D_{\text{B}} }},\,E = \frac{{E_{\text{a}} }}{{\kappa T_{\infty } }},\,\delta = \frac{{T_{\text{w}} - T_{\infty } }}{{T_{\infty } }},\,\beta^{ * } = \frac{{\mu_{\infty } }}{{\mu_{0} }}. \\ \end{aligned}$$
(14)

Physical quantities

Mathematically, the expression of Nusselt and Sherwood numbers \(\left( {C_{fx} ,\,Nu_{x} } \right)\) in dimensional form is:

$$C_{fx} = \frac{{\tau_{\text{w}} }}{{\rho_{\text{f}} U_{\text{w}}^{2} }},$$
(15)
$$Nu_{x} = \frac{{xq_{\text{w}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}},$$
(16)

where

$$\tau_{\text{w}} = \mu \frac{\partial u}{\partial y}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right],$$
(17)
$$q_{\text{w}} = - k\frac{\partial T}{\partial y} - \frac{{16\sigma^{ * * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{\partial T}{\partial y}.$$
(18)

From Eqs. (17) and (18), one obtains:

$$C_{fx} Re_{x}^{1/2} = \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + \left( {Wef^{{^{\prime \prime } }} \left( 0 \right)} \right)^{n} }}} \right]\,f^{{^{\prime \prime } }} \left( 0 \right),$$
(19)
$$Nu_{x} Re_{x}^{ - 1/2} = - \left[ {1 + \frac{4}{3}R} \right]\,\theta^{{^{\prime } }} \left( 0 \right),$$
(20)

where \(Re_{x} = \tfrac{{xU_{w} }}{\nu }.\)

Analysis of entropy generation

Mathematical relation of volumetric entropy generation for Cross fluid in dimensional form is expressed as

$$\begin{aligned} S_{\text{G}}=\frac{{k }}{{T_{\infty }^{2} }}\left[ {1 + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k k^{ * } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \frac{\mu }{{T_{\infty } }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\,\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right]\, \\ + \frac{{\sigma^{ * } B_{0}^{2} u^{2} }}{{T_{\infty } }} + \frac{RD}{{C_{\infty } }}\left( {\frac{\partial C}{\partial y}} \right)^{2} + \frac{RD}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}} \right). \\ \end{aligned}$$
(21)

In dimensionless, one has:

$$\begin{aligned} N_{\text{G}} & = \alpha_{1} \left[ {1 + \frac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + Br\left[ {\beta^{ * } + \frac{{\left( {1 - \beta^{ * } } \right)}}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right]\,f^{{^{\prime \prime } 2}} \\ & + MBrf^{{^{\prime } 2}} + \frac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} , \\ \end{aligned}$$
(22)

where

$$Br = \frac{{\mu U_{\text{w}}^{2} }}{\kappa \Delta T},\quad \alpha_{1} = \frac{\Delta T}{{T_{\infty } }},\quad N_{\text{G}} = \frac{{\nu T_{\infty } S_{\text{G}} }}{\kappa c\Delta T},\quad L = \frac{{RC_{\infty }D}}{{k }}.$$
(23)

\(Be\) is expressed as

$$Be = \frac{\text{Entropy generation subject to heat and mass transfer}}{\text{Total entropy generation}},$$
(24)
$$Be = \frac{{\alpha_{1} \left[ {1 + \tfrac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} }}{{\alpha_{1} \left[ {1 + \tfrac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + Br\left[ {\beta^{ * } + \tfrac{{1 - \beta^{ * } }}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right]\,f^{{^{\prime \prime } 2}} + MBrf^{{^{\prime } 2}} + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} }}.$$
(25)

Discussion

Here our emphasis is to scrutinize features of entropy generation for Cross nanofluid. Transportation of heat is analyzed in the presence of heat sink–source and radiation aspects. Set of Eqs. (8)–(13), (22) and (15) along with associated conditions are tackled numerically via MATLAB tool bvp4c.

Nanofluid velocity profiles

Figure 1 reveals the features of \(We\) on \(f^{{^{\prime } }} .\) We observed from obtained data that \(f^{{^{\prime } }}\) enhances via larger \(We\) for shear thinning liquid. Figure 2 is plotted to scrutinize the impact of \(\beta^{ * }\) on \(f^{{^{\prime } }} .\) We observed that \(f^{{^{\prime } }}\) enhances for higher estimation of \(\beta^{ * } .\) Analysis for features of \(Nr\) on \(f^{{^{\prime } }}\) is addressed in Fig. 3. Here \(f^{{^{\prime } }}\) is increasing function for larger \(Nr.\) The curve of \(f^{{^{\prime } }}\) for different values of \(\lambda\) is investigated in Fig. 4. We noticed an improvement in \(f^{{^{\prime } }}\) subject to larger \(\lambda .\) Physically, the enhancement in buoyancy forces yields higher liquid velocity. The impact of \(M\) on \(f^{{^{\prime } }}\) is presented in Fig. 5. Here \(f^{{^{\prime } }}\) decays via larger \(M\). The liquid velocity is much smaller in hydromagnetic case when compared with hydrodynamic case. It is due to the fact that Lorentz force becomes stronger when \(M\) increases. Therefore, stronger Lorentz force creates resistance to transport phenomenon which is accountable for diminishment in the velocity \(f^{{^{\prime } }}\).

Fig. 1
figure 1

\(f^{{^{\prime } }}\) impact for different \(We\)

Full size image
Fig. 2
figure 2

\(f^{{^{\prime } }}\) impact for different \(\beta^{ * }\)

Full size image
Fig. 3
figure 3

\(f^{{^{\prime } }}\) impact for different \(Nr\)

Full size image
Fig. 4
figure 4

\(f^{{^{\prime } }}\) impact for different \(\lambda\)

Full size image
Fig. 5
figure 5

\(f^{{^{\prime } }}\) impact for different \(M\)

Full size image

Nanofluid temperature profiles

Figure 6 interprets \(\theta\) variation for \(Ec\). Here \(\theta\) augments when \(Ec\) is increased. Relation between the flow of enthalpy difference and KE (kinetic energy) is called Eckert number. It elaborates change of KE (kinetic energy) into internal energy by work done versus the viscous liquid stresses. The larger \(Ec\) causes loss of heat from the plate to the liquid, i.e. cooling of the plate. In other words, larger energy dissipation produces higher liquid temperature. Features of \(Pr\) on \(\theta\) is exhibited in Fig. 7. Here \(\theta\) decays when \(Pr\) is increased. In fact, larger \(Pr\) reduces the thermal diffusivity which accordingly decay liquid temperature. Figure 8 portrays the impact of \(Nt\) on \(\theta .\) Clearly, larger \(Nt\) yields higher \(\theta .\) Physically, small number of particles are pulled away from hot region to cold one in thermophoresis phenomenon. Hence, a large number of nanomaterials are moved away from the heated region which inflates the liquid temperature. The role of \(R\) on \(\theta\) is explored in Fig. 9. Clearly, a rise in \(R\) augments \(\theta .\) Physically, radiation process produces more heat in the working liquid; therefore, \(\theta\) and related thermal layer thickness enhance. Figure 10 is plotted to examine the impact of \(\beta^{ * }\) on \(\theta .\) We observed that \(\theta\) decreases for higher estimation of \(\beta^{ * } .\)

Fig. 6
figure 6

\(\theta\) impact for different \(Ec\)

Full size image
Fig. 7
figure 7

\(\theta\) impact for different Pr

Full size image
Fig. 8
figure 8

\(\theta\) impact for different \(Nt\)

Full size image
Fig. 9
figure 9

\(\theta\) impact for different \(R\)

Full size image
Fig. 10
figure 10

\(\theta\) impact for different \(\beta^{ * }\)

Full size image

Nanofluid concentration profiles

Figure 11 depicts the behavior of \(E\) for \(\phi .\) It is examined that the term \(\exp \left( { - \tfrac{{E_{\text{a}} }}{\kappa T}} \right)\) decreases for higher estimation of \(E_{\text{a}}\). This eventually generates a chemical reaction due to which \(\phi\) improves. Figure 12 is plotted to examine the impact of \(\sigma\) on \(\phi .\) We observed that \(\phi\) enhances for higher estimation of \(\sigma\). Actually, the consumption of reactive species decays rapidly for larger \(\sigma\). The impacts of \(N_{\text{t}}\) and \(N_{\text{b}}\) on \(\phi\) are interpreted in Figs. (13 and 14). For larger \(N_{\text{t}}\) and thickness of nanoparticles, concentration boundary layer escalates. Actually, thermophoretic force increases for higher estimation of \(N_{\text{t}}\) due to which nanoparticles moves from higher to lower temperature and boosts up (See Fig. 13). Moreover, \(\phi\) and its associated concentration layer reduce when \(N_{\text{b}}\) is increased (See Fig. 14).

Fig. 11
figure 11

\(\varphi\) impact for different \(E\)

Full size image
Fig. 12
figure 12

\(\varphi\) impact for different \(\sigma\)

Full size image
Fig. 13
figure 13

\(\varphi\) impact for different \(N_{\text{b}}\)

Full size image
Fig. 14
figure 14

\(\varphi\) impact for different \(N_{\text{t}}\)

Full size image

Entropy generation rate and Bejan number

Figures 15 and 16 depict the salient features of \(Br\) on \(N_{\text{G}}\) and \(Be.\) In fact, Brinkman number \(Br\) has characteristic to propagate heat by viscous flowing liquid to heat transport through molecular conduction, e.g. in polymer processing. Heat transport via molecular conduction is much greater than heat propagation via viscous effects. Consequently, movement of liquid particles generates more heat between the adjacent layers. It enhances the entropy and system disorderness (see Fig. 15). Figure 16 displays that \(Be\) decays via larger \(Br.\) It is due to the fact that larger \(Br\) corresponds to increase in entropy rate which decays the \(Be.\) Figure 17 reports the impact of \(L\) on \(N_{\text{G}} .\) Clearly, \(N_{\text{G}}\) shows a decreasing trend for \(L\). Figure 18 discloses the characteristics of \(M\) on \(N_{\text{G}} .\) Here, it is noticed that \(N_{\text{G}}\) augments when \(M\) is increased. Physically, rise in \(M\) creates greater Lorentz force due to which resistance in liquid flow increases and \(N_{\text{G}}\) enhances. Figure 19 Illustrates the characteristics of \(\alpha_{1}\) on \(N_{\text{G}} .\) Here, \(N_{\text{G}}\) enhances via larger \(\alpha_{1}\). Physically, liquid temperature increases for larger \(\alpha_{1}\) which accordingly enhances entropy generation rate. The curves of \(\alpha_{2}\) on \(N_{G}\) is displayed in Fig. 20. It is evaluated that liquid concentration increases when \(\alpha_{2}\) is increased and consequently \(N_{\text{G}}\) enhances. Figures 21 reveals the impact of \(R\) on \(Be.\) Here, \(Be\) enhances when \(R\) is augmented.

Fig. 15
figure 15

\(N_{\text{G}}\) impact for different \(Br\)

Full size image
Fig. 16
figure 16

\(Be\) impact for different \(Br\)

Full size image
Fig. 17
figure 17

\(N_{\text{G}}\) impact for different \(L\)

Full size image
Fig. 18
figure 18

\(N_{\text{G}}\) impact for different \(M\)

Full size image
Fig. 19
figure 19

\(N_{\text{G}}\) impact for different \(\alpha_{1}\)

Full size image
Fig. 20
figure 20

\(N_{\text{G}}\) impact for different \(\alpha_{2}\)

Full size image
Fig. 21
figure 21

\(Be\) impact for different \(R\)

Full size image

Features of drag force and heat transportation rate

Table 1 portrays the influences of \(We,\,\;\lambda ,\;\,n,\;\,Nr,\,\;M\) and \(\beta^{ * }\) on surface drag force. Here, surface drag force enhances via larger \(We\) and \(M\), whereas it decays for larger \(\lambda ,\) \(n,\) \(Nr\) and \(\beta^{ * }\). Table 2 points out the features of several embedded physical parameters on heat transfer rate. It is examined that heat transfer rate increases via larger \(Pr\) and \(R\), whereas it decays for larger \(Ec,\) \(\beta^{ * } ,\,\;Nt\) and \(Nb\).

Table 1 Computational outcomes of surface drag forces (Re1/2\(C_{fx}\))
Full size table
Table 2 Computational outcomes for rate of heat transfer (Re−1/2Nu)
Full size table

Conclusions

This research scrutinizes the influence of entropy generation minimization for Cross nanoliquid with Joule heating. Thermal radiation, thermophoresis and Brownian movement are taken into account for modeling and analysis. This research leads to following outcomes:

  • Liquid velocity is decreasing function for larger \(We\).

  • Increments in \(R_{\text{d}}\) intensifies liquid temperature.

  • Thermal and nanoparticle profiles are boosted via larger \(Nt\) .

  • Stronger Lorentz’s force leads to higher entropy generation rate while decays for Bejan number.

  • Larger Brinkman gives rise to entropy generation rate in comparison with Bejan number.

  • Surface drag force reduces for larger magnetic parameter.

  • Heat transfer rate enhances via larger Prandtl number and radiative parameter when compared with Eckert number and thermophoretic parameter.