1 Introduction

Nowadays, the dynamics of non-Newtonian liquids is a subject of abundant researches for the scientists and engineers due to its practical implementation. The technological and industrial applications of such liquids include molten polymers, drilling muds, volcanic lava, oils, certain paints, liquid suspensions, cosmetic products, poly crystal melts, food stuffs and many more. The flow phenomenon of such materials can be elaborated by the nonlinear relationships of shear rate and shear stresses. The viscosity of such liquids is shear dependent. The Carreau liquid model is one of the non-Newtonian liquid models which have the constitutive relationship for both high and low shear rates. This fact enhanced the utilization of Carreau model in technological and industrial processes. Hsu et al. [1] developed a model to describe the importance of electrophoresis on Carreau liquid in a spherical cavity. Peristaltic motion in an asymmetric channel filled with Carreau fluid has been addressed by Ali and Hayat [2]. Shamekhi and Sadeghy [3] explored characteristics of Carreau-Yasuda liquid in a cavity by employing PIM mesh-free method. The flow phenomenon of Carreau fluid over an inclined free surface has been reported by Tshehla [4]. Olajuwon [5] described the analysis convective heat and mass transport in magnetohydrodynamic flow of Carreau liquid induced by a porous plat. He also examined the thermal diffusion and radiation effects in this study. The boundary layer flow analysis of Carreau liquid due to a convectively heated sheet has been made by Hayat et al. [6]. Magnetohydrodynamic (MHD) Falkner-Skan wedge flow of Carreau liquid with cross-diffusion effects is presented by Raju and Sandeep [7]. Machireddy and Naramgari [8] examined the characteristics of cross-diffusion in MHD flow of Carreau liquid over a stretched surface with Robin boundary condition. Stagnation point flow of Carreau nanofluid with transpiration is explored by Sulochana et al. [9]. Raju and Sandeep [10] studied the three-dimensional (3D) flow of Casson-Carreau fluids over a stretched surface subject to homogeneous/heterogeneous reactions and nonlinear thermal radiation. Hayat et al. [11] explored the stretching flow phenomenon of Carreau nanoliquid.

The stagnation point flow arises whenever a flow imposes on a solid object. The motion of liquid near stagnation region is described by stagnation point flow which exists for both cases of moving or fixed body in a liquid. Hiemenz [12] firstly explored the phenomenon of stagnation point flow over a stationary semi-infinite wall. He demonstrated that the Navier–Stokes expressions which govern the flow can be converted into ordinary differential equations by the utilization of similarity transformation. Mahaputra and Gupta [13] studied the heat transport analysis of stagnation point flow over a moving sheet. Nazar et al. [14] studied the flow of micropolar fluid over a stretched sheet. Mustafa et al. [15] studied the stagnation point flow of a nanofluid towards a stretching surface. Alsaedi et al. [16] achieved the results for the effects of heat sink/source of nanofluid near a stagnation point over a surface with convective conditions. Turkyilmazoglu and Pop [17] investigated the boundary layer flow of Jeffrey fluid near a stagnation point over a shrinking/stretching sheet. Hayat et al. [18] addressed the stagnation point flow of second grade liquid. Shehzad et al. [19] reported the effect of chemical reaction in steady stagnation point flow of thixotropic liquid.

The aim of this investigation is to make an analysis of mixed convective stagnation point flow of Carreau liquid over a stretched sheet. The governing mathematical expressions are coupled due to occurrence of mixed convection. Analytical solutions via homotopy analysis method (HAM) [20–29] are constructed. Relevant convergence criteria of solutions is established and examined. Plots of various quantities are elaborated and discussed.

2 Mathematical formulation

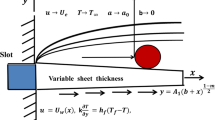
Here, we consider the two-dimensional steady mixed convection flow of an incompressible Carreau liquid towards a stretched surface near a stagnation point. The sheet is stretched in such a manner that \(x\)-axis is along the surface of sheet and \(y\)-axis perpendicular to it. An incompressible fluid flow is confined to y > 0. The thermo-physical characteristics of liquid at surface are taken variable. The constitutive relation for Carreau material is [6]:

$${\varvec{\uptau}} = \left[ {\eta_{0} \left( {1 + \lambda^{2} \dot{\gamma }^{2} } \right)^{{\frac{n - 1}{2}}} } \right]{\mathbf{A}}_{1} ,$$
(1)

where

$${\mathbf{A}}_{1} = \nabla {\mathbf{V + }}\left( {\nabla {\mathbf{V}}} \right)^{tr} ,$$
(2)
$$\dot{\gamma } = \sqrt {\frac{1}{2}tr\left( {{\mathbf{A}}_{1} } \right)^{2} ,}$$
(3)
$${\mathbf{V = }}\left[ {u\left( {x,\,y} \right),\,v\left( {x,\,y} \right),\,0} \right],$$
(4)
$$\dot{\gamma }^{2} = 2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} ,$$
(5)

or

$$\dot{\gamma }^{2} = 4\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} .$$
(6)

Now

$${\mathbf{\tau = }}\eta_{0} \left[ {1 + \lambda^{2} \left\{ {4\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right\}} \right]^{{\tfrac{n - 1}{2}}} {\mathbf{A}}_{1} ,$$
(7)

with

$${\varvec{\uptau}}_{xx} = 2\eta_{0} \left[ {1 + \lambda^{2} \left\{ {4\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right\}} \right]^{{\tfrac{n - 1}{2}}} \frac{\partial u}{\partial x},$$
(8)
$${\varvec{\uptau}}_{xy} = \eta_{0} \left[ {1 + \lambda^{2} \left\{ {4\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right\}} \right]^{{\tfrac{n - 1}{2}}} \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)={\varvec{\uptau}}_{yx} ,$$
(9)
$${\varvec{\uptau}}_{yy} = 2\eta_{0} \left[ {1 + \lambda^{2} \left\{ {4\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right\}} \right]^{{\tfrac{n - 1}{2}}} \frac{\partial v}{\partial y}.$$
(10)

Since

$$\rho( \nabla {\mathbf{.V }}) = \nabla {\mathbf{.\tau }},$$
(11)

so inserting Eqs. (4), (8) and (9) in Eq. (11) we obtain

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \left( {\frac{n - 1}{2}} \right)\,\lambda^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]$$
$$+\, \nu (n - 1)\lambda^{2} \left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} } \right)\,\left( {1 + \left( {\frac{n - 3}{2}} \right)\,\lambda^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right).$$
(12)

Two-dimensional flow equations for Carreau liquid in the presence of stagnation point, variable viscosity, mixed convection, thermal radiation and temperature-dependent thermal conductivity are:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(13)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{1}{\rho }\frac{\partial }{\partial y}\left( {\eta_{0} \left( T \right)\,\frac{\partial u}{\partial y}} \right)+\nu\frac{{\partial^2 u}}{{\partial y^2 }}\left[ {1 + \left( {\frac{n - 1}{2}} \right)\,\lambda^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} }\right]+(n-1)\lambda^2 \left[\frac{\partial^2 u}{\partial y^2}\left(\frac{{\partial u}}{{\partial y }}\right)^2\right] \left[ {1 + \left( {\frac{n - 3}{2}} \right)\,\lambda^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]$$
$$+ u_{e} \frac{{{\text{d}}u_{e} }}{{{\text{d}}x}} + g\beta_{T} \left( {T - T_{\infty } } \right),$$
(14)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{1}{{\rho c_{p} }}\frac{\partial }{\partial y}\left( {K\left( T \right)\,\frac{\partial T}{\partial y}} \right) + \frac{{16\sigma^{ * } }}{{3k^{ * } \rho c_{p} }}\frac{\partial }{\partial y}\left( {T^{3} \frac{\partial T}{\partial y}} \right),$$
(15)
$$\begin{aligned} u = & u_{w} (x) = cx,\quad \, \, v = v_{w} ,\,\quad \, T = T_{w} \left( x \right) = T_{\infty } + bx\quad {\text{ at}}\quad \, y = 0,\, \\ u \to & u_{e} (x) = ax,\quad \, \, T \to T_{\infty } \, \quad {\text{as}}\quad \, y \to \infty . \\ \end{aligned}$$
(16)

In the above equations, u and v denote the velocity components in the x and y-directions, respectively, λ the time constant, T the fluid temperature, \(\nu\) the kinematic viscosity, ρ the density, \(c_{p}\) the specific heat, η0(T) the variable dynamic viscosity depending on temperature, g the gravitational acceleration, \(\beta_{\text{T}}\) the thermal expansion coefficient, the \(\sigma^{*}\) Steafan-Boltzmann constant, \(k^{ * }\) the mean absorption coefficient, (a, b, c) the dimensional constants, \(v_{\text{w}}\) is the mass transfer velocity and \(T_{\text{w}}\) the variable temperature at the sheet and \(T_{\infty }\) the ambient temperature. The constant mass transfer velocity is taken as \(v_{\text{w}} .\) Here \(v_{\text{w}} > 0\) denotes injection or blowing, \(v_{\text{w}} < 0\) for suction and \(u_{e}\) the free stream velocity.

Thermal conductivity \(K(T)\) and variable viscosity \(\eta_{0} \left( T \right)\) are [30, 31]:

$$K\left( T \right) = k_{\infty } \left( {1 + \varepsilon \frac{{T - T_{\infty } }}{\Delta T}} \right),\, \,$$
(17)
$$\frac{1}{\eta_{0} \left( T \right)} = \frac{1}{{\eta_{\infty } }}\left[ {1 + \gamma \left( {T - T_{\infty } } \right)} \right],$$
(18)

or

$$\frac{1}{\eta_{0} \left( T \right)} = \delta \left( {T - T_{r} } \right),$$
(19)

where

$$\delta = \frac{\gamma }{{\eta_{\infty } }}\quad {\text{ and}}\quad \, T_{\text{r}} = T_{\infty } - \frac{1}{\gamma },$$
(20)

here \(k_{\infty }\) is the thermal conductivity of the ambient fluid, \(\varepsilon\) is a small scalar parameter which portrays the impact of temperature on variable thermal conductivity, \(\Delta T = T_{\text{w}} - T_{\infty } ,\) \(\eta_{\infty }\) the ambient dynamic viscosity, γ the thermal property of fluid, \(\left( {\delta ,\,T_{\text{r}} } \right)\) are the constants and their values depend upon the thermal state and thermal property, i.e., γ. Also δ > 0 for liquids and δ < 0 for gases.

To transform the above problem in dimensionless form, we employ

$$\eta = y\sqrt {\frac{c}{\nu },} \, \quad u = cxf^{\prime}\left( \eta \right),\,\quad \, v = - \sqrt {c\nu } f^{\prime}\left( \eta \right),\quad \, \, \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}.$$
(21)

The continuity Eq. (13) is identically satisfied, and the resulting problems in f and θ are reduced to the following forms

$$f^{{^{\prime \prime \prime } }} \left[ {1 + \left( {\frac{n - 1}{2}} \right)\,\lambda_{1} f^{{^{\prime \prime } 2}} } \right) + 2\left( {\left( {\frac{n - 1}{2}} \right)\,\lambda_{1} f^{{^{\prime \prime } 2}} } \right)\,\left( {1 + \left( {\frac{n - 3}{2}} \right)\,\lambda_{1} f^{{^{\prime \prime } 2}} } \right]$$
$$+ \left( {\frac{{\theta^{\prime} }}{{\theta_{r} - \theta }}} \right)\,f^{\prime\prime} + \left( {\frac{{\theta_{r} - \theta }}{{\theta_{r} }}} \right)\,\left( {ff^{{^{\prime \prime } }} - f^{{^{\prime } 2}} } + G\theta + A^{2}\right) = 0,$$
(22)
$$\left( {1 + \frac{4}{3}N + \varepsilon \theta } \right)\,\theta^{\prime\prime} + \varepsilon \theta^{\prime 2} + \mathop {\Pr }\limits \left( {f\theta^{\prime} - f^{\prime}\theta } \right) = 0,$$
(23)
$$\begin{aligned} f = & S,\quad f^{\prime } = 1,\quad \theta = 1\quad {\text{at}}\quad \eta = 0,\, \\ f^{\prime } = & A,\quad \, \theta = 0\quad {\text{as}}\quad \eta \to \infty , \\ \end{aligned}$$
(24)

where prime signifies differentiation with respect to η and dimensionless quantities can be expressed as follows:

$$\begin{aligned} & \lambda_{1} = \lambda^{2} c^{2} ,\quad S = - \frac{{v_{\text{w}} }}{{\sqrt {c\nu } }},\quad \mathop {\Pr }\limits = \frac{{\nu }}{\alpha},\, \, \theta_{\text{r}} = \frac{{T_{\text{r}} - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }} = - \frac{\eta_{\infty}}{{\gamma \left( {T_{\text{w}} - T_{\infty } } \right)}},\quad G = \frac{{Gr_{x} }}{{Re_{x}^{2} }} = \frac{{g\beta_{T} b}}{{c^{2} }},\, \\ & Gr_{x} = \frac{{g\beta_{\text{T}} (T_{\text{w}} - T_{\infty } )x^{3} }}{{\nu^{2} }},\quad Re_{x} = \frac{{u_{\text{w}} (x)x}}{\nu },\quad A = \frac{a}{c},\quad N = \frac{{4\sigma^{ * } T_{\infty }^{3} }}{{k^{ * } K\left( T \right)}}. \\ \end{aligned}$$
(25)

Here, λ 1 denotes the material parameter, S the mass transfer parameter with S > 0 for suction and S < 0 for injection, Pr the Prandtl number, θ r the variable viscosity parameter, G the mixed convection parameter, Gr x the Grashof number, Re x the Reynolds numbers, A the ratio of rate constants and N the thermal radiation parameter.

The terms \(\left( {1 + \tfrac{4}{3}N} \right)\) and Pr in Eq. (23) can be combined. In this way, a single parameter is obtained i.e. \(\Pr_{\text{eff}} = \tfrac{3\Pr }{3 + 4N}.\) Hence Eq. (23) takes the form [32, 33]:

$$\theta^{\prime\prime} + { \Pr }_{\text{eff}} \left( {f\theta^{\prime} - f^{\prime}\theta } \right) + \varepsilon \theta \theta^{\prime\prime} + \varepsilon \theta^{{\prime^{2} }} = 0,$$
(26)

in which \(\Pr_{\text{eff}}\) is known as the effective Prandtl number. Benefit of aforementioned combination is that effects of linear radiation are neglected and the problem reduces to the case of without radiation. Idea of such combination can be found in the analysis provided in [32, 33].

The skin friction coefficient C f and local Nusselt number Nu x are defined as

$$C_{\text{f}} = \frac{{\tau_{\text{w}} }}{{\tfrac{1}{2}\rho u_{\text{w}}^{2} }},\quad Nu_{\text{x}} = - \frac{{xq_{\text{w}} }}{{K\left( T \right)\left( {T_{\text{w}} - T_{\infty } } \right)}},$$
(27)

where

$$\tau_{\text{w}} = \eta_{0} \left( T \right)\,\left[ {\left( {\frac{\partial u}{\partial y}} \right) + \left( {\frac{n - 1}{2}} \right)\,\lambda^{2} \left\{ {\begin{array}{*{20}c} {\tfrac{\partial u}{\partial y}\left( {\tfrac{\partial u}{\partial x}} \right)^{2} + } \\ {3\tfrac{\partial v}{\partial x}\left( {\tfrac{\partial u}{\partial y}} \right)^{2} } \\ \end{array} } \right\}} \right]_{y = 0} ,\quad q_{\text{w}} = - \left( {K\left( T \right) + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}} \right)\,\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} .$$
(28)

In terms of dimensionless form one has

$$C_{f} Re_{x}^{{\tfrac{1}{2}}} = \left( {\frac{{\theta_{r} }}{{\theta_{r} - 1}}} \right)\,\left( {1 + \left( {\frac{n - 1}{2}} \right)\,\lambda_{1} \left( {f^{\prime}\left( 0 \right)} \right)^{2} } \right)\,f^{{^{\prime \prime } }} (0),\, \, Re_{x}^{{ - \tfrac{1}{2}}} Nu_{x} = - \left( {1 + \frac{4}{3}N} \right)\,\theta^{\prime}\left( 0 \right).$$
(29)

3 Series solutions

The initial guesses and auxiliary linear operators are given below:

$$f_{0} (\eta ) = A\eta + \left( {1 - A} \right)\,\left( {1 - {\text{e}}^{ - \eta } } \right),\quad \theta_{0} (\eta ) = {\text{e}}^{ - \eta } ,$$
(30)
$$L_{\text{f}} = f^{\prime\prime\prime} - f^{\prime},\quad L_{\theta } = \theta^{\prime\prime} - \theta .$$
(31)

The above auxiliary linear operators satisfy the following properties

$$\begin{aligned} L_{\text{f}} (C_{1} + C_{2} {\text{e}}^{\eta } + C_{3} {\text{e}}^{ - \eta } ) = \,0, & \\ \, L_{\theta } (C_{4} {\text{e}}^{\eta } + C_{5} {\text{e}}^{ - \eta } ) = 0, & \\ \end{aligned}$$
(32)

where C i (i = 1–5) indicate the arbitrary constants.

The corresponding problems at the zeroth order are given in the following forms [22–24]:

$$\left( {1 - p} \right)L_{f} \left[ {\hat{f}(\eta ;\,p) - f_{0} (\eta )} \right] = p\hbar_{f} {\mathbf{N}}_{f} \left[ {\hat{f}(\eta ;\,p),\,\hat{\theta }(\eta ,\,p)} \right],$$
(33)
$$\left( {1 - p} \right)L_{\theta } \left[ {\hat{\theta }(\eta ;\,p) - \theta_{0} (\eta )} \right] = p\hbar_{\theta } {\mathbf{N}}_{\theta } \left[ {\hat{f}(\eta ;\,p),\,\hat{\theta }(\eta ,\,p)} \right],$$
(34)
$$\begin{aligned} \hat{f}(0;\,p) = & 0,\quad \hat{f}^{\prime } (0;\,p) = 1,\quad \hat{f}^{\prime } (\infty ;\,p) = A,\, \\ \hat{\theta }^{\prime } (0,\,p) = & 1,\quad \hat{\theta }(\infty ,\,p) = 0, \\ \end{aligned}$$
(35)

When p = 0 and p = 1 one has [25, 26]:

$$\hat{f}(\eta ;\,0) = f_{0} (\eta ),\quad \hat{\theta }(\eta ,\,0) = \theta_{0} (\eta ),\quad \, \hat{f}(\eta ;\,1) = f(\eta ),\quad \hat{\theta }(\eta ,\,1) = \theta (\eta ).$$
(36)

Clearly when p is increased from 0 to 1 then f(η, p) and θ(η, p) vary from f 0(η), θ 0(η) to f(η) and θ(η). By Taylor’s expansion we have [27, 28]:

$$f(\eta ,\,p) = f_{0} (\eta ) + \mathop \sum \limits_{m = 1}^{\infty } f_{m} (\eta )p^{m} ,\, \, f_{m} (\eta ) = \frac{1}{m!}\left. {\frac{{\partial^{m} f(\eta ;\,p)}}{{\partial \eta^{m} }}} \right|_{p = 0} ,$$
(37)
$$\theta (\eta ,\,p) = \theta_{0} (\eta ) + \mathop \sum \limits_{m = 1}^{\infty } \theta_{m} (\eta )p^{m} ,\, \, \theta_{m} (\eta ) = \frac{1}{m!}\left. {\frac{{\partial^{m} \theta (\eta ;\,p)}}{{\partial \eta^{m} }}} \right|_{p = 0} .$$
(38)

The convergence of above series strongly depends upon \(\hbar_{f}\) and \(\hbar_{\theta } .\) Considering that \(\hbar_{f}\) and \(\hbar_{\theta }\) are selected properly so that Eqs. (37) and (38) converge at p = 1, then we can write

$$f(\eta ) = f_{0} (\eta ) + \mathop \sum \limits_{m = 1}^{\infty } f_{m} (\eta ),$$
(39)
$$\theta (\eta ) = \theta_{0} (\eta ) + \mathop \sum \limits_{m = 1}^{\infty } \theta_{m} (\eta ).$$
(40)

The resulting problems at mth order deformation can be constructed as follows:

$$L_{f} [f_{m} (\eta ) - \chi_{m} f_{m - 1} (\eta )] = \hbar_{f} {\mathbf{R}}_{f}^{m} (\eta ),$$
(41)
$$L_{\theta } [\theta_{m} (\eta ) - \chi_{m} \theta_{m - 1} (\eta )] = \hbar_{\theta } {\mathbf{R}}_{\theta }^{m} (\eta ),$$
(42)
$$f_{m} (0) = f_{m}^{\prime } (0) = f_{m}^{\prime } (\infty ) = 0,\quad \theta_{m} (0) = \theta_{m} (\infty ) = 0,$$
(43)
$$\begin{aligned} {\mathbf{R}}_{f}^{m} (\eta ) = & f_{m - 1}^{\prime \prime \prime } (\eta ) + f_{m - 1}^{\prime \prime } (\eta ) + \frac{1}{{\theta_{r} }}\mathop \sum \limits_{k = 0}^{m - 1} f_{m - 1 - k}^{\prime \prime } \theta_{k} - \frac{1}{{\theta_{r} }}\mathop \sum \limits_{k = 0}^{m - 1} \mathop \sum \limits_{l = 0}^{k} \theta_{m - 1 - k} f_{k - l} f_{l}^{\prime \prime } \\ & + \frac{1}{{\theta_{r} }}\mathop \sum \limits_{k = 0}^{m - 1} \mathop \sum \limits_{l = 0}^{k} \theta_{m - 1 - k} f_{k - l}^{\prime } f_{l}^{\prime } + \lambda_{1} \left( {\frac{n - 1}{2}} \right)\mathop \sum \limits_{k = 0}^{m - 1} \mathop \sum \limits_{l = 0}^{k} f_{m - 1 - k}^{\prime \prime \prime } f_{k - l}^{\prime \prime } f_{l}^{\prime \prime } + \mathop \sum \limits_{k = 0}^{m - 1} \left[ {f_{m - 1 - k} f_{k}^{\prime \prime } - f_{m - 1 - k}^{\prime } f_{k}^{\prime } } \right] \\ &- \frac{1}{{\theta_{r} }}G\mathop \sum \limits_{k = 0}^{m - 1} \theta_{m-1-k} \theta_{k}-\frac{1}{\theta_{r}}A^{2}\theta_{m-1}+ 2\left( {\frac{n - 1}{2}} \right)\,\lambda_{1} \mathop \sum \limits_{k = 0}^{m - 1} f_{m - 1 - k}^{\prime \prime } f_{k}^{\prime \prime } \left[ {1 + \lambda_{1} \left( {\frac{n - 3}{2}} \right)\mathop \sum \limits_{l = 0}^{k} f_{k - l}^{\prime \prime } f_{l}^{\prime \prime } } \right] \\ & + \left( {1 - \chi_{m} } \right)\,A^{2} + \lambda \theta_{m - 1} \\ \end{aligned}$$
(44)
$$\begin{aligned} {\mathbf{R}}_{m}^{\theta } \left( \eta \right) = & \left( {1 + \frac{4}{3}N} \right)\,\theta_{m - 1}^{\prime \prime } \left( \eta \right) + \varepsilon \mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k} \theta_{k}^{\prime \prime } + \varepsilon \mathop \sum \limits_{k = 0}^{m - 1} \theta_{m - 1 - k}^{\prime } \theta_{k}^{\prime } \\ & + \mathop {Pr_{eff} }\limits \mathop \sum \limits_{k = 0}^{m - 1} \left( {\theta_{m - 1 - k}^{\prime } f_{k} - f_{m - 1 - k}^{{^{\prime } }} \theta_{k} } \right), \\ \end{aligned}$$
(45)

Solving the above mth order deformation problems, the general solutions can be written as follows:

$$f_{m} (\eta ) = f_{m}^{ * } (\eta ) + C_{1} + C_{2} e^{\eta } + C_{3} e^{ - \eta } ,$$
(46)
$$\theta_{m} (\eta ) = \theta_{m}^{ * } (\eta ) + C_{4} e^{\eta } + C_{5} e^{ - \eta } ,$$
(47)

in which the \(f_{m}^{ * }\) and \(\theta_{m}^{ * }\) indicate the special solutions.

4 Convergence of the homotopy solutions

Here, our desire is to ensure the convergence of the obtained series solutions. Thus Fig. 1 has been plotted for the admissible values of \(\hbar_{f}\) and \(\hbar_{\theta }\) regarding convergence of the solutions (39) and (40). Ultimate the admissible values have been noticed in the ranges \(- 1.30 \le \hbar_{f} \le - 0.20\) and \(- 1.40 \le \hbar_{\theta } \le - 0.30.\)

Fig. 1
figure 1

ℏ-curve for f and θ

Full size image

5 Discussion

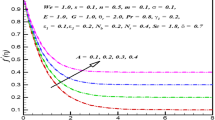
This section elaborates the influence of different parameters on velocity fʹ and temperature profile θ. Figures 2, 3, 4, 5, 6 and 7 show the variations of different parameters A, λ 1, G, S, n and θ r on the velocity fʹ. The effects of A on the velocity fʹ are shown in Fig. 2. It is revealed that the velocity fʹ enhances for larger values of A. The thickness of boundary layer is stronger for A < 1. Here the stretching rate dominates over the free stream rate. For A > 1 (the stretching rate of velocity is lower than free stream velocity rate) the thickness of boundary layer reduces while the velocity fʹ enhances. For A = 1, no boundary layer situation appeared. Figure 3 explores the effect of material parameter λ 1 on fʹ. By increasing λ 1 the velocity enhances and the profiles approaches to zero as \(\eta \to \infty .\) This shows an enhancement in hydrodynamic boundary layer. It is pointed out that the values of Carreau number vary from 0.1 to 20. Figure 4 shows the influence of mixed convection parameter G on velocity fʹ. We can see that velocity profile increases with an enhancement in the mixed convection parameter G. Physically, the buoyancy force takes place due to consideration of mixed convective parameter which enhances the velocity fʹ. The impacts of suction parameter S on velocity fʹ are visualized in Fig. 5. The liquid particles are sucked by sheet due to the larger suction parameter that offers a resistance to fluid flow and hence the velocity fʹ decreases. Figure 6 elucidates the variation of power law index n on velocity fʹ. The liquid velocity increases due to presence of power law index. The non-linearity of sheet is enhanced for larger n due to which the resistive force decreases and hence a reduction in velocity fʹ is achieved. Characteristics of θ r on fʹ(η) are addressed through Figs. 7 and 8. Here fʹ(η) decays for θ r  > 0 (i.e. for gases) whereas reverse behavior is noted for θ r  < 0 (i.e. for liquids). Physically larger θ r diminishes convective potential between the heated surface and ambient liquid and so fʹ(η) decays.

Fig. 2
figure 2

Effects of A on fʹ(η)

Full size image
Fig. 3
figure 3

Effects of λ 1 on fʹ(η)

Full size image
Fig. 4
figure 4

Effects of G on fʹ(η)

Full size image
Fig. 5
figure 5

Effects of S on fʹ(η)

Full size image
Fig. 6
figure 6

Effects of n on fʹ(η)

Full size image
Fig. 7
figure 7

Effects of θ r  > 0 on fʹ(η)

Full size image
Fig. 8
figure 8

Effects of θ r  < 0 on fʹ(η)

Full size image

Figures 9, 10, 11, 12, 13, 14 and 15 show the influence of different parameters A, S, Pr, N, ɛ and θ r on temperature profile θ(η). The effects of A on temperature profile θ are shown in Fig. 9. We can see that the temperature profile decreases by increasing A. Higher values of A correspond to more pressure which provides less resistance to fluid. Hence less heat is produced and temperature profile reduces. Figure 10 shows the behavior of S on temperature profile. Clearly, temperature profile reduces for larger S. In fact some fluid particles are absorbed by the sheet and each particle has energy which is transferred to the environment. Therefore, temperature of the fluid decreases. The conduction phenomenon decreases while pure convection enhanced due to an increase in Prandtl number Pr. That fact leads to lower temperature and thickness of thermal boundary layer (see Fig. 11). Small values of the Prandtl number Pr ≪ 1 means the thermal diffusivity dominates whereas the large values Pr ≫ 1 implies the momentum diffusivity dominates the behavior. It depends on the fluid properties like for gases Pr ranges 0.7–1.0, for water Pr ranges 1–10, for liquid metals Pr ranges 0.001–0.03 and for oils Pr ranges 50–2000. Figure 12 explores the variations of N on temperature θ. Here, we revealed that the temperature and its related thickness of boundary layer are higher for larger N. Influence of ɛ on temperature profile is presented in Fig. 13 It is examined that large amount of heat transfers from surface to material and thus θ(η) increases. Figures 14 and 15 are disclosed to analyze the impacts of θ r  > 0 and θ r  < 0 on temperature θ(η). Clearly θ(η) boosts when θ r  > 0. However, opposite situation is examined for θ r  < 0.

Fig. 9
figure 9

Effects of A on θ(η)

Full size image
Fig. 10
figure 10

Effects of S on θ(η)

Full size image
Fig. 11
figure 11

Effects of Pr on θ(η)

Full size image
Fig. 12
figure 12

Effects of N on θ(η)

Full size image
Fig. 13
figure 13

Effects of ɛ on θ(η)

Full size image
Fig. 14
figure 14

Effects of θ r  > 0 on θ(η)

Full size image
Fig. 15
figure 15

Effects of θ r  < 0 on θ(η)

Full size image

Table 1 is presented to find that how much order of computations is required for a convergent solution. It is noticed that 15th and 20th order of deformations are required for the velocity and temperature solutions respectively. Table 2 is made to analyze the numerical values of skin friction coefficient and local Nusselt number for different values of A, G, S, θ r , Pr and N. This Table elaborates that heat transfer rate become larger when we increase the values of A, G, S, Pr and N; however, opposite situation is noticed for larger θ r . Moreover, skin friction coefficient becomes larger when we increase Pr and S while it reduces via larger A, G, θ r and N. Tables 3 and 4 provides a comparative analysis of existing solutions with the previous results in a limiting case. From these Tables, we have examined that our present solutions have an excellent match with the previous published data that shows the reliability and validity of technique used for the computations.

Table 1 Convergence of homotopy solutions when n = 3, G = 0.3, λ 1 = ɛ = 0.2, A = 0.1, S = 0.6, Pr = 2.0, θ r  = 1.1 and N = 0.3
Full size table
Table 2 Numerical data of skin friction coefficient and local Nusselt number for various values of A, G, S, θ r , Pr, and N when λ 1 = 0.2, ɛ = 0.2 and n = 3.0
Full size table
Table 3 Comparison of present results of fʹ’(0) with [34] for different values of A when n = 1.0, and S = 0.0 = λ 1 = G = θ r
Full size table
Table 4 Comparison of present results of θ ′(0) with those of [35] when N = ɛ = 0
Full size table

6 Concluding remarks

Mixed convective flow of Carreau liquid near a stagnation point considering variable properties is examined. The following conclusions can be extracted from this investigation:

  • Impact of A on temperature and velocity fields is quite reverse. Velocity is increased while temperature reduces with an increase in A.

  • Suction parameter S reduced the velocity of liquid while it increases the momentum boundary layer thickness.

  • Prandtl number Pr creates a reduction in temperature θ(η) and thickness of thermal boundary layer.

  • The increasing values of θ r (i.e. θ r  > 0) correspond to lower velocity and higher temperature.

  • The effects of S and Pr on temperature θ(η) are similar in a qualitatively way.