Influence of thermal stratification on the radiative flow of Maxwell fluid

Abstract

We carried out analysis of the effects of thermal stratification in the boundary layer mixed convection flow of Maxwell fluid. The thermal radiation effect is considered. The derived equations with appropriate boundary conditions are solved for series solutions of velocity and temperature. Graphical results lead to the interesting observations. Local Nusselt number is tabulated and discussed. It is found that there is an opposite effect of fluid characteristics on the velocity and temperature. However, the velocity and temperature have similar effects for thermal stratification and radiation.

1 Introduction

The dynamics of non-Newtonian fluids is of great interest amongst the recent researchers of both the theoretical and applied fields. This type of fluids cannot be explained by using Newton’s law of viscosity. Many fluids such as polymer melts, mud, soaps, apple sauce, certain oils, lubricants, suspension solutions, ketchup and many others exhibit the rheological properties and thus cannot be described by one constitutive relationship. Therefore, the existing information regarding non-Newtonian fluids has been presented through the differential, rate and integral types. It is further seen that the rate type fluids are not given due attention. Maxwell fluid is a subclass of rate type fluids describing the relaxation time effects. Jamil and Fetecau [1] in a recent study reported an analysis for the helical flows of Maxwell fluid. They discussed the flow situation when the inner cylinder begins to rotate around its axis and to slide along the same axis due to time-dependent shear stresses. Hankel transform method is employed for the development of exact solution. Couette flow of fractional Maxwell fluid with accelerated shear rate was studied by Athar et al. [2]. Expressions for velocity and shear stress are obtained using Laplace and finite Hankel transforms. Wang and Tan [3] provided the stability analysis of Maxwell fluid with Soret-driven double diffusive convection in a porous medium. Hayat et al. [4] examined the flow of Maxwell fluid subject to convective boundary conditions. Thermophoresis effects in the two-dimensional flow of Maxwell fluid was analyzed by Hayat et al. [5]. Few other recent attempts involving Maxwell fluid model may be mentioned by the Refs. [6–10].

Mixed convection flow with heat transfer over a continuously moving surface is encountered in extrusion processes, cooling of metallic sheets and electronic chips, melt spinning, crystal blowing, continuous casting, glass blowing, etc. Further, mixed convection flow also has a pivotal role in the environment when the temperature difference between land and air leads to complicated flow patterns. Slip effects on the unsteady mixed convection flow over a moving surface was examined by Mukhopadhyay [11]. Turkyilmazoglu [12] provided the analytic solutions for mixed hydrodynamic thermal slip flow past a stretching surface. Two-dimensional flow of viscous fluid over an inclined stretching surface was numerically investigated by Noor et al. [13]. Convective heat transfer in two-dimensional flow of Maxwell fluid over a non-isothermal stretching sheet was investigated by Vajravelu et al. [14]. Hayat and Alsaedi [15] studied the mixed convection boundary layer flow of an Oldroyd-B fluid over a moving surface. They explored the effects of thermophoresis and Joule heating. Simultaneous effects of heat and mass transfer in MHD mixed convection flow with porous medium and internal heat generation were studied by Makinde [16]. Series solutions for mixed convection Falkner-Skan flow of Maxwell fluid was addressed by Hayat et al. [17].

Thermal radiation effect has a vital role in operations carried out at high temperature. Such effect is particularly important in the industrial and engineering applications including nuclear power plant, satellites, missiles, propulsion devices for aircraft and other space vehicles. Further, the study of thermally stratified fluid is significant in various industrial, environment and engineering processes. In fact the thermal stratification is a property of all fluid bodies surrounded by differentially heated side walls [18]. Thermal stratification for vertical consideration is due to temperature variations, concentration difference or presence of different density fluids. Having such in mind, Kulkarni et al. [19] carried out a study to investigate the similarity solution over an isothermal vertical surface in a thermally stratified medium. Natural convection flow in a thermally stratified medium over a vertical cylinder was examined by Thakhar et al. [20]. Hossain et al. [21] discussed the effects of viscous dissipation and thermal stratification on the flow of viscous fluid in the presence of uniform surface heat flux. Singh et al. [22] examined the thermal stratification effects on MHD flow of viscous fluid. Recently, Mukhopadhyay and Ishak [23] provided the numerical solutions for the thermally stratified flow over a stretching cylinder.

To the best of our information, the boundary layer due to temperature gradient in non-Newtonian fluid with radiation effects has not been attained so far. This interest motivated us to examine such effects for the flow of Maxwell fluid over a stretched surface. This article is arranged in the following pattern. Next section deals with the definitions of problem and some physical quantities. Series solutions and related convergence analysis are given in the Sects. 3 and 4 respectively by homotopy analysis method [24–28]. Physical results are presented in Sect. 5. Section 6 contains main conclusions.

2 Governing problems

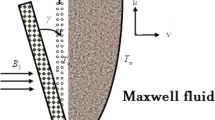
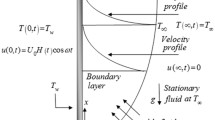
We consider the mixed convection flow of an incompressible Maxwell fluid over a stretching surface. Thermal stratification and radiation effects are present. The vertical surface has temperature T _w and further $T_{\infty }$ denotes the temperature of ambient fluid. The x and y-axes are chosen along and normal to the surface. The equation of continuity, the equations of momentum in the absence of pressure gradient [6] and the equation of energy can be written as

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, $$

(1)

$$ \rho \left( u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} \right) =\frac{\partial \tau _{xx}}{\partial x}+\frac{\partial \tau _{xy}}{ \partial y}+g\beta _{T}(T-T_{\infty }), $$

(2)

$$ \rho \left( u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} \right) =\frac{\partial \tau _{yx}}{\partial x}+\frac{\partial \tau _{yy}}{ \partial y}, $$

(3)

$$ \rho C_{p}\left( u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y }\right) =k\frac{\partial ^{2}T}{\partial y^{2}}-\frac{\partial q_{r}}{ \partial y},\;$$

(4)

where u and v denote the velocity components in the x- and y-directions, ρ the fluid density, T the fluid temperature, k the thermal conductivity of fluid, g the gravitational acceleration, β _T the thermal expansion coefficient, C _p the specific heat at constant pressure and q _r the radiative heat flux. The extra stress tensor τ _ij related to the deformation rate tensor d _ij for a Maxwell fluid can be defined as [29]:

$$ \tau _{ij}+\lambda \frac{\triangle }{\triangle t}\tau _{ij}=2\delta d_{ij},\;$$

(5)

in which δ is the coefficient of viscosity, λ is the relaxation time and $\frac{\triangle }{\triangle t}$ is the upper convected time derivative. By applying this time derivative to the stress tensor, we have [29]

$$ \frac{\triangle }{\triangle t}\tau _{ij}=\frac{D}{Dt}\tau _{ij}-L_{jk}\tau _{ik}-L_{ik}\tau _{kj},\;$$

(6)

where L _ij denote the velocity gradient tensor. For an incompressible flow of Maxwell fluid, the x-component of the momentum equation and energy equation after employing the boundary layer theory [30] has the following forms:

$$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\lambda _{1}\left( u^{2}\frac{\partial ^{2}u}{\partial x^{2}}+v^{2}\frac{\partial ^{2}u}{\partial y^{2}}+2uv\frac{\partial ^{2}u}{\partial x\partial y}\right) =\nu \frac{\partial ^{2}u}{\partial y^{2}}+g\beta _{T}(T-T_{\infty }), $$

(7)

$$ \rho C_{p}\left( u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y }\right) =k\frac{\partial ^{2}T}{\partial y^{2}}-\frac{\partial q_{r}}{ \partial y},\;$$

(8)

where ν is the kinematic viscosity. The subjected boundary conditions are

$$ u=u_{w}(x)=cx,\,v=0,\,T=T_{w}=T_{0}+bx\, \quad \hbox {at} \quad y=0, $$

(9)

$$ u\rightarrow 0,\,T\rightarrow T_{\infty }=T_{0}+ax \quad \hbox { as}\, y\rightarrow \infty,\;$$

(10)

in which c is the stretching rate, a, b are dimensional constants and T ₀ is the reference temperature.

The radiative flux is accounted by the Rosseland approximation in the energy equation [31]:

$$ q_{r}=-\frac{4\sigma ^{\ast }}{3k^{\ast }}\frac{\partial T^{4}}{\partial y},\;$$

(11)

in which $\sigma ^{\ast }$ the Stefan-Boltzmann constant and $k^{\ast }$ the mean absorption coefficient. Further, the differences of temperature within the flow is assumed to be small such that T ⁴ may be expressed as a linear function of temperature. Expansion of T ⁴ about $T_{\infty }$ via Taylor’s series and ignoring higher order terms, we have

$$ T^{4}\cong T_{\infty }^{4}+(T-T_{\infty })4T_{\infty }^{3}=4T_{\infty }^{3}T-3T_{\infty }^{4}. $$

(12)

By employing Eqs. (11) and (12), Eq. (8) has the form

$$ \rho C_{p}\left( u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y }\right) =k\frac{\partial ^{2}T}{\partial y^{2}}+\frac{16\sigma T_{\infty }^{3}}{3k^{\ast }}\frac{\partial ^{2}T}{\partial y^{2}}. $$

(13)

Setting

$$ u=cxf^{\prime }(\eta ),\,v=-\sqrt{c\nu }f(\eta ),\hbox { }\eta =y\sqrt{ \frac{c}{\nu }},\,\theta (\eta )=\frac{T-T_{\infty }}{T_{w}-T_{0}}, $$

(14)

Equation (1) is satisfied automatically and reduced forms of Eqs. (7)–(10) and (13) are

$$ f^{\prime \prime \prime }+ff^{\prime \prime }-f^{\prime 2}+\beta (2ff^{\prime }f^{\prime \prime }-f^{2}f^{\prime \prime \prime })+\lambda \theta =0, $$

(15)

$$ (1+\frac{4}{3}N)\theta ^{\prime \prime }+Prf\theta ^{\prime }-Prf^{\prime }\theta -PrSf^{\prime }=0, $$

(16)

and the boundary conditions in dimensionless form has the following form:

$$ f=0,\,f^{\prime }=1,\,\theta =1-S \quad \hbox {at}\ \eta =0, $$

(17)

$$ f^{\prime }=0,\,\theta =0\quad \hbox{as}\ \eta \rightarrow \infty . $$

(18)

Here De = λ ₁ c is the Deborah number, λ = Gr _x /Re ² _x the mixed convection parameter with $Gr_{x}=g\beta _{T}(T-T_{\infty })x^{3}/\nu ^{2}$ the local Grashof number and Re _x  = u _w (x)x/ν the local Reynolds number, Pr = ν /α the Prandtl number, $\alpha =\frac{k}{\rho C_{p}}$ the thermal diffusivity, $N=\frac{4\sigma ^{\ast }T_{\infty }^{3}}{kk^{\ast }}$ the thermal radiation parameter, S = b/a the thermal stratification parameter, θ the dimensionless temperature and η the similarity variable.

Local Nusselt number is defined by

$$ Nu_{x}=\frac{xq_{w}}{k(T-T_{\infty })}, $$

(19)

where the heat transfer from the surface q _w is

$$ q_{w}=-k\left( \frac{\partial T}{\partial y}\right) _{y=0}. $$

(20)

Equation (13) in dimensionless variables is given as

$$ Nu_{x}/Re_{x}^{1/2}=-\theta ^{\prime }(0). $$

(21)

3 Development of the series solutions

For an interest in the homotopy analysis solutions we choose the initial guesses and operators in the form given below:

$$ f_{0}(\eta )=(1-\exp (-\eta )),\,\theta _{0}(\eta )=(1-S)\exp (-\eta ), $$

(22)

$$ {{\mathcal{L}}} _{f}=f^{\prime \prime \prime }-f^{\prime },\, {{\mathcal{L}}} _{\theta }=\theta ^{\prime \prime }-\theta , $$

(23)

with

$$ {{\mathcal{L}}} _{f}(C_{1}+C_{2}e^{\eta }+C_{3}e^{-\eta })=0,\, {{\mathcal{L}}}_{\theta }(C_{4}e^{\eta }+C_{5}e^{-\eta })=0, $$

(24)

where C _i  (i = 1–5) are the arbitrary constants. The zeroth order deformation equations together with the boundary conditions are

$$ \left( 1-p\right) {{\mathcal{L}}} _{f}\left( \hat{f}(\eta ;p)-f_{0}(\eta )\right) =p\hbar _{f}{\mathcal{N}}_{f}\left( \hat{f}(\eta ;p),\hat{\theta} (\eta ;p)\right) , $$

(25)

$$ \left( 1-p\right) {{\mathcal{L}}} _{\theta }\left( \hat{\theta}(\eta ;p)-\theta _{0}(\eta )\right) =p\hbar _{\theta }{\mathcal{N}}_{\theta }\left( \hat{f} (\eta ;p),\hat{\theta}(\eta ,p)\right) , $$

(26)

$$ \hat{f}(0;p)=0,\,\hat{f}^{\prime }(0;p)=1,\,\hat{f}^{\prime }(\infty ;p)=0,\,\hat{\theta}(0,p)=1-S,\,\hat{\theta}(\infty ,p)=0, $$

(27)

$$ {\mathcal{N}}_{f}{\mathcal{[}}\hat{f}(\eta ,p)] =\frac{\partial ^{3}\hat{f} (\eta ,p)}{\partial \eta ^{3}}+\hat{f}(\eta ,p)\frac{\partial ^{2}\hat{f} (\eta ,p)}{\partial \eta ^{2}}-\left( \frac{\partial \hat{f}(\eta ,p)}{ \partial \eta }\right) ^{2}+\lambda \hat{\theta}(\eta ,p) $$

(28)

$$ +De\left( 2\hat{f}(\eta ,q)\frac{\partial \hat{f}(\eta ,q)}{\partial \eta } \frac{\partial ^{2}\hat{f}(\eta ,q)}{\partial \eta ^{2}}-(\hat{f}(\eta ,q))^{2}\frac{\partial ^{3}\hat{f}(\eta ,q)}{\partial \eta ^{3}}\right) , $$

(29)

$$ \begin{aligned} {\mathcal{N}}_{\theta }[\hat{\theta}(\eta ,p),\hat{f}(\eta ,p)] &= (1+\frac{4}{ 3}N)\frac{\partial ^{2}\hat{\theta}(\eta ,p)}{\partial \eta ^{2}}-Pr\hat{ \theta}(\eta ,p)\frac{\partial \hat{f}(\eta ,p)}{\partial \eta }+Pr\hat{f} (\eta ,p)\frac{\partial \hat{\theta}(\eta ,p)}{\partial \eta } \\ &-PrS\frac{\partial \hat{f}(\eta ,p)}{\partial \eta }, \end{aligned} $$

(30)

where p is an embedding parameter, $\hbar _{f}$ and $\hbar _{\theta }$ the non-zero auxiliary parameters and $\mathcal{N}_{f}$ and $\mathcal{N}_{\theta }$ the nonlinear operators. For p = 0 and p = 1 one has

$$ \hat{f}(\eta ;0)=f_{0}(\eta ),\,\hat{\theta}(\eta ,0)=\theta _{0}(\eta )\hbox { and }\hat{f}(\eta ;1)=f(\eta ),\,\hat{\theta}(\eta ,1)=\theta (\eta ). $$

(31)

When variation of p is taken into account from 0 to 1 then f(η, p) and θ (η, p) vary from f ₀(η), θ ₀(η) to f(η) and θ(η). We expand f and θ in the following forms:

$$ f(\eta ,p)=f_{0}(\eta )+\sum\limits_{m=1}^{\infty }f_{m}(\eta )p^{m},\,f_{m}(\eta )=\frac{1}{m!}\left. \frac{\partial ^{m}f(\eta ;p)}{\partial \eta ^{m}}\right\vert _{p=0}, $$

(32)

$$ \theta (\eta ,p)=\theta _{0}(\eta )+\sum\limits_{m=1}^{\infty }\theta _{m}(\eta )p^{m},\,\theta _{m}(\eta )=\frac{1}{m!}\left. \frac{ \partial ^{m}\theta (\eta ;p)}{\partial \eta ^{m}}\right\vert _{p=0}, $$

(33)

where the convergence of above series strongly depends upon $\hbar _{f}$ and $\hbar _{\theta }.$ Considering that $\hbar _{f}$ and $\hbar _{\theta }$ are selected properly such that Eqs. (32) and (33) converge for p = 1 and thus

$$ f(\eta )=f_{0}(\eta )+\sum\limits_{m=1}^{\infty }f_{m}(\eta ), $$

(34)

$$ \theta (\eta )=\theta _{0}(\eta )+\sum\limits_{m=1}^{\infty }\theta _{m}(\eta ). $$

(35)

The general solutions are derived as follows:

$$ f_{m}(\eta )=f_{m}^{\ast }(\eta )+C_{1}+C_{2}e^{\eta }+C_{3}e^{-\eta} $$

(36)

$$ \theta _{m}(\eta )=\theta _{m}^{\ast }(\eta )+C_{4}e^{\eta}+C_{5}e^{-\eta } $$

(37)

where $f_{m}^{\ast }$ and $\theta _{m}^{\ast }$ are the special solutions.

4 Convergence analysis

The auxiliary parameters $\hbar _{f}$ and $\hbar _{\theta }$ appearing in the series solutions have the key role regarding the control and adjustment of the convergence of the homotopy solutions. Hence, the $\hbar$—curves are sketched for 21st order of approximations to find the range of admissible values of $\hbar _{f}$ and $\hbar _{\theta }.$ It is obvious from Fig. 1 that the range of admissible values of $\hbar _{f}$ and $\hbar _{\theta }$ are $-1.15\!\leq \hbar _{f}\leq -\!0.2$ and $-1.1\leq \hbar _{\theta }\leq -\!0.15.$ Both series are convergent in the whole region of η for $\hbar _{f}=-0.7$ and $\hbar _{\theta }=-0.6.$

Fig. 1

$\hbar$ —curves for the functions f(η) and θ (η)

5 Results and discussion

The purpose of this section is to describe the role of emerging parameters through plots and construction of tabular values of Nusselt number. Such objective is achieved for the variations of Deborah number De, mixed convection parameter λ, thermal stratified parameter S, Prandtl number Pr and radiation parameter N on the velocity $f^{\prime }(\eta )$ and temperature θ (η). The effects of Deborah number on velocity and temperature are seen in the Figs. 2 and  3. We observed that the velocity and associated boundary layer thickness are decreased by increasing De. This is attributed to the fact that the relaxation time opposes the fluid flow. De is dependent on the relaxation time and an increase in De increases the relaxation time and thus decreases the velocity and boundary layer thickness. From Fig. 3, one can see that Deborah number has quite opposite effects on temperature in comparison to velocity. This reverse behavior is due to the relaxation time. In fact increase in Deborah number leads to an increase in the relaxation time. For larger relaxation time, the velocity is increased but temperature decreases. Hence, an increase in the Deborah number gives rise to the velocity and reduced the temperature. Figures 4 and  5 show that the velocity increases by increasing mixed convection parameter but the temperature decreases by increasing λ. This is because of the buoyancy force. The effects of thermal stratification parameter on velocity and temperature are observed from the Figs. 6 and  7. It is seen that both the velocity and temperature are decreasing functions of S. We also noticed that the variation in temperature is more significant when compared with velocity. This shows that the temperature decreases rapidly while the decrease in velocity is slow. There is a reduction in the effective convective potential between the surface and the ambient fluid for the increasing values of thermal stratification parameter. This reduction causes a decrease in the momentum and thermal boundary layer thicknesses. From Figs. 8 and  9, we see that both the velocity and temperature decrease by increasing Prandtl number. This is because of the fact that higher Prandtl number fluid has lower thermal diffusivity which decreases the temperature and thermal boundary layer thickness. Comparison of Figs. 8 and  9 shows that the thermal boundary layer thickness is more dominant than the velocity boundary layer thickness. The thermal radiation parameter N has similar effects on the velocity and temperature. Both the velocity and temperature increase by increasing N. An increase in the radiation parameter provides more heat to the fluid due to which the velocity and temperature are increased. It is also seen that an increase in temperature is rapid than velocity (see Figs. 10,  11). Figures 12 and 13 are plotted for the different values of radiation by considering smaller value of Prandtl number. Here we examined that the fluid velocity corresponding to $Pr =1.0$ dies out quickly in comparison to the fluid velocity for $Pr =0.2.$ A comparison of Figs. 11 and  13 shows that increase in radiation increases the temperature for $Pr =1.0$ and $Pr =0.2$ but the temperature is higher for $Pr =0.2.$ Figure 14 shows the variations of S when $Pr=0.2$ on the fluid velocity. The fluid velocity increased by increasing the values of S. From Figs. 6 and  14, we have seen that the fluid velocity is large for $Pr =0.2$ when compared with the velocity for $Pr =1.0.$ From Fig. 15, one can see that the temperature is zero for S = 1.0. Also we see that the temperature decreases rapidly in Fig. 15 in comparison to Fig. 7. Figures 16 and 17 illustrate the effects of S and N vs. De on the local Nusselt number $-\theta ^{\prime }(0).$ The local Nusselt number reduced with an increase in S and N vs. De but the local Nusselt number corresponding to N is greater than the local Nusselt number for S.

Fig. 2

Influence of De on $f^{\prime }(\eta)$

Fig. 3

Influence of De on $\theta (\eta)$

Fig. 4

Influence of $\lambda$ on $f^{\prime }(\eta)$

Fig. 5

Influence of $\lambda$ on $\theta (\eta )$

Fig. 6

Influence of S on $f^{\prime }(\eta)$

Fig. 7

Influence of S on $\theta (\eta)$

Fig. 8

Influence of $Pr$ on $f^{\prime }(\eta)$

Fig. 9

Influence of $Pr$ on $\theta (\eta)$

Fig. 10

Influence of N on $f^{\prime }(\eta)$

Fig. 11

Influence of N on $\theta (\eta)$

Fig. 12

Influence of N on $f^{\prime }(\eta )$ when $Pr =0.2$

Fig. 13

Influence of N on $\theta (\eta )$ when $Pr =0.2$

Fig. 14

Influence of S on $f^{\prime }(\eta )$ when $Pr=0.2$

Fig. 15

Influence of S on $\theta (\eta )$ when $Pr =0.2$

Fig. 16

Influence of S vs. De on $-\theta ^{\prime }(0)$

Fig. 17

Influence of N vs. De on $-\theta ^{\prime }(0)$

Table 1 is prepared to see the convergent values and to find that how much deformations are required for the convergent series solutions. We see that the solutions for velocity and temperature start to repeat from 25th order of deformations. So it is concluded from this table that 25th order approximations are enough for the convergent series solutions of velocity and temperature. Numerical values of local Nusselt number $-\theta ^{\prime }(0)$ for different values of De,  λ,  Pr,  S and N are examined in Table 2. The values of Nusselt number increase by increasing the values of Prandtl number and mixed convection parameter. Such values reduce by increasing the Deborah number, thermal stratification parameter and radiation parameter. Table 3 provides the comparison for different values of De on $f^{\prime \prime }(0)$ and $\theta ^{\prime }(0)$ with Vajravelu et al. [14]. Here we see that our homotopic solution has good agreement with that presented by Vajravelu et al. [14].

Table 1 Convergence of homotopy solution for different order of approximations when $De=0.1,\;\lambda =0.5,\;Pr=1.0,\,S=0.1,\;N=0.5,\;\hbar _{f}=-0.7$ and $\hbar _{\theta}=-0.6$

Table 2 Numerical values of local Nusselt number $-\theta ^{\prime }(0)$ for different values of De,   λ,   S,   Pr and N

Table 3 Comparison values of $f^{\prime \prime }(0)$ and $\theta ^{\prime }(0)$ for different values of β when λ = N = S = 0.0

6 Conclusions

Influence of thermal stratification on the mixed convection flow of upper convected Maxwell fluid over a stretching sheet is explored. Similarity transformations are utilized for the reduction of partial differential equations into the ordinary differential equations. The governed nonlinear ordinary differential equations with the subjected boundary conditions are solved by homotopy analysis method. The main points of the presented study can be summed up as follows.

• Deborah number has reverse effects on the dimensionless velocity and temperature.

• There is decrease in both the velocity and temperature when thermal stratified parameter increases. However, the decrease in velocity is more significant than the temperature.

• Decrease in temperature and thermal boundary layer thickness is rapid when compared with an increase in velocity by increasing Prandtl number.

• The velocity and temperature increase by increasing the radiation parameter N.

• Values of local Nusselt number decrease when Deborah number and stratification parameter are increased.

• Increase in Prandtl number causes an increase in the values of $-\theta ^{\prime }(0).$