1 Introduction

Rapid advancement in nanotechnology with potential heat transport features has been communicated by many researchers in recent years. Nanofluids are a class of fluids that are formed by adding nanosized materials in base fluids. The scattered solid particles in the base fluid enhance thermophysical properties and conserve important properties like thermal resistance, heat exchanger functioning, cooling of nuclear reactors, etc. Choi [1] first introduced the concept of increasing the thermal conductance of the base fluids by adding nanoparticles. Khan et al [2] reported the activation and chemical reaction of the cross nanofluid. Sultan et al [3] theoretically studied the thermophoresis and Brownian motion of the cross fluid. Abbas et al [4] considered a mathematical model for the cross nanofluid flow with entropy generation. Ali et al [5] investigated thermal radiative and non-uniform source on Sisko nanofluid in the presence of Lorentz forces on a curved surface. Khan et al [6] studied numerical simulation of the Casson nanofluid over heated surface. Feature of magnetic field and nanofluid over a stretching sheet are reported by Ganga et al [7]. Hakeem et al [8] analysed the non-uniform heat source/sink and MHD flow of a nanofluid over a stretching sheet. Govindaraju et al [9] introduced nanofluid over a stretching sheet with Lorentz forces and heat source/sink. Hakeem et al [10] designed hydromagnetic flow of the Buongiorno model nanofluid through a vertical plate.

Non-Newtonian fluids are very important in modern sciences which include industrial and mechanical fields. These types of fluids do not follow Newton’s viscosity law. They include ketchup, blood, yogurt, toothpaste, paints, etc. Therefore, Navier–Stokes statements are not enough to indicate the behaviour of such types of materials due to their complex nature. Many researchers [11,12,13,14,15,16,17,18,19,20,21] presented non-Newtonian models. Nowadays, viscoelastic fluids are commonly used in the movement of biological fluids, bioengineering, paint production, plastic films, pharmaceuticals, extrusion, drawing sheet, solution suspension and several other production processes. Various important applications of convective thermal transport which include nuclear reactors, solar collectors, aeronautics, heating and cooling devices, many other experimental and theoretical investigations on the buoyant movement of different fluids in various geometries have been investigated [22,23,24].

This communication presents a discussion about the physical properties of nanoparticle with variable properties over a starching sheet. The Carreau fluid is assumed to be a base fluid. The shear-thinning nature of the Carreau fluid is more affected. Studies by many researchers concerning new developments in different fluid flow models are listed in refs [25,26,27,28]. The applications of the base fluid are mostly referred to lubricating oil production.

2 Formulation

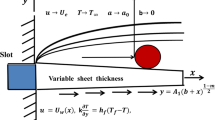
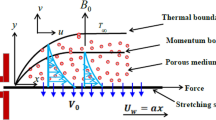
In this computational model, we consider the convective flow of steady Carreau fluid by continuously starched surface near the stagnation point under the influence of nanoparticles. The direction of flow on a stretchable surface is in such a manner that the x-axis is along the surface of the sheet and the y-axis is orthogonal to the flow. An incompressible flow is confined to \(y>0\). Also, thermophysical features of the fluid at the surface are taken as variables. The constitutive relation for a Carreau material is

$$\begin{aligned} \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}=0. \end{aligned}$$
(1)

Momentum equation:

$$\begin{aligned} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}&=\frac{1}{\rho }\frac{\partial }{\partial y} \left[ \eta _{0}\left[ 1+\lambda ^{2} \left( \frac{\partial u}{\partial y} \right) ^{2} \right] ^{\frac{n-1}{2}} \left( \frac{\partial u}{\partial y} \right) \right] \nonumber \\&\quad +u_{e}\frac{\mathrm {d}u_{e}}{\mathrm {d}x}+g\beta _{T} \left( T-T_{\infty } \right) . \end{aligned}$$
(2)

Energy equation:

$$\begin{aligned} u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}&=\frac{1}{{\rho c\!}_{p} }\frac{\partial }{\partial y} \left( {K(T)\frac{\partial T}{\partial y}} \right) \nonumber \\&\quad +\tau \left[ {D_{B} \left( {\frac{\partial C}{\partial y} \frac{\partial T}{\partial y}} \right) +\frac{D_{T}}{T_{\infty }} \left( {\frac{\partial T}{\partial y}} \right) ^{2}} \right] . \end{aligned}$$
(3)

Concentration:

$$\begin{aligned} u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}&=\frac{1}{{\rho c\!}_{p}}\frac{\partial }{\partial y} \left( D(C)\frac{\partial C}{\partial y}\right) \nonumber \\&\quad +D_{B}\frac{\partial ^{2}C}{\partial y^{2}} +\frac{D_{T}}{T_{\infty }} \frac{\partial ^{2}T}{\partial y^{2}}\nonumber \\&\quad -k_{c}^{2} \left( C-C_{\infty }\right) \left( \frac{T}{T_{\infty }}\right) ^{m}\nonumber \\&\quad \times \exp {\left( -\frac{E_{a}}{KT} \right) .} \end{aligned}$$
(4)

Boundary conditions:

$$\begin{aligned}&u=u_{w}(x)=cx,\quad v=v_{w},\, -K(T) \frac{\partial T}{\partial y}=\left( T-T_{w} \right) ,\nonumber \\&D_{B}\frac{\partial C}{\partial y}+\frac{D_{T}}{T_{\infty }} \frac{\partial T}{\partial y}=0\quad \mathrm{at}\, y=0, \end{aligned}$$
(5)
$$\begin{aligned}&u\rightarrow u_{e}=ax,\quad T\rightarrow T_{\infty },\quad C \rightarrow C_{\infty }\quad \mathrm{as}\, y\rightarrow \infty , \end{aligned}$$
(6)

where

$$\begin{aligned}&K(T)=k_{\infty }\left( 1+\varepsilon _{1} \frac{T-T_{\infty }}{\varDelta T} \right) ,\nonumber \\&D(C)=D_{\infty }\left( 1+\varepsilon _{2} \frac{C-C_{\infty }}{\varDelta C} \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\frac{1}{\mu }=\frac{1}{\mu _{\infty } }\left[ {1+\gamma _{1} \left( {T-T_{\infty } } \right) } \right] , \end{aligned}$$
(8)

This equation can be rewritten as

$$\begin{aligned} \frac{1}{\mu }=\alpha (T-T_{\Gamma }). \end{aligned}$$
(9)

Consider

$$\begin{aligned}&\Psi =x\sqrt{cv} f( \eta ),\quad u=cxf^{\prime } ( \eta ),\quad v=-\sqrt{cv} f(\eta ),\nonumber \\&\theta \left( \eta \right) =\frac{T-T_{\infty }}{T_{w}-T_{\infty }},\quad \phi \left( \eta \right) =\frac{C-C_{\infty }}{C_{w} -C_{\infty }},\quad \eta =y\sqrt{\frac{c}{v}}. \end{aligned}$$
(10)

Equation (1) holds while eqs (2) and (6) become

$$\begin{aligned}&f'''\left[ 1+\left( Wef'' \right) ^{2} \right] ^{\frac{n-3}{2}} \left[ 1+n(Wef'')^{2} \right] \nonumber \\&\quad +\left( \frac{\theta ^{\prime }}{\theta _{r}-\theta }\right) f'' \left[ 1+(Wef'')^{2}\right] ^{\frac{n-1}{2}}\nonumber \\&\quad +\left( \frac{\theta _{r}-\theta }{\theta _{r}} \right) \big [ff''-\big (f^{\prime } \big )^{2}+G\theta +A^{2} \big ]=0, \end{aligned}$$
(11)
$$\begin{aligned}&\left( 1+\varepsilon _{1}\theta \right) \theta {''}+\varepsilon _{1} \left( \theta ^{\prime } \right) ^{2}+P_r{N_{b}\theta ^{\prime }\phi ^{\prime }}+P_r{N_{t} \theta ^{\prime 2}}\nonumber \\&\quad +P_r\left[ f\theta {'}-f{'}\theta \right] =0, \end{aligned}$$
(12)
$$\begin{aligned}&\left( 1+\varepsilon _{2}\phi \right) \phi {''}+\varepsilon _{2} \phi ^{\prime 2}+\frac{N_{t}}{N_{b}}\theta {''}+Sc\big [ f\phi {'}-f{'} \phi \big ]\nonumber \\&\quad -Sc\sigma \left( 1+\delta \theta \right) ^{m}\phi \exp \left( -\frac{E}{1+\delta \theta } \right) =0. \end{aligned}$$
(13)

Boundary conditions are

$$\begin{aligned}&f=s,{\, \, \, f}^{\prime }=1,\quad \theta ^{\prime }=-\gamma (1-\theta ),\nonumber \\&N_{b}\phi ^{\prime }+N_{t}\theta ^{\prime } =0\quad \mathrm{at}\, \eta =0, \end{aligned}$$
(14)
$$\begin{aligned}&f^{\prime }=A,\quad \theta =0,\quad \phi ^{\prime }=0 \quad \mathrm{as}\, \eta \rightarrow \infty . \end{aligned}$$
(15)

Involved physical parameters are

$$\begin{aligned}&We=\frac{\lambda ^{2}x^{2}c^{3}}{v},\quad s=-\frac{v_{w}}{\sqrt{cv}},\quad P_r=\frac{v}{\alpha },\nonumber \\&\theta _{r}=\frac{T_{r}-T_{\infty }}{T_{w} -T_{\infty }}=-\frac{1}{\gamma (T_{w}-T_{\infty })},\nonumber \\&G=\frac{Gr_{x}}{{Re}^{2}x}=\frac{g\beta _{T}b}{c^{2}}, \, \, \, N_{t}=\frac{\tau D_{T}(T_{w} -T_{\infty })}{\upsilon T_{\infty }},\nonumber \\&Gr_{x}=\frac{g\beta _{T}(T_{w}-T_{\infty })x^{3}}{v^{2}},\quad Re_{x}=\frac{u_{w}(x)x}{v},\nonumber \\&N_b=\frac{\tau D_{B}\left( C_{w}-C_{\infty } \right) }{\upsilon },\quad A=\frac{a}{c},\quad \sigma =\frac{k_{c}^{2}}{a},\nonumber \\&E=\frac{E_{a}}{k_{\infty }T_{\infty }},\quad \delta =\frac{T_{w}-T_{\infty }}{T_{\infty }}. \end{aligned}$$
(16)

Non-dimensional skin friction \(C_{f} \) and local Nusselt number \(Nu_{x}\) become

$$\begin{aligned}&\frac{1}{2}C_{f}{Re}_{x}^{\frac{1}{2}} =\left( \frac{\theta _{r}}{\theta _{r}-\theta }\right) \left[ 1+(We f{''}(0))^{2}\right] ^{\frac{n-1}{2}}f{''}(0), \end{aligned}$$
(17)
$$\begin{aligned}&{Re}_{x}^{-\frac{-1}{2}}Nu_{x} =-\left( 1+\frac{4}{3}N \right) \theta ^{\prime }(0). \end{aligned}$$
(18)

3 Solution of the proposed problem

The ruling governed system of first-order ODEs for the flow field is solved by utilising the MATLAB tool bvp4c technique. The bvp4c technique is applied for first-order initial boundary value problems. Thus, we have used the bvp4c technique which controls the convergences of the dimensional parameter.

Fig. 1
figure 1

Influence of A on velocity \((f^{\prime }(\eta ))\).

Full size image
Fig. 2
figure 2

Influence of G on velocity \((f^{\prime }(\eta ))\).

Full size image
Fig. 3
figure 3

Influence of s on velocity \((f^{\prime }(\eta ))\).

Full size image
Fig. 4
figure 4

Influence of We on velocity \((f^{\prime }(\eta ))\).

Full size image
Fig. 5
figure 5

Influence of A on temperature \((\theta (\eta ))\).

Full size image
Fig. 6
figure 6

Influence of \(\varepsilon _{1}\) on temperature \((\theta (\eta ))\).

Full size image
Fig. 7
figure 7

Influence of Pr on temperature \((\theta (\eta ))\).

Full size image
Fig. 8
figure 8

Influence of \(\gamma _{1}\) on temperature \((\theta (\eta ))\).

Full size image
Fig. 9
figure 9

Influence of s on temperature \((\theta (\eta ))\).

Full size image
Fig. 10
figure 10

Influence of E on concentration \((\phi (\eta ))\).

Full size image
Fig. 11
figure 11

Influence of \(\varepsilon _{2}\) on concentration \((\phi (\eta ))\).

Full size image

4 Analysis

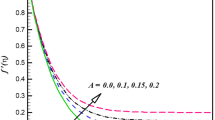
The main aim of this paper is to investigate the variation of dimensionless parameters of flow, temperature and concentration field. The velocity components \((f^{\prime }(\eta ))\), temperature \((\theta (\eta ))\) and concentration field \((\phi (\eta ))\) of the fluid are examined in figures 1–14. Figures 1–4 show the variation in velocity field \((f^{\prime }(\eta ))\), due to an increase in \(A,\, G,\, s\, \hbox {and}\, We\). Figure 1 displays the variation of velocity with A, the ratio of rate constant. The boundary layer thickness is stronger for \(A<1\) and starching rate controls the free stream rate. Similarly, for \(A>1\) the boundary layer thickness is reduced while velocity field \((f^{\prime }(\eta ))\) increases. The effect of mixed convection parameter (G) on the velocity field is explored in figure 2. Here, we observe that when mixed convection parameter (G) increases, velocity field \((f^{\prime }(\eta ))\) increases. Buoyancy forces occur when the mixed convection parameter due to velocity \((f^{\prime }(\eta ))\) increases. Figure 3 illustrates the influence of section parameter (s) on velocity field \((f^{\prime }(\eta ))\). The fluid particle is sucked by the starching sheet because of some resistances occurring in fluid flow and then velocity decreases. The impact of local Weissenberg number We on velocity field \((f^{\prime }(\eta ))\) is shown in figure 4. Figures 5–9 indicate variation in temperature field \((\theta (\eta ))\). Figure 5 shows the effect of A on the temperature field \((\theta (\eta ))\). Temperature field \((\theta (\eta ))\) decreases for increasing values of A. Physically, by increasing the value of A, more pressure is produced which gives less resistance to the fluid. Figure 6 demonstrates the influence of variable conductivity \((\varepsilon _{1})\) on the temperature field \((\theta (\eta ))\). This figure shows that increasing the values of variable conductivity \((\varepsilon _{1})\) enhances the temperature field \((\theta (\eta ))\). The influence of Pr on the temperature field \((\theta (\eta ))\) is displayed in figure 7. Figure 7 shows that increase Pr tends to decrease the temperature field \((\theta (\eta ))\). Temperature field declines as Pr strengthens. This is the reason for the reduction in thermal conductivity of the fluid with increasing Pr. The temperature field \((\theta (\eta ))\) is sketched in figure 8 for increasing values of generalised Biot number \((\gamma )\). This figure shows that temperature field \((\theta (\eta ))\) decreases for increasing values of generalised Biot number \((\gamma _1)\). Physically, less resistance from the thermal wall causes augmentation in convective heat transfer to the fluid. Figure 9 explores the deviation of section parameter (s) on the temperature field \((\theta (\eta ))\). Here, temperature field \((\theta (\eta ))\) decreases for increasing section parameter (s). Physically, the liquid particle observes the stretching sheet and each particle transfers energy to the environment. Figures 10–13 indicate variation in concentration field \((\phi (\eta ))\). Figure 10 shows the effect of activation energy (E) on concentration field \((\phi (\eta ))\). It can be seen that the concentration field \((\phi (\eta ))\) is increasing with an increment in activation energy (E). We have detected that higher activation energy and temperature reduce the reaction rate because the reaction mechanism is reduced. Thus, the concentration field increases for the activation energy. Figure 11 shows the variation in temperature of the Carreau nanofluid with variable conductivity (\(\varepsilon _2\)). Graphical data show that the Carreau nanofluid temperature increases with increasing \(\varepsilon _2\). Figure 12 is plotted to investigate the Brownian motion parameter (\({N}_{b}\)) on concentration field \((\phi (\eta ))\). Here, we detect that increasing the values of thermophoresis parameter \((N_{t})\) decreases the concentration field \((\phi (\eta ))\). Figure 14 is plotted to show the effect of Schmidt number (Sc) on \((\theta (\eta ))\). Here is a decreasing function for larger Schmidt number (Sc).

Fig. 12
figure 12

Influence of \(N_{b}\) on concentration \((\phi (\eta ))\).

Full size image
Fig. 13
figure 13

Influence of \(N_{t}\) on concentration \((\phi (\eta ))\).

Full size image
Fig. 14
figure 14

Influence of Sc on concentration \((\phi (\eta ))\).

Full size image

Table 1 shows how much order of computation is required for convergent solution. Table 1 shows that the present solutions are in excellent agreement with other previously published data. Table 2 examines the skin friction \((\frac{1}{2}Re^{1/2}C_{fx})\) and Nusselt number \((Re^{-1/2}Nu_{x})\) for dimensionless parameters \(A,\, N,\, G\) and \(\theta _{r}\). Table 2 shows that the skin friction becomes less for increasing parameter A while the opposite occurs for \(N,\, G\) and \(\theta _{r}\). Similarly, the rate of heat transport increases for increasing values of dimensionless parameters \(A,\, N\) and G. However, opposite behaviour is observed for \(\theta _{r}\).

Table 1 Comparison of the current results of \(f{''}(0)\) with previous results [29] and [30] for different values of A when \(n=1.0\), and \(S=0.0=\lambda _{1} = G = \theta _{r}\).
Full size table
Table 2 Numerical outcomes \(\frac{1}{2}Re^{1/2}C_{fx}\) for various physical parameters with \(n=0.8\).
Full size table

5 Main outcomes

Carreau flow of nanomaterial and variable properties are examined in the present analysis. Heat and mass transport via convection and activation energy are studied, respectively. The main theme of this study is to control the flow of fluid, skin friction using heat and mass transport rate. The velocity of fluid \((f^{\prime }(\eta ))\) is increased by increasing the values of A. Section parameter (s) decay is observed in the component of velocity field \((f^{\prime }(\eta ))\). Increase in mixed convection parameter (G) increases velocity \((f^{\prime }(\eta ))\). The fluid concentration \((\phi (\eta ))\) decreases for increasing values of Brownian motion parameter \((N_{b})\). The concentration of Carreau nanofluid decreases with increasing values of Sc. The augmentation in activation energy parameter (E) corresponds to a higher concentration \((\phi (\eta ))\). Skin friction decreases with increasing values of \(A,\, N,\, G\) and \(\theta _{r}\). Heat transfer rate increases with increasing values of \(A,\, N,\, G\) and \(\theta _{r}\).