Analysis of non-linear radiative stagnation point flow of Carreau fluid with homogeneous-heterogeneous reactions

Abstract

Current work focuses on stagnation point flow of MHD Carreau fluid with heterogeneous–homogeneous reactions. Non-linear stretched sheet of variable thickness is the main agent for flow induction. Liquid is assumed an electrically conducted. Nonlinear thermal radiation and heat generation/absorption aspects are addressed. Proper transformations lead to dimensionless the governing problem. Resultant systems are tackled numerically via NDSolve based Shooting scheme. Importance of emerging variables is addressed through graphical illustrations. Tables regarding the estimations of skin friction and rate of heat transfer are computed and examined for various physical variables. It is found that convective and radiation variables improve the liquid temperature. Obtained outcomes are also compared in limiting way and found an excellent agreement.

1 Introduction

There is a wide range of chemical reactions in nature which have widespread practical applications. These reactions are involved in various processes especially in fog formation and dispersion, food processing, hydrometallurgical industry, air and water pollutions, atmospheric flows, fibres insulation and crops damage due to freezing etc. In these process the molecular diffusion of species on the boundary or inside the chemical reaction is very intricate. Some of the reactions have the capacity to proceed gradually or do not react at the moment with out catalyst. In this direction (Merkin 1996) studied a model for isothermal homogeneous–heterogeneous reactions in boundary layer flow over a flat plate. Forced convection stagnation point flow of viscous fluid with homogeneous–heterogeneous reactions was explored by (Chaudhary and Merkin 1995). (Khan and Pop 2015) put forward such effects on the flow of viscoelastic fluid towards a stretching sheet. The boundary layer flow of Maxwell fluid over a stretching surface with homogeneous-heterogeneous reactions was examined by Hayat et al. (2015a). The characteristics of homogeneous–heterogeneous reactions in the region of stagnation point flow of carbon nanotubes over a stretching cylinder with Newtonian heating was presented by Hayat et al. (2015b). (Farooq et al. 2015) discussed the homogeneous–heterogeneous reaction in flow of Jeffrey liquid. Aspects of homogeneous–heterogeneous reactions in flow of Sisko liquid was studied by Hayat et al. (2018a). Temperature based heat source and nonlinear radiative flow of third grade liquid with homogeneous-heterogeneous reactions is explored by Hayat et al. (2018b).

Heat transport and flow phenomena because of stretching surface have various practical uses in technological and engineering processes. Such phenomenon encountered in paper production, fiber production, extrusion of polymer and metal, wire drawing, hot rolling, refrigeration and heat conduction in tissues etc. Both stretching and kinematics of heat transport during such procedure have a crucial consequence on standard of final outcomes. Initially (Sakiadis 1961) provided the study of boundary layer flow bounded by a stretching sheet. (Crane 1970) and (Gupta and Gupta 1977) inspected heat/mass transport analysis over a stretching sheet with constant surface temperature. Afterwards several theoretical attempts have been performed by several researchers (Bhattacharyya 2011; Turkyilmazoglu 2011; Malvandi et al. 2014; Shehzad et al. 2015; Hayat et al. 2016a; Ibrahim et al. 2013; Hayat et al. 2016b; Meraj et al. 2017; Zhu et al. 2017; Mahanthesh et al. 2016; Abbasi et al. 2016; Hayat et al. 2017a, b; Sheikholeslami and Shehzad 2017; Hayat et al. 2018c). Further, the stretching sheet with variable thickness occur in practical uses more frequently than a flat sheet. Such flow phenomenon are used in marine structures, aeronautical, mechanical and civil. Variable thickness is used for reduction of structural elements weight and advance way to use material (Shufrin and Eisenberger 2005) Some notable attempts in this direction can be seen via (Fang 2012; Subhashini et al. 2013; Hayat et al. 2015c, 2016c, 2017c, 2018d; Hayat et al. 2018e).

Present study disclose the aspects of homogeneous–heterogeneous reactions and magnetohydrodynamic (MHD) flow of Carreau fluid past a nonlinear starching sheet with variable thickness. It is assumed that plate is heated and exposed to transverse magnetic field. Features of heat generation/absorption and nonlinear thermal radiation are considered in mathematical modeling. Further we imposed convective condition at the surface. Mathematical formulation is constructed through boundary layer and small magnetic Reynolds number assumptions. Resulting nonlinear systems are then attempted numerically by NDSolve technique. Numerical computations and discussion of plots are carried out for various influential variables. Further comparative analysis is provided to validate our current outcomes.

2 Formulation

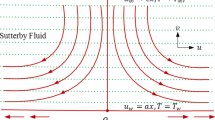
We intend to inspect steady two-dimensional flow of Carreau fluid in the region of stagnation point flow towards a nonlinear stretching sheet with variable thickness. Liquid is conducting electrically via constant magnetic field of strength $B_{0}$ (see Fig.1). We ignored the contribution of induced magnetic field utilizing the small magnetic Reynolds number assumptions. Let $U_{e} = U_{\infty } (x + b_{1} )^{m}$ and $U_{w} = U_{0} (x + b_{1} )^{m}$ indicate the respective velocities of external and sheet flow. Where reference velocities are signified by $U_{0}$ and $U_{\infty }$. Features of radiation and heat generation/absorption are addressed in governing expression. In addition the contribution of homogeneous-heterogeneous reactions are considered. For cubic autocatalysis the homogeneous reaction can be written as (Merkin 1996; Chaudhary and Merkin 1995):

$$A + 2B \to 3B,\, \, rate = K_{c} ab^{2} .$$

(1)

On catalyst surface the first-order isothermal reaction is expressed as

$$A \to B,\, \, rate = K_{s} a,\,$$

(2)

where $a$ and $b$ the respective concentrations of chemical species $A$ and $B$ and $K_{c}$ and $K_{s}$ show the rate constants. Both the reaction processes are assume to be isothermal. The governing expression for flow under consideration are:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,\,$$

(3)

$$\begin{aligned} u\frac{\partial u}{\partial x} + \upsilon \frac{\partial u}{\partial y} = & \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} + \nu (n - 1)\varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} \\ & \, + \frac{{\sigma B_{0}^{2} }}{\rho }(U_{e} - u) + U_{e} \frac{{dU_{e} }}{dx},\, \\ \end{aligned}$$

(4)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{k}{{\rho c_{p} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\rho c_{p} }}\frac{{16\sigma^{ * } }}{{3m^{ * } }}\frac{\partial }{\partial y}\left( {T^{3} \frac{\partial T}{\partial y}} \right) + \frac{{Q_{0} (T - T_{\infty } )}}{{\rho c_{p} }},\,$$

(5)

$$u\frac{\partial a}{\partial x} + v\frac{\partial a}{\partial y} = D_{A} \frac{{\partial^{2} a}}{{\partial y^{2} }} - K_{c} ab^{2} ,\,$$

(6)

$$u\frac{\partial b}{\partial x} + v\frac{\partial b}{\partial y} = D_{B} \frac{{\partial^{2} b}}{{\partial y^{2} }} + K_{c} ab^{2} .$$

(7)

$$\left. {\begin{array}{*{20}c} {u = U_{w} = U_{0} (x + b_{1} )^{m} ,\, \, v = 0,\, \, - k\tfrac{\partial T}{\partial y} = h_{f} (T_{f} - T),} \\ {D_{A} \tfrac{\partial a}{\partial y} = K_{s} a,\, \, D_{B} \tfrac{\partial b}{\partial y} = - K_{s} a{\text{ at }}y = A_{1} (x + b_{1} )^{{\tfrac{1 - m}{2}}} ,} \\ \end{array} } \right\}\,$$

(8)

$$u \to U_{e} = U_{\infty } (x + b_{1} )^{m} ,\, \, T \to T_{\infty } ,\, \, a \to a_{0} ,\, \, b \to 0{\text{ as }}y \to \infty ,\,$$

(9)

Fig. 1

Schematic flow diagram

where ($u$, $v$) denotes the respective velocity components in ($x$, $y)$ directions, $Q_{0}$ the coefficient of heat generation/absorption, $\nu = \tfrac{\mu }{\rho }$ the kinematic viscosity, $\rho$ the liquid density, $\varGamma$ the material time constant, $\mu$ the dynamic viscosity, $k$ the thermal conductivity, $\sigma$ the electrical conductivity, $m^{ * }$ the mean absorption coefficient, $\sigma^{ * }$ the Stefan-Boltzmann constant, $b_{1}$ the stretching constant, ($D_{A}$, $D_{B}$) the diffusion species coefficients of $A$ and $B$, ($a$, $b$) the chemical species of concentration, ($T_{\infty }$, $T$) the ambient and surface temperatures and $n$ expresses the power law index. Noted that $n = 1$ corresponds to viscous fluid. The transformations are defined as follow:

$$\left. {\begin{array}{*{20}c} {u = U_{0} \left( {x + b_{1} } \right)^{m} F^{\prime}\left( \eta \right),\, \, v = - \sqrt {\left( {\tfrac{m + 1}{2}} \right)\,\nu U_{0} \left( {x + b_{1} } \right)^{m - 1} } \left[ {F\left( \eta \right) + \eta F^{\prime}\left( \eta \right)\,\left( {\tfrac{m - 1}{m + 1}} \right)} \right],} \\ {\eta = y\sqrt {\left( {\tfrac{m + 1}{2}} \right)\,\tfrac{{U_{0} \left( {x + b_{1} } \right)^{m - 1} }}{\nu },\, \, } \theta (\eta ) = \tfrac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\, \, g(\eta ) = \tfrac{a}{{a_{0} }},\, \, h(\eta ) = \tfrac{b}{{a_{0} }}.} \\ \end{array} } \right\}\,$$

(10)

On using Eq. (10), the continuity expression is identically satisfied while Eqs. (4, 5, 6, 7, 8, 9) become

$$\begin{array}{*{20}c} {F^{\prime\prime\prime}\left[ {1 + We^{2} F^{{\prime \prime^{2} }} } \right]^{{\tfrac{n - 3}{2}}} \left[ {1 + nWe^{2} F^{{\prime \prime^{2} }} } \right] + FF^{\prime\prime} - \left( {\tfrac{2m}{m + 1}} \right)\,F^{{\prime^{2} }} } \\ { + \left( {\tfrac{2}{m + 1}} \right)\,M^{2} \left( {\lambda - F^{\prime}} \right) + \left( {\tfrac{2m}{m + 1}} \right)\,\lambda^{2} = 0,} \\ \end{array}$$

(11)

$$\left. {\begin{array}{*{20}c} {(1 + Rd)\theta^{\prime\prime} + Rd[(\varTheta_{w} - 1)^{3} (3\varTheta^{{^{{\prime^{2} }} }} \varTheta^{\prime 2} + \varTheta^{3} \varTheta^{\prime\prime}) + 3(\varTheta_{w} - 1)^{2} (2\varTheta^{{^{{\prime^{2} }} }} \varTheta + \varTheta^{2} \varTheta^{\prime\prime})} \\ { + 3(\varTheta_{w} - 1)(\varTheta^{{^{{\prime^{2} }} }} + \varTheta \varTheta^{\prime\prime})] + \Pr F\varTheta^{\prime} + \left( {\tfrac{2}{n + 1}} \right)\,\Pr \gamma_{1} \varTheta = 0,} \\ \end{array} } \right\}\,$$

(12)

$$\frac{1}{Sc}g^{\prime\prime} + Fg^{\prime} - \left( {\frac{1}{m + 1}} \right)\,K_{1} gh^{2} = 0,\,$$

(13)

$$\frac{{\delta_{1} }}{Sc}h^{\prime\prime} + Fh^{\prime} + \left( {\frac{1}{m + 1}} \right)\,K_{1} gh^{2} = 0,\,$$

(14)

$$\left. {\begin{array}{*{20}c} {F\left( \alpha \right) = \alpha \left( {\tfrac{1 - m}{1 + m}} \right),\, \, F^{\prime}(\alpha ) = 1,\, \, \theta^{\prime}(\alpha ) = - \gamma (1 - \theta (\alpha )),} \\ {g^{\prime}(\alpha ) = K_{2} g(\alpha ),\, \, \delta_{1} h^{\prime}(\alpha ) = - K_{2} h(\alpha )}, \end{array} } \right\}\,$$

(15)

$$F^{\prime}(\alpha ) \to \lambda ,\, \, \theta \left( \alpha \right) \to 0,\, \, g(\alpha ) \to 1,\, \, h(\eta ) \to 0{\text{ as }}\alpha \to \infty ,\,$$

(16)

where prime represents differentiation via $\eta$, $\alpha = A \sqrt {\left( {\tfrac{m + 1}{2}} \right)\,\tfrac{{U_{0} }}{\nu }}$ the wall thickness parameter and $\eta = \alpha = A \sqrt {\left( {\tfrac{n + 1}{2}} \right)\,\tfrac{{U_{0} }}{v}}$ indicates the flat surface. By considering $F(\eta ) = f(\eta - \alpha ) = f(\xi ),$$\varTheta (\eta ) = \theta (\eta - \alpha ) = \theta (\xi ),$ Eqs. 11, 12, 13, 14, 15, 16 reduced to the from

$$\begin{array}{*{20}l} {f^{\prime\prime\prime}\left[ {1 + We^{2} f^{{\prime \prime^{2} }} } \right]^{{\tfrac{n - 3}{2}}} \left[ {1 + nWe^{2} f^{{\prime \prime^{2} }} } \right] + ff^{\prime\prime} - \left( {\tfrac{2m}{m + 1}} \right)\,f^{{\prime^{2} }} } \hfill \\ { + \left( {\tfrac{2}{m + 1}} \right)\,M^{2} \left( {\lambda - f^{\prime}} \right) + \left( {\tfrac{2m}{m + 1}} \right)\,\lambda^{2} = 0,} \hfill \\ \end{array}$$

(17)

$$\left. {\begin{array}{*{20}c} {(1 + Rd)\theta^{\prime\prime} + Rd[(\theta_{w} - 1)^{3} (3\theta^{{^{{\prime^{2} }} }} \theta^{2} + \theta^{3} \theta^{\prime\prime}) + 3(\theta_{w} - 1)^{2} (2\theta^{{^{{\prime^{2} }} }} \theta + \theta^{2} \theta^{\prime\prime})} { + 3(\theta_{w} - 1)(\theta^{{^{{\prime^{2} }} }} + \theta \theta^{\prime\prime})] + \Pr f\theta^{\prime} + \Pr \left( {\tfrac{2}{m + 1}} \right)\,\gamma_{1} \theta = 0,} \\ \end{array} } \right\}\,$$

(18)

$$\frac{1}{Sc}g^{\prime\prime} + fg^{\prime} - \left( {\frac{1}{m + 1}} \right)\,K_{1} gh^{2} = 0,\,$$

(19)

$$\frac{{\delta_{1} }}{Sc}h^{\prime\prime} + fh^{\prime} + \left( {\frac{1}{m + 1}} \right)\,K_{1} gh^{2} = 0,\,$$

(20)

$$\left. {\begin{array}{*{20}c} {f\left( 0 \right) = \alpha \left( {\tfrac{1 - m}{1 + m}} \right),\, \, f^{\prime}(0) = 1,\, \, \theta^{\prime}(0) = - \gamma (1 - \theta (0)),} \\ {g^{\prime}(0) = K_{2} g(0),\, \, \delta_{1} h^{\prime}(0) = - K_{2} h(0),} \\ \end{array} } \right\}\,$$

(21)

$$f^{\prime}(\infty ) \to \lambda ,\, \, \theta \left( \infty \right) \to 0,\, \, g(\infty ) \to 1,\, \, h(\infty ) \to 0.$$

(22)

Here $Rd( = \tfrac{{4\sigma^{ * } T_{\infty }^{3} }}{{km^{ * } }})$ the radiation parameter, $\gamma_{1} ( = \tfrac{{Q_{0} }}{{\rho c_{p} U_{0} }})$ the heat generation/absorption variable, $\theta_{w} ( = \tfrac{{T_{f} }}{{T_{\infty } }})$ the temperature parameter, $We( = \sqrt {\tfrac{{U_{0}^{3} (m + 1)(x + b_{1} )^{3m - 1} }}{2\nu}} )$ the local Weissenberg number, $\gamma (=\tfrac{{h_{f} }}{k\sqrt {\tfrac{2U_0(x+b_1)^{m-1} }{(1+n)\nu}}} )$ the Biot number, $M(=\tfrac{{\sigma B_{0}^{2} }}{{\rho U_{0} (x + b_{1} )^{m - 1} }})$ represents the magnetic parameter, $\lambda ( = \tfrac{U\infty }{{U_{0} }})$ the velocity ratio, $\Pr$ stands for Prandtl number, $K_{1} ( = \tfrac{{K_{c} a_{0}^{2} (x + b_{1} )}}{{U_{w} }})$ the measure of the strength of homogeneous reaction, $Sc(=\tfrac{\nu }{{D_{A} }})$ the Schmidt number, $\delta_{1} ( = \tfrac{{D_{B} }}{{D_{A} }})$ the diffusion coefficient ratio, $K_{2} (=\tfrac{{K_{s} }}{{D_{A} }}\sqrt {\tfrac{{\nu (x + b_{1} )}}{{U_{w} }}} )$ the measure of the strength of heterogeneous reaction and prime designates differentiation via $\xi .$

Here assume that $D_{B}$ and $D_{A}$ are equal i.e., $\delta_{1} = 1$ and thus:

$$g(\eta ) + h(\eta ) = 1.$$

(23)

Therefore Eqs. 19, 20 yield

$$\frac{1}{Sc}g^{\prime\prime} + fg^{\prime} - K_{1} g(1 - g)^{2} = 0,\,$$

(24)

and

$$g^{\prime}(0) = K_{2} g(0),\, \, g(\infty ) \to 1.$$

(25)

The skin friction and Nusselt number are

$$C_{f_{x}} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} /2}},\, \, Nu_{x} = \frac{{(x + b_{1} )q_{w} }}{{k\left( {T_{f} - T_{\infty } } \right)}},\,$$

(26)

where

$$\left. {\begin{array}{*{20}c} {\tau_{w} = \eta_{0} \tfrac{\partial u}{\partial y}\left[ {1 + \varGamma^{2} \left( {\tfrac{\partial u}{\partial y}} \right)^{2} } \right]_{{y = A_{1} (x + b_{1} )^{{\tfrac{1 - m}{2}}} }}^{{\tfrac{n - 1}{2}}} ,} \\ {q_{w} = - k\left( {1 + \tfrac{{16\delta^{ * } T^{3} }}{{3km^{ * } }}} \right)\,\left( {\tfrac{\partial T}{\partial y}} \right)_{{y = A_{1} (x + b_{1} )^{{\tfrac{1 - m}{2}}} }} .} \\ \end{array} } \right\}\,$$

(27)

Non-dimensional form of skin friction and local Nusselt number are

$$\left. {\begin{array}{*{20}c} {Re_{x}^{1/2} C_{{f_{x} }} = \sqrt {2(m + 1)} \left( {f^{\prime\prime}\left[ {1 + We^{2} f^{{\prime \prime^{2} }} } \right]^{{\tfrac{n - 1}{2}}} } \right)_{\xi = 0} ,} \\ {Re_{x}^{ - 1/2} Nu_{x} = - \sqrt {(\tfrac{m + 1}{2})} \left( {1 + \tfrac{4}{3}Rd(\theta_{w} - 1)\theta (0))^{3} } \right)\,\theta^{\prime}(0),} \\ \end{array} } \right\}\,$$

(28)

where $Re_{x} = U_{w} (x + b_{1} )^{m + 1} /\nu$ indicates local Reynolds number.

3 Discussion

In order to find the numerical solutions valid locally for Eqs. 17, 18, 19, 20, 21, 22, we employ NDSolve based Shooting technique. Using the numerical technique the interpretations have been performed for numerous estimations of embedded variables. Aspects of $\lambda$ on $f^{\prime}(\xi )$ is captured in Fig. 2. Clearly velocity enhances for $\lambda > 1$ but for $\lambda < 1$ the layer thickness reduces. Further it is noted that for $\lambda = 1$ there is no boundary layer due to same free stream and velocities. Influence of $M$ on $f^{\prime}(\xi )$ is disclosed in Fig. 3. Higher $M$ leads to rise the Lorentz forces (resistive forces) which consequently decay the liquid velocity. Figure 4 indicates behavior of $n$ on $f^{\prime}(\xi ).$ It is found that $f^{\prime}(\xi )$ substantially rise the velocity. Features of $We$ on $f^{\prime}(\xi )$ is plotted in Fig. 5. As expected, higher $We$ result in an increment of velocity. Variations of $\Pr$ on $\theta \left( \xi \right)$ is drawn in Fig. 6. Here we see that higher estimations of $\Pr$ decay thermal conductivity and thus decline the liquid temperature. Figure 7 exhibits the impact of $\gamma_{1}$ on temperature distributions. This Fig. indicates that thermal field enhances for larger estimations of $\gamma_{1}$. Effects of $Rd$ on $\theta \left( \xi \right)$ is declared in Fig. 8. As expected the heat is generated due to radiation process in working liquid which consequently rise the temperature. Temperature for $\gamma$ is captured in Fig. 9. Clearly $\theta \left( \xi \right)$ is enhanced via $\gamma .$ Figure 10 disclose the impact of $We$ on $\theta \left( \xi \right).$ Higher values of $We$ correspond to enhancement of fluid temperature. Figure 11 depicts impact of $K_{1}$ on $g\left( \xi \right)$. Higher estimations of $K1$ enhance $g\left( \xi \right)$. Figure 12 presents effect of $K_{2}$ on $g\left( \xi \right).$ Here $g\left( \xi \right)$ reduces for larger $K_{2}$. Behavior of $Sc$ on $g\left( \xi \right)$ is noticed in Fig. 13 Decaying feature of $g\left( \xi \right)$ is seen for higher $Sc$. Table 1 reports numerical outcomes of drag force ($- \left( {Re} \right)^{1/2} C_{{f_{x} }}$) for distinct flow variables $We$, $M$, $\lambda$, $n$ and $\;m$. It is shown that $- \left( {Re} \right)^{1/2} C_{{f_{x} }}$ enhances for $n$, $We$, and $M$. Table 2 is prepared for variations of Nusselt number $- \theta^{\prime}\left( 0 \right)$ against various embedded variables. It scrutinizes that Nusselt number is enhanced for $n$, $\Pr$, $\lambda$ and $\;\gamma$ while it diminishes for $M$. Table 3 certifies the validation of present analysis with limiting study provided by Hayat et al. (2017d). Clearly obtained outcomes are an exellent agreement.

Fig. 2

$f^{\prime}(\xi )$ through $\lambda$

Fig. 3

$f^{\prime}(\xi )$ through $M$

Fig. 4

$f^{\prime}(\xi )$ through $n$

Fig. 5

$f^{\prime}(\xi )$ through $We$

Fig. 6

$\theta (\xi )$ through $\Pr$

Fig. 7

$\theta (\xi )$ through $\gamma_{1}$

Fig. 8

$\theta (\xi )$ through $Rd$

Fig. 9

$\theta (\xi )$ through $\gamma$

Fig. 10

$\theta (\xi )$ through $We$

Fig. 11

$g(\xi )$ through $K_{1}$

Fig. 12

$g(\xi )$ through $K_{2}$

Fig. 13

$g(\xi )$ through $Sc$

Table 1 Numerical values of skin friction $- Re^{1/2} C_{fx}$ for $M$, $We$, $\lambda$ and $m$

Table 2 Numerical outcomes of surface temperature gradient $- \theta^{\prime}(0)$ for different values of $\gamma_{1}$, $\lambda$, $We$, $Rd$$\theta_{w}$ and $\gamma$ when $\Pr = 6.2$, $M = \lambda = 0.3$, $m = 0.5$, $n = 1.0$, $K_{1} = 0.5 = K_{2}$ and $Sc = 0.9.$

Table 3 Comparison for numerical estimations of $- \sqrt {\tfrac{m + 1}{2}} \theta^{\prime}(0)$ with Hayat et al. (2017) for distinct values of $\lambda$ and $We$ when $\gamma_{1} = Rd = \theta_{w} = 0$

4 Final remarks

Main points include:

• Velocity enhances via We and n while it diminishes through M.

• Temperature field decays through higher Pr and We.

• Thermal layer thickness and temperature are enhanced for higher Rd, $\gamma$ and $\gamma_{1}$.

• Concentration shows reverse trend for higher estimations of K₂ and K₁.

• Surface drag force enhances via $\;\lambda ,\,\;m$ and M.

• Nusselt number reduces for Rd and θ_w