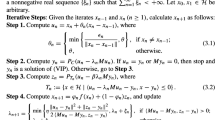On modified subgradient extragradient methods for pseudomonotone variational inequality problems with applications

Abstract

This paper presents several modified subgradient extragradient methods with inertial effects to approximate solutions of variational inequality problems in real Hilbert spaces. The operators involved are either pseudomonotone Lipschitz continuous or pseudomonotone non-Lipschitz continuous. The advantage of the suggested algorithms is that they can work adaptively without the prior information of the Lipschitz constant of the mapping involved. Strong convergence theorems of the proposed algorithms are established under some suitable conditions. Finally, some numerical experiments are given to verify the advantages and efficiency of the proposed iterative algorithms with respect to previously known ones.

1 Introduction and preliminaries

The goal of this paper is to provide several efficient and adaptive numerical methods to solve pseudomonotone variational inequality problems in real Hilbert spaces. Recall that the classical variational inequality problem (shortly, VIP) is given as follows:

$$\begin{aligned} \text {find } x^{*} \in C \text{ such } \text{ that } \left\langle M x^{*}, z-x^{*}\right\rangle \ge 0,\quad \forall z \in C, \end{aligned}$$

(VIP)

where C is a nonempty, closed and convex subset of a real Hilbert space $\mathcal {H}$ with inner product $\langle \cdot , \cdot \rangle$ and induced norm $\Vert \cdot \Vert$, and $M: \mathcal {H} \rightarrow \mathcal {H}$ is an operator. Throughout the paper, the solution set of the (VIP) is denoted by $\mathrm {VI}(C,M)$, and is assumed to be nonempty. The variational inequality, as one of the fundamental problems in mathematics, provides a unified and useful framework for the study of many linear and nonlinear problems. It has become one of the effective mathematical methods and research tools in solving optimization problems, and has been widely used in many research fields (such as engineering, finance, mechanics, transportation modeling, operations management and optimal control), see, e.g., Mordukhovich (2018), Vuong and Shehu (2019), Bonacker et al. (2020), Cuong et al. (2020), Khan et al. (2015) and Sahu et al. (2021).

Let us first review the basic definitions of some mappings in nonlinear analysis, which will be used in the next sequel. Recall that a mapping $M: \mathcal {H} \rightarrow \mathcal {H}$ is said to be:

• L-Lipschitz continuous with $L > 0$ if $\Vert M x-M y\Vert \le L\Vert x-y\Vert , \; \forall x,y\in \mathcal {H}$.

• monotone if $\langle M x-M y, x-y\rangle \ge 0, \; \forall x,y\in \mathcal {H}$.

• pseudomonotone if $\langle M x, y-x\rangle \ge 0 \Rightarrow \langle M y, y-x\rangle \ge 0, \; \forall x,y\in \mathcal {H}$.

• sequentially weakly continuous if for each sequence $\left\{ x_{n}\right\}$ converges weakly to x implies $\left\{ M x_{n}\right\}$ converges weakly to Mx.

In the past decades, researchers proposed a large number of iterative methods to solve variational inequality problems, among which the methods based on extragradient types are the focus of this paper. Recall that the classical extragradient method (shortly, EGM), which was introduced by Korpelevich (1976), requires computing the projection on the feasible set twice in each iteration. The computation of the projection is difficult if the feasible set is complex. In order to improve the computational efficiency of the iterative algorithm, scholars have proposed many improvements to the EGM, see, e.g., (He 1997; Solodov and Svaiter 1999; Tseng 2000; Censor et al. 2011; Malitsky 2015) and the references therein. It should be mentioned that the subgradient extragradient method (SEGM) proposed by Censor et al. (2011) replaces the projection on the feasible set in the second step of the EGM with a projection on the half-space in each iteration. It is known that the projection on a half-space can be computed explicitly (see, e.g., Cegielski 2012). Thus, the SEGM greatly improves the computational efficiency of the EGM. Note that the SEGM can only obtain the weak convergence in infinite-dimensional Hilbert spaces. From the viewpoint of the physically tangible property, the strong convergence, which is norm convergence, is often much more desirable than the weak convergence. This shows the theoretical value and potential applications of analyzing the strong convergence of iterative algorithms in infinite-dimensional Hilbert spaces. In the last decades, many techniques were developed to obtain strongly convergent numerical methods for solving variational inequality problems in infinite-dimensional Hilbert spaces; see, e.g., Mann-type methods (Kraikaew and Saejung 2014; Tan et al. 2021), viscosity-type methods (Shehu and Iyiola 2017; Thong et al. 2019), and projection-based methods (Censor et al. 2011; Cho 2020). In this paper, we consider several strongly convergent numerical algorithms for variational inequalities in the framework of real Hilbert spaces, which is motivated by the real applications of the (VIP) in infinite-dimensional spaces, such as machine learning and quantum mechanics.

On the other hand, it is noted that the Lipschitz constants of the operators corresponding to the problems studied in practical applications are difficult to obtain and estimate, which will further affect the use of those algorithms whose step size is related to the prior information of the Lipschitz constant. Recently, some adaptive algorithms that do not require the prior information of the Lipschitz constant of the operator involved were proposed to solve variational inequality problems, see, e.g., Thong and Hieu (2018), Yang et al. (2018), Yang and Liu (2019), Liu and Yang (2020), Cai et al. (2021), Hieu et al. (2021) and the references therein. Among the step size selections of these methods, a non-monotonic step size criterion proposed by Liu and Yang (2020), and a new Armijo-type step size approach introduced by Cai et al. (2021) are desired to be mentioned. Their numerical experiments demonstrated the advantages and efficiency of the proposed algorithms over previously known ones.

It is known that the class of pseudomonotone mappings contains the class of monotone mappings. Recently, many algorithms were proposed in the literature to solve pseudomonotone variational inequalities in real Hilbert spaces; see, e.g., Hieu et al. (2021), Shehu et al. (2019), Jolaoso et al. (2020), Thong et al. (2020), Yang (2021), Grad and Lara (2021) and the references therein. However, a common feature enjoyed by these algorithms is the requirement that the operator satisfies the Lipschitz continuity, which may be difficult to be satisfied in practical applications. To overcome this drawback, scholars proposed many iterative schemes for solving non-Lipschitz continuous monotone (or pseudomonotone) variational inequality problems (see, e.g., Cai et al. 2021; Shehu et al. 2019; Cho 2020; Malitsky 2020; Reich et al. 2021; Tan and Cho 2021). On the other hand, the inertial extrapolation method based on discrete versions of a second-order dissipative dynamic system was widely studied as one of the acceleration techniques. Recently, inertial-type methods attracted a great deal of attention and interest from researchers in the optimization community, who proposed a large number of inertial-type numerical algorithms to solve image processing, signal recovery, variational inequality problems, equilibrium problems, split feasibility problems, fixed point problems, and variational inclusion problems, see, e.g., Hieu and Gibali (2020), Ceng and Shang (2021), Shehu and Yao (2020), Shehu and Gibali (2021) and the references therein. The main feature of inertial-type methods is the inclusion in each iteration of an inertial term, which is obtained from the combination of some previously known iteration points. This small change can improve the convergence speed of the original algorithm without the inertial term.

Inspired and motivated by the above work, this paper proposes several adaptive inertial subgradient extragradient methods to solve variational inequality problems in infinite-dimensional real Hilbert spaces. Our contributions in this paper are stated as follows: (1) the subgradient extragradient method introduced by Censor et al. (2011) is modified in two simple ways by using two different step sizes in each iteration; (2) two non-monotonic adaptive step size criteria are used to make the proposed algorithms work adaptively; (3) the variational inequality operators involved in the proposed methods are pseudomonotone Lipschitz continuous (or non-Lipschitz continuous); (4) the strong convergence of the iterative sequences generated by the proposed algorithms is established without the prior knowledge of the Lipschitz constant of the operator; (5) inertial extrapolation terms are added to the proposed algorithms to accelerate their convergence speed; and (6) some numerical experiments are given to verify the computational efficiency of the proposed iterative schemes compared to some known algorithms in the literature (Cai et al. 2021; Thong and Vuong 2019; Thong et al. 2020).

In the whole paper, we use the symbol $x_{n} \rightarrow x$ ($x_{n} \rightharpoonup x$) to represent the strong convergence (weak convergence) of the sequence $\left\{ x_{n}\right\}$ to x, and use $P_{C}: \mathcal {H} \rightarrow C$ to denote the metric projection from $\mathcal {H}$ onto C, i.e., $P_{C}(x):= \arg \min \{\Vert x-y\Vert ,\, y \in C\}$. We conclude the section by giving the following lemma that is crucial in the convergence analysis of the proposed algorithms.

Lemma 1.1

(Saejung and Yotkaew 2012) Let $\left\{ p_{n}\right\}$ be a positive sequence, $\left\{ s_{n}\right\}$ be a sequence of real numbers, and $\left\{ \alpha _{n}\right\}$ be a sequence in (0, 1) such that $\sum _{n=1}^{\infty } \alpha _{n}=\infty$. Assume that

$$\begin{aligned} p_{n+1} \le (1-\alpha _{n}) p_{n}+\alpha _{n} s_{n}, \quad \forall n \ge 1. \end{aligned}$$

If $\limsup _{k \rightarrow \infty } s_{n_{k}} \le 0$ for every subsequence $\left\{ p_{n_{k}}\right\}$ of $\left\{ p_{n}\right\}$ satisfying $\lim \inf _{k \rightarrow \infty }$ $(p_{n_{k}+1}-p_{n_{k}}) \ge 0$, then $\lim _{n \rightarrow \infty } p_{n}=0$.

2 Main results

In this section, we introduce several modified subgradient extragradient algorithms with inertial effects for solving pseudomonotone variational inequality problems in infinite-dimensional Hilbert spaces. The advantage of our algorithms is that they can work without the prior knowledge of the Lipschitz constant of the mapping and the strong convergence of the iterative sequence generated by the proposed algorithms can be guaranteed.

2.1 The first type of modified subgradient extragradient methods

In this subsection, two new iterative schemes are proposed for solving the (VIP) in real Hilbert spaces. We first introduce a new modified subgradient extragradient algorithm with a non-monotonic sequence of step sizes (see Algorithm 2.1 below) and assume that the proposed algorithm satisfies the following conditions.

• (C1) The feasible set C is a nonempty, closed and convex subset of the real Hilbert space $\mathcal {H}$ and the solution set of the problem (VIP) is nonempty.

• (C2) The operator $M: \mathcal {H} \rightarrow \mathcal {H}$ is pseudomonotone, L-Lipschitz continuous on $\mathcal {H}$ and sequentially weakly continuous on C.

• (C3) Let $\{\epsilon _{n}\}$ be a positive sequence such that $\lim _{n \rightarrow \infty } \frac{\epsilon _{n}}{\tau _{n}}=0$, where $\{\tau _{n}\}\subset (0,1)$ satisfies $\lim _{n \rightarrow \infty } \tau _{n}=0$ and $\sum _{n=1}^{\infty } \tau _{n}=\infty$. Let $\left\{ \sigma _{n}\right\} \subset (a, b) \subset \left( 0,1-\tau _{n}\right)$ for some $a>0, b>0$.

We now state the first iterative scheme in Algorithm 2.1.

The following lemmas are important for the convergence analysis of our main results.

Lemma 2.1

Suppose that Condition (C2) holds. Then the sequence $\{\lambda _{n}\}$ generated by (2.3) is well defined and $\lim _{n \rightarrow \infty } \lambda _{n}=\lambda$ and $\lambda \in \left[ \min \{{\mu }/{L}, \lambda _{1}\}, \lambda _{1}+\sum _{n=1}^{\infty }\xi _{n}\right]$.

Proof

The proof is similar to Lemma 3.1 in Liu and Yang (2020) and thus we omit the details. $\square$

Lemma 2.2

Assume that Condition (C2) holds. Let $\left\{ q_{n}\right\}$ be a sequence generated by Algorithm 2.1. Then, for all $p \in \mathrm {VI}(C, M)$,

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\beta ^{*}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned} \end{aligned}$$

where $\beta ^{*}=2-\beta -\frac{\beta \mu \lambda _{n}}{\lambda _{n+1}}$ if $\beta \in [1,2/(1+\mu ))$ and $\beta ^{*}=\beta -\frac{\beta \mu \lambda _{n}}{\lambda _{n+1}}$ if $\beta \in (0,1)$.

Proof

From the definition of $q_{n}$ and the property of projection $\Vert P_{C} (x)-y\Vert ^{2} \le \Vert x-y\Vert ^{2}-\Vert x-P_{C} (x)\Vert ^{2},\; \forall x \in \mathcal {H}, y \in C$, we have

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2}&=\left\| P_{T_{n}}\left( u_{n}-\beta \lambda _{n} M v_{n}\right) -p\right\| ^{2} \nonumber \\&\le \left\| u_{n}-\beta \lambda _{n} M v_{n}-p\right\| ^{2}-\left\| u_{n}-\beta \lambda _{n} M v_{n}-q_{n}\right\| ^{2} \nonumber \\&=\left\| u_{n}-p\right\| ^{2}+\left( \beta \lambda _{n}\right) ^{2}\left\| M v_{n}\right\| ^{2}-2\left\langle u_{n}-p, \beta \lambda _{n} M v_{n}\right\rangle -\left\| u_{n}-q_{n}\right\| ^{2} \nonumber \\&\quad -\left( \beta \lambda _{n}\right) ^{2}\left\| M v_{n}\right\| ^{2}+2\left\langle u_{n}-q_{n}, \beta \lambda _{n} M v_{n}\right\rangle \nonumber \\&=\left\| u_{n}-p\right\| ^{2}-\left\| u_{n}-q_{n}\right\| ^{2}-2\left\langle \beta \lambda _{n} M v_{n}, q_{n}-p\right\rangle \nonumber \\&=\left\| u_{n}-p\right\| ^{2}-\left\| u_{n}-q_{n}\right\| ^{2}-2\left\langle \beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle -2\left\langle \beta \lambda _{n} M v_{n}, v_{n}-p\right\rangle . \end{aligned}$$

(2.4)

Since $p \in \mathrm {VI}(C, M)$ and $v_{n} \in C$, we obtain $\langle M p, v_{n}-p\rangle \ge 0$. By the pseudomonotonicity of mapping M, we have $\langle M v_{n}, v_{n}-p\rangle \ge 0$. Thus the inequality (2.4) reduces to

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2} \le \left\| u_{n}-p\right\| ^{2}-\left\| u_{n}-q_{n}\right\| ^{2}-2\left\langle \beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.5)

Now we estimate $2\left\langle \beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle$. Note that

$$\begin{aligned} -\left\| u_{n}-q_{n}\right\| ^{2} =-\left\| u_{n}-v_{n}\right\| ^{2}-\left\| v_{n}-q_{n}\right\| ^{2}+2\left\langle u_{n}-v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.6)

In addition,

$$\begin{aligned}&\left\langle u_{n}-v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\quad =\left\langle u_{n}-v_{n}-\lambda _{n} M u_{n}+\lambda _{n} M u_{n}-\lambda _{n} M v_{n}+\lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\quad =\left\langle u_{n}-\lambda _{n} M u_{n}-v_{n}, q_{n}-v_{n}\right\rangle +\lambda _{n}\left\langle M u_{n}-M v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\qquad +\left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.7)

Since $q_{n}\in T_{n}$, one sees that

$$\begin{aligned} \left\langle u_{n}-\lambda _{n} M u_{n}-v_{n}, q_{n}-v_{n}\right\rangle \le 0. \end{aligned}$$

(2.8)

According to the definition of $\lambda _{n+1}$, it follows that

$$\begin{aligned} \begin{aligned} \left\langle M u_{n}-M v_{n}, q_{n}-v_{n}\right\rangle \le \frac{\mu }{2\lambda _{n+1}}\left\| u_{n}-v_{n}\right\| ^{2}+\frac{\mu }{2\lambda _{n+1}}\left\| q_{n}-v_{n}\right\| ^{2} . \end{aligned} \end{aligned}$$

(2.9)

Substituting (2.7), (2.8), and (2.9) into (2.6), we have

$$\begin{aligned} \begin{aligned} -\left\| u_{n}-q_{n}\right\| ^{2} \le -\left( 1-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) +2\left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle , \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} -2\left\langle \beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle&\le -\beta \left( 1-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad +\beta \left\| u_{n}-q_{n}\right\| ^{2}. \end{aligned}$$

(2.10)

Combining (2.5) and (2.10), we conclude that

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\beta \left( 1-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad -(1-\beta )\left\| u_{n}-q_{n}\right\| ^{2}. \end{aligned}$$

(2.11)

Note that

$$\begin{aligned} \left\| u_{n}-q_{n}\right\| ^{2}\le 2\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned}$$

which yields that

$$\begin{aligned} -(1-\beta )\left\| u_{n}-q_{n}\right\| ^{2}\le -2(1-\beta )\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta \ge 1. \end{aligned}$$

This together with (2.11) implies

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\left( 2-\beta -\frac{\beta \mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta \ge 1. \end{aligned} \end{aligned}$$

On the other hand, if $\beta \in (0,1)$, then we obtain

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2} \le \left\| u_{n}-p\right\| ^{2} -\beta \left( 1-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta \in (0,1). \end{aligned} \end{aligned}$$

This completes the proof of the lemma. $\square$

Remark 2.1

From Lemma 2.1 and the assumptions of the parameters $\mu$ and $\beta$ (i.e., $\mu \in (0,1)$ and $\beta \in (0,2/(1+\mu ))$), we can obtain that $\beta ^{*}>0$ for all $n\ge n_{0}$ in Lemma 2.2 always holds.

Lemma 2.3

(Thong et al. 2020, Lemma 3.3) Suppose that Conditions (C1)–(C3) hold. Let $\{u_{n}\}$ and $\{v_{n} \}$ be two sequences formulated by Algorithm 2.1. If there exists a subsequence $\left\{ u_{n_{k}}\right\}$ of $\left\{ u_{n}\right\}$ such that $\left\{ u_{n_{k}}\right\}$ converges weakly to $z \in \mathcal {H}$ and $\lim _{k \rightarrow \infty }\Vert u_{n_{k}}-v_{n_{k}}\Vert =0$, then $z \in \mathrm {VI}(C, M)$.

We now in a position to prove our first main result of this section.

Theorem 2.1

Suppose that Conditions (C1)–(C3) hold. Then the sequence $\left\{ x_{n}\right\}$ generated by Algorithm 2.1 converges to $p \in \mathrm {VI}(C, M)$ in norm, where $\Vert p\Vert =\min \{\Vert z\Vert : z \in \mathrm {VI}(C, M)\}$.

Proof

To begin with, our first goal is to show that the sequence $\left\{ x_{n}\right\}$ is bounded. Indeed, thanks to Lemma 2.2 and Remark 2.1, one sees that

$$\begin{aligned} \Vert q_{n}-p\Vert \le \Vert u_{n}-p\Vert , \quad \forall n \ge n_{0}. \end{aligned}$$

(2.12)

From the definition of $u_{n}$, one sees that

$$\begin{aligned} \Vert u_{n}-p\Vert&\le \Vert x_{n}-p\Vert +\tau _{n} \cdot \frac{\phi _{n}}{\tau _{n}}\Vert x_{n}-x_{n-1}\Vert . \end{aligned}$$

(2.13)

According to Condition (C3), we have $\frac{\phi _{n}}{\tau _{n}}\Vert x_{n}-x_{n-1}\Vert \rightarrow 0$ as $n\rightarrow \infty$. Therefore, there exists a constant $Q_{1}>0$ such that

$$\begin{aligned} \frac{\phi _{n}}{\tau _{n}}\Vert x_{n}-x_{n-1}\Vert \le Q_{1}, \quad \forall n \ge 1, \end{aligned}$$

which together with (2.12) and (2.13) implies that

$$\begin{aligned} \Vert q_{n}-p\Vert \le \Vert u_{n}-p\Vert \le \Vert x_{n}-p\Vert +\tau _{n} Q_{1}, \quad \forall n \ge n_{0}. \end{aligned}$$

(2.14)

Using the definition of $x_{n+1}$ and (2.14), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert (1-\tau _{n}-\sigma _{n})(u_{n}-p)+\sigma _{n}(q_{n}-p)-\tau _{n} p\Vert \nonumber \\&\le (1-\tau _{n}-\sigma _{n})\Vert u_{n}-p\Vert +\sigma _{n}\Vert q_{n}-p\Vert +\tau _{n}\Vert p\Vert \nonumber \\&\le (1-\tau _{n})\Vert u_{n}-p\Vert +\tau _{n}\Vert p\Vert \nonumber \\&\le (1-\tau _{n})\Vert x_{n}-p\Vert +\tau _{n}(\Vert p\Vert +Q_{1})\nonumber \\&\le \max \left\{ \Vert x_{n}-p\Vert ,\Vert p\Vert +Q_{1}\right\} ,\quad \forall n\ge n_{0} \nonumber \\&\le \cdots \le \max \left\{ \Vert x_{n_{0}}-p\Vert ,\Vert p\Vert +Q_{1}\right\} . \end{aligned}$$

(2.15)

This implies that the sequence $\left\{ x_{n}\right\}$ is bounded. We have that the sequences $\left\{ u_{n}\right\}$ and $\left\{ q_{n}\right\}$ are also bounded.

From (2.14), one sees that

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2}&\le (\Vert x_{n}-p\Vert +\tau _{n} Q_{1})^{2} \nonumber \\&=\Vert x_{n}-p\Vert ^{2}+\tau _{n}(2 Q_{1}\Vert x_{n}-p\Vert +\tau _{n} Q_{1}^{2}) \nonumber \\&\le \Vert x_{n}-p\Vert ^{2}+\tau _{n} Q_{2} \end{aligned}$$

(2.16)

for some $Q_{2}>0$. Combining (2.16), Lemma 2.2 and the inequality $\Vert \tau x+\sigma y+\delta z\Vert ^{2}= \tau \Vert x\Vert ^{2}+\sigma \Vert y\Vert ^{2}+\delta \Vert z\Vert ^{2}-\tau \sigma \Vert x-y\Vert ^{2} -\tau \delta \Vert x-z\Vert ^{2}-\sigma \delta \Vert y-z\Vert ^{2}$, where $\tau , \sigma , \delta \in [0, 1]$ and satisfies $\tau +\sigma +\delta =1$, we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&=\Vert (1-\tau _{n}-\sigma _{n})(u_{n}-p)+\sigma _{n}(q_{n}-p)+\tau _{n}(-p)\Vert ^{2} \nonumber \\&\le (1-\tau _{n}-\sigma _{n})\Vert u_{n}-p\Vert ^{2}+\sigma _{n}\Vert q_{n}-p\Vert ^{2}+\tau _{n}\Vert p\Vert ^{2}\nonumber \\&\le (1-\tau _{n}-\sigma _{n})\Vert u_{n}-p\Vert ^{2}+\sigma _{n}\Vert u_{n}-p\Vert ^{2}+\tau _{n}\Vert p\Vert ^{2}\nonumber \\&\quad -\sigma _{n}\beta ^{*}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\le \Vert x_{n}-p\Vert ^{2}-\sigma _{n}\beta ^{*}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad +\tau _{n}(\Vert p\Vert ^{2}+Q_{2}),\quad \forall n\ge n_{0}. \end{aligned}$$

(2.17)

It follows from (2.17) that

$$\begin{aligned}&\sigma _{n}\beta ^{*}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p\Vert ^{2} +\tau _{n}(\Vert p\Vert ^{2}+Q_{2}),\quad \forall n\ge n_{0}. \end{aligned}$$

(2.18)

From the definition of $u_{n}$, we have

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2}&\le \Vert x_{n}-p\Vert ^{2}+2 \phi _{n}\Vert x_{n}-p\Vert \Vert x_{n}-x_{n-1}\Vert +\phi _{n}^{2}\Vert x_{n}-x_{n-1}\Vert ^{2}\nonumber \\&\le \Vert x_{n}-p\Vert ^{2}+3Q\phi _{n}\Vert x_{n}-x_{n-1}\Vert , \end{aligned}$$

(2.19)

where $Q:=\sup _{n \in \mathbb {N}}\{\Vert x_{n}-p\Vert , \phi \Vert x_{n}-x_{n-1}\Vert \}>0$. Setting $g_{n}=(1-\sigma _{n}) u_{n}+\sigma _{n} q_{n}$, one has

$$\begin{aligned} \Vert g_{n}-u_{n}\Vert =\sigma _{n}\Vert u_{n}-q_{n}\Vert . \end{aligned}$$

(2.20)

It follows from (2.12) that

$$\begin{aligned} \Vert g_{n}-p\Vert&=\Vert (1-\sigma _{n})(u_{n}-p)+\sigma _{n}(q_{n}-p)\Vert \nonumber \\&\le (1-\sigma _{n})\Vert u_{n}-p\Vert +\sigma _{n}\Vert u_{n}-p\Vert \nonumber \\&=\Vert u_{n}-p\Vert , \quad \forall n \ge n_{0}. \end{aligned}$$

(2.21)

Combining (2.19), (2.20), (2.21), and the inequality $\Vert x+y\Vert ^{2} \le \Vert x\Vert ^{2}+2\langle y, x+y\rangle ,\;\forall x,y \in \mathcal {H}$, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&=\Vert (1-\sigma _{n}) u_{n}+\sigma _{n} q_{n}-\tau _{n} u_{n}-p\Vert ^{2} \nonumber \\&=\Vert (1-\tau _{n})(g_{n}-p)-\tau _{n}(u_{n}-g_{n})-\tau _{n} p\Vert ^{2} \nonumber \\&\le (1-\tau _{n})^{2}\Vert g_{n}-p\Vert ^{2}-2\tau _{n}\left\langle u_{n}-g_{n}+ p, x_{n+1}-p\right\rangle \nonumber \\&=(1-\tau _{n})^{2}\Vert g_{n}-p\Vert ^{2}+2 \tau _{n}\left\langle u_{n}-g_{n}, p-x_{n+1}\right\rangle +2 \tau _{n}\left\langle p, p-x_{n+1}\right\rangle \nonumber \\&\le (1-\tau _{n})\Vert g_{n}-p\Vert ^{2}+2 \tau _{n}\Vert u_{n}-g_{n}\Vert \Vert x_{n+1}-p\Vert +2 \tau _{n}\left\langle p, p-x_{n+1}\right\rangle \nonumber \\&\le (1-\tau _{n})\Vert x_{n}-p\Vert ^{2}+\tau _{n}\Big [2 \sigma _{n}\Vert u_{n}-q_{n}\Vert \Vert x_{n+1}-p\Vert \Big .\nonumber \\&\quad \Big .+2\left\langle p, p-x_{n+1}\right\rangle + \frac{3 Q \phi _{n}}{ \tau _{n}}\Vert x_{n}-x_{n-1}\Vert \Big ],\,\, \forall n \ge n_{0}. \end{aligned}$$

(2.22)

Finally, we need to show that the sequence $\{\Vert x_{n}-p\Vert \}$ converges to zero. We set

$$\begin{aligned} p_{n}=\Vert x_{n}-p\Vert ^{2},\;\;s_{n}=\frac{3Q\phi _{n}}{ \tau _{n}}\Vert x_{n}-x_{n-1}\Vert +2\left\langle p, p-x_{n+1}\right\rangle +2 \sigma _{n}\Vert u_{n}-q_{n}\Vert \Vert x_{n+1}-p\Vert . \end{aligned}$$

Then the last inequality in (2.22) can be written as $p_{n+1} \le (1- \tau _{n}) p_{n}+ \tau _{n} s_{n}$ for all $n \ge n_{0}$. Note that the sequence $\left\{ \tau _{n}\right\}$ is in (0, 1) and $\sum _{n=1}^{\infty } \tau _{n}=\infty$. By Lemma 1.1, it remains to show that $\limsup _{k \rightarrow \infty } s_{n_{k}} \le 0$ for every subsequence $\left\{ p_{n_{k}}\right\}$ of $\left\{ p_{n}\right\}$ satisfying $\liminf _{k \rightarrow \infty }\left( p_{n_{k+1}}-p_{n_{k}}\right) \ge 0$. For this purpose, we assume that $\left\{ p_{n_{k}}\right\}$ is a subsequence of $\left\{ p_{n}\right\}$ such that $\liminf _{k \rightarrow \infty }\left( p_{n_{k+1}}-p_{n_{k}}\right) \ge 0$. From (2.18) and the assumption on $\{\tau _{n}\}$, one obtains

$$\begin{aligned} \begin{aligned}&\sigma _{n_{k}}\beta ^{*}\left( \left\| u_{n_{k}}-v_{n_{k}}\right\| ^{2}+\left\| q_{n_{k}}-v_{n_{k}}\right\| ^{2}\right) \\&\quad \le \limsup _{k \rightarrow \infty }\tau _{n_{k}}(\Vert p\Vert ^{2}+Q_{2})+\limsup _{k \rightarrow \infty } \left( p_{n_{k}}-p_{n_{k}+1}\right) \\&\quad \le -\liminf _{k \rightarrow \infty } \left( p_{n_{k}+1}-p_{n_{k}}\right) \le 0 , \end{aligned} \end{aligned}$$

which together with Remark 2.1 yields

$$\begin{aligned} \lim _{k \rightarrow \infty }\Vert v_{n_{k}}-u_{n_{k}}\Vert =0\;\; \text { and } \lim _{k \rightarrow \infty }\Vert q_{n_{k}}-v_{n_{k}}\Vert =0. \end{aligned}$$

This implies that $\lim _{k \rightarrow \infty }\Vert q_{n_{k}}-u_{n_{k}}\Vert =0$, which combining with the boundedness of $\{x_{n}\}$ yields that

$$\begin{aligned} \lim _{k \rightarrow \infty } \sigma _{n_{k}}\Vert u_{n_{k}}-q_{n_{k}}\Vert \Vert x_{n_{k}+1}-p\Vert =0. \end{aligned}$$

(2.23)

Moreover, we have

$$\begin{aligned} \left\| x_{n_{k}+1}-u_{n_{k}}\right\| \le \tau _{n_{k}}\left\| u_{n_{k}}\right\| +\sigma _{n_{k}}\left\| u_{n_{k}}-q_{n_{k}}\right\| \rightarrow 0 \text{ as } k \rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \Vert x_{n_{k}}-u_{n_{k}}\Vert =\tau _{n_{k}} \cdot \frac{\phi _{n_{k}}}{\tau _{n_{k}}}\Vert x_{n_{k}}-x_{n_{k}-1}\Vert \rightarrow 0 \text { as } k\rightarrow \infty . \end{aligned}$$

It follows that

$$\begin{aligned} \Vert x_{n_{k}+1}-x_{n_{k}}\Vert \le \Vert x_{n_{k}+1}-u_{n_{k}}\Vert +\Vert u_{n_{k}}-x_{n_{k}}\Vert \rightarrow 0 \text { as } k\rightarrow \infty . \end{aligned}$$

(2.24)

Since the sequence $\{x_{n_{k}}\}$ is bounded, there exists a subsequence $\{x_{n_{k_{j}}}\}$ of $\{x_{n_{k}}\}$ such that $x_{n_{k_{j}}}\rightharpoonup z$. Furthermore,

$$\begin{aligned} \limsup _{k \rightarrow \infty }\left\langle p, p-x_{n_{k}}\right\rangle =\lim _{j \rightarrow \infty }\langle p, p-x_{n_{k_{j}}}\rangle =\langle p, p-z\rangle . \end{aligned}$$

(2.25)

We obtain that $u_{n_{k}} \rightharpoonup z$ since $\Vert x_{n_{k}}-u_{n_{k}}\Vert \rightarrow 0$. This together with $\lim _{k \rightarrow \infty }\Vert u_{n_{k}}-v_{n_{k}}\Vert =0$ and Lemma 2.3 yields $z \in \mathrm {VI}(C, M)$. From the definition of p, the property of projection $\langle x-P_{C} (x), y-P_{C} (x)\rangle \le 0,\; \forall x \in \mathcal {H}, y \in C$ and (2.25), we have

$$\begin{aligned} \limsup _{k \rightarrow \infty }\left\langle p, p-x_{n_{k}}\right\rangle =\langle p, p-z\rangle \le 0. \end{aligned}$$

(2.26)

Combining (2.24) and (2.26), we obtain

$$\begin{aligned} \limsup _{k \rightarrow \infty }\left\langle p, p-x_{n_{k}+1}\right\rangle \le 0. \end{aligned}$$

(2.27)

This together with $\lim _{n \rightarrow \infty } \frac{\phi _{n}}{\tau _{n}}\Vert x_{n}-x_{n-1}\Vert =0$ and (2.23) yields that $\limsup _{k \rightarrow \infty } s_{n_{k}} \le 0$. Therefore, we conclude that $\lim _{n \rightarrow \infty }\Vert x_{n}-p\Vert =0$. That is, $x_{n}\rightarrow p$ as $n\rightarrow \infty$. This completes the proof. $\square$

Next, we provide a new Armijo-type iterative scheme (see Algorithm 2.2 below) for finding solutions to the non-Lipschitz continuous and pseudomonotone (VIP) in real Hilbert spaces. The following condition (C4) will replace the condition (C2) in Algorithm 2.1.

• (C4) The mapping $M: \mathcal {H} \rightarrow \mathcal {H}$ is pseudomonotone, uniformly continuous on $\mathcal {H}$ and sequentially weakly continuous on C.

The Algorithm 2.2 is stated as follows.

We need the following lemmas in order to analyze the convergence of Algorithm 2.2.

Lemma 2.4

Suppose that Condition (C4) holds. Then the Armijo-like criteria (2.28) is well defined.

Proof

The proof is similar to Lemma 3.1 in Tan and Cho (2021). Therefore, we omit the details. $\square$

Lemma 2.5

Assume that Condition (C4) holds. Let $\left\{ q_{n}\right\}$ be a sequence generated by Algorithm 2.2. Then, for all $p \in \mathrm {VI}(C, M)$,

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\beta ^{**}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned} \end{aligned}$$

where $\beta ^{**}=2-\beta -\beta \mu$ if $\beta \in [1,2/(1+\mu ))$ and $\beta ^{**}=\beta -\beta \mu$ if $\beta \in (0,1)$.

Proof

The proof is omitted since it follows the argument of Lemma 2.2. $\square$

Remark 2.2

Note that $\beta ^{**}>0$ for all $n\ge 1$ in Lemma 2.5 always holds.

Lemma 2.6

Suppose that Conditions (C1), (C3), and (C4) hold. Let $\{u_{n}\}$ and $\{v_{n} \}$ be two sequences generated by Algorithm 2.2. If there exists a subsequence $\left\{ u_{n_{k}}\right\}$ of $\left\{ u_{n}\right\}$ such that $\left\{ u_{n_{k}}\right\}$ converges weakly to $z \in \mathcal {H}$ and $\lim _{k \rightarrow \infty }\Vert u_{n_{k}}-v_{n_{k}}\Vert =0$, then $z \in \mathrm {VI}(C, M)$.

Proof

A simple modification of Cai et al. (2021, Lemma 3.2) yields the desired conclusion and thus it is omitted. $\square$

Theorem 2.2

Suppose that Conditions (C1), (C3), and (C4) hold. Then the sequence $\left\{ x_{n}\right\}$ created by Algorithm 2.2 converges to $p \in \mathrm {VI}(C, M)$ in norm, where $\Vert p\Vert =\min \{\Vert z\Vert : z \in \mathrm {VI}(C, M)\}$.

Proof

The proof is similar to the proof of Theorem 2.1. Therefore, we omit some details of the proof. By Lemma 2.5 and similar statements in (2.12)–(2.14), we have

$$\begin{aligned} \Vert q_{n}-p\Vert \le \Vert u_{n}-p\Vert \le \Vert x_{n}-p\Vert +\tau _{n} Q_{1}, \quad \forall n \ge 1. \end{aligned}$$

Applying a similar procedure as in (2.15), we can obtain that $\{x_{n}\}$, $\{u_{n}\}$, and $\{q_{n}\}$ are bounded. Combining (2.16), (2.17) and Lemma 2.5, we can show that

$$\begin{aligned} \begin{aligned}&\sigma _{n}\beta ^{**}\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \\&\quad \le \Vert x_{n}-p\Vert ^{2}-\Vert x_{n+1}-p\Vert ^{2} +\tau _{n}(\Vert p\Vert ^{2}+Q_{2}),\quad \forall n\ge 1. \end{aligned} \end{aligned}$$

Reviewing the statements from (2.19)–(2.22), we obtain

$$\begin{aligned} \begin{aligned} \Vert x_{n+1}-p\Vert ^{2}&\le (1-\tau _{n})\Vert x_{n}-p\Vert ^{2}+\tau _{n}\Big [2 \sigma _{n}\Vert u_{n}-q_{n}\Vert \Vert x_{n+1}-p\Vert \Big .\\&\quad \Big .+2\left\langle p, p-x_{n+1}\right\rangle + \frac{3 Q \phi _{n}}{ \tau _{n}}\Vert x_{n}-x_{n-1}\Vert \Big ],\,\, \forall n \ge 1. \end{aligned} \end{aligned}$$

The rest of the proof follows in the same way as that of Theorem 2.1 but we need apply Lemma 2.6 in place of Lemma 2.3. $\square$

2.2 The second type of modified subgradient extragradient methods

In this subsection, two modified versions of the suggested Algorithms 2.1 and 2.2 are proposed to solve the pseudomonotone and Lipschitz continuous (or non-Lipschitz continuous) variational inequality problem in real Hilbert spaces. We first present a modified form of the suggested Algorithm 2.1, see Algorithm 2.3 below for more details. Note that this method is different from the proposed Algorithm 2.1 in computing the values of the sequences $\{v_{n}\}$ and $\{q_{n}\}$.

The following lemma plays a crucial role in the convergence analysis of Algorithm 2.3.

Lemma 2.7

Assume that Condition (C2) holds. Let $\left\{ q_{n}\right\}$ be a sequence generated by Algorithm 2.3. Then, for all $p \in \mathrm {VI}(C, M)$,

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\beta ^{\dagger }\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned} \end{aligned}$$

where $\beta ^{\dagger }=2-\frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}$ if $\beta \in (0,1]$ and $\beta ^{\dagger }=\frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}$ if $\beta >1$.

Proof

From (2.4) and (2.5), we obtain

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2} \le \left\| u_{n}-p\right\| ^{2}-\left\| u_{n}-q_{n}\right\| ^{2}-2\left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.29)

Now we estimate $2\left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle$. Note that

$$\begin{aligned} -\left\| u_{n}-q_{n}\right\| ^{2} =-\left\| u_{n}-v_{n}\right\| ^{2}-\left\| v_{n}-q_{n}\right\| ^{2}+2\left\langle u_{n}-v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.30)

One can show that

$$\begin{aligned}&\left\langle u_{n}-v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\quad =\left\langle u_{n}-v_{n}-\beta \lambda _{n} M u_{n}+\beta \lambda _{n} M u_{n}-\beta \lambda _{n} M v_{n}+\beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\quad =\left\langle u_{n}-\beta \lambda _{n} M u_{n}-v_{n}, q_{n}-v_{n}\right\rangle +\beta \lambda _{n}\left\langle M u_{n}-M v_{n}, q_{n}-v_{n}\right\rangle \nonumber \\&\qquad +\left\langle \beta \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle . \end{aligned}$$

(2.31)

Since $q_{n}\in H_{n}$, one has

$$\begin{aligned} \left\langle u_{n}-\beta \lambda _{n} M u_{n}-v_{n}, q_{n}-v_{n}\right\rangle \le 0. \end{aligned}$$

(2.32)

According to the definition of $\lambda _{n+1}$, we deduce that

$$\begin{aligned} \left\langle M u_{n}-M v_{n}, q_{n}-v_{n}\right\rangle \le \frac{\mu }{2\lambda _{n+1}}\left\| u_{n}-v_{n}\right\| ^{2}+\frac{\mu }{2\lambda _{n+1}}\left\| q_{n}-v_{n}\right\| ^{2} . \end{aligned}$$

(2.33)

Substituting (2.31), (2.32), and (2.33) into (2.30), we have

$$\begin{aligned} \begin{aligned} -\left\| u_{n}-q_{n}\right\| ^{2} \le -\left( 1-\frac{\beta \mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) +2\beta \left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle , \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} -2\left\langle \lambda _{n} M v_{n}, q_{n}-v_{n}\right\rangle&\le -\left( \frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad +\frac{1}{\beta }\left\| u_{n}-q_{n}\right\| ^{2}. \end{aligned}$$

(2.34)

Combining (2.29) and (2.34), we conclude that

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\left( \frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) \nonumber \\&\quad -\left( 1-\frac{1}{\beta }\right) \left\| u_{n}-q_{n}\right\| ^{2}. \end{aligned}$$

(2.35)

Note that

$$\begin{aligned} \left\| u_{n}-q_{n}\right\| ^{2}\le 2\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned}$$

which yields that

$$\begin{aligned} -\left( 1-\frac{1}{\beta }\right) \left\| u_{n}-q_{n}\right\| ^{2}\le -2\left( 1-\frac{1}{\beta }\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta \in (0,1]. \end{aligned}$$

This together with (2.35) implies

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\left( 2-\frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta \in (0,1] . \end{aligned} \end{aligned}$$

On the other hand, if $\beta >1$, then we obtain

$$\begin{aligned} \left\| q_{n}-p\right\| ^{2} \le \left\| u_{n}-p\right\| ^{2} -\left( \frac{1}{\beta }-\frac{\mu \lambda _{n}}{\lambda _{n+1}}\right) \left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) ,\quad \forall \beta >1 . \end{aligned}$$

The proof is completed. $\square$

Remark 2.3

From Lemma 2.1 and the assumptions of the parameters $\mu$ and $\beta$ (i.e., $\mu \in (0,1)$ and $\beta \in (1/(2-\mu ),1/\mu )$), we can obtain that $\beta ^{\dagger }>0$ for all $n\ge n_{1}$ in Lemma 2.7 always holds.

Lemma 2.8

Suppose that Conditions (C1)–(C3) hold. Let $\{u_{n}\}$ and $\{v_{n} \}$ be two sequences formulated by Algorithm 2.3. If there exists a subsequence $\left\{ u_{n_{k}}\right\}$ of $\left\{ u_{n}\right\}$ such that $\left\{ u_{n_{k}}\right\}$ converges weakly to $z \in \mathcal {H}$ and $\lim _{k \rightarrow \infty }\Vert u_{n_{k}}-v_{n_{k}}\Vert =0$, then $z \in \mathrm {VI}(C, M)$.

Proof

The conclusion can be obtained by applying a similar statement in Thong et al. (2020, Lemma 3.3). $\square$

Theorem 2.3

Suppose that Conditions (C1)–(C3) hold. Then the sequence $\left\{ x_{n}\right\}$ formed by Algorithm 2.3 converges to $p \in \mathrm {VI}(C, M)$ in norm, where $\Vert p\Vert =\min \{\Vert z\Vert : z \in \mathrm {VI}(C, M)\}$.

Proof

It follows from Lemma 2.7 that $\beta ^{\dagger }>0$ for all $n\ge n_{1}$, which is similar to the conclusion of Remark 2.1. Thus, we can obtain the conclusion required by replacing Lemmas 2.2 and 2.3 in the proof of Theorem 2.1 with Lemmas 2.7 and 2.8, respectively. We omit the details of the proof to avoid repetition. $\square$

Now, we state the last iterative scheme proposed in this paper in Algorithm 2.4 below. The difference between this scheme and the proposed Algorithm 2.3 is that it can solve the pseudomonotone and non-Lipschitz continuous (VIP) because it uses an Armijo-type step size (2.28) instead of the adaptive step size criterion (2.3).

The Algorithm 2.4 is described as follows.

Lemma 2.9

Assume that Condition (C4) holds. Let $\left\{ q_{n}\right\}$ be a sequence generated by Algorithm 2.4. Then, for all $p \in \mathrm {VI}(C, M)$,

$$\begin{aligned} \begin{aligned} \left\| q_{n}-p\right\| ^{2}&\le \left\| u_{n}-p\right\| ^{2} -\beta ^{\ddag }\left( \left\| u_{n}-v_{n}\right\| ^{2}+\left\| q_{n}-v_{n}\right\| ^{2}\right) , \end{aligned} \end{aligned}$$

where $\beta ^{\ddag }=2-\frac{1}{\beta }-\mu$ if $\beta \in (0,1]$ and $\beta ^{\ddag }=\frac{1}{\beta }-\mu$ if $\beta >1$.

Proof

The proof follows the proof of Lemma 2.7 and so it is omitted. $\square$

Remark 2.4

Note that $\beta ^{\ddag }>0$ for all $n\ge 1$ in Lemma 2.9 always holds.

Lemma 2.10

Suppose that Conditions (C1), (C3), and (C4) hold. Let $\{u_{n}\}$ and $\{v_{n} \}$ be two sequences generated by Algorithm 2.4. If there exists a subsequence $\left\{ u_{n_{k}}\right\}$ of $\left\{ u_{n}\right\}$ such that $\left\{ u_{n_{k}}\right\}$ converges weakly to $z \in \mathcal {H}$ and $\lim _{k \rightarrow \infty }\Vert u_{n_{k}}-v_{n_{k}}\Vert =0$, then $z \in \mathrm {VI}(C, M)$.

Proof

We can obtain the conclusion by a simple modification of Cai et al. (2021, Lemma 3.2). $\square$

Theorem 2.4

Suppose that Conditions (C1), (C3), and (C4) hold. Then the sequence $\left\{ x_{n}\right\}$ generated by Algorithm 2.4 converges to $p \in \mathrm {VI}(C, M)$ in norm, where $\Vert p\Vert =\min \{\Vert z\Vert : z \in \mathrm {VI}(C, M)\}$.

Proof

The proof is similar to that of Theorem 2.2. However, we need to replace Lemmas 2.5 and 2.6 in Theorem 2.2 with Lemmas 2.9 and 2.10, respectively. Therefore, we omit the details of the proof. $\square$

Remark 2.5

We now explain the contribution of this paper in detail as follows.

• 1. We modify the subgradient extragradient method (SEGM) introduced by Censor et al. (2011) in two simple ways. Specifically, our algorithms use two different step sizes for computing the values of $v_{n}$ and $q_{n}$ in each iteration, while the SEGM by Censor et al. (2011) employs the same step size for computing these two values in each iteration. Numerical experimental results will show that this modification improves the convergence speed and computational efficiency of the original method (see numerical results for our algorithms when $\beta =1$ and $\beta \ne 1$ in Sect. 3).

• 2. The idea of step size selection (i.e., (2.1) and (2.28)) for the methods proposed in this paper comes from the recent work in Liu and Yang (2020) and Cai et al. (2021). The two step size criteria generate non-monotonic step size sequences, which improves the algorithms in the literature (see, e.g., Tan et al. 2021; Yang et al. 2018; Yang and Liu 2019; Hieu et al. 2021; Thong et al. 2020) that use non-increasing step size sequences. In addition, our Algorithms 2.2 and 2.4 can be used to solve non-Lipschitz continuous variational inequalities, which extends a large number of algorithms in the literature (see, e.g., Hieu et al. 2021; Shehu et al. 2019; Jolaoso et al. 2020; Thong et al. 2020; Yang 2021; Grad and Lara 2021) for solving Lipschitz continuous variational inequalities. On the other hand, the four iterative schemes suggested in this paper are designed to solve pseudomonotone variational inequalities. Therefore, our results extend many methods in the literature (see, e.g., Tan et al. 2021; Shehu and Iyiola 2017; Thong et al. 2019; Censor et al. 2011; Thong and Hieu 2018; Yang et al. 2018; Yang and Liu 2019) that can only solve monotone variational inequalities.

• 3. Our algorithms added inertial terms, which accelerates the convergence speed of our algorithms without inertial terms. In addition, the proposed schemes use the Mann-type method to obtain strong convergence. Thus, the results obtained in this paper are preferable to the weakly convergent algorithms in the literature (see, e.g., He 1997; Solodov and Svaiter 1999; Tseng 2000; Censor et al. 2011; Malitsky 2015; Hieu et al. 2021) in infinite-dimensional Hilbert spaces.

3 Numerical experiments

In this section, we provide several numerical examples to demonstrate the efficiency of our algorithms compared to some known ones in Cai et al. (2021), Thong and Vuong (2019) and Thong et al. (2020). All the programs are implemented in MATLAB 2018a on a Intel(R) Core(TM) i5-8250S CPU @1.60 GHz computer with RAM 8.00 GB.

Example 3.1

Consider the linear operator $M: \mathbb {R}^{m}\rightarrow \mathbb {R}^{m}\,(m=20)$ in the form $M(x)=Sx+q$, where $q\in \mathbb {R}^m$ and $S=NN^{\mathsf {T}}+Q+D$, N is a $m\times m$ matrix, Q is a $m\times m$ skew-symmetric matrix, and D is a $m\times m$ diagonal matrix with its diagonal entries being nonnegative (hence S is positive symmetric definite). The feasible set C is given by $C=\left\{ x \in {\mathbb {R}}^{m}:-2 \le x_{i} \le 5, \, i=1, \ldots , m\right\}$. It is clear that M is monotone and Lipschitz continuous with constant $L= \Vert S\Vert$. In this experiment, all entries of N, Q are generated randomly in $[-2,2]$, D is generated randomly in [0, 2] and $q = \mathbf {0}$. It can be checked that the solution of the (VIP) is $x^{*}=\{\mathbf {0}\}$. We apply the proposed algorithms to solve this problem. Take $\phi =0.6$, $\epsilon _{n}=100/(n+1)^{2}$, $\tau _{n}=1/(n+1)$ and $\sigma _{n}=0.9(1-\tau _{n})$ for the suggested Algorithms 2.1–2.4. Choose $\lambda _{1}=1$, $\mu =0.2$ and $\xi _{n}=1/(n+1)^{1.1}$ for the proposed Algorithms 2.1 and 2.3. Select $\delta =2$, $\ell =0.5$, $\mu =0.2$ for the stated Algorithms 2.2 and 2.4. The maximum number of iterations 500 is used as a common stopping criterion. We use $D_{n}=\Vert x_{n}-x^{*}\Vert$ to measure the error of the nth iteration step. Figure 1 shows the numerical performance of the proposed algorithms for different parameter $\beta$.

Fig. 1

Numerical results of our algorithms with different $\beta$ in Example 3.1

Example 3.2

Let $\mathcal {H}=L^{2}([0,1])$ be an infinite-dimensional Hilbert space with inner product

$$\begin{aligned} \langle x, y\rangle =\int _{0}^{1} x(t) y(t)\, \mathrm {d} t, \quad \forall x,y\in \mathcal {H}, \end{aligned}$$

and induced norm

$$\begin{aligned} \Vert x\Vert =\left( \int _{0}^{1} |x(t)|^{2}\, \mathrm {d} t\right) ^{1 / 2}, \quad \forall x\in \mathcal {H}. \end{aligned}$$

Let r, R be two positive real numbers such that $R/(k+1)<r/k<r<R$ for some $k>1$. Take the feasible set as $C=\{x \in \mathcal {H}:\Vert x\Vert \le r\}$. The operator $M: \mathcal {H} \rightarrow \mathcal {H}$ is given by

$$\begin{aligned} M(x)=(R-\Vert x\Vert ) x, \quad \forall x \in \mathcal {H}. \end{aligned}$$

It is not hard to check that operator M is pseudomonotone rather than monotone. For the experiment, we choose $R=1.5$, $r=1$, $k=1.1$. The solution of the (VIP) with M and C given above is $x^{*}(t)=0$. We compare the proposed Algorithms 2.1–2.4 with the Algorithm 2 introduced by Thong and Vuong (2019) (shortly, TV Alg. 2). Set $\tau _{n}=1/(n+1)$ and $\sigma _{n}=0.9(1-\tau _{n})$ for all algorithms. Choose $\phi =0.3$, $\epsilon _{n}=100/(n+1)^{2}$ for the suggested Algorithms 2.1–2.4. Take $\mu =0.4$, $\lambda _{1}=1$ and $\xi _{n}=1/(n+1)^{1.1}$ for the suggested Algorithms 2.1 and 2.3. Select $\delta =1$, $\ell =0.5$ and $\mu =0.4$ for the proposed Algorithm 2.2, Algorithm 2.4 and TV Alg. 2. The maximum number of iterations 50 is used as a common stopping criterion. The numerical behavior of the function $D_{n}=\Vert x_{n}(t)-x^{*}(t)\Vert$ of all algorithms with four starting points $x_{0}(t)=x_{1}(t)$ is shown in Fig. 2 and Table 1, where “CPU" in Table 1 indicates the execution time of all algorithms in seconds.

Fig. 2

Numerical behavior of all algorithms at $x_{0}(t)=x_{1}(t)=t^{4}$ for Example 3.2

Table 1 Numerical results of all algorithms for Example 3.2

Example 3.3

Consider the Hilbert space $\mathcal {H}=l_{2}:=\{x=\left( x_{1}, x_{2}, \ldots , x_{i}, \ldots \right) \mid \sum _{i=1}^{\infty }\left| x_{i}\right| ^{2}<+\infty \}$ equipped with the inner product

$$\begin{aligned} \langle x, y\rangle =\sum _{i=1}^{\infty } x_{i} y_{i}, \quad \forall x,y\in \mathcal {H}, \end{aligned}$$

and the induced norm

$$\begin{aligned} \Vert x\Vert =\sqrt{\langle x, x\rangle }, \quad \forall x\in \mathcal {H}. \end{aligned}$$

Let $C:=\left\{ x\in \mathcal {H}:\left| x_{i}\right| \le {1}/{i}\right\}$. Define an operator $M: C \rightarrow \mathcal {H}$ by

$$\begin{aligned} M x=\left( \Vert x\Vert +\frac{1}{(\Vert x\Vert +\alpha )}\right) x \end{aligned}$$

for some $\alpha >0$. It can be verified that mapping M is pseudomonotone on $\mathcal {H}$, uniformly continuous and sequentially weakly continuous on C, but not Lipschitz continuous on $\mathcal {H}$ (see Thong et al. 2020, Example 1). In the following cases, we take $\alpha =0.5$, $\mathcal {H}=\mathbb {R}^{m}$ for different values of m. In these situations, the feasible set C is a box given by

$$\begin{aligned} C=\left\{ x \in \mathbb {R}^{m}: \frac{-1}{i} \le x_{i} \le \frac{1}{i}, \,\,i=1,2, \ldots , m\right\} . \end{aligned}$$

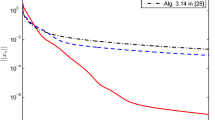
We compare the proposed Algorithms 2.2 and  2.4 with several strongly convergent algorithms that can solve the (VIP) with uniformly continuous operators, including the Algorithm 3.1 introduced by Cai et al. (2021) (shortly, CDP Alg. 3.1) and the Algorithm 3 suggested by Thong et al. (2020) (shortly, TSI Alg. 3). Take $\tau _{n}=1/(n+1)$, $\delta =2$, $\ell =0.5$, $\mu =0.1$ for all the algorithms. Select $\sigma _{n}=0.9(1-\tau _{n})$, $\phi =0.4$ and $\epsilon _{n}={100}/{(n+1)^2}$ for the suggested Algorithms 2.2 and 2.4. Set $f(x)=0.1x$ for CDP Alg. 3.1 and TSI Alg. 3. The initial values $x_{0}=x_{1}=5rand(m,1)$ are randomly generated by MATLAB. The maximum number of iterations 200 is used as a common stopping criterion. The numerical performance of the function $D_{n}=\Vert x_{n}-x_{n-1}\Vert$ of all algorithms with four different dimensions is reported in Fig. 3 and Table 2, where “CPU” in Table 2 represents the execution time of all algorithms in seconds.

Fig. 3

Numerical behavior of all algorithms at $m=200000$ for Example 3.3

Table 2 Numerical results of all algorithms for Example 3.3

Next, we use the proposed algorithms to solve the (VIP) that appears in optimal control problems. Assume that $L_{2}\left( [0, T], \mathbb {R}^{m}\right)$ represents the square-integrable Hilbert space with inner product $\langle p, q\rangle =\int _{0}^{T}\langle p(t), q(t)\rangle \,\mathrm {d} t$ and norm $\Vert p\Vert =\sqrt{\langle p, p\rangle }$. The optimal control problem is described as follows:

$$\begin{aligned} \left\{ \begin{aligned}&p^{*}(t) \in {\text {Argmin}}\{g(p) \mid p \in V\},\\&g(p)=\Phi (x(T)),\\&V=\left\{ p(t) \in L_{2}\left( [0, T], \mathbb {R}^{m}\right) : p_{i}(t) \in \left[ p_{i}^{-}, p_{i}^{+}\right] , i=1,2, \ldots , m\right\} ,\\&\text {such that }\dot{x}(t)=Q(t) x(t)+W(t) p(t), \;\;0 \le t \le T, \;\;x(0)=x_{0}, \end{aligned}\right. \end{aligned}$$

(3.1)

where g(p) means the terminal objective function, $\Phi$ is a convex and differentiable defined on the attainability set, p(t) denotes the control function, V represents a set of feasible controls composed of m piecewise continuous functions, x(t) stands for the trajectory, and $Q(t) \in \mathbb {R}^{n \times n}$ and $W(t) \in \mathbb {R}^{n \times m}$ are given continuous matrices for every $t \in$ [0, T] . By the solution of problem (3.1), we mean a control $p^{*}(t)$ and a corresponding (optimal) trajectory $x^{*}(t)$ such that its terminal value $x^{*}(T)$ minimizes objective function g(p) . It is known that the optimal control problem (3.1) can be transformed into a variational inequality problem (see Preininger and Vuong 2018; Vuong and Shehu 2019). We first use the classical Euler discretization method to decompose the optimal control problem (3.1) and then apply the proposed algorithms to solve the variational inequality problem corresponding to the discretized version of the problem (see Preininger and Vuong 2018; Vuong and Shehu 2019 for more details). In the proposed Algorithms 2.1–2.4, we set $N=100$, $\phi =0.01$, $\epsilon _{n}={10^{-4}}/{(n+1)^2}$, $\tau _{n}={10^{-4}}/{(n+1)}$ and $\sigma _{n}=0.9(1-\tau _{n})$. Pick $\lambda _{1}=0.4$, $\mu =0.5$ and $\xi _{n}=1/(n+1)^{1.1}$ for the proposed Algorithms 2.1 and 2.3. Select $\delta =2$, $\ell =0.5$ and $\mu =0.5$ for the suggested Algorithms 2.2 and 2.4. The initial controls $p_{0}(t)=p_{1}(t)$ are randomly generated in $[-1,1]$ and the stopping criterion is $D_{n}=\left\| p_{n+1}-p_{n}\right\| \le 10^{-4}$.

Example 3.4

(Rocket car (Bressan and Piccoli 2007))

$$\begin{aligned} \begin{aligned} \text {minimize} \;\;\;&-x_{1}(2)+\left( x_{2}(2)\right) ^{2}, \\ \text {subject to} \;\;\;&\dot{x}_{1}(t)=x_{2}(t), \;\;\; \dot{x}_{2}(t)=p(t), \;\;\forall t \in [0,2], \\ \;\;\;&x_{1}(0)=0, \;\;x_{2}(0)=0, \;\;\; p(t) \in [-1,1]. \end{aligned} \end{aligned}$$

The exact optimal control of Example 3.4 is $p^{*}(t)=1$ if $t \in [0,1.2)$ and $p^{*}(t)=-1$ if $t \in (1.2,2]$. The approximate optimal control of the stated Algorithm 2.2 is plotted in Fig. 4a. Moreover, the numerical behavior of the proposed algorithms is shown in Fig. 4b.

Fig. 4

Numerical results for Example 3.4

Remark 3.1

We have the following observations for Examples 3.1–3.4: (i) as can be seen in Examples 3.2 and 3.3, the algorithms proposed in this paper converge faster than some known methods in the literature (Cai et al. 2021; Thong and Vuong 2019; Thong et al. 2020), and these results are independent of the choice of initial values and the size of the dimensions (see Figs. 2, 3, Tables 1,  2); (ii) our four algorithms can obtain a faster convergence speed when the appropriate value of $\beta$ is chosen; in other words, our algorithms can achieve a higher error accuracy when the two step sizes used in each iteration are different (i.e., $\beta \ne 1$) than when they are the same (i.e., $\beta =1$), see Figs. 1, 2,  3,  4 and Tables 1,  2; (iii) from Fig. 2 and Table 1, it can be seen that our Armijo-type Algorithms 2.2 and 2.4 take more computation time than the adaptive step size Algorithms 2.1 and 2.3, because the Armijo-type methods may take extra time to find a suitable step size in each iteration, while the adaptive step size type methods can use previously known information to automatically compute the next iteration step size; (iv) the proposed algorithms can work well in solving optimal control problems (see Fig. 4); and (v) notice that the operator M in Example 3.3 is non-Lipschitz continuous rather than Lipschitz continuous, which means that the algorithms proposed in the literature (see, e.g., Hieu et al. 2021; Shehu et al. 2019; Jolaoso et al. 2020; Thong et al. 2020; Yang 2021; Grad and Lara 2021) for solving Lipschitz continuous variational inequalities will not be available in this example. In summary, the iterative schemes suggested in this paper are useful, efficient and robust.

4 Conclusions

In this paper, we presented four new iterative schemes inspired by the inertial method, the subgradient extragradient method and the Mann-type method for solving the variational inequality problem with a pseudomonotone and Lipschitz continuous (or non-Lipschitz continuous) operator. Our algorithms use two non-monotonic step size criteria allowing them to work without the prior information about the Lipschitz constant of the operator. Strong convergence theorems of the proposed iterative algorithms are proved under some mild conditions in the framework of real Hilbert spaces. Finally, some numerical experimental results show the computational efficiency of the suggested methods compared to previously known schemes.