A Strong Convergence Theorem for Solving Pseudo-monotone Variational Inequalities Using Projection Methods

Abstract

Several iterative methods have been proposed in the literature for solving the variational inequalities in Hilbert or Banach spaces, where the underlying operator A is monotone and Lipschitz continuous. However, there are very few methods known for solving the variational inequalities, when the Lipschitz continuity of A is dispensed with. In this article, we introduce a projection-type algorithm for finding a common solution of the variational inequalities and fixed point problem in a reflexive Banach space, where A is pseudo-monotone and not necessarily Lipschitz continuous. Also, we present an application of our result to approximating solution of pseudo-monotone equilibrium problem in a reflexive Banach space. Finally, we present some numerical examples to illustrate the performance of our method as well as comparing it with related method in the literature.

1 Introduction

In 1959, A. Signorini posed a contact problem (well known as “Signorini Problem”), which was reformulated as VI by Fichera [1] in 1963. In 1964, the first cornerstone for the theory of VI was recorded by Stampacchia [2]. Later in 1966, Hartman and Stampacchia [3] proved the first existence theorem for the solution of the VI. In 1967, the first exposition result for the existence and uniqueness of solution of the VI appeared in the work of Lion and Stampacchia [4]. Since then, the VI has served as an important tool in studying a wide class of unilateral optimization problems arising in several branches of pure and applied sciences in a general framework (see, for example, [5]). Several methods have also been developed for solving a VI (1) and related optimization problems; see [6,7,8] and references therein.

One of the important methods for solving the VI is the extragradient method (EM) introduced by Korpelevich [9] (also by Antipin [10] independently) for solving VI in a finite dimensional space. The EM requires two projections onto the feasible set C and two evaluations of A per each iteration (a fact which affect the usage of the EM). This method was further extended to infinite-dimensional spaces by many authors; see, for example, [11]. In order to improve the EM, Censor et al. [12] introduced a subgradient extragradient method (SEM), which involves only one projection onto the feasible set and another projection onto a constructible half-space. The weak convergence of the SEM was proved in [12] and, by modifying the SEM with Halpern iterative scheme (see [13, 14]), some authors proved the strong convergences of the SEM under certain mild conditions (see, for instance, [12, 15,16,17]).

An obvious disadvantage of the EM and SEM is the assumption that the underlying operator A admits a Lipschitz constant, which is known or can be estimated. In fact, in many problems, operators may not satisfy the Lipschitz condition. Iusem and Svaiter [18] introduced a projection-type algorithm, which does not require the Lipschitz continuity of A and proved a weak convergence result for approximating solutions of VI (1) in a finite dimensional space, where A is a monotone operator. The projection method was later extended to an infinite dimensional Hilbert space by Bello Cruz and Iusem [19]. Recently, Kanzow and Shehu [20] proved a strong convergence theorem for solving VI (1) by combining the projection method with a Halpern method in a real Hilbert space H. Very recently, Gibali [21] proposed a new Bregman projection method for solving the VI in a Hilbert space. Gibali’s algorithm is an extension of the SEM with Bregman projection, which makes only one projection per iteration. The Bregman projection is well known as a generalization of the metric projection. Several other alternatives to the EM or its modifications have also been proposed in the literature by many authors; see, for example, [7, 22, 23] and references there in.

It is worth mentioning that many important real life problems are generally defined in Banach spaces. Hence, it is of interest to consider solving the VI in a Banach space, which is more general than the Hilbert space. Some recent attempts in this direction are the works of Cai et al. [24] and Chidume and Nnakwe [25] in a 2-uniformly convex and uniformly smooth Banach space E. It is also important to find the solutions of variational inequalities, which are also the fixed point of a particular mapping due to its possible application to mathematical models, whose constraint can be expressed as fixed point and variational inequalities. This happens, in particular, in the practical problems such as signal processing, network resource allocation and image recovery; see, for instance, [26,27,28].

Motivated by the works of Gibali [21], Cai et al. [24], Chidume and Nnakwe [25] and Kanzow and Shehu [20], in this paper, we present a new projection-type algorithm for approximating a common solution of VI (1) and fixed point of Bregman quasi-nonexpansive mapping in a real reflexive Banach space. We also take A to be a pseudo-monotone operator and prove a strong convergence theorem for the sequence generated by our algorithm. This result extends and generalizes many other results in the literature.

2 Preliminaries

In this section, we present some basic notions and results that are needed in the sequel. Throughout this paper, $E^*$ denotes the dual space of a Banach space E and C is a nonempty, closed and convex subset of E. The norm and the duality pairing between E and $E^*$ are denoted by $||\cdot ||$ and $\langle \cdot ,\cdot \rangle ,$ respectively. Also, the strong and weak convergence of a sequence $\{x_n\} \subseteq E$ to a point $p \in E$ are denoted by $x_n \rightarrow p$ and $x_n \rightharpoonup p,$ respectively.

Let $f:E \rightarrow ]-\infty ,+\infty ]$ be a proper, convex and lower semicontinuous function. The Fenchel conjugate of f is the functional $f^*:E^{*} \rightarrow ]-\infty ,+\infty ]$ defined by $f^*(\xi ) = \sup \{\langle \xi ,x\rangle - f(x): x \in E\}.$

The domain of f is defined by $\hbox {dom}f:= \{x \in E: f(x) < +\infty \}$ and if $\hbox {dom}f \ne \emptyset$, we say that f is proper.

Let $x \in$ int($\hbox {dom}f$), for any $y \in E$, the directional derivative of f at x is defined by $f^{o}(x,y) = \lim _{t \downarrow 0}\dfrac{f(x+ty)-f(x)}{t}.$ If the limit as ${t \downarrow 0}$ exists for each y, then f is said to be Gâteaux differentiable at x. When the limit as ${t \downarrow 0}$ is attained uniformly for any $y \in E$ with $||y||=1$, we say that f is Fréchet differentiable at x. Throughout this paper, we take f to be an admissible function, i.e., a proper, convex and lower semicontinuous function. Under this condition, we know that f is continuous in int($\hbox {dom}f$); see, [29].

Let E be a reflexive Banach space. The function f is called Legendre if and only if it satisfies the following two conditions:

• (L1) f is Gâteaux differentiable, int(dom $f) \ne \emptyset$ and dom $\nabla f$ = int(dom f),

• (L2) $f^*$ is Gâteaux differentiable, int(dom $f^*) \ne \emptyset$ and dom $\nabla f^*$ = int(dom $f^*)$.

Since E is reflexive, we know that $(\nabla f)^{-1}= \nabla f^*$, this together with conditions (L1) and (L2) implies that $ran \nabla f = dom \nabla f^* = int(domf^*) \quad \text {and}\quad ran \nabla f^* = dom \nabla f = int(domf).$

The variational inequalities (VI) is defined as finding a point $x^{*} \in C$ such that

$$\begin{aligned} \langle Ax^{*}, y- x^{*} \rangle \ge 0, \quad \forall y \in C, \end{aligned}$$

(1)

where $A: E \rightarrow E^*$ is a single-valued mapping. The set of solutions of a VI is denoted by VI(C, A).

Definition 2.1

[30] The operator A is said to be

• (a) strongly monotone on C,  if there exists $\gamma >0$ such that $\langle Au - Av, u-v\rangle \ge \gamma ||u-v||^2 \quad \forall ~~ u,v \in C;$

• (b) monotone on C,  if $\langle Au-Av, u-v \rangle \ge 0 \quad \forall ~~u,v \in C;$

• (c) strongly pseudo-monotone on C,  if there exists $\gamma >0$ such that

  $$\begin{aligned} \langle Au, v-u \rangle \ge 0 \Rightarrow \langle Av, v-u \rangle \ge \gamma ||u-v||^2, \quad \text {for all}\ u,v \in C; \end{aligned}$$

• (d) pseudo-monotone on C,  if for all $u,v \in C$$\langle Au,v-u\rangle \ge 0 \Rightarrow \langle Av,v-u \rangle \ge 0;$

Remark 2.1

It is easy to see that the following implications hold: (a) $\Rightarrow$ (b) $\Rightarrow$ (d) and (a) $\Rightarrow$ (c) $\Rightarrow$ (d) .

Recall that a point $x \in C$ is called a fixed point of an operator $T:C\rightarrow C,$ if $Tx =x.$ We shall denote the set of fixed points of T by F(T). It is well known that in a real Hilbert space, $x^{*}$ solves the VI (1) if and only if $x^{*}$ solves the fixed point equation $x^{*} = P_C(x^{*} - \lambda Ax^{*}),$ or equivalently, $x^{*}$ solves the residual equation

$$\begin{aligned} r_{\lambda }(x^{*}) = x^{*} - P_C(x^{*} - \lambda A x^{*})=0, \end{aligned}$$

where $\lambda >0$ and $P_C$ is the metric projection from H onto C. Hence, the knowledge of fixed point algorithms can be used to solve the VI (1); see, for example, [6].

Definition 2.2

Let $f:E \rightarrow {\mathbb {R}}\cup \{+ \infty \}$ be a Gâteaux differentiable function. The function

$D_f:$$\hbox {dom}f \times$ int($\hbox {dom}f) \rightarrow [0, +\infty [$ defined by

$$\begin{aligned} D_f(y,x) := f(y)-f(x) - \langle \nabla f(x),y-x \rangle \end{aligned}$$

(2)

is called the Bregman distance with respect to f (see, [31, 32]). The Bregman distance does not satisfy the well-known properties of a metric, but it has the following important property, called three point identity (see, [29]): for any $x \in$$\hbox {dom}f$ and $y,z \in$ int($\hbox {dom}f$),

$$\begin{aligned} D_f(y,z)+D_f(z,x)-D_f(y,x) = \langle \nabla f(z)- \nabla f(x), z-y \rangle . \end{aligned}$$

(3)

Definition 2.3

Let $f:E \rightarrow ]-\infty ,+\infty ]$ be a convex and G${\hat{a}}$teaux differentiable function. The function f is called:

• (i) totally convex at x if its modulus of totally convexity at $x \in$ int($\hbox {dom}f$), that is, the bifunction $v_f:$ int($\hbox {dom}f) \times [0, +\infty [ \rightarrow [0, + \infty [$ defined by $v_f(x,t):= \inf \{D_f(y,x): y \in dom f, ||y-x||=t\}$ is positive for any $t>0.$

• (ii) cofinite if $\hbox {dom}f^*=E^*$; coercive if $\lim \limits _{||x|| \rightarrow +\infty }\Big (\frac{f(x)}{||x||}\Big )= +\infty ;$ and sequentially consistent if for any two sequences $\{x_n\}$ and $\{y_n\}$ in E such that $\{x_n\}$ is bounded, $\lim \limits _{n \rightarrow \infty }D_f(y_n,x_n)=0 \Rightarrow \lim \limits _{n \rightarrow \infty }||y_n-x_n||=0.$ For further details and examples on totally convex functions; see, [33,34,35,36].

Remark 2.2

[36, 37] The function $f:E\rightarrow {\mathbb {R}}$ is totally convex on bounded subsets, if and only if it is sequentially consistent. Also, if f is Fréchet differentiable and totally convex, then, f is cofinite.

The function $V_f: E \times E^* \rightarrow [0,\infty [$ associated with f is defined by

$$\begin{aligned} V_f(x,x^*) = f(x) - \langle x^*,x \rangle + f^*(x^*), \qquad \forall x \in E, x^* \in E^*. \end{aligned}$$

$V_f$ is non-negative and $V_f(x,x^*) = D_f(x, \nabla f^*(x^*))$ for all $x \in E$ and $x^* \in E^*$. It is known that $V_f$ is convex in the second variable, i.e., for all $z \in E,$$D_f\Big (z, \nabla f^*(\sum \nolimits _{i=1}^Nt_i \nabla f(x_i))\Big ) \le \sum \nolimits _{i=1}^N t_i D_f(z,x_i),$ where $\{x_i\} \subset E$ and $\{t_i\} \subset ]0,1[$ with $\sum \nolimits _{i=1}^N t_i =1$.

The Bregman projection $Proj_C^f:$ int($\hbox {dom}f$)$\rightarrow C$ is defined as the necessarily unique vector $\hbox {Proj}_C^f(x) \in C$ satisfying $D_f(Proj_C^f(x),x) = \inf \{D_f(y,x):y\in C \}.$ The Bregman projection is characterized by the following properties (see, [38]): for $x \in$int($\hbox {dom}f$) and ${\hat{x}} \in C$, then the following conditions are equivalent:

• (i) the vector ${\hat{x}}$ is the Bregman projection of x onto C, with respect to f,

• (ii) the vector ${\hat{x}}$ is the unique solution of the variational inequality

  $$\begin{aligned} \langle \nabla f(x)- \nabla f(z), z-y \rangle \ge 0 \qquad \forall y\in C, \end{aligned}$$

  (4)

• (iii) the vector ${\hat{x}}$ is the unique solution of the inequality

  $$\begin{aligned} D_f(y,z)+D_f(z,x) \le D_f(y,x)\qquad \forall y \in C. \end{aligned}$$

  (5)

A point $x^* \in C$ is said to be an asymptotic fixed point of T if C contains a sequence $\{x_n\}_{n=1}^\infty ,$ which converges weakly to $x^*$ and $\lim \limits _{n \rightarrow \infty }||x_n- Tx_n||=0$ (see, [39]). The set of asymptotic fixed points of T is denoted by ${\hat{F}}(T)$. A mapping $T: C \rightarrow$ int(dom f) is called

• (i) Bregman Firmly Nonexpansive (BFNE for short) if

  $$\begin{aligned} \langle \nabla f(Tx) - \nabla f(Ty), Tx-Ty \rangle \le \langle \nabla f(x)- \nabla f(y), Tx-Ty \rangle \qquad \forall x,y \in C.\nonumber \\ \end{aligned}$$

  (6)

• (ii) Bregman quasi-nonexpansive (BQNE) if $F(T) \ne \emptyset$ and $D_f(p,Tx) \le D_f(p,x) \qquad \forall x \in C, p \in F(T).$

It is easy to see that if ${\hat{F}}(T)= F(T) \ne \emptyset$, then $BFNE \subset BQNE.$

Definition 2.4

(see, [40]) The Minty Variational Inequality (MVI) is defined as finding a point ${\bar{x}} \in C$ such that $\langle Ay, y - {\bar{x}} \rangle \ge 0, \quad \forall y \in C.$ We denote by M(C, A), the set of solution of MVI. Some existence results for the MVI have been presented in [41].

Lemma 2.1

(see, p. 69, Proposition 2.9 of [42]) Let f be a totally convex and Gâteaux differentiable such that $\hbox {dom}f = E$. Then for all $x^* \in E^{*}\setminus \{0\}$, ${\tilde{y}} \in E$, $x \in H^{+}$ and ${\bar{x}} \in H^{-}$, it holds that

$$\begin{aligned} D_f({\bar{x}},x) \ge D_f({\bar{x}},z) +D_f(z,x), \end{aligned}$$

where $z = argmin_{y \in H}D_f(y,x)$ and $H = \{y \in E:\langle x^*,y - {\tilde{y}} \rangle = 0\}$, $H^{+} = \{y \in E: \langle x^*, y-{\tilde{y}} \rangle \ge 0\}$ and $H^{-} = \{y \in E: \langle x^*, y - {\tilde{y}} \rangle \le 0\}$.

3 Main Results

In this section, we give a precise statement of our projection-type method and discuss some of its convergence analysis.

Let E be a real reflexive Banach space and let C be a nonempty, closed and convex subset of E. Let $f: E \rightarrow {\mathbb {R}}$ be a coercive, Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E such that $C \subset int(domf)$. Let $A: E \rightarrow E^{*}$ be a continuous pseudo-monotone operator and $T:C \rightarrow C$ be a Bregman quasi-nonexpansive mapping such that $\varGamma := VI(C,A) \cap F(T) \ne \emptyset$. Let $\{\alpha _n\}$ and $\{\beta _n\}$ be nonnegative sequences in ]0, 1[.

Remark 3.1

Note that if $x_n - Proj_C^f(z_n) =0$ and $x_n - Tx_n =0$, then we are at a common solution of the VI (1) and fixed point of the Bregman quasi-nonexpansive mapping. In our convergence analysis, we will implicitly assume that this does not occur after finitely many iterations so that Algorithm 3.1 generates an infinite sequences.

We first show that Algorithm 3.1 is well defined. To do this, it is sufficient to show that the inner loop in the stepsize rule in Step 2 is well defined.

Lemma 3.1

• (i) The stepsize process in Step 2 of Algorithm 3.1 is well defined.

• (ii) Let $\{x_n\}$ and $\{y_n\}$ be sequences generated by Algorithm 3.1, then $\langle Ay_n, x_n -y_n \rangle > 0.$

Proof

• (i) Assume that (8) does not hold for $n \in {\mathbb {N}}$. This implies that

  $$\begin{aligned} \langle Ay_n(t_n), x_n - Proj_C^fz_n \rangle < \dfrac{\sigma D_f(Proj_C^fz_n,x_n)}{\lambda _n} \quad for~~n \in {\mathbb {N}}. \end{aligned}$$

  Thus, we have

  $$\begin{aligned} \langle A((1-s \gamma ^m)x_n + s\gamma ^m Proj_C^f z_n), x_n - Proj_C^fz_n \rangle < \dfrac{\sigma D_f(Proj_C^f z_n,x_n)}{\lambda _n} \quad \forall m \ge 0. \end{aligned}$$

  Since A is continuous and $y_n(t_n) \rightarrow x_n$ as $m \rightarrow \infty$, it follows that

  $$\begin{aligned} \langle \lambda _n Ax_n, x_n -Proj_C^fz_n \rangle < \sigma D_f(Proj_C^fz_n,x_n), \end{aligned}$$

  equivalently, by (7), we have

  $$\begin{aligned} \langle \nabla f(x_n) - \nabla f(z_n), x_n - Proj_C^fz_n \rangle < \sigma D_f(Proj_C^fz_n,x_n). \end{aligned}$$

  Applying the three point identity (3) to the left-hand side of the above inequality, we obtain

  $$\begin{aligned} D_f(Proj_C^fz_n,x_n) +D_f(x_n,z_n) - D_f(Proj_C^fz_n,z_n) < \sigma D_f(Proj_C^fz_n,x_n). \end{aligned}$$

  Since f is strictly convex and $\sigma \in (0,1)$, then $D_f(x_n,z_n) < D_f(Proj_C^fz_n,z_n).$ This contradicts the definition of the Bregman projection. Hence, the stepsize rule in Step 2 of Algorithm 3.1 is well defined.

• (ii) Furthermore, from (8), we have

  $$\begin{aligned} \langle Ay_n, x_n - y_n \rangle= & {} \langle Ay_n, x_n - (1-t_n)x_n - t_n Proj_C^f z_n \rangle = t_n \langle Ay_n, x_n - Proj_C^fz_n \rangle \\\ge & {} \dfrac{\sigma t_n D_f(Proj_C^f z_n,x_n)}{\lambda _n} > 0. \end{aligned}$$

$\square$

In order to establish our main result, we make the following assumptions:

• (C1) $\lim \limits _{n\rightarrow \infty }\alpha _n = 0$ and $\sum \limits _{n=0}^\infty \alpha _n = \infty$.

• (C2) $0< \liminf \limits _{n\rightarrow \infty }\beta _n \le \limsup \limits _{n \rightarrow \infty }\beta _n < 1$.

We proceed to prove the following lemmas before proving the convergence of our main Algorithm 3.1.

Lemma 3.2

The sequence $\{x_n\}$ generated by Algorithm 3.1 is bounded.

Proof

For each $n \in {\mathbb {N}},$ define the sets:

$$\begin{aligned}&Q_n^{-}:= \{u\in E: \langle Ax_n, u - x_n\rangle \le 0\}, \ Q_n := \{u\in E: \langle Ax_n, u - x_n \rangle = 0\}, \ \text {and}\ Q_n^{+} \\&\quad :=\{u\in E: \langle Ax_n, u - x_n \rangle \ge 0\}. \end{aligned}$$

Let $p \in \varGamma$, then since A is pseudo-monotone, we have $\langle Ap, x - p \rangle \ge 0 \Rightarrow \langle Ax, x-p \rangle \ge 0 \quad \forall x \in E.$ This implies that $p \in Q_n^{-}$ for all $n \in {\mathbb {N}}$. Furthermore, since we implicitly assumed that Algorithm 3.1 does not terminate after finitely many steps with an exact solution, we have from Lemma 3.1(ii) that $\langle Ay_n, x_n - y_n \rangle > 0$. This implies that $x_n \in Q_n^{+}$ and $x_n \notin Q_n^{-}$ for all $n \in N$. Therefore, using Lemma 2.1, we obtain

$$\begin{aligned} D_f(p,x_n) \ge D_f(p,u_n) + D_f(u_n,x_n). \end{aligned}$$

(10)

Now, since $v_n = Proj_C^f(u_n)$, then from (5), we have

$$\begin{aligned} D_f(p,u_n) \ge D_f(p,v_n) +D_f(v_n,u_n). \end{aligned}$$

(11)

Combining (10) and (11), we have

$$\begin{aligned} D_f(p,x_n) \ge D_f(p,v_n) + D_f(v_n,u_n) +D_f(u_n,x_n). \end{aligned}$$

This implies that

$$\begin{aligned} D_f(p,v_n) \le D_f(p,x_n) -D_f(v_n,u_n) - D_f(u_n,x_n). \end{aligned}$$

(12)

From (9) and (12), we have

$$\begin{aligned} D_f(p,x_{n+1})\le & {} D_f\Big (p, \nabla f^*\Big (\alpha _n \nabla f(u)+(1-\alpha _n)(\beta _n \nabla f(v_n)+(1-\beta _n)\nabla f(Tv_n))\Big ) \Big ),\\\le & {} \alpha _n D_f(p, u) + (1-\alpha _n)\beta _n D_f(p,v_n) + (1-\alpha _n)(1-\beta _n)D_f(p,Tv_n) \\\le & {} \alpha _n D_f(p,u) + (1-\alpha _n)D_f(p,x_n) \\\le & {} \max \{D_f(p,u), D_f(p,x_n)\} \le \dots \le \max \{D_f(p,u), D_f(p,x_1)\}. \end{aligned}$$

Hence $\{D_f(p,x_n)\}$ is bounded. Then by using Lemma 3.1 of [37], p. 31, we obtain $\{x_n\}$ is bounded. Consequently, $\{y_n\}$, $\{Ay_n\}$, $\{u_n\}$, $\{v_n\}$ and $\{Tv_n\}$ are bounded. $\square$

Lemma 3.3

Let $\{x_n\}$, $\{y_n\}$, $\{z_n\}$ and $\{u_n\}$ be sequences generated by Algorithm 3.1. Suppose there exist subsequences $\{x_{n_k}\}$ and $\{u_{n_k}\}$ of $\{x_n\}$ and $\{u_n\}$ respectively such that $\lim \limits _{k \rightarrow \infty }||x_{n_k} - u_{n_k}|| = 0$. Let $\{y_{n_k}\}$ and $\{z_{n_k}\}$ be subsequences of $\{y_n\}$ and $\{z_n\}$ respectively, then

• (a) $\lim \limits _{k\rightarrow \infty }\langle Ay_{n_k}, x_{n_k} - y_{n_k} \rangle = 0,$

• (b) $\lim \limits _{k \rightarrow \infty }||Proj_C^f(z_{n_k}) - x_{n_k}|| = 0,$

• (c) $0 \le \liminf \limits _{k \rightarrow \infty }\langle Ax_{n_k}, x - x_{n_k} \rangle ,$ for all $x \in C$.

Proof

• (a) Since $u_n \in Q_n$, then we have $0 = \langle Ay_{n_k}, u_{n_k} - y_{n_k} \rangle = \langle Ay_{n_k}, u_{n_k} - x_{n_k} \rangle + \langle Ay_{n_k}, x_{n_k} - y_{n_k} \rangle ,$ which implies that

  $$\begin{aligned} \langle Ay_{n_k}, x_{n_k} - y_{n_k} \rangle= & {} \langle Ay_{n_k}, x_{n_k} - u_{n_k} \rangle \le ||Ay_{n_k}||_{*}||x_{n_k}-u_{n_k}||. \end{aligned}$$

  Taking the limit of the above inequality as $k \rightarrow \infty$ yields $\lim \limits _{k \rightarrow \infty }\langle Ay_{n_k}, x_{n_k} -y_{n_k} \rangle = 0.$

• (b) Let $\{t_{n_k}\}$ be a subsequence of $\{t_n\}$. We consider the following two cases based on the behaviour of $t_{n_k}$.

Case I: Suppose $\lim \limits _{k \rightarrow \infty }t_{n_k} \ne 0$; i.e., there exists some $\delta >0$ such that $t_{n_k} \ge \delta >0$ for all $k \in {\mathbb {N}}$. It follows from Step 2 of Algorithm 3.1 that $\langle Ay_{n_k}, x_{n_k} - y_{n_k} \rangle \ge \dfrac{\sigma D_f(Proj_C^fz_{n_k}, x_{n_k})}{\lambda _n} .$ Hence, from Lemma 3.3(a), we have $\lim \limits _{k\rightarrow \infty }D_f(Proj_C^fz_{n_k}, x_{n_k}) = 0\Rightarrow \lim \limits _{k \rightarrow \infty } ||Proj_C^fz_{n_k} - x_{n_k}|| = 0.$

Case II: On the other hand, suppose $t_{n_k} \rightarrow 0$ as $k \rightarrow \infty$. Let $t_{n_k} <s$ so that the stepsize get reduced at least once for all iterations belonging to this subsequence. This implies that the trial stepsize does not satisfy the test from Step 2 of Algorithm 3.1. Assume that $\lim \limits _{k \rightarrow \infty }D_f(Proj_C^fz_{n_k},x_{n_k}) \ne 0,$ i.e., there exists a positive constant $\delta < +\infty$ such that $\limsup \limits _{k\rightarrow \infty }(Proj_C^fz_{n_k},x_{n_k}) = \delta .$

Define ${\bar{y}}_k = (1-t_{n_k})x_{n_k} + t_{n_k} Proj_C^f(z_{n_k})$. Then ${\bar{y}}_k - x_{n_k} = t_{n_k}(Proj_C^fz_{n_k} - x_{n_k}).$ Since $\{Proj_C^fz_{n_k} - x_{n_k}\}$ is bounded and $t_{n_k} \rightarrow 0$ as $k \rightarrow \infty$, it follows that $\lim \limits _{k \rightarrow \infty }||{\bar{y}}_k - x_{n_k}||= 0$. From the stepsize rule in Step 2 and the definition of ${\bar{y}}_k$, we have $\langle A{\bar{y}}_k, x_{n_k} - Proj_C^f z_{n_k} \rangle < \dfrac{\sigma D_f(Proj_C^fz_{n_k}, x_{n_k})}{\lambda _{n_k}} \quad \forall k \in {\mathbb {N}}.$ Since A is uniformly continuous on bounded subsets of C and $\sigma \in (0,1)$, we obtain that there exists $N \in {\mathbb {N}}$ such that

$$\begin{aligned} \langle \lambda _{n_k} Ax_{n_k}, x_{n_k} - Proj_C^fz_{n_k} \rangle < D_f(Proj_C^f z_{n_k}, x_{n_k}) \quad \forall k \in {\mathbb {N}}, ~~k \ge N. \end{aligned}$$

Therefore

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \nabla f(z_{n_k}), x_{n_k} - Proj_C^fz_{n_k} \rangle < D_f(Proj_C^f z_{n_k}, x_{n_k}), \quad \forall k\in {\mathbb {N}},~~k \ge N. \end{aligned}$$

Using the three points identity (3) in the last inequality, we get

$$\begin{aligned}&D_f(Proj_C^fz_{n_k}, x_{n_k}) + D_f(x_{n_k}, z_{n_k}) - D_f(Proj_C^f z_{n_k}, z_{n_k}) < D_f(Proj_C^fz_{n_k}, z_{n_k}) \\ \quad \forall k \ge N. \end{aligned}$$

Hence $D_f(x_{n_k}, z_{n_k}) < D_f(Proj_C^fz_{n_k}, z_{n_k}) \quad \forall k \ge N.$ This contradicts the definition of the Bregman projection. Hence $\lim _{k \rightarrow \infty } D_f(Proj_C^fz_{n_k}, x_{n_k}) = 0.$ Therefore, by using Proposition 2.5 in [36], we obtain that $\lim \limits _{k \rightarrow \infty }||Proj_C^fz_{n_k} - x_{n_k}|| = 0.$

(c) From (4), we have that $\langle \nabla f(z_{n_k}) - \nabla f(Proj_C^f z_{n_k}), y - Proj_C^fz_{n_k} \rangle \le 0 \quad \forall y \in C.$ This implies from (7) that

$$\begin{aligned} \langle \nabla f(x_{n_k}) - \nabla f(Proj_C^fz_{n_k}), y -Proj_C^fz_{n_k} \rangle \le \langle \lambda _{n_k} Ax_{n_k}, y - Proj_C^f z_{n_k} \rangle \quad \forall y \in C. \end{aligned}$$

Therefore

$$\begin{aligned}&\langle \nabla f(x_{n_k}) -\nabla f(Proj_C^fz_{n_k}), y - Proj_C^fz_{n_k} \rangle + \langle \lambda _{n_k}Ax_{n_k} , Proj_C^fz_{n_k} - x_{n_k} \rangle \nonumber \\&\quad \le \langle \lambda _{n_k} Ax_{n_k}, y - x_{n_k} \rangle . \end{aligned}$$

(13)

Thus, we have from (b) that $\lim \limits _{k \rightarrow \infty }||\nabla f(Proj_C^f(z_{n_k})) - \nabla f(x_{n_k})||_{*} = 0.$ Taking the limit of the inequality in (13) and noting that $\{\lambda _{n_k}\} \subset [a,b]$, we have $0 \le \liminf \limits _{k \rightarrow \infty } \langle Ax_{n_k}, y - x_{n_k} \rangle \quad \forall y \in C.$$\square$

Lemma 3.4

The sequence $\{x_n\}$ generated by Algorithm 3.1 satisfies the following estimates:

• (i) $s_{n+1} \le (1-\alpha _n)s_n + \alpha _nb_n$,

• (ii) $-1 \le \limsup \limits _{n \rightarrow \infty }b_n < + \infty$,

where $p \in \varGamma$, $s_n = D_f(p, x_{n})$,    $b_n = \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle .$

Proof

• (i) Let $w_n = \nabla f^*(\beta _n \nabla f(v_n) + (1-\beta _n)\nabla f(Tv_n))$ and $p \in \varGamma$, then from (9), we have

  $$\begin{aligned} D_f(p, x_{n+1})= & {} D_f(p, \nabla f^*(\alpha _n \nabla f(u) + (1-\alpha _n)\nabla f (w_n))) \nonumber \\\le & {} V_f \Big ( p, \alpha _n \nabla f(u) + (1-\alpha _n)\nabla f(w_n) - \alpha _n(\nabla f(u) - \nabla f(p)) \Big ) \nonumber \\&+ \langle \alpha _n (\nabla f(u) - \nabla f(p)), x_{n+1} - p \rangle \nonumber \\= & {} V_f\Big (p, \alpha _n \nabla f(p) +(1-\alpha _n) \nabla f(w_n) \Big ) + \alpha _n \langle \nabla f(u) \nonumber \\&- \nabla f(p), x_{n+1} - p \rangle \nonumber \\\le & {} (1-\alpha _n)D_f(p,w_n) + \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle \end{aligned}$$

  (14)
  $$\begin{aligned}= & {} (1-\alpha _n)\Big ( D_f(p, \nabla f^*(\beta _n \nabla f(v_n) + (1-\beta _n)\nabla f(Tv_n))) \Big ) \nonumber \\&+ \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle \nonumber \\\le & {} (1-\alpha _n)\beta _n D_f(p, v_n) + (1-\alpha _n)(1-\beta _n)D_f(p,Tv_n) \nonumber \\&+ \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle \nonumber \\\le & {} (1-\alpha _n)D_f(p,v_n) + \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

  (15)

  Therefore from (12), we have

  $$\begin{aligned} D_f(p, x_{n+1})\le & {} (1-\alpha _n)\Big ( D_f(p,x_n) -D_f(v_n,u_n) - D_f(u_n,x_n) \Big ) \nonumber \\&+ \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

  (16)

  Since $\{\alpha _n\} \subset ]0,1[$, then

  $$\begin{aligned} D_f(p,x_{n+1}) \le (1-\alpha _n)D_f(p,x_{n}) + \alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

  (17)

  This established (i).

• (ii) Since $\{x_{n}\}$ is bounded, then we have

  $$\begin{aligned} \sup _{n \ge 0} b_n\le \sup ||\nabla f(u) - \nabla f(p)||_{*}||x_{n+1}-p|| < \infty . \end{aligned}$$

  This implies that $\limsup \limits _{n \rightarrow \infty }b_n < \infty$. Next, we show that $\limsup \limits _{n \rightarrow \infty }b_n \ge -1.$ Assume the contrary, i.e. $\limsup \limits _{n \rightarrow \infty }b_n < -1$. Then there exists $n_0 \in {\mathbb {N}}$ such that $b_n < -1$, for all $n \ge n_0$. Then for all $n \ge n_0$, we get from (i) that

  $$\begin{aligned} s_{n+1}\le & {} (1-\alpha _n)s_n + \alpha _n b_n < (1-\alpha _n)s_n - \alpha _n = s_n - \alpha _n(s_n +1) \le s_n - \alpha _n. \end{aligned}$$

  Taking $\limsup$ of the last inequality, we have

  $$\begin{aligned} \limsup _{n \rightarrow \infty }s_{n} \le s_{n_0} - \lim _{n\rightarrow \infty }\sum _{i = n_0}^n \alpha _i = - \infty . \end{aligned}$$

  This contradicts the fact that $\{s_n\}$ is a non-negative real sequence. Therefore $\limsup \limits _{n \rightarrow \infty }b_n \ge -1$.

$\square$

We are now in position to state and prove our main theorem.

Theorem 3.1

Let $\{x_n\}$ be the sequence generated by Algorithm 3.1. Then, $\{x_n\}$ converges strongly to a point ${\bar{x}} = Proj_\varGamma ^f(u)$, where $Proj_\varGamma ^f$ is the Bregman projection from C onto $\varGamma$.

Proof

Let $p \in \varGamma$, and denote $D_f(p,x_{n})$ by $\varPhi _{n}$. We consider the following two possible cases.

CASE A: Suppose there exists $n_0 \in {\mathbb {N}}$ such that $\varPhi _{n}$ is monotonically nonincreasing for all $n \ge n_0$. Since $\varPhi _{n}$ is bounded, then it is convergent and so $\varPhi _{n} - \varPhi _{n+1} \rightarrow 0$ as $n \rightarrow \infty$.

We first show that $||x_n -u_n|| \rightarrow 0,$$||v_n - Tv_n|| \rightarrow 0$ and $||x_{n+1} - x_{n}|| \rightarrow 0$ as $n \rightarrow \infty$. Since $\{\alpha _n\} \subset (0,1)$, we obtain from (16) that

$$\begin{aligned}&(1-\alpha _n)D_f(u_n,x_n) \le (1-\alpha _n)D_f(p,x_{n}) - D_f(p,x_{n+1}) + \alpha _n \langle \nabla f(u) \\&\quad - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

Using condition(C1), we obtain that $D_f(u_n,x_n) \rightarrow 0$ as $n \rightarrow \infty$. Using Lemma 3.1 in [37], p. 31, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }||u_n - x_n|| = 0. \end{aligned}$$

(18)

Similarly from (16), we can obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }||v_n - u_n|| = 0 \Rightarrow \lim _{n\rightarrow \infty }||v_n -x_n|| = 0. \end{aligned}$$

(19)

Recall that $w_n = \nabla f^*(\beta _n \nabla f(v_n) + (1-\beta _n)\nabla f(Tv_n))$. Thus, we have

$$\begin{aligned} D_f(p,w_{n})= & {} D_f(p, \nabla f^*(\beta _n \nabla f(v_n) + (1-\beta _n)\nabla f(Tv_n))) \nonumber \\\le & {} \beta _n D_f(p,v_n) + (1-\beta _n)D_f(p,Tv_n) \nonumber \\&- \beta _n(1-\beta _n)\rho _r(||\nabla f(v_n)- \nabla f(Tv_n)||_{*}) \nonumber \\\le & {} D_f(p, v_n) - \beta _n(1-\beta _n)\rho _r(||\nabla f(v_n)- \nabla f(Tv_n)||_{*}). \end{aligned}$$

(20)

Thus from (12), (14) and (20), we have

$$\begin{aligned} D_f(p, x_{n+1})\le & {} (1-\alpha _n)D_f(p,v_n) - (1-\alpha _n)\beta _n(1-\beta _n)\rho _r(||\nabla f(v_n)- \nabla f(Tv_n)||) \\&+\,\alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle \\\le & {} (1-\alpha _n)D_f(p,x_n) - (1-\alpha _n)\beta _n(1-\beta _n)\rho _r(||\nabla f(v_n)- \nabla f(Tv_n)||_{*}) \\&+\,\alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

Hence

$$\begin{aligned} (1-\alpha _n)\beta _n(1-\beta _n)\rho _r(||\nabla f(v_n)- \nabla f(Tv_n)||)\le & {} (1-\alpha _n)D_f(p,x_n) - D_f(p, x_{n+1}) \\&+\alpha _n \langle \nabla f(u) - \nabla f(p), x_{n+1} - p \rangle . \end{aligned}$$

It follows from conditions (C1), (C2) and the properties of $\rho _r$ that

$$\begin{aligned} \lim _{n\rightarrow \infty }||\nabla f(v_n)- \nabla f(Tv_n)||_{*} = 0. \end{aligned}$$

(21)

Since f is uniformly Fréchet differentiable on bounded subsets of E, it is also uniformly continuous and $\nabla f$ is norm-to-norm uniformly continuous on bounded subsets of E, hence from (21), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }||f(v_n) - f(Tv_n)|| = 0\ \text {and} \ \lim _{n\rightarrow \infty }||v_n - Tv_n|| = 0. \end{aligned}$$

(22)

In addition, it is easy to see from definition of Bregman distance that $D_f(v_n,Tv_n) \rightarrow 0$ as $n \rightarrow \infty$. Thus

$$\begin{aligned} D_f(v_n, x_{n+1})&\le \alpha _n D_f(v_n,u) + (1-\alpha _n)\beta _n D_f(v_n,v_n) \\&\quad + (1-\alpha _n)(1-\beta _n)D_f(v_n,Tv_n). \end{aligned}$$

This implies that $\lim \limits _{n \rightarrow \infty }||v_n - x_{n+1}|| = 0 \Rightarrow \lim \limits _{n \rightarrow \infty }\Vert x_{n+1}- x_{n}\Vert = 0.$

Next, we show that $\varOmega _w (x_n) \subset VI(C,A)\cap F(T)$, where $\varOmega _w(x_n)$ is the weak subsequential limit of $\{x_n\}$. Let ${\bar{x}} \in \varOmega _w(x_n)$, there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $x_{n_k} \rightharpoonup {\bar{x}}$ as $k \rightarrow \infty$. Consequently from (22), $v_{n_k} \rightharpoonup {\bar{x}}$. Since $||v_{n_k} - Tv_{n_k}|| \rightarrow 0$, then ${\bar{x}} \in {\hat{F}}(T) = F(T)$. Furthermore, let $z \in C$ be an arbitrary point and $\{\varepsilon _k\}$ be a sequence of decreasing nonnegative numbers such that $\varepsilon _k \rightarrow 0$ as $k \rightarrow \infty$. Using Lemma 3.3(c), we can find a large enough $N_k$ such that $\langle Ax_{n_k}, z - x_{n_k} \rangle + \varepsilon _k \ge 0, \quad \forall k \ge N_k.$ This implies that

$$\begin{aligned} \langle Ax_{n_k}, z + \varepsilon _kt_k - x_{n_k} \rangle \ge 0, \quad \forall k \ge N_k, \end{aligned}$$

(23)

for some $t_k \in E$ satisfying $1 = \langle Ax_{n_k}, t_k \rangle$ (since $Ax_{n_k} \ne 0$). Since A is pseudo-monotone, then we have from (23) that $\langle A(z+ \varepsilon _kt_k), z + \varepsilon _k t_k - x_{n_k} \rangle \ge 0, \quad \forall k \ge N_k.$ This implies that

$$\begin{aligned} \langle Az, z - x_{n_k} \rangle \ge \langle Az - A(z + \varepsilon _k t_k), z + \varepsilon _k t_k - x_{n_k} \rangle - \varepsilon _k \langle Az, t_{n_k} \rangle \quad \forall k \ge N_k. \end{aligned}$$

(24)

Since $\epsilon _{k} \rightarrow 0$ and A is continuous, then the right-hand side of (24) tends to zero. Thus, we obtain that $\liminf \limits _{k \rightarrow \infty }\langle Az, z- x_{n_k} \rangle \ge 0, \quad \forall z \in C.$ In view of Lemma 3.3(c), we have that

$$\begin{aligned} \langle Az, z - {\bar{x}} \rangle = \lim _{k \rightarrow \infty }\langle Az, z -x_{n_k} \rangle \ge 0, \quad \forall z \in C. \end{aligned}$$

We know from Lemma 2.2 of [40], p. 2090 and the above inequality that ${\bar{x}} \in VI(C,A).$

Therefore ${\bar{x}} \in \varGamma : = VI(C,A)\cap F(T)$.

We now show that $\{x_n\}$ converges strongly to $x^* = Proj_\varGamma ^f u$. It is easy to show that

$$\begin{aligned} \limsup _{n \rightarrow \infty }\langle \nabla f(u) - \nabla f(x^*), x_{n+1} -x^* \rangle \le 0. \end{aligned}$$

Now using Lemma 2.5 of [43], p. 243 with Lemma 3.4(i), we obtain that $D_f(x^*,x_{n}) \rightarrow 0$ as $n \rightarrow \infty$. Hence, $\lim \limits _{n \rightarrow \infty }||x_{n} - x^*|| = 0.$ Therefore, $\{x_{n}\}$ converges strongly to $x^*= Proj_\varGamma ^f u$.

CASE B: Suppose $\{D_f(p,x_n)\}$ is not monotonically decreasing. Let $\phi : {\mathbb {N}} \rightarrow {\mathbb {N}}$ for all $n \ge n_0$ (for some $n_0$ large enough) be defined by $\phi _{n} = \max \{k \in {\mathbb {N}}: \phi _k \le \phi _{k+1}\}.$ Clearly, $\phi$ is nondecreasing, $\phi (n) \rightarrow \infty$ as $n \rightarrow \infty$ and

$$\begin{aligned} 0 \le D_f(p, x_{\phi (n)}) \le D_f(p, x_{\phi (n)+1}), \quad \forall n \ge n_0. \end{aligned}$$

Following similar argument as in CASE A, we obtain

$$\begin{aligned} ||x_{\phi (n)} - u_{\phi (n)}|| \rightarrow 0, \quad ||v_{\phi (n)} - Tv_{\phi (n)}|| \rightarrow 0, \quad ||x_{\phi (n)+1} - x_{\phi (n)}|| \rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$ and $\varOmega _w(x_{\phi (n)}) \subset VI(C,A)\cap F(T),$ where $\varOmega _w(x_{\phi (n)})$ is the weak subsequential limit of $\{x_{\phi (n)}\}$. Also,

$$\begin{aligned} \limsup _{n \rightarrow \infty }\langle \nabla f(u) - \nabla f(p), x_{\phi (n)+1} - p \rangle \le 0. \end{aligned}$$

(25)

From Lemma 3.4(i), we have that $D_f(p, x_{\phi (n)+1}) \le (1-\alpha _{\phi (n)})D_f(p, x_{\phi (n)}) + \alpha _{\phi (n)}\langle \nabla f(u) - \nabla f(p), x_{\phi (n)+1} - p \rangle .$ Since $D_f(p, x_{\phi (n)}) \le D_f(p, x_{\phi (n)+1})$, then

$$\begin{aligned} 0\le & {} D_f(p, x_{\phi (n)+1}) - D_f(p, x_{\phi (n)}) \\\le & {} (1-\alpha _{\phi (n)})D_f(p,x_{\phi (n)}) + \alpha _{\phi (n)}\langle \nabla f(u) - \nabla f(p), x_{\phi (n)+1} -p \rangle -D_f(p, x_{\phi (n)}). \end{aligned}$$

Hence from (25), we obtain

$$\begin{aligned} D_f(p, x_{\phi (n)}) \le \langle \nabla f(u) - \nabla f(p), x_{\phi (n)+1} - p \rangle \rightarrow 0, ~~as~~n \rightarrow \infty . \end{aligned}$$

As a consequence, we obtain that for all $n \ge n_0$,

$$\begin{aligned} 0 \le D_f(p, x_n) \le \max \{D_f(p, x_{\phi (n)}), D_f(p, x_{\phi (n)+1})\} = D_f(p, x_{\phi (n)+1}). \end{aligned}$$

Hence $\lim \limits _{n \rightarrow \infty }D_f(p, x_{n}) = 0\Rightarrow \lim \limits _{n \rightarrow \infty }||x_{n} - p|| = 0.$ This implies that $\{x_n\}$ converges strongly to p. This completes the proof. $\square$

4 Application to Equilibrium Problems

Let E be a real reflexive Banach space and C be a nonempty, closed and convex subset of E. Let $g:C \times C \rightarrow {\mathbb {R}}$ be a bifunction such that $g(x,x) = 0$ for all $x \in C$. The equilibrium problem (shortly, EP) with respect to g on C is stated as follows:

$$\begin{aligned} \text {Find} \quad x^* \in C \quad \text {such that}\quad g(x^*,y) \ge 0, \quad \forall ~y \in C. \end{aligned}$$

(26)

We denote the solution set of EP (26) by EP(C, g). The bifunction $g: C \times C \rightarrow {\mathbb {R}}$ is said to be

• (i) monotone on C if $g(x,y) + g(y,x) \le 0 \quad \forall ~~x,y \in C;$

• (ii) pseudo-monotone on C if $g(x,y) \ge 0 \Rightarrow g(y,x) \le 0 \quad \forall ~~x,y \in C.$

Remark 4.1

[44] Every monotone bifunction on C is pseudo-monotone but the converse is not true. A mapping $A: C \rightarrow E^{*}$ is pseudo-monotone if and only if the bifunction $g(x,y) = \langle Ax, y-x \rangle$ is pseudo-monotone on C.

Several algorithms have been introduced for solving the EP (26) when the bifunction g is monotone (see, for instance, [45,46,47,48]). However, when g is pseudo-monotone, very few iterative methods are known for solving the EP.

Assume that the bifunction g satisfies the following:

Assumption 4.1

(A1) g is weakly continuous on $C \times C$,

• (A2) $g(x,\cdot )$ is convex lower semicontinuous and subdifferentiable on C for every fixed $x \in C$,

• (A3) for each $x,y,z \in C$, $\limsup _{t \downarrow 0}g(tx + (1-t)y,z) \le g(y,z).$

Lemma 4.1

[49] Let E be a nonempty convex subset of a Banach space E and $f:E \rightarrow {\mathbb {R}}$ be a convex and subdifferentiable function, then f is minimal at $x \in E$ if and only if

$$\begin{aligned} 0 \in \partial f(x) + N_C(x), \end{aligned}$$

where $N_C(x)$ is the normal cone of C at x, that is, $N_C(x) := \{x^* \in E^* : \langle x^*, x - z \rangle \ge 0,~~\forall z \in C\}.$

Lemma 4.2

[50] Let E be a real reflexive Banach space. If f and g are two convex functions such that there is a point $x_0 \in$ dom $f ~\cap$ dom g where f is continuous, then $\partial (f+g)(x) = \partial f(x) + \partial g(x) \quad \forall x \in E.$

Proposition 4.1

Let E be a real reflexive Banach space and C be a nonempty, closed and convex subset of E. Let $g:C \times C \rightarrow {\mathbb {R}}$ be a bifunction such that $g(x,x) = 0$ and $f:E \rightarrow {\mathbb {R}}$ be a Legendre and totally coercive function. Then a point $x^* \in EP(C,g)$ if and only if $x^*$ solves the following minimization problem:

$$\begin{aligned} \min \bigg \{\lambda g(x,y) + D_f(y,x) : y \in C\bigg \},\quad \text {where}\ x \in C, \text {and}\ \lambda >0. \end{aligned}$$

Proof

Let $x^* = argmin_{y \in C}\bigg \{ \lambda g(x,y) +D_f(y,x)\bigg \},$ then from Lemmas 4.1 and 4.2, we have

$$\begin{aligned} 0 \in \partial \lambda g(x,x^*) + \nabla D_f(x^*,x) + N_C(x^*). \end{aligned}$$

Hence, there exist $w \in \partial g(x,x^*)$ and ${\bar{w}} \in N_C(x^*)$ such that

$$\begin{aligned} \lambda w + \nabla f(x^*) - \nabla f(x) + {\bar{w}} = 0. \end{aligned}$$

(27)

Since ${\bar{w}} \in N_C(x^*)$, then $\langle {\bar{w}},z -x^* \rangle \le 0$ for all $z \in C$. This together with (27) implies that

$$\begin{aligned} \langle \lambda w + \nabla f(x^*) - \nabla f(x), z -x^* \rangle \ge 0 \quad \forall ~~z \in C, \end{aligned}$$

and hence

$$\begin{aligned} \lambda \langle w, z -x^* \rangle \ge \langle \nabla f(x^*) - \nabla f(x), x^* - z \rangle \quad \forall ~~z \in C. \end{aligned}$$

(28)

Also, since $w \in \partial g(x,x^*)$, then we have $g(x,z) - g(x,x^*) \ge \langle w, z -x^* \rangle \quad \forall ~~z \in C.$ This together with (28) yields

$$\begin{aligned} \lambda \Big ( g(x,z) - g(x,x^*)\Big ) \ge \langle \nabla f(x^*) - \nabla f(x), x^* - z \rangle \quad \forall ~~z \in C. \end{aligned}$$

(29)

Replacing x with $x^*$ in (29), we have $g(x^*,z) \ge 0, \quad \forall z \in C.$ Therefore, $x^* \in EP(C,g).$ The converse follows clearly. $\square$

It is easy to show that, if $x \in VI(C,A),$ then x is the unique solution of the minimization problem

$$\begin{aligned} \min \bigg \{ \lambda \langle Au,y-u \rangle + D_f (y,u) : y \in C\bigg \}, \end{aligned}$$

where $u \in C$ and $\lambda >0$. By setting $\langle Ax, y-x \rangle = g(x,y)$ in Theorem 3.1, we have the following result for approximating solution of pseudo-monotone equilibrium problem.

Theorem 4.1

Let E be a real reflexive Banach space, and let C be a nonempty, closed and convex subset of E. Let $f: E \rightarrow {\mathbb {R}}$ be a coercive, Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subsets of E such that $C \subset int(domf)$. Let $g: C \times C \rightarrow {\mathbb {R}}$ be a pseudo-monotone bifunction such that $g(x,x) =0$ for all $x \in C$ and satisfying Assumption 4.1. Let $T:C \rightarrow C$ be a Bregman quasi-nonexpansive mapping with ${\hat{F}}(T)= F(T)$ such that $\varGamma := EP(C,g) \cap F(T) \ne \emptyset$. Let $\{\alpha _n\}$ and $\{\beta _n\}$ be nonnegative sequences in ]0, 1[ and such that conditions (C1) and (C2) are satisfied. Let $\{x_n\}$ be generated by the following algorithm:

Then, the sequence $\{x_n\}$ converges strongly to a point ${\bar{x}} = Proj_\varGamma ^f(u)$, where $Proj_\varGamma ^f$ is the Bregman projection from C onto $\varGamma$.

5 Numerical Examples

In this section, we present two numerical examples which demonstrate the performance of our Algorithm 3.1.

Example 5.1

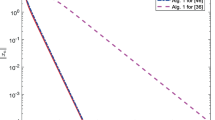
Let $E = {\mathbb {R}}^n$ with standard topology and $T: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ be defined by $Tx = -\frac{1}{2}x.$ Consider an operator $A: {\mathbb {R}}^m \rightarrow {\mathbb {R}}^m$ ($m = 20, 50,100,200$) define by $Ax = Mx+q$ where $M =NN^{T} + S+D,$N is a $m\times m$ matrix, S is an $m \times m$ skew-symmetric matrix, D is a $m \times m$ diagonal matrix, whose diagonal entries are non-negative so that M is positive definite and q is a vector in ${\mathbb {R}}^m$. The feasible set $C\subset {\mathbb {R}}^m$ is closed and convex (polyhedron), which is defined as $C = \{x = (x_1,x_2,\dots , x_m) \in {\mathbb {R}}^m: Qx \le b\}$, where Q is a $l \times m$ matrix and b is a non-negative vector. Clearly, A is monotone (hence, pseudo-monotone) and L-Lipschitz continuous with $L = ||M||$. For experimental purpose, all the entries of N, S, D and b are generated randomly as well as the starting point $x_1 \in [0,1]^m$ and q is equal to the zero vector. In this case, the solution to the corresponding variational inequality is $\{0\}$ and thus, $\varGamma : = VI(C,A) \cap F(T) =\{0\}$. We fix the stopping criterion as $\frac{\Vert x_{n+1}-x_{n}\Vert ^2}{\Vert x_2 - x_1\Vert ^2}=\epsilon <10^{-5}$, $\sigma = 0.7$, $\gamma = 0.9$, $s = 10$, $\lambda _n = 0.15$ and let $\alpha _n = \frac{1}{n+1}$ and $\beta _n = \frac{1}{4}$. The projection onto the feasible set C is carry-out by using the MATLAB solver ‘fmincon’ and the projection onto an hyperplane $Q = \{x \in {\mathbb {R}}^m: \langle a,x\rangle = 0\}$ is defined by $P_Q(x) = x -\frac{\langle a,x \rangle }{||a||^2}a.$ Since A is monotone, we compare the output of our Algorithm 3.1 with Algorithm 3.3 of [20] (Alg 1.5). The numerical result is reported in Fig. 1 and Table 1. We see that our Algorithm 3.1 converges faster than Algorithm 3.3 of [20]. This is expected because the stepsize rule in STEP 2 of our algorithm tends to determine a larger stepsize closer to the solution of the problem (Tables 2, 3).

Table 1 Comparison between Algorithm 3.1 and Algorithm 3.3 of [20] for Example 5.1

Fig. 1

Example 5.1, $m =20$; $m =50$; $m=100$ and $m=200$ respectively

Finally, we give a concrete example in $\ell _p$ space ($1 \le p < \infty$ with $p \ne 2$), which is not a Hilbert space. It is well known that the dual space $(\ell _p)^*$ is isomorphic to $\ell _q$ provided that $\frac{1}{q}+\frac{1}{p} =1$ (see, for instance, [51], Lemma 2.2, p. 11). Also, the $\ell _p$ space is a reflexive Banach space and in this case, we take $f(x) = \frac{1}{p}||x||^p.$

Example 5.2

Let $E = \ell _3({\mathbb {R}})$ define by $\ell _3({\mathbb {R}}):= \{{\bar{x}}= (x_1,x_2,x_3,\dots ), x_i \in {\mathbb {R}}: \sum _{i=1}^\infty |x_i|^3 < \infty \},$ with norm $||\cdot ||_{\ell _3}:\ell _3 \rightarrow [0,\infty )$ defined by $||{\bar{x}}||_{\ell _3} = \left( \sum _{i=1}^\infty |x_i|^3\right) ^\frac{1}{3},$ for arbitrary ${\bar{x}} = (x_1,x_2,x_3,\dots )$ in $\ell _3.$ Let $C:=\{x\in E:||x||_{\ell _3}\le 1\}$ and define the mapping $A:C \rightarrow (\ell _3)^*$ by $Ax = 2x + (1,1,1,0,0,0,\dots ),$ with $(x_1,x_2,x_3,\dots ) \in \ell _3({\mathbb {R}}).$ It is easy to show that A is monotone (hence, pseudo monotone). Take $Tx = \frac{x}{2},$$\alpha _n = \frac{1}{100n+1}, \beta _n = \frac{3n+5}{7n+8}, \sigma = 0.14,\gamma = 0.4, s = 3, \lambda = 0.78.$ The projections onto the feasibility set are carried out using optimization tool box in MATLAB. We carried out two numerical tests for approximating the common solution of the VI and FPP using Algorithm 3.1. The initial value of $x_1$ and fixed u used are

• Case I: $x_1 = (0.3241,0.5387,-0.1256,0,0,0,\dots )$ and $u = (-0.0988,0.2679,0.2890,0,0,0,\dots )$

• Case II: $x_1 = (-4.5289,-1.2345,5.2238,0,0,0\dots )$ and $u = (1.3268,-5.3420,3.2890,0,0,0,\dots ),$ with stopping criterion $\frac{||x_{n+1}-x_{n}||_{\ell _3}}{||x_2 -x_1||_{\ell _3}} < 10^{-7}$ in each case. The following are the computational results obtain for these tests.

Table 2 Computation result for Example 5.2, Case I; Time: 0.1336 s

Table 3 Computation result for Example 5.2, Case 2; Time: 0.2182 s

Remark 5.1

The numerical experiments showed that the performance of the algorithm is essentially independent of the value of $x_1$ used in the computation.

6 Conclusions

In this paper, we have proposed a strong convergence projection-type algorithm for solving pseudo-monotone VI and fixed point of Bregman quasi-nonexpansive mapping in a real reflexive Banach space. A convergence theorem was established without a Lipschitz condition imposed on the cost operator of the VI. We also give an application of our results to approximating the solution of pseudo-monotone equilibrium problems in reflexive Banach spaces. Some numerical examples are also provided to demonstrate the behavior of our algorithm. The following are the contributions made in this paper:

• (i) The main result in this paper extends the result of Denisov et al [52] and Kanzow and Shehu [20] from Hilbert space to a reflexive Banach space and also from monotone variational inequality to pseudo-monotone variational inequalities.

• (ii) The operator involved in our method need not be Lipschitz continuous. Our main result extends many recent results (e.g., [16, 24, 25]) on VI, where the underlying operator is monotone and Lipschitz continuous.

• (iii) The (w, s) sequential continuity of a pseudo-monotone operator A,  assumed by Ceng et al. [53] and Yao and Postolache [54] to establish weak and strong convergence results for solving VI in a Hilbert space, was relaxed in our result and also the strong convergence result obtained in this paper improves the weak convergence result of Vuong [55] in a real Hilbert space.