1 Introduction

The paper concerns with some new iterative methods for approximating a solution of an equilibrium problem in a Banach space E.

Recall that an equilibrium problem (EP) is stated as follows:

$$\begin{aligned} \text{ Find }\,x^*\in C\,\text{ such } \text{ that }\,f(x^*,y)\ge 0\,\text{ for } \text{ all }\, y\in C, \end{aligned}$$
(EP)

where C is a nonempty closed convex subset in E, \(f:C \times C \rightarrow \mathfrak {R}\) is a bifunction with \(f(x,x)=0\) for all \(x\in C\). Let us denote by EP(f, C) the solution set of the problem (EP).

Mathematically, the problem (EP) has a simple and convenient structure. This problem is quite general, and it unifies several known models in applied sciences as optimization problems, variational inequalities, hemivariational inequalities, fixed point problems and others [3, 12, 15, 28, 35, 43, 44].

In recent years, this problem has received a lot of attention by many authors in both theory and algorithm. Some methods have been proposed for solving the problem (EP) such as the proximal point method [30, 34], the extragradient method [13, 38], the descent method [4,5,6, 29], the linesearch extragradient method [38], the projected subgradient method [42] and others [7, 36, 48, 51].

The proximal-like method was early introduced in [13] and its convergence was also studied. Recently, this method has been extended and investigated further the convergence by Quoc et al. in [38] under different assumptions. The method in [13, 38] is also called the extragradient method due to Korpelevich’s contributions for saddle point problems in [31]. Precisely, in Euclidean spaces, the extragradient method (EGM) generates two sequences \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \), from a starting point \(x_0\in C\), defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=\arg \min \left\{ \rho f(x_n,y)+G(x_n,y):y\in C\right\} ,\\ x_{n+1}=\arg \min \left\{ \rho f(y_n,y)+G(x_n,y):y\in C\right\} ,\;\;\forall n\ge 0, \end{array}\right. } \end{aligned}$$
(EGM)

where \(\rho \) is a suitable parameter and G(x, y) is a given Bregman distance function defined on \(C \times C\). Observe that, at each iteration, the method EGM needs to compute two values of bifunction f at \(x_n\) and \(y_n\). In recent years, the method EGM has been developed naturally in setting of Hilbert spaces. The convergence of this method was proved in [38] under the hypotheses of the pseudomonotonicity and the Lipschitz-type condition (MLC) introduced recently by Mastroeni in [32].

Recall that a bifunction \(f:C \times C \rightarrow \mathfrak {R}\) is called pseudomonotone on C, if

$$\begin{aligned} f(x,y) \ge 0 \;\; \Longrightarrow \;\; f(y,x) \le 0, \;\; \forall x,y \in C, \end{aligned}$$

and we say that f satisfies a Lipschitz-type condition (MLC) [32] on C, if there exist two constants \(c_1,\,c_2>0\) such that, for all \(x,\,y\in C\),

$$\begin{aligned} f(x,y)+f(y,z)\ge f(x,z)-c_1||x-y||^2-c_2||y-z||^2. \end{aligned}$$
(MLC)

In recent years, the method EGM has been intensively studied in both finite and infinite dimensional Hilbert spaces under various different conditions (see, e.g., [2, 8, 16, 17, 20,21,22, 45, 46]).

In setting of Banach spaces, the well-known method for solving the problem (EP) is the proximal point method (PPM). The description of this method is as follows: from a starting point \(x_0\in C\), at the current step, given \(x_n\), find the next iterate \(x_{n+1} \in C\) such that

$$\begin{aligned} f(x_{n+1},y)+\frac{1}{r}\left\langle y-x_{n+1},Jx_{n+1}-Jx_n\right\rangle \ge 0,\;\;\forall y\in C. \end{aligned}$$
(PPM)

Here r is a positive parameter, \(J:E\rightarrow 2^{E^*}\) is the normalized duality mapping on E and \(\left\langle \cdot ,\cdot \right\rangle \) stands for the dual product in E.

The convergence of the method (PPM) was obtained under the monotonicity of the bifunction f and some other suitable conditions. This method was developed further in combining with other methods as the Halpern iteration, the viscosity method, hybrid (outer approximation) or shrinking projection method to obtain the convergence in norm which is useful in infinite dimensional Banach spaces (see, e.g., [25, 33, 39,40,41, 47, 50, 52]).

Some other methods with linesearch can be found, for example, in [23, 24]. The linesearch method in general requires many extra-computations. More precisely, at each iterative step, a linesearch algorithm often uses an inner loop running until some finite stopping criterion is satisfied. This can be expensive and time-consuming.

Remark that the method (PPM) is not easy to implement numerical computations in practise. This comes from the proceeding of a non-linear inequality in the method at each iteration, especially in huge-scale problems. In that case, the method (EGM) [13, 38] can be easily applied by using some tools of optimization. However, as mentioned above, the method (EGM) requires to proceed many values of cost bifunction at each iteration. This can affect the effectiveness of the method, if the feasible set and the cost bifunction have complicated structures. In this paper, we propose some new extragradient-like algorithms for solving a pseudomonotone problem (EP) with a different Lipschitz-type condition in a Banach space. Unlike the method EGM in [13, 38], our algorithms only require to proceed one value of the bifunction f at the current approximation. The first algorithm can work with the requirement that the Lipschitz-type constant needs to be known as an input parameter of the algorithm. The next two algorithms use new stepsize rules and they can be implemented more easily without the prior knowledge of the Lipschitz-type constant. A reason is that the two latter algorithms use variable stepsizes which are either chosen previously or updated at each iteration by a simple computation not depending on the Lipschitz-type constant. This makes the algorithms particularly interesting because the Lipschitz-type constant in general is unknown or difficult to estimate in huge-scale nonlinear problems. Some experiments are performed to illustrate the numerical behavior of the new algorithms.

The rest of this paper is organized as follows: Sect. 2 recalls some concepts and preliminary results used in the paper. Sect. 3 deals with proposing an extragradient-like algorithm with previously known constant, while Sect. 4 presents two different algorithms with new variable stepsize rules. In Sect. 5, some numerical experiments are provided. Finally, in Sect. 6, we present some conclusions and forthcoming works.

2 Preliminaries

Let E be a Banach space with the dual \(E^*\). Throughout this paper, for the sake of simplicity, the norms of E and \(E^*\) are denoted by the same symbol ||.||. The dual product of any pair \((x,f) \in E\times E^*\) is denoted by \(\left\langle x, f\right\rangle \).

Let us begin with several concepts and properties of a Banach space (see, e.g., [1, 14] for more details).

Definition 2.1

A Banach space E is called:

  1. (a)

    strictly convex if the unit sphere \(S_1(0) = \{x \in E: ||x||\le 1\}\) is strictly convex, i.e., the inequality \(||x+y|| <2\) holds for all \(x, y \in S_1(0), x \ne y ;\)

  2. (b)

    uniformly convex if for any given \(\epsilon >0\) there exists \(\delta = \delta (\epsilon ) >0\) such that, for all \(x,y \in E\) with \(\left\| x\right\| \le 1, \left\| y\right\| \le 1,\left\| x-y\right\| = \epsilon \), the inequality \(\left\| x+y\right\| \le 2(1-\delta )\) holds;

  3. (c)

    smooth if the limit

    $$\begin{aligned} \lim \limits _{t \rightarrow 0} \frac{\left\| x+ty\right\| -\left\| x\right\| }{t} \end{aligned}$$
    (1)

    exists for all \(x,y \in S_1(0)\);

  4. (d)

    uniformly smooth if the limit (1) exists uniformly for all \(x,y\in S_1(0)\).

The modulus of convexity of E is the function \(\delta _E:[0,2]\rightarrow [0,1]\) defined by

$$\begin{aligned} \delta _{E}(\epsilon )=\inf \Big \{1-\frac{\left\| x+y\right\| }{2}: \left\| x\right\| = \left\| y\right\| = 1,\left\| x-y\right\| =\epsilon \Big \},\;\;\forall \epsilon \in [0,2]. \end{aligned}$$

Note that E is uniformly convex if and only if \(\delta _{E}(\epsilon )>0\) for all \(0<\epsilon \le 2\) and \(\delta _{E}(0)=0\).

Let \(p>1\). A uniformly convex Banach space E is said to be p-uniformly convex if there exists some constant \(c>0\), such that

$$\begin{aligned} \delta _{E}(\epsilon )\ge c \epsilon ^p. \end{aligned}$$

It is well known that the functional spaces \(L^p\), \(l^p\) and \(W_m^p\) are p-uniformly convex when \(p>2\) and 2-uniformly convex when \(1< p \le 2\). Furthermore, any Hilbert space H is uniformly smooth and 2-uniformly convex.

The normalized duality mapping \(J:E\rightarrow 2^{E^*}\) is defined by

$$\begin{aligned} J(x)=\big \{f\in E^*: \left\langle x,f \right\rangle =\left\| x\right\| ^2=\left\| f\right\| ^2\big \},\;\; \forall x\in E. \end{aligned}$$

We have the following properties (see for instance [9]):

  1. (a)

      if E is a smooth, strictly convex, and reflexive Banach space, then the normalized duality mapping \(J:E\rightarrow 2^{E^*}\) is single-valued, one-to-one and onto;

  2. (b)

      if E is a reflexive and strictly convex Banach space, then \(J^{-1}\) is norm to weak \(^*\) continuous;

  3. (c)

      if E is a uniformly smooth Banach space, then J is uniformly continuous on each bounded subset of E;

  4. (d)

      Aa Banach space E is uniformly smooth if and only if \(E^*\) is uniformly convex.

Let E be a smooth, strictly convex, and reflexive Banach space. The Lyapunov functional \(\phi : E\times E \rightarrow [0, \infty )\) is defined by

$$\begin{aligned} \phi (x,y)=\left\| x\right\| ^2-2\left\langle x,Jy\right\rangle +\left\| y\right\| ^2,\;\;\forall x, y \in E. \end{aligned}$$

The followings are some characteristics of the Lyapunov functional \(\phi \):

  1. (a)

      For all \(x,\,y,\,z\in E\),

    $$\begin{aligned} \left( \left\| x\right\| -\left\| y\right\| \right) ^2\le \phi (x,y)\le \left( \left\| x\right\| +\left\| y\right\| \right) ^2. \end{aligned}$$
    (2)
  2. (b)

      For all \(x,\,y,\,z\in E\),

    $$\begin{aligned} \phi (x,y)=\phi (x,z)+\phi (z,y)+2\left\langle z-x,Jy-Jz\right\rangle . \end{aligned}$$
    (3)

Particularly, when \(x=y\), we have

$$\begin{aligned} \left\langle y-z,Jy-Jz\right\rangle =\frac{1}{2}\phi (y,z)+\frac{1}{2}\phi (z,y). \end{aligned}$$

We need the following lemmas in our analysis:

Lemma 2.1

[10] Let E be a 2-uniformly convex and smooth Banach space. Then there exists a \(\tau >0\) such that

$$\begin{aligned} \left\langle x-y,Jx-Jy\right\rangle \ge \tau ||x-y||^2,\;\;\forall x,y\in E. \end{aligned}$$

Lemma 2.2

[49] Let E be a 2-uniformly convex and smooth Banach space. Then there exists some number \(\alpha >0\), such that for all \(x,y\in E\),

$$\begin{aligned} \alpha ||x-y||^2\le \phi (x,y). \end{aligned}$$

The normal cone \(N_C\) of a set C at the point \( x \in C\) is defined by

$$\begin{aligned} N_C(x)=\left\{ x^*\in E^*:\left\langle x-y,x^*\right\rangle \ge 0,\; \forall y\in C\right\} . \end{aligned}$$

Let \(g:C\rightarrow \mathfrak {R}\) be a function. The subdifferential of g at x is defined by

$$\begin{aligned} \partial g(x)=\left\{ w\in E^*: g(y)-g(x)\ge \left\langle y-x,w\right\rangle ,\,\forall y\in C\right\} . \end{aligned}$$

Remark 2.1

It follows easily from the definitions of the subdifferential and \(\phi (x,y)\) that

$$\begin{aligned} \partial _1\phi (x,y):=\partial \phi (.,y)(x)=\left\{ 2(Jx-Jy)\right\} . \end{aligned}$$

Let \(g:C\rightarrow \mathfrak {R}\cup \left\{ +\infty \right\} \) be a convex, subdifferentiable and lower semi-continuous function. The \(\phi \)-proximal mapping associated with g for a parameter \(\lambda >0\) is defined by

$$\begin{aligned} \mathrm{prox}_{\lambda g}^\phi (x)=\arg \min \left\{ \lambda g(y)+\frac{1}{2}\phi (y,x):y\in C\right\} . \end{aligned}$$

Remark 2.2

A characteristic of the \(\phi \)-proximal mapping is that, if \(x=\mathrm{prox}^\phi _{\lambda g}(x)\), then

$$\begin{aligned} x\in \mathrm{Arg}\min \left\{ g(y):y\in C\right\} :=\left\{ x\in C: g(x)=\min _{y\in C}g(y)\right\} . \end{aligned}$$

Throughout this paper, we assume that E is a 2-uniformly convex and uniformly smooth Banach space and consider the following standard assumptions (see, [19]) imposed on the bifunction \(f:C\times C\rightarrow \mathfrak {R}\):

Condition A. We need the following assumptions:

  1. (A0)

    Either \(int(C)\ne \emptyset \) or, for each \(x\in C\), the function f(x, .) is continuous at a point in C;

  2. (A1)

      f is pseudomonotone on C, i.e., the following implication holds

    $$\begin{aligned} f(x,y) \ge 0 \; \Longrightarrow \; f(y,x) \le 0, \;\; \forall x,y \in C; \end{aligned}$$
  3. (A2)

    f satisfies the Lipschitz-type condition (LC) on C, i.e., there exists a positive constant L, such that

    $$\begin{aligned} f(x,y)+f(y,z)\ge f(x,z)-L||x-y|| ||y-z||,\;\;\forall x,y\in C; \end{aligned}$$
  4. (A3)

      \(\lim \sup _{n\rightarrow \infty }f(x_n,y)\le f(x,y)\) for each sequence \(x_n\rightharpoonup x \in C\) and \(y \in C\);

  5. (A4)

    \(f(x,\cdot )\) is convex and subdifferentiable on C for every \(x\in C\);

  6. (A5)

      The solution set EP(f, C) of the problem (EP) is nonempty.

Remark 2.3

It follows from hypotheses (A1)–(A2) that \(f(x,x)=0\) for all \(x\in C\). Indeed, by (A2), we obtain that \(f(x,x) \ge 0\) for all \(x \in C\). Thus, by (A1), we have \(f(x,x) \le 0\) for all \(x \in C\). Consequently, \(f(x,x) = 0\) for all \(x \in C\).

3 Modified extragradient-like algorithm with prior constant

In this section, we introduce a new algorithm for finding a solution of problem (EP) in a Banach space. The algorithm is constructed around the \(\phi \)-proximal mapping associated with cost bifunction f when the Lipschitz-type constant (or an estimate) of f is explicitly known. The algorithm is of the following form.

Algorithm 3.1

[Modified extragradient-like algorithm with prior constant]

Initialization: Choose \(x_0,\,y_0\in C\) and a sequence \(\left\{ \lambda _n\right\} \subset (0,+\infty )\), such that

$$\begin{aligned} 0<\lambda _*\le \lambda _n\le \lambda ^*<\frac{(\sqrt{2}-1)\alpha }{L}, \end{aligned}$$

where \(\alpha \) is defined in Lemma 2.2.

Iterative Steps:

Step 1. :

Compute

$$\begin{aligned} x_{n+1}=\mathrm{prox}_{\lambda _n f(y_n,.)}^\phi (x_n). \end{aligned}$$
Step 2. :

Compute

$$\begin{aligned} y_{n+1}=\mathrm{prox}_{\lambda _{n+1} f(y_n,.)}^\phi (x_{n+1}). \end{aligned}$$

Stopping criterion: If \(x_{n+1}=y_n=x_n\), then stop and \(x_n\) is a solution of problem (EP).

Remark 3.4

The sequence \(\left\{ \lambda _n\right\} \) of stepsizes in Algorithm 3.1 is taken previously which is bounded and separated from zero. This sequence depends on the Lipschitz-type constant L of bifunction f. This means that the information of L needs to be known and it is an input parameter of Algorithm 3.1.

Remark 3.5

From the definition of the \(\phi \)-proximal mapping, the two approximations \(x_{n+1}\) and \(y_{n+1}\) in Algorithm 3.1 can be rewritten under the form of optimization programs as

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n+1}=\arg \min \left\{ \lambda _n f(y_n,y)+\frac{1}{2}\phi (y,x_n):y\in C\right\} ,\\ y_{n+1}=\arg \min \left\{ \lambda _{n+1} f(y_n,y)+\frac{1}{2}\phi (y,x_{n+1}):y\in C\right\} . \end{array}\right. } \end{aligned}$$

Moreover, since \(\phi (x,y)=||x||^2-2\left\langle x,Jy\right\rangle +||y||^2\) and the fact

$$\begin{aligned} \arg \min \left\{ g(y)+a:y\in C\right\} =\arg \min \left\{ g(y):y\in C\right\} , \end{aligned}$$

we can write

$$\begin{aligned} {{\left\{ \begin{array}{ll} x_{n+1}=\arg \min \left\{ \lambda _n f(y_n,y)+\frac{1}{2}||y||^2-\left\langle y,Jx_n\right\rangle :y\in C\right\} ,\\ y_{n+1}=\arg \min \left\{ \lambda _{n+1} f(y_n,y)+\frac{1}{2}||y||^2-\left\langle y,Jx_{n+1}\right\rangle :y\in C\right\} . \end{array}\right. }} \end{aligned}$$

Observe that at each iteration in Algorithm 3.1, it requires to proceed only one value of bifunction f at the approximation \(y_n\). This is different from the extragradient method (EGM) in [13, 19, 38], where at each iteration,, the two values of f need to be computed.

Remark 3.6

In the case when \(E=H\) is a Hilbert space, then \(J=I\) and \(\phi (x,y)=||x-y||^2\). Thus Algorithm 3.1 reduces to the result in [18, Corollary 3.5]. In addition, if \(f(x,y)=\left\langle Ax,y-x\right\rangle \), where \(A:C \rightarrow H\) is an operator, our Algorithm 3.1 becomes Popov’s extragradient method in [37] for saddle point problems as well as variational inequality problems.

Remark 3.7

It follows immediately from Remark 2.2 that, if \(x_{n+1}=y_n=x_n\), then \(x_n\) is a solution of the problem (EP). Another stopping criterion can be used as: if \(y_{n+1}=y_n=x_{n+1}\), then stop and \(y_n\) is a solution of the problem (EP).

Lemma 3.1

The following estimates hold: for each \(n\ge 0\) and \(y\in C\),

  1. (a)

      \(\lambda _{n}(f(y_n,y)-f(y_n,x_{n+1}))\ge \left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle \).

  2. (b)

      \(\lambda _{n}(f(y_{n-1},y)-f(y_{n-1},y_n))\ge \left\langle y_n-y,Jy_n-Jx_n\right\rangle \).

Proof

(a) By the definitions of \(x_{n+1}\) and the \(\phi \)-proximal mapping, the iterate \(x_{n+1}\) can be rewritten as

$$\begin{aligned} x_{n+1}=\arg \min \left\{ \lambda _n f(y_n,y)+\frac{1}{2}\phi (y,x_n):y\in C\right\} . \end{aligned}$$

Thus, from the first-order necessary condition (see, Lemma 2.8 in [19]), we have

$$\begin{aligned} 0 \in \lambda _n \partial _2 f(y_n,x_{n+1})+\frac{1}{2}\partial _1\phi (x_{n+1},x_n)+N_C(x_{n+1}), \end{aligned}$$

which, by Remark 2.1, implies that

$$\begin{aligned} 0 \in \lambda _n \partial _2 f(y_n,x_{n+1})+Jx_{n+1}-Jx_n+N_C(x_{n+1}). \end{aligned}$$

Hence, there exists \(w_n \in \partial _2 f(y_n,x_{n+1})\) such that

$$\begin{aligned} -\lambda _n w_n +Jx_n -Jx_{n+1} \in N_C(x_{n+1}). \end{aligned}$$

It follows from the definition of \(N_C(x_{n+1})\) that

$$\begin{aligned} \left\langle x_{n+1}-y,-\lambda _n w_n +Jx_n -Jx_{n+1}\right\rangle \ge 0,\,\,\forall y \in C, \end{aligned}$$

or, equivalently

$$\begin{aligned} \lambda _n\left\langle y-x_{n+1},w_n\right\rangle \ge \left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle ,\,\,\forall y \in C. \end{aligned}$$

By \(w_n \in \partial _2 f(y_n,x_{n+1})\), we obtain

$$\begin{aligned} f(y_n,y) - f(y_n,x_{n+1}) \ge \left\langle y-x_{n+1},w_n\right\rangle ,\,\,\forall y \in C. \end{aligned}$$

Combining the last two inequalities, we come to the following one

$$\begin{aligned} \lambda _n\left( f(y_n,y) - f(y_n,x_{n+1})\right) \ge \left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle ,\,\,\forall y \in C. \end{aligned}$$

(b) By arguing similarly as the conclusion (a), from the definition of \(y_n\), we also obtain the desired conclusion. Lemma 3.1 is proved. \(\square \)

The following theorem ensures the convergence of Algorithm 3.1:

Theorem 3.1

Under Condition A, the sequences \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \) generated by Algorithm 3.1converge weakly to a solution of the problem (EP).

Proof

From Lemma 3.1 (b) with \(y=x_{n+1} \in C\), we derive

$$\begin{aligned} \lambda _{n}(f(y_{n-1},x_{n+1})-f(y_{n-1},y_n))\ge \left\langle y_n-x_{n+1},Jy_n-Jx_n\right\rangle . \end{aligned}$$
(4)

Combining relation (4) and Lemma 3.1(a), we obtain

$$\begin{aligned}&2\lambda _{n}f(y_n,y)+2\lambda _{n}(f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1})) \nonumber \\&\quad \ge 2\left\langle y_n-x_{n+1},Jy_n-Jx_n\right\rangle +2\left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle . \end{aligned}$$
(5)

Since f satisfies the Lipschit-type condition, there exists \(L>0\) such that

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1})\le L||y_n-y_{n-1}|| ||x_{n+1}-y_n||, \end{aligned}$$
(6)

which, together with the relation (5), implies that

$$\begin{aligned}&2\lambda _{n}f(y_n,y)+2\lambda _{n}L||y_n-y_{n-1}|| ||x_{n+1}-y_n||\nonumber \\&\quad \ge 2\left\langle y_n-x_{n+1},Jy_n-Jx_n\right\rangle +2\left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle ,\;\;\forall y\in C. \end{aligned}$$
(7)

Using the relation (3), it follows that, for all \(x^*\in EP(f,C)\),

$$\begin{aligned}&2\left\langle y_n-x_{n+1},Jy_n-Jx_n\right\rangle +2\left\langle x_{n+1}-x^*,Jx_{n+1}-Jx_n\right\rangle \nonumber \\&\quad =\phi (x_{n+1},y_n)+\phi (y_n,x_n)-\phi (x_{n+1},x_n)\nonumber \\&\qquad +\phi (x^*,x_{n+1})+\phi (x_{n+1},x_n)-\phi (x^*,x_n)\nonumber \\&\quad =\phi (x^*,x_{n+1})-\phi (x^*,x_n)+\phi (x_{n+1},y_n)+\phi (y_n,x_n). \end{aligned}$$
(8)

Substituting \(y=x^*\) into relation (7), and afterward combining the obtained inequality with relation (8), we obtain

$$\begin{aligned} \phi (x^*,x_{n+1})\le & {} \phi (x^*,x_n)-\phi (x_{n+1},y_n)-\phi (y_n,x_n)+2\lambda _{n}f(y_n,x^*)\nonumber \\&+2\lambda _{n}L||y_n-y_{n-1}|| ||x_{n+1}-y_n||. \end{aligned}$$
(9)

Applying the two inequalities \(2ab\le \frac{1}{\sqrt{2}}a^2+\sqrt{2}b^2\) and \((a+b)^2\le (2+\sqrt{2})a^2+\sqrt{2}b^2\), we obtain

$$\begin{aligned}&2||y_n-y_{n-1}|| ||x_{n+1}-y_n||\\&\quad \le \frac{1}{\sqrt{2}}||y_n-y_{n-1}||^2+\sqrt{2}||x_{n+1}-y_n||^2\\&\quad \le \frac{1}{\sqrt{2}}(||y_n-x_n||+||x_n-y_{n-1}||)^2+\sqrt{2}||x_{n+1}-y_n||^2\\&\quad \le \frac{1}{\sqrt{2}}\left( (2+\sqrt{2})||y_n-x_n||^2 +\sqrt{2}||x_n-y_{n-1}||^2\right) +\sqrt{2}||x_{n+1}-y_n||^2\\&\quad =(1+\sqrt{2})||y_n-x_n||^2+||x_n-y_{n-1}||^2+\sqrt{2}||x_{n+1}-y_n||^2. \end{aligned}$$

This together with Lemma 2.2 implies that

$$\begin{aligned} 2||y_n-y_{n-1}|| ||x_{n+1}-y_n||\le \frac{1+\sqrt{2}}{\alpha }\phi (y_n,x_n)+\frac{1}{\alpha } \phi (x_n,y_{n-1})+\frac{\sqrt{2}}{\alpha }\phi (x_{n+1},y_n). \end{aligned}$$
(10)

From the relations (9) and (10), we get

$$\begin{aligned} \phi (x^*,x_{n+1})\le & {} \phi (x^*,x_n)-\Big (1-\frac{\sqrt{2}\lambda _n L}{\alpha }\Big )\phi (x_{n+1},y_n)-\Big (1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha }\Big )\phi (y_n,x_n)\nonumber \\&+\frac{\lambda _n L}{\alpha }\phi (x_n,y_{n-1})+2\lambda _{n}f(y_n,x^*). \end{aligned}$$
(11)

Adding both sides of the inequality (11) to the term \(\frac{\lambda _{n+1} L}{\alpha }\phi (x_{n+1},y_n)\), we come to the following estimate:

$$\begin{aligned}&\phi (x^*,x_{n+1})+\frac{\lambda _{n+1} L}{\alpha }\phi (x_{n+1},y_n)\nonumber \\&\quad \le \phi (x^*,x_n)+\frac{\lambda _n L}{\alpha }\phi (x_n,y_{n-1})+2\lambda _{n}f(y_n,x^*)\nonumber \\&\qquad -\Big (1-\frac{\sqrt{2}\lambda _n L}{\alpha }-\frac{\lambda _{n+1} L}{\alpha }\Big )\phi (x_{n+1},y_n)-\Big (1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha }\Big )\phi (y_n,x_n). \end{aligned}$$
(12)

Since f is pseudomonotone and the fact \(f(x^*,y_n)\ge 0\), we obtain that \(f(y_n,x^*)\le 0\). Thus the relation (12) can be shortly rewritten as

$$\begin{aligned} a_{n+1}\le a_n-b_n, \end{aligned}$$
(13)

where

$$\begin{aligned} a_n=\phi (x^*,x_n)+\frac{\lambda _n L}{\alpha }\phi (x_n,y_{n-1}), \end{aligned}$$
$$\begin{aligned} b_n= \Big (1-\frac{\sqrt{2}\lambda _n L}{\alpha }-\frac{\lambda _{n+1} L}{\alpha }\Big )\phi (x_{n+1},y_n)+\Big (1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha }\Big )\phi (y_n,x_n). \end{aligned}$$

Since \(0<\lambda _*\le \lambda _n\le \lambda ^*<\frac{(\sqrt{2}-1)\alpha }{L}\), we obtain

$$\begin{aligned}&1-\frac{\sqrt{2}\lambda _n L}{\alpha }-\frac{\lambda _{n+1} L}{\alpha }\ge 1-\frac{(1+\sqrt{2})\lambda ^* L}{\alpha }>0. \end{aligned}$$
(14)
$$\begin{aligned}&1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha }\ge 1-\frac{(1+\sqrt{2})\lambda ^* L}{\alpha }>0. \end{aligned}$$
(15)

Thus, \(b_n\ge 0\) for each \(n\ge 1\). The relation (13) ensures that the limit of \(\left\{ a_n\right\} \) exists and \(\lim \nolimits _{n\rightarrow \infty }b_n=0\). This together with the relations (14), (15) and the definition of \(b_n\) implies that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\phi (x_{n+1},y_n) =\lim \limits _{n\rightarrow \infty }\phi (y_n,x_n)=0. \end{aligned}$$
(16)

Since the limit of \(\left\{ a_n\right\} \) exists, the sequence \(\left\{ \phi (x^*,x_n)\right\} \) is bounded. Thus, from the relation (2), we also get that the sequence \(\left\{ x_n\right\} \) is bounded. Moreover, from the relation (16) and Lemma 2.2, one derives that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||x_{n+1}-y_n||^2 =\lim \limits _{n\rightarrow \infty }||y_n - x_n||^2=0. \end{aligned}$$
(17)

Thus, since \(||x_{n+1}-x_n||^2\le 2||x_{n+1}-y_n||^2+2||y_n - x_n||^2\), we come to the following limit:

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||x_{n+1}-x_n||^2 =0. \end{aligned}$$
(18)

Since J is uniformly continuous on each bounded set, it follows from the relations (17) and (18) that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||Jx_{n+1}-Jx_n||^2 =\lim \limits _{n\rightarrow \infty }||Jy_n-Jx_n||^2 =0. \end{aligned}$$
(19)

Now, assume that \({\bar{x}}\) is a weak cluster point of \(\left\{ x_n\right\} \), i.e., there exists a subsequence \(\left\{ x_m\right\} \) of \(\left\{ x_n\right\} \) converging weakly to \({\bar{x}}\in C\). Since \(||x_n-y_n||\rightarrow 0\), we also have that \(y_m\rightharpoonup {\bar{x}}\) as \(m\rightarrow \infty \). It follows from the relation (7) that

$$\begin{aligned} f(y_{n},y)\ge & {} -L||y_n-y_{n-1}|| ||x_{n+1}-y_n||+ \frac{1}{\lambda _n}\left\langle y_n-x_{n+1},Jy_n-Jx_n\right\rangle \nonumber \\&+\frac{1}{\lambda _n}\left\langle x_{n+1}-y,Jx_{n+1}-Jx_n\right\rangle \nonumber \\\ge & {} -L||y_n-y_{n-1}|| ||x_{n+1}-y_n||- \frac{1}{\lambda _n}||Jy_n-Jx_n|| ||y_n-x_{n+1}||\nonumber \\&-\frac{1}{\lambda _n}||Jx_{n+1}-Jx_n|| ||x_{n+1}-y||,\;\;\forall y\in C. \end{aligned}$$
(20)

Passing to the limit in (20) as \(n=m\rightarrow \infty \) and using (A3), the relations (17), (19), we obtain

$$\begin{aligned} f({\bar{x}},y)\ge \limsup \limits _{m\rightarrow \infty }f(y_m,y)\ge 0,\;\;\forall y\in C, \end{aligned}$$

or \({\bar{x}}\) is a solution of the problem (EP).

In order to finish the proof, now, we prove the whole sequence \(\left\{ x_n\right\} \) converges weakly to \({\bar{x}}\). Indeed, assume that \({\widehat{x}}\) is another weak cluster point of \(\left\{ x_n\right\} \), i.e., there exists a subsequence \(\left\{ x_k\right\} \) of \(\left\{ x_n\right\} \) converging weakly to \({\widehat{x}}\) such that \({\bar{x}}\ne {\widehat{x}}\). As mentioned above, it follows that \({\widehat{x}}\) also belongs to the solution set EP(f, C). From the definition of the Lyapunov functional \(\phi (\cdot ,\cdot )\), we have

$$\begin{aligned} 2\left\langle x_n,J{\bar{x}}-J{\widehat{x}}\right\rangle =\phi (x_n,{\widehat{x}}) -\phi (x_n,{\bar{x}})+||{\bar{x}}||^2-||{\widehat{x}}||^2. \end{aligned}$$
(21)

Since the limit of \(\left\{ a_n\right\} \) exists and the relation (16), also it follows from the definition of \(a_n\) that the limit of \(\phi (x_n,x^*)\) exists for each \(x^*\in EP(f,C)\). Thus, from the relation (21), we find that the limit of \(\left\{ \left\langle x_n,J{\bar{x}}-J{\widehat{x}}\right\rangle \right\} \) exists and set

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\langle x_n,J{\bar{x}}-J{\widehat{x}}\right\rangle =K. \end{aligned}$$
(22)

Passing to the limit in (22) as \(n=m\rightarrow \infty \) and afterward as \(n=k\rightarrow \infty \), we obtain

$$\begin{aligned} \left\langle {\bar{x}},J{\bar{x}}-J{\widehat{x}}\right\rangle =\lim _{m\rightarrow \infty }\left\langle x_m,J{\bar{x}}-J{\widehat{x}}\right\rangle =K =\lim _{k\rightarrow \infty }\left\langle x_k,J{\bar{x}}-J{\widehat{x}}\right\rangle =\left\langle {\widehat{x}},J{\bar{x}}-J{\widehat{x}}\right\rangle . \end{aligned}$$

Thus we have

$$\begin{aligned} \left\langle {\bar{x}}-{\widehat{x}},J{\bar{x}}-J{\widehat{x}}\right\rangle =0, \end{aligned}$$

which, together with Lemma 2.1, implies that \({\bar{x}}={\widehat{x}}\). This completes the proof. \(\square \)

Remark 3.8

We have used hypothesis (A3), the sequentially weakly upper semi-continuity of bifunction f respect to the first argument, to prove the convergence of Algorithm 3.1. We can replace this hypothesis by a weaker one which was presented in [26, condition (2.1)] (also, see [26, Remark 2.1]).

4 Modified extragradient-like algorithms without prior constant

In this section, we introduce some new stepsize rules and propose two extragradient-like algorithms of explicit form for solving the problem (EP). The algorithms are explicit in the sense that the prior knowledge of the Lipschitz-type constant of the bifunction is not necessary, i.e., the Lipschitz-type constant is not an input parameter of the algorithms. Our algorithms thus can be more easily implemented.

The first algorithm in this section is of the following form:

Algorithm 4.1

[Modified extragradient-like algorithm with diminishing stepsizes]

Initialization: Choose \(x_0,\,y_0\in C\) and a sequence \(\left\{ \lambda _n\right\} \subset (0,+\infty )\) such that

$$\begin{aligned} \text{(H1) }\;\,\lim _{n\rightarrow \infty }\lambda _n=0,\,\quad \text{(H2) }\,\, \sum _{n=1}^\infty \lambda _n=+\infty . \end{aligned}$$

Iterative Steps:

Step 1.:

Compute

$$\begin{aligned} x_{n+1}=\mathrm{prox}_{\lambda _n f(y_n,.)}^\phi (x_n). \end{aligned}$$
Step 2.:

Compute

$$\begin{aligned} y_{n+1}=\mathrm{prox}_{\lambda _{n+1} f(y_n,.)}^\phi (x_{n+1}). \end{aligned}$$

Stopping criterion: If \(x_{n+1}=y_n=x_n\), then stop and \(x_n\) is a solution of problem (EP).

A sequence \(\left\{ \lambda _n\right\} \) satisfies the conditions (H1)-(H2) as \(\lambda _n=1/n^p\) with \(p\in (0,1]\). In order to get the convergence of Algorithm 4.1, we assume that the bifunction f satisfies the following condition:

Condition B. Conditions (A0), (A2), (A4) in Condition A hold, and

  1. (A6)

      f(., y) is hemi-continuous for each \(y \in C\);

  2. (A7)

      f is strongly pseudomonotone (SP), i.e., the following implication holds:

    $$\begin{aligned} \text{(SP) }\,\qquad f(x,y) \ge 0 \; \Longrightarrow \; f(y,x) \le -\gamma ||x-y||^2, \;\; \forall x,y \in C, \end{aligned}$$

where \(\gamma \) is some positive constant.

Under conditions (A4), (A6) and (A7), the problem (EP) has a unique solution. Let us denote this unique solution by \(x^\dagger \).

We have the following result:

Theorem 4.1

Under Condition B, the sequences \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \) generated by Algorithm 4.1converge strongly to the unique solution \(x^\dagger \) of the problem (EP).

Proof

Applying the strong pseudomonotonicity of f on the relation (11) with \(x^*=x^\dagger \) and repeating the proof of the relations (12) and (13), we obtain

$$\begin{aligned} {\widetilde{a}}_{n+1}\le {\widetilde{a}}_n-{\widetilde{b}}_n-2\gamma \lambda _n ||y_n-x^\dagger ||^2 \end{aligned}$$

or

$$\begin{aligned} {\widetilde{b}}_n+2\gamma \lambda _n ||y_n-x^\dagger ||^2\le {\widetilde{a}}_n-{\widetilde{a}}_{n+1}, \end{aligned}$$
(23)

where

$$\begin{aligned} {\widetilde{a}}_n= & {} \phi (x^\dagger ,x_n)+\frac{\lambda _n L}{\alpha }\phi (x_n,y_{n-1}),\nonumber \\ {\widetilde{b}}_n= & {} \Big (1-\frac{\sqrt{2}\lambda _n L}{\alpha }-\frac{\lambda _{n+1} L}{\alpha }\Big )\phi (x_{n+1},y_n)+\Big (1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha }\Big )\phi (y_n,x_n). \end{aligned}$$

Let \(\epsilon \in (0,1)\) be a fixed number. Since \(\lambda _n\rightarrow 0\), there exists \(n_0\ge 1\) such that

$$\begin{aligned}&1-\frac{\sqrt{2}\lambda _n L}{\alpha }-\frac{\lambda _{n+1} L}{\alpha }\ge \epsilon >0, \end{aligned}$$
(24)
$$\begin{aligned}&1-\frac{(1+\sqrt{2})\lambda _n L}{\alpha } \ge \epsilon >0. \end{aligned}$$
(25)

Thus \({\widetilde{b}}_n\ge 0\) for all \(n\ge n_0\). Letting \(N\ge n_0\), applying the inequality (23) for each \(n=n_0,\cdots , N\) and summing up these obtained inequalities, we obtain

$$\begin{aligned} \sum _{n=n_0}^N{\widetilde{b}}_n+2\gamma \sum _{n=n_0}^N\lambda _n ||y_n-x^\dagger ||^2\le {\widetilde{a}}_{n_0}-{\widetilde{a}}_{N+1}\le {\widetilde{a}}_{n_0}<+\infty . \end{aligned}$$

This is true for all \(N \ge n_0\). Thus we have

$$\begin{aligned} \sum _{n=n_0}^\infty {\widetilde{b}}_n+2\gamma \sum _{n=n_0}^\infty \lambda _n ||y_n-x^\dagger ||^2<+\infty , \end{aligned}$$
(26)

which implies that \(\lim _{n\rightarrow \infty }{\widetilde{b}}_n=0\) and

$$\begin{aligned} \sum _{n=n_0}^\infty \lambda _n ||y_n-x^\dagger ||^2<+\infty . \end{aligned}$$
(27)

Combining the relation (27) and the fact \(\sum _{n=n_0}^\infty \lambda _n=+\infty \), we derive

$$\begin{aligned} \liminf _{n\rightarrow \infty } ||y_n-x^\dagger ||^2=0. \end{aligned}$$
(28)

Since \(\lim _{n\rightarrow \infty }{\widetilde{b}}_n=0\), it follows from the relations (24), (25) and the definition of \({\widetilde{b}}\) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\phi (x_{n+1},y_n)=\lim _{n\rightarrow \infty }\phi (y_n,x_n)=0. \end{aligned}$$
(29)

Thus, from Lemma 2.2, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_{n+1}-y_n||=\lim _{n\rightarrow \infty }||y_n-x_n||=0. \end{aligned}$$
(30)

From the relations (28) and (30), we derive

$$\begin{aligned} \liminf _{n\rightarrow \infty } ||x_n-x^\dagger ||^2=0. \end{aligned}$$
(31)

Thus there exists a subsequence \(\left\{ x_{n_k}\right\} \) of \(\left\{ x_n\right\} \) such that \(\lim _{k\rightarrow \infty } ||x_{n_k}-x^\dagger ||^2=0\), i.e., \(x_{n_k}\rightarrow x^\dagger \) as \(k\rightarrow \infty \). Since J is uniformly continuous on each bounded set, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\phi (x^\dagger ,x_{n_k})= & {} \lim _{k\rightarrow \infty }\left( ||x^\dagger ||^2-2 \left\langle x^\dagger , Jx_{n_k}\right\rangle +||x_{n_k}||^2\right) \nonumber \\= & {} \lim _{k\rightarrow \infty }\left( ||x^\dagger ||^2-2 \left\langle x^\dagger , Jx^\dagger \right\rangle +||x^\dagger ||^2\right) \nonumber \\= & {} \phi (x^\dagger ,x^\dagger )=0. \end{aligned}$$
(32)

Moreover, by the definition, we see that the sequence \(\left\{ {\widetilde{a}}_n\right\} _{n\ge n_0}\) is bounded from below by zero. It follows from the relation (23) that the sequence \(\left\{ {\widetilde{a}}_n\right\} _{n\ge n_0}\) is non-increasing. Hence the limit of \(\left\{ {\widetilde{a}}_n\right\} _{n\ge n_0}\) exists. Thus, by the relation (29) and the definition of \({\widetilde{a}}_n\), we observe that the limit of \(\left\{ \phi (x^\dagger ,x_n)\right\} \) exists. This together with (32) implies

$$\begin{aligned} \lim _{n\rightarrow \infty } \phi (x^\dagger ,x_n)=0. \end{aligned}$$

Thus, from Lemma 2.2, we can conclude that \(x_n\rightarrow x^\dagger \) and thus \(y_n\rightarrow x^\dagger \). This completes the proof. \(\square \)

Next, we introduce the second algorithm in this section with a different stepsize rule. Unlike Algorithm 4.1, the next algorithm uses variable stepsizes which are updated at each iteration. The stepsizes are found by some cheap computations and without any linesearch procedure. The algorithm also does not require to previously know the Lipschitz-type constant. The convergence of the algorithm is obtained under the standard assumptions as in Theorem 3.1.

For the sake of simplicity, we use a notation \([t]_+\) and adopt a convention \(\frac{0}{0}\) as follows:

$$\begin{aligned}{}[t]_+=\max \{0,t\},\quad \frac{0}{0}=+\infty . \end{aligned}$$

The following is the algorithm in details:

Algorithm 4.2

[Modified extragradient-like algorithm with new stepsize rule]

Initialization: Choose \(x_0,\,y_{-1},\,y_0\in C\) and two numbers \(\lambda _0>0\), \(\mu \in (0,(\sqrt{2}-1)\alpha )\).

Iterative Steps:

Step 1. :

Compute

$$\begin{aligned} x_{n+1}=\mathrm{prox}_{\lambda _n f(y_n,.)}^\phi (x_n). \end{aligned}$$
Step 2. :

Compute

$$\begin{aligned} y_{n+1}=\mathrm{prox}_{\lambda _{n+1} f(y_n,.)}^\phi (x_{n+1}), \end{aligned}$$

   where

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \lambda _n, \frac{\mu ||y_n-y_{n-1}|| ||y_n-x_{n+1}||}{\left[ f(y_{n-1},x_{n+1})-f(y_{n-1},y_n) -f(y_n,x_{n+1})\right] _+}\right\} . \end{aligned}$$
(33)

Stopping criterion: If \(x_{n+1}=y_n=x_n\), then stop and \(x_n\) is a solution of problem (EP).

Remark 4.9

In fact, with the aforementioned convention, in the case when

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1})\le 0, \end{aligned}$$

then \(\lambda _{n+1}:=\lambda _n\). From the definition of \(\lambda _n\) in Algorithm 4.2, it is easy to see that \(\left\{ \lambda _n\right\} \) is non-increasing. Moreover, since f satisfies the Lipschitz-type condition, there exists some \(L>0\) such that

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1}) \le L||y_n-y_{n-1}|| ||y_n-x_{n+1}||. \end{aligned}$$

Thus, from the definition, we obtain immediately that \(\left\{ \lambda _n\right\} \) is bounded from below by \(\min \left\{ \lambda _0,\frac{\mu }{L}\right\} \). Thus there exists \(\lambda >0\) such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\lambda _n=\lambda >0. \end{aligned}$$
(34)

Remark 4.10

Unlike Algorithm 3.1, the sequence \(\left\{ \lambda _n\right\} \) in Algorithm 4.2 is sequentially computed at each iteration, from a starting number \(\lambda _0 >0\), by using simple formula (33). This sequence, as Remark 4.9, is also separated from zero. This is different to the stepsize rule in Algorithm 4.1 where \(\lambda _n \rightarrow 0\) as \(n \rightarrow \infty \) (see, condition (H1)).

Theorem 4.2

Under Condition A, the sequences \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \) generated by Algorithm 4.2converge weakly to a solution of the problem (EP).

Proof

We use some estimates in the proof of Theorem 3.1. From the definition of \(\lambda _{n+1}\), in the case when \(f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1})>0\), we have

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1})\le \frac{\mu }{\lambda _{n+1}}||y_n-y_{n-1}|| ||x_{n+1}-y_n||. \end{aligned}$$
(35)

It is emphasized here that the relation (35) also remains valuable when

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_n)-f(y_n,x_{n+1}) \le 0. \end{aligned}$$

Thus, by replacing the inequality (6) by the inequality (35) and repeating the proof of the relation (12), we obtain

$$\begin{aligned}&\phi (x^*,x_{n+1})+\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\phi (x_{n+1},y_n)\nonumber \\&\quad \le \phi (x^*,x_n)+\frac{\lambda _n \mu }{\lambda _{n+1}\alpha }\phi (x_n,y_{n-1})+2\lambda _{n}f(y_n,x^*)\nonumber \\&\qquad -\Big (1-\frac{\sqrt{2}\lambda _n \mu }{\lambda _{n+1}\alpha }-\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\Big )\phi (x_{n+1},y_n)-\Big (1-\frac{(1+\sqrt{2})\lambda _n \mu }{\lambda _{n+1}\alpha }\Big )\phi (y_n,x_n). \end{aligned}$$
(36)

Since f is pseudomonotone and \(f(x^*,y_n)\ge 0\), we have \(f(y_n,x^*)\le 0\). This together with the relation (36) implies that

$$\begin{aligned} {\bar{a}}_{n+1}\le {\bar{a}}_n-{\bar{b}}_n, \end{aligned}$$
(37)

where

$$\begin{aligned} {\bar{a}}_n= & {} \phi (x^*,x_n)+\frac{\lambda _n \mu }{\lambda _{n+1}\alpha }\phi (x_n,y_{n-1}), \\ {\bar{b}}_n= & {} \Big (1-\frac{\sqrt{2}\lambda _n \mu }{\lambda _{n+1}\alpha }-\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\Big )\phi (x_{n+1},y_n)+\Big (1-\frac{(1+\sqrt{2})\lambda _n \mu }{\lambda _{n+1}\alpha }\Big )\phi (y_n,x_n). \end{aligned}$$

From the relation (34) that \(\lambda _n \rightarrow \lambda >0\), we observe

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \Big (1-\frac{\sqrt{2}\lambda _n \mu }{\lambda _{n+1}\alpha }-\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\Big ) =\lim \limits _{n\rightarrow \infty }\Big (1-\frac{(1+\sqrt{2})\lambda _n \mu }{\lambda _{n+1}\alpha }\Big )=1-\frac{(1+\sqrt{2})\mu }{\alpha }>0. \end{aligned}$$

Thus, for a fixed number \(\epsilon \in \Big (0, 1-\frac{(1+\sqrt{2})\mu }{\alpha }\Big )\), there exists a number \({\bar{n}}_0\ge 1\) such that, for all \(n\ge {\bar{n}}_0\),

$$\begin{aligned} 1-\frac{\sqrt{2}\lambda _n \mu }{\lambda _{n+1}\alpha }-\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }>\epsilon>0,\quad 1-\frac{(1+\sqrt{2})\lambda _n \mu }{\lambda _{n+1}\alpha }>\epsilon >0. \end{aligned}$$
(38)

This implies that \({\bar{b}}_n\ge 0\) for all \(n\ge {\bar{n}}_0\). Using the relations (37), (38) and arguing similarly to the proof of Theorem 3.1, we also obtain the desired conclusion. This completes the proof. \(\square \)

Remark 4.11

We consider the case where f is strongly pseudomonotone. Using the relation (36) and taking into account the fact \(f(y_n,x^\dagger )\le -\gamma ||y_n-x^\dagger ||^2\), we derive

$$\begin{aligned}&\phi (x^\dagger ,x_{n+1})+\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\phi (x_{n+1},y_n)\\&\quad \le \phi (x^\dagger ,x_n) +\frac{\lambda _n \mu }{\lambda _{n+1}\alpha }\phi (x_n,y_{n-1}) -2\lambda _{n}\gamma ||y_n-x^\dagger ||^2\\&\qquad -\Big (1-\frac{\sqrt{2}\lambda _n \mu }{\lambda _{n+1}\alpha }-\frac{\lambda _{n+1} \mu }{\lambda _{n+2}\alpha }\Big )\phi (x_{n+1},y_n) -\Big (1-\frac{(1+\sqrt{2})\lambda _n \mu }{\lambda _{n+1}\alpha }\Big )\phi (y_n,x_n) \end{aligned}$$

for all \(n\ge {\bar{n}}_0\) or

$$\begin{aligned} {\bar{a}}_{n+1}\le {\bar{a}}_n-{\bar{b}}_n-2\lambda _{n}\gamma ||y_n-x^\dagger ||^2 \end{aligned}$$

for all \(n\ge {\bar{n}}_0\). This implies that the limit of \(\left\{ {\bar{a}}_n\right\} \) exists and

$$\begin{aligned} \sum \limits _{n=n_0}^\infty \left( {\bar{b}}_n+2\lambda _{n}\gamma ||y_n -x^\dagger ||^2\right) <+\infty . \end{aligned}$$

Thus we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }{\bar{b}}_n=\lim \limits _{n\rightarrow \infty } \lambda _{n}\gamma ||y_n-x^\dagger ||^2=0, \end{aligned}$$

which, together with the definition of \({\bar{b}}_n\), the relation (38) and the fact \(\lambda _n\rightarrow \lambda >0\), implies that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||y_n-x^\dagger ||^2=\lim \limits _{n\rightarrow \infty } \phi (x_{n+1},y_n)=\lim \limits _{n\rightarrow \infty }\phi (y_n,x_n)=0. \end{aligned}$$
(39)

The relation (39) and Lemma 2.2 ensure that \(||y_n-x_n||^2\rightarrow 0\). Thus the sequence \(\left\{ x_n\right\} \) converges strongly to the unique solution \(x^\dagger \) of the problem (EP). This conclusion is also true for Algorithm 3.1. The proof here is simpler than the one of Theorem 4.1 thanks to the relation (34), which is different from (H1) in Algorithm 4.1. Moreover, in this case, hypothesis (A3) is not necessary.

Remark 4.12

The sequences \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \) generated by Algorithm 3.1 or Algorithm 4.2 converge weakly to some solution of the problem (EP). As in [26, Theorem 3.3] (also, see [27, Theorem 5.2]), if we assume additionally that the bifunction f satisfies one of the following conditions:

  1. (a)

    f(x, .) is strongly convex for each \(x \in C\),

  2. (b)

    f(., y) is strongly concave for each \(y \in C\),

then \(\left\{ x_n\right\} \) and \(\left\{ y_n\right\} \) generated by Algorithm 3.1 (or Algorithm 4.2) converges strongly to the unique element of EP(f, C). We will prove this conclusion for Algorithm 3.1 (without the condition (A3)), and with Algorithm 4.2, it is done similarly. Indeed, note that in each case (a) or (b), the solution of problem (EP) is unique and denoded by \(x^\dagger \). Recall relation (20) that

$$\begin{aligned} f(y_{n},y)\ge & {} -L||y_n-y_{n-1}|| ||x_{n+1}-y_n||- \frac{1}{\lambda _n}||Jy_n-Jx_n|| ||y_n-x_{n+1}||\nonumber \\&-\frac{1}{\lambda _n}||Jx_{n+1}-Jx_n|| ||x_{n+1}-y||,\;\;\forall y\in C. \end{aligned}$$
(40)

Firstly, we prove the conclusion in the case (a). Take \(w_n=ty_n+(1-t)x^\dagger \) for some \(t \in (0,1)\) and all \(n\ge 0\). Since \(f(y_{n},.)\) is strongly convex, we get \(f(y_{n},w_n) \le tf(y_{n},y_n)+ (1-t)f(y_{n},x^\dagger )-t(1-t)||y_n-x^\dagger ||^2\). Thus, from the facts \(f(y_{n},y_n)=0\) and \(f(y_{n},x^\dagger ) \le 0\), we obtain

$$\begin{aligned} f(y_{n},w_n) \le -t(1-t)||y_n-x^\dagger ||^2. \end{aligned}$$
(41)

Substituting \(y=w_n\) into the relation (40), and combining the obtained inequality with the relation (41), we come to the following one

$$\begin{aligned} ||y_n-x^\dagger ||^2\le & {} \frac{L}{t(1-t)}||y_n-y_{n-1}|| ||x_{n+1}-y_n|| + \frac{1}{t(1-t)\lambda _n}||Jy_n-Jx_n|| ||y_n-x_{n+1}||\nonumber \\&\frac{1}{t(1-t)\lambda _n}||Jx_{n+1}-Jx_n|| ||x_{n+1}-w_n||. \end{aligned}$$
(42)

Passing to the limit in (42) as \(n \rightarrow \infty \) and using relations (17), (19), we obtain \(\lim \nolimits _{n\rightarrow \infty }||y_n-x^\dagger ||^2=0\). Thus \(\lim \nolimits _{n\rightarrow \infty }||x_n-x^\dagger ||^2=0\) because \(\lim \nolimits _{n\rightarrow \infty }||y_n-x_n||^2=0\). In order to get the conclusion in case (b), we also take \(w_n=ty_n+(1-t)x^\dagger \). Since \(f(.,x^\dagger )\) is strongly concave,

$$\begin{aligned} t f(y_n,x^\dagger )+(1-t)f(x^\dagger ,x^\dagger )+t(1-t)||y_n-x^\dagger ||^2 \le f(w_n,x^\dagger ) \le 0. \end{aligned}$$

Thus, \(f(y_n,x^\dagger ) \le -(1-t)||y_n-x^\dagger ||^2\), which together with relation (40) for \(y=x^\dagger \), implies that

$$\begin{aligned} ||y_n-x^\dagger ||^2\le & {} \frac{L}{1-t}||y_n-y_{n-1}|| ||x_{n+1}-y_n|| + \frac{1}{(1-t)\lambda _n}||Jy_n-Jx_n|| ||y_n-x_{n+1}||\nonumber \\&\frac{1}{(1-t)\lambda _n}||Jx_{n+1}-Jx_n|| ||x_{n+1}-x^\dagger ||. \end{aligned}$$
(43)

As case (a), from relation (43), we also obtain the desired conclusion. Remark that hypothesis (A3) is also not necessary here.

5 Numerical illustrations

Consider the space \(E=\mathfrak {R}^m\) with the norm \(||x||=\sqrt{\sum \nolimits _{i=1}^m x_i^2}\) which is generated by the inner product \(\left\langle x,y\right\rangle =\sum \nolimits _{i=1}^m x_i y_i\). The bifunction f is of the form:

$$\begin{aligned} f(x,y)=\left\langle Px+Qy+q,y-x\right\rangle +h(y)-h(x), \end{aligned}$$

where \(q\in E = \mathfrak {R}^m\) and \(P,\,Q\) are two matrices of order m such that Q is symmetric and positive semidefinite, \(Q-P\) is negative semidefinite, \(h(x)=\sum _{j=1}^m h_j(x_j)\) with

$$\begin{aligned} h_j(x_j)= & {} \max \left\{ {\bar{h}}_j(x_j),{\widehat{h}}_j(x_j)\right\} , \\ {\bar{h}}_j(x_j)= & {} {\bar{a}}_j x_j^2+{\bar{b}}_j x_j+{\bar{c}}_j, \\ {\widehat{h}}_j(x_j)= & {} {\widehat{a}}_j x_j^2+{\widehat{b}}_j x_j+{\widehat{c}}_j, \end{aligned}$$

where \({\bar{a}}_j,\,{\bar{b}}_j,\,{\bar{c}}_j,\,{\widehat{a}}_j,\,{\widehat{b}}_j,\,{\widehat{c}}_j\) are real numbers such that \({\bar{a}}_j>0,\,{\widehat{a}}_j>0\) for all \(j=1,\cdots ,m\).

The feasible set C is a box defined by \(C=\left\{ x\in \mathfrak {R}^m: x_{\min }\le x\le x_{\max }\right\} \), where

$$\begin{aligned} x_{\min }=(-2,-2,\cdots ,-2)^T,\quad x_{\max }=(5,5,\ldots ,5)^T. \end{aligned}$$

The bifunction f is generalized from the Nash-Cournot market equilibrium model in [11, 12, 38] with the nonsmooth price function. The bifunction f satisfies Condition A with the Lipschitz-type constant \(L=||Q-P||\). In this case, the normalized duality mapping \(J=I\), the Lyapunov functional \(\phi (x,y)=||x-y||^2\) and the number \(\alpha \) in Lemma 2.2 is 1.

All the optimization problems are effectively solved by the Optimization Toolbox in Matlab 7.0 and all the programs are performed on a PC Desktop Intel(R) Core(TM) i5-3210M CPU @ 2.50GHz RAM 2.00 GB.

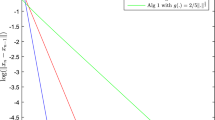
We illustrate the numerical behavior of the new algorithms involving Algorithm 3.1 (MEGM1), Algorithm 4.1 (MEGM2) and Algorithm 4.2 (MEGM3). For experiment, the data are randomly generated. The parameters are \(\lambda _n=0.4/L\) for MEGM1, \(\lambda _n=1/(n+1)\) for MEGM2, and \(\lambda _0=1\), \(\mu =0.4\) for MEGM3. The last two algorithms do not use the information of the Lipschitz-type constant L.

Observe a characteristic of a solution of the problem (EP) is that \(x\in EP(f,C)\) if and only if \(x=\mathrm{prox}^\phi _{\lambda f(x,\cdot )}(x)\) for some \(\lambda >0\). Then, in order to show the computational performance of the algorithms, we use the function

$$\begin{aligned} D(x)=||x-\mathrm{prox}^\phi _{\lambda f(x,\cdot )}(x)||^2. \end{aligned}$$

The numerical results are shown in Figures 1, 2, 3, 4. In each figure, the x-axis represents for the number of iterations while the y-axis is for the value of \(D(x_n)\) generated by each algorithm. In view of these figures, we see that Algorithm 4.1 is the worst, especially when the dimensional number of our problem increases.

Fig. 1
figure 1

Experiment in \(\mathfrak {R}^{50}\)

Full size image
Fig. 2
figure 2

Experiment in \(\mathfrak {R}^{100}\)

Full size image
Fig. 3
figure 3

Experiment in \(\mathfrak {R}^{120}\)

Full size image
Fig. 4
figure 4

Experiment in \(\mathfrak {R}^{150}\)

Full size image

6 Conclusions and forthcoming works

In this paper, we have presented three extragradient-like algorithms for solving an equilibrium problem involving a pseudomonotone bifunction with a Lipschitz-type condition in a 2 - uniformly convex and uniformly smooth Banach space. Some new stepsize rules have been introduced which allow the algorithms work with or without the prior knowledge of Lipschitz-type constant of bifunction. The paper can help us in the design and analysis of practical algorithms and enrich methods for solving equilibrium problems in Banach spaces. The numerical behavior of the new algorithms have been also demonstrated by some experiments on a test problem.

An open question arising in infinite dimensional spaces is how to obtain the strong convergence of Algorithm 3.1 (also, Algorithm 4.2) without the additional assumptions as in Remarks 4.11 and 4.12. Besides, how to develop our algorithms for finding a solution of an equilibrium problem which is also a solution of a fixed point problem. This problem is useful for some problems where their constraint are expressed as solution sets of fixed point problems. These are surely our future goals.