Finite-time $H_{\infty }$ control of uncertain fractional-order neural networks

Abstract

The problem of finite-time $H_{\infty }$ control for uncertain fractional-order neural networks is investigated in this paper. Using finite-time stability theory and the Lyapunov-like function method, we first derive a new condition for problem of finite-time stabilization of the considered fractional-order neural networks via linear matrix inequalities (LMIs). Then a new sufficient stabilization condition is proposed to ensure that the resulting closed-loop system is not only finite-time bounded but also satisfies finite-time $H_{\infty }$ performance. Three examples with simulations have been given to demonstrate the validity and correctness of the proposed methods.

1 Introduction

In recent years, fractional-order neural networks (FONNs) have received considerable attention due to its extensive applications in real life (Li 2018). Much interesting works with respect to FONNs have been considered. For example, some sufficient conditions on Lyapunov stability for FONNs with or without time delays were derived via LMIs using Lyapunov functional method (Wu et al. 2016; Zhang et al. 2017a, b, 2018; Yang et al. 2018). With the help of the fractional-order Razumikhin theorem and LMIs, the authors of the work (Chen et al. 2019) presented some delay-dependent criteria for asymptotic stability of a class of delayed fractional-order memristive neural networks. The authors of the work (Chen et al. 2015b) derived sufficient condition for global asymptotic stability of fractional memristor-based neural networks with time-varying delays by employing a comparison theorem for a class of linear fractional-order systems with time delay. Very recently, some interesting results on robust stability analysis have been investigated in Pahnehkolaei et al. (2019a, b) for delayed fractional quaternion-valued leaky integrator echo state neural networks. The problem of finite-time stability or finite-time boundedness for FONNs was investigated in Rakkiyappan et al. (2014), Yang et al. (2015), Chen et al. (2016), Wang et al. (2017), Dinh et al. (2017), Xu and Li (2019) and Rajivganthi et al. (2018). Some delay-independent sufficient conditions on finite-time stability problem for a class of nonlinear fractional-order systems were proposed in Chen et al. (2015a) based on using the technique of inequalities. Using linear matrix inequality approach and finite-time stability theory, the authors in Thuan et al. (2019) solved the problem of finite-time passivity for FONNs. The problem of finite-time guaranteed cost control for FONNs was considered in Thuan et al. (2018). Recently, problem of global nonfragile synchronization in finite time for fractional-order discontinuous neural networks with nonlinear growth activations functions has been studied in Peng et al. (2019) using nonsmooth analysis method combined with Lur’e Postnikov-type Lyapunov functional.

As we known, due to many reasons such as measurement errors, linear approximation, modeling inaccuracies, external noises and so on, disturbances are usually unavoidable in neural network systems. It is significant for scholars to study the disturbance attenuation performance via $H_{\infty }$ control approach. Some interesting and important results on finite-time $H_{\infty }$ control for integer order dynamical systems have been shown in recent years (Xiang and Xiao 2011; Xiang et al. 2012; Wang et al. 2015; Song and He 2015; Cheng et al. 2015; Guo et al. 2018; Ban et al. 2018; Lin et al. 2014; Liu and Lin 2015; Xie et al. 2017). The authors (Xiang and Xiao 2011) investigated problem of finite-time $H_{\infty }$ control for switched nonlinear discrete-time systems. Using the average dwell time approach, problems of finite-time stability analysis and $H_{\infty }$ stabilization for switched neutral systems were solved in Xiang et al. (2012) via LMIs. The results in Xiang et al. (2012) was improved in Wang et al. (2015) for both stable and unstable subsystems. Using Lyapunov–Krasovskii functional method, some sufficient conditions on finite-time boundedness of Markovian jump systems was shown in Cheng et al. (2015). For neural networks, some important results have been addressed. Using finite-time bounded average dwell time and LMI approaches, finite-time $H_{\infty }$ control for neutral-type uncertain switched neural networks with mixed time varying delays was investigated in Ali and Saravanan (2016). The authors (Baskar et al. 2018) investigated finite-time $H_{\infty }$ control problem for neutral Markovian jumping neural networks based on LMI approach. However, all the above results are limited to integer order systems. Noting that the analysis on finite-time stability of FONNs is more complex and difficult than that of integer-order neural networks due to the fact that fractional derivatives are nonlocal and have weakly singular kernels. This is the main reason that there are very few results on finite-time $H_{\infty }$ control for fractional-order systems. To the best of authors’ knowledge, so far, no result on the finite-time $H_{\infty }$ control for FONNs with uncertainties has been reported. This is the primary motivation of this work.

Motivated by the above discussions, the problem of finite-time $H_{\infty }$ control for FONNs with uncertainties is considered. The crucial novelty of this paper is stated as follows:

• (1) Using the Lyapunov-like function method and an important fractional derivative inequality of quadratic function, we derive a new stabilization criteria in terms of LMIs.

• (2) Based on the obtained finite-time stabilization result, the finite-time $H_{\infty }$ control problem is investigated for the concerned FONNs, and the corresponding state feedback controller design is given simultaneously.

• (3) New results are derived in the form of LMIs. They are less conservative and generalize those proposed in the literature.

  The organization of this paper is as follows. In Sect. 2, we summarize some definitions, notations and give auxiliary lemmas which will be used in the proof of the main results in the next section. We present our main results on finite-time stabilization and $H_{\infty }$ control problems for FONNs in Sect. 3. Three numerical examples are provided in Sect. 4 to illustrate the effectiveness of the proposed method.

Notation The following notations will be used in this paper: $\mathbb {R}^n$ denotes the n-dimensional linear vector space over the reals with the Euclidean norm $\Vert .\Vert$ given by $\Vert x\Vert = \sqrt{x_1^2 + \cdots + x_n^2}$, $x= (x_1, \ldots , x_n)^{\text {T}} \in \mathbb {R}^n;$$\mathbb {R}^{n\times m}$ denotes the space of $n\times m$ matrices. For a real matrix $A, \lambda _{\max }(A)$ and $\lambda _{\min }(A)$ denote the maximal and the minimal eigenvalue of A, respectively. A matrix P is positive definite $(P > 0)$ if $x^{\text {T}}Px> 0, \forall x \not = 0; P > Q$ means $P-Q > 0$. The symmetric term in a matrix is denoted by $*$. Let $\mathbb {S}_n^{+}$ denote the set of symmetric positive definite matrices in $\mathbb {R}^{n \times n}$.

2 Problem statement and preliminaries

To describe the model, some useful definitions and properties on Riemann–Liouville fractional integral and Caputo fractional derivative of order $\alpha > 0$ is recalled.

Definition 1

(Kilbas et al. 2006) The Riemann–Liouville fractional integral operator of order $\alpha > 0$ of a function f(t) is defined by

$$\begin{aligned} {}_{0}I_{t}^{\alpha }f(t) = \frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha - 1}f(s)\,{\text {d}}s, \end{aligned}$$

where $\varGamma (.)$ is the gamma function, $\varGamma (s) = \int \limits _{0}^{\infty }e^{-t}t^{s-1}{\text {d}}t, s > 0$.

Definition 2

(Kilbas et al. 2006) The Caputo fractional-order derivative of order $\alpha > 0$ for a function f(t) is defined as

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }f(t) = \frac{1}{\varGamma (n - \alpha )}\int _{0}^{t}\frac{f^{(n)}(s)}{(t-s)^{\alpha + 1 - n}}{\text {d}}s, \quad t \ge 0,\ n-1 < \alpha \le n, \end{aligned}$$

where n is a positive integer. In particular, when $0< \alpha < 1$, we have

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }f(t) = \frac{1}{\varGamma (1 - \alpha )}\int _{0}^{t}\frac{\dot{f}(s)}{(t-s)^{\alpha }}{\text {d}}s, \quad t \ge 0. \end{aligned}$$

The following are some useful properties about fractional-order calculus:

P1:

(Li and Deng 2007): for any constants $\lambda _1, \lambda _2$, and two functions f(t), g(t), we have

$$\begin{aligned} {}^C_{0}D_t^{\alpha }\left( \lambda _1 f(t) + \lambda _2 g(t)\right) = \lambda _1\,^C_{0}D_t^{\alpha }f(t) + \lambda _2\,^C_{0}D_t^{\alpha }g(t). \end{aligned}$$

P2:

(Li and Deng 2007): if $f(t) \in C^{n}([0, +\infty ), \mathbb {R})$ and $n-1< \alpha < n, (n \ge 1, n \in \mathbb {Z}^{+})$, then

$$\begin{aligned} {}_{0}I_{t}^{\alpha }\left( \,^C_{0}D_t^{\alpha }f(t)\right) = f(t) - \sum \limits _{i=0}^{n-1}\frac{t^i}{i!}f^{(i)}(0). \end{aligned}$$

In particular, when $0< \alpha < 1$, we have

$$\begin{aligned} {}_{0}I_{t}^{\alpha }\left( \,^C_{0}D_t^{\alpha }f(t)\right) = f(t) - f(0). \end{aligned}$$

P3:

(Lemma 2.3, pp. 73 in the work of Kilbas et al. 2006) If f(t) is continuous function, then we have

$$\begin{aligned} {}_{0}I_{t}^{\alpha }\left( \,_{0}I_{t}^{\beta }f(t)\right) = \, _{0}I_{t}^{\beta }\left( \,_{0}I_{t}^{\alpha }f(t)\right) =\, _{0}I_{t}^{\alpha +\beta }(f(t)), \forall t \ge 0. \end{aligned}$$

Consider a class of FONNs with parameter uncertainties described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}^C_{0}D_{t}^{\alpha }x(t) = -\left[ A + \varDelta A(t)\right] x(t) + [D + \varDelta D(t)]f(x(t))+ [W + \varDelta W(t)]\omega (t)\\ &{} \qquad \qquad \qquad \qquad + [B + \varDelta B(t)]u(t) , \quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}, \end{array}\right. } \end{aligned}$$

(1)

where $0<\alpha < 1$ is the fractional commensurate order of the system, $x(t) = \left( x_1(t), \ldots , x_n(t)\right) ^{\text {T}} \in \mathbb {R}^{n}$ is the state vector, $z(t) \in \mathbb {R}^{p}$ is the output vector, $\omega (t) \in \mathbb {R}^{q}$ is the disturbance input, $u(t) \in \mathbb {R}^m$ is the control vector, n is the number of neurals, $f(x(t)) = \left( f_1(x_1(t)), f_2(x_2(t)), \ldots , f_n(x_n(t))\right) ^{\text {T}} \in \mathbb {R}^n$ denotes the activation function, $A = {{\,\mathrm{diag}\,}}\{a_1, a_2, \ldots , a_n\} \in \mathbb {R}^{n \times n}$ is a positive diagonal matrix, $D \in \mathbb {R}^{n \times n}$ is the interconnection weight matrix, $W \in \mathbb {R}^{n \times q}, B \in \mathbb {R}^{n \times m}, C \in \mathbb {R}^{p \times n}$, are known real matrices, $x_0$ is the initial condition.

To obtain the main results on finite-time $H_{\infty }$ control of system (1), the following conditions are needed for further study.

Assumption 1

$$\begin{aligned} \varDelta A(t) = E_aF_a(t)H_a, \varDelta D(t) {=} E_dF_d(t)H_d, \varDelta W(t) = E_wF_w(t)H_w, \varDelta B(t) = E_bF_b(t)H_b, \end{aligned}$$

(2)

where $E_a, E_d, E_w, E_b, H_a, H_d, H_w, H_b$ are known real constant matrices of appropriate dimensions; $F_a(t), F_d(t), F_w(t), F_b(t)$ are unknown real-time-varying matrices satisfying $F_a^T(t)F_a(t) \le I, F_d^T(t)F_d(t) \le I, F_w^T(t)F_w(t) \le I, F_b^T(t)F_b(t) \le I, \forall t \ge 0$.

Assumption 2

The activation functions $f_i(.)$ are continuous, $f_i(0) = 0 \, (i = 1, \ldots , n)$, and satisfies Lipschitz condition on $\mathbb {R}$ with Lipschitz constant $l_i > 0:$

$$\begin{aligned} |f_i(\eta _1) - f_i(\eta _2)| \le l_i|\eta _1-\eta _2|,\quad \forall \eta _1,\quad \eta _2 \in \mathbb {R}. \end{aligned}$$

(3)

Especially, when $\eta _2 = 0$, we have

$$\begin{aligned} \Vert f_i(\eta _1)\Vert \le l_i |\eta _1|, \quad \forall \eta _1 \in \mathbb {R}. \end{aligned}$$

(4)

Assumption 3

The disturbance input $\omega (t) \in \mathbb {R}^{q}$ is satisfied

$$\begin{aligned} \exists \overline{d} > 0: \, \omega ^T(t)\omega (t) < \overline{d}, \forall t \in [0, T_f]. \end{aligned}$$

(5)

For system (1) and a given positive scalar $\gamma$ , the $H_{\infty }$ performance measure is

$$\begin{aligned} J = \int _{0}^{T_f}\left( z^T(t)z(t) - \gamma ^2 \omega ^T(t)\omega (t)\right) {\text {d}}t. \end{aligned}$$

The nominal unforced systems of system (1) can be written as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = -\left[ A + \varDelta A(t)\right] x(t) + [D + \varDelta D(t)]f(x(t))+ [W + \varDelta W(t)]\omega (t), t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}. \end{array}\right. } \end{aligned}$$

(6)

Definition 3

(Finite-time boundedness Ma et al. 2016) Given positive numbers $T_f, c_1, c_2 (c_1 < c_2), {\overline{d}}$, and a symmetric positive definite matrix $R \in \mathbb {R}^{n \times n}$. System (6) with the output $z(t) = 0$ is robustly finite-time bounded with respect to $(c_1, c_2, T_f, R, {\overline{d}})$ if $x_0^TRx_0 \le c_1 \Longrightarrow x^T(t)Rx(t) < c_2, \forall t \in [0, T_f]$, for all the disturbance input $\omega (t) \in \mathbb {R}^{q}$ satisfying Assumption 3.

Definition 4

(Finite-time $H_{\infty }$ performance Xiang et al. 2012; Lin et al. 2014) System (6) is said to be finite-time $H_{\infty }$ performance with respect to $(c_1, c_2, T_f, R, {\overline{d}})$ if the following conditions are satisfied:

• (i) When the input $z(t) \equiv 0$, system (6) is robustly finite-time bounded with respect to $(c_1, c_2, T_f, R, {\overline{d}})$.

• (ii) Under the zero initial condition, the following inequality holds

  $$\begin{aligned} J = \int _{0}^{T_f}\left( z^T(t)z(t) - \gamma ^2 \omega ^T(t)\omega (t)\right) {\text {d}}t < 0, \end{aligned}$$

  for all $\omega (t) \in L^2([0, T_f], \mathbb {R}^q)$.

In this paper, we are interested in designing the state feedback controller $u(t) = Kx(t)$ such that the following closed-loop system

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = \left[ -A + BK - \varDelta A(t) + \varDelta B(t)K \right] x(t) + [D + \varDelta D(t)]f(x(t))\\ &{} \qquad \qquad \qquad \quad + [W + \varDelta W(t)]\omega (t),\quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n} \end{array}\right. } \end{aligned}$$

(7)

is finite-time $H_{\infty }$ performance with respect to $(c_1, c_2, T_f, R, {\overline{d}})$.

Now, we recalled the following auxiliary lemmas which are essential to derive our main results in this paper.

Lemma 1

(Duarte-Mermoud et al. 2015) Let $x(t) \in \mathbb {R}^n$ be a vector of differentiable function. Then for any time instant $t \ge t_0$, the following relationship holds:

$$\begin{aligned} \frac{1}{2}\,^C_{t_0}D_{t}^{\alpha }\left( x^T(t)Px(t)\right) \le x^T(t)P\,\,^C_{t_0}D_{t}^{\alpha }x(t), \quad \forall \alpha \in (0, 1),\quad \forall t \ge t_0 \ge 0, \end{aligned}$$

where $P \in \mathbb {R}^{n \times n}$ is a symmetric positive definite matrix.

Lemma 2

(Boyd et al. 1994). Given constant matrices X, Y, Z with appropriate dimensions satisfying $Y = Y^T > 0, X = X^T$, then $X + Z^TY^{-1}Z < 0$ if and only if

$$\begin{aligned} \begin{bmatrix}X &{} Z^T \\ Z &{} -Y \end{bmatrix} < 0. \end{aligned}$$

3 Main results

First, we derive a result on finite-time boundedness for the closed-loop system (7). Let us denote

$$\begin{aligned} L&= {{\,\mathrm{diag}\,}}\{l_1, l_2, \ldots , l_n\}, \, \hat{X} = R^{-\frac{1}{2}}X^{-1}R^{-\frac{1}{2}}, \lambda _1 = \lambda _{\min }( \hat{X}), \lambda _2 = \lambda _{\max }( \hat{X}),\\ \varXi _{11}&= -AX - XA + BY + Y^TB^T + \varepsilon _1 E_aE_a^T + \varepsilon _2E_bE_b^T + E_dE_d^T + E_wE_w^T,\\ \varXi _{22}&= H_d^TH_d - I,\\ \varXi _{33}&= H_w^TH_w - \varepsilon I. \end{aligned}$$

Theorem 1

Assume that Assumptions 1, 2 and 3 are satisfied. Given positive scalars $c_1, c_2, \overline{d}, T_f$ and $R \in \mathbb {S}_n^{+}$. The closed-loop system (7) is finite-time bounded with respect to $(c_1, c_2, T_f, R, \overline{d})$ if there exist positive scalars $\varepsilon , \varepsilon _1, \varepsilon _2$, a matrix $X \in \mathbb {S}_n^{+}$, a matrix $Y \in \mathbb {R}^{m \times n}$ such that the following conditions hold:

$$\begin{aligned}&\begin{bmatrix} \varXi _{11} &{} D &{} W &{} XH_a^T &{} Y^TH_b^T &{} XL^T \\ * &{} \varXi _{22} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} \varXi _{33} &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} -\varepsilon _1 I &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -\varepsilon _2 I &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -I \end{bmatrix} < 0, \end{aligned}$$

(8a)

$$\begin{aligned}&\lambda _2c_1 + \frac{\varepsilon \overline{d}}{\varGamma (\alpha + 1)}T_f^{\alpha } < \lambda _1c_2. \end{aligned}$$

(8b)

Moreover, the state feedback controller is given by

$$\begin{aligned} u(t) = YX^{-1}x(t), \quad t \in [0, T_f]. \end{aligned}$$

Proof

Since X is symmetric positive definite matrix, $X^{-1}$ is also symmetric positive definite matrix. Consider the candidate Lyapunov function:

$$\begin{aligned} V(x(t)) = x^T(t)X^{-1}x(t). \end{aligned}$$

Using Lemma 2, we get the $\alpha$-order $(0< \alpha < 1)$ Caputo derivative of V(x(t)) along the trajectories of the closed-loop system (7) as follows:

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }V(x(t))&\le 2x^T(t)X^{-1}\,^C_{0}D_{t}^{\alpha }x(t) \nonumber \\&= x^T(t)\left[ -X^{-1}A - AX^{-1} + X^{-1}{} { BK} + K^TB^TX^{-1}\right] x(t)\nonumber \\&\quad - 2x^T(t)X^{-1}E_aF_a(t)H_ax(t) + 2x^T(t)X^{-1}E_bF_b(t)H_bKx(t)\nonumber \\&\quad + 2x^T(t)X^{-1}Df(x(t)) + 2x^T(t)X^{-1}E_dF_d(t)H_df(x(t)) \nonumber \\&\quad + 2x^T(t)X^{-1}W\omega (t) + 2x^T(t)X^{-1}E_wF_w(t)H_w\omega (t). \end{aligned}$$

(9)

The following estimates are obtained based on using Cauchy matrix inequality and Assumption 1:

$$\begin{aligned}&- 2x^T(t)X^{-1}E_aF_a(t)H_ax(t) \le \varepsilon _1 x^T(t)X^{-1}E_aE_a^TX^{-1}x(t) + \varepsilon _1^{-1}x^T(t)H_a^TH_ax(t), \nonumber \\&2x^T(t)X^{-1}E_bF_b(t)H_bKx(t) \le \varepsilon _2 x^T(t)X^{-1}E_bE_b^TX^{-1}x(t) + \varepsilon _2^{-1}x^T(t)K^TH_b^TH_bKx(t),\nonumber \\&2x^T(t)X^{-1}E_dF_d(t)H_df(x(t)) \le x^T(t)X^{-1}E_dE_d^TX^{-1}x(t) + f^T(x(t))H_d^TH_df(x(t)),\nonumber \\&2x^T(t)X^{-1}E_wF_w(t)H_w\omega (t) \le x^T(t)X^{-1}E_wE_w^TX^{-1}x(t) + \omega ^T(t)H_w^TH_w\omega (t). \end{aligned}$$

(10)

From Assumption 2, we have

$$\begin{aligned} 0 \le -f^T(x(t))f(x(t)) + x^T(t)L^TLx(t). \end{aligned}$$

(11)

Submitting inequalities (10) and (11) into (9), we obtain

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }V(x(t)) \le \xi ^T(t)\varOmega \xi (t) + \varepsilon \omega ^T(t)\omega (t), \end{aligned}$$

(12)

where

$$\begin{aligned} \xi (t) = \begin{bmatrix} x(t) \\ f(x(t)) \\ \omega (t) \end{bmatrix}, \, \varOmega = \begin{bmatrix} \varOmega _{11} &{} X^{-1}D &{} X^{-1}W \\ * &{} \varOmega _{22} &{} 0 \\ * &{} * &{} \varOmega _{33} \end{bmatrix}, \end{aligned}$$

with

$$\begin{aligned} \varOmega _{11}&= - X^{-1}A - AX^{-1} + X^{-1}BK + K^TB^TX^{-1} + \varepsilon _1 X^{-1}E_aE_a^TX^{-1} + \varepsilon _1^{-1}H_a^TH_a \\&\qquad + \varepsilon _2 X^{-1}E_bE_b^TX^{-1} + \varepsilon _2^{-1}K^TH_b^TH_bK + X^{-1}E_dE_d^TX^{-1} + X^{-1}E_wE_w^TX^{-1} + L^TL,\\ \varOmega _{22}&= H_d^TH_d - I,\\ \varOmega _{33}&= H_w^TH_w - \varepsilon I. \end{aligned}$$

Now, pre- and post-multiply both sides $\varOmega$ by $\mathscr {X} = {{\,\mathrm{diag}\,}}\{X, I, I\}$ and letting $K = YX^{-1}$, we have

$$\begin{aligned} \mathscr {X} \varOmega \mathscr {X} = \begin{bmatrix}\, \overline{\varOmega }_{11} &{} D &{} W\\ * &{} \varOmega _{22} &{} 0 \\ * &{} * &{} \varOmega _{33} \end{bmatrix}, \end{aligned}$$

(13)

where

$$\begin{aligned} \overline{\varOmega }_{11}&= -AX - XA + BY + Y^TB^T + \varepsilon _1 E_aE_a^T + \varepsilon _1^{-1}XH_a^TH_aX + \varepsilon _2 E_bE_b^T \\&\qquad + \varepsilon _2^{-1}Y^TH_b^TH_bY + E_dE_d^T + E_wE_w^T + XL^TLX. \end{aligned}$$

Note that $\varOmega < 0$ is equivalent to $\mathscr {X} \varOmega \mathscr {X} < 0$. Using the Schur complement Lemma (Lemma 2), we have $\mathscr {X} \varOmega \mathscr {X} < 0$ is equivalent to (8a). From (8a) and (12), we have

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }V(x(t)) \le \varepsilon \omega ^T(t)\omega (t), \quad \forall t \in [0, T_f]. \end{aligned}$$

(14)

Integrating with order $\alpha$ both sides of (14) from 0 to t$(0< t < T_f)$ and using Lemma 1, we have

$$\begin{aligned} x^T(t)X^{-1}x(t)&\le x^T(0)X^{-1}x(0) + \frac{\varepsilon }{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha - 1}\omega ^T(s)\omega (s){\text {d}}s \nonumber \\&\le x^T(0)X^{-1}x(0) + \frac{\varepsilon \overline{d}}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha - 1}{\text {d}}s \nonumber \\&\le x^T(0)X^{-1}x(0) + \frac{\varepsilon \overline{d}}{\varGamma (\alpha +1)}T_f^{\alpha }. \end{aligned}$$

(15)

On the other hand, the following conditions hold:

$$\begin{aligned} x^T(t)X^{-1}x(t)&= x^T(t)R^{\frac{1}{2}}\hat{X}R^{\frac{1}{2}}x(t) \ge \lambda _{\min }(\hat{X})x^T(t)Rx(t) = \lambda _1 x^T(t)Rx(t), \end{aligned}$$

(16)

$$\begin{aligned} x^T(0)X^{-1}x(0)&= x^T(0)R^{\frac{1}{2}}\hat{X}R^{\frac{1}{2}}x(0) \le \lambda _{\max }(\hat{X})x^T(0)Rx(0) = \lambda _2 x^T(0)Rx(0) \le \lambda _2 c_1. \end{aligned}$$

(17)

From (15), (16) and (17), we have

$$\begin{aligned} \lambda _1 x^T(t)Rx(t) \le V(x(t)) = x^T(t)X^{-1}x(t) \le \lambda _2c_1 + \frac{\varepsilon \overline{d}}{\varGamma (\alpha + 1)}T_f^{\alpha }. \end{aligned}$$

(18)

Condition (8b) implies that $x^T(t)Rx(t) < c_2$. Thus, the closed-loop system (7) with $z(t) \equiv 0$ is finite-time bounded with respect to $(c_1, c_2, T_f, R, \overline{d})$. $\square$

Remark 1

Many results have been reported in the literature for the problem of finite-time stability or finite-time boundedness for FONNs (Yang et al. 2015; Chen et al. 2016; Dinh et al. 2017; Xu and Li 2019). The approaches used in existing works mainly based on Hölder inequality, Bellman–Gronwall inequalities and Laplace transform (Yang et al. 2015; Chen et al. 2016; Wang et al. 2017), differential mean value theorem and contraction mapping principle (Rajivganthi et al. 2018). It should be mentioned here that the above approaches cannot be easily extended to finite-time stabilization problems. Using Lyapunov-like function method, Theorem 1 solves the problem of finite-time stabilization for uncertain fractional-order neural networks in terms of LMIs, which can be effectively solved using existing computationally effective convex algorithms.

To comparing with existing works in the literature, we consider the following linear fractional-order system:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = Ax(t) + W\omega (t) + Bu(t), \, t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}, \end{array}\right. } \end{aligned}$$

(19)

where $\alpha \in (0, 1)$, $x(t) \in \mathbb {R}^n$ is the state vector, $\omega (t) \in \mathbb {R}^{p}$ is the disturbance input, $u(t) \in \mathbb {R}^m$ is the control, $x_0$ is the initial condition, $A \in \mathbb {R}^{n \times n}, W \in \mathbb {R}^{n \times p}, B \in \mathbb {R}^{n \times m}$ are given real constant matrices. The disturbance input vector $\omega (t)$ satisfies the Assumption 3. Under state feedback controller $u(t) = Kx(t)$, the closed-loop systems of system (19) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = (A + BK)x(t) + W\omega (t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}. \end{array}\right. } \end{aligned}$$

(20)

Using the same techniques as in the proof of Theorem 1, we obtain the following corollary.

Corollary 1

Assume that Assumption 3 is satisfied. Given positive scalars $c_1, c_2, \overline{d}, T_f$ and $R \in \mathbb {S}_n^{+}$. The closed-loop system (20) is finite-time bounded with respect to $(c_1, c_2, T_f, R, \overline{d})$ if there exist a matrix $X \in \mathbb {S}_n^{+}$, a matrix $Y \in \mathbb {R}^{m \times n}$ such that the following conditions hold:

$$\begin{aligned}&\begin{bmatrix} AX + XA^T + BY + Y^TB^T &{} W \\ * &{} -I \end{bmatrix} < 0, \end{aligned}$$

(21a)

$$\begin{aligned}&\lambda _2c_1 + \frac{\overline{d}}{\varGamma (\alpha + 1)}T_f^{\alpha } < \lambda _1c_2, \end{aligned}$$

(21b)

where

$$\begin{aligned} \hat{X} = R^{-\frac{1}{2}}X^{-1}R^{-\frac{1}{2}}, \lambda _1 = \lambda _{\min }( \hat{X}), \lambda _2 = \lambda _{\max }( \hat{X}). \end{aligned}$$

Moreover, the state feedback controller is given by

$$\begin{aligned} u(t) = YX^{-1}x(t), \quad t \in [0, T_f]. \end{aligned}$$

Now, we consider the problem of finite-time $H_{\infty }$ control for system (1). Let us denote

$$\begin{aligned} L&= {{\,\mathrm{diag}\,}}\{l_1, l_2, \ldots , l_n\}, \, \hat{X} = R^{-\frac{1}{2}}X^{-1}R^{-\frac{1}{2}}, \lambda _1 = \lambda _{\min }( \hat{X}), \lambda _2 = \lambda _{\max }( \hat{X}),\\ \mathscr {M}_{11}&= - AX - XA + BY + Y^TB^T + \varepsilon _1 E_aE_a^T + \varepsilon _2 E_bE_b^T + E_dE_d^T + E_wE_w^T, \\ \mathscr {M}_{22}&= H_d^TH_d - I,\\ \mathscr {M}_{33}&= H_w^TH_w - \varepsilon I - \gamma ^2 I. \end{aligned}$$

Theorem 2

Assume that Assumptions 1, 2 and 3 are satisfied. Given positive scalars $c_1, c_2, \overline{d}, T_f$ and $R \in \mathbb {S}_n^{+}$. If there exist a matrix $X \in \mathbb {S}_n^{+}$, a matrix $Y \in \mathbb {R}^{m \times n}$, positive scalars $\varepsilon , \varepsilon _1, \varepsilon _2$ such that the following conditions hold:

$$\begin{aligned}&\begin{bmatrix} \mathscr {M}_{11} &{} D &{} W &{} XH_a^T &{} Y^TH_b^T &{} XL^T &{} XC^T\\ * &{} \mathscr {M}_{22} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} \mathscr {M}_{33} &{} 0 &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} -\varepsilon _1 I &{} 0 &{} 0 &{} 0\\ * &{} * &{} * &{} * &{} -\varepsilon _2 I &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -I &{} 0 \\ * &{} * &{} * &{} * &{} * &{} * &{} - I\end{bmatrix} < 0, \end{aligned}$$

(22a)

$$\begin{aligned}&\lambda _2c_1 + \frac{\varepsilon \overline{d}}{\varGamma (\alpha + 1)}T_f^{\alpha } < \lambda _1c_2, \end{aligned}$$

(22b)

then the closed-loop system (7) is finite-time bounded with $H_{\infty }$ performance $\gamma$ with respect to $(c_1, c_2, T_f, R, \overline{d})$ under state feedback controller is given by

$$\begin{aligned} u(t) = YX^{-1}x(t), \quad t \in [0, T_f]. \end{aligned}$$

Proof

When $z(t) \equiv 0$, (22a) and (22b) imply (8a) and (8b), respectively. Therefore, from Theorem 1, the closed-loop system is finite-time bounded with respect to $(c_1, c_2, T_f, R, \overline{d})$. To show the finite-time bounded with $H_{\infty }$ performance $\gamma$ of the closed-loop system (7), we choose the Lyapunov function as given in the proof of Theorem 1. Then we obtain the following estimate:

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }V(x(t)) + z^T(t)z(t) - \gamma ^2 \omega ^T(t)\omega (t) \le { \xi ^T(t)}\varPsi { \xi (t)}, \end{aligned}$$

(23)

where

$$\begin{aligned}&{ \xi (t)} = \begin{bmatrix} x(t) \\ f(x(t)) \\ \omega (t) \end{bmatrix}, \, \varPsi = \begin{bmatrix} \varPsi _{11} &{} X^{-1}D &{} X^{-1}W \\ * &{} \varPsi _{22} &{} 0 \\ * &{} * &{} \varPsi _{33} \end{bmatrix}, \\&\varPsi _{11} = - X^{-1}A - AX^{-1} + X^{-1}BK + K^TB^TX^{-1} + \varepsilon _1 X^{-1}E_aE_a^TX^{-1} + \varepsilon _1^{-1}H_a^TH_a \\&\qquad \quad + \varepsilon _2 X^{-1}E_bE_b^TX^{-1} + \varepsilon _2^{-1}K^TH_b^TH_bK + X^{-1}E_dE_d^TX^{-1}\\&\qquad \quad + X^{-1}E_wE_w^TX^{-1} + L^TL + C^TC,\\&\varPsi _{22} = H_d^TH_d - I,\\&\varPsi _{33} = H_w^TH_w - \varepsilon I -\gamma ^2 I. \end{aligned}$$

Now, pre- and post-multiply both sides $\varPsi$ by $\mathscr {X} = {{\,\mathrm{diag}\,}}\{X, I, I\}$ and letting $K = YX^{-1}$ and using Schur complement Lemma, we have $\varPsi < 0$ is equivalent to (22a). Hence, we get

$$\begin{aligned} {}^C_{0}D_{t}^{\alpha }V(x(t)) + z^T(t)z(t) - \gamma ^2 \omega ^T(t)\omega (t) < 0, \forall t \in [0, T_f]. \end{aligned}$$

(24)

Integrating (24) with respect to t from 0 to $T_f$, we have

$$\begin{aligned} {}_{0} I_{T_f}^{1}\,^C_{0}D_{T_f}^{\alpha }V(x(t)) + \int _{0}^{T_f}z^T(t)z(t){\text {d}}t - \int _{0}^{T_f}\gamma ^2 \omega ^T(t)\omega (t){\text {d}}t < 0. \end{aligned}$$

(25)

Using Properties P2 and P3 on fractional-order calculus, we obtain

$$\begin{aligned}&{}_{0} I_{T_f}^{1}\,^C_{0}D_{T_f}^{\alpha }V(x(t)) \\&\quad = \,_{0}I_{T_f}^{1-\alpha }\,_{0}I_{T_f}^{\alpha }\,^C_{0}D_{T_f}^{\alpha }V(x(t))\\&\quad = \,_{0}I_{T_f}^{1-\alpha }\left( \,_{0}I_{T_f}^{\alpha }\,^C_{0}D_{T_f}^{\alpha }V(x(t))\right) \\&\quad = \, _{0}I_{T_f}^{1-\alpha }\left( V(x(t)) - V((0))\right) = \, _{0}I_{T_f}^{1-\alpha }V(x(t)) - \,_{0} I_{T_f}^{1-\alpha }V(x(0)). \end{aligned}$$

On the other hand, we have

$$\begin{aligned} {}_{0} I_{T_f}^{1-\alpha }V(x(t)) = \frac{1}{\varGamma (1-\alpha )}\int _{0}^{T_f}(T_f -s)^{-\alpha }x^T(s)X^{-1}x(s){\text {d}}s \ge 0,\quad \forall T_f \ge 0. \end{aligned}$$

Under zero initial condition, we have the following estimate:

$$\begin{aligned} {}_{0} I_{T_f}^{1-\alpha }V(x(0)) = \frac{1}{\varGamma (1-\alpha )}\int _{0}^{T_f}(T_f -s)^{-\alpha }x^T(0)X^{-1}x(0){\text {d}}s = 0,\quad \forall T_f \ge 0. \end{aligned}$$

Hence, $\,_{0}I_{T_f}^{1}\,^C_{0}D_{T_f}^{\alpha }V(x(t)) \ge 0, \forall T_f \ge 0$ with zero initial condition. Therefore, we have

$$\begin{aligned} J = \int _{0}^{T_f}\left( z^T(t)z(t) - \gamma ^2 \omega ^T(t)\omega (t)\right) {\text {d}}t < 0. \end{aligned}$$

Hence, it can be concluded that the closed-loop system (7) is finite-time bounded with $H_{\infty }$ performance $\gamma$ with respect to $(c_1, c_2, T_f, R, \overline{d})$. $\square$

Remark 2

Based on MATLAB LMI Control Toolbox (Gahinet et al. 1995), we now propose an effective algorithm to solve the $H_{\infty }$ control problem for system (1).

Algorithm 1

Step 1 Solve LMI (22a) and obtain three positive scalars $\varepsilon , \varepsilon _1, \varepsilon _2$, a matrix $X \in \mathbb {S}_{n}^{+}$ and a matrix $Y \in \mathbb {R}^{m \times n}$.

Step 2 Check condition (22b) in Theorem 2. If they hold, enter Step 3; else return to Step 1.

Step 3 The state feedback gain matrix K can be designed as $K = YX^{-1}$. The $H_{\infty }$ control problem is solved.

Remark 3

In recent years, many results have been reported for finite-time $H_{\infty }$ control problem for integer-order dynamical systems with or without time delays (Xiang and Xiao 2011; Xiang et al. 2012; Wang et al. 2015; Song and He 2015; Cheng et al. 2015; Guo et al. 2018; Ban et al. 2018; Liu and Lin 2015; Xie et al. 2017). However, similar tools have not been developed for fractional-order systems. Since the fact that fractional derivatives are nonlocal and have weakly singular kernels (Chen et al. 2015b, 2019), these approaches could not be extended to FONNs easily. This is the main reason that there are very few results on finite-time $H_{\infty }$ control for FONNs. Thus, to find out new ways to cope with the problems is very challenging. Using LMI approach and using some auxiliary properties on fractional calculus, we solve the problem of finite-time $H_{\infty }$ control for Caputo FONNs with uncertainties for the first time. Hence, our results are new and novel.

In the case of system (1) without parameter uncertainties, that is, $\varDelta A(t) \equiv 0, \varDelta D(t) \equiv 0, \varDelta W(t) \equiv 0, \varDelta B(t) \equiv 0$, the model reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = -Ax(t) + Df(x(t))+ W\omega (t) + Bu(t) , \quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}. \end{array}\right. } \end{aligned}$$

(26)

Under state feedback controller $u(t) = Kx(t)$, the closed-loop systems of system (26) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{\alpha }x(t) = (-A + BK)x(t) + Df(x(t))+ W\omega (t), \quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{n}. \end{array}\right. } \end{aligned}$$

(27)

We can easily get the following result as the special case of Theorem 2.

Corollary 2

Assume that Assumptions 2 and 3 are satisfied. Given positive scalars $c_1, c_2, \overline{d}, T_f$ and $R \in \mathbb {S}_n^{+}$. If there exist a matrix $X \in \mathbb {S}_n^{+}$, a matrix $Y \in \mathbb {R}^{m \times n}$ and a positive scalar $\varepsilon$ such that the following conditions hold:

$$\begin{aligned}&\begin{bmatrix} \mathscr {N}_{11} &{} D &{} W &{} XL^T &{} XC^T \\ * &{} - I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\varepsilon I - \gamma ^2 I &{} 0 &{} 0 \\ * &{} * &{} * &{} - I &{} 0 \\ * &{} * &{} * &{} * &{} - I \end{bmatrix} < 0, \end{aligned}$$

(28a)

$$\begin{aligned}&\lambda _2c_1 + \frac{\varepsilon \overline{d}}{\varGamma (\alpha + 1)}T_f^{\alpha } < \lambda _1c_2, \end{aligned}$$

(28b)

where

$$\begin{aligned} \mathscr {N}_{11} = - AX - XA^T + BY + Y^TB^T, \end{aligned}$$

then the closed-loop system (27) is finite-time bounded with $H_{\infty }$ performance $\gamma$ with respect to $(c_1, c_2, T_f, R, \overline{d})$ under state feedback controller is given by

$$\begin{aligned} u(t) = YX^{-1}x(t), \quad t \in [0, T_f]. \end{aligned}$$

4 Numerical examples

We provide three numerical examples to demonstrate the effectiveness of the proposed method.

Example 1

Consider the following linear fractional-order system (Example 2 in the work of Ma et al. 2016):

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.8}x(t) = Ax(t) + W\omega (t) + Bu(t),\\ &{} x(0) = (x_1(0), x_2(0) )^T \in \mathbb {R}^{2}, \end{array}\right. } \end{aligned}$$

(29)

where

$$\begin{aligned} A = \begin{bmatrix} 7 &{} 3\\ 9 &{} 6 \end{bmatrix}, \, B = \begin{bmatrix} 3 &{} 0 \\ 0 &{} 4 \end{bmatrix}, \, W = \begin{bmatrix} 1 \\ 0.6 \end{bmatrix}, \end{aligned}$$

$x(t) = (x_1(t), x_2(t))^T \in \mathbb {R}^2, u(t) = (u_1(t), u_2(t)) \in \mathbb {R}^2, \omega (t) = \sin t \in \mathbb {R}$. The closed-loop system with a state feedback controller $u(t) = Kx(t)$ of system (29) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.8}x(t) = (A+BK)x(t) + W\omega (t),\\ &{} x(0) = (x_1(0), x_2(0) )^T \in \mathbb {R}^{2}. \end{array}\right. } \end{aligned}$$

(30)

To comparing our results with the existing work (Ma et al. 2016), we consider two cases:

Case I: Let us take $c_1 = 5, T_f = 0.1, R = I, \overline{d} = 1$. By Corollary 1, the closed-loop system (30) is finite-time bounded with respect to $(5, c_2, 0.1, I, 1)$ for any $c_2 \ge 5.9$ by state feedback controller is given by $u(t) = \begin{bmatrix} -2.500 &{} -4.9939 \\ 0.7454 &{} -1.6250 \end{bmatrix}x(t)$. Note that in Ma et al. (2016), the minimum value of $c_2$ is $c_{2\min } = 15$.

Case II: Let us take $c_1 = 5, c_2 = 15, R = I, \overline{d} = 1$. By Corollary 1, the closed-loop system (30) is finite-time bounded with respect to $(5, 15, T_f, I, 1)$ for any finite time $0< T_f < T_{f \max } = 6$ by state feedback controller is given by $u(t) = \begin{bmatrix} -2.500 &{} -4.9939 \\ 0.7454 &{} -1.6250 \end{bmatrix}x(t)$. Note that in Ma et al. (2016), the maximum value of $T_f$ is $T_{f \max } = 0.1$.

Therefore, our results may be wider applications than the results in the work of Ma et al. (2016).

Simulation results:

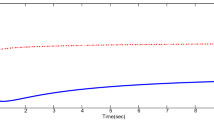
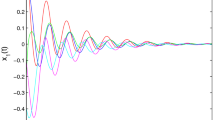
• Choosing the initial values $x(0) = (2, 2)^T \in \mathbb {R}^2, c_1 = 5, c_2 = 5.9, T_f = 0.1, R = I, \overline{d} = 1$. Figure 1 shows the evolution of the states $x_1(t), x_2(t)$ of the open-loop system. Figure 2 shows the evolution of the states $x_1(t), x_2(t)$ of the closed-loop system. Figures 3 and 4 show the state trajectory of $x^T(t)Rx(t)$ of the open-loop system and the closed-loop system, respectively. It is easy to see that the closed-loop system is finite-time bounded with respect to (5, 5.9, 0.1, I, 1).

• Choosing the initial values $x(0) = (2, 2)^T \in \mathbb {R}^2, c_1 = 5, c_2 = 15, T_f = 6, R = I, \overline{d} = 1$. Figures 5 and 6 show the state trajectory of $x^T(t)Rx(t)$ of the open-loop system and the closed-loop system, respectively. It is easy to see that the closed-loop system is finite-time bounded with respect to (5, 15, 6, I, 1).

Fig. 1

Trajectories of $x_1(t), x_2(t)$ of the open-loop system in Example 1

Fig. 2

Trajectories of $x_1(t), x_2(t)$ of the closed-loop system in Example 1

Fig. 3

Trajectory $x^T(t)Rx(t)$ of the open-loop system in Example 1

Fig. 4

Trajectory $x^T(t)Rx(t)$ of the closed-loop system in Example 1

Fig. 5

Trajectory $x^T(t)Rx(t)$ of the open-loop system in Example 1

Fig. 6

Trajectory $x^T(t)Rx(t)$ of the closed-loop system in Example 1

Example 2

Consider the following fractional-order neural networks:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.49}x(t) = -Ax(t) + Df(x(t)) + W\omega (t) + Bu(t), \, t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{2}, \end{array}\right. } \end{aligned}$$

(31)

where $x(t) = (x_1(t), x_2(t))^T \in \mathbb {R}^2, u(t) = (u_1(t), u_2(t)) \in \mathbb {R}^2, z(t) \in \mathbb {R}, \omega (t) = 0.01 \cos t \in \mathbb {R}$ and

$$\begin{aligned} A = \begin{bmatrix} 2 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \, D = \begin{bmatrix} 1 &{} 0.5 \\ 0 &{} 9 \end{bmatrix}, \, W = \begin{bmatrix}2 \\ 3 \end{bmatrix}, \, B = \begin{bmatrix} 4 &{} 0 \\ 0 &{} 5 \end{bmatrix}, \, C = \begin{bmatrix} 0.5&0.1 \end{bmatrix}. \end{aligned}$$

The closed-loop system with a state feedback controller $u(t) = Kx(t)$ of system (31) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.49}x(t) = (-A+BK)x(t) + Df(x(t)) + W\omega (t), \, t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{2}. \end{array}\right. } \end{aligned}$$

(32)

The activation function is choose as $f(x(t)) = (\tanh x_1(t), \tanh x_2(t))^T \in \mathbb {R}^2$. We have the activation function f(x(t)) satisfies Assumption 2 with $L = {{\,\mathrm{diag}\,}}\{1, 1\}$. Let $c_1 = 1, c_2 = 2, T_f = 5$ and matrix $R = I$. Using LMI Control Toolbox in MATLAB (Gahinet et al. 1995), we found that conditions (28a) and (28b) in Corollary 2 are satisfied with $\varepsilon = 128.2634$ and

$$\begin{aligned}&X = \begin{bmatrix} 7.6032 &{} 0.1030 \\ 0.1030 &{} 8.9494 \end{bmatrix}, \, Y = \begin{bmatrix} -29.5516 &{} 2.9265 \\ -0.2045 &{} -24.7392 \end{bmatrix}. \end{aligned}$$

According to Corollary 2, the closed-loop system (32) is finite-time bounded with respect to (1, 2, 5, I, 0.0001) with $H_{\infty }$ disturbance attenuation level $\gamma = 1.2598$ under state feedback controller is given by

$$\begin{aligned} u(t) = \begin{bmatrix} -3.8918 &{} 0.3718 \\ 0.0106 &{} -2.7645 \end{bmatrix}x(t), \, t \in [0, 5]. \end{aligned}$$

Simulation results: choosing the initial values $x(0) = (1, 0.9)^T \in \mathbb {R}^2, c_1 = 1, c_2 = 2, T_f = 5, R = I, \overline{d} = 0.0001$. Figures 7 and 8 show the state trajectory of $x^T(t)Rx(t)$ of the open-loop system and the closed-loop system, respectively. It is easy to see that the closed-loop system is finite-time bounded with respect to (1, 2, 5, I, 0.0001).

Fig. 7

The response of $x^T(t)Rx(t)$ of the open-loop system in Example 2

Fig. 8

The response of $x^T(t)Rx(t)$ of the closed-loop system in Example 2

Example 3

Consider the uncertain fractional-order neural networks:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.96}x(t) = -\left[ A + E_aF_a(t)H_a\right] x(t) + [D + E_dF_d(t)H_d]f(x(t))\\ &{} \qquad \qquad \qquad \qquad + [W + E_wF_w(t)H_w]\omega (t) + [B + E_bF_b(t)H_b]u(t) , \quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{2}, \end{array}\right. } \end{aligned}$$

(33)

where $x(t) = (x_1(t), x_2(t))^T \in \mathbb {R}^2$ and

$$\begin{aligned}&{ A = \begin{bmatrix} 0.5 &{} 0\\ 0 &{} 0.6 \end{bmatrix}}, \, E_a = \begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix}, \, H_a = \begin{bmatrix} 0.5&0.6 \end{bmatrix}, \, F_a(t) = \sin t, \\&D = \begin{bmatrix} 2 &{} 1 \\ 0 &{} 2.5 \end{bmatrix}, \, E_d = \begin{bmatrix} 0.5 \\ 0.8 \end{bmatrix}, \, H_d = \begin{bmatrix} 0.1&0.2 \end{bmatrix}, \, F_d(t) = \sin t,\\&W = \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \, E_w = \begin{bmatrix} 0.2 \\ 0.3 \end{bmatrix}, \, H_w = \begin{bmatrix} 0.1&0.3 \end{bmatrix}, \, F_w(t) = \cos t,\\&{ B = \begin{bmatrix} 2 &{} 0\\ 0 &{} 3 \end{bmatrix}}, \, E_b = \begin{bmatrix} 1\\ 2 \end{bmatrix}, \, { H_b = \begin{bmatrix} 0.4&0.5 \end{bmatrix}}, \, F_b(t) = \sin t, \, {C = \begin{bmatrix} 1&1 \end{bmatrix}}. \end{aligned}$$

The closed-loop system with a state feedback controller $u(t) = Kx(t)$ of system (33) is described by

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} ^C_{0}D_{t}^{0.96}x(t) = \left[ -A -E_aF_a(t)H_a + BK +E_bF_b(t)H_bK \right] x(t) \\ &{} \qquad \qquad \qquad + [D + E_dF_d(t)H_d]f(x(t)) + [W + E_wF_w(t)H_w]\omega (t), \quad t \ge 0,\\ &{} z(t) = Cx(t), \quad t \ge 0,\\ &{} x(0) = x_{0} \in \mathbb {R}^{2}. \end{array}\right. } \end{aligned}$$

(34)

The disturbance is chosen as $\omega (t) = \begin{bmatrix} 0.01 \sin t \\ 0.01 \cos t \end{bmatrix}$. Hence, the disturbance satisfying Assumption 3 with $\overline{d} = 0.0001$. The activation function is chosen as $f(x(t)) = (\tanh x_1(t), \tanh x_2(t))^T \in \mathbb {R}^2$. We have the activation function f(x(t)) satisfies Assumption 2 with $L = {{\,\mathrm{diag}\,}}\{1, 1\}$. Let $c_1 = 1, c_2 = 1.6, T_f = 10$ and matrix $R = I$. Given $\gamma = 1.2391$. Using LMI Control Toolbox in MATLAB (Gahinet et al. 1995), we found that conditions (22a) and (22b) in Theorem 2 are satisfied with $\varepsilon = 14.1493, \varepsilon _1 = 17.3301, \varepsilon _2 = 14.7246$ and

$$\begin{aligned} X = \begin{bmatrix} 2.0174 &{} -0.4117 \\ -0.4117 &{} 1.9908 \end{bmatrix}, \, Y = \begin{bmatrix} -10.8208 &{} -2.6891 \\ -10.4999 &{} -14.3833 \end{bmatrix}. \end{aligned}$$

According to Theorem 2, the closed-loop system (34) is finite-time bounded with respect to (1, 1.6, 10, I, 0.0001) with $H_{\infty }$ disturbance attenuation level $\gamma = 1.2391$ under state feedback controller is given by

$$\begin{aligned} u(t) = \begin{bmatrix} -5.8879 &{} -2.5683 \\ -6.9733 &{} -8.6667 \end{bmatrix}x(t), \, t \in [0, 10]. \end{aligned}$$

Simulation results: Choosing the initial values $x(0) = (1, 0.9)^T \in \mathbb {R}^2, c_1 = 1, c_2 = 1.6, T_f = 10, R = I, \overline{d} = 0.0001$. Figures 9 and 10 show the state trajectory of $x^T(t)Rx(t)$ of the open-loop system and the closed-loop system, respectively. It is easy to see that the closed-loop system is finite-time bounded with respect to (1, 1.6, 10, I, 0.0001).

Fig. 9

The response of $x^T(t)Rx(t)$ of the open-loop system in Example 3

Fig. 10

The response of $x^T(t)Rx(t)$ of the closed-loop system in Example 3

5 Conclusion

This paper considers finite-time $H_{\infty }$ control problem for uncertain fractional-order neural networks. We first derive a new condition for finite-time stabilization problem of the considered fractional-order neural networks in terms of LMIs. Next, by extending the concept of $H_{\infty }$ performance methods for integer-order neural networks to fractional-order neural networks and using Lyapunov-like function, a new sufficient condition is derived that ensure the resulting closed-loop system is not only finite-time bounded but also satisfies finite-time $H_{\infty }$ performance. Finally, three numerical examples have been shown to illustrate the effectiveness of the obtained results.