Reduced-Order $H_{\infty }$ Filtering with Intermittent Measurements for a Class of 2D Systems

Abstract

The problem of $H_{\infty }$ filter design for a class of 2D systems is solved here in the presence of intermittent measurements. Data dropouts are characterized using a stochastic variable satisfying the Bernoulli random binary distribution. Our attention is focused on the design of reduced-order $H_{\infty }$ filters such that the filtering error 2D stochastic system is robust mean-square asymptotically stable and fulfills a given $H_{\infty }$ disturbance attenuation level. We use a new formulation for a class of 2D system Fornasini–Marchesini (FM) models. A sufficient condition is established by means of the linear matrix inequalities (LMI) technique. The efficiency and viability of the proposed techniques and tools are demonstrated through a set of numerical examples.

1 Introduction

Design problems concerning multi-dimensional signals are currently being extensively studied in the scientific literature. In particular, two-dimensional (2D) signals and systems (Benzaouia et al. 2016) have been studied in many engineering fields, such as image processing, seismographic data processing, biomedical imaging processing, thermal processes, process control, and iterative learning control. This paper deals with general 2D signal processing: The investigation of 2D systems in signal processing applications has attracted considerable attention, and many important results have been reported to the literature. Among these results, the problem of the $H_{\infty }$ filtering for 2D linear systems, described by the Roesser and Fornasini–Marchesini (FM) models, has been investigated in Benzaouia et al. (2016), Boukili et al. (2014b, (2016a), Souza et al. (2010) and Hmamed et al. (2013) and references there in Du and Xie (2002), El-Kasri et al. (2012, (2013a), Kririm et al. (2015), Wang and Liu (2013), Tuan et al. (2002) and Li and Gao (2014, (2013), the $H_{\infty }$ filtering problem for 2D Takagi–Sugeno systems is addressed in Boukili et al. (2014a), the $H_{\infty }$ filtering problems for 2D systems with delays are studied in El-Kasri et al. (2013b), and stability and stabilization of 2D systems is studied in Benhayoun et al. (2015), Li and Gao (2012a), Duan et al. (2013) and Duan and Xiang (2014).

For the 2D systems with stochastic perturbation, the $H_{\infty }$ filtering problem is given in Gao et al. (2004) and Boukili et al. (2016b), the state estimation and of 2D stochastic systems is solved in Cui and Hu (2010), the Refs. Boukili et al. (2015) and Li et al. (2013) investigate the $H_{\infty }$ control for TS fuzzy with stochastic perturbation, and the problems of stability and robust $H_{\infty }$ control for 2D stochastic systems are given in Cui et al. (2011), Dai et al. (2013) and Duan et al. (2014).

In this context, we consider the problem of the $H_{\infty }$ filter for a class of 2D systems with intermittent measurements. This $H_{\infty }$ filtering and the related $H_{\infty }$ control problems have already been studied in Liu et al. (2009), Bu et al. (2014a, (2014b), Shi et al. (2012) and Gao et al. (2009). Following the literature, the phenomenon of missing measurements is assumed here to satisfy a Bernoulli random binary distribution. Our attention is focused on the design of reduced-order $H_{\infty }$ filters that make the filter error system robustly stable and provide a guaranteed $H_{\infty }$ performance. Some slack variables are included in the design, to provide extra degrees of freedom that makes it possible to optimize the filter, by minimizing the guaranteed $H_{\infty }$ performance. A sufficient condition is then established by means of an LMI technique, with formulas for the filter law design derived in parallel. Numerical examples are also given to illustrate the effectiveness of the proposed approach.

The remainder of this paper is organized as follows. In Sect. 2, the system description and the design objectives are presented. In Sect. 3, a sufficient condition guaranteeing robust mean-square asymptotic stability with $H_{\infty }$ performance for such 2D stochastic systems is derived by means of LMI technique. Using this result, the filter design problem is solved in Sect. 4. Examples are given in Sect. 5, and conclusions are drawn in Sect. 6.

Notations The superscript T stands for matrix transposition; the asterisk $*$ represents a term that is induced by symmetry; diag{$\ldots$} stands for a block-diagonal matrix; $\mathbb {E}\{.\}$ denotes the mathematical expectation. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.

The $l_{2}$ norm for a 2D signal w(i, j) is given by

$$\begin{aligned} \parallel w\parallel _{2}=\sqrt{\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }w^{T}(i,j)w(i,j)} \end{aligned}$$

where w(i, j) is said to be in the space $l_{2}\{[0,\infty ),[0,\infty )\}$ or $l_{2}$, for simplicity, if $\parallel w\parallel _{2}<\infty$. we define $\parallel e\parallel _{E}$ as

$$\begin{aligned} \parallel e\parallel _{E}=\sqrt{\mathbb {E}\left\{ \sum _{i=0}^{\infty }\sum _{j=0}^{\infty }e^{T}(i,j)e(i,j) \right\} .} \end{aligned}$$

2 Problem Formulation

Consider the uncertain 2D stochastic system described by the following Fornasini–Marchesini (FM) model (Liu et al. 2009):

$$\begin{aligned} x_{i+1,j+1}= & {} A_{1}(\alpha )x_{i,j+1}+A_{2}(\alpha )x_{i+1,j}\nonumber \\&+\,B_{1}(\alpha )w_{i,j+1}+ B_{2}(\alpha )w_{i+1,j}\nonumber \\ y_{i,j}= & {} C(\alpha ) x_{i,j}+ D(\alpha )w_{i,j}\nonumber \\ z_{i,j}= & {} L(\alpha ) x_{i,j}\;\;\;\; i,j=0,1,2,\ldots ,\nonumber \\ x_{0,j}= & {} \varphi (j)\;\forall j\ge 0\; \hbox {and} \; x_{i,0}=\phi (i) \;\forall i\ge 0 \end{aligned}$$

(1)

where $x_{i ,j}\in \mathbb {R}^{n}$ is the state vector, $z_{i,j}\in \mathbb {R}^{p}$ is the signal to be estimated, $y_{i ,j}\in \mathbb {R}^{m}$ is the measured output, and $w_{i ,j}\in \mathbb {R}^{q}$ is the disturbance input that belongs to $l_{2}\{[0,\infty ),[0,\infty )\}$. The system matrices

$$\begin{aligned} \varOmega (\alpha )= & {} \{A_{1}(\alpha ),\; A_{2}(\alpha ),\; B_{1}(\alpha ) ,\; B_{2}(\alpha ),\; C(\alpha ),\;D(\alpha ),\nonumber \\&\; L(\alpha )\}\in \varGamma \end{aligned}$$

(2)

have partially unknown parameters. $\varOmega (\alpha )$ is a given convex-bounded polyhedral domain, described by its s vertices as follows:

$$\begin{aligned} \varGamma =\left\{ \varOmega (\alpha )|\varOmega (\alpha )=\sum _{i=1}^{s}\alpha _{i}\varOmega _{i};\; \sum _{i=1}^{s}\alpha _{i}=1,\; \alpha _{i}\ge 0\right\} \end{aligned}$$

(3)

where

$$\begin{aligned} \varOmega _{i}:=(A_{1i},\; A_{2i},\; B_{1i},\; B_{2i},\; C_{i},\; D_{i},\; L_{i}) \end{aligned}$$

(4)

denotes the ith vertex of the polytope.

Throughout the paper, we make the following assumption on the boundary condition:

Assumption 2.1

Cui et al. (2011) The boundary condition is assumed to satisfy

$$\begin{aligned} \hbox {lim}_{k\mapsto \infty } \mathbb {E}\{\parallel x_{0,k}\parallel ^{2}\}=0,\;\; \hbox {lim}_{k\mapsto \infty } \mathbb {E}\{\parallel x_{k,0}\parallel ^{2}\}=0\nonumber \\ \parallel x_{0,k}\parallel ^{2}<\infty ,\;\;\;\; \parallel x_{k,0}\parallel ^{2}<\infty \;\; \hbox {for}\;\; \hbox {any}\;\; k\ge 1. \end{aligned}$$

(5)

In this paper, we consider the following $H_{\infty }$ filter to estimate $z_{i,j}$:

$$\begin{aligned} \hat{x}_{i+1,j+1}= & {} A_{f1}\hat{x}_{i,j+1}+A_{f2}\hat{x}_{i+1,j}+ B_{f1}\tilde{y}_{i,j+1}\nonumber \\&+\,B_{f2}\tilde{y}_{i+1,j}\nonumber \\ \hat{z}_{i,j}= & {} L_{f} \hat{x}_{i,j}\nonumber \\ \hat{x}_{0,j}= & {} 0 \;\;\;\forall j\ge 0\; \hbox {and} \; \hat{x}_{i,0}=0 \;\;\;\forall i\ge 0 \end{aligned}$$

(6)

where $\hat{x}_{i ,j}\in \mathbb {R}^{n_{f}}$ ($n_{f}\le n$) is the filter state vector (for reduced-order case $n_{f}<n$), $\tilde{y}_{i ,j}\in \mathbb {R}^{m}$ is the input of the filter, and $\hat{z}_{i,j}\in \mathbb {R}^{q}$ is the output of the filter. The matrices $A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$ and $L_{f}$ are the filter matrices to be determined.

It is assumed that measurements are intermittent, that is, the data may be lost during their transmission. In this case, the input $\tilde{y}_{i,j}$ of the filter is no longer equivalent to the output $y_{i,j}$ of the system (that is, $\tilde{y}_{i,j}\ne \theta _{i,j}y_{i,j}$). In this paper, the data loss phenomenon is modeled via a stochastic approach:

$$\begin{aligned} \tilde{y}_{i,j}=\theta _{i,j}y_{i,j} \end{aligned}$$

(7)

where the stochastic variable $\{\theta _{i,j}\}$ is a Bernoulli distributed white sequence taking the values of 0 and 1 with

$$\begin{aligned} \hbox {Prob}\{\theta _{i,j}=1\}= & {} \mathbf {E}\{\theta _{i,j}\}=\theta \\ \hbox {Prob}\{\theta _{i,j}=0\}= & {} 1-\mathbf {E}\{\theta _{i,j}\}=1-\theta \end{aligned}$$

and $\theta$ is a known positive scalar.

Based on this, we have

$$\begin{aligned} \hat{x}_{i+1,j+1}= & {} A_{f1}\hat{x}_{i,j+1}+A_{f2}\hat{x}_{i+1,j}+ B_{f1}\theta _{i,j+1}y_{i,j+1}\nonumber \\&+\,B_{f2}\theta _{i+1,j}y_{i+1,j}\nonumber \\ \hat{z}_{i,j}= & {} L_{f} \hat{x}_{i,j} \end{aligned}$$

(8)

From (1) and (8), the filtering error system can be expressed as follows is given by:

$$\begin{aligned} \xi _{i+1,j+1}= & {} \bar{A}_{1}(\alpha )\xi _{i,j+1}+\bar{A}_{2}(\alpha )\xi _{i+1,j}+ \bar{B}_{1}(\alpha )w_{i,j+1}\nonumber \\&+\,\bar{B}_{2}(\alpha )w_{i+1,j}+\bar{\theta }_{i,j+1}\bar{A}_{3}(\alpha )\xi _{i,j+1}\nonumber \\&+\,\bar{\theta }_{i+1,j}\bar{A}_{4}(\alpha )\xi _{i+1,j}+ \bar{\theta }_{i,j+1}\bar{B}_{3}(\alpha )w_{i,j+1} \nonumber \\&+\,\bar{\theta }_{i+1,j}\bar{B}_{4}(\alpha )w_{i+1,j}\nonumber \\ e_{i,j}= & {} \bar{L}(\alpha ) \xi _{i,j}\nonumber \\ \xi _{0,j}= & {} [\varphi (j)^{T},0^{T}]^{T},\;\;\;\; \xi _{i,0}= [\phi (i)^{T},0^{T}]^{T},\;\;\;\forall j,i\ge 0\nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned} \bar{A}_{1}(\alpha )= & {} \left[ \begin{array}{cc} A_{1}(\alpha ) &{} 0 \\ \theta B_{f1}C(\alpha ) &{} A_{f1} \\ \end{array} \right] , \bar{A}_{2}(\alpha )=\left[ \begin{array}{cc} A_{2}(\alpha ) &{} 0 \\ \theta B_{f2}C(\alpha ) &{} A_{f2} \\ \end{array} \right] \nonumber \\ \bar{A}_{3}(\alpha )= & {} \left[ \begin{array}{cc} 0 &{} 0 \\ B_{f1}C(\alpha ) &{} 0 \\ \end{array} \right] , \bar{A}_{4}(\alpha )=\left[ \begin{array}{cc} 0 &{} 0 \\ B_{f2}C(\alpha ) &{} 0 \\ \end{array} \right] ,\nonumber \\ \bar{B}_{1}(\alpha )= & {} \left[ \begin{array}{cc} B_{1}(\alpha ) \\ \theta B_{f1}D(\alpha ) \\ \end{array} \right] , \bar{B}_{2}(\alpha )=\left[ \begin{array}{cc} B_{2}(\alpha ) \\ \theta B_{f2}D(\alpha ) \\ \end{array} \right] ,\nonumber \\ \bar{B}_{3}(\alpha )= & {} \left[ \begin{array}{cc} 0 \\ B_{f1}D(\alpha ) \\ \end{array} \right] , \bar{B}_{4}(\alpha )=\left[ \begin{array}{cc} 0 \\ B_{f2}D(\alpha ) \\ \end{array} \right] ,\nonumber \\ \bar{L}(\alpha )= & {} \left[ \begin{array}{cc} L(\alpha ) &{} -L_{f} \\ \end{array} \right] , \bar{\theta }_{i,j} =\theta _{i,j}- \theta . \end{aligned}$$

$\xi _{i , j}=[x_{i , j}^{T}\;,\;\hat{x}_{i , j}^{T}]^{T}$ and $e_{i,j}= z_{i,j}-\hat{z}_{i,j}$. It is clear that

$$\begin{aligned} \mathbf {E}\{\bar{\theta }_{i,j}\}=0,\;\;\;\;\; \mathbf {E}\{\bar{\theta }_{i,j}\bar{\theta }_{i,j}\}=\theta (1-\theta ) \end{aligned}$$

(10)

Before giving the main results, it is necessary to introduce some lemmas that will be used for our derivations.

Lemma 2.2

(Theorem 1 in Liu et al. (2009)): Consider system in (1) and suppose the filter matrices ($A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$, $L_{f}$) in (6) are given. Then, the filtering error systems in (9) for any $\alpha \in \varGamma$ is mean-square asymptotically stable with an $H_{\infty }$ disturbance attenuation level bound $\gamma$ if there exist matrices $P(\alpha )>0$ and $Q(\alpha )>0$ satisfying

$$\begin{aligned} \varPsi\triangleq & {} \varXi _{1}^{T}P(\alpha )\varXi _{1}+\beta ^{2}\varXi _{2}^{T}P(\alpha )\varXi _{2}+\varXi _{3}^{T}\varXi _{3}+\varXi _{4}^{T}\varXi _{4}\nonumber \\&+\varXi _{5}<0 \end{aligned}$$

(11)

where

$$\begin{aligned} \varXi _{1}= & {} \left[ \begin{array}{cccc} \bar{A}_{1}(\alpha ) \;\;&{}\;\; \bar{A}_{2}(\alpha ) \;\;&{}\;\; \bar{B}_{1}(\alpha ) \;\;&{}\;\; \bar{B}_{2}(\alpha ) \\ \end{array} \right] ,\\ \varXi _{2}= & {} \left[ \begin{array}{cccc} \bar{A}_{3}(\alpha ) \;\;&{}\;\; \bar{A}_{4}(\alpha ) \;\;&{}\;\; \bar{B}_{3}(\alpha ) \;\;&{}\;\; \bar{B}_{4}(\alpha ) \\ \end{array} \right] ,\\ \varXi _{3}= & {} \left[ \begin{array}{cccc} \bar{L}(\alpha ) \;\;&{}\;\; 0 \;\;&{}\;\; 0 &{}\;\; 0\\ \end{array} \right] ,\\ \varXi _{4}= & {} \left[ \begin{array}{cccc} 0 \;\;&{}\;\; \bar{L}(\alpha ) \;\;&{}\;\; 0 &{}\;\; 0 \\ \end{array} \right] ,\\ \varXi _{5}= & {} diag\left\{ \begin{array}{cccc} Q(\alpha )-P(\alpha ), \;&{}\; -Q(\alpha ), \;&{}\; -\gamma ^{2}I, \;&{}\; -\gamma ^{2}I \\ \end{array} \right\} ,\\ \beta= & {} \sqrt{\theta (1-\theta )} \end{aligned}$$

Lemma 2.3

(Lemma 2.1 in Qiu et al. (2010)) Given matrices $\mathcal {W}=\mathcal {W}^{T}\in \mathbf {R}^{n\times n}$, $\mathcal {U}\in \mathbf {R}^{k\times n}$, $\mathcal {V}\in \mathbf {R}^{m\times n}$, the following LMI problem:

$$\begin{aligned} \mathcal {W}+\mathcal {U}^{T}\mathcal {X}^{T}\mathcal {V} +\mathcal {V}^{T}\mathcal {X}\mathcal {U}<0 \end{aligned}$$

(12)

is solvable with respect to the variable $\mathcal {X}$ if and only if

$$\begin{aligned} \mathcal {U}_{\perp }^{T}\mathcal {W} \mathcal {U}_{\perp }< & {} 0,\;\;\;\; when\;\;\;\; \mathcal {U}_{\perp }\ne 0, \;\; \mathcal {V}_{\perp }=0 \end{aligned}$$

(13)

$$\begin{aligned} \mathcal {V}_{\perp }^{T}\mathcal {W} \mathcal {V}_{\perp }< & {} 0, \;\;\;\; when\;\;\;\; \mathcal {U}_{\perp }=0,\;\; \mathcal {V}_{\perp }\ne 0 \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {U}_{\perp }^{T}\mathcal {W} \mathcal {U}_{\perp }<&0, \mathcal {V}_{\perp }^{T}\mathcal {W} \mathcal {V}_{\perp }<0, when \;\mathcal {U}_{\perp }, \mathcal {V}_{\perp }\ne 0 \end{aligned}$$

(15)

where $\mathcal {U}_{\perp }$ and $\mathcal {V}_{\perp }$ denote the right null spaces of $\mathcal {U}$ and $\mathcal {V}$, respectively.

Problem Description The filtering error system (9) is said to mean-square asymptotically stable with $H_{\infty }$ performance $\gamma$, if the following requirements are satisfied:

• 1. The filtering error system (9) with $w_{i,j}\equiv 0$ is mean-square asymptotically stable.

• 2. Under zero boundary condition, $\parallel \bar{e}_{i,j}\parallel _{E}<$ $\gamma \parallel \bar{w}_{i,j} \parallel _{2}$ is guaranteed for all non-zero $w\in l_{2}$ and a prescribed $\gamma >0$, where $\bar{e}_{i,j}=[e^{T}_{i,j}\;\; e^{T}_{i,j}]^{T}$ and $\bar{w}_{i,j}=[w^{T}_{i,j}\;\; w^{T}_{i,j}]^{T}$.

3 $H_{\infty }$ Filtering Analysis

In this section, the analysis of stability and performance of the $H_{\infty }$ filter is carried out. Thus, we temporarily assume that the filter matrices are known, to study the condition under which the filter error system is mean-square asymptotically stable with $H_{\infty }$-norm bounded. For this, Lemma 2.2 can be rewritten as follows:

Lemma 3.1

Consider the system in (1) and suppose that the filter matrices ($A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$, $L_{f}$) in (6) are given. Then, the filtering error systems in (9) for any $\alpha \in \varGamma$ is mean-square asymptotically stable and guarantees an $H_{\infty }$ disturbance attenuation level $\gamma$ if there exist matrices $P(\alpha )>0$ and $Q(\alpha )>0$ satisfying

$$\begin{aligned} \left[ \begin{array}{cccc} -\bar{P}(\alpha ) \;\;&{}\;\; 0 \;\;&{}\;\; \bar{P}(\alpha )A(\alpha ) \;\;&{}\;\; \bar{P}(\alpha )B(\alpha ) \\ * &{} -I &{} \tilde{L}(\alpha ) &{} 0 \\ * &{} * &{} -R(\alpha ) &{} 0 \\ * &{} * &{} * &{} -\gamma ^{2} I \\ \end{array} \right] <0 \end{aligned}$$

(16)

where

$$\begin{aligned} \bar{P}(\alpha )= & {} \left[ \begin{array}{cc} P(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; P(\alpha ) \\ \end{array} \right] , R(\alpha )=\left[ \begin{array}{cc} P(\alpha )-Q(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; Q(\alpha ) \\ \end{array} \right] ,\nonumber \\ A(\alpha )= & {} \left[ \begin{array}{cc} \bar{A}_{1}(\alpha ) \;&{}\;\bar{A}_{2}(\alpha ) \\ \beta \bar{A}_{3}(\alpha ) \;&{}\; \beta \bar{A}_{4}(\alpha ) \\ \end{array} \right] = \varUpsilon ^{T}\left[ \begin{array}{cc} \breve{A}(\alpha ) \;&{}\; 0 \\ \varLambda B_{f}\breve{C}(\alpha ) \;&{}\; A_{f} \\ \end{array} \right] \varUpsilon ,\nonumber \\ B(\alpha )= & {} \left[ \begin{array}{cc} \bar{B}_{1}(\alpha ) \;&{}\; \bar{B}_{2}(\alpha ) \\ \beta \bar{B}_{3}(\alpha ) \;&{}\; \beta \bar{B}_{4}(\alpha ) \\ \end{array} \right] = \varUpsilon ^{T}\left[ \begin{array}{c} \breve{B}(\alpha ) \\ \varLambda B_{f}\breve{D}(\alpha ) \\ \end{array} \right] ,\\ \tilde{L}(\alpha )= & {} \left[ \begin{array}{cc} \bar{L}(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; \bar{L}(\alpha ) \\ \end{array} \right] = \left[ \begin{array}{cc} \breve{L}(\alpha ) \;&{}\; -\breve{L}_{f} \\ \end{array} \right] \varUpsilon .\nonumber \end{aligned}$$

(17)

and

$$\begin{aligned} \breve{A}(\alpha )= & {} \left[ \begin{array}{cc} A_{1}(\alpha ) \;&{}\; A_{2}(\alpha ) \\ 0 \;&{}\; 0 \\ \end{array} \right] ,\; \breve{B}(\alpha )=\left[ \begin{array}{cc} B_{1}(\alpha ) \;&{}\; B_{2}(\alpha ) \\ 0 \;&{}\; 0 \\ \end{array} \right] ,\nonumber \\ \breve{D}(\alpha )= & {} \left[ \begin{array}{cc} D(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; D(\alpha ) \\ \end{array} \right] ,\; \breve{L}(\alpha )=\left[ \begin{array}{cc} L(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; L(\alpha ) \\ \end{array} \right] ,\\ A_{f}= & {} \left[ \begin{array}{cc} A_{f1} \;&{}\; A_{f2} \\ 0 \;&{}\; 0 \\ \end{array} \right] , B_{f}=\left[ \begin{array}{cc} B_{f1} \;&{}\; B_{f2} \\ B_{f1} \;&{}\; B_{f2} \\ \end{array} \right] , \varLambda =\left[ \begin{array}{cc} \theta \;&{}\; 0 \\ 0 \;&{}\; \beta \\ \end{array} \right] ,\nonumber \\ \breve{L}_{f}= & {} \left[ \begin{array}{cc} L_{f} \;&{}\; 0 \\ 0 \;&{}\; L_{f} \\ \end{array} \right] ,\;\; \breve{C}(\alpha )=\left[ \begin{array}{cc} C(\alpha ) \;&{}\; 0 \\ 0 \;&{}\; C(\alpha ) \\ \end{array} \right] .\nonumber \end{aligned}$$

(18)

$$\begin{aligned} P(\alpha )= & {} \left[ \begin{array}{cc} P_{1}(\alpha ) &{} P_{2}(\alpha ) \\ P_{2}^{T}(\alpha ) &{} P_{3}(\alpha ) \\ \end{array} \right] , Q(\alpha )=\left[ \begin{array}{cc} Q_{1}(\alpha ) &{} Q_{2}(\alpha ) \\ Q_{2}^{T}(\alpha ) &{} Q_{3}(\alpha ) \\ \end{array} \right] ,\nonumber \\ \varUpsilon= & {} \left[ \begin{array}{cccc} I \;\;&{}\;\; 0 \;\;&{}\;\; 0 \;\;&{}\;\; 0 \\ 0 &{} 0 &{} I &{} 0 \\ 0 &{} I &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} I \\ \end{array} \right] \end{aligned}$$

(19)

Proof 3.2

By the Schur complement, the relation (16) is equivalent to the relation (18) given in Liu et al. (2009), which is equivalent to the relation (11). Consequently, (16) and (11) are equivalent, completing the proof. $\square$

Based on this, we present the following new result.

Theorem 3.3

Consider the system in (1) and suppose that the filter matrices ($A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$, $L_{f}$) in (6) are given. Then, the filtering error system in (9) for any $\alpha \in \varGamma$ is mean-square asymptotically stable and guarantee an $H_{\infty }$ disturbance attenuation level $\gamma$ if there exist matrices $K(\alpha )$, $E(\alpha )$, $F(\alpha )$, $S(\alpha )$ and symmetric positive definite matrices $\bar{P}(\alpha )$ and $R(\alpha )$ satisfying

$$\begin{aligned} \varXi =\left[ \begin{array}{cccc} \varTheta _{1}(\alpha ) \;&{}\; \varTheta _{2}(\alpha ) \;&{}\; \varTheta _{3}(\alpha ) \;&{}\; -F^{T}(\alpha ) \\ * &{} \varTheta _{4}(\alpha ) &{} \varTheta _{5}(\alpha ) &{} \varTheta _{6}(\alpha ) \\ * &{} * &{} \varTheta _{7}(\alpha ) &{} B^{T}(\alpha )F^{T}(\alpha ) \\ * &{} * &{} * &{} -I \\ \end{array} \right] <0, \end{aligned}$$

(20)

where

$$\begin{aligned} \varTheta _{1}(\alpha )= & {} \bar{P}(\alpha )-E(\alpha )-E^{T}(\alpha );\\ \varTheta _{2}(\alpha )= & {} E(\alpha )A(\alpha )-K^{T}(\alpha );\\ \varTheta _{3}(\alpha )= & {} E(\alpha )B(\alpha )-S^{T}(\alpha );\\ \varTheta _{4}(\alpha )= & {} -R(\alpha ) + K(\alpha )A(\alpha ) +A^{T}(\alpha )K^{T}(\alpha );\\ \varTheta _{5}(\alpha )= & {} K(\alpha )B(\alpha )+A^{T}(\alpha )S^{T}(\alpha );\\ \varTheta _{6}(\alpha )= & {} A^{T}(\alpha )F^{T}(\alpha )+\tilde{L}^{T}(\alpha );\\ \varTheta _{7}(\alpha )= & {} B^{T}(\alpha )S^{T}(\alpha )+S(\alpha )B(\alpha )-\gamma ^{2} I. \end{aligned}$$

In addition, $\bar{P}(\alpha )$, $R(\alpha )$, $A(\alpha )$, $B(\alpha )$ and $\tilde{L}(\alpha )$ are given in (17).

Proof 3.4

To show the equivalence between Theorem 3.3 and Lemma 3.1, define the following matrices:

$$\begin{aligned} \mathcal {U}= & {} \left[ \begin{array}{ccccc} -I \;\;&{}\;\; A(\alpha ) \;\;&{}\;\; B(\alpha ) \;\;&{}\;\; 0 \\ \end{array} \right] ;\; \;\;\;\mathcal {V}=I; \end{aligned}$$

(21)

$$\begin{aligned} \mathcal {W}= & {} \left[ \begin{array}{cccc} \bar{P}(\alpha )&{} 0 &{} 0&{} 0 \\ 0 &{} -R(\alpha ) &{} 0 &{} \tilde{L}^{T}(\alpha ) \\ 0 &{} 0 &{} -\gamma ^{2}I &{} 0 \\ 0 &{} \tilde{L}(\alpha ) &{}0 &{} -I \\ \end{array} \right] ;\; \mathcal {X}=\left[ \begin{array}{c} E(\alpha )\\ K(\alpha )\\ S(\alpha )\\ F(\alpha )\\ \end{array} \right] \end{aligned}$$

(22)

and

$$\begin{aligned} \mathcal {U}_{\perp }= & {} \left[ \begin{array}{ccc} A(\alpha ) &{} B(\alpha ) &{} 0 \\ I &{} 0 &{} 0 \\ 0 &{} I &{} 0 \\ 0 &{} 0 &{} I \\ \end{array} \right] ;\;\;\;\;\;\; \mathcal {V}_{\perp }=0. \end{aligned}$$

(23)

Using the projection Lemma 2.3 and the Schur complement, (16) is equivalent to (20). Thus, Theorem 3.3 is equivalent to Lemma 3.1. This completes the proof. $\square$

Remark 3.5

In the derivation of Theorem 3.3, four slack variables E, K, S and F are introduced. By setting $E=diag\{V^{T},V^{T}\}$, $K=0$, $S=0$ and $F=0$, Theorem 3.3 coincides with the results of Propostion 1 in Liu et al. (2009), so Theorem 3.3 would generally render a less conservative evaluation of the upper bound of the $H_{\infty }$ norm, as will be seen in the examples at the end of the paper.

Remark 3.6

Theorem 3.3 provides a sufficient condition of the mean-square asymptotic stability and $H_{\infty }$ disturbance attenuation level for 2D systems with intermittent measurements. If the communication link between the plant and the filter is perfect (that is, there is no packet dropout during transmission), then $\theta =1$ and $\beta =0$. In this case, the condition in Theorem 3.3 collapses to the condition obtained in the deterministic case.

4 $H_{\infty }$ Filtering Design

In this section, we propose a sufficient condition for the existence of an $H_{\infty }$ filter and characterize the filter matrices that provide the required robust stability and disturbance attenuation requirements. Using the previous result and choosing an appropriate linearizing transformation, we obtain a strict LMI condition for the filter design.

Theorem 4.1

Consider the system in (1) and suppose that the filter matrices $A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$, $L_{f}$ in (8) are given. Then, the filtering error system in (9) for any $\alpha \in \varGamma$ is mean-square asymptotically stable and guarantees an $H_{\infty }$ disturbance attenuation level $\gamma$ if there exist matrices $K_{1}(\alpha )$, $K_{2}(\alpha )$, $E_{1}(\alpha )$, $E_{2}(\alpha )$, $F_{1}(\alpha )$, $S_{1}(\alpha )$, $\breve{B}_{f}$, $\breve{A}_{f}$, $\breve{L}_{f}$, U, $\tilde{P}_{2}(\alpha )=diag\{P_{2}(\alpha ),P_{2}(\alpha )\}$, $\tilde{R}_{2}(\alpha )=diag\{P_{2}(\alpha )-Q_{2}(\alpha ),Q_{2}(\alpha )\}$ symmetric matrices $\tilde{P}_{k}(\alpha )=diag\{P_{k}(\alpha ),P_{k}(\alpha )\}>0$, the scalars $\lambda _{i},\; i=1,\ldots ,3$ and $\tilde{R}_{k}(\alpha )$ = $diag\{P_{k}(\alpha )-Q_{k}(\alpha ),Q_{k}(\alpha )\}>0$, $k=1,3$ satisfying

$$\begin{aligned} \varDelta (\alpha )= \left[ \begin{array}{cccccc} T_{11} &{} T_{12} &{} T_{13} &{} T_{14} &{} T_{15} &{} -F_{1}(\alpha )^{T}\\ * &{} T_{22} &{} T_{23} &{} T_{24} &{} T_{25} &{} 0 \\ * &{} * &{} T_{33} &{} T_{34} &{} T_{35} &{} T_{36}\\ * &{} * &{} * &{} T_{44} &{} T_{45} &{} -\breve{L}_{f}^{T}\\ * &{} * &{} * &{} * &{} T_{55} &{} T_{56}\\ * &{} * &{} * &{} * &{} * &{} -I\\ \end{array}\right] <0 \end{aligned}$$

(24)

$$\begin{aligned} T_{11}= & {} \tilde{P}_{1}(\alpha ) - E_{1}(\alpha ) - E_{1}^{T}(\alpha );\\ T_{12}= & {} \tilde{P}_{2}(\alpha ) - \mathcal {V}_{1}U - E_{2}^{T}(\alpha );\\ T_{13}= & {} E_{1}(\alpha )\breve{A}(\alpha ) + \mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{C}(\alpha ) - K_{1}^{T}(\alpha );\\ T_{14}= & {} \mathcal {V}_{1}\breve{A}_{f} - K_{2}^{T}(\alpha );\\ T_{15}= & {} E_{1}(\alpha )\breve{B}(\alpha ) + \mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{D}(\alpha ) - S_{1}^{T}(\alpha );\\ T_{22}= & {} \tilde{P}_{3}(\alpha ) - \lambda _{1}(U + U^{T});\\ T_{23}= & {} E_{2}(\alpha )\breve{A}(\alpha ) + \lambda _{1}\varLambda \breve{B}_{f}\breve{C}(\alpha ) - \lambda _{2}U^{T}\mathcal {V}_{1}^{T};\\ T_{24}= & {} \lambda _{1}\breve{A}_{f} - \lambda _{3}U^{T}; \end{aligned}$$

$$\begin{aligned} T_{25}= & {} E_{2}(\alpha )\breve{B}(\alpha ) + \lambda _{1}\varLambda \breve{B}_{f}\breve{D}(\alpha );\\ T_{56}= & {} \breve{B}^{T}(\alpha )F_{1}^{T}(\alpha );\\ T_{33}= & {} -\tilde{R}_{1}(\alpha ) + K_{1}(\alpha )\breve{A}(\alpha ) + \breve{A}^{T}(\alpha )K_{1}^{T}(\alpha )\\&+\,\lambda _{2}(\mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{C}(\alpha ) + \breve{C}^{T}(\alpha )\breve{B}_{f}^{T}\varLambda ^{T}\mathcal {V}_{1}^{T});\\ T_{34}= & {} -\tilde{R}_{2}(\alpha ) + \lambda _{2}\mathcal {V}_{1}\breve{A}_{f} + \breve{A}^{T}(\alpha )K_{2}^{T}(\alpha )\\&+\,\lambda _{3}\breve{C}^{T}(\alpha )\breve{B}_{f}^{T}\varLambda ^{T};\\ T_{35}= & {} K_{1}(\alpha )\breve{B}(\alpha ) + \lambda _{2}\mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{D}(\alpha ) + \breve{A}^{T}(\alpha )S_{1}^{T}(\alpha );\\ T_{36}= & {} \breve{A}^{T}(\alpha )F_{1}^{T}(\alpha )+ \breve{L}^{T}(\alpha );\\ T_{44}= & {} -\tilde{R}_{3}(\alpha ) + \lambda _{3}(\breve{A}_{f} + \breve{A}_{f}^{T});\\ T_{45}= & {} K_{2}(\alpha )\breve{B}(\alpha ) + \lambda _{3}\varLambda \breve{B}_{f}\breve{D}(\alpha );\\ T_{55}= & {} S_{1}(\alpha )\breve{B}(\alpha ) + \breve{B}^{T}(\alpha )S_{1}^{T}(\alpha )- \gamma ^{2}I ; \end{aligned}$$

The filter parameter obtained by

$$\begin{aligned} A_{f}=U^{-1}\breve{A}_{f};\;\;\;\; B_{f}=U^{-1}\breve{B}_{f};\;\;\;\; L_{f}=\breve{L}_{f}. \end{aligned}$$

Proof 4.2

For the slack matrices in (20), we first structurize them as the following block form (Feng and Han 2015; Li and Gao 2012b):

$$\begin{aligned} E(\alpha )= & {} \varUpsilon \left[ \begin{array}{cc} E_{1}(\alpha ) \;\;&{}\;\; \mathcal {V}_{1}U \\ E_{2}(\alpha ) \;\;&{}\;\; \lambda _{1}U \\ \end{array} \right] \varUpsilon ^{T},\end{aligned}$$

(25)

$$\begin{aligned} K(\alpha )= & {} \varUpsilon \left[ \begin{array}{cc} K_{1}(\alpha ) \;\;&{}\;\; \lambda _{2}\mathcal {V}_{1}U \\ K_{2}(\alpha ) \;\;&{}\;\; \lambda _{3}U \\ \end{array} \right] \varUpsilon ^{T},\nonumber \\ S(\alpha )= & {} \left[ \begin{array}{cc} S_{1}(\alpha ) \;\;&{}\;\; 0 \\ \end{array} \right] \varUpsilon ^{T},\; F(\alpha )=\left[ \begin{array}{cc} F_{1}(\alpha ) \;\;&{}\;\; 0 \\ \end{array} \right] . \end{aligned}$$

(26)

where

$$\begin{aligned} U=\left[ \begin{array}{cc} U_{1} \;\;&{}\;\; 0 \\ 0 \;\;&{}\;\; U_{1} \\ \end{array} \right] ,\;\;\;\;\;\;\;\; \mathcal {V}_{1}= \left[ \begin{array}{c} I_{2n_{f}\times 2n_{f}} \\ 0_{(2n - 2n_{f})\times 2n_{f}} \\ \end{array} \right] \end{aligned}$$

(27)

with $\varUpsilon$ in (18). Moreover, for matrix variables $\bar{P}$ and R in (20), we introduce the following definitions:

$$\begin{aligned} \bar{P}(\alpha )= & {} \varUpsilon \left[ \begin{array}{cc} \tilde{P}_{1}(\alpha ) \;\;&{}\;\; \tilde{P}_{2}(\alpha ) \\ \tilde{P}_{2}(\alpha ) \;\;&{}\;\; \tilde{P}_{3}(\alpha ) \\ \end{array} \right] \varUpsilon ^{T},\nonumber \\ R(\alpha )= & {} \varUpsilon \left[ \begin{array}{cc} \tilde{R}_{1}(\alpha ) \;\;&{}\;\; \tilde{R}_{2}(\alpha ) \\ \tilde{R}_{2}(\alpha ) \;\;&{}\;\; \tilde{R}_{3}(\alpha ) \\ \end{array} \right] \varUpsilon ^{T} \end{aligned}$$

(28)

where $\tilde{P}_{k}(\alpha )$, $\tilde{R}_{k}(\alpha )$ are from Theorem 4.1.

As $\varUpsilon ^{T}\varUpsilon =I$, by substituting (9)–(18) into (20) and combining (25)–(28), we have that

$$\begin{aligned} \varPhi =J^{T}\varXi J \end{aligned}$$

(29)

where $\varXi$ is in (20) and

$$\begin{aligned}&J=diag\{\varUpsilon ,\;\;\varUpsilon ,\;\;I_{p},\;\;I_{q}\},\nonumber \\&\breve{A}_{f}=UA_{f},\;\;\; \breve{B}_{f}=UB_{f},\;\;\; \breve{L}_{f}=L_{f}. \end{aligned}$$

(30)

This completes the proof. $\square$

One way to facilitate the use of Theorem 4.1 for the construction of a filter is to convert (24) into a finite set of LMI constraints. The following results give a methodology to achieve this.

Theorem 4.3

Consider the system in (1) and suppose that the filter matrices $A_{f1}$, $A_{f2}$, $B_{f1}$, $B_{f2}$, $L_{f}$ in (8) are given. Then, the filtering error system in (9) for any $\alpha \in \varGamma$ is mean-square asymptotically stable and guarantees an $H_{\infty }$ disturbance attenuation level $\gamma$ if there exist matrices $K_{1i}$, $K_{2i}$, $E_{1i}$, $E_{2i}$, $F_{1i}$, $S_{1i}$, $\breve{B}_{f}$, $\breve{A}_{f}$, $\breve{L}_{f}$, U, $\tilde{P}_{2i}=diag\{P_{2i},P_{2i}\}$, $\tilde{R}_{2i}=diag\{P_{2i}-Q_{2i},Q_{2i}\}$, symmetric matrices $\tilde{P}_{ki}=diag\{P_{ki},P_{ki}\}>0$, $\tilde{R}_{ki}=diag\{P_{ki}-Q_{ki},Q_{ki}\}>0$, $k=1,3$ and scalars $\lambda _{t},\; t=1,2,3$ satisfying

$$\begin{aligned} \varDelta _{ij}+\varDelta _{ji}<0,\;\;\;\; 1\le i \le j \le s, \end{aligned}$$

(31)

where

$$\begin{aligned} \varDelta _{ij}=\left[ \begin{array}{cc} \varOmega _{11}\;\;\; &{}\;\;\;\varOmega _{12} \\ * &{} \varOmega _{22}\\ \end{array} \right] \end{aligned}$$

(32)

and

$$\begin{aligned} \varOmega _{11}=\left[ \begin{array}{ccc} T_{11}^{ij} \;\;&{}\;\; \tilde{P}_{2i} - \mathcal {V}_{1}U - E_{2i}^{T} \;\;&{}\;\; T_{13}^{ij}\\ * &{} \tilde{P}_{3i} - \lambda _{1}(U + U^{T}) &{} T_{23}^{ij} \\ * &{} * &{} T_{33}^{ij} \end{array} \right] \end{aligned}$$

(33)

$$\begin{aligned} \varOmega _{12}=\left[ \begin{array}{cccccc} T_{14}^{ij} \;\;&{}\;\; T_{15}^{ij} \;\;&{}\;\; -F_{1i}^{T}\\ T_{24} &{} T_{25}^{ij} &{} 0\\ T_{34}^{ij} &{} T_{35}^{ij} &{} \breve{A}^{T}_{j}F_{1i}^{T}+ \breve{L}^{T}_{j}\\ \end{array} \right] \end{aligned}$$

(34)

$$\begin{aligned} \varOmega _{22}=\left[ \begin{array}{ccc} T_{44}^{ii} &{} T_{45}^{ij} &{} -\breve{L}_{f}^{T}\\ * &{} T_{55}^{ij}- \gamma ^{2}I &{} \breve{B}^{T}_{j}F_{1i}^{T}\\ * &{} * &{} -I\\ \end{array} \right] \end{aligned}$$

(35)

and

$$\begin{aligned} T_{11}^{ii}= & {} \tilde{P}_{1i} - E_{1i} - E_{1i}^{T};\\ T_{13}^{ij}= & {} E_{1i}\breve{A}_{j} + \mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{C}_{j} - K_{1i}^{T};\\ T_{14}^{ii}= & {} \mathcal {V}_{1}\breve{A}_{f} - K_{2i}^{T};\\ T_{15}^{ij}= & {} E_{1i}\breve{B}_{j} + \mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{D}_{j} - S_{1i}^{T};\\ T_{23}^{ij}= & {} E_{2i}\breve{A}_{j} + \lambda _{1}\varLambda \breve{B}_{f}\breve{C}_{j} - \lambda _{2}U^{T}\mathcal {V}_{1}^{T};\\ T_{24}= & {} \lambda _{1}\breve{A}_{f} - \lambda _{3}U^{T};\\ T_{25}^{ij}= & {} E_{2i}\breve{B}_{j} + \lambda _{1}\varLambda \breve{B}_{f}\breve{D}_{j};\\ T_{33}^{ij}= & {} -\tilde{R}_{1i} + K_{1i}\breve{A}_{j} + \breve{A}^{T}_{j}K_{1i}^{T} + \lambda _{2}(\mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{C}_{j}\\&+\,\breve{C}^{T}_{j}\breve{B}_{f}^{T}\varLambda ^{T}\mathcal {V}_{1}^{T});\\ T_{34}^{ij}= & {} -\tilde{R}_{2i} + \lambda _{2}\mathcal {V}_{1}\breve{A}_{f} + \breve{A}^{T}_{j}K_{2i}^{T} + \lambda _{3}\breve{C}^{T}_{j}\breve{B}_{f}^{T}\varLambda ^{T};\\ T_{35}^{ij}= & {} K_{1i}\breve{B}_{j} + \lambda _{2}\mathcal {V}_{1}\varLambda \breve{B}_{f}\breve{D}_{j} + \breve{A}^{T}_{j}S_{1i}^{T};\\ T_{44}^{ii}= & {} -\tilde{R}_{3i} + \lambda _{3}(\breve{A}_{f} + \breve{A}_{f}^{T});\\ T_{45}^{ij}= & {} K_{2i}\breve{B}_{j} + \lambda _{3}\varLambda \breve{B}_{f}\breve{D}_{j};\\ T_{55}^{ij}= & {} S_{1i}\breve{B}_{j} + \breve{B}^{T}_{j}S_{1i}^{T}. \end{aligned}$$

The filter parameter obtained by

$$\begin{aligned} A_{f}=U^{-1}\breve{A}_{f}.;\;\;\;\; B_{f}=U^{-1}\breve{B}_{f};\;\;\;\; L_{f}=\breve{L}_{f}. \end{aligned}$$

Proof 4.4

Suppose that there exist matrices $K_{1}(\alpha )$, $K_{2}(\alpha )$, $E_{1}(\alpha )$, $E_{2}(\alpha )$, $F_{1}(\alpha )$, $S_{1}(\alpha )$, $\breve{B}_{f}$, $\breve{A}_{f}$, $\breve{L}_{f}$, U, $\tilde{P}_{2}(\alpha )=diag\{P_{2}(\alpha ),P_{2}(\alpha )\}$,$\tilde{R}_{2}(\alpha )=diag\{P_{2}(\alpha )-Q_{2}(\alpha ),Q_{2}(\alpha )\}$ and symmetric matrices $\tilde{P}_{k}(\alpha )=diag\{P_{k}(\alpha ),P_{k}(\alpha )\}>0$, $\tilde{R}_{k}(\alpha )=diag\{P_{k}(\alpha )-Q_{k}(\alpha ),Q_{k}(\alpha )\}>0$, $k=1,3$ satisfying (24), then a filter in the form of (6) exists. Now, we use these matrices and $\alpha$ in the unit simplex $\varGamma$ to fix the matrices as follows:

$$\begin{aligned} K_{1}(\alpha )= & {} \sum _{i=1}^{s}\alpha _{i} K_{1i}; \;\;\;\;\;\; K_{2}(\alpha )=\sum _{i=1}^{s}\alpha _{i} K_{2i};\\ E_{1}(\alpha )= & {} \sum _{i=1}^{s}\alpha _{i} E_{1i};\;\;\;\;\;\; E_{2}(\alpha )=\sum _{i=1}^{s}\alpha _{i} E_{2i};\\ F_{1}(\alpha )= & {} \sum _{i=1}^{s}\alpha _{i} F_{1i}; \;\;\;\;\;\; S_{1}(\alpha )=\sum _{i=1}^{s}\alpha _{i} S_{1i};\\ \tilde{P}_{2}(\alpha )= & {} \sum _{i=1}^{s}\alpha _{i} \tilde{P}_{2i}; \;\;\;\;\;\;\;\;\; \tilde{R}_{2}(\alpha )=\sum _{i=1}^{s}\alpha _{i} \tilde{R}_{2i};\\ \tilde{P}_{k}(\alpha )= & {} \sum _{i=1}^{s}\alpha _{i} \tilde{P}_{ki}; \;\;\;\;\;\;\;\;\; \tilde{R}_{k}(\alpha )=\sum _{i=1}^{s}\alpha _{i} \tilde{R}_{ki};\\&k=1,3. \end{aligned}$$

By (36), it is easy to rewrite $\varDelta (\alpha )$ in (24) as

$$\begin{aligned} \varDelta (\alpha )= & {} \sum _{j=1}^{s}\sum _{i=1}^{s}\alpha _{i}\alpha _{j}\varDelta _{ij}\nonumber \\= & {} \sum _{i=1}^{s}\alpha _{i}^{2}\varDelta _{ii}+\sum _{i=1}^{s}\sum _{j=i+1}^{s}\alpha _{i}\alpha _{j}(\varDelta _{ij} +\varDelta _{ij}) \end{aligned}$$

(36)

where $\varDelta _{ij}$ takes the form of (32). On the other hand, from (31), we have

$$\begin{aligned} \varDelta _{ii}<0,\; i=1,\ldots ,s,\;\hbox {and}\; \varDelta _{ij}+\varDelta _{ji}<0,\; 1\le i < j\le s. \end{aligned}$$

(37)

Considering $\sum _{j=1}^{s}\alpha _{i}=1,\;\; \alpha _{i}\ge 0$, then from (36)–(37), we have $\varDelta (\alpha )<0$. Based on Theorem 4.1, there exists a filter in the form of (6) such that the filtering error system in (9) is stochastically stable with a given $H_{\infty }$ performance. This completes the proof. $\square$

Remark 4.5

When the scalars $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ of Theorem 4.3 are fixed to be constants, then (31) is an LMI linear in the variables. To select values for these scalars, optimization can be used (for instance, fminsearch in MATLAB) to obtain the scalars that improve some measure of performance (for instance, the value of the bound on the disturbance attenuation level $\gamma$).

5 Numerical Examples

In this section, simulation examples are provided to illustrate the effectiveness of the proposed filtering design approach.

5.1 Example 1

Consider the 2D static field model presented in Liu et al. (2009), which is described by the following equation:

$$\begin{aligned} \eta _{i+1,j+1}=\alpha _{1}\eta _{i,j+1}+\alpha _{2}\eta _{i+1,j}-\alpha _{1}\alpha _{2}\eta _{i,j} +\omega _{1(i,j)} \end{aligned}$$

(38)

where $\eta _{i,j}$ is the state vector at coordinates (i, j) and $\alpha _{1}$, $\alpha _{2}$ are the vertical and horizontal correlative coefficients, respectively, satisfying: $\alpha _{1}^{2}<1$ and $\alpha _{2}^{2}<1$. Defining the augmented state vector $x_{i,j}=[\eta _{i,j+1}^{T}-\alpha _{2}\eta _{i,j}^{T}\eta _{i,j}^{T}]^{T}$, and supposing that the measurement equation and the signal to be estimated are, respectively,

$$\begin{aligned} y_{i,j}= & {} \alpha _{1}\eta _{i,j+1}+(1-\alpha _{1}\alpha _{2})\eta _{i+1,j}+\omega _{2},\nonumber \\ z_{i,j}= & {} \eta _{i,j}, \end{aligned}$$

(39)

It is not difficult to transform these equations into a 2D FM model in the form of (1), with the system matrices given by

$$\begin{aligned} A_{1}(\alpha )= & {} \left[ \begin{array}{cc} \alpha _{1} &{} 0 \\ 0 &{} 0 \\ \end{array} \right] , A_{2}(\alpha )=\left[ \begin{array}{cc} 0 &{} 0 \\ 1 &{} \alpha _{2} \\ \end{array} \right] , B_{1}(\alpha )=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \\ \end{array} \right] ,\nonumber \\ B_{2}(\alpha )= & {} \left[ \begin{array}{cc} 0 \;&{}\; 0 \\ 0 \;&{}\; 0 \\ \end{array} \right] ,\; C(\alpha )=\left[ \begin{array}{cc} \alpha _{1} \;&{}\; 1 \\ \end{array} \right] ,\; D(\alpha )=\left[ \begin{array}{cc} 0 \;&{} \; 1\\ \end{array} \right] ,\nonumber \\ L(\alpha )= & {} \left[ \begin{array}{cc} 0 \;\;\;&{} \;\;\; 1\\ \end{array} \right] . \end{aligned}$$

(40)

The uncertain parameters $\alpha _{1}$ and $\alpha _{2}$ are now assumed to be $0.15\le \alpha _{1}\le 0.45$, and $0.35\le \alpha _{2}\le 0.85$, so the above system is represented by a four-vertex polytope. It is assumed that measurements transmitted between the plant and the filter are imperfect, that is, data may be lost during their transmission. Based on this, our aim is to design a filter in the form of (6) such that the resulting filtering error system in (9) is mean-square asymptotically stable with a guaranteed $H_{\infty }$ disturbance attenuation level.

5.1.1 The Measurements Transmitted Between the Plant and Filter are Perfect ($\theta$=1)

First, the stochastic variable is assumed to be $\theta _{i,j}=1 (\theta =1)$, which means that the measurements always reach the filter. Applying the filter design method in Theorem (4.3), for this particular case, the minimum $H_{\infty }$ performance $\gamma ^{*}=2.4924$ is obtained, with the associated filter matrices given by equation (41).

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} &{} B_{f1} \\ \hline A_{f2} &{} B_{f2} \\ \hline L{f} &{} \\ \end{array} \right] = \left[ \begin{array}{cc|c} 0.5456 \;&{}\; -0.1778 \;&{}\; -0.0908 \\ 0.0510 \;&{}\; -0.0171 \;&{}\; -0.0089\\ \hline -0.0910 \;&{}\; 0.0035 \;&{}\; 0.0205\\ 0.2213 \;&{}\; 0.2792 \;&{}\; -0.2664\\ \hline 0.0313 \;&{}\; -2.1730 \;&{}\; \\ \end{array} \right] \end{aligned}$$

(41)

It is noticeable that the value of $\gamma$ obtained in this case ($\gamma =2.4924$) is smaller than the one found in Liu et al. (2009) and Gao et al. (2008).

5.1.2 The Measurements Transmitted Between the Plant and Filter are Imperfect ($\theta$=0.8)

We assume that data may be lost during their transmission: $\theta =0.8$, so the probability of a data packet going missing is 20 %. With this assumption, applying the filter design method in Theorem (4.3), the achieved $H_{\infty }$ disturbance attenuation level is $\gamma ^{*}=4.6287$, and the corresponding filter matrices are

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} &{} B_{f1} \\ \hline A_{f2} &{} B_{f2} \\ \hline L{f} &{} \\ \end{array} \right] = \left[ \begin{array}{cc|c} 0.3503 \;\;\;&{}\;\;\; -0.0663 \;\;\;&{}\;\;\; -0.0327 \\ 0.1648 \;\;\;&{}\;\;\; -0.0315 \;\;\;&{}\;\;\; -0.0190\\ \hline 0.0328 \;\;\;&{}\;\;\; 0.0043 \;\;\;&{}\;\;\; -0.0328\\ 0.5952 \;\;\;&{}\;\;\; 0.5458 \;\;\;&{}\;\;\; -0.1737\\ \hline 0.5107 \;\;\;&{}\;\;\; -2.2695 \;\;\;&{}\;\;\; \\ \end{array} \right] \end{aligned}$$

(42)

Fig. 1

Disturbance input w(i, j) for example 1

Fig. 2

Filtering error e(i, j) for $w(i,j)\ne 0$ and $(\alpha _{1}=0.15,\; \alpha _{2}=0.35)$

Fig. 3

Filtering error e(i, j) for $w(i,j)\ne 0$ and $(\alpha _{1}=0.15,\; \alpha _{2}=0.85)$

Fig. 4

Filtering error e(i, j) for $w(i,j)\ne 0$ and $(\alpha _{1}=0.45,\; \alpha _{2}=0.35)$

Fig. 5

Filtering error e(i, j) for $w(i,j)\ne 0$ and $(\alpha _{1}=0.45,\; \alpha _{2}=0.85)$

Fig. 6

Data packet dropout

For simulation, the disturbance input w(i, j), depicted in Fig. 1, is

$$\begin{aligned} w(i,j)=\left\{ \begin{array}{ll} [0.1\;\;\; 0.1]^{T}, &{}\;\; 3\le i, j \le 19 \\ 0 &{} \mathrm{otherwise}\\ \end{array} \right. \end{aligned}$$

(43)

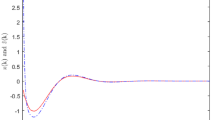
The filtering error signal e(i, j) obtained with the designed filter matrices is shown in Figs. 2, 3, 4 and 5 for the random data packet dropouts presented in Fig. 6: we can confirm that e(i, j) converges to zero despite the data dropouts and the disturbance.

The minimum guaranteed performance $\gamma$ for different values of $\theta$ are given in Table 1.

Table 1 Minimum $\gamma$ for different values of $\theta$ for example 1

Table 2 Minimum $\gamma$ for different values of $\theta$ for example 2

5.2 Example 2

Consider systems (1) and (2) with s = 4 and with the following data:

$$\begin{aligned} A_{11}= & {} A_{12}=\left[ \begin{array}{cc} 0.4 \;&{}\; -0.5;\\ 0.5 &{} 0.2 \\ \end{array} \right] , A_{13}=A_{14}=\left[ \begin{array}{cc} 0 \;&{}\; -0.5;\\ 0.5 &{} 0.2 \\ \end{array} \right] ,\\ A_{21}= & {} \left[ \begin{array}{cc} 0.1 \;&{}\; 0\\ 0 &{} 0.3 \\ \end{array} \right] , A_{22}=A_{23}=A_{24}=\left[ \begin{array}{cc} 0.25 \;&{}\; 0.1;\\ 0 &{} 0.3 \\ \end{array} \right] ,\nonumber \\ B_{1j}= & {} \left[ \begin{array}{c} 0.2 \\ 0.5 \\ \end{array} \right] ,\;\; B_{2j}=\left[ \begin{array}{c} 0 \\ 0.5 \\ \end{array} \right] ,\;\;\;\; L_{j}=\left[ \begin{array}{cc} -2 \;&{}\; 1 \\ \end{array} \right] ,\\ C_{1}= & {} C_{3}=\left[ \begin{array}{cc} 0.5 \;&{}\; -3 \\ \end{array} \right] ,\;\;\; C_{2}=C_{4}=\left[ \begin{array}{cc} 0.5 \;&{}\; 3 \\ \end{array} \right] .\\ D_{j}= & {} \left[ \begin{array}{c} 0.1\\ \end{array} \right] , \;\; j=1,2,3,4. \end{aligned}$$

With these data, the optimal values $\gamma$ of problem (31) are given in Table 2.

5.2.1 The Measurements Transmitted Between the Plant and Filter are Perfect ($\theta$=1)

Full Order $(n_{f}=n)$ Case In this case , for $\lambda _{1}=2.0433$, $\lambda _{2}=-0.0002$ and $\lambda _{3}=0.0130$, the minimum $H_{\infty }$ performance is $\gamma ^{*}=5.4933$ and the filter gains obtained are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} &{} B_{f1} \\ \hline A_{f2} &{} B_{f2} \\ \hline L{f} &{} \\ \end{array} \right] = \left[ \begin{array}{cc|c} 0.1140 \;&{}\; -0.5007 \;&{}\; -0.0040 \\ 0.0147 \;&{}\; -0.0496 \;&{}\; -0.0425\\ \hline 0.1120 \;&{}\; 0.1363 \;&{}\; -0.0095\\ -0.1501 \;&{}\; 0.3178 \;&{}\; 0.0026\\ \hline 4.1101 \;&{}\; -2.0349 \;&{}\; \\ \end{array} \right] \end{aligned}$$

(44)

We can notice that the value of $\gamma =5.4933$ is smaller than the one found in Liu et al. (2009).

Fig. 7

Filtering error e(i, j) for $w(i,j)\ne 0$

Fig. 8

Filtering error e(i, j) for $w(i,j)\ne 0$

For simulation, the disturbance input w(i, j), is

$$\begin{aligned} w(i,j)=\left\{ \begin{array}{cc} 0.4, &{}\;\; 3\le i, j \le 19 \\ \\ 0 &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$

(45)

The filtering error signal e(i, j) obtained with the designed filter matrices is shown in Figs. 7, 8, 9 and 10 for the random data packet dropouts presented in Fig. 6: we can confirm that e(i, j) converges to zero despite the disturbance.

Fig. 9

Filtering error e(i, j) for $w(i,j)\ne 0$

Fig. 10

Filtering error e(i, j) for $w(i,j)\ne 0$

Reduced Order $(n_{f}<n)$ Case In this case, for $\lambda _{1}=1.9797$, $\lambda _{2}=-0.6339$ and $\lambda _{3}=0.0038$, the minimum $H_{\infty }$ performance is $\gamma ^{*}=6.1731$ and the filter gains obtained are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} \;\;\;&{}\;\;\; B_{f1} \\ \hline A_{f2} \;\;\;&{}\;\;\; B_{f2} \\ \hline L{f} \;\;\;&{}\;\;\; \\ \end{array} \right] = \left[ \begin{array}{c|c} 0.0458 \;\;\;&{}\;\;\; 0.2365 \\ \hline -0.3481 \;\;\;&{}\;\;\; -0.0369\\ \hline 0.4996 \;\;\;&{}\;\;\; \\ \end{array} \right] . \end{aligned}$$

(46)

5.2.2 The Measurements Transmitted Between the Plant and Filter are Imperfect ($\theta$=0.8)

Full Order $(n_{f}=n)$ Case In this case , for $\lambda _{1}=2.0302$, $\lambda _{2}=-0.0014$ and $\lambda _{3}=0.0131$, the minimum $H_{\infty }$ performance is $\gamma ^{*}=6.2240$ and the filter gains obtained are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} &{} B_{f1} \\ \hline A_{f2} &{} B_{f2} \\ \hline L{f} &{} \\ \end{array} \right] = \left[ \begin{array}{cc|c} 0.1322 \;&{}\; -0.5416 \;&{}\; -0.0035 \\ 0.1262 \;&{}\; -0.0340 \;&{}\; -0.0344\\ \hline -0.0186 \;&{}\; 0.1318 \;&{}\; -0.0185\\ -0.2338 \;&{}\; 0.3796 \;&{}\; -0.0085\\ \hline 4.0910 \;&{}\; -2.0220 \;&{}\; \\ \end{array} \right] \end{aligned}$$

(47)

It is noticeable that the value of $\gamma =5.5459$ is better than the one found in Liu et al. (2009).

Reduced order $(n_{f}<n)$ case In this case, for $\lambda _{1}=1.3162$, $\lambda _{2}=-0.7450$ and $\lambda _{3}=0.0108$, the minimum $H_{\infty }$ performance is $\gamma ^{*}=6.2240$ and the filter gains obtained are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f1} \;\;\;&{}\;\;\; B_{f1} \\ \hline A_{f2} \;\;\;&{}\;\;\; B_{f2} \\ \hline L{f} \;\;\;&{}\;\;\; \\ \end{array} \right] = \left[ \begin{array}{c|c} 0.0050 \;\;\;&{}\;\;\; 0.3631 \\ \hline -0.1949 \;\;\;&{}\;\;\; -0.1403\\ \hline 0.3352 \;\;\;&{}\;\;\; \\ \end{array} \right] . \end{aligned}$$

(48)

6 Conclusions

This paper has investigated the $H_{\infty }$ filtering problem for a class of two-dimensional systems with intermittent measurements. These measurements are characterized using a stochastic variable that follows a Bernoulli random binary distribution, which makes it possible to derive a sufficient condition guaranteeing mean-square asymptotic stability and a certain level of $H_{\infty }$ disturbance attenuation by means of an LMI technique. Numerical examples are provided to illustrate the effectiveness of the proposed approach. It must be pointed out that the methodology presented here can be used to solve parallel problems, such as $H_{\infty }$ control and $H_{\infty }$ filtering for other multi-dimensional systems, maybe with delays.