Robust $H_{\infty }$ Filtering for Uncertain 2D Singular Roesser Models

Abstract

This paper addresses the design of robust $H_{\infty }$ filters for polytopic 2D discrete singular systems described by a Roesser model. By establishing a novel version of the bounded real lemma, a polynomially parameter-dependent approach is developed to solve this filter design problem, with a new linear matrix inequality condition obtained for the existence of those $H_{\infty }$ filters. It is also shown that the proposed filter design method is general, in the sense that the results are also useful for standard (non-singular) systems. To show the applicability of the proposed filter design methodology, some examples are solved and compared with previous results.

1 Introduction

As it is well known, many practical systems, such as those in image data processing and transmission, thermal processes, gas absorption, and water stream heating, are correctly modelled as two-dimensional (2D) systems [4, 18]. The investigation of 2D systems is then attracting considerable attention among the control and signal processing fields. Many important results have already been reported. Among these results, the $H_{\infty }$ filtering problem for 2D systems described by Roesser and Fornasini-Marchesini (FM) models has been studied in [1, 6, 7, 10–12, 16, 24, 26–31, 38]; for 2D parameter-varying systems, the related work can be found in [8, 29], whereas the $H_{\infty }$ filtering problems for 2D state-delayed systems are investigated in [24, 28], the stability and stabilization of 2D systems in [2, 23], and the $H_{\infty }$ control for 2D nonlinear systems with delays and the non-fragile $H_{\infty }$ and $l_{2}-l_{1}$ problems in [33]. However, as there is no systematic and general approach to analyze 2D singular Roesser models (SRM), many problems still remain open in this specific subject, which justifies the work presented here.

In fact, 2D singular systems have already received interest due to their applications in many practical areas [5, 17]. A great number of fundamental results on 1D singular systems has been extended to 2D singular systems: in [32, 35], the general response formula and minimum energy control problem for 2D general descriptor models were studied in the shift-invariant and shift-varying coefficient cases, using the $Z$-transformation approach; [20] has extended the geometric method to the 2D singular case, whereas the input admissibility of 2D singular systems was investigated in [19]. Finally, we cite [40], where an asymptotic stability theory based on the concept of jump modes was proposed. It should be pointed out that in the 2D singular case, the acceptability and jump modes play an important role in the problem of robust stability of a 2D singular system [40]. The existence of the jump modes implies that the systems are non-casual and the structural stability of the systems will be violated. Hence, in many synthesis topics such as robust $H_\infty$ control [34], the closed loops have to be designed as jump-mode-free.

This paper concentrates on 2D singular Roesser models (2D SRM) as they are the simplest (and most popular) 2D singular system models: Although they resemble 1D singular systems in their forms, there is no Kronecker canonical form for 2D system, which is one of the most powerful tools for the extensive basic studies of 1D singular systems. This makes it more difficult to study 2D singular systems. For examples, the problems of the robust $H_\infty$ control, model reduction, and duality for 2D SRM have been shown to be quite complex [34, 36, 42]. As far as we know, there is no relevant progress reported on the full-order $H_\infty$ filtering for 2D uncertain SRM, which motivates the investigations in this paper.

In summary, this paper seeks new techniques to design robust $H_\infty$ filters for uncertain 2D singular systems. Given a 2D system described by the Roesser model with uncertain parameters residing in a convex bounded polytope, the focus is on designing a robust filter such that the filtering error system is acceptable, robustly asymptotically stable, causal, and has a prescribed $H_\infty$ disturbance attenuation performance for the entire uncertainty domain. By establishing a new version of bounded real lemma, the polynomially parameter-dependent idea is introduced to solve the robust $H_\infty$ filtering problem. A linear matrix inequality condition is obtained for the existence of admissible filters, and based on this, the filter design is cast into a convex optimization problem that can be readily solved via standard numerical software. The merit of the proposed approach lies in the reduced conservatism, when compared with alternative conventional robust filter design methods; moreover, it includes the quadratic and the linearly parameter-dependent frameworks as special cases.

$\mathbf {Notations:}$ For real symmetric matrices $X$ and $Y$, the notation $X\ge Y$ (respectively, $X>Y$) means that the matrix $X-Y$ is positive semidefinite (respectively, positive definite). $*$ stands for the symmetric term of a square symmetric matrix. $I$ denotes the identity matrix with appropriate dimension. The superscript $^T$ represents the transpose of a matrix. $\mathrm{diag}(\ldots )$ stands for a block-diagonal matrix. The Euclidean vector norm is denoted by $\parallel .\parallel$. The $l_{2}$ norm of a 2D signal $w(i,j)$ is given by

$$\begin{aligned} \parallel w(i,j)\parallel _{2}=\sqrt{\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }w^{T}(i,j)w(i,j)} \end{aligned}$$

where $w(i,j)$ is said to be in the space $l_{2}{[0, \infty ), [0, \infty )}$ or $l_{2}$, for simplicity, if $\parallel w(i,j)\parallel _{2}<\infty$.

2 Preliminaries

Consider a 2D singular Roesser model (2D SRM) of the following form

$$\begin{aligned} E_{\alpha }\left[ \begin{array}{lll} x^h(i+1,j) \\ x^v(i,j+1) \end{array}\right]&= A_{\alpha } \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] + B_{\alpha }w(i,j) \nonumber \\ y(i,j)&= C_{\alpha } \left[ \begin{array}{cccc} x^h(i,j) \\ x^v(i,j) \end{array}\right] +D_{\alpha }w(i,j)\nonumber \\ z(i,j)&= H_{\alpha } \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] \end{aligned}$$

(2.1)

with the so-called standard quarter plane boundary conditions ([18])

$$\begin{aligned} \begin{array}{cccc} x_{h}(0,j)=x_{h}^{j},&{} x_{v}(i,0)=x_{v}^{i},&{} i,j=0,1,2,\cdots ,\\ \end{array} \end{aligned}$$

(2.2)

where $x^h(i,j)\in \mathbb {R}^{n_{h}}$ and $x^v(i,j)\in \mathbb {R}^{n_{v}}$ are the horizontal and vertical states, respectively, and $w(i,j)\in \mathbb {R}^{q}$ is a disturbance (or noise) vector that belongs to $l_{2} \{[0, \infty ), [0, \infty )\}, y(i,j)\in \mathbb {R}^{m}$ is the measured output, and $z(i,j)\in \mathbb {R}^{p}$ is the signal to be estimated.

The system matrices are assumed to belong to a known polyhedral domain $\varGamma$ described by $s$ vertices, that is,

$$\begin{aligned} P_{\alpha } \triangleq [E_{\alpha }, A_{\alpha }, B_{\alpha }, C_{\alpha }, D_{\alpha }, H_{\alpha }]\in \varGamma \end{aligned}$$

(2.3)

where

$$\begin{aligned} \varGamma \triangleq \left\{ P_{\alpha }/P_{\alpha }=\sum _{m=1}^{s}\alpha _{m}P_{m}; \sum _{m=1}^{s}\alpha _{m}=1, \alpha _{m}\ge 0\right\} \end{aligned}$$

(2.4)

with $P_{m}\triangleq \{E_{m}, A_{m}, B_{m}, C_{m}, D_{m}, H_{m}\}$ denoting the $m$th vertex of the polyhedral domain $\varGamma$. It is assumed that the parameter $\alpha$ is unknown (not measured online) and does not depend explicitly on the variables $i,j$.

$E_{\alpha }$ is possibly singular, satisfying the 2D regular pencil condition, i.e., for some finite pairs $(z,w)$

$$\begin{aligned} \mathrm{det}[E_{\alpha }I(z,w)-A_{\alpha }]=\sum _{k=0}^{\bar{n}_{1}}\sum _{l=0}^{\bar{n}_{2}}a_{kl}z^{k}w^{l} \end{aligned}$$

where $I(z,w)=\mathrm{diag}\{zI_{n_{h}}, wI_{n_{v}}\}$, where $a_{\bar{n}_{1},0}\ne 0$ and $a_{0,\bar{n}_{2}}\ne 0$. When $a_{\bar{n}_{1},\bar{n}_{2}}\ne 0$, system (2.1) is called acceptable [18, 40].

It has been shown [40] that the unacceptable systems are usually ill-posed in a certain sense, so they are discarded from this study.

The jump modes of 2D SRM (2.1) can be defined equivalently by the nonzero positive power items $(a_{ij}z^{i}w^{j}, i>0 \; or\; j>0)$ in the Laurent expansion of the matrices $[E_{\alpha }I(z,w)-A_{\alpha }]^{-1}, 1\le \mid z\mid <\infty , 1\le \mid w\mid <\infty$ [3]. The freedom from jump modes of 2D singular systems is equivalent to the systems that are causal.

Recently, the authors of [40] suggested that if the 2D acceptable SRM (2.1) is causal, then, via linear transformations, it can be equivalently transferred into a 2D SRM of separated standard from, which is of the form (2.1) with $E=\mathrm{diag}(E_{h}, E_{v})$, where $E_{h\alpha } \in \mathbb {R}^{n_{h} \times n_{h}}, E_{v\alpha } \in \mathbb {R}^{n_{v} \times n_{v}}$. Therefore, for simplicity and convenience, in the problem of Robust $H_\infty$ filtering for uncertain 2D SRM, it can be assumed that $E_{\alpha }=\mathrm{diag}(E_{h\alpha }, E_{v\alpha })$.

Assumption 2.1

Throughout this article, $E_{\alpha }=\mathrm{diag}(E_{h\alpha }, E_{v\alpha })$, where $E_{h\alpha } \in \mathbb {R}^{n_{h} \times n_{h}}, E_{v\alpha } \in \mathbb {R}^{n_{v} \times n_{v}}$, and $n_{h}+n_{v}=n$.

Definition 2.2

[3, 37, 40] An acceptable 2D SRM system (2.1) is said to be internally stable if for every uniformly bounded boundary condition (2.2), $\lim _{i,j\longrightarrow \infty }x(i,j)=0$, where $x(i,j)=\left[ \begin{array}{c} x_{h}(i,j) \\ x_{v}(i,j) \end{array}\right]$.

Lemma 2.3

[37, 40] The 2D SRM system (2.1) is acceptable and internally stable if and only if

$$\begin{aligned} \begin{array}{cccc} p(z,w)\ne 0,&{} 0<\mid z\mid \le 1,&{} 0<\mid w\mid \le 1.\\ \end{array} \end{aligned}$$

(2.5)

Here, $p(z,w)=\mathrm{det}[E_{\alpha }-A_{\alpha }I(z,w)]$.

Lemma 2.4

[37, 40] The acceptable 2D SRM system (2.1) is causal if and only if

$$\begin{aligned} \mathrm{deg}\quad \mathrm{det}[sE_{\alpha }-A_{\alpha }]&= \mathrm{rank}E_{\alpha }\end{aligned}$$

(2.6)

$$\begin{aligned} \mathrm{rank}E_{\alpha }&= \mathrm{rank}E_{h\alpha }+\mathrm{rank}E_{v\alpha } \end{aligned}$$

(2.7)

Now, we want to find a 2D discrete-time filter, with input $y(i,j)$ and output $\bar{z}(i,j)$, which is an estimation of $z(i,j)$. Here, we consider the following 2D state-space description for this filter

$$\begin{aligned} \left[ \begin{array}{lll} \bar{x}^h(i+1,j) \\ \bar{x}^v(i,j+1) \end{array}\right]&= A_{f} \left[ \begin{array}{llll} \bar{x}^h(i,j) \nonumber \\ \bar{x}^v(i,j) \end{array}\right] + B_{f}y(i,j) \nonumber \\ \bar{z}(i,j)&= H_{f} \left[ \begin{array}{llll} \bar{x}^h(i,j) \\ \bar{x}^v(i,j) \end{array}\right] \end{aligned}$$

(2.8)

with the boundary conditions $\bar{x}^h(0,k)=0, \bar{x}^v(0,k)=0$ $\forall k$, where $\bar{x}^h(i,j)\in \mathbb {R}^{n_{h}}$ and $\bar{x}^v(i,j)\in \mathbb {R}^{n_{v}}$ are, respectively, the horizontal and vertical states of the filter, and $\bar{z}(i,j)\in \mathbb {R}^{p}$ is the estimation of signal $z(i,j)$. Defining the error system

$$\begin{aligned} \bar{E}_{\alpha }\left[ \begin{array}{lll} \xi ^h(i+1,j) \\ \xi ^v(i,j+1) \end{array}\right]&= \bar{A}_{\alpha } \left[ \begin{array}{llll} \xi ^h(i,j) \\ \xi ^v(i,j) \end{array}\right] + \bar{B}_{\alpha }w(i,j) \nonumber \\ e(i,j)&= \bar{C}_{\alpha } \left[ \begin{array}{llll} \xi ^h(i,j) \\ \xi ^v(i,j) \end{array}\right] \end{aligned}$$

(2.9)

where

$$\begin{aligned} \xi ^h(i,j)&= [x^{hT}(i,j) \quad \bar{x}^{hT}(i,j)]^{T}\\ \xi ^v(i,j)&= [x^{vT}(i,j) \quad \bar{x}^{vT}(i,j)]^{T}, e(i,j)=z(i,j)- \bar{z}(i,j) \end{aligned}$$

and

$$\begin{aligned} \bar{A}_{\alpha }&= \varUpsilon \left[ \begin{array}{c@{\quad }c} A_{\alpha }&{} 0\\ B_{f}C_{\alpha } &{} A_{f} \end{array} \right] \varUpsilon ^{T}=\varUpsilon \tilde{A}_{\alpha }\varUpsilon ^{T}, \bar{E}_{\alpha }=\varUpsilon \left[ \begin{array}{cc} E_{\alpha }&{} 0\\ 0 &{} I \end{array} \right] \varUpsilon ^{T}=\varUpsilon \tilde{E}_{\alpha }\varUpsilon ^{T},\nonumber \\ \bar{B}_{\alpha }&= \varUpsilon \left[ \begin{array}{cc} B_{\alpha }\\ B_{f}D_{\alpha } \end{array} \right] =\varUpsilon \tilde{B}_{\alpha }, \bar{C}_{\alpha }=\left[ \begin{array}{cc} H_{\alpha }&{}-C_{f}\\ \end{array} \right] \varUpsilon ^{T}=\tilde{C}_{\alpha }\varUpsilon ^{T}, \end{aligned}$$

(2.10)

with $\varUpsilon =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} I_{n_{h}}&{}0&{}0&{}0\\ 0&{}0&{}I_{n_{h}}&{}0\\ 0&{}I_{n_{v}}&{}0&{}0\\ 0&{}0&{}0&{} I_{n_{v}} \end{array} \right]$.

When the error system (2.9) is regular, its transfer function is given by

$$\begin{aligned} \bar{G}_{\alpha }(z,w)=\bar{C}_{\alpha }[\bar{E}_{\alpha }I(z,w)-\bar{A}_{\alpha }]^{-1}\bar{B}_{\alpha } \end{aligned}$$

and the $H_{\infty }$ norm of the system is, by definition,

$$\begin{aligned} \Vert \bar{G}_{\alpha }(z,w)\Vert _{\infty }=\sup _{z,w\in [0,2 \pi ]}\sigma _{\max }[\bar{G}_{\alpha }(e^{jz},e^{jw})], \end{aligned}$$

where $\sigma$ denotes the maximum singular value.

Remark 2.5

By using the 2D Parseval’s theorem [21], it is not difficult to show that, under zero-boundary conditions and with internal stability of (2.9), the condition $\Vert \bar{G}_{\alpha }(z,w)\Vert _{\infty }<\gamma$ is equivalent to

$$\begin{aligned} \sup _{0\ne w(i,j)\in \ell _{2}}\frac{\Vert e(i,j)\Vert _{2}}{\Vert w(i,j)\Vert _{2}}<\gamma \end{aligned}$$

The parameter uncertainties considered in this paper are assumed to be of polytopic type. The polytopic uncertainty has been widely used in the problems of robust control and filtering for uncertain systems (see, for instance, [15] and the references therein); moreover, many practical systems have parameter uncertainties that can be either exactly modeled or overbounded by the polytope $\varGamma$. Then, the 2D SRM $H_\infty$ filtering problem to be addressed in this paper is expressed as follows: given the 2D SRM system (2.1), design a suitable full-order filter (2.8) such that the following two requirements are satisfied

• 1. The error system (2.9) with $w(i,j)\equiv 0$ is acceptable, internally stable, causal (in ([40]) called jump-mode-free) for all $\alpha \in \varGamma$.

• 2. Under zero-boundary conditions, the $H_\infty$ performance $\Vert \bar{G}_{\alpha }(z,w)\Vert _{\infty }<\gamma$ is guaranteed for all nonzero $w(i,j) \in L_{2}$

We conclude this section by introducing the following two lemmas, which will be used in the proof of our main results; they are an extension of the results in ([34]) to uncertain systems, dependent on the parameter $\alpha \in \varGamma$.

Lemma 2.6

2D SRM system (2.9) is acceptable, internally stable, and causal for all $\alpha \in \varGamma$ if there exists symmetric matrices $P_{\alpha }=\mathrm{diag}(P_{h\alpha }, P_{v\alpha })\in \mathbb {R}^{2n_{h} \times 2n_{v}}$ such that

$$\begin{aligned}&\bar{E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }\ge 0\end{aligned}$$

(2.11)

$$\begin{aligned}&\bar{A}^{T}_{\alpha }P_{\alpha } \bar{A}_{\alpha }-\bar{ E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }<0 \end{aligned}$$

(2.12)

Moreover, if (2.12) holds, then $P_{\alpha }$ is non-singular.

Lemma 2.7

Given a scalar $\gamma >0$, the 2D SRM system (2.9) is acceptable, internally stable, and causal and satisfies $\Vert \bar{G}_{\alpha }(z,w)\Vert _{\infty }<\gamma$ for all $\alpha \in \varGamma$ if there exists symmetric matrices $P_{\alpha }=\mathrm{diag}(P_{h\alpha }, P_{v\alpha })\in \mathbb {R}^{n_{h} \times n_{v}}$ such that the following LMI holds

$$\begin{aligned}&\bar{E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }\ge 0\end{aligned}$$

(2.13)

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \bar{A}^{T}_{\alpha }P_{\alpha } \bar{A}_{\alpha }-\bar{ E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }&{}\bar{A}^{T}_{\alpha }P_{\alpha } \bar{B}_{\alpha }&{}\bar{C}^{T}_{\alpha }\\ *&{}-\gamma ^{2}I+\bar{B}^{T}_{\alpha }P_{\alpha } \bar{B}_{\alpha }&{}0\\ *&{}*&{}-I\\ \end{array} \right] <0 \end{aligned}$$

(2.14)

Lemma 2.8

[9] (Finsler’s Lemma) Let $\xi \in \mathbb {R}^{n}, Q \in \mathbb {R}^{n\times n}$ and $B\in \mathbb {R}^{m \times n}$ with $\mathrm{rank}(B)<n$ and $B^{\bot }$ such that $BB^{\bot }=0$. Then, the following conditions are equivalent

• (i) $\xi ^{T}Q\xi <0,\forall \xi \ne 0:B\xi =0$

• (ii) ${B^{\bot }}^{T}QB^{\bot }<0$

• (iii) $\exists \mu \in \mathfrak {R}: Q-\mu B^{T}B<0$

• (iv) $\exists \chi \in \mathfrak {R}^{n\times m}: Q+\chi B+B^{T}\chi ^{T}<0$

3 Robust $H_{\infty }$ Filtering Analysis

Now, we are in a position to present a new bounded real lemma for 2D SRM

Theorem 3.1

The filtering error 2D SRM (2.9) is acceptable, internally stable, and causal and satisfies $\Vert \bar{G}_{\alpha }(z,w)\Vert _{\infty }<\gamma$ for all $\alpha \in \varGamma$ if there exist symmetric matrices $P_{\alpha }=\mathrm{diag}(P_{h\alpha }, P_{v\alpha })\in \mathbb {R}^{2n_{h} \times 2n_{v}}$ and parameter-dependent matrices $K_{\alpha }\in \mathbb {R}^{(n_{h}+n_{v})\times (n_{h}+n_{v})}$, $M_{\alpha }\in \mathbb {R}^{(n_{h}+n_{v})\times (n_{h}+n_{v})}$, $Q_{\alpha }\in \mathbb {R}^{q\times (n_{h}+n_{v})}$ and $F_{\alpha }\in \mathbb {R}^{p\times ((n_{h}+n_{v}))}$ such that the following LMIs hold for all $\alpha \in \varGamma$:

$$\begin{aligned}&\bar{E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }\ge 0\end{aligned}$$

(3.1)

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \varTheta _{11}&{} K_{\alpha }\bar{B}_{\alpha }+\bar{A}^{T}_{\alpha }Q^{T}_{\alpha }&{} -K_{\alpha }+\bar{A}^{T}_{\alpha }M^{T}_{\alpha }&{} \bar{C}^{T}_{\alpha }+\bar{A}^{T}_{\alpha }F^{T}_{\alpha }\\ *&{} \varTheta _{22}&{} -Q_{\alpha }+\bar{B}^{T}_{\alpha }M^{T}_{\alpha }&{} \bar{B}^{T}_{\alpha }F^{T}_{\alpha }\\ *&{}*&{}-M_{\alpha }-M^{T}_{\alpha }+P_{\alpha } &{} -F^{T}_{\alpha }\\ *&{}*&{}*&{} -I_{p} \end{array} \right] <0 \end{aligned}$$

(3.2)

where

$$\begin{aligned} \varTheta _{11}&= -\bar{ E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }+K_{\alpha }\bar{A}_{\alpha }+\bar{A}^{T}_{\alpha }K^{T}_{\alpha }\\ \varTheta _{22}&= Q_{\alpha }\bar{B}_{\alpha }+\bar{B}^{T}_{\alpha }Q^{T}_{\alpha }-\gamma ^{2}I_{q} \end{aligned}$$

Proof 3.2

The LMIs (3.2) is obtained by considering

$$\begin{aligned} \chi&= \left[ \begin{array}{c} K_{\alpha }\\ Q_{\alpha }\\ M_{\alpha }\\ F_{\alpha }\\ \end{array} \right] ,\\ B&= \left[ \begin{array}{cccc} \bar{A}(\alpha )&\bar{B}(\alpha )&-I_{n_{h}+n_{v}}&0_{(n_{h}+n_{v})\times p} \end{array} \right] \\ Q&= \left[ \begin{array}{cccc} -\bar{ E}^{T}_{\alpha }P_{\alpha } \bar{E}_{\alpha }&{}0_{(n_{h}+n_{v}) \times q}&{} 0_{(n_{h}+n_{v})\times (n_{h}+n_{v})}&{} \bar{C}^{T}_{\alpha }\\ *&{}-\gamma ^{2}I_{q}&{}0_{q\times (n_{h}+n_{v})}&{}0_{q\times p}\\ *&{}*&{}P_{\alpha }&{}0_{(n_{h}+n_{v})\times P}\\ *&{}*&{}*&{}-I_{P} \end{array} \right] \\ \end{aligned}$$

in condition $(iv)$ of Lemma  2.8, with

$$\begin{aligned} B^{\bot }=\left[ \begin{array}{cccc} I_{n_{h}+n_{v}}&{}0_{(n_{h}+n_{v})\times q}&{} 0_{(n_{h}+n_{v})\times p}\\ 0_{q\times (n_{h}+n_{v})}&{}I_{q} &{}0_{q \times p}\\ \bar{A}_{\alpha } &{}\bar{B}_{\alpha }&{}0_{(n_{h}+n_{v})\times p}\\ 0_{p\times (n_{h}+n_{v})}&{}0_{p \times q}&{}I_{p} \end{array}\right] \end{aligned}$$

and then by calculation and Schur complement, using condition $(ii)$ of Lemma  2.8, we can obtain the equality between $B^{\bot T}QB^{\bot }<0$ and the LMIs in (2.14). Thus, (2.14) is equivalent to (3.2) using Lemma  2.8.

Remark 3.3

When the parameters of the filter $A_{f}, B_{f}$, and $H_{f}$ are known, then the matrices $\bar{E}_{\alpha }, \bar{A}_{\alpha }, \bar{B}_{\alpha }$, and $\bar{C}_{\alpha }$ belong to an uncertain polytope $\varGamma$, (3.1) and (3.2) would render a less conservative evaluation of the upper bound of the $H_{\infty }$ norm of the system (2.9), thanks to the degrees of freedom given by the slack variables $K_{\alpha }, Q_{\alpha }, M_{\alpha }$, and $F_{\alpha }$, and the fact that $P_{\alpha }$ is allowed to be vertex-dependent in (3.1) and (3.2). This enables us to derive a less conservative robust full-order filtering design.

Remark 3.4

In the case when $E=I$, Theorem  3.1 reduces to the parameter-dependent robust $H_{\infty }$ filtering results for regular 2D discrete Roesser model systems, which is general than the results in [14] and [39](if $K_{\alpha }=0, Q_{\alpha }=0, F_{\alpha }=0, M^{T}_{\alpha }=T_{\alpha }$ we have LMIs 7 in [14] and if $K^{T}_{\alpha }=F_{\tau }, Q_{\alpha }=0, F_{\alpha }=0, M^{T}_{\alpha }=V_{\tau }$ we have Theorem 1 in [39]), the slack variables $K_{\alpha }, Q_{\alpha }$, $F_{\alpha }=$ in Theorem  3.1 provide free dimensions in the solution space for the robust $H_{\infty }$ filtering problem.

Remark 3.5

When the 2D SRM (2.1)–(2.2) reduces to a 1D singular system, it is easy to show that Theorem  3.1 (with $Q_{\alpha }=0$ and $F_{\alpha }=0$) coincides with Lemma 2 in [41]; thus, the method used in this paper is more general than the method used in [41]. In the case when $\bar{E}_{\alpha }=I$, Theorem 3.1 reduces to the parameter-dependent bounded real lemma same as in [22], which has been shown to be less conservative than the filtering results using a common Lyapunov matrix for the entire uncertainty. Therefore, Theorem  3.1 can be viewed as an extension of the parameter-dependent bounded real lemma for discrete-time regular state-space systems to singular systems.

4 Robust $H_{\infty }$ Filter Design

In the previous section, the robust $H_{\infty }$ filter analysis problem was studied. Unfortunately, in the result of Theorem  3.1, there exist products of unknown matrices $P_{\alpha }, K_{\alpha }, M_{\alpha }, F_{\alpha }$ and $Q_{\alpha }$ with filter parameters $A_{f}, B_{f}, C_{f}$, so Theorem  3.1 cannot be used directly for the filter design problem. In this section, robust $H_{\infty }$ filter design problems for polytopic 2D SRM systems are investigated, giving a solution to this problem.

Theorem 4.1

The filtering error 2D SRM (2.9) is acceptable, internally stable, and causal with prescribed $H_{\infty }$ performance level $\gamma >0$ if there exist parameter-dependent symmetric positive definite matrices $P_{11\alpha }=\mathrm{diag}(P_{11h\alpha }, P_{11v\alpha })$ and $P_{22\alpha }=\mathrm{diag}(P_{22h\alpha }, P_{22v\alpha })$, and parameter-dependent matrices

$P_{12\alpha }=\mathrm{diag}(P_{12h\alpha }, P_{12v\alpha }), K_{11\alpha }, K_{21\alpha }, M_{11\alpha }, M_{21\alpha }, Q_{1\alpha }, F_{1\alpha }$ and matrices $\hat{K}, \bar{A}_{f}, \bar{B}_{f}, \bar{C}_{f}$ and scalars $\lambda _{1}, \lambda _{2}$ such that the following LMIs hold for all $\alpha \in \varGamma$

$$\begin{aligned}&\left[ \begin{array}{cc} E^{T}_{\alpha }P_{11\alpha } E_{\alpha }&{}E^{T}_{\alpha }P_{12\alpha }\\ *&{} P_{22\alpha } \end{array} \right] \ge 0\end{aligned}$$

(4.1)

$$\begin{aligned}&\left[ \begin{array}{cccccc} \varLambda _{11}&{}\varLambda _{12}&{}\varLambda _{13}&{}\varLambda _{14}&{}\varLambda _{15}&{}\varLambda _{16}\\ *&{} \varLambda _{22}&{}\varLambda _{23}&{}\varLambda _{24}&{}\varLambda _{25}&{}-\bar{C}^{T}_{f}\\ *&{} *&{} \varLambda _{33} &{} \varLambda _{34}&{}\varLambda _{35}&{} B^{T}_{\alpha }F^{T}_{1\alpha }\\ *&{}*&{}*&{}\varLambda _{44}&{}\varLambda _{45}&{}-F^{T}_{1\alpha }\\ *&{}*&{}*&{}*&{}\varLambda _{55}&{}0\\ *&{}*&{}*&{}*&{}*&{}-I \end{array} \right] <0 \end{aligned}$$

(4.2)

where

$$\begin{aligned} \varLambda _{11}&= -E^{T}_{\alpha }P_{11\alpha } E_{\alpha }+K_{11\alpha }A_{\alpha }+A^{T}_{\alpha }K^{T}_{11\alpha }+\lambda _{1}(C^{T}_{\alpha }\bar{B}^{T}_{f}+\bar{B}_{f}C_{\alpha })\\ \varLambda _{12}&= -E^{T}_{\alpha }P_{12\alpha }+\lambda _{1}\bar{A}_{f}+A^{T}_{\alpha }K^{T}_{21\alpha }+\lambda _{2}C^{T}_{\alpha }\bar{B}^{T}_{f}\\ \varLambda _{13}&= A^{T}_{\alpha }Q^{T}_{1\alpha }+K_{11\alpha }B_{\alpha }+\lambda _{1}\bar{B}_{f}D_{\alpha }\\ \varLambda _{14}&= A^{T}_{\alpha }M^{T}_{11\alpha }+C^{T}_{\alpha }\bar{B}^{T}_{f}-K_{11\alpha }\\ \varLambda _{15}&= A^{T}_{\alpha }M^{T}_{21\alpha }+C^{T}_{\alpha }\bar{B}^{T}_{f}-\lambda _{1}\hat{K}\\ \varLambda _{16}&= A^{T}_{\alpha }F^{T}_{1\alpha }+H^{T}_{\alpha }\\ \varLambda _{22}&= -P_{22\alpha }+\lambda _{2}(\bar{A}_{f}+\bar{A}^{T}_{f})\\ \varLambda _{23}&= K_{21\alpha }B_{\alpha }+\lambda _{2}\bar{B}_{f}D_{\alpha }\\ \varLambda _{24}&= \bar{A}^{T}_{f}-K_{21\alpha }\\ \varLambda _{25}&= \bar{A}^{T}_{f}-\lambda _{2}\hat{K}\\ \varLambda _{33}&= Q_{1\alpha }B_{\alpha }+B^{T}_{\alpha }Q^{T}_{1\alpha }-\gamma ^{2}I\\ \varLambda _{34}&= B^{T}_{\alpha }M^{T}_{11\alpha }+D^{T}_{\alpha }\bar{B}^{T}_{f}-Q_{1\alpha }\\ \varLambda _{35}&= B^{T}_{\alpha }M^{T}_{21\alpha }+D^{T}_{\alpha }\bar{B}^{T}_{f}\\ \varLambda _{44}&= -M_{11\alpha }-M^{T}_{11\alpha }+P_{11\alpha }\\ \varLambda _{45}&= -\hat{K}-M^{T}_{21\alpha }+P_{12\alpha }\\ \varLambda _{55}&= -\hat{K}-\hat{K}^{T}+P_{22\alpha } \end{aligned}$$

Then, there exists a filter of the form of (2.8) such that the filtering error dynamics are acceptable, asymptotically stable, and causal, and the prescribed $H_{\infty }$ performance level $\gamma$ is achieved. This $H_{\infty }$ filter can be computed from

$$\begin{aligned} \left[ \begin{array}{cc} A_{f}&{}B_{f}\\ C_{f}&{}0 \end{array} \right] = \left[ \begin{array}{cc} \hat{K}^{-1}&{}0\\ 0&{}I \end{array} \right] \times \left[ \begin{array}{lll} \bar{A}_{f}&{}\bar{B}_{f}\\ \bar{C}_{f}&{}0 \end{array} \right] \end{aligned}$$

Proof 4.2

As $\varUpsilon ^{T}=\varUpsilon ^{-1}$, pre- and post-multiplying (3.1) by $\varUpsilon ^{T}$ and (3.2) by $\mathrm{diag}(\varUpsilon ^{T},I,\varUpsilon ^{T},I)$ gives

$$\begin{aligned}&\displaystyle \tilde{E}^{T}_{\alpha }\varUpsilon ^{T}P_{\alpha }\varUpsilon \tilde{E}_{\alpha }\ge 0\end{aligned}$$

(4.3)

$$\begin{aligned}&\displaystyle \left[ \begin{array}{cccc} \varPhi _{11}&{}\varPhi _{12}&{}-\varUpsilon ^{T}K_{\alpha }\varUpsilon +\tilde{A}^{T}_{\alpha }\varUpsilon ^{T}M^{T}_{\alpha }\varUpsilon &{}\tilde{A}^{T}_{\alpha }\varUpsilon ^{T}F^{T}_{\alpha }+\tilde{C}^{T}_{\alpha }\\ *&{}\varPhi _{22}&{}-Q_{\alpha }\varUpsilon +\tilde{B}^{T}_{\alpha }\varUpsilon ^{T}M^{T}_{\alpha }\varUpsilon &{}\tilde{B}^{T}_{\alpha }\varUpsilon ^{T}F^{T}_{\alpha }\\ *&{}*&{}-\varUpsilon ^{T}M^{T}_{\alpha }\varUpsilon -\varUpsilon ^{T}M_{\alpha }\varUpsilon +\varUpsilon ^{T} P_{\alpha }\varUpsilon &{}-\varUpsilon ^{T}F^{T}_{\alpha }\\ *&{}*&{}*&{}-I \end{array} \right] <0\quad \end{aligned}$$

(4.4)

where

$$\begin{aligned} \varPhi _{11}&= -\tilde{E}^{T}_{\alpha }\varUpsilon ^{T} P_{\alpha }\varUpsilon \tilde{E}_{\alpha }+\varUpsilon ^{T}K_{\alpha }\varUpsilon \tilde{A}_{\alpha }+\tilde{A}^{T}_{\alpha }\varUpsilon ^{T}K^{T}_{\alpha }\varUpsilon \\ \varPhi _{12}&= \varUpsilon ^{T}K_{\alpha }\varUpsilon \tilde{B}_{\alpha }+\tilde{A}^{T}_{\alpha }\varUpsilon ^{T}Q^{T}_{\alpha }\\ \varPhi _{22}&= Q_{\alpha }\varUpsilon \tilde{B}_{\alpha }+\tilde{B}^{T}_{\alpha }\varUpsilon ^{T}Q^{T}_{\alpha }-\gamma ^{2}I \end{aligned}$$

$\tilde{E}_{\alpha }, \tilde{A}_{\alpha }, \tilde{B}_{\alpha }$, and $\tilde{C}_{\alpha }$ are given in (2.10). The rest of the matrices have the following structures

$$\begin{aligned} \varUpsilon ^{T} P_{\alpha }\varUpsilon&= \varUpsilon ^{T} \mathrm{diag}\{P_{h\alpha }, P_{v\alpha }\}\varUpsilon = \left[ \begin{array}{cc} P_{11\alpha }&{}P_{12\alpha }\\ P^{T}_{12\alpha }&{}P_{22\alpha } \end{array} \right] ,\\ \varUpsilon ^{T} K_{\alpha }\varUpsilon&= \left[ \begin{array}{cc} K_{11\alpha }&{}\lambda _{1}\hat{K}\\ K_{21\alpha }&{}\lambda _{2}\hat{K} \end{array} \right] , \varUpsilon ^{T} M_{\alpha }\varUpsilon =\left[ \begin{array}{cc} M_{11\alpha }&{}\hat{K}\\ M_{21\alpha }&{}\hat{K} \end{array} \right] \\ Q_{\alpha }\varUpsilon&= [Q_{1\alpha } \quad 0], F_{\alpha }\varUpsilon =[F_{1\alpha } \quad 0] \end{aligned}$$

Now, defining $\hat{K}A_{f}= \bar{A}_{f}, \hat{K}B_{f}= \bar{B}_{f}$ and $C_{f}= \bar{C}_{f}$ gives (4.1) and (4.2), which completes the proof. $\square$

5 Solution Using Parameter-Dependent Polynomials

To solve the parameter-dependent LMI conditions of Theorems  4.1, the polynomially parameter-dependent method is used; this method includes results in the quadratic framework and the linearly parameter-dependent framework as particular cases, for polynomials of degrees 0 and 1, respectively.

Now, before presenting the Theorem  4.1 using homogeneous parameter-dependent polynomials, some definitions and preliminaries from [14] are recalled. For the matrices $P_{11\alpha }$, we take a homogeneous polynomially dependent Lyapunov function given by

$$\begin{aligned} P_{11\alpha (g)}=\sum _{j=1}^{J(g)}\alpha _{1}^{k_{1}}\alpha _{2}^{k_{2}}\ldots \alpha _{N}^{k_{N}}P_{11\kappa _{j}(g)}; k_{1}k_{2}\ldots k_{N}=\kappa _{j}(g) \end{aligned}$$

(5.1)

Similar definitions for the matrices $P_{22\alpha }, P_{12\alpha }, K_{11\alpha }, K_{21\alpha }, M_{11\alpha }, M_{21\alpha }, Q_{1\alpha }$ and $F_{1\alpha }$ are used.

To facilitate the presentation, we denote $\beta ^{j}_{i}(j+1)$ in [14] by $\vartheta$; using this notation. we now present the Theorem  5.1.

Theorem 5.1

The filtering error 2D SRM (2.9) is acceptable, asymptotically stable, and causal with prescribed $H_{\infty }$ performance level $\gamma >0$ if there exist parameter-dependent symmetric positive definite matrices $P_{11\kappa _{j}(g)}=\mathrm{diag}(P_{11h\kappa _{j}(g)}, P_{11v\kappa _{j}(g)})$ and $P_{22\kappa _{j}(g)}=\mathrm{diag}(P_{22h\kappa _{j}(g)}, P_{22v\kappa _{j}(g)})$, and parameter-dependent matrices

$P_{12\kappa _{j}(g)}=\mathrm{diag}(P_{12h\kappa _{j}(g)}, P_{12v\kappa _{j}(g)}), K_{11\kappa _{j}(g)}, K_{21\kappa _{j}(g)}, M_{11\kappa _{j}(g)},$ $M_{21\kappa _{j}(g)}, Q_{1\kappa _{j}(g)}, F_{1\kappa _{j}(g)}, \kappa _{j}(g) \in \kappa (g), j=1,\cdots ,J(g)$ and matrices $\hat{K},$ $\bar{A}_{f}, \bar{B}_{f}, \bar{C}_{f}$ and scalars $\lambda _{1}$, $\lambda _{2}$ such that the following LMIs hold for all $\kappa _{l}(g+1) \in \kappa (g+1), l=1,\cdots ,J(g+1)$:

$$\begin{aligned}&\sum _{i\in I_{l}(g+1)}\left[ \begin{array}{c@{\quad }c} E^{T}_{i}P_{11\kappa ^{i}_{l}(g)} E_{i}&{}E^{T}_{i}P_{12\kappa ^{i}_{l}(g)}\\ *&{} P_{22\kappa ^{i}_{l}(g)} \end{array} \right] \ge 0\end{aligned}$$

(5.2)

$$\begin{aligned}&\sum _{i\in I_{l}(g+1)}\left[ \begin{array}{cccccc} \varLambda _{11}&{}\varLambda _{12}&{}\varLambda _{13}&{}\varLambda _{14}&{}\varLambda _{15}&{}\varLambda _{16}\\ *&{} \varLambda _{22}&{}\varLambda _{23}&{}\varLambda _{24}&{}\varLambda _{25}&{}-\vartheta \bar{C}^{T}_{f}\\ *&{} *&{} \varLambda _{33} &{} \varLambda _{34}&{}\varLambda _{35}&{} B^{T}_{\alpha }F^{T}_{1\kappa ^{i}_{l}(g)}\\ *&{}*&{}*&{}\varLambda _{44}&{}\varLambda _{45}&{}-F^{T}_{1\kappa ^{i}_{l}(g)}\\ *&{}*&{}*&{}*&{}\varLambda _{55}&{}0\\ *&{}*&{}*&{}*&{}*&{}-\vartheta I \end{array} \right] <0 \end{aligned}$$

(5.3)

where

$$\begin{aligned} \varLambda _{11}&= -E^{T}_{i}P_{11\kappa ^{i}_{l}(g)} E_{i}+K_{11\kappa ^{i}_{l}(g)}A_{i}+A^{T}_{i}K^{T}_{11\kappa ^{i}_{l}(g)}+\lambda _{1}\vartheta (C^{T}_{i}\bar{B}^{T}_{f}+\bar{B}_{f}C_{i})\\ \varLambda _{12}&= -E^{T}_{i}P_{12\kappa ^{i}_{l}(g)}+\lambda _{1}\vartheta \bar{A}_{f}+A^{T}_{i}K^{T}_{21\kappa ^{i}_{l}(g)}+\lambda _{2}\vartheta C^{T}_{i}\bar{B}^{T}_{f}\\ \varLambda _{13}&= A^{T}_{i}Q^{T}_{1\kappa ^{i}_{l}(g)}+K_{11\kappa ^{i}_{l}(g)}B_{i}+\lambda _{1}\vartheta \bar{B}_{f}D_{i}\\ \varLambda _{14}&= A^{T}_{i}M^{T}_{11\kappa ^{i}_{l}(g)}+\vartheta C^{T}_{i}\bar{B}^{T}_{f}-K_{11\kappa ^{i}_{l}(g)}\\ \varLambda _{15}&= A^{T}_{i}M^{T}_{21\kappa ^{i}_{l}(g)}+\vartheta C^{T}_{i}\bar{B}^{T}_{f}-\lambda _{1}\vartheta \hat{K}\\ \varLambda _{16}&= A^{T}_{i}F^{T}_{1\kappa ^{i}_{l}(g)}+H^{T}_{i}\\ \varLambda _{22}&= -P_{22\kappa ^{i}_{l}(g)}+\lambda _{2}\vartheta (\bar{A}_{f}+\bar{A}^{T}_{f})\\ \varLambda _{23}&= K_{21\kappa ^{i}_{l}(g)}B_{i}+\lambda _{2}\vartheta \bar{B}_{f}D_{i}\\ \varLambda _{24}&= \vartheta \bar{A}^{T}_{f}-K_{21\kappa ^{i}_{l}(g)}\\ \varLambda _{25}&= \vartheta \bar{A}^{T}_{f}-\lambda _{2}\vartheta \hat{K}\\ \varLambda _{33}&= Q_{1\kappa ^{i}_{l}(g)}B_{i}+B^{T}_{i}Q^{T}_{1\kappa ^{i}_{l}(g)}-\gamma ^{2}\vartheta I\\ \varLambda _{34}&= B^{T}_{i}M^{T}_{11\kappa ^{i}_{l}(g)}+\vartheta D^{T}_{i}\bar{B}^{T}_{f}-Q_{1\kappa ^{i}_{l}(g)}\\ \varLambda _{35}&= B^{T}_{i}M^{T}_{21\kappa ^{i}_{l}(g)}+\vartheta D^{T}_{i}\bar{B}^{T}_{f}-Q_{1\kappa ^{i}_{l}(g)}\\ \varLambda _{44}&= -M_{11\kappa ^{i}_{l}(g)}-M^{T}_{11\kappa ^{i}_{l}(g)}+P_{11\kappa ^{i}_{l}(g)}\\ \varLambda _{45}&= -\vartheta \hat{K}-M^{T}_{21\kappa ^{i}_{l}(g)}+P_{12\kappa ^{i}_{l}(g)}\\ \varLambda _{55}&= -\vartheta \hat{K}-\vartheta \hat{K}^{T}+P_{22\kappa ^{i}_{l}(g)} \end{aligned}$$

then the homogeneous polynomially parameter-dependent matrices given by (5.1) ensure that (4.1) and (4.2) are fulfilled for all $\alpha \in \varGamma$. Moreover, if the LMIs (5.2) and (5.3) are fulfilled for a given degree $g$, then the LMIs corresponding to any degree $\hat{g}>g$ are also satisfied.

Proof 5.2

The proof is parallel to that of Theorem 3 in [14], using the result in Theorem  4.1, so it is omitted. $\square$

Remark 5.3

The parameters $\lambda _{1}$ and $\lambda _{2}$ in Theorem  5.1 can be searched using, for example, the MATLAB fminsearch program, to attain an optimized result. When they are set to be fixed constants, (5.3) is linear in the variables. Thus, an optimal $H_{\infty }$ filter is obtained by solving the following convex optimization problem, minimize $\delta$ subject to (5.2) and (5.3) with $\delta =\gamma ^{2}$ using Yalmip ([13]) and SeDumi ([25]).

Remark 5.4

for degrees $g=0$ and $g=1$ of variable matrices dependent on the parameter $\alpha$ given in Theorem  5.1, we obtain, respectively, the quadratic framework and the linearly parameter-dependent framework, so Theorem  5.1 is general for all degrees $g$.

6 Illustrative Examples

In this section, examples are given to illustrate the effectiveness of the proposed method. The robust $H_{\infty }$ filter design for 2D singular systems using Theorem  5.1 is presented in Examples 1, 2 (Case 1), and 3. To show that the Theorem  5.1 is a general filter design method including both singular and non-singular systems, comparisons between the existing paper [14] and Theorem  5.1 are illustrated in Example 2 (Case 2).

6.1 Example 1

Consider a 2D SRM with the following parameters, based on a system in [36]:

with $-0.6\le \sigma _{1} \le 0.6$ and $-0.6\le \sigma _{2} \le 0.6$.

since

$\mathrm{det}[E_{\alpha }I(z,w)-A_{\alpha }]=(2-z)(w-\sigma _{1})(1+\sigma _{2})$ and $\mathrm{deg}\; \mathrm{det}(sE_{\alpha }-A_{\alpha })=2=\mathrm{rank}E_{\alpha }$

so the given system is acceptable when $\sigma _{2}\ne -1$.

From Lemma  2.4, the system is causal.

For this system, the $H_\infty$ disturbance attenuation levels are $g=0$ (quadratic method) and $g=1$ (linearly parameter-dependent method) in Theorem  5.1 are 0.3241 and 0.2946, respectively. Now, we apply the filter design method corresponding to $g=2$, the obtained guaranteed performance $\gamma =0.2946$ with $\lambda _{1}=0.0070, \lambda _{2}=-0.0132$, and the associated filter matrices are

$$\begin{aligned} A_{f}&= \left[ \begin{matrix} 0.1715 &{} 0.3763&{} 1.5876\\ -0.2648&{} 0.7612 &{} 6.2572\\ -0.0022&{} -0.0039&{} 0.3959\\ \end{matrix}\right] ,\\ B_{f}&= \left[ \begin{matrix} -1.8468\\ -0.2674\\ -0.0022\\ \end{matrix}\right] ,\\ C_{f}&= \left[ \begin{matrix}-0.0990 &{} -0.0603&{} -0.1698\\ \end{matrix}\right] \end{aligned}$$

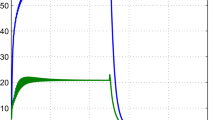
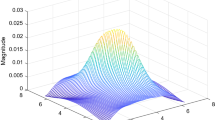
The obtained results show that the larger the value of $g$, the smaller the value of $\gamma$, which indicate the less conservatism of filtering results. For the designed filter with $g=2$, the actual $H_{\infty }$ norms calculated at the two vertices are shown in Figs. 1, 2, 3, and 4, all of which are below the guaranteed bound 0.2946.

Fig. 1

Frequency response of filtering error system: First vertex

Fig. 2

Frequency response of filtering error system: Second vertex

Fig. 3

Frequency response of filtering error system: Third vertex

Fig. 4

Frequency response of filtering error system: Fourth vertex

6.2 Example 2

Consider a 2D SRM with the following parameters, adapted from [14]:

Case 1: singular system

with $0.15\le a_{1}\le 0.8$ and $0.35\le a_{2}\le 1.9$.

since

$\mathrm{det}[E_{\alpha }I(z,w)-A_{\alpha }]=(z-a_{1})a_{2}$ and $\mathrm{deg}\; \mathrm{det}(sE_{\alpha }-A_{\alpha })=1=\mathrm{rank}E_{\alpha }$

so the given system is acceptable when $a_{2}\ne 0$.

From Lemma  2.4, the system is causal.

For this system, the $H_{\infty }$ disturbance attenuation level for $g=0$ (quadratic method) and $g=1$ (linearly parameter-dependent method) in Theorem  5.1 is 8.7299 and 6.0443, respectively. Now, we apply the filter design method corresponding to $g=2$, the obtained guaranteed performance $\gamma =5.8514$ with $\lambda _{1}=-0.5869, \lambda _{2}=0.0544$, and the associated filter matrices are

$$\begin{aligned} A_{f}=\left[ \begin{matrix} 0.2568&{}0 \\ 0.4614&{}-0.0497 \end{matrix}\right] , B_{f}=\left[ \begin{matrix} 0.3197 \\ 0.9147 \end{matrix}\right] , C_{f}=\left[ \begin{matrix}4.3087&{}0\\ \end{matrix}\right] \end{aligned}$$

The obtained results show that the larger the value of $g$, the smaller the value of $\gamma$, which indicate the less conservatism of filtering results. For the designed filter with $g=2$, the actual $H_{\infty }$ norms calculated at the four vertices are shown in Figs. 5, 6, 7, and 8, all of which are below the guaranteed bound 5.8514 (Table 1).

Fig. 5

Frequency response of filtering error system: First vertex

Fig. 6

Frequency response of filtering error system: Second vertex

Fig. 7

Frequency response of filtering error system: Third vertex

Fig. 8

Frequency response of filtering error system: Fourth vertex

Case 2: non-singular system

with $0.15\le a_{1}\le 0.45$ and $0.35\le a_{2}\le 0.85$.

Table 1 The minimum $\gamma$ obtained with several arbitrary degree $g$

Applying the filter design method corresponding to $g=2$, the associated filter matrices are

$$\begin{aligned} A_{f}=\left[ \begin{matrix} 0.7112&{}-0.1682\\ 0.1400&{}0.2534 \end{matrix}\right] , B_{f}=\left[ \begin{matrix} -0.3408 \\ -1.3154 \end{matrix}\right] , C_{f}=\left[ \begin{matrix}-0.0479&{}-0.4577\\ \end{matrix}\right] \end{aligned}$$

For the designed filter with $g=2$, the actual $H_{\infty }$ norms calculated at the four vertices are shown in Figs. 9, 10, 11, and 12: it can be seen that all the norms are effectively below the guaranteed bound 1.8055.

Fig. 9

Frequency response of filtering error system: First vertex

Fig. 10

Frequency response of filtering error system: Second vertex

Fig. 11

Frequency response of filtering error system: Third vertex

Fig. 12

Frequency response of filtering error system: Fourth vertex

6.3 Example 3

In this example, we consider a thermal processes in chemical reactors, heat exchangers, and pipe furnaces, which can be described by the partial differential equation [37]:

$$\begin{aligned} \frac{\partial T(x,t)}{\partial x}=-\frac{\partial T(x,t)}{\partial t}-T(x,t) \end{aligned}$$

(6.1)

where $T(x,t)$ is usually the temperature at $x(space)\in [0,xf]$ and $t(time)\in [0,\infty ]$.

Assuming that the disturbance input is given by $w(i,j)$,

the partial differential equation can be modeled into the following 2D SRM: (see [37] for more details)

$$\begin{aligned} \begin{array}{ccccc} \left[ \begin{matrix} 1&{}0 \\ 1&{}0 \end{matrix}\right] \left[ \begin{array}{lll} x^h(i+1,j) \\ x^v(i,j+1) \end{array}\right] &{}=&{}\left[ \begin{matrix} a_{1}&{}0 \\ 0&{}1 \end{matrix}\right] \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] &{}+&{} \left[ \begin{matrix} 0.1\\ 0 \end{matrix}\right] w(i,j) \\ \end{array} \end{aligned}$$

(6.2)

It is easy to check that the given system is converted to

$$\begin{aligned} \begin{array}{ccccc} \left[ \begin{matrix} 1&{}0 \\ 0&{}0 \end{matrix}\right] \left[ \begin{array}{lll} x^h(i+1,j) \\ x^v(i,j+1) \end{array}\right] &{}=&{}\left[ \begin{matrix} a_{1}&{}0 \\ -a_{1}&{}1 \end{matrix}\right] \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] &{}+&{} \left[ \begin{matrix} 0.1\\ -0.1 \end{matrix}\right] w(i,j) \\ \end{array} \end{aligned}$$

(6.3)

We now assume that the measured output and the signal to be estimated are given by

$$\begin{aligned} y(i,j)&= \left[ \begin{matrix} 0.1&{}0 \\ 0&{}0.1 \end{matrix}\right] \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] \end{aligned}$$

(6.4)

$$\begin{aligned} z(i,j)&= \left[ \begin{matrix} 0.2&{}0.1 \\ 0.1&{}0 \end{matrix}\right] \left[ \begin{array}{llll} x^h(i,j) \\ x^v(i,j) \end{array}\right] \end{aligned}$$

(6.5)

In this example, we also suppose that $-0.99\le a_{1}\le 0.99$

since

$\mathrm{det}[E_{\alpha }I(z,w)-A_{\alpha }]=(a_{1}-z)$ and $\mathrm{deg}\; \mathrm{det}(sE_{\alpha }-A_{\alpha })=1=\mathrm{rank}E_{\alpha }$

so the given system is acceptable, and from Lemma  2.4, the system is causal.

For this system, the value of the $H_\infty$ disturbance attenuation level for $g=0$ (quadratic method) and $g=1$ (linearly parameter-dependent method) in Theorem  5.1 is 1.0001 and 0.4472, respectively. Now, we apply the filter design method corresponding to $g=2$, the obtained guaranteed performance $\gamma =0.4471$ with $\lambda _{1}=0.0596, \lambda _{2}=-0.3484$, and the associated filter matrices are

$$\begin{aligned} A_{f}=\left[ \begin{matrix} 0.2527 &{}0.0002\\ -0.0847&{}0.3482 \end{matrix}\right] , B_{f}=\left[ \begin{matrix} -1.7080&{}-10.4444\\ -0.9840 &{}-0.9893 \end{matrix}\right] , C_{f}=\left[ \begin{matrix}-0.1721&{}0.0000\\ -0.0861 &{}0.0000 \end{matrix}\right] \end{aligned}$$

For the designed filter with $g=2$, the actual $H_{\infty }$ norms calculated at the two vertices are shown in Figs. 13 and 14: all the norms are clearly below the guaranteed bound 0.4471.

Fig. 13

Frequency response of filtering error system: First vertex

Fig. 14

Frequency response of filtering error system: Second vertex

7 Conclusions

New parameter-dependent LMI conditions for the design of full-order robust and $H_{\infty }$ filters have been proposed, for uncertain 2D singular systems with time-invariant parameters. LMI relaxations based on homogeneous polynomials of arbitrary degrees are used to reduce the conservatism, based on an improved version of bounded real lemma. The developed filter design method has been illustrated by numerical examples to show the general robust $H_{\infty }$ filter design algorithm for both singular systems and non-singular systems. The main results in this paper may be further extended to robust $H_{\infty }$ filter design for uncertain 2D singular delayed systems, $H_{\infty }$ control for uncertain 2D singular systems, and $H_{\infty }$ control for uncertain 2D singular delayed systems.