1 Introduction

Two-dimensional (2-D) systems have important applications in many fields such as signal and image processing, seismographic data processing, biomedical imaging processing, process control, and iterative learning control [5, 13, 16]. Thus the design of 2-D control systems is of practical significance and has attracted a lot of interest in the past decade. Hinamoto and Lu investigated the stability of 2-D systems through Lyapunov approaches [11, 17], Xie et al. and Du et al. are concerned with controller and filter design problems [4, 19]. It is known that the H ∞ control has been a most active area of control systems in the past two decades [18]. The main advantage of H ∞ control is that its performance specification takes into account the worst case performance of the system in terms of the system energy gain. This is more appropriate for system robustness analysis and robust control under modeling uncertainties and disturbances than the other performance specifications such as the LQ-optimal control specification. Thus the development of the H ∞ control theory has greatly advanced the methods for analysis and design of robust control systems.

In the past few decades, the study of stochastic systems has received much attention over the past few decades due to the extensive application of stochastic systems in biology, economics, mechanical system and other areas [18]. A great number of fundamental results for stochastic systems have been reported in the literature. For example, the analysis of asymptotic behavior can be found in [2, 22], optimal control problems were reported in [10, 18], robust control and filtering results were studied in [6, 10, 12]. Most of the aforementioned results are concerned with 1-D stochastic systems. In the 2-D case, the robust stabilization problem for 2-D systems with stochastic uncertainties was addressed in [9], where stabilizing state feedback controllers were designed via an LMI approach. The problem of H∞ filter design for 2-D systems with stochastic perturbations was presented in [8]. On the other hand, the nonlinearity is another important feature existing in almost all practical systems. Since nonlinearities may cause undesirable dynamic behaviors such as oscillation or even instability, the analysis and synthesis problems for nonlinear systems have been extensively investigated [7, 15, 18, 20]. Due to stochastic and nonlinear phenomena frequently exhibited in many branches of science and engineering applications, growing research interests have been paid to the study of stability and control problems for nonlinear stochastic systems, and a great number of results on this subject were reported in the literature; The stabilization problem was investigated in [9] for nonlinear stochastic systems. In [20], a global decentralized stabilization algorithm was given for a class stochastic nonlinear system with nonlinear interconnections in the drift vector fields. Most recently, in [16], the extended Kalman filtering problem has been investigated for a class of nonlinear systems with multiple missing measurements over a finite horizon. It is worth pointing out that the sector nonlinearity [17] has gained much attention for deterministic systems among different descriptions of the nonlinearities.

Very recently, the problems of stability analysis and stabilization for a class of 2-D nonlinear discrete systems have been studied in [21], in which sufficient conditions for the solvability of this problem were obtained and an LMI approach was proposed. However, the above mentioned results were obtained in the context of 2-D nonlinear discrete systems. When 2-D discrete systems with stochastic and nonlinear uncertainties are concerned, no results on H ∞ control for such systems have been available in the literature so far, which motivates the present study.

In this paper, we consider the problem of stability and robust H ∞ control for 2-D stochastic systems with sector nonlinearities. Our attention is focused on the design of a state feedback controller for a nonlinear discrete time 2-D stochastic system, such that the closed-loop 2-D stochastic system is asymptotically stable and has a prescribed H ∞ disturbance attenuation performance. Similar to the result of 1-D systems [2], the bounded realness property of 2-D stochastic systems with sector nonlinearities plays a key role for the H ∞ control solution. We will first extend the bounded real lemma for 2-D systems to 2-D stochastic systems with nonlinearities. Based on this lemma, solvability conditions for the H ∞ control of 2-D nonlinear stochastic systems in the form of LMIs (linear matrix inequalities) are derived, and the corresponding controller design is cast into a convex optimization problem that can be efficiently handled by using MATLAB LMI Toolbox. A numerical example is provided to illustrate the usefulness of the proposed controller design procedures.

2 Stability Analysis of 2-D Stochastic System with Sector Nonlinearity

In this section, we discuss mean-square asymptotic stability for 2-D discrete stochastic system with sector nonlinearity. Consider the 2-D stochastic system with sector nonlinearity in the following Roesser model [9]:

(1)
(2)

where \(x^{h} \in R^{n_{1}}\) and \(x^{v} \in R^{n_{2}}\) represent the horizontal and vertical states. The function ψ(•) denotes the standard vector-valued sector nonlinearity (see Definition 2). A is system matrix with compatible dimensions, A 1, M and M 1 are appropriately dimensions matrix, and v i,j is a standard random scalar signal satisfying E{v i,j }=0, where E{•}stands for the mathematical expectation and

$$ E\{ v_{i,j}v_{m,n}\} = \begin{cases} 1 & (i,j) = (m,n)\\ 0& (i,j) \ne(m,n) \end{cases} $$
(3)

Throughout the paper, we make the following assumption on the boundary condition:

Assumption 1

The boundary condition is independent of v i,j and is assumed to satisfy

$$\lim_{N \to\infty} E \Biggl\{ \sum_{k = 0}^{N} \bigl[ \bigl \Vert x^{h}(0,k) \bigr \Vert ^{2} + \bigl \Vert x^{v}(k,0) \bigr \Vert ^{2} \bigr] \Biggr\} < \infty $$

Similar to [9], we give the following definition which will be used throughout the paper.

Definition 1

([3]) The two-dimensional discrete stochastic system (1) with Assumption 1 is said to be mean-square asymptotically stable if under the zero input and for every initial condition E{∥x 0,0∥2}<∞,

$$\lim_{i + j \to\infty} E \bigl\{ \Vert x_{i,j} \Vert ^{2} \bigr\} = 0 $$

Definition 2

([15]) A memoryless vector nonlinear function ψ:R n→R n is said to satisfy a sector condition if

$$ \bigl( \psi(q) - K_{1}q \bigr)^{T} \bigl( \psi(q) - K_{2}q \bigr) \le0,\quad \forall q \in R^{n} $$
(4)

for some diagonal real matrices K 1,K 2∈R n×n. In this case, we say that ψ belongs to the sector K=[K 1,K 2] and denote it by ψ∈[K 1,K 2].

Lemma 1

(Schur complement)

For matrices Σ 1, Σ 2 and Σ 3 whereΣ 1>0 and \(\varSigma_{3} = \varSigma _{3}^{T}\) then \(\varSigma_{3} + \varSigma _{2}^{T}\varSigma_{1}^{ - 1}\varSigma_{2} < 0\) if and only if

$$\left [ \begin{array}{c@{\quad }c} \varSigma_{3} & \varSigma_{2}^{T} \\ \varSigma_{2} & - \varSigma_{1} \end{array} \right ] < 0\quad\mbox{\textit{or}} \quad \left [ \begin{array}{c@{\quad }c} - \varSigma_{1} & \varSigma_{2} \\ \varSigma_{2}^{T} & \varSigma_{3} \end{array} \right ] < 0 $$

The following theorem gives the criterion of stability for the system (1)–(2).

Theorem 1

For the system (1)–(2), ψ belonging to the sector K=[K 1,K 2], if there exist a positive definite symmetric matrix P=diag{P h ,P v }>0 and a scalar ε>0 satisfying

$$ \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} - P & PC^{T}K & P ( A + A_{1}K_{1}C )^{T} & P ( M + M_{1}K_{1}C )^{T} \\ * & - 2\varepsilon I & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} \\ * & * & - P & 0 \\ * & * & * & - P \end{array} \right ] < 0 $$
(5)

where K=K 2−K 1 is a positive definite symmetric matrix, the asterisk (∗) represents a term that is induced by symmetry. Then, the system (1)–(2) is asymptotically stable for any ψ(q)∈[K 1,K 2].

Proof

We decompose the nonlinear function ψ(q) into a linear and a nonlinear part as ψ(q)=ψ n (q)+K 1 q, where the nonlinearity ψ n (q) belongs to the set Φ given by [21]

$$ \varPhi= \bigl\{ \psi_{n}(q)\mid \bigl( \psi_{n}(q) \bigr)^{T} \bigl( \psi_{n}(q) - Kq \bigr) \le0,\forall q \in R^{n} \bigr\} $$
(6)

Since ψ belongs to the sector K=[K 1,K 2], the system (1) becomes

(7)

To establish the stability of system (1)–(2). Consider the following index:

$$J: = \mathbb{E} \bigl\{ x'^{T}Qx'|x \bigr \} - x^{T}Qx $$

where , and Q is a symmetric positive definite matrix to be determined. Then along the solution of the system (1)–(2) we have

where

$$\varPsi= \left [ \begin{array}{c@{\quad }c} \left ( \begin{array}{c} ( A + A_{1}K_{1}C )^{T}Q ( A + A_{1}K_{1}C ) + \\ ( M + M_{1}K_{1}C )^{T}Q ( M + M_{1}K_{1}C ) - Q \end{array} \right ) & \left ( \begin{array}{l} ( A + A_{1}K_{1}C )^{T}QA_{1} + \\ ( M + M_{1}K_{1}C )^{T}QM_{1} + \mu C^{T}K \end{array} \right ) \\ * & A_{1}^{T}QA_{1} + M_{1}^{T}QM_{1} - 2\mu I \end{array} \right ], $$

, Q=P −1,E{x|y} stands for the mathematical expectation of x conditional on y.

By the Schur complement, LMI (5) implies Ψ<0. Then for all x≠0, we have

$$\frac{E\{ x'^{T}Qx'|x\} - x^{T}Qx}{x^{T}Qx} = - \frac{\eta^{T}( - \varPsi )\eta}{x^{T}Qx} \le- \frac{\lambda_{\min} ( - \varPsi)\eta^{T}\eta}{\lambda_{\max} (Q)x^{T}x} \le- \frac{\lambda _{\min} ( - \varPsi)}{\lambda_{\max} (Q)} = \alpha- 1 $$

where λ min(⋅), λ max(⋅) denote the minimum and the maximum eigenvalue of the corresponding matrix, respectively. \(\alpha= 1 - \frac{\lambda_{\min} ( - \varPsi )}{\lambda_{\max} (Q)}\), since \(\frac{\lambda_{\min} ( - \varPsi )}{\lambda_{\max} (Q)} > 0\), we have α<1, obviously

$$\alpha\ge\frac{E\{ x'^{T}Qx'\mid x\}}{x^{T}Qx} > 0 $$

That is, α belongs to (0,1) and is independent of x. Therefore, we have

$$E \bigl\{ x'^{T}Qx'\mid x \bigr\} \le \alpha x^{T}Qx $$

Taking expectation of both sides yields

$$ E\bigl\{ x'^{T}Qx'\bigr\} \le\alpha E\bigl \{ x^{T}Qx\bigr\} $$
(8)

Upon the relationship (8), it can be established that

(9)

Adding both sides of the inequality system (9) yields

Using this relationship iteratively, we can obtain

Therefore, we have

(10)

where \(\kappa: = \frac{\lambda_{\max} (Q)}{\lambda_{\min} (Q)}\).

Now, denote \(\chi_{k}: = \sum_{j = 0}^{k} \Vert x_{k - j,j} \Vert ^{2}\). Then from the inequality (10) we have

Adding both sides of this inequality system yields

Then, under Assumption 1, the right side of this inequality is bounded, which means lim k→0 E{χ k }=0, that is, lim i +j→∞ E{∥x i,j ∥2}=0. Then the 2-D discrete stochastic system (1) is mean-square asymptotically stable. □

Remark 1

Theorem 1 provides an LMI condition for the mean-square asymptotic stability of 2-D nonlinear stochastic system in the Roesser model which can be solved by LMI Toolbox.

3 Bounded Realness of 2-D Stochastic System with Sector Nonlinearity

In this section, we will analyses the bounded realness for 2-D stochastic discrete system with sector nonlinearity. We consider the following system [9]:

(11)
(12)
(13)

where w∈R p is the noise input which belongs to ℓ 2, z∈R q is the controlled output, B 1, N 1, H, H 1 and L 1 are known real constant matrices with appropriate dimensions. Using the transformation (6), the above system (11)–(13) becomes

(14)
(15)

Definition 3

Given a scalar γ>0 and weighting matrices R 1>0 and R 2>0, the 2-D system (11)–(13) with unknown boundary condition is said to have an H ∞ disturbance attenuation level γ if it is mean-square asymptotically stable and satisfies

$$ \Vert z \Vert _{E}^{2} < \gamma^{2} \Biggl( \Vert w \Vert _{2}^{2} + \sum _{k = 0}^{\infty} \bigl[ E \bigl\{ x^{v}(k,0)^{T}R_{2}x^{v}(k,0) \bigr\} + E \bigl\{ x^{h}(0,k)^{T}R_{1}x^{h}(0,k) \bigr\} \bigr] \Biggr) $$
(16)

In the case when the boundary condition is known to be zero, the H ∞ performance measure (10) reduces to

$$ \Vert z \Vert _{E} < \gamma \Vert w \Vert _{2} $$
(17)

where

$$\Vert z \Vert _{E}: = \sqrt{E \Biggl\{ \sum _{i = 0}^{\infty} \sum_{j = 0}^{\infty} \vert z_{i,j} \vert ^{2} \Biggr\}},\qquad \Vert w \Vert _{2}: = \sqrt{\sum_{i = 0}^{\infty} \sum_{j = 0}^{\infty} \vert w_{i,j} \vert ^{2}} $$

Remark 2

Note that the definition is a natural extension of 2-D Roesser model to 2-D stochastic Roesser model case.

The following bounded real lemma will play an important role in solving the robust H ∞ control problem formulated in the next section.

Theorem 2

Given a positive scalar γ, the 2-D system (11)–(13)with unknown boundary condition has an H ∞ disturbance attenuation level γ if there exist a scalar ε>0 and a block-diagonal matrix P=diag{P h ,P v }>0, where \(P_{h} \in R^{n_{1} \times n_{1}}\) and \(P_{v} \in R^{n_{2} \times n_{2}}\) satisfy \(P_{h}^{\ - 1} < \gamma^{2}R_{1}\) and \(P_{v}^{\ - 1} < \gamma^{2}R_{2}\) such that

$$ \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} - P & PC^{T}K & 0 & P ( A + A_{1}K_{1}C )^{T} & P ( M + M_{1}K_{1}C )^{T} & P ( H + H_{1}K_{1}C )^{T} \\[3pt] * & - 2\varepsilon I & 0 & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} & \varepsilon H_{1}^{T} \\[3pt] * & * & - \gamma^{2}I & B_{1}^{T} & N_{1}^{T} & L_{1}^{T} \\[3pt] * & * & * & - P & 0 & 0 \\ * & * & * & * & - P & 0 \\ * & * & * & * & * & - I \end{array} \right ] < 0 $$
(18)

Proof

By (18), it is easy to see that

$$\left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} - P & PC^{T}K & P ( A + A_{1}K_{1}C )^{T} & P ( M + M_{1}K_{1}C )^{T} \\ * & - 2\varepsilon I & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} \\ * & * & - P & 0 \\ * & * & * & - P \end{array} \right ] < 0 $$

By Theorem 1, we see that system (11)–(13) with w(i,j)=0 is asymptotically stable. Suppose now that there exists a block-diagonal matrix P=diag{P h ,P v }>0, such that the matrix inequality (18) holds, we denote the system sate as

$$x = \left [ \begin{array}{c} x^{h}(i,j) \\ x^{v}(i,j) \end{array} \right ],\qquad x' = \left [ \begin{array}{c} x^{h}(i + 1,j) \\ x^{v}(i,j + 1) \end{array} \right ] $$

Consider the following index:

where

By the Schur complement, LMI (18) implies Ω<0.

Then for ξ≠0, we have δ(i,j)<0, that is

$$ E \bigl\{ x'^{T}Qx'|x \bigr\} < x^{T}Qx - z^{T}(i,j)z(i,j) + \gamma ^{2}w^{T}(i,j)w(i,j) $$

Taking the expectation of both sides yields

$$ E \bigl\{ x'^{T}Qx'|x \bigr\} < E \bigl\{ x^{T}Qx - z^{T}(i,j)z(i,j) \bigr\} + \gamma ^{2}w^{T}(i,j)w(i,j) $$
(19)

Due to the relationship (19), it can be established that

Adding both sides of the inequality system

Summing up both sides of this inequality from k=0 to k=N, we have

(20)

Since Q h <γ 2 R 1 and Q v <γ 2 R 2 (Q=P −1), the inequality (20) leads to

That is

$$\Vert z \Vert _{E}^{2} < \gamma^{2} \Biggl( \Vert w \Vert _{2}^{2} + \sum _{k = 0}^{\infty} \bigl[ E \bigl\{ x^{v}(k,0)^{T}R_{2}x^{v}(k,0) \bigr\} + E \bigl\{ x^{h}(0,k)^{T}R_{1}x^{h}(0,k) \bigr\} \bigr] \Biggr) $$

Therefore, from Definition 3, the system (11)–(13) is mean-square asymptotically stable and have an H ∞ disturbance attenuation level γ. The proof is completed. □

Remark 3

Theorem 2 provides an H ∞ performance index for 2-D nonlinear stochastic system. When we assume v i,j =0, A 1=0, that is, no nonlinear and stochastic uncertainty is in the system (11)–(12), it is easy to show that Theorem 2 coincides with the existing bounded real lemma for discrete 2-D Roesser model [5]. Therefore, Theorem 2 in this paper can be regarded as an extension of existing results on bounded realness for 2-D systems to 2-D nonlinear stochastic system described by the Roesser model.

4 Robust H ∞ Control of 2-D Stochastic System with Sector Nonlinearity

Consider the following 2-D stochastic system with sector nonlinearity expressed by [9]:

(21)
(22)
(23)

where u∈R m is the control input, B 2, N 2 and L 2 are known real constant matrices with appropriate dimensions.

Now, we consider the following state feedback controller:

$$ u(i,j) = Gx(i,j) $$
(24)

Applying this controller to 2-D stochastic system (21)–(23) results in the following closed-loop system:

(25)
(26)

For the closed-loop system (25)–(26), we state the 2-D H ∞ control problem as: find a 2-D state feedback controller of the form (24) for the 2-D stochastic system, such that the closed-loop system has a specified H ∞ performance γ.

In the following theorem, we present a sufficient condition for the 2-D stochastic system (18)–(20) to have an H ∞ disturbance attenuation level γ.

Theorem 3

Consider the 2-D stochastic system (21)–(23). Given a positive scalar γ, if there exist a scalar ε>0 and two matrices Y, X=diag{X h ,X v }>0 such that

$$ \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} - X & XC^{T}K & 0 & \left ( \begin{array}{l} X(A + A_{1}K_{1} \\ \times C)^{T} + YB_{2}^{T} \end{array} \right ) & \left ( \begin{array}{l} X(M + M_{1}K_{1} \\ \times C)^{T} + YN_{2}^{T} \end{array} \right ) & \left ( \begin{array}{l} X(H + H_{1}K_{1} \\ \times C)^{T} + YL_{2}^{T} \end{array} \right ) \\ * & - 2\varepsilon I & 0 & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} & \varepsilon H_{1}^{T} \\[2pt] * & * & - \gamma^{2}I & B_{1}^{T} & N_{1}^{T} & L_{1}^{T} \\ * & * & * & - X & 0 & 0 \\ * & * & * & * & - X & 0 \\ * & * & * & * & * & - I \end{array} \right] < 0 $$
(27)

Then the closed-loop system (25)–(26) has a specified H ∞ performance γ, and

$$ u(i,j) = \bigl( X^{ - 1}Y \bigr)^{T}x(i,j) $$
(28)

is a γ—suboptimal state feedback H ∞ controller for the 2-D stochastic system (21)–(23).

Proof

By applying Theorem 2, a sufficient condition for the closed-loop system (25)–(26) to have a specified H ∞ performance γ is that there exist a scalar ε>0 and a block-diagonal matrix P=diag{P h ,P v }>0 such that

$$ \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} - P & PC^{T}K & 0 & \left ( \begin{array}{l} P(A + A_{1}K_{1}C \\ + B_{2}G)^{T} \end{array} \right ) & \left ( \begin{array}{l} P(M + M_{1}K_{1}C \\ + N_{2}G)^{T} \end{array} \right ) & \left ( \begin{array}{l} P(H + H_{1}K_{1}C \\ + L_{2}G)^{T} \end{array} \right ) \\ * & - 2\varepsilon I & 0 & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} & \varepsilon H_{1}^{T} \\[3pt] * & * & - \gamma^{2}I & B_{1}^{T} & N_{1}^{T} & L_{1}^{T} \\[3pt] * & * & * & - P & 0 & 0 \\ * & * & * & * & - P & 0 \\ * & * & * & * & * & - I \end{array} \right] < 0 $$
(29)

denoting X=P, Y=XG T, it follows that inequality (29) is equal to the linear matrix inequality (27). This completes this proof.

In view of Theorem 3, in what follows, attention will be focused on the design of a state feedback controller to solve the robust H ∞ control problem for the following 2-D stochastic system.

Consider the 2-D stochastic system in the following Roesser model [9]:

(30)
(31)
(32)

where ΔA, ΔA 1, ΔM, ΔM 1, ΔH, ΔH 1, ΔB i , ΔN i and ΔL i (i=1,2) are unknown matrices representing norm-bounded parameter uncertainties, and are assumed to be of the form:

$$ \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \Delta A & \Delta A_{1} & \Delta B_{1} & \Delta B_{2} \\ \Delta M & \Delta M_{1} & \Delta N_{1} & \Delta N_{2} \\ \Delta H & \Delta H_{1} & \Delta L_{1} & \Delta L_{2} \end{array} \right] = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} U_{1} \\ U_{2} \\ U_{3} \end{array} \right]F(i,j) \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} V_{1} & V_{2} & V_{3} & V_{4} \end{array} \right] $$
(33)

where F(i,j) is an unknown real matrix satisfying:

$$ F^{T}(i,j)F(i,j) \le I $$
(34)

and U i , V i (i=1,2,3) are known real constant matrices with appropriate dimensions. □

Lemma 2

([14]) Let L, E, F and Q be real matrices of appropriate dimensions with Q satisfying Q=Q T, then Q+LFE+(LFE)T<0 for all F satisfying F T F≤I, if and only if there exists a scalar ε>0 such that

$$Q + \varepsilon LL^{T} + \varepsilon^{ - 1}E^{T}E < 0 $$

The main result of this section is given in the following theorem.

Theorem 4

Consider the 2-D stochastic system (30)–(32) with parameter uncertainties. Given a positive scalar γ, if there exist two matrices Y and X=diag{X h ,X v }>0, and scalar ε>0, μ>0 such that

$$ \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} - X & XC^{T}K & 0 & \varXi_{1} & \varXi_{2} & \varXi_{3} & \varXi _{4} \\ * & - 2\varepsilon I & 0 & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} & \varepsilon H_{1}^{T} & \varepsilon V_{2}^{T} \\[3pt] * & * & - \gamma^{2}I & B_{1}^{T} & N_{1}^{T} & L_{1}^{T} & V_{3}^{T} \\[3pt] * & * & * & \mu U_{1}U_{1}^{T} - X & \mu U_{1}U_{2}^{T} & \mu U_{1}U_{3}^{T} & 0 \\[3pt] * & * & * & * & \mu U_{2}U_{2}^{T} - X & \mu U_{2}U_{3}^{T} & 0 \\[3pt] * & * & * & * & * & \mu U_{3}U_{3}^{T} - I & 0 \\ * & * & * & * & * & * & - \mu I \end{array} \right] < 0 $$
(35)

where

Then

$$ u(i,j) = \bigl( X^{ - 1}Y \bigr)^{T}x(i,j) $$
(36)

is a robust γ—suboptimal state feedback H ∞ controller for the uncertain 2-D stochastic system (30)–(32).

Proof

Suppose the uncertain 2-D stochastic system (30)–(32) has H ∞ performance γ, that is, there exist two matrices Y and X=diag{X h ,X v }>0, and a scalar ε>0 such that the following LMI (34) holds:

$$ \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} - X & XC^{T}K & 0 & \varXi_{5} & \varXi_{6} & \varXi_{7} \\ * & - 2\varepsilon I & 0 & \varepsilon A_{1}^{T} & \varepsilon M_{1}^{T} & \varepsilon H_{1}^{T} \\[3pt] * & * & - \gamma ^{2}I & B_{1}^{T} & N_{1}^{T} & L_{1}^{T} \\ * & * & * & - X & 0 & 0 \\ * & * & * & * & - X & 0 \\ * & * & * & * & * & - I \end{array} \right] < 0 $$
(37)

where

That is

for all F satisfying (34). Therefore, using Lemma 1, there exists a scalar μ>0 such that

(38)

By the Schur complement, LMI (35) implies LMI (32) holds. This completes this proof.

In addition, by solving the following optimization problem [1]:

(39)

we can obtain a state feedback controller such that the H ∞ disturbance attenuation γ of the corresponding closed-loop system is minimized. This controller (24) is said to be the robust optimal H ∞ controller for the uncertain 2-D stochastic system (30)–(32).

Theorem 4 provides a sufficient condition for the solvability of the robust H ∞ control problem for the 2-D nonlinear stochastic system described by Roesser model. A desired state feedback controller can be constructed by solving the LMI in (35). The optimization problem proposed above can be carried out automatically by using the function mincx in the LMI control toolbox. □

5 Numerical Example

This section gives an example to illustrate the proposed results.

Example 1

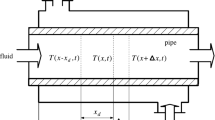
We consider the dynamical processes in gas absorption, water stream heating and air drying, which can be described by the following partial differential equation [13]:

(40)

where s(x,t) is an unknown function at x (space) ∈[0,x f ] and t (time) ∈[0,∞]. a 0, a 1,a 2 and b are coefficients, and f(x,t) is the input function. v ij is a standard random scalar signal satisfying E{v ij }=0.

Similar to the technique used in [5]. We define

Taking:

$$\frac{\partial s(x,t)}{\partial t} \approx\frac{s(i,j + 1) - s(i,j)}{\Delta t},\qquad \frac{\partial r(x,t)}{\partial x} \approx \frac{r(i + 1,j) - r(i,j)}{\Delta x} $$

We can write (40) in the discrete form

(41)

It is easy to verify that Eq. (41) can be converted into the following 2-D Roesser model:

Let Δt=0.5, Δx=0.1, a 0=0.2, a 1=−3, a 2=−1 and b=0.3. To consider the problem of H ∞ disturbance attenuation, the thermal process is modeled in the form (1)–(2) with

By applying Theorem 4 and solving the optimization problem (39), the minimum H ∞ disturbance attenuation level for the corresponding closed-loop system is γ=0.2830 (based on feasibility of the corresponding LMIs). Meanwhile, we obtain

Thus, the robust optimal H ∞ controller is obtained as

$$u(i,j) = \left[ \begin{array}{c@{\quad }c} - 0.9622 & - 2.2282 \end{array} \right]x(i,j). $$

6 Conclusions

This paper has investigated the problem of stability and robust H ∞ control for 2-D stochastic systems with sector nonlinearities. To the authors’ knowledge, it is possibly the first attempt to consider robust control and stability for this class of 2-D nonlinear stochastic systems. The stability and H ∞ disturbance attenuation condition has been developed via the LMI approach. The design of the H ∞ controller can be recast as a convex optimization with constraints of LMI. Finally, a dynamical processes with stochastic perturbation to serve as a simulation example of 2-D stochastic system is given to illustrate the effectiveness of the proposed result. Further development for this class of systems will be studied.