Perturbed HEO Satellite Hovering Investigation in the Earth-Moon System

Abstract

The relative hovering of satellites in highly elliptic orbits (HEO), as one of the most crucial space operations, is modeled and analyzed in this paper. The proposed modeling is based on the new perturbed relative dynamics equations, uses the time-varied parameters depending on the motion of the target satellite. This proposed model considered the dynamic air drag, oblateness of Earth (including all zonal harmonics coefficients) and the Lunar perturbation as an inclined third-body disturbing effect on both follower and target orbits. The non-simplified relative motion model has been obtained by employing the Lagrangian mechanics principals and completed along with the target satellite’s motion characteristic. Then the required thrust for relative hovering mission has been obtained without any simplifications to ensure the accuracy of long-duration flight analyses. To validate the presented model, another model has been built as an ECI based Relative Motion (ERM) model. Then, according to effective parameters on hovering mission design around HEOs such as the eccentricity and inclination of the target obit, the fuel consumption, optimal positioning of the follower, maximum required thrust, and the appropriate time to perform the operation, several examples are provided. Furthermore, the hybrid IWO/PSO algorithm has been used to find the location and the minimum/maximum amounts of thrust force.

Introduction

New on-orbit servicing space missions such as inspection, refueling, upgrading and the repairing require a high degree of precision in modeling and computations [1]. These missions can be accomplished with high reliability if the follower is assumed to remain stationary relative to the target satellite. Accordingly, the space hovering problem has been studied in recent years by adopting a new approach as relative hovering of two spacecraft. The aim of relative hovering is to keep the velocity and acceleration of the controllable satellite zero in the relative frame attached to the centroid of the target [2]. Also, this article is focused on hovering around a highly elliptic orbit. Therefore, it is necessary to include the effects of Moon as a perturbing body, oblate Earth and the air drag as a non-conservative force.

The early studies in the field of hovering were dedicated to controlling a spacecraft near a celestial body [3]. In this problem, the spacecraft should be controlled in such a way that it hovers at a specific position relative to the celestial body [4, 5]. The major complexity of this situation is that the spacecraft is affected by the gravitational forces of the Sun as well as the target asteroid [6]. In relative hovering of two spacecraft, several issues such as relative position control, relative attitude control, fuel consumption, and the determination of a suitable hovering position are taken into account. Wang et al. [7] employed a dynamic model to simulate the hovering operation in an elliptical orbit. Dang et al. [8] investigated the problem of hovering from the standpoint of finding a suitable hovering position to minimize the control effort and fuel consumption. He also presented a kinematic model for the perturbed state of J₂ but employed unperturbed models for studying the hovering problem. By designing an LQR controller, Zhang et al. [9] analyzed the hovering control for an elliptic Keplerian orbit based on the frozen parameters. With consideration of the Earth’s magnetic field, Huang et al. [10] obtained the relative motion equations for a Lorentz spacecraft. The Lorenz spacecraft was assumed as a charged particle in the Earth’s magnetic field. This Lorenz force can be effectively used in the hovering and configuration problems. Huang et al. [11] focused on the use of a nonlinear controller for the Lorentz spacecraft in order to minimize fuel consumption in hovering. The dynamic model was applied in Huang’s work for unperturbed elliptical orbits. Zhang et al. [6] explored three different kinds of hovering about the elliptical perturbed orbits. By presenting a state feedback control scheme for unperturbed circular orbits, Zhou [12] proposed a Multi-objective feedback control based on HCW dynamic model for orbital transfer and hovering upkeeping. Huang [13] proposed a nonlinear controller for a hovering without an actuator in the radial direction or outside the orbital plane.

The previous studies have not addressed the hovering model in the presence of perturbed target orbit, which will lead to large error in prolonged missions. Moreover, the effects of a third-body, air drag and also all zonal harmonics perturbation have not been examined in relative hovering, even on the follower or target satellite. In this paper, the main focus is to obtain a proper model for relative motion and hovering in highly elliptic orbit in long time flight. For high altitudes orbits (higher than the GEO orbit’s altitude), the Moon effect as a third-body perturbation, will be the dominant disturbing force. Therefore, it is necessary to consider the influences of the Moon in this work.

The Moon gravity, as third-body perturbation on hovering mission, has not been formulated and investigated yet. The effect of a third-body on absolute motion of a satellite has been extensively studied [14,15,16,17]. Prado [18] presented a simple model for applying the third-body effect on the motion of a satellite that was based on the restricted three-body problem. In previous works like as [19,20,21], for simplification, the X-Y plane was introduced as a third-body’s orbital plane instead of the equatorial plane of the main-body. Later, Ortore [22] expanded the third-body gravity function as a Legendre polynomial up to second order, and analytically established the absolute equations motion of satellite with consideration of inclined third-body. Nevertheless, the perturbation effect of an inclined third-body on the relative motion of a spacecraft has attracted any attention. However, the third-body effect on the relative motion of satellites has been studied in only a very few research works. By employing Prado model, Roscoe [23] investigated the effect of a third-body in the relative motion for the first time.

In this study, the hovering problem is modeled based on the non-simplified relative motion equations of satellites. In view of the previous works, the relative motion equations are divided into two kinematic [24,25,26] and dynamic [27, 28] categories. With this regards, dynamic equations in the form of a set of differential equations are considered here. The dynamic equations are appropriate for configuration, navigation, guidance, control and optimization problems. Schweighart [29] obtained a model for a circular reference orbit with consideration of J₂ perturbation. However, due to the linearity of this model, its precision reduced when the relative distances become large. Huang [30] presented a new J₂ perturbed nonlinear model based on Lagrangian mechanics. Also, Wei [31] presented a linear relative dynamic model in the presence of the J₂ perturbation. It should be noted that, deriving these models was more complicated than Zhou’s model, and involved some simplifications.

The relative hovering mission under the perturbation effects, including the disturbing third-body, air drag and Earth’s oblateness has not been investigated so far. Also, in the previous models, the hovering equation was obtained for undisturbed target orbits. Therefore, the previous models are only valid for short-duration hovering in low-altitude orbits. The presented model considers the perturbing effects of Moon’s gravitation, Earth’s oblateness and the effect of drag force on the orbits of target and follower satellites in order to provide a suitable model for high-altitude and highly-eccentric orbits. To derive the relative motion equations, first, the perturbed target satellite’s motion is developed based on the six hybrid orbital elements which are introduced in the presence of third-body [32, 33]. Then, by applying the Lagrangian mechanics, the new relative motion equations are derived with consideration of air drag, Earth’s oblateness (all zonal harmonics) and Moon’s gravitation perturbation. The comparison between this model and the former models indicates that the proposed model has a higher accuracy in long-duration flights. Also, to clearly validate the presented model, another model is introduced as the ERM model. Since the fuel consumption is one of the key issues in relative hovering operations, the IWO/PSO hybrid algorithm is applied to obtain the proper position of follower. Fuel consumption with regard to the hovering position, mission duration and different eccentricities of the target satellite are also investigated. Finally, the perturbation effect of Moon’s gravitation on hovering position is examined.

The Dynamic Model of Relative Hovering

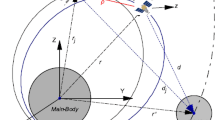
Figure 1 shows the configurations of two satellites in a hovering mission. Both satellites are affected by oblate Earth, air drag, and Lunar perturbation. The center of the relative coordinate is located at the mass center of the target satellite to measure the position and velocity of follower at all times. This rotating frame generally rotates about the cross-track direction (z-axis), and experiences another rotation about the radial direction (x-axis) when the perturbations are applied. Also, the LVLH frame [34] does not sense any rotation around the along-track direction (y-axis). The x-axis is directed from the Earth’s center towards the target, and the z-axis is normal to the orbital plane [35]. Also, the y-axis completes the coordinate system. Besides, the motion of the target satellite in the geocentric coordinates is expressed by the X, Y, Z components. The ECI coordinate system is an Earth-fixed frame and it does not rotate with the Earth. The origin of the ECI frame is located at the Earth’s center, and its X-Y plane is the Earth’s equatorial plane and the Z-axis is directed towards the North Pole. In addition to, a perifocal frame [36] has been used to express the motion of Moon relative to Earth. It is fixed and centered at the focus of the Moon’s orbit around Earth. Its $\overline{xy}$ plane is the plane of the Earth-Moon system, and its $\overline{x}$-axis is directed from the focus through the periapsis of Lunar orbit.

Fig. 1

Schematic diagram of ECI and LVLH frame in presence of Moon

The implementation of the relative hovering operation means to keep the controllable satellite stationary relative to the target, respect to the LVLH frame. The hovering is based on two factors: first, keeping the relative position of the controllable satellite constant and second, keeping the relative speed of the controllable satellite always equal to zero in LVLH coordinate [12]. Therefore, the follower has to utilize a various amount of energy continuously depending on hovering position. The amount of fuel consumption is one of the most fundamental and key parameters in designing space missions. Therefore, in this paper the optimal relative position of the follower for achieving the minimum fuel consumption is investigated.

In this section, the relative hovering model is developed for the case of a target spacecraft in a perturbed highly elliptic orbit. First, the perturbed nonlinear equations of motion of target are developed by six hybrid orbital elements and then, by employing the principles of Lagrangian mechanics, the new relative motion equations are derived. Eventually by achieving the required thrust, the hovering model becomes completed.

The Exact Nonlinear Dynamics of a Satellite in a Perturbed Highly Elliptic Orbit

With consideration of the oblate Earth, air drag and Lunar perturbation, the motion equations of the target on highly elliptic orbits are obtained by proposed hybrid orbital elements. These elements (r, v_x, i, h, θ, Ω) represent the distance from the Earth’s center r = |r|, velocity in the radial direction, inclination, angular momentum$h=\left|\boldsymbol{r}\times \dot{\boldsymbol{r}}\right|$, argument of latitude, and the right ascension of ascending node, respectively.

$$ \dot{r}={v}_x $$

(1)

$$ {\dot{v}}_x=-\frac{\mu }{r^2}+\frac{h^2}{r^3}-\psi -C\left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert \left(h-{\omega}_e{r}^2{c}_i\right)-{\kappa}_m\ {x}_m-\frac{\mu_m}{d^3}r $$

(2)

$$ \dot{h}=- r\chi {c}_{\theta }{s}_{\theta }-C\left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert \left(h-{\omega}_e{r}^2{c}_i\right)-{\kappa}_m\ {y}_mr $$

(3)

$$ \dot{\theta}=\frac{h}{r^2}+\frac{r\chi {c}_i^2{s}_{\theta }}{h{s}_i}+\frac{C\left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert {\omega}_e{r}^2{c}_i{s}_{2\theta }}{2h}+\frac{r}{h}\frac{c_i{s}_{\theta }}{s_i}\ {\kappa}_m\ {z}_m $$

(4)

$$ \overset{\cdot }{i}=-\frac{r\chi {c}_i{c}_{\theta }}{h}-\frac{C\left\Vert {V}_a\right\Vert {\omega}_e{r}^2{s}_i{c}_{\theta}^2}{2h}-\frac{r}{h}{c}_{\theta }\ {\kappa}_m\ {z}_m $$

(5)

$$ \dot{\Omega}=-\frac{r\chi {c}_i{s}_{\theta }}{h{s}_i}-\frac{C\left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert {\omega}_e{r}^2{s}_{2\theta }}{2h}-\frac{r}{h}\frac{s_{\theta }}{s_i}\ {\kappa}_m\ {z}_m $$

(6)

where, in order to better display the equations,$C={C}_d\left(\frac{A}{m}\right)\rho /2$ and ${\kappa}_m={\mu}_m\left(\frac{1}{r_m^3}-\frac{1}{d^3}\right)$. Also, R_e is the Earth radius at the equator and μ is the Earth’s gravitational constant. V_a = V − ω_e × r is the velocity of the target relative to the atmosphere. ω_e = ω_eZ is the vector of Earth’s rotation about itself in the ECI coordinate system. μ_m is the gravitational constant of Moon and r_m is the distance between the centers of Earth and Moon.

The motion equations obtained are independent of Ω (i.e. Eq. 6) and this is due to the symmetry of the spherical gravitational potential. Therefore, the motion of the target satellite can be analyzed by using five eqs. (1–5). In addition, these equations are able to compute the short-term and long-term effect which can influence the hovering operations.

Proof Eqs. (1–6)

The LVLH frame rotates with respect to the ECI frame, with the angular velocity vector of ω = ω_xx + ω_yy + ω_zz. Using the orbital elements of (i, θ, Ω) related to the target satellite, this rotation vector components are expressed as [37]:

$$ {\omega}_x=\overset{\cdot }{i}{c}_{\theta }+\overset{\cdot }{\varOmega }{s}_{\theta }{s}_i $$

(7)

$$ {\omega}_y=-\overset{\cdot }{i}{s}_{\theta }+\overset{\cdot }{\varOmega }{c}_{\theta }{s}_i=0 $$

(8)

$$ {\omega}_z=\dot{\theta}+\dot{\Omega}{c}_i $$

(9)

Furthermore, the unit vectors of the LVLH frame are defined as follows:

$$ x=r/\mid r\mid, z=h/\mid h\mid, \kern0.5em y=z\times x $$

(10)

Also, the derivatives of these unit vectors are established as below:

$$ \dot{\boldsymbol{x}}=\boldsymbol{\omega} \times \boldsymbol{x}={\omega}_z\boldsymbol{y} $$

(11)

$$ \dot{\boldsymbol{y}}=\boldsymbol{\omega} \times \boldsymbol{y}={\omega}_x\boldsymbol{z}-{\omega}_z\boldsymbol{x} $$

(12)

$$ \dot{\boldsymbol{z}}=\boldsymbol{\omega} \times \boldsymbol{z}=-{\omega}_x\boldsymbol{y} $$

(13)

The connecting vector from the Earth’s center to the target orbit shows the target position as r = rx. By taking the derivative and employing (11–13), the velocity and acceleration vectors of the target in the relative coordinate system will be obtained [38]:

$$ \dot{\boldsymbol{r}}=\boldsymbol{V}={v}_x\boldsymbol{x}+\frac{\boldsymbol{h}}{r}\boldsymbol{y} $$

(14)

$$ \ddot{\boldsymbol{r}}=\left({\dot{v}}_x-\frac{h^2}{r^3}\right)\boldsymbol{x}+\frac{\dot{h}}{r}\boldsymbol{y}+\frac{\omega_xh}{r}\boldsymbol{z} $$

(15)

Also, based on Newton’s laws, the motion of the target spacecraft under the perturbations caused by Moon gravity, oblateness of Earth and air drag is expressed as:

$$ \ddot{\boldsymbol{r}}=-\nabla U-\nabla {U}^M+{\boldsymbol{a}}_{drag} $$

(16)

where $\ddot{\boldsymbol{r}}$ is the acceleration vector of satellite, also U and U^M are the gravitational potential functions of Earth and Moon, respectively. Now, the acceleration due to the air drag and the gradient of gravitation potential of Earth and Moon should be determined. The air dynamic acceleration is expressed as follows with consideration of the rotation of atmospheric with the Earth’s rotation [34].

$$ {\boldsymbol{a}}_{drag}=-\frac{1}{2}{C}_d\frac{A}{m}\rho \left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert {\boldsymbol{V}}_{\boldsymbol{a}} $$

(17)

In the above equation, V_a = V − ω_e × r is the velocity of the target relative to the atmosphere. ω_e = ω_eZ is the vector of Earth’s rotation about itself in the ECI coordinate system that must be transformed to the LVLH frame. This transformation is achieved as follows:

$$ {\boldsymbol{\omega}}_{\boldsymbol{e}}={\omega}_e\boldsymbol{Z}={\omega}_e\left({s}_{\theta }{s}_i\boldsymbol{x}+{c}_{\theta }{s}_i\boldsymbol{y}+{c}_i\boldsymbol{z}\right) $$

(18)

with consideration of Eqs. (14) and (18), the satellite’s velocity relative to air will have the following form:

$$ {\boldsymbol{V}}_{\boldsymbol{a}}=\left({v}_x\right)\boldsymbol{x}-\left(\frac{h}{r}-{\omega}_er{c}_i\right)\boldsymbol{y}+\left({\omega}_er{c}_{\theta }{s}_i\right)\boldsymbol{z} $$

(19)

Now, to complete of Eq. (16), the gradient of the Earth’s gravitational potential function that can be written in the form of $\overset{\sim }{U}\left(r,\varphi, \lambda \right)=U\left(r,\cos \varphi \right)$ must be expressed in LVLH frame as follows:

$$ \nabla \tilde{U}=\frac{\partial \tilde{U}}{\partial r}r+\frac{1}{r}\frac{\partial \tilde{U}}{\partial \varphi}\boldsymbol{\upvarphi} +\frac{1}{rsin\varphi}\frac{\partial \tilde{U}}{\partial \lambda}\boldsymbol{\uplambda} $$

(20)

$$ \nabla U=\frac{\partial U}{\partial r}\boldsymbol{r}+\frac{1}{r}\frac{\partial U}{\partial \left({c}_{\varphi}\right)}\frac{\partial \left({c}_{\varphi}\right)}{\partial \varphi}\boldsymbol{\varphi} =\frac{\partial U}{\partial r}\boldsymbol{r}-\frac{1}{r}\frac{\partial U}{\partial \left({c}_{\varphi}\right)}{s}_{\varphi}\boldsymbol{\varphi} $$

(21)

To express the gradient equations of the potential function in the LVLH frame, it is necessary to define vectors φ and r in terms of the unit vectors of the LVLH system. For this purpose, first, the unit vector Z in the ECI coordinate system is written using the unit components of the spherical and the LVLH frame as in Eqs. (22–23):

$$ \boldsymbol{Z}={c}_{\varphi}\boldsymbol{r}-{s}_{\varphi}\boldsymbol{\varphi} $$

(22)

$$ \boldsymbol{Z}={s}_{\theta }{s}_i\boldsymbol{x}+{c}_{\theta }{s}_i\boldsymbol{y}+{c}_i\boldsymbol{z} $$

(23)

With consideration of geometrical relationships among the spherical and LVLH coordinate, the following relation is obtained between the zenith angle, inclination and argument of latitude [39].

$$ {c}_{\varphi }={s}_{\theta }{s}_i $$

(24)

Now, by substituting Eqs. (22–24) into Eq. (21) and knowing relation between unit vectors r = x, the general form of the Earth’s gravitational potential function in the LVLH frame will be formed as:

$$ \nabla U=\frac{\partial U}{\partial r}\boldsymbol{x}+\frac{1}{r}\frac{\partial U}{\partial \left({c}_{\varphi}\right)}\left({c}_{\theta }{s}_i\boldsymbol{y}+{c}_i\boldsymbol{z}\right) $$

(25)

In this regard, the Earth’s gravitational potential function U can be written by considering the all zonal harmonic coefficients [40]:

$$ U\left(r,{c}_{\varphi}\right)=-\frac{\mu }{r}+\frac{\mu }{r}{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n{P}_n\left({c}_{\varphi}\right) $$

(26)

Where c_φ = s_θ s_i, and P_n is the Legendre function. To complete the motion equations of the reference satellite, it is necessary to express the ∇U in the LVLH frame. By combining Eq. (26) and (25) we will obtain:

$$ \nabla U=\frac{\partial U}{\partial r}\boldsymbol{x}+\frac{1}{r}\frac{\partial U}{\partial \left({c}_{\varphi}\right)}\left({c}_{\theta }{s}_i\boldsymbol{y}+{c}_i\boldsymbol{z}\right)=\left(\frac{\mu }{r^2}+\psi \right)\boldsymbol{x}+\chi {c}_{\theta }{s}_i\boldsymbol{y}+\chi {c}_{\theta}\boldsymbol{z} $$

(27)

in which

$$ \psi \left(r,{c}_{\varphi}\right)=-\frac{\mu }{r^2}+{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n\left(n+1\right)\ {P}_n\left({c}_{\varphi}\right) $$

(28)

$$ \chi \left(r,{c}_{\varphi}\right)=\frac{1}{r}\frac{\partial U}{\partial {c}_{\varphi }}=\frac{\mu }{r^2}+{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n\ {P}_n^{\prime}\left({c}_{\varphi}\right) $$

(29)

$$ {P}_n^{\prime}\left({c}_{\varphi}\right)=\frac{1}{2^nn!}\frac{d^{n+1}}{d{\left({c}_{\varphi}\right)}^{n+1}}{\left({\left({c}_{\varphi}\right)}^2-1\right)}^n $$

(30)

After obtaining Eqs. (15), (21) and (17), the motion equation (Eq. (16)) should be completely expressed in the LVLH frame that needed to express the Moon’s gravitational potential function in the LVLH coordinate. The Lunar gravitational potential function as a third-body effect is expressed as [41]:

$$ {U}^m=-{\mu}_m\left(\frac{1}{d}-\frac{1}{r_m^3}\boldsymbol{r}.{\boldsymbol{r}}_{\boldsymbol{m}}\right) $$

(31)

where μ_m is the Moon’s gravitational constant, r_m is the distance between the centers of Earth and Moon, and d = |r_m − r| is the distance between Moon and target satellite. So, the gradient of Moon’s gravitational potential function will be as follows:

$$ {\nabla U}^m=\frac{\mu_m}{d^3}\boldsymbol{r}+\left(\frac{\mu_m}{r_m^3}-\frac{\mu_m}{d^3}\right){\boldsymbol{r}}_{\boldsymbol{m}} $$

(32)

Regarding vector r_m in the LVLH frame as r_m = x_mx + y_my + z_mz, and noting that r = rx, the gradient of Moon’s gravitational potential function in the LVLH frame can be shown as:

$$ {\nabla U}^m=\left(\frac{\mu_m}{d^3}r+{\kappa}_m\ {x}_m\right)\boldsymbol{x}+{\kappa}_m\ {y}_m\boldsymbol{y}+{\kappa}_m\ {z}_m\boldsymbol{z} $$

(33)

$$ {\kappa}_m={\mu}_m\left(\frac{1}{r_m^3}-\frac{1}{d^3}\right) $$

(34)

$$ d=\sqrt{{\left({x}_m-r\right)}^2+{y}_m^2+{z}_m^2} $$

(35)

By using Eqs. (17), (27) and (33), and considering s_φ = Z/r, the right side of Eq. (16) (i.e., a sum of both the gradient of the gravitational potential function and the acceleration due to atmosphere drag) can be written as:

$$ {\displaystyle \begin{array}{l}-\nabla U-\nabla {U}^m+{\boldsymbol{a}}_{\boldsymbol{drag}}=-\left[\frac{\mu }{r^2}+\psi -C\left\Vert {V}_a\right\Vert {v}_x+\frac{\mu_m}{d^3}+{\kappa}_m{x}_m\right]\boldsymbol{x}\\ {}-\left[\chi {s}_i{c}_i+C\left\Vert {V}_a\right\Vert \left(\frac{h}{r}-{\omega}_er{c}_i\right)+\frac{\mu_m}{d^3}+{\kappa}_m{x}_m\right]\boldsymbol{y}-\left[\chi {c}_i+C\left\Vert {V}_a\right\Vert {\omega}_er{c}_{\theta }{s}_i+{\kappa}_m{z}_m\right]z\end{array}} $$

(36)

It should be noted that the left side of Eq.(16) has been extracted by twice taking the derivative of vector r in Eq. (15). Now, by equating Eqs. (15) and (36), referring to Eq. (16), the mentioned expression can be obtained.

Furthermore, the orbital rate ω_z is equal to [31]:

$$ {\omega}_z=\frac{h}{r^2} $$

(37)

Also, by comparing Eqs. (15) and (36), the steering rate of orbital plane will be determined as:

$$ {\omega}_x=-\frac{r\chi\ {s}_i}{h}-\frac{r}{h}{\kappa}_m{z}_m-\frac{C\left\Vert {\boldsymbol{V}}_{\boldsymbol{a}}\right\Vert {\omega}_e{r}^2{s}_i{c}_{\theta }}{h} $$

(38)

Now, the motion equations with hybrid elements (1–6) can be obtained by employing Eqs. (15) and (36) and using Eqs. (37), (38) and (7–9).

Finally, the time derivative of the rotation components of the LVLH axes relative to the ECI frame are achieved in Eqs. (39) and (40) by using Eqs. (37), (38) as well as Eqs. (4) and (5).

$$ {\displaystyle \begin{array}{l}{\alpha}_x=-\frac{c_i}{r{\omega}_z}\left(\dot{\chi}+\frac{\chi {v}_x}{r}+\frac{2{\chi}^2{s}_i{c}_{\theta }}{r{\omega}_z}\right)-\frac{C{\omega}_e}{\omega_z}\left(\frac{\partial \left\Vert {V}_a\right\Vert }{\partial t}{s}_i{c}_{\theta }-\frac{\alpha_z}{\omega_z}\right\Vert {V}_a\left\Vert {s}_i{c}_{\theta }-\dot{\theta}\right\Vert {V}_a\Big\Vert {s}_i{c}_{\theta }+\\ {}i\left\Vert {V}_a\right\Vert {c}_i{c}_{\theta}\Big)-\frac{r{\kappa}_m}{h}\left(\frac{\dot{r}}{r}-\frac{\dot{h}}{h}\right){z}_{m-}\frac{r{\kappa}_m}{h}{\dot{z}}_m-\frac{r}{h}{\dot{\kappa}}_m{z}_m\end{array}} $$

(39)

$$ {\alpha}_z={\dot{\omega}}_z=-\frac{2{v}_xh}{r^3}-\frac{\chi {c}_{\theta }{s}_i}{r}-\frac{\kappa_m}{r}{y}_m-\frac{C\left\Vert {V}_a\right\Vert \left(h-{\omega}_e{r}^2{c}_i\right)}{r^2} $$

(40)

Also, In the above equations, the following expressions are employed:

$$ \dot{\chi}=\frac{\mu {v}_x}{r^3}{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n\left(n+1\right)\ {P}_n^{\prime}\left({c}_{\varphi}\right)+\frac{\mu {\omega}_z}{r^2}{s}_i{c}_{\theta }{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n{P}_n^{\prime \prime}\left({c}_{\varphi}\right) $$

(41)

$$ {P}_n^{\prime \prime}\left({c}_{\varphi}\right)=\frac{d^2}{d{c}_{\varphi}^2}{p}_n\left({c}_{\varphi}\right)=\frac{1}{2^nn!}\frac{d^{n+2}}{d{\left({c}_{\varphi}\right)}^{n+2}}{\left({\left({c}_{\varphi}\right)}^2-1\right)}^n $$

(42)

$$ \dot{\kappa}=3\left(\frac{\dot{d}}{d^4}-\frac{{\dot{r}}_m}{r_m^4}\right) $$

(43)

$$ \dot{d}=\left[\left({\dot{x}}_m-\dot{r}\right)+{\dot{y}}_m+{\dot{z}}_m\right]/d $$

(44)

For completing of equations (1–6), the displacement [x_m, y_m, z_m] and velocity $\left[{\dot{x}}_m,{\dot{y}}_m,{\dot{z}}_m\right]$ components of Moon in the LVLH frame must be known. These vectors are achieved by introducing procedure in Appendix1.

The Dynamic Model of Relative Hovering in HEO

By considering the perturbation forces including oblate Earth, Moon’s gravity, and air drag, the required thrust force for hovering operations will be obtained as follows:

$$ {\displaystyle \begin{array}{l}{T}_{x_j}={x}_j\left({\eta}_j^2-{\omega}_z^2\right)-{y}_j{\alpha}_z+{z}_j{\omega}_x{\omega}_z+\left({\chi}_j-\chi \right){s}_i{s}_{\theta }+r\left({\eta}_j^2-\eta \right)+{x}_m\left({\kappa}_j-{\kappa}_m\right)+\\ {}\frac{\mu_m}{d_j^3}{x}_m+r{\mu}_m\left(\frac{1}{d_j^3}-\frac{1}{d^3}\right)+{C}_j\left\Vert {V}_a\right\Vert \left({y}_j{\omega}_z\right)+\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right){v}_x\end{array}} $$

(45)

$$ {\displaystyle \begin{array}{l}{T}_{y_j}={x}_j{\alpha}_z+{y}_j\left({\eta}_j^2-{\omega}_z^2-{\omega}_x^2\right)-{z}_j{\alpha}_x+\left({\chi}_j-\chi \right){s}_i{c}_{\theta }+{y}_m\left({\kappa}_j-{\kappa}_m\right)+\frac{\mu_m}{d_j^3}{y}_m+\\ {}\kern0.24em {C}_j\left\Vert {V}_{aj}\right\Vert \left({x}_j{\omega}_z-{z}_j{\omega}_x\right)+\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right)\left(\frac{h}{r}-{\omega}_er{c}_i\right)\end{array}} $$

(46)

$$ {\displaystyle \begin{array}{l}{T}_{z_j}=-{x}_j{\omega}_x{\omega}_z-{y}_j{\alpha}_x-{z}_j\left({\eta}_j^2-{\omega}_z^2\right)-\left({\chi}_j-\chi \right){c}_i+{z}_m\left({\kappa}_j-{\kappa}_m\right)+\kern0.5em \frac{\mu_m}{d_j^3}{z}_m\\ {}\kern4.079998em +{C}_j\left\Vert {V}_{aj}\right\Vert \left({\dot{z}}_j-{y}_j{\omega}_x\right)+\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right){\omega}_e\ r\ {c}_{\theta }{s}_i\end{array}} $$

(47)

where ζ_j, r_j, η_j, κ_j are defined as follows:

$$ {\chi}_j=\frac{1}{r_j}\frac{\partial U}{\partial {c}_{\varphi_j}}=\frac{\mu }{r_j^2}{\sum}_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n\ {P}_n^{\prime}\left({c}_{\varphi}\right) $$

(48)

$$ {r}_j=\sqrt{{\left(r+{x}_j\right)}^2+{y}_j^2+{z}_j^2} $$

(49)

$$ {\eta}^2=\frac{\mu }{r^3}+\frac{\psi }{r}-\frac{\chi\ {s}_i{s}_{\theta }}{r} $$

(50)

$$ {\eta}_j^2=\frac{\mu }{r_j^3}+\frac{\psi_j}{r_j}-\frac{\chi_j\ {s}_i{s}_{\theta }}{r_j} $$

(51)

$$ {r}_{jZ}=\left(r+{x}_j\right){s}_i{s}_{\theta }+{y}_j\ {s}_i{c}_{\theta }+{z}_j{c}_i $$

(52)

$$ {\kappa}_j={\mu}_m\left(\frac{1}{r_m^3}-\frac{1}{d_j^3}\right) $$

(53)

$$ {d}_j=\left|{\boldsymbol{r}}_{\boldsymbol{m}}-{\boldsymbol{r}}_{\boldsymbol{j}}\right|=\sqrt{{\left({x}_m-\left(r+{x}_j\right)\right)}^2+{\left({y}_m-{y}_j\right)}^2+{\left({z}_m-{z}_j\right)}^2} $$

(54)

The equations (45–54) are obtained by applying hovering conditions (the relative position of the follower with respect to the target must be fixed and the time derivative of the relative position vector calculated in the rotating LVLH frame is zero during the mission, but the relative velocity and acceleration of the follower relative to the target measured in the ECI frame are not zero.) in the proposed relative motion equations. To obtain these proposed equations of relative motion, a Lagrangian approach was adopted (seeAppendix2for details). The exact dynamic model of satellites relative motion has the following form:

$$ {\displaystyle \begin{array}{l}{\ddot{x}}_j=2{\dot{y}}_j{\omega}_z-{x}_j\left({\eta}_j^2-{\omega}_z^2\right){y}_j{\alpha}_z-{z}_j{\omega}_x{\omega}_z-\left({\chi}_j-\chi \right){s}_i{s}_{\theta }-r\left({\eta}_j^2-\eta \right)-{x}_m\left({\kappa}_j-{\kappa}_m\right)-\\ {}\frac{\mu_m}{d_j^3}{x}_m-r{\mu}_m\left(\frac{1}{d_j^3}-\frac{1}{d^3}\right)-{C}_j\left\Vert {V}_a\right\Vert \left({\dot{x}}_j-{y}_j{\omega}_z\right)-\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right){v}_x+{T}_{xj}\end{array}} $$

(55)

$$ {\displaystyle \begin{array}{l}{\ddot{y}}_j=-2{\dot{x}}_j{\omega}_z+2{z}_j{\omega}_x-{x}_j{\alpha}_z-{y}_j\left({\eta}_j^2-{\omega}_z^2-{\omega}_x^2\right)+{z}_j{\alpha}_x-\left({\chi}_j-\chi \right){s}_i{c}_{\theta }-{y}_m\Big({\kappa}_j-\\ {}{\kappa}_m\left)-\frac{\mu_m}{d_j^3}{x}_m-{C}_j\right\Vert {V}_a\Big\Vert \left({\dot{y}}_j-{x}_j{\omega}_z-{z}_j{\omega}_x\right)-\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right)\left(\frac{h}{r}-{\omega}_er{c}_i\right)+{T}_{yj}\end{array}} $$

(56)

$$ {\displaystyle \begin{array}{l}\ddot{z}=2{\dot{y}}_j{\omega}_x-{x}_j{\omega}_x{\omega}_z-{y}_j{\alpha}_x-{z}_j\left({\eta}_j^2-{\omega}_z^2\right)-\left({\chi}_j-\chi \right){c}_i-{z}_m\left({\kappa}_j-{\kappa}_m\right)-\frac{\mu_m}{d_j^3}{z}_m+\\ {}\left({C}_j\left\Vert {V}_{aj}\right\Vert -C\left\Vert {V}_j\right\Vert \right){\omega}_er{c}_{\theta }{s}_i+{T}_{zj}\end{array}} $$

(57)

The relative motion equations (55–57) are obtained without any simplification, and the perturbation effects of the Moon, all zonal harmonic perturbation due to the Earth’s oblateness, and the non-conservative perturbation effect of the air dynamic drag are considered in deriving the equations. In this situation (derived by Lagrangian principle) classical orbital elements couldn’t be made effective help to complete the relative motion equations, but the advantage of hybrid orbital elements is fully cleared in deriving and completing of relative equations (seeAppendix2for details). To analyze the relative hovering mission, it is necessary to use equations (1–6) with equations (55–57) as well as equations (45–47) simultaneously, so that changes in the orbital elements of the target orbit are calculated at each time instant, and applied to the hovering model.

Results Analysis

To investigate the relative hovering problem, it is necessary to validate the proposed dynamic model and it should be compared to other models. Due to the lack of an appropriate model that consider the perturbations intended in the presented model, the structure of an ECI based Relative Motion (ERM) model is constructed. To establish such a structure, the equations of the target and follower satellites should be written in the ECI frame. Then, by means of a transformation matrix, the position and velocity vectors of both satellites should be transformed into the LVLH frame. Finally, by subtracting the position and velocity components of satellites, the relative position and velocity of the follower satellite will be obtained as shown in Fig. 2. Due to lack of data, the proposed absolute motion of target (Eq. 1–6) and relative motion model (Eq. 55–57) will be compared with the introduced ERM model by considering the perturbation effects. All of the test cases are performed by constructing a general MATHEMATICA® code and runs on a personal computer with following properties: Intel(R) Core(TM) i5–3770 CPU @ 3.40 GHz and 4 GB RAM.

Fig. 2

ERM model building procedure

In this paper, the focus of work was on the missions on high eccentric orbits with low perigee altitude. Therefore, the air drag was considered in modeling. Moreover, based on [42], the order of magnitude of the main perturbations acting on objects under the GEO region demonstrated that the oblateness of the Earth (like as J₂) and Lunar perturbation are more important than Sun perturbation and tesseral resonances. Also, lunar perturbation was dominated to the disturbing force of Sun, thus the Sun gravity effect was ignored to be able to better study on other perturbation force on hovering mission. However, the equations are so general that the Sun perturbation effect can add to introduced equations in the same way of considering lunar perturbation.

Validating the Motion Model of the Reference Satellite

In this section, the motion model of the reference satellite (1–6) is compared with the ECI based model (Fig. 2) with consideration of all the perturbation effects. The presented dynamic model is valid for all the values of eccentricity. In this example, a highly elliptical orbit is discussed:

$$ a=23331\ km,e=0.7,i={10}^{{}^{\circ}},\Omega ={30}^{{}^{\circ}},\uptheta ={30}^{{}^{\circ}},\upomega ={130}^{{}^{\circ}} $$

(58)

Figures 3 and 4 show the position and velocity components of the reference satellite, respectively. The difference between the presented model and the ECI based model is negligible and close to zero. The considered simulation time is equal to 95 h. Furthermore, the accuracy of the proposed model will be maintained for long-term missions as well.

Fig. 3

Position components of target satellite in highly elliptical orbit with consideration of zonal harmonics, air drag and Lunar perturbation (e = 0.7). (bullet correspond to result based on ECI based model)

Fig. 4

Velocity components of target satellite in highly elliptical orbit with consideration of zonal harmonics, air drag and Lunar perturbation (e = 0.7). (bullet correspond to result based on ECI based model)

Moreover, another comparison is conducted between the presented model and the model introduced in [41], to verify the accuracy of model in prolonged flight in presence of a third-body perturbation. Figure 5 compares the double-averaged model and the exact model proposed in this article. As seen in Fig. 5, the agreements of the eccentricity and inclination obtained by the two models becomes lower, over time.

Fig. 5

Variation of eccentricity over 400 canonical time units (1737 days) for different initial inclinations, double-averaged model [41] (dashed-line), the proposed model (solid line)

In Fig. 5, the exact proposed model of satellite motion by Eqs. (1–6) was compared with the double-averaged model [41] to show the accuracy of the model in long-time flight in presence of a third-body perturbation. In Liu’s work, some simplifications were considered to derive the motion equation of a satellite under inclined third-body perturbation. Also, the only perturbing force that considered in Liu’s paper was third-body gravity effect that orbiting in a 6.68^o inclined orbit. Furthermore, in double-averaged model the short-term oscillations are ignored and cause to accumulate of error in prolonged analyses.

Achieving the exact position of the target orbit in the hovering is undoubtedly one of the most important issues encountered in long-term missions. The lack of information about a reference satellite and ignoring its perturbation effects can gradually reduce the accuracy of the hovering mission evaluations.

Validating the Relative Motion

At this point, the accuracy of the presented relative dynamic model will be evaluated by the ERM model. The specifications of the target orbit were given in Eq. (58), and the orbital elements of the follower satellite are as follow:

$$ a=23330\ km,e=0.71,i={9}^{{}^{\circ}},\Omega ={29}^{{}^{\circ}},\uptheta ={129}^{{}^{\circ}},\upomega ={129}^{{}^{\circ}} $$

(59)

Also, the initial condition of the follower satellite in the LVLH frame is obtained as follow:

$$ {\displaystyle \begin{array}{l}x=-238.45,y=-234.03,-104.53\ km\\ {}{v}_x=0.0195,{v}_y=0.5266,{v}_z=0.0864\kern0.5em km/s\end{array}} $$

(60)

To obtain the relative initial values, it is required to solve the ERM equations. Since no approximations have been considered in obtaining the relative motion equations, these equations are expected to be valid for prolonged evaluation. Figure 6 shows the displacement components of relative motion in the presented model (55–57) and the ERM model (Fig. 2). The results obtained indicate that the two models have very good agreement with each other. Also, the velocity components of relative motion in both models are shown in Fig. 7.

Fig. 6

The relative position components of follower satellite in LVLH frame obtained by the ERM and the presented model

Fig. 7

The relative velocity components of follower satellite in LVLH frame obtained by the ERM and the presented model

The results obtained confirm that the proposed relative motion model has good accuracy and the relative hovering model can be derived on the basis of these equations. Due to the hovering sensitivity and the need for high precision in long-duration flights, besides the importance of the short-term effects, the proposed model can be a good basis for analyzing and investigating the hovering operations.

Minimum and Maximum of Required Thrust

In practice, hovering control requires a continuous consumption of fuel. A major objective in designing space missions is to reduce the amount of energy utilized during a mission. Therefore, a proper hovering location must be determined for a follower in order to minimize fuel consumption. Thus, an optimization problem is constructed to find the maximum and minimum of required thrust, their timing and the position of follower satellite. This optimization problem will be solved by the fast and powerful IWO/PSO hybrid algorithm [32, 43, 44].

It was assumed that the orbit target has a perigee altitude of a_p = 622 km orbital elements of Ω = 30^°, θ = 30^°, ω = 130^° with all the perturbations. The flight duration in this simulation is considered equal to 10 orbital periods. The above analyses are carried out for different eccentricities and inclinations of target orbit with a constant perigee altitude, so that the effects of inclination and eccentricity on the follower position and the maximum and minimum required thrust can be observed in the results. The possible hovering position is given as a sphere around the target with a constant radius of 2 km. The results obtained are presented in Table 1.

Table 1 IWO/ PSO optimization result for determining maximum and minimum of required thrust per unit mass of a satellite (N/kg) and their position in different inclination and eccentricity of target satellite with the constant perigee

As seen in Table 1, at a constant eccentricity, the maximum thrust increases up until the 70° inclination and then decreases. Of course, this trend is more prominent at smaller eccentricities. A careful examination reveals that, at a constant inclination, the maximum thrust increases slightly with the increase of eccentricity. Also, the results obtained indicate that the maximum thrust is generated in the vicinity of perigee. This is due to the fact that the target has a fixed perigee altitude and at low altitudes, the Earth’s oblateness and air drag perturbation have a greater effect on the target motion.

Angles α, β in spherical coordinates specify the position of follower in the following way:

$$ {\displaystyle \begin{array}{l}x=\rho \cos \left(\alpha \right)\sin \left(\beta \right)\\ {}y=\rho \cos \left(\alpha \right)\sin \left(\beta \right)\\ {}z=\rho \cos \left(\beta \right)\end{array}} $$

(61)

The results obtained indicate that minimum thrust occurs when the follower is located in the orbital plane of target satellite around the along-track axis. This trend becomes more regular at the location that required maximum thrust. This means that the maximum thrust occurs in the vicinity of the x-z plane, closer to the radial axis, and closer to Earth.

For more investigation on relative hovering distant effect on results, two simulations were accomplished: first, in Table 2 the results were demonstrated that there was same behavior in different hovering distance. The generated thrust was decreased with decreasing the hovering distance. These results are provided in same eccentricity 0.6 and different inclinations.

Table 2 IWO/ PSO optimization result for determining maximum and minimum of required thrust per unit mass of a satellite (N/kg) and their position in different hovering distance (e = 0.6)

In the second simulation, in constant inclination 70^o and different eccentricities, effect of relative distance (2, 3, 4 km) on generated thrust was obtained. As shown in Table 3, there is the same trend in different hovering distance. Also, the required thrust was increased with increasing the hovering distance.

Table 3 IWO/ PSO optimization result for determining maximum and minimum of required thrust per unit mass of a satellite (N/kg) and their position in different hovering distance (i = 70^o)

Another key parameter in the design of a hovering operation is the distribution of maximum and minimum thrust based on the follower location. The magnitude of the total thrust is considered as follows:

$$ {T}_t=\left(\left|{T}_x\right|+\left|{T}_y\right|+\left|{T}_z\right|\right) $$

(62)

For more clarity, in Fig. 8, a group of contours is shown to indicate the distributions of the thrust required at different times and eccentricities. By getting further away from the Earth, the magnitude of the needed thrusts diminishes.

Fig. 8

The pattern of the required thrust at different times and different target orbit eccentricities in hovering distance of 2 km. T_r(×10⁸) )

The Effects of Eccentricity and the Altitude of HEO Target Orbit on the Required Thrust

The history of the generated thrust and the effects of eccentricity and perigee altitude of target orbit will be considered in this section. The orbital elements are similar to the previous simulation and the hovering position is ρ = (−1, 0, 1) km. Figure 9 shows the thrusts at three different target orbit eccentricities with constant perigee altitude for one period of Moon’s orbit. The results indicate that the extreme value of thrust for relative hovering is required in the radial direction. Also, in the along-track direction, the lowest value of thrust is required rather than two other directions. Moreover, the amplitude of the required thrust decreases with the increase of eccentricity and altitude. As shown in Fig. 9, the pattern of the generated thrust has changed around the apogee.

Fig. 9

Time history of required thrust per unit mass of a satellite (N/kg) (×10⁶) in different eccentricity with a constant perigee of 622 km. (hovering distance is 10 km)

To evaluate the effect of HEO orbit altitude on the generated thrust, the altitude of perigee is changed from 20,000 to 25,000 km, while the eccentricity is kept constant at 0.8. This investigation is carried out for three different kinds of hovering missions. The R-bar hovering means that the follower satellite is fixed on the radial axis (x), H-bar hovering demonstrates that the controllable satellite is located on the cross-track axis (z), and in the V-bar hovering, the follower satellite is stationary on the along-track axis (y).

With the increase of altitude, the orbit of the satellite will get closer to the Moon at the apogee point, and the effects of HEO orbit altitude on the generated thrust, becomes more evident (As seen in Fig. 10).

Fig. 10

Time history of required thrust per unit mass of a satellite (N/kg) in different perigee altitude e = 0.8, ρ = 10 km, ap = 25,000 km (solid line), ap = 20,000 km (dashed line)

The Produced Deviation Due to Perturbation Ignorance

In the modeling of hovering missions in highly eccentric orbits, the perturbation effect of the Moon has to be considered in addition to air drag and Earth’s oblateness. To demonstrate the Lunar perturbation effect, the required thrust is obtained from a model without consideration of the Moon. Then this thrust is applied to the complete relative motion equations with all perturbations. Based on the definition of hovering, the follower must preserve its desired position by using the resulting thrust. But, when Moon as the perturbing body is ignored (as shown in Fig. 11), the follower gradually deviates and cannot keep its position. This demonstrates the need for a high-precision model for long-duration hovering operations. The deviations from the desired hovering point in the three directions of the LVLH frame have been calculated based on three different types of hovering. The same investigation was accomplished to show the importance of oblate Earth perturbation and the results are presented in Fig. 12.

Fig. 11

Position deviation during three kinds of hovering due to ignorance of Lunar perturbation (ρ = 2 km)

Fig. 12

Position deviation during three kinds of hovering due to ignorance of zonal harmonics perturbation (ρ = 2 km)

As shown in Figs. 11 and 12, the greatest amount of deviation has occurred in R-bar hovering and along-track direction in both simulations. These deviations have belonged to the duration of mission and characteristic of target orbit. If the eccentricity of orbit increases, the effect of Moon will be more important. Also, the drift is happened from the almost initial time of mission due to ignorance of Earth oblateness. From another view, the distribution of the follower’s deviation from its desired hovering point is illustrated in Fig. 13 in the anywhere feasible hovering region. These deviations are occurred due to ignorance of Earth oblateness and Lunar perturbation.

Fig. 13

The distribution of the follower’s deviation after two period of target orbit due to ignorance of zonal harmonics and Lunar perturbation in different target eccentricities

Comparing the Fuel Consumption

In hovering missions, the fuel consumption is one of the most crucial factors in designing of such operations. In practice, relative hovering is implemented through continuous control and fuel consumption. The space missions are planned with the goal of minimum fuel consumption. So, knowing the amount of fuel consumption based on the hovering position can greatly help the space mission designers. Here, the amount of utilized fuel is expressed as Eq. (63) [9]:

$$ \Delta V={\int}_{t_0}^{t_f}\left(\left|{T}_x\right|+\left|{T}_y\right|+\left|{T}_z\right|\right) dt $$

(63)

Where t₀ and t_f indicate the start and end times of the relative hovering, respectively. Due to the significance and importance of cognizing the pattern of fuel consumption in different situations, a batch of fuel consumption contours for different target eccentricities are shown in Fig. 14.

Fig. 14

Fuel consumption (per unit mass of satellite) distribution at different time intervals and different target orbit eccentricities

These contours indicate that the fuel consumption will be minimized during the time intervals when the satellite is passing the apogee point. It is shown that as eccentricity increases, the fuel consumption is decreased in specific time interval.

Conclusion

In this study, the modeling and analyzing of hovering mission about highly elliptic orbit (HEO) was investigated. In HEOs, depending on the satellite altitude, one of the following perturbations was becoming more important. At very low altitudes, the air drag as a non-conservative force, dominates the motion of satellites. After that the major perturbation is due to the oblateness of Earth. By moving away from the Earth (at altitudes higher than the GEO), the oblate Earth perturbation step down and the Lunar perturbation as a third-body, put more influence on satellite motion.

To achieve suitable modeling, first, the new motion equations of target satellite were developed under abovementioned perturbations. Then, by employing the target orbit equations, the proposed equations were derived for the relative motion of satellites. Finally, the hovering model was completed by applying the hovering conditions on the proposed relative equation to obtain the required thrust. Moreover, an appropriate model was obtained with consideration of short-term orbital effect as well as the target orbit perturbation variations in the relative motion equations. To validate this modeling, another model was introduced as the ERM (ECI based Relative Motion) model.

By applying the powerful IWO/PSO hybrid algorithm, the location and also the maximum and minimum values of thrust were obtained for different inclinations and eccentricities of target orbit. According to the results obtained, the maximum amount of thrust generates near the x-z plane closed to the x-axis and around the perigee. It was demonstrated that the fuel consumption decreases with increasing the orbital eccentricity, while the perigee altitude was kept constant. The perturbation effects of the Moon on the generated thrust were also investigated and it was shown that the consideration of small perturbation terms in the hovering equations can lead to large deviations in the controllable satellite. Finally, the contours of fuel consumption with respect to the hovering position were presented and analyzed. Base on the results obtained in the present study, it should be stated that the analysis of the relative hovering operations about the highly eccentric orbits can play a key role in the planning of new space missions.

Appendices

Appendix 1

For completing of absolute and relative equations of motion of target and follower satellites, the displacement [x_m, y_m, z_m] and velocity $\left[{\dot{x}}_m,{\dot{y}}_m,{\dot{z}}_m\right]$ components of Moon in the LVLH frame must be known. These vectors are achieved by introducing procedure:

• 1- The Lunar classical orbital elements (a_m, i_m, e_m, ω_m, Ω_m, f_m.) are obtained in the mean ecliptic and mean equinox of date coordinate system from [45]. The Moon’s orbital elements are provided in the form of time series, and based on some specific coefficients [36].

• 2- From classical orbital elements, the position and velocity vectors of the Moon in the Earth-Moon perifocal frame are obtained by:

$$ {\overline{r}}_m=\frac{h_m}{\mu_m}\frac{1}{1+{e}_m\ {c}_{f_m}}\left({c}_{f_m}\boldsymbol{p}+{s}_{f_m}\boldsymbol{q}\right) $$

(64)

$$ {\dot{\overline{r}}}_m={\overline{v}}_m=\frac{h_m}{\mu_m}\left[-{c}_{f_m}\boldsymbol{p}+\left({e}_m+{c}_{f_m}\right)\boldsymbol{q}\right] $$

(65)

• 3- the position and velocity vectors of the Moon in the ECI frame is obtained from the perifocal frame by:

$$ {Q}_p^E=\left[\begin{array}{ccc}{c}_{\omega_m}{c}_{\Omega_m}-{s}_{\omega_m}{c}_{{\mathrm{i}}_m}{s}_{\Omega_m}& -{s}_{\omega_m}{c}_{\Omega_m}-{c}_{\omega_m}{c}_{{\mathrm{i}}_m}{s}_{\Omega_m}& {s}_{\omega_m}{s}_{\Omega_m}\\ {}{c}_{\omega_m}{s}_{\Omega_m}+{s}_{\omega_m}{c}_{{\mathrm{i}}_m}{c}_{\Omega_m}& -{s}_{\omega_m}{s}_{\Omega_m}-{c}_{\omega_m}{c}_{{\mathrm{i}}_m}{c}_{\Omega_m}& -{s}_{i_m}{c}_{\Omega_m}\\ {}{s}_{\omega_m}{s}_{{\mathrm{i}}_m}& {c}_{\omega_m}{s}_{{\mathrm{i}}_m}& {c}_{{\mathrm{i}}_m}\end{array}\right] $$

(66)

$$ {r}_m^E={Q}_p^E{\overline{r}}_m $$

(67)

$$ {v}_m^E={Q}_p^E{\overline{v}}_m $$

(68)

• 4- Finally, the position and velocity of the Moon in the LVLH coordinate system (located on the target satellite) can be obtained by:

$$ {\Phi}_E^L=\left[-\begin{array}{ccc}{c}_{\theta }{c}_{\Omega}-{s}_{\theta }{c}_i{s}_{\Omega}& {c}_{\theta }{c}_{\Omega}+{s}_{\theta }{c}_i{c}_{\Omega}& {s}_{\theta }{s}_i\\ {}{s}_{\theta }{c}_{\Omega}-{c}_{\theta }{s}_i{s}_{\Omega}& -{s}_{\theta }{s}_{\Omega}-{c}_{\theta }{c}_i{c}_{\Omega}& {c}_{\theta }{s}_i\\ {}{s}_i{s}_{\Omega}& -{s}_i{c}_{\Omega}& {c}_i\end{array}\right] $$

(69)

$$ {r}_m={\Phi}_E^L\ {r}_m^E={\left[{x}_m\kern0.5em {y}_m\kern0.5em {z}_m\right]}^T $$

(70)

$$ {v}_m={\Phi}_E^L\ {v}_m^E={\left[{\dot{x}}_m\kern0.5em {\dot{y}}_m\kern0.5em {\dot{z}}_m\right]}^T $$

(71)

Appendix 2: Proof of relative motion equations

In this appendix, the procedure to obtain the proposed satellite relative motion by employing of the Lagrangian principle of is briefly summarized.

The Lagrange’s equation used for developing the relative motion model for satellite j is as follows [46]:

$$ \frac{d}{dt}\left(\frac{\partial {K}_j}{\partial {\dot{q}}_n}\right)-\frac{\partial {K}_j}{\partial {q}_n}+\frac{\partial {U}_j}{\partial {q}_n}={Q}_n $$

(72)

In this equation, ${q}_j={\left[{x}_j\kern0.5em {y}_j\kern0.5em {z}_j\right]}^T$is the generalized displacement and ${\dot{q}}_j={\left[{\dot{x}}_j\kern0.5em {\dot{y}}_j\kern0.5em {\dot{z}}_j\right]}^T$ is the generalized velocity. K_j and U_j are kinetic and potential energy (per unit mass) for satellite j. Also, Q_n represents the sum of the non-conservative forces (Here, includes the air drag and the control force) applied on controllable satellite. Now, by exactly computing the potential and kinetic functions for the jth satellite and the non-conservative forces applied on the jth satellite, the relative dynamic motion equations of satellite in the LVLH frame can be derived.

The kinetic energy (per unit mass) for satellite j is obtained by means of:

$$ {K}_j=\frac{1}{2}{\dot{\boldsymbol{r}}}_{\boldsymbol{j}}{\dot{\boldsymbol{r}}}_{\boldsymbol{j}}=\frac{1}{2}\left[{\left({v}_x-{\dot{x}}_j-{y}_i{\omega}_z\right)}^2+{\left(\frac{h}{r}+{\dot{y}}_j+{x}_j{\omega}_x\right)}^2+{\left({\dot{z}}_j+{y}_j{\omega}_x\right)}^2\right] $$

(73)

By substituting Eq. (73) into the first two terms of the Lagrange’s equation (72) will have:

$$ {\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial {K}_j}{\partial {\dot{q}}_n}\right)-\frac{\partial {K}_j}{\partial {q}_n}=\\ {}\left[\begin{array}{c}{\ddot{x}}_j-2{\dot{y}}_j{\omega}_z-2{\dot{y}}_j{\omega}_z-{y}_j{\alpha}_z+{z}_j{\omega}_x{\omega}_z-r{\left({\omega}_z\right)}^2+\left({\dot{v}}_x\right)\\ {}{\ddot{y}}_j+2{\dot{x}}_j{\omega}_z-2{\dot{z}}_j{\omega}_x+{x}_j{\alpha}_z-{y}_j{\omega}_z^2-{y}_j{\omega}_x^2+{z}_j{\alpha}_x+2{V}_x\left({\omega}_z\right)+\mathrm{r}\left({\alpha}_z\right)\\ {}\ddot{z}+2{\dot{x}}_j{\omega}_z+{x}_j{\omega}_x{\omega}_z+{y}_j{\alpha}_x-{z}_j{\omega}_x^2-r\left({\omega}_z{\omega}_x\right)\end{array}\right]\end{array}} $$

(74)

By using Equations (2), (37), (38) and (40) and substituting into the expression within parenthesis in Eq. (74), the following expression is obtained:

$$ {\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial {K}_j}{\partial {\dot{q}}_n}\right)-\frac{\partial {K}_j}{\partial {q}_n}=\\ {}\left[\begin{array}{c}{\ddot{x}}_j-2{\dot{y}}_j{\omega}_z-{x}_j{\omega}_z^2-{y}_j{\alpha}_z+{z}_j{\omega}_x{\omega}_z-r{\eta}^2-\zeta {s}_i{s}_{\theta }-C\left\Vert {V}_a\right\Vert {v}_x-\frac{\mu_m}{d^3}-{\kappa}_m\ {x}_m\\ {}{\ddot{y}}_j+2{\dot{x}}_j{\omega}_z-2{\dot{z}}_j{\omega}_x+{x}_j{\alpha}_z-{y}_j{\omega}_z^2-{y}_j{\omega}_x^2-{z}_j{\alpha}_x-\zeta {s}_i{c}_{\theta }-C\left\Vert {V}_a\right\Vert \left(\frac{h}{r}-{\omega}_er{c}_i\right)-{\kappa}_m{y}_m\\ {}\ddot{z}+2{\dot{y}}_j{\omega}_x+{x}_j{\omega}_x{\omega}_z+{y}_j{\alpha}_x-{z}_j{\omega}_x^2-\zeta {c}_i-C\left\Vert {V}_a\right\Vert {\omega}_er{c}_{\theta }{s}_i-{\kappa}_m\ {z}_m\end{array}\right]\end{array}} $$

(75)

The sum of gravitational potential functions of satellite j due to the gravitational fields of Earth and Moon as a third-body is expressed as equation (76):

$$ {U}_j\left({r}_j,{c}_{\varphi_j}\right)=-\frac{\mu }{r_j}+\frac{\mu }{r_j}\left[\sum \limits_{n=2}^{\infty }{J}_n{\left(\frac{R_e}{r}\right)}^n\ {P}_n\left({c}_{\varphi_j}\right)\ \right]-{\mu}_m\left(\frac{1}{d_j}-\frac{1}{r_m^3}{\boldsymbol{r}}_{\boldsymbol{j}}\ {\boldsymbol{r}}_{\boldsymbol{m}}\right) $$

(76)

where r_j = (r + x_j)x + y_j y + z_j z.

Also, ${c}_{\phi_j}={r}_{jZ}/{r}_j$; and r_jz is the projection of satellite j’s position vector on the Z axis in the ECI frame.

$$ {\boldsymbol{r}}_{\boldsymbol{j}\boldsymbol{Z}}={\boldsymbol{r}}_{\boldsymbol{j}}\ \boldsymbol{Z}=\left(r+{x}_j\right){s}_i{s}_{\theta }+{y}_j{c}_{\theta }{s}_i+{z}_j{c}_i $$

(77)

Therefore, by using Equations (48), (51) and (77) will have:

$$ \frac{\partial {U}_j}{\partial {q}_j}=\left[\begin{array}{c}{\eta}_j^2\left(r+{x}_i\right)+\zeta {s}_i{s}_{\theta }+{\kappa}_j{x}_m+{\mu}_m\left(r+{x}_m\right)/{d}_j^3\\ {}{\eta}_j^2{y}_j+\zeta {s}_i{c}_{\theta }+{\kappa}_j{y}_m+{\mu}_m{x}_m/{d}_j^3\\ {}{\eta}_j^2{z}_j+{\zeta}_j{c}_i+{\kappa}_j{z}_m+{\mu}_m{z}_m/{d}_j^3\end{array}\right] $$

(78)

At this point, the effects of the non-conservative air drag and control forces should be considered in the relative nonlinear equations of motion. So in this paper, in addition to the gravitational effect, the effects of the control force and the air drag have been incorporated into the Lagrange’s equations as Q_n terms. To extract the drag force, the relative velocity of satellite j should be determined first. This term is expressed as follows:

$$ {\boldsymbol{V}}_{\boldsymbol{j}}=\boldsymbol{V}+{\boldsymbol{\rho}}_{\boldsymbol{j}}+\boldsymbol{\omega} \times {\boldsymbol{\rho}}_{\boldsymbol{j}} $$

(79)

$$ {\boldsymbol{V}}_{\boldsymbol{aj}}={\boldsymbol{V}}_{\boldsymbol{j}}-{\boldsymbol{\omega}}_{\boldsymbol{e}}\times {\boldsymbol{r}}_{\boldsymbol{j}} $$

(80)

Now by using Equations (18) and (78) and substituting into Eq. (79), the velocity vector of the jth satellite will be obtained:

$$ {\boldsymbol{V}}_{{\boldsymbol{a}}_{\boldsymbol{j}}}=\left[\begin{array}{c}{v}_x+{\dot{x}}_j-{y}_j{\omega}_z-{\omega}_e{z}_j{c}_{\theta }{s}_i+{\omega}_e{y}_j{c}_i\\ {}\frac{h}{r}+{\dot{y}}_j+{x}_j{\omega}_x-{z}_j{\omega}_x+{z}_j{\omega}_e{s}_i{s}_{\theta }-{\omega}_e\left(r+{x}_j\right){c}_i\\ {}{\dot{z}}_j+{\omega}_e{y}_j{s}_i{s}_{\theta }+{\omega}_e\left(r+{x}_j\right){c}_{\theta }{s}_i\end{array}\right] $$

(81)

Now, the radial, along-track and cross-track components of non-conservative force can be obtained with consideration of drag force ${F}_{drag}=-{C}_j\ \left\Vert {\mathbf{V}}_{a_j}\right\Vert {\mathbf{V}}_{a_j}$ as follows:

$$ {Q}_{xj}={C}_j\left\Vert {\boldsymbol{V}}_{\boldsymbol{aj}}\right\Vert \left({v}_x+{\dot{x}}_j-{y}_j{\omega}_z-{\omega}_e{z}_j{c}_{\theta }{s}_i+{\omega}_e{y}_j{c}_i\right)+{T}_{xj} $$

(82)

$$ {Q}_{yj}={C}_j\left\Vert {\boldsymbol{V}}_{\boldsymbol{aj}}\right\Vert \left(\frac{h}{r}+{\dot{y}}_j+{x}_j{\omega}_x-{z}_j{\omega}_x+{z}_j{\omega}_e{s}_i{s}_{\theta }-{\omega}_e\left(r+{x}_j\right){c}_i\right)+{T}_{yj} $$

(83)

$$ {Q}_{zj}={C}_j\left\Vert {\boldsymbol{V}}_{\boldsymbol{aj}}\right\Vert \left({\dot{z}}_j+{\omega}_e{y}_j{s}_i{s}_{\theta }+{\omega}_e\left(r+{x}_j\right){c}_{\theta }{s}_i\right)+{T}_{zj} $$

(84)

Finally, by substituting Equations (75), (78) and (82–84) into Eq. (72) and considering the conditions of the hovering operation and with consideration of Appendix1, Equations (45–47) will be proved.