Astrodynamics

Abstract

To specify the functional requirements of STS, it is essential to understand the orbital motion of the injected satellites under the influence of a central gravitational force and other disturbing forces. This chapter deals with astrodynamics which explains the motion of celestial bodies as well as human-made satellites under the influence of gravitational force field of celestial bodies and other external forces. Orbital motions of Low Earth Orbit (LEO) satellites are the solutions of two-body problems i.e. the Earth and the satellite, in the specified reference frame, considering the Earth’s gravitational force as the primary central body force field. The deviation of the gravity force away from the central force field and other disturbance forces affect the orbital motion of the satellites. In addition to the central force field, gravitational forces of other planets and Moon also influence the higher altitude orbital motions. Solutions for such motions are achieved by solving restricted three body problem, considering the Earth’s gravity force as the central gravity field whereas the perturbing gravitational force is from the third body such as Moon. Depending on the type of trajectory, different reference frames are used and theses aspects are explained first. Then, this chapter discusses the orbital mechanics of satellites and various aspects of orbital motions of two-body problems. The restricted three body problem and the resulting orbital motion are also briefly explained. Even though the launch vehicles are capable of injecting the satellites in the near Earth orbits, for certain scientific applications, these satellites have to reach and orbit around Moon or distant planets. The interplanetary trajectories of such satellites from the Earth bound orbits to the target planets are also included. In an integrated mission management, optimum strategies like transferring the satellite at suitable time from the initial orbit to the required one in an optimum fashion are required. Various optimum orbital transfer maneuver strategies are explained in this chapter.

3.1 Introduction

The functional requirement of a space transportation system (STS) is to lift a specified satellite with a defined mass and to inject it into the mission defined orbit (within allowable dispersion band) in space. To achieve the above requirements, the subsystems of the STS are designed to achieve the targeted state with the specified accuracy bands in space, which in turn lead to the specified orbit within the allowable error bounds. In order to specify the functional requirements in terms of the required final state of STS, it is essential to understand the orbital motion of the injected satellites under the influence of a central gravitational force and other disturbing forces which can alter the orbits achieved by the STS.

Astrodynamics deals with the motion of celestial bodies as well as human-made satellites under the influence of gravitational force field of celestial bodies and other external forces. While the motion of celestial bodies are referred as celestial mechanics, that of the human-made satellites are classified under orbital mechanics.

Generally, orbital motions of Low Earth Orbit (LEO) satellites are the solutions of two-body problems in the specified reference frame, considering the Earth’s gravitational force as the primary central body force field. In these problems, the Earth and the satellite are the two bodies. The deviation of the gravity force away from the central force field changes the characteristics of Earth-bound satellite orbits. In certain cases, these particular orbital characteristics are favorably used to achieve the satellite-specific mission requirements. In addition, other disturbance forces also affect the orbital motion of the satellites.

In addition to the central force field, gravitational forces of other planets and Moon also influence the higher altitude orbital motions. Solutions for such motions are achieved by solving restricted three body problem, considering the Earth’s gravity force as the central gravity field whereas the perturbing gravitational force is from the third body such as Moon. Depending on the type of trajectory, different reference frames are used and theses aspects are explained first. Then, this chapter deals with the orbital mechanics of satellites and various aspects of orbital motions of two-body problems. The restricted three body problem and the resulting orbital motion are also briefly explained.

Even though the launch vehicles are capable of injecting the satellites in the near Earth orbits, for certain scientific applications, these satellites have to reach and orbit around Moon or distant planets. The interplanetary trajectories of such satellites from the Earth-bound orbits to the target planets are also included.

In the integrated satellite mission management, optimum strategies are being adopted considering: (i) launching satellites into a suitable Earth bound orbit and (ii) transfer the satellite at suitable time from the initial orbit to the finally required orbit in an optimum fashion. Various optimum orbital transfer maneuvers are also brought out in this chapter.

Considering the integrated mission requirements and the various factors as defined above, the mission target defined for the STS is also explained.

3.2 Reference Frames

Orbital mechanics deals with the trajectories of satellites around central bodies. The motion of a satellite is described in terms of its position and velocity vectors as functions of time. Therefore, a reference frame is required with respect to which the position and velocity vectors are defined. In order to define a coordinate reference frame, three fundamental elements are required:

• 1. Origin

• 2. A reference plane passing through the origin

• 3. A reference axis, lying in the reference plane, originating from the origin and pointing towards a well-defined reference point

The three dimensional coordinate system is defined by specifying one axis along the direction of reference axis, second axis normal to the reference plane and third axis in the reference plane, thus completing the right-handed orthogonal system.

Once the origin and reference plane are fixed in space and reference axis is pointed towards distant stars, then the reference frame is fixed in space. The reference frames, either fixed in space or moving with uniform velocity, without rotation with respect to distant stars are un-accelerated. Such frames are called inertial reference frames. If a reference frame is inertial, then every other reference frame which is in uniform motion relative to it is also an inertial reference frame.

Inertial reference frames are important as it is useful to define motion of an object as per the Newtonian mechanics. Alternatively, inertial reference frame is one in which Newton’s laws of motion are valid.

In order to describe the motion of a satellite, the inertial reference frame makes use of celestial references. Therefore, the corresponding celestial references are explained first, followed by the reference frames being used in orbital mechanics to describe the motion of satellite orbits.

3.2.1 Celestial Sphere and Ecliptic

Celestial sphere is a fictitious sphere of infinitely large radius with the Earth at its center. All the celestial bodies appear to be on the surface of the sphere and move westward over the celestial sphere due to the rotation of the Earth about its spin axis. This is called diurnal motion. The extensions of the Earth’s equator and the spin axis intersect with the celestial sphere and are called celestial equator and celestial poles respectively. For an observer on the Earth, in addition to its daily motion, there is a motion of the Sun towards eastwards over the celestial sphere at the rate of approximately 1°/day and return to its initial position on the celestial sphere in one year. The path of this apparent motion of the Sun over the celestial sphere is called the ecliptic. With respect to the Sun, ecliptic is the Earth’s orbit around the Sun. The ecliptic plane is inclined to the equatorial plane by an angle ∈, which is called as the obliquity of the ecliptic. The present value of ∈ is about 23.5°. Axis of the ecliptic intersects the celestial sphere at the ecliptic poles. Therefore, obliquity of the ecliptic ∈ is the angle between celestial North Pole and ecliptic pole.

Sun in apparent motion along ecliptic crosses the celestial equator at two points, called equinoxes, and reaches highest point with respect to celestial equator, called solstices. During its motion from the southern hemisphere to northern hemisphere, the Sun crosses the celestial equator at Vernal equinox and reaches Summer solstice in northern hemisphere. Subsequently, the Sun crosses the celestial equator at Autumnal equinox during its motion from northern hemisphere to southern hemisphere and reaches the Winter solstice. Approximate dates of occurrence of these events over a year are:

• Vernal equinox: March 21st

• Summer solstice: June 21st

• Autumnal equinox: September 21st

• Winter solstice: December 21st

However, there could be a variation of ±1 day due to the variation of prediction methodologies and perturbations of planetary orbital characteristics. In effect, the line joining the equinox points is the intersecting line of equatorial plane and ecliptic plane. Due to the Sun, planets and Moon gravitational effects on Earth’s orbit and spin axis, the equinox line is not fixed in space as given below:

• 1. The obliquity angle oscillates between 22.1° and 24.5° with a period of about 41,000 years. Currently the angle is 23.44° and decreasing.

• 2. The effect of other planets on the plane of Earth orbit causes smaller motion of the ecliptic about 0.114″/year. This is known as planetary precision.

• 3. Due to the gravitational effect of the Sun and Moon on the Earth’s gravitational bulge, the Earth spin axis rotates about the poles of ecliptic with the period of approximately 26,000 years. This motion is called lunisolar precession.

Orbital plane of the Moon is also precessing with the period of 18.6 years. This causes a nutation of smaller amplitude with a period of 18.6 years on the Earth spin axis.

However, as the period involved in the variation of equinox line is very large compared to the mission durations of STS and human-made satellites, the equinox line can be considered as fixed in space and this plays a fundamental role for the definition of inertial reference frames.

3.2.2 Heliocentric Inertial Reference Frame

Origin of the heliocentric reference frame is the Sun’s mass center. The fundamental plane is the ecliptic, X-axis of this frame is passing through the Vernal equinox, Z-axis is along the ecliptic north pole direction and Y-axis lies in the ecliptic plane and completes the right-handed system as given in Fig. 3.1. Even though the Vernal equinox is not fixed in space, still the heliocentric reference frame is considered as an inertial frame for most of our missions since the time duration of most of the missions are much smaller than the period of variations of the reference X-axis (Vernal equinox).

Fig. 3.1

Heliocentric inertial frame

This frame is useful for describing planetary motions or motion of human-made satellites for the interplanetary missions.

3.2.3 Earth Centered/Geocentric Inertial (ECI) Reference Frame

Origin of ECI is the Earth’s center. The fundamental plane is the equator, X-axis is the reference axis, passing through the Vernal equinox, Z-axis is along the Earth’s North Pole direction and Y-axis lies in the equatorial plane and completes the right-handed system as shown in Fig. 3.2. It is pertinent to note that XYZ is not fixed with the Earth and that it is non-rotating with respect to the distant stars, whereas the Earth rotates.

Fig. 3.2

Earth centered inertial and Earth centered rotating frames

As in the case of heliocentric reference frame, though the reference direction towards Vernal equinox is not truly inertial, for the purpose of missions carried out by the STS as well as for the orbital motions of satellites around the Earth, the ECI frame can be considered as inertial reference. Earth gravitational accelerations are calculated in this reference frame and the orbital elements of satellites are computed based on the state vector given with respect to this ECI reference frame.

3.2.4 Earth-Centered Rotating (ECR) Frame

Origin of ECR is the Earth’s center. The fundamental plane is the equatorial plane. The reference axis, X_R-axis is in the equatorial plane, passes through the Greenwich meridian and rotates along with it, Z_R-axis is along the Earth’s north pole and Y_R lies in the equatorial plane, completes the right-handed system as given in Fig. 3.2. The ECR frame rotates about Z_R-axis at the spin rate of the Earth, i.e., 15.0411°/h with respect to the ECI frame. This frame is also termed as World Geodetic System (WGS) and is mostly used in Satellite Navigation System.

3.3 Laws of Motion

3.3.1 Kepler’s Laws

Many astronomers studied the motions of planetary bodies. Aristotle hypothesized that all planetary bodies move in circular paths. Danish astronomer Tycho Brahe (1546–1606) collected huge amount of accurate data on planetary motions for many years. Johannes Kepler (1571–1630) joined Tycho Brahe as his assistant in 1600 and studied the Tycho’s data in detail during 1601–1606. Based on the extensive studies, he deduced three laws of planetary motions as given below:

• 1. The orbit of each planet lies in a fixed plane containing the Sun and is an ellipse with Sun at one focus.

• 2. The line joining a planet to the Sun sweeps equal areas in equal intervals of time.

• 3. The square of the period of revolution of a planet is proportional to the cube of the semi-major axis of its elliptical orbit.

While the Kepler’s laws describe the motions of planets, orbital mechanics based on the applications of Sir Issac Newton’s (1642–1727) law of universal gravitation and his three laws of motion provide more general explanations for the motions of the bodies. Kepler’s laws can be proved through Newtonian mechanics. Since the velocities involved in the motion of the bodies are small compared to the velocity of light, classical or Newtonian mechanics is sufficient for describing the motion of satellites.

3.3.2 Newton’s Laws of Motion

Newton’s three laws of motion are given below:

• 1. A body continues its state of rest or of uniform motion in a straight line unless compelled by external force to change the state.

• 2. The rate of change of momentum of a body is directly proportional to the applied force and this change takes place in the direction of the applied force.

• 3. For every action there is always an equal and opposite reaction.

The first law is about the motion, which is relative. It is necessary to describe the motion with respect to a reference frame. Therefore, the first law can be interpreted as that there exists a reference frame with respect to which a body, free of all external forces, is in uniform motion. Such a reference frame is inertial reference frame. Therefore, Newton’s laws of motion are valid in inertial frame only.

While the first law gives qualitative statement that a force is the cause of motion, the Newton’s second law provides the quantitative definition of the force. The second law is valid only with respect to an inertial frame.

Consider a body of mass, m, moving with velocity V, then the linear momentum of P of the body is given by,

$$ \mathbf{P}=\mathrm{m}\mathbf{V} $$

(3.1)

As per the Newton second law,

$$ \mathbf{F}\propto \frac{\mathrm{d}\kern-0.14em \mathrm{p}}{\mathrm{d}\mathrm{t}} $$

(3.2)

Considering mass, m is constant, then the Eq. (3.2) can be written as

$$ \mathbf{F}\propto \mathrm{m}\frac{\mathrm{d}\mathbf{V}}{\mathrm{d}\mathrm{t}} $$

(3.3)

Considering the rate of change of velocity as acceleration, a, Eq. (3.3) can be written as

$$ \mathbf{F}=\mathrm{km}\mathbf{a} $$

(3.4)

where a is the acceleration and k is the constant of proportionality, which depends on the units of the parameters used in the equation. Considering force in Newton (N), mass in kilogram (kg), acceleration in $\mathrm{m}/{\mathrm{s}}^2$, for the case of F = 1 N, m = 1 kg, a = 1 $\mathrm{m}/{\mathrm{s}}^2$ then k = 1. Therefore, Eq. (3.4) can be written as

$$ \mathbf{F}=\mathrm{m}\mathbf{a} $$

(3.5)

There are two types of masses viz., inertial mass and gravitational mass. The mass used in Eq. (3.5) is the inertial mass whereas the mass used in the Newton law of gravitation (as explained later) is gravitational mass. The inertial mass of a body depends on the motion and is given by

$$ \mathrm{m}=\frac{{\mathrm{m}}_0}{\sqrt{1-\frac{{\mathrm{V}}^2}{{\mathrm{c}}^2}}} $$

(3.6)

where m₀ is the mass at rest, C is speed of light and V is the speed of the body in motion. As the speed of the body considered is much less than the speed of light, in Newtonian mechanics, mass can be assumed as constant, which corresponds to the value at rest, m₀.

Newton’s third law of motion explained that mutual forces of two bodies acting upon each other are equal in magnitude and opposite in direction, and these actions and reactions are collinear. Consider body 2 exerts a force F₁₂ on body 1 as given in Fig. 3.3, then body 1 exerts an opposite force F₁₂ on body 2, so that

Fig. 3.3

Two bodies separated by distance r

$$ {\mathbf{F}}_{12}+{\mathbf{F}}_{21}=0 $$

(3.7)

and

$$ {\mathbf{F}}_{12}= - {\mathbf{F}}_{21} $$

(3.8)

In summary, Newton’s first law of motion tells that the state of motion of a body can be changed only if there is a force acting on it. The second law tells how much change in the state of motion of the body, if there is a force and the third law tells how the forces are exerted.

3.3.3 Newton’s Law of Universal Gravitation

Newton’s law of universal gravitation states that two bodies exert a force on each other along the line joining them and is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. Consider two homogenous bodies with masses m₁ and m₂ as shown in Fig. 3.3. The two bodies are subject to mutual gravitational forces. The gravitational force acting on each body can be written as

$$ \mathrm{F}\kern0.4em \propto \frac{{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2} $$

(3.9)

i.e.,

$$ \mathrm{F}=\frac{\mathrm{G}{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2} $$

(3.10)

where the proportionality constant G is known as the Universal gravitational constant and the value is about 6.67 × 10⁻¹¹ Nm²/kg².

Assuming F₂₁ is the gravitational force exerted on body 2 by body 1 and is given as

$$ {\mathrm{F}}_{21}=\frac{\mathrm{G}{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2} $$

(3.11)

Similarly, the force on body 1 by body 2 is given by

$$ {\mathrm{F}}_{12}=\frac{\mathrm{G}{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2} $$

(3.12)

In vector notations, F₂₁ and F₁₂ are in the opposite direction.

3.4 Two-Body Problem

In universe, each and every body is attracted to each other. Since the distance between the bodies is large, the motion of two close bodies is influenced by their gravitational forces alone where the other body effects are negligible. Therefore, most of the orbital mechanics can be treated as the solution of a two-body problem. Two-body orbital mechanics is the determination of the motion of two point masses which are subjected only by their own mutual gravitational forces. This is the case when both the bodies are homogeneous spheres. The deviations in the solutions of two-body problems may arise when the bodies are not true point masses or some other forces are exerted on the bodies apart from the mutual gravitational forces. Such forces can be considered small compared to the gravitational forces and the effects can be treated as perturbations over the solutions of two-body problems.

In this section, general two-body problem is explained first, and then the special case of motion of a very small body compared to the primary central body (as in the case of satellite motion about the Earth) is described in detail. The perturbations due to non-central force field are explained in a later section of this chapter.

Consider two homogeneous spherical bodies in inertial frame as shown in Fig. 3.4. As per Newton’s law of universal gravitation, F₂₁ is the force exerted on body 2 by body 1 and is given as

Fig. 3.4

Two-body system: (a) two bodies in inertial frame (b) free-body diagram

$$ {\mathrm{F}}_{21}=\frac{\mathrm{G}\;{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2} $$

(3.13)

where r is the distance between the bodies. Let r be the position vector of m₂ with respect to m₁, and u_r is the unit vector along the r, then

$$ {\mathbf{u}}_{\mathbf{r}}=\frac{\mathbf{r}}{\mathrm{r}} $$

(3.14)

In vector notation, Eq. (3.13) can be written as

$$ {\mathbf{F}}_{21}=-\frac{\mathrm{G}\;{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2}{\mathbf{u}}_{\mathbf{r}} $$

(3.15)

and the same can be expressed as

$$ {\mathbf{F}}_{21}=-\frac{\mathrm{G}\;{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^3}\mathbf{r} $$

(3.16)

Using Newton’s second law of motion and referring Fig. 3.4a, the force, F ₂₁ , can also be written as

$$ {\mathbf{F}}_{21}={\mathrm{m}}_2{\ddot{\mathbf{R}}}_2 $$

(3.17)

Using Eqs. (3.16) and (3.17),

$$ {\mathrm{m}}_2{\ddot{\mathbf{R}}}_2=-\frac{\mathrm{G}\;{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^3}\mathbf{r} $$

(3.18)

Using Newton’s third law, the force exerted on body 1 by body 2 can be written as

$$ {\mathbf{F}}_{12}=-{\mathbf{F}}_{21} $$

(3.19)

As explained earlier,

$$ {\mathrm{m}}_1{\ddot{\mathbf{R}}}_1=\frac{\mathrm{G}\;{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^3}\mathbf{r} $$

(3.20)

Let R_c be the center of mass of the two body system. Then,

$$ {\mathbf{R}}_{\mathrm{c}}=\frac{{\mathrm{m}}_1{\mathbf{R}}_1+{\mathrm{m}}_2{\mathbf{R}}_2}{{\mathrm{m}}_1+{\mathrm{m}}_2} $$

(3.21)

and

$$ {\ddot{\mathbf{R}}}_{\mathbf{c}}=\frac{{\mathrm{m}}_1{\ddot{\mathbf{R}}}_1+{\mathrm{m}}_2{\ddot{\mathbf{R}}}_2}{{\mathrm{m}}_1+{\mathrm{m}}_2} $$

(3.22)

Adding Eqs. (3.18) and (3.20) yields

$$ {\mathrm{m}}_1{\ddot{\mathbf{R}}}_1+{\mathrm{m}}_2{\ddot{\mathbf{R}}}_2=0 $$

(3.23)

Applying Eq. (3.23) in Eq. (3.22) shows that the acceleration of the center of mass is zero. Therefore, center of mass of a two-body system can be considered for inertial frame.

Eqs. (3.18) and (3.20) can be written as

$$ {\ddot{\mathbf{R}}}_2=-\frac{{\mathrm{G}\;\mathrm{m}}_1}{{\mathrm{r}}^3}\mathbf{r} $$

(3.24)

and

$$ {\ddot{\mathbf{R}}}_1=\kern0.36em \frac{\mathrm{G}\;{\mathrm{m}}_2}{{\mathrm{r}}^3}\mathbf{r} $$

(3.25)

Subtracting Eq. (3.25) from Eq. (3.24),

$$ {\ddot{\mathbf{R}}}_2 - {\ddot{\mathbf{R}}}_1=-\frac{\mathrm{G}\;\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}{{\mathrm{r}}^3}\mathbf{r} $$

(3.26)

By the definition of position vectors,

$$ \mathbf{r}={\mathbf{R}}_2 - {\mathbf{R}}_1 $$

(3.27)

which gives

$$ \ddot{\mathbf{r}}={\ddot{\mathbf{R}}}_2 - {\ddot{\mathbf{R}}}_1 $$

(3.28)

Using Eq. (3.28), Eq. (3.26) can be written as

$$ \ddot{\mathbf{r}}= - \frac{\mathrm{G}\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}{{\mathrm{r}}^3}\mathbf{r} $$

(3.29)

Equation (3.29) governs the motion of mass m₂ relative to mass m₁. This can also be written as

$$ \ddot{\mathbf{r}}= - \frac{\upmu}{{\mathrm{r}}^3}\mathbf{r} $$

(3.30)

where $\upmu = \mathrm{G}\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)$ is the gravitational constant of the specified two-body system.

Since center of mass has zero acceleration, it can be considered as an inertial reference and motion of each body can be defined about the center of mass. Let r₁ and r₂ be the position vectors of masses m₁ and m₂ with respect to the center of mass. Then,

$$ \mathbf{r}={\mathbf{r}}_2 - {\mathbf{r}}_1 $$

(3.31)

Since the position vector of center of mass relative to itself is zero,

$$ {\mathrm{m}}_1{\mathbf{r}}_1+{\mathrm{m}}_2{\mathbf{r}}_2=0 $$

(3.32)

Therefore,

$$ {\mathbf{r}}_1 = -\frac{{\mathrm{m}}_2}{{\mathrm{m}}_1}\kern0.18em {\mathbf{r}}_2 $$

(3.33)

Using Eq. (3.33) in Eq. (3.31) yields

$$ \mathbf{r}=\frac{{\mathrm{m}}_1+{\mathrm{m}}_2}{{\mathrm{m}}_1}{\mathbf{r}}_2 $$

(3.34)

The equations of motion of m₂ with respect to the center of mass is given by

$$ {\mathrm{m}}_2{\ddot{\mathbf{r}}}_2=-\frac{\mathrm{G}{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^3}\mathbf{r} $$

(3.35)

Using Eq. (3.34) in Eq. (3.35) yields

$$ {\ddot{\mathbf{r}}}_2= - \frac{\mathrm{G}{{\mathrm{m}}_1}^3}{{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}^2}\frac{{\mathbf{r}}_2}{{{\mathrm{r}}_2}^3} $$

(3.36)

Equation (3.36) gives the motion of m₂ about center of mass. The path of m₂ relative to center of mass is a conic with C as a focus, which is explained later. If V₂ is the velocity and r₂ is the position of m₂, with respect to C, then this conic can be

$$ \left.\begin{array}{c}\hfill \kern-1.4em \mathrm{Ellipse}\hfill \\ {}\hfill \hfill \\ {}\hfill \kern-0.7em \mathrm{Parabola}\hfill \\ {}\hfill \hfill \\ {}\hfill \mathrm{Hyperbola}\hfill \end{array}\right\}\kern0.5em \mathrm{if}\kern0.5em \left\{\begin{array}{c}\hfill {{\mathrm{V}}_2}^2<2\mathrm{G}{{\mathrm{m}}_1}^3\ /\left[{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}^2{\mathrm{r}}_2\right]\hfill \\ {}\hfill {{\mathrm{V}}_2}^2=2\mathrm{G}{{\mathrm{m}}_1}^3\ /\left[{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}^2{\mathrm{r}}_2\right]\hfill \\ {}\hfill {{\mathrm{V}}_2}^2>2\mathrm{G}{{\mathrm{m}}_1}^3\ /\left[{\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}^2{\mathrm{r}}_2\right]\hfill \end{array}\right. $$

Similarly, the expression for the path of m₁ about center of mass can be derived. Typical paths (ellipse) of the two bodies with respect to center of mass of two-body problem are represented in Fig. 3.5.

Fig. 3.5

Two-body motions

Consider the Sun-Earth system, the ratio of masses is $\cong 1/332900\left({\mathrm{m}}_2/{\mathrm{m}}_1\right)$. The distance between the Sun and the Earth is of the order of 150 million kilometers (r), whereas the center of mass of the system is of the order of 455 km from the center of the Sun. The angular velocity of line joining the Sun and Earth, ω is given by

$$ \upomega =\frac{{\mathrm{V}}_1}{{\mathrm{r}}_1}=\frac{{\mathrm{V}}_2}{{\mathrm{r}}_2} $$

(3.37)

where V₁ and V₂ are velocity of Sun and Earth with respect to center of mass respectively, and r₁ and r₂ are distance of center of Sun and Earth with respect to the center of mass of the system.

Therefore, the velocity V₂ of the Earth (m₂) about center of mass is of the order of 30,000 m/s whereas that of the Sun (m₁) of the order of 0.1 m/s.

When ${\mathrm{m}}_1\gg {\mathrm{m}}_2$, as in the case of Earth-satellite systems, then the center of the principal attracting body (in this case the larger body is Earth) can be taken as the center of mass and hence can be considered as the origin of the inertial system. The governing equations of such two-body system can be given using Eq. (3.29) as such.

$$ \ddot{\mathbf{r}}= - \frac{\mathrm{G}{\mathrm{m}}_1}{{\mathrm{r}}^3}\mathbf{r} $$

(3.38)

and

$$ \ddot{\mathbf{r}}= - \frac{\upmu}{{\mathrm{r}}^3}\kern0.18em \mathbf{r} $$

(3.39)

where m₁ is the mass of the larger body (Earth). In this case, the gravitational constant, μ, is Gm₁. The value of Earth’s gravitational constant is 3.986013 × 10⁵ km³/s². The Eq. (3.39) describes the motion of the restricted two-body system.

Cross product of Eq. (3.39) with r leads to

$$ \mathbf{r}\times \ddot{\mathbf{r}}=0 $$

(3.40)

As

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{r}\times \dot{\mathbf{r}}\right)=\dot{\mathbf{r}}\times \dot{\mathbf{r}}+\mathbf{r}\times \ddot{\mathbf{r}} $$

(3.41)

Using Eq. (3.40), the Eq. (3.41) leads to

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{r}\times \dot{\mathbf{r}}\right)=0 $$

(3.42)

Therefore, the angular momentum per unit mass H, given by

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{r}\times \dot{\mathbf{r}}\right)=0 $$

(3.43)

As r and ṙ are normal to the angular momentum, the orbital motion of the mass m₂ is in a plane normal to H.

Let A be the area swept by the line joining the two bodies in a specified time. Then,

$$ \frac{\mathrm{dA}}{\mathrm{dt}}=\frac{1}{2}\left|\mathbf{r}\times \dot{\mathbf{r}}\right|=\frac{1}{2}\left|\mathbf{H}\right|=\mathrm{constant} $$

(3.44)

This proves Kepler’s second law. Solution to Eq. (3.39) can be obtained by taking cross product of Eq. (3.39) with H.

$$ \mathbf{H}\times \ddot{\mathbf{r}}=-\frac{\upmu}{{\mathrm{r}}^3}\left(\mathbf{H}\times \mathbf{r}\right) $$

(3.45)

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{H}\times \dot{\mathbf{r}}\right)=\dot{\mathbf{H}}\times \dot{\mathbf{r}}+\mathbf{H}\times \ddot{\mathbf{r}} $$

(3.46)

Since the angular momentum is constant, $\dot{\mathbf{H}}=0$. Therefore, Eq. (3.46) can be written as

$$ \mathbf{H}\times \ddot{\mathbf{r}}=\frac{\mathbf{d}}{\mathbf{d}\mathbf{t}}\left(\mathbf{H}\times \dot{\mathbf{r}}\right) $$

(3.47)

The right-hand side of Eq. (3.45) can be written as

$$ \frac{1}{{\mathrm{r}}^3}\left(\mathbf{H}\times \mathbf{r}\right)=\frac{1}{{\mathbf{r}}^3}\left[\left(\mathbf{r}\times \dot{\mathbf{r}}\right)\times \mathbf{r}\right] $$

(3.48)

Using vector rule,

$$ \left(\mathbf{r}\times \dot{\mathbf{r}}\right)\times \mathbf{r}=\left(\mathbf{r}\cdotp \mathbf{r}\right)\dot{\mathbf{r}}-\left(\mathbf{r}\cdotp \dot{\mathbf{r}}\right)\mathbf{r} $$

(3.49)

Using Eq. (3.49), Eq. (3.48) can be written as

$$ \frac{\frac{1}{{\mathrm{r}}^3}\left(\mathbf{H}\times \mathbf{r}\right)=\mathrm{r}\;\dot{\mathbf{r}}-\dot{\mathrm{r}}\;\mathbf{r}}{{\mathrm{r}}^2} $$

(3.50)

But,

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\frac{\mathbf{r}}{\mathrm{r}}\right)=\frac{\mathrm{r}\kern0.28em \dot{\mathbf{r}}-\dot{\mathrm{r}}\kern0.28em \mathbf{r}}{{\mathrm{r}}^2} $$

(3.51)

Therefore, using Eqs. (3.47) and (3.51), Eq. (3.45) can be written as

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{H}\times \dot{\mathbf{r}}\right)=-\upmu \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\frac{\mathbf{r}}{\mathrm{r}}\right) $$

(3.52)

Integrating the Eq. (3.52) gives

$$ \mathbf{H}\times \dot{\mathbf{r}}=-\upmu \left[\frac{\mathbf{r}}{\mathrm{r}}+\mathbf{e}\right] $$

(3.53)

where e is the dimensionless vector constant of integration called eccentricity.

Equation (3.53) can be written as

$$ \frac{\mathbf{r}}{\mathrm{r}}+\mathbf{e}=\frac{\dot{\mathbf{r}}\times \mathbf{H}}{\upmu} $$

(3.54)

Taking dot product of Eq. (3.54) with H gives

$$ \frac{\mathbf{r}\cdotp \mathbf{H}}{\mathrm{r}}+\mathbf{e}\cdotp \mathbf{H}=\frac{\left(\dot{\mathbf{r}}\times \mathbf{H}\right)\cdotp \mathbf{H}}{\upmu} $$

(3.55)

H is perpendicular to both r and ṙ. Therefore, $\mathbf{r}\cdot \mathbf{H} = 0$. Similarly, the vector $\left(\dot{\mathbf{r}} \times \mathbf{H}\right)$ is perpendicular to both ṙ and H. Therefore, $\left(\dot{\mathbf{r}} \times \mathbf{H}\right)\ .\ \mathbf{H}=0$. Considering the above aspects, Eq. (3.55) can be written as

$$ \mathbf{e}\cdotp \mathbf{H}=0 $$

(3.56)

Equation (3.56) shows the eccentricity vector, e is perpendicular to H and therefore lies in the orbital plane formed by r and ṙ. e vector lies along the line of apsides as explained below.

To express scalar equation of motion of two-body problem, take the dot product of Eq. (3.54) with r as given below:

$$ \frac{\mathbf{r}\cdotp \mathbf{r}}{\mathrm{r}}+\mathbf{r}\cdotp \mathbf{e}=\mathbf{r}\cdotp \frac{\left(\dot{\mathbf{r}}\times \mathbf{H}\right)}{\upmu} $$

(3.57)

Using the vector identity of interchange of dot and cross products, Eq. (3.57) can be written as

$$ \frac{\mathbf{r}\cdotp \mathbf{r}}{\mathrm{r}}+\mathbf{r}\cdotp \mathbf{e}=\frac{\left(\mathbf{r}\times \dot{\mathbf{r}}\right)\cdotp \mathbf{H}}{\upmu} $$

(3.58)

Since $\mathbf{r} \cdot \mathbf{r} = {\mathrm{r}}^2$, $\mathbf{r} \times \dot{\mathbf{r}}=\mathbf{H}$ and $\mathbf{H}\cdot \mathbf{H} = {\mathrm{H}}^2$, Eq. (3.58) can be written as

$$ \mathrm{r}+\mathbf{r}\cdotp \mathbf{e}=\frac{{\mathrm{H}}^2}{\upmu} $$

(3.59)

$\mathbf{r}\cdot \mathbf{e}$ can be expressed as

$$ \mathbf{r}\cdot \mathbf{e}=\mathrm{r}\mathrm{e}\kern0.28em \cos \uptheta $$

(3.60)

where e is the magnitude of eccentricity vector, θ is the angle between eccentricity vector (line of apsides) and position vector r. Then Eq. (3.59) is written as

$$ \mathbf{r}=\frac{{\mathrm{H}}^2/\upmu}{1+\mathrm{e}\kern0.28em \cos \uptheta} $$

(3.61)

In general, conic section is the locus of all points which follow the constant ratio for (r_c/d_c) as shown in Fig. 3.6, where r_c is the distance of a point from focus and d_c is the distance of the point from a given line called directrix. The constant ratio (r_c/d_c) is called the eccentricity, e_c of the conic section.

Fig. 3.6

Conic section

From Fig. 3.6,

$$ {\mathrm{d}}_0 = {\mathrm{d}}_{\mathrm{c}} + {\mathrm{r}}_{\mathrm{c}} \cos {\uptheta}_{\mathrm{c}} $$

(3.62)

As per the definition of eccentricity,

$$ \frac{{\mathrm{p}}_{\mathrm{c}}}{{\mathrm{d}}_0}=\frac{{\mathrm{r}}_{\mathrm{c}}}{{\mathrm{d}}_{\mathrm{c}}}={\mathrm{e}}_{\mathrm{c}} $$

(3.63)

Using Eqs. (3.62) and (3.63), it can be shown that a conic equation is represented as

$$ {\mathrm{r}}_{\mathrm{c}}=\frac{{\mathrm{p}}_{\mathrm{c}}}{1+{\mathrm{e}}_{\mathrm{c}}\kern0.18em \cos {\uptheta}_{\mathrm{c}}} $$

(3.64)

The value of e_c decides the various conic sections as represented in Fig. 3.7.

Fig. 3.7

Conic sections

• ${\mathrm{e}}_{\mathrm{c}}=0$, conic is circle

• $0<{\mathrm{e}}_{\mathrm{c}}<1$, conic is ellipse

• ${\mathrm{e}}_{\mathrm{c}}=1$, conic is parabola

• ${\mathrm{e}}_{\mathrm{c}}>1$, conic is hyperbola

Therefore, it can be concluded that the trajectory of a smaller body (in this case, satellite) with respect to the bigger body (in this case, Earth) in the central gravitational force field as represented in Eq. (3.61) is a conic as given below:

$$ \mathrm{r}=\frac{\mathrm{p}}{1+\mathrm{e}\kern0.18em \cos \uptheta} $$

(3.65)

where the semi-latus rectum of the trajectory is given by

$$ \mathrm{p}=\frac{{\mathrm{H}}^2}{\upmu} $$

(3.66)

The eccentricity, e, of the Eq. (3.65) decides the shape and type of the trajectory of small body with respect to the bigger one as given below:

• e = 1 represents a closed trajectory called circular orbit of smaller body around the central body, whereas 0 < e < 1 also represents a closed trajectory, and in this case, the orbit is an ellipse. If e = 1, the trajectory of smaller body is an open trajectory with the shape of parabola and e > 1 represents the motion of smaller body as an open trajectory of hyperbola about the central body. This gives the mathematical statement of Kepler’s first law. The orbit of a body under central force field is called Keplerian orbit. Typical orbits and trajectories for various values of e which have the same focus and common periapsis are represented in Fig. 3.8.

  Fig. 3.8

  

  Orbits with various eccentricities with the same focus and common periapsis

As explained above, the cross product of Eq. (3.39) with specific relative angular momentum (angular momentum per unit mass), gives the equation for the motion of a smaller body in central force field. The dot product of Eq. (3.39) with specific relative linear momentum gives the energy at any point on the orbit as explained below:

The relative linear momentum of mass m₂ is given by

$$ \mathbf{L}={\mathrm{m}}_2\dot{\mathbf{r}} $$

(3.67)

Therefore, the specific linear momentum is ṙ. Taking dot product of Eq. (3.39) with ṙ gives

$$ \ddot{\mathbf{r}}\cdot \dot{\mathbf{r}}=-\upmu \frac{\mathbf{r}\cdot \dot{\mathbf{r}}}{{\mathrm{r}}^3} $$

(3.68)

It is to be noted that

$$ \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\dot{\mathbf{r}}\cdot \dot{\mathbf{r}}\right)=\ddot{\mathbf{r}}\cdot \dot{\mathbf{r}} $$

(3.69)

Assuming $\mathbf{V} = \dot{\mathbf{r}}$,

$$ \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\dot{\mathbf{r}}\cdot \dot{\mathbf{r}}\right)=\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\mathbf{V}\cdot \mathbf{V}\right)=\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left({\mathrm{V}}^2\right) $$

(3.70)

Therefore, Eq. (3.69) can be written as

$$ \ddot{\mathbf{r}}\cdot \dot{\mathbf{r}}=\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\frac{{\mathrm{V}}^2}{2}\right) $$

(3.71)

The right-hand side of Eq. (3.68) can be written as

$$ \upmu \frac{\mathbf{r}\cdot \dot{\mathbf{r}}}{{\mathrm{r}}^3}=\upmu \frac{\dot{\mathbf{r}}}{{\mathrm{r}}^2}=-\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\frac{\upmu}{\mathrm{r}}\right) $$

(3.72)

Substituting Eqs. (3.71) and (3.72) in Eq. (3.68) gives

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left(\frac{{\mathrm{V}}^2}{2}-\frac{\upmu}{\mathrm{r}}\right)=0 $$

(3.73)

This gives

$$ \frac{{\mathrm{V}}^2}{2}-\frac{\upmu}{\mathrm{r}}=\upvarepsilon $$

(3.74)

where ε is a constant called total energy. (V²/2) is the specific relative kinetic energy (kinetic energy per unit mass) and (μ/r) is the specific potential energy (potential energy per unit mass) of the body m₂ in the gravity field of m₁. The Eq. (3.74) gives the total mechanical energy per unit mass. Also the Eq. (3.74) gives the conservation of the specific mechanical energy for the defined trajectory, i.e., the total energy at any point of the trajectory is same and is given by the relation (3.74). Equation (3.74) is also called vis-viva (living force) integral.

3.4.1 Some Important Trajectory Parameters of Two-Body Problem

As explained above, motion of the smaller body with respect to the bigger one is a conic, which can be either a closed trajectory in terms of circular and elliptic orbits or an open trajectory defined by a parabola or hyperbola depending on the eccentricity value. Also, depending on the velocity magnitude at the instantaneous location, energy of the trajectory is defined.

In the trajectory, the closest point to the primary focus (central body) is called periapsis, and the farthest point is called apoapsis. The line joining the apses is called apse line. In the case of motion of a satellite about the Earth, the periapsis and apoapsis are referred to as perigee and apogee, respectively. For the case of motion about the Sun, the corresponding points are called perihelion and aphelion, respectively. Typical trajectory of a smaller body m₂ about the bigger body m₁ is represented in Fig. 3.9.

Fig. 3.9

Trajectory of orbiting body (m₂) with respect to the primary body (m₁)

The eccentricity vector is always defined from the primary focus towards periapsis and this becomes the reference for the measure of true anomaly, θ, the location of the body with respect to the apse line. The flight path angle, γ, at any location on the trajectory is defined as the angle between the velocity vector and the local horizontal.

Angular velocity of the position vector r is $\dot{\ \uptheta}$. Therefore, the horizontal velocity, V_h is given by

$$ {\mathrm{V}}_{\mathrm{h}}=\mathrm{r}\ \dot{\uptheta} $$

(3.75)

Magnitude of angular momentum is the product of r and horizontal velocity. Thus

$$ \mathrm{H}={\mathrm{r}}^2\dot{\uptheta} $$

(3.76)

Equation (3.76) along with Eq. (3.65) gives

$$ {\mathrm{V}}_{\mathrm{h}}=\frac{\upmu}{\mathrm{H}}\left(1+\mathrm{e}\ \cos \kern0.22em \uptheta \right) $$

(3.77)

The radial velocity, V_r is ṙ. Therefore,

$$ {\mathrm{V}}_{\mathrm{r}}=\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{{\mathrm{H}}^3}{\upmu {\mathrm{r}}^2}\frac{\mathrm{e}\ \sin \uptheta}{{\left(1+\mathrm{e}\ \cos \uptheta \right)}^2} $$

(3.78)

Using Eq. (3.66) gives

$$ {\mathrm{V}}_{\mathrm{r}}=\frac{\upmu}{\mathrm{H}}\ \mathrm{e}\ \sin \uptheta $$

(3.79)

From the Fig. 3.9,

$$ \tan \upgamma =\frac{{\mathrm{V}}_{\mathrm{r}}}{{\mathrm{V}}_{\mathrm{h}}} $$

(3.80)

Substituting Eq. (3.77), Eqs. (3.79) and (3.80) becomes

$$ \tan \upgamma =\frac{\mathrm{e}\ \sin \uptheta}{1+\mathrm{e}\ \cos \uptheta} $$

(3.81)

The magnitude of angular momentum at any location r is also expressed as

$$ \mathrm{H}=\mathrm{r}\mathrm{V}\ \cos \upgamma $$

(3.82)

where V is the velocity of the smaller body and γ is the flight path angle.

Assume r_p and r_a are the distances of periapsis and apoapsis respectively with respect to the primary focus and the corresponding velocities are V_p and V_a respectively. r_p is the location when $\uptheta =0$ and r_a is the location of satellite when θ becomes 180°. Using Eqs. (3.65) and (3.66),

$$ {\mathrm{r}}_{\kern-0.18em \mathrm{p}}=\frac{{\mathrm{H}}^2}{\upmu}\frac{1}{\left(1+\mathrm{e}\right)} $$

(3.83)

and

$$ {\mathrm{r}}_{\mathrm{a}}=\frac{{\mathrm{H}}^2}{\upmu}\frac{1}{\left(1-\mathrm{e}\right)} $$

(3.84)

r_p and r_a are the minimum and maximum distances of the trajectory about the primary body. At the periapsis and apoapsis, the flight path angle is zero.

The semi-major axis, a is given by

$$ \mathrm{a}=\frac{{\mathrm{r}}_{\kern-0.18em \mathrm{p}}+{\mathrm{r}}_{\mathrm{a}}}{2}=\frac{{\mathrm{H}}^2}{\upmu}\frac{1}{\left(1-{\mathrm{e}}^2\right)} $$

(3.85)

Since the angular momentum is constant along the trajectory,

$$ \mathrm{H}={\mathrm{r}}_{\kern-0.18em \mathrm{p}}{\mathrm{V}}_{\kern-0.18em \mathrm{p}}={\mathrm{r}}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{a}} $$

(3.86)

This gives

$$ {\mathrm{V}}_{\kern-0.18em \mathrm{p}}=\frac{\mathrm{H}}{{\mathrm{r}}_{\kern-0.18em \mathrm{p}}} $$

(3.87)

and

$$ {\mathrm{V}}_{\mathrm{a}}=\frac{\mathrm{H}}{{\mathrm{r}}_{\mathrm{a}}} $$

(3.88)

From the above, it can be seen that V_p and V_a are the maximum and minimum velocities along the trajectory.

Since the energy along the trajectory, ε is constant, at the periapsis,

$$ \upvarepsilon =\frac{{{\mathrm{V}}_{\kern-0.18em \mathrm{p}}}^2}{2}-\frac{\upmu}{{\mathrm{r}}_{\kern-0.18em \mathrm{p}}} $$

(3.89)

Using Eq.(3.87) into (3.89) yields

$$ \upvarepsilon =\frac{1\ }{2}\frac{{\mathrm{H}}^2}{{{\mathrm{r}}_{\kern-0.18em \mathrm{p}}}^2}-\frac{\upmu}{{\mathrm{r}}_{\kern-0.18em \mathrm{p}}} $$

(3.90)

Using Eq. (3.83) in Eq. (3.90) gives

$$ \upvarepsilon =-\frac{1}{2}\frac{\upmu^2}{{\mathrm{H}}^2}\left(1-{\mathrm{e}}^2\right) $$

(3.91)

It can be seen from Eq. (3.91) that the energy is function of trajectory parameters. Also, it can be concluded that:

• 1. For elliptic orbit (including circular orbit), ε is negative value

• 2. For parabolic orbit, $\upvarepsilon =0$

• 3. For hyperbolic orbit, ε is positive value

Using Eq. (3.85) in Eq. (3.91) gives

$$ \upvarepsilon =-\frac{\upmu}{2\mathrm{a}} $$

(3.92)

Alternatively,

$$ \mathrm{a}=-\frac{\upmu}{2\upvarepsilon} $$

(3.93)

Thus, the semi-major axis is dependent only on the specific total energy. Using Eq. (3.93) in Eq. (3.74) yields

$$ {\mathrm{V}}^2=\upmu\ \left(\frac{2}{\mathrm{r}}-\frac{1}{\mathrm{a}}\right) $$

(3.94)

Using Eq. (3.93) in Eq. (3.94) with the initial conditions of velocity and distance as V₀ and r₀ respectively, the achieved trajectory characteristics can be identified as follows:

$$ \left.\begin{array}{c}\hfill \kern-3.5em \mathrm{Elliptic}\ \mathrm{orbit}\hfill \\ {}\hfill \hfill \\ {}\hfill \kern-.7em \mathrm{Parabolic}\ \mathrm{trajectory}\hfill \\ {}\hfill \hfill \\ {}\hfill \mathrm{Hyperbolic}\ \mathrm{trajectory}\hfill \end{array}\right\}\kern0.5em \mathrm{if}\kern0.5em \left\{\begin{array}{c}\hfill {\mathrm{V}}_0<\sqrt{\frac{2\upmu}{{\mathrm{r}}_0}}\hfill \\ {}\hfill {\mathrm{V}}_0=\sqrt{\frac{2\upmu}{{\mathrm{r}}_0}}\hfill \\ {}\hfill {\mathrm{V}}_0>\sqrt{\frac{2\upmu}{{\mathrm{r}}_0}}\hfill \end{array}\right. $$

Therefore, the following conclusions can be arrived at: At r₀, for the lower velocity V₀, the orbit is ellipse. As V₀ is increased the closed orbit gradually changes into open trajectory. The minimum velocity required to achieve open trajectory is called escape velocity and is given by

$$ {\mathrm{V}}_{\mathrm{esc}}=\sqrt{\frac{2\upmu}{{\mathrm{r}}_0}} $$

(3.95)

At this velocity, the trajectory of the smaller body with respect to the bigger body is a parabola. Any increase in velocity leads to hyperbolic trajectory of the body with respect to the primary body.

In summary, the following conclusions are arrived at:

• 1. Eccentricity determines the shape and type of trajectory

• 2. Semi-major axis defines the size and energy of the trajectory

The relations between these parameters and the trajectory are summarized below in Table 3.1.

Table 3.1 Trajectories in two-body problem

The following sections give the significance and specific features of each of the above orbits and open trajectories.

3.4.2 Circular Orbits

Applying $\mathrm{e}=0$ in the Eq. (3.65) gives the radial distance of the circular orbit as

$$ \mathrm{r}=\frac{{\mathrm{H}}^2}{\upmu} $$

(3.96)

Also, for circular orbit, there is no radial velocity and the velocity, V, is always tangential. Therefore, angular momentum of circular orbit is

$$ \mathrm{H}=\mathrm{r}\mathrm{V} $$

(3.97)

and

$$ \mathrm{V}=\frac{\mathrm{H}}{\mathrm{r}} $$

(3.98)

Equations (3.96) and (3.98) show that the radial distance and velocity at any point on the orbit are constants. Using Eq. (3.97) into Eq. (3.96) yields

$$ {\mathrm{V}}_{\mathrm{cir}}=\sqrt{\frac{\upmu}{\mathrm{r}}} $$

(3.99)

Equation (3.99) gives velocity of satellite along the circular orbit of distance of r.

Time required to travel along the orbit once is called the period of the orbit, T, and given by

$$ \mathrm{T} = \frac{\mathrm{Circumference}}{\mathrm{Speed}} $$

(3.100)

For the circular orbit of radius r, period is as given in Eqn. 3.100

For the circular orbit of radius r, period is given by

$$ {\mathrm{T}}_{\mathrm{cir}}=\frac{2\uppi \mathrm{r}}{{\mathrm{V}}_{\mathrm{cir}}}=\frac{2\uppi \mathrm{r}}{\sqrt{\left(\upmu /\mathrm{r}\right)}} $$

(3.101)

The specific energy of a satellite at circular orbit is obtained by substituting $\mathrm{e}=0$ in Eq. (3.91) as

$$ {\mathrm{T}}_{\mathrm{cir}}=2\uppi \sqrt{\frac{{\mathrm{r}}^3}{\upmu}} $$

(3.102)

Using Eq. (3.96) in Eq. (3.102) yields

$$ \upvarepsilon =-1/2\left({\upmu}^2/{\mathrm{H}}^2\right) $$

(3.103)

$$ {\upvarepsilon}_{\mathrm{cir}}=-\frac{\upmu}{2\mathrm{r}} $$

(3.104)

Equation (3.104) gives shows that the energy along a circular orbit is negative. As r increases, the energy becomes less negative, indicating higher specific energy for the higher circular orbits.

3.4.3 Elliptical Orbits

For the cases of $0<\mathrm{e}<1$, the relative radial distance calculated by the Eq. (3.65) remains bounded for θ ranging from 0 to 2π and the orbit is elliptic one as shown in Fig. 3.10. The minimum distance r_p is from focus to the periapsis (P) and the maximum distance r_a is from F to apoapsis (A). r_a and r_p are values of r corresponding to $\uptheta =0$ and $\uptheta =180{}^{\circ}$ respectively as are explained in Sect. 3.4.1:

Fig. 3.10

Elliptic orbit parameters

Some additional parameters are explained in this section. Using Eq. (3.85) in Eq. (3.65) an alternate form of orbit equation can be written as

$$ \mathrm{r}=\frac{\mathrm{a}\left(1-{\mathrm{e}}^2\right)}{1+\mathrm{e}\ \cos \uptheta} $$

(3.105)

From the above equation, the r_p and r_a are expressed as

$$ {\mathrm{r}}_{\kern-0.18em \mathrm{p}}=\mathrm{a}\left(1-\mathrm{e}\right) $$

(3.106)

$$ {\mathrm{r}}_{\mathrm{a}}=\mathrm{a}\left(1+\mathrm{e}\right) $$

(3.107)

From Fig. 3.10, CF is expressed as

$$ \mathrm{C}\mathrm{F}=\mathrm{a}\mathrm{e} $$

(3.108)

Also, from the Fig. 3.10,

$$ \mathrm{C}\mathrm{F}=\mathrm{a}\mathrm{e}={\mathrm{r}}_{\mathrm{B}}\ \cos \left(\uppi -\upbeta \right)=-\left[\frac{\mathrm{a}\left(1-{\mathrm{e}}^2\right)}{\left(1+\mathrm{e}\ \cos \upbeta \right)}\right] \cos \upbeta $$

(3.109)

From Eq. (3.109), e can be expressed as

$$ \mathrm{e}=- \cos \upbeta $$

(3.110)

Using this, the value of r_B can be given as

$$ {\mathrm{r}}_{\mathrm{B}}=\mathrm{a} $$

(3.111)

Therefore, the semi-minor axis, b is given by

$$ \mathrm{b}=\mathrm{a}\left(\sqrt{1-{\mathrm{e}}^2}\right) $$

(3.112)

The area of ellipse is given by

$$ \mathrm{A}=\uppi \mathrm{ab} $$

(3.113)

As per Eq. (3.44),

$$ \frac{\mathrm{dA}}{\mathrm{dt}}=\frac{\mathrm{H}}{2} $$

(3.114)

which can be used to obtain

$$ \Delta \mathrm{A}=\left(\frac{\mathrm{H}}{2}\right)\Delta \mathrm{t} $$

(3.115)

For one complete revolution, ΔA is πab and Δt is the period, T. Therefore,

$$ \mathrm{T}=\left(\frac{2\uppi \mathrm{a}\mathrm{b}}{\mathrm{H}}\right) $$

(3.116)

Using Eq. (3.85) and (3.112) for a and b respectively yields

$$ \mathrm{T}=\frac{2\uppi}{\upmu^2}{\left[\frac{\mathrm{H}}{\sqrt{1-{\mathrm{e}}^2}}\right]}^3 $$

(3.117)

Using Eq. (3.85) the period, T given as

$$ \mathrm{T}=2\uppi \sqrt{\frac{{\mathrm{a}}^3}{\upmu}} $$

(3.118)

which proves Kepler’s third law.

This expression reveals that the period of elliptic orbit is independent of eccentricity and depends only on the semi-major axis. The two orbits having the same period are represented in Fig. 3.11.

Fig. 3.11

Elliptic and circular orbits with same energy and period: (a) orbits comparison with center aligned (b) orbits about the focus

The eccentricity of the elliptical orbit can also be represented using Eq.(3.83) and (3.84) as

$$ \frac{{\mathrm{r}}_{\mathrm{p}}}{{\mathrm{r}}_{\mathrm{a}}}=\frac{1-\mathrm{e}}{1+\mathrm{e}} $$

(3.119)

which can be used to derive e as

$$ \mathrm{e}=\frac{{\mathrm{r}}_{\mathrm{a}}-{\mathrm{r}}_{\mathrm{p}}}{{\mathrm{r}}_{\mathrm{a}}+{\mathrm{r}}_{\mathrm{p}}} $$

(3.120)

The Eq. (3.120) shows that

$$ \mathrm{e} = \frac{\mathrm{distance}\ \mathrm{between}\ \mathrm{the}\ \mathrm{two}\ \mathrm{focii}}{\mathrm{distance}\ \mathrm{between}\ \mathrm{the}\ \mathrm{apsi}\ \mathrm{points}} $$

It can be seen from the above that the size of the elliptic orbit is defined by ‘a’ whereas the shape is decided by ‘e’. Together ‘a’ and ‘e’ define the elliptical orbit characteristics.

Using the eccentric anomaly E, the position on an elliptic orbit is given by

$$ \mathrm{r}=\mathrm{a}\left(1-\mathrm{e}\kern0.35em \cos \mathrm{E}\right) $$

(3.121)

Another important relation is Kepler’s equation defined by

$$ \mathrm{M}=\mathrm{E}-\mathrm{e}\kern0.35em \sin \mathrm{E} $$

(3.122)

where M is the Mean anomaly and

$$ \mathrm{M}={\mathrm{t}}_{\mathrm{p}}\sqrt{\frac{\upmu}{{\mathrm{a}}^3}} $$

(3.123)

where

• t_p = time elapsed since the previous passage of periapsis

3.4.4 Parabolic Trajectories

Consider the orbit equation

$$ \mathrm{r}=\left(\frac{{\mathrm{H}}^2}{\upmu}\right)\left(\frac{1}{1+\mathrm{e}\kern0.35em \cos \uptheta}\right) $$

and the orbit energy equation

$$ \upvarepsilon =-\frac{1}{2}\frac{\upmu^2}{{\mathrm{H}}^2}\left(1-{\mathrm{e}}^2\right) $$

and

$$ \upvarepsilon =\frac{{\mathrm{V}}^2}{2}-\frac{\upmu}{\mathrm{r}} $$

From the above equations, it can be observed that, for the case of $\mathrm{e}=$ 1, the specific energy ε is zero and as the true anomaly tends to 180°, the radial distance approaches infinity.

The velocity at $\mathrm{r} = \infty$ is called residual velocity, ${\mathrm{V}}_{\infty }$ (sometimes referred as excess velocity). For the case of parabolic trajectory, ${\mathrm{V}}_{\infty }$ is 0, meaning that, once the body is placed in parabolic trajectory, it won’t come back, thus referred to as open trajectory. Also, since the residual velocity ${\mathrm{V}}_{\infty }$ is zero, parabolic trajectory is the boundary between the closed elliptical orbit and open hyperbolic trajectory. Thus, the velocity on the parabolic trajectory is referred as escape velocity and is given by

$$ {\mathrm{V}}_{\mathrm{esc}}=\sqrt{\frac{2\upmu}{\mathrm{r}}} $$

(3.124)

Considering the Eq. (3.99), it can be seen that

$$ {\mathrm{V}}_{\mathrm{esc}}=\sqrt{2}\ {\mathrm{V}}_{\mathrm{cir}} $$

(3.125)

Thus at any distance, the required escape velocity is about 41.4 % more than the circular orbital velocity at that location. Typical values of escape velocities are given below:

• 11.12 km/s for escape from Earth from the Earth’s surface

• 617 km/s for escape from Sun from the Sun’s surface

• 42.1 km/s for escape from Sun from the Earth orbit

It is to be noted that if a body (satellite) is injected into a parabolic trajectory about the primary body (Earth) with the escape velocity, V_esc, the satellite does not go to infinity. As the distance increases, gravitational attraction of the Earth reduces, and the influence of the Sun becomes predominant. At one point of time, the satellite velocity with respect to Earth becomes zero; but the satellite velocity about the Sun is same as that of the Earth and therefore both the Earth and the satellite move about the Sun in the same orbit.

Typical parabolic trajectory is given in Fig. 3.12. Considering the Eq. (3.81), the flight path angle at any location of a parabolic trajectory is given by

Fig. 3.12

Typical parabolic orbit

$$ \tan \boldsymbol{\upgamma} =\frac{ \sin \boldsymbol{\uptheta}}{1+ \cos \boldsymbol{\uptheta}} $$

(3.126)

On simplifying the Eq. (3.126), it can be seen that

$$ \boldsymbol{\upgamma} =\frac{\boldsymbol{\uptheta}}{2} $$

(3.127)

Thus, along parabolic trajectory, the flight path angle at any location is half of the true anomaly.

3.4.5 Hyperbolic Trajectories

Hyperbola is an open trajectory as represented in Fig. 3.13. Since the trajectory is open one, the distance r can increase without limit. When r approaches $\infty$, the tip of the position vector meets the asymptote. The asymptotes intersect at the centre, O. The centre falls outside the trajectory.

Fig. 3.13

Hyperbolic trajectory

The angle between the asymptote and major axis is ${\uptheta}_{\infty }$. Since the trajectory meets the asymptote at infinity, ${\uptheta}_{\infty }$, is the true anomaly at infinity. Using the equation,

$$ \mathrm{r}=\frac{{\mathrm{H}}^2}{\upmu}\frac{1}{1+\mathrm{e}\ \cos \uptheta} $$

at $\mathrm{r} = \infty$, the term $1+\mathrm{e} \cos \uptheta =0$. Therefore, ${\uptheta}_{\infty }$ can be expressed as

$$ {\uptheta}_{\infty }= \cos {\kern-0.14em }^{-1}\left(\kern-0.5em -\frac{1}{\mathrm{e}}\right) $$

(3.128)

The angle between the asymptotes is turning angle, δ. As the body travels from $-\infty$ to $+\infty$, δ is the angle through which the velocity along the hyperbolic trajectory turns. From Fig. 3.13, it can be seen that

$$ \cos \kern-0.18em \left(\uppi -{\uptheta}_{\infty}\right)= \cos \kern-0.18em \left(\frac{\pi }{2},-,\frac{\delta }{2}\right) $$

(3.129)

Using Eq. (3.128), Eq. (3.129) gives

$$ \updelta =2{ \sin}^{\kern-0.18em -1}\left(\frac{1}{\mathrm{e}}\right) $$

(3.130)

For the case of parabola, $\mathrm{e}=1$ which gives ${\uptheta}_{\infty }$ as 180°. Therefore, for parabola, the asymptotes are parallel and do not intersect, and this is the limiting case between closed elliptical orbits and the open hyperbola trajectory.

Consider the energy equation,

$$ \frac{{\mathrm{V}}^2}{2}-\frac{\upmu}{\mathrm{r}}=\upvarepsilon $$

As for hyperbolic trajectory, ε is a positive value; at $\mathrm{r}=\infty$, the velocity is not zero and this is called residual velocity, ${\mathrm{V}}_{\infty }$ which is given by

$$ {{\mathrm{V}}_{\infty}}^2=2\upvarepsilon $$

(3.131)

For the case of hyperbolic trajectory of a satellite from the Earth, at $\mathrm{r}=\infty$, there is a positive residual velocity and therefore the satellite has its own orbit around Sun, which is different from that of the Earth.

At any point on the hyperbolic trajectory, the velocity is given by

$$ \mathrm{V}=\sqrt{2\left(\upvarepsilon +\frac{\upmu}{\mathrm{r}}\right)} $$

(3.132)

This gives,

$$ \mathrm{V}=\sqrt{{{\mathrm{V}}_{\mathrm{esc}}}^2+{{\mathrm{V}}_{\infty}}^2} $$

(3.133)

3.5 Satellite Orbit and Trajectory Requirements

The previous section deals with two-body problem, which defines the motion of a smaller body with respect to a bigger body. From the human-made satellite requirements point of view, these solutions can be used to define the motion of satellites (small body) about the Earth (bigger body). The requirements of orbits can be classified into two categories: (i) closed orbits (circular and elliptic) and (ii) open trajectories.

Closed orbits are used for the near Earth space utilization. These types of orbits are used for the utilization of Earth for survey of natural resources, Earth observation and its surrounding environments, communication and navigational systems. In another important application, these orbits are used as parking orbits, from which the satellites are injected into interplanetary trajectories which are open trajectories. This section gives uses of various types of orbits/trajectories required for various applications.

3.5.1 Circular Orbits

Circular orbits of different altitudes are utilized for various applications. Circular orbits are generally classified as Low Earth Orbit (LEO), Medium Earth Orbit (MEO) and High Earth Orbit (HEO). There is a hazardous Van Allen radiation belt around Earth, which starts at about 2400 km. The Van Allen belt consists of an inner zone of high energy protons and an outer zone of high energy electrons. Generally, the circular orbits are planned below the high intensity inner zone peak (altitude ~ 3700 km) or above the high intensity outer zone peak (altitude ~ 28,000 km). Low Earth circular orbits limit between around 150 km (where the atmospheric drag effect on orbit is less) to 1000 km (which is well below the Van Allen belt). The HEO is above the Geosynchronous Earth Orbit (GEO). In between, orbits are referred as MEO.

A circular orbit which skim the surface of the Earth (assumes a spherical Earth with no atmosphere) is referred as Earth-surface circular orbit and is many times used as reference orbit. This orbit has the minimum energy, maximum circular orbit velocity and minimum period. The period of this orbit is 84.4 min. This period is called Schuler period and is used in inertial navigation.

Solar day (synodic day) is the time from noon to noon, which is the time taken by Earth to rotate one full rotation about its axis, which is 24 h. But Earth also moves around the Sun. The siderial day is time taken by the Earth to complete one rotation relative to inertial space. Siderial day period is 23 h 56 min 4.091 s.

Orbit with the period equal to a siderial day is called Geosynchronous orbit. If such orbit is circular one and over equator and a satellite is placed on such orbit looks stationary with respect to a specified point on the Earth. Such orbit is called Geostationary Earth Orbit (GEO). The radial distance of GEO is 42,164 km and the altitude is 35,786 km. Such orbits are useful for communication satellites and weather satellites due to global coverage.

A satellite placed in GEO covers the latitudes range of ±81.3° and Earth surface area of 42.4 %. Therefore, 3 such satellites are required to cover the entire globe.

3.5.2 Elliptic Orbits

The elliptical orbits are used for reconnaissance satellites. The targets are near the perigee of such orbits whereas the apogee phase is utilized for transmitting the acquired information as well as to make the intercept problem more difficult. Also, elliptic orbits with high eccentricity are used for communications of high latitude regions as explained later.

Elliptic orbits are also used as the intermediate Geo Transfer Orbit (GTO) to place a satellite into GEO. In order to achieve the maximum performance, initially the launch vehicle places the satellite into an elliptic orbit of perigee altitude of about 200 km with apogee altitude of about 36,000 km. The satellite further uses its own propulsion system to transfer the satellite to GEO. This aspect is explained later.

3.5.3 Open Trajectories

The open trajectories, primarily hyperbolic trajectories, have been used for escaping Earth’s gravitational force field and to place a satellite in interplanetary or lunar trajectories. Also, when the satellite enters or reenters the sphere of gravitational attraction of another planet, the satellite follows hyperbolic trajectory. These aspects are also covered in later part of this chapter.

3.6 A Note on Orbital Energy and Launching of Satellites into Orbit

The previous section defines specified orbits or trajectories for specified spacecraft depending upon application. This section gives the launch vehicle requirements to achieve the specified orbits for the specified satellite.

Specific energy of an elliptical orbit (circular orbit is a special case of elliptical orbit) is given by

$$ \upvarepsilon =\frac{{\mathrm{V}}^2}{2}-\frac{\upmu}{\mathrm{r}} $$

(3.134)

where V²/2 is the specific kinetic energy and $\left(-\upmu /\mathrm{r}\right)$ is the specific potential energy. Considering a satellite of mass, m in the specified orbit, then the mechanical energy of the satellite E is given by

$$ \mathrm{E}=\mathrm{m}\upvarepsilon $$

(3.135)

Therefore, even though specific energy of an orbit is a defined value, depending on the mass of the satellite, the mechanical energy of the satellite in that orbit would vary. Therefore, for a heavier satellite, the mechanical energy of the satellite is larger. Similarly, the mechanical energy of a satellite in a bigger orbit is higher than that of the lower orbit. For the specified satellite to be placed in the defined orbit, the satellite has to be injected into the orbit with the mechanical energy as given by Eq. (3.135).

The specific kinetic energy depends on the square of orbital velocity at the specified radial distance. As the velocity increases, the kinetic energy also increases. For the radial distance close to zero, the potential energy is near to negative infinity. At the surface of Earth, the specific potential energy is about −62.6 MJ/kg, i.e., the energy becomes less negative and thus the energy increases. Similarly, for the Earth bound orbit at the altitude of 360 km (r = 6738 km), the specific potential energy is −59.2 MJ/kg. Thus at the altitude of 360 km above the surface of Earth, there is potential energy increase by 3.4 MJ/kg. From these it can be seen that as r increases, the negative value decreases, thus causing an increase in the potential energy compared to that at the surface of Earth.

Therefore, while defining the energy of satellite orbit, one should not confuse with its negative value. Even though the energy is negative, increase in the energy with respect to its value at the surface of Earth has to be considered for all the computations. From these explanations, it can be concluded

• 1. Energy increases for the orbits with larger r

• 2. Energy increases for the orbits with higher velocity

In order to launch a satellite of mass m from the surface of the Earth to the specified orbit, it is essential to impart the mechanical energy, $\mathrm{E}=\mathrm{m}\upvarepsilon$, to the satellite, where ε is the specific energy as per the requirements of the specified orbit. The mechanical energy to the satellite is imparted by the launch vehicle. The following are the requirements of the launch vehicle:

• 1. For the specified satellite mass, a larger launch vehicle is required to position the satellite to a higher orbit than that required to launch the same satellite into a lower orbit.

• 2. A specified launch vehicle can launch higher mass satellite into a lower orbit or a lesser mass satellite into a higher orbit.

These discussions give the total energy required to be generated by a launch vehicle. In reality, the velocity addition and correspondingly the increase in r happens during the STS operation time. The pattern of increase of these parameters depends on the vehicle configuration, the type of propulsion system and the vehicle attitude history during thrusting phase and thrusting duration. In order to reach the required orbit with the specified energy, at satellite injection at the specified distance r, the velocity components and the flight parameters are to be achieved by the launch vehicle as specified in Eqs. (3.77), (3.79) and (3.81). These functions are carried out by the launch vehicle subsystems as per the details provided in the subsequent chapters of this book.

During the launch vehicle operation, while propulsion system is adding energy which in turn increases the velocity and altitude to the vehicle and satellite systems, the Earth gravity reduces the velocity. The velocity loss due to gravity depends on the vehicle attitude with respect to gravity acceleration direction during thrusting phase and thrusting duration. Therefore, the energy provided by the propulsion system has to be effectively utilized to impart the maximum mechanical energy to the satellite to achieve the maximum performance. Generally, maximum energy utilization of the launch vehicle and in turn the maximum performance can be achieved if the satellites are injected at a lower orbit. However, depending on the complexities of integrated launch vehicle – satellite mission, a trade-off between the altitude of injection and velocity losses, suitable mission strategies are to be defined.

3.7 Orbital Elements

The state of a satellite at any instant in inertial space is defined by its instantaneous position and velocity components along the three axis of a specified reference frame.

The solution of two-body problem as discussed earlier gives the motion of the satellite in a plane, and the motion is along a closed orbit (circular or elliptic) or open trajectory (parabola or hyperbolic). The two body solution thus defines only type, shape and size of the orbits through two constants namely, eccentricity (e) and semi-major axis (a). But these two constants are not sufficient to define completely the location and velocity of the satellite at any instant. The additional constants required are: (i) orientation of the orbit with respect to a reference frame (3 constants) and (ii) position of the satellite in the orbit at any instant (1 constant). Together, these six constants are called orbital elements. It is to be noted that the components of position and velocity vectors in the defined Cartesian reference frame is related to these orbital elements.

The six orbital elements corresponding to a geocentric orbit as defined in Fig. 3.14 are summarized below:

Fig. 3.14

Orbital elements

• 1. Orientation of orbital plane in inertial space is given by inclination (i) and right ascension of ascending node (Ω)

• 2. Location of perigee in the orbital plane is defined by the argument of perigee (ω)

• 3. Type, shape and size of the orbit is defined by eccentricity (e) and semi-major axis (a)

• 4. Location of the satellite in the orbit is defined by the true anomaly (θ). Other equivalent parameters viz., mean anomaly, time since elapse of perigee, etc. can also be defined as the sixth element.

The parameters ‘a’ and ‘e’ define size, shape and type of orbit. The orientation of the orbital plane is defined by ‘Ω’ and ‘i’ and the location of perigee in that plane is defined by ω. The position of satellite in the defined orbit as above is decided by ‘θ’. These six orbital elements are explained below:

• 1. Right Ascension of Ascending Node (Ω)

The satellite during its orbital motion from southern hemisphere to northern hemisphere crosses the equator at ascending node, while its motion from northern hemisphere to southern hemisphere crosses the equator at descending node. The line joining the nodes is called the line of nodes. The nodal line is the line of intersection of orbital plane with equatorial plane. The angle of nodal line at ascending node location measured eastward from the X-axis of ECI frame is called the right ascension of ascending node.

• 2. Orbital Inclination (i)

The angle between the equator and orbit at the location of ascending node, measured from equator along the counter clockwise direction is called the inclination of the orbit.

• 3. Argument of Perigee (ω)

The angle between the line of nodes at the ascending node to the apsis line at the perigee location is called argument of perigee. This angle is measured counter clockwise from the line of nodes to the apsis line along the orbital plane.

• 4. Eccentricity (e)

This constant defines the type and shape of the orbit as explained earlier.

• (v) Semi-major axis (a)

This constant defines the size of the orbit as explained earlier.

• 5. True anomaly (θ)

This is the angle measured clockwise from the apsis line at perigee location to the position vector of the satellite. This is defined earlier as part of two-body motion.

3.8 Orbital Perturbations

Perturbations of geocentric orbital elements are explained in this section. The two-body problem as explained in the previous sections considered central gravitational force field. In reality, the actual force field is not central force field due to the asphericity of Earth and due to the presence of atmospheric drag, third body perturbations such as Moon, Sun and solar radiation pressure.

These perturbation forces can be added to the central force field and the equation of motion of the satellite can be written as

$$ \ddot{\mathbf{r}}=-\frac{\upmu}{{\mathrm{r}}^3}\mathbf{r}+\mathbf{f} $$

(3.136)

The solution of Eq. (3.136) is not a Keplerian orbit as defined by the first part of right hand side (RHS) of Eq. (3.136). However, the major force is the gravity force (central force) due to spherical Earth which keeps the satellite in the Keplerian orbit whereas the perturbation forces cause the variations in the Keplerian orbital elements.

Variations in the orbital elements consist of the following components: (i) secular, (ii) short period variation and (iii) long-period term as shown in Fig. 3.15. Depending on the types of disturbing forces and orbital characteristics, each orbital element has the specific variations.

Fig. 3.15

Typical variation of anorbital element

For near Earth satellites orbits, Earth’s asphericity causes major disturbing force compared to the other sources and its effects are explained in the following section.

3.8.1 Effects of Earth’s Asphericity on Orbital Elements

Earth is an irregular shaped body which causes the gravitational force not passing through its center and its gravitational potential is defined as

$$ \mathrm{U}=-\frac{\upmu}{\mathrm{r}}\left[1-{\displaystyle \sum_{\mathrm{n}=2}^{\infty }}{\mathrm{J}}_{\mathrm{n}}{\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{n}}\left(\kern-0.25em , \sin \uplambda \right)\right.\left. - {\displaystyle \sum_{\mathrm{n}=2}^{\infty }}{\displaystyle \sum_{\mathrm{m}=1}^{\mathrm{n}}}{\mathrm{J}}_{\mathrm{n},\kern0.05em \mathrm{m}}{\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^{\mathrm{n}}{{\mathrm{P}}_{\mathrm{n}}}^{\mathrm{m}}\left(\kern-0.25em \sin \uplambda \right) \cos \mathrm{m}\left(\Phi -{\Phi}_{\mathrm{n},\kern0.05em \mathrm{m}}\right)\right] $$

(3.137)

where r, λ, ϕ are geocentric distance, latitude and longitude respectively. P_n(sin λ) is Legendre’s polynomial of degree n in sin λ, P_n ^m(sin λ) is the associated Legendre function of degree n and order m. R_e is the equatorial radius of Earth. J_n, J_n, m and ϕ_n, m are numerical coefficients that describe the mass distribution. The terms having J_n are called zonal harmonics, which describe the deviation of gravity away from Newtonian in the north-south direction. The terms having J_n, m, $\mathrm{n}\ne \mathrm{m}$ are called tesseral harmonics and J_n, m, $\mathrm{n}=\mathrm{m}$ is known as sectorial harmonics, which represent the deviation of gravity acceleration in the east-west direction.

The term with $\mathrm{n}=1$ is absent due to the assumption that the origin of reference frame coincides with center of mass of the Earth. The term J₂ represents the oblateness of Earth, J₃ represents the Earth as pear shaped, J_2,2 represents ellipticity of the equator and so on. For an orbit inclined to the equator, the effects of tesseral and sectorial harmonics can be assumed to be averaged out over a long period of time. In this case, the Earth can be assumed to be an axi-symmetric body with zonal harmonics terms alone. However, for equatorial orbit, especially geostationary orbit, wherein the satellite is positioned at same location with respect to the Earth, tesseral and sectorial harmonics play a major role in the orbital elements variations. Considering only zonal harmonics terms, the value of J₂ is 1.0826 × 10⁻³ and other coefficients are of the order of 10⁻⁶. Therefore, J₂ term is having the major impact on the orbital perturbations and is further analyzed as given below.

Considering only J₂ in Earth potential, define the Earth as oblate spheroid, and due to this feature, the gravity acceleration is away from the center of Earth as shown in Fig. 3.16, and the deviation is the function of latitude and radial distance.

Fig. 3.16

Oblate Earth

The gravity component g_r towards center of the Earth defines Keplerian orbital elements whereas the disturbance component g_d causes perturbation to the Keplerian orbital elements. The disturbing potential considering only J₂ term is given as

$$ \Delta \mathrm{U}=-\frac{\upmu}{\mathrm{r}}\left({\mathrm{J}}_2\right){\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^2{\mathrm{P}}_2\left( \sin \uplambda \right) $$

(3.138)

In this case, the gravitational acceleration of oblate Earth as defined by Eq. (3.136) is

$$ \ddot{\mathbf{r}}=-\frac{\upmu}{{\mathrm{r}}^3}\mathbf{r}+\mathbf{f} $$

where

$$ \mathbf{f}={\mathrm{f}}_{\mathrm{r}}{\mathbf{u}}_{\mathbf{r}}+{\mathrm{f}}_{\mathrm{h}}{\mathbf{u}}_{\mathbf{h}}+{\mathrm{f}}_{\mathrm{v}}{\mathbf{u}}_{\mathbf{v}} $$

(3.139)

f_r, f_v and f_h are the radial, normal (to orbital plane) and perpendicular to r and lying in the orbital plane components of f and u _r , u _v and u _h are the corresponding unit vectors along these directions respectively. The disturbing force components corresponding to J₂ term, with respect to the orbital plane in terms of orbital elements, can be expressed as

$$ {\mathrm{f}}_{\mathrm{r}}=-\frac{\upmu}{{\mathrm{r}}^2}\left(\frac{3}{2}\right){\mathrm{J}}_2{\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^2\left[1-3\kern0.15em \sin {\kern-0.17em }^2\mathrm{i}\kern0.20em \sin {\kern-0.17em }^2\left(\upomega +\uptheta \right)\right] $$

(3.140)

$$ {\mathrm{f}}_{\mathrm{h}}=-\frac{\upmu}{{\mathrm{r}}^2}\left(\frac{3}{2}\right){\mathrm{J}}_2{\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^2 \sin {\kern-0.18em }^2\mathrm{i}\kern0.20em \sin \kern-0.20em \left[2\left(\upomega +\uptheta \right)\right] $$

(3.141)

$$ {\mathrm{f}}_{\mathrm{v}}=-\frac{\upmu}{{\mathrm{r}}^2}\left(\frac{3}{2}\right){\mathrm{J}}_2{\left(\frac{{\mathrm{R}}_{\mathrm{e}}}{\mathrm{r}}\right)}^2 \sin 2\mathrm{i}\kern0.45em \sin \kern-0.25em \left(\upomega +\uptheta \right) $$

(3.142)

The disturbance forces as given in Eqs. (3.140), (3.141), and (3.142) induce rates of change of all the orbital elements. The rate of change of two orbital elements of interest is given below:

$$ \dot{\mathsf{\varOmega}}=\frac{\mathrm{H}}{\upmu}\frac{ \sin \kern-0.20em \left(\upomega +\uptheta \right)}{ \sin \mathrm{i}\left(1+\mathrm{e}\kern0.20em \cos \uptheta \right)}{\mathrm{f}}_{\mathrm{v}} $$

(3.143)

$$ \dot{\upomega}=-\frac{\mathrm{r}\kern0.20em \cos \uptheta}{\mathrm{eH}}{\mathrm{f}}_{\mathrm{r}}+\frac{\left(2+\mathrm{e}\kern0.20em \cos \uptheta \right) \sin \uptheta}{\mathrm{eH}}{\mathrm{f}}_{\mathrm{h}}-\frac{\mathrm{r} \sin \kern-0.20em \left(\upomega +\uptheta \right)}{\mathrm{H}\kern0.20em \tan \mathrm{i}}{\mathrm{f}}_{\mathrm{v}} $$

(3.144)

It can be seen that the rate of change of $\mathsf{\varOmega}$ is caused by disturbance normal to orbital plane whereas disturbances in all the directions caused $\dot{\upomega}$. Integrating $\dot{\mathit{\mathsf{\varOmega}}}$ and $\dot{\upomega}$ over one orbit gives the average rate of change and is given by

$$ {\dot{\mathsf{\varOmega}}}_{\mathrm{av}}=\frac{1}{\mathrm{T}}\underset{0}{\overset{\mathrm{T}}{\int }}\dot{\mathsf{\varOmega}}\mathrm{d}\mathrm{t};\kern1em {\dot{\upomega}}_{\mathrm{av}}=\frac{1}{\mathrm{T}}\underset{0}{\overset{\mathrm{T}}{\int }}\dot{\upomega}\mathrm{d}\mathrm{t} $$

where T is orbital period

After simplifications, the average rate of change of $\mathsf{\varOmega}$ is given by

$$ {\dot{\mathsf{\varOmega}}}_{\mathrm{a}\mathrm{v}}=-\left[\frac{3}{2}\frac{\sqrt{\upmu}{\mathrm{J}}_2{{\mathrm{R}}_{\mathrm{e}}}^2}{{\left(1-{\mathrm{e}}^2\right)}^2\ {\mathrm{a}}^{7/2}}\right] \cos \mathrm{i} $$

(3.145)

and the average rate of change of ω is given by

$$ {\dot{\upomega}}_{\mathrm{a}\mathrm{v}}=-\left[\frac{3}{2}\frac{\sqrt{\upmu}{\mathrm{J}}_2{{\mathrm{R}}_{\mathrm{e}}}^2}{{\left(1-{\mathrm{e}}^2\right)}^2\ {\mathrm{a}}^{7/2}}\right]\left[\frac{5}{2} \sin {\kern-0.20em }^2\mathrm{i}-2\right] $$

(3.146)

Equations (3.145) and (3.146) are the secular variations on $\mathsf{\varOmega}$ and ω respectively.

For the case of orbits with $0\le \mathrm{i}<90{}^{\circ}$, which are called posigrade orbits, the nodal line drifts westward and this phenomenon is called regression of the nodes. For the case of retrograde orbits, i.e., $90{}^{\circ}<\mathrm{i}\le 180{}^{\circ}$, the nodal line advances. Similarly for the orbits with $0\le \mathrm{i}<63.4{}^{\circ}$, or $116.6{}^{\circ}<\mathrm{i}\le 180{}^{\circ}$, the perigee advances in the direction of orbital motion. i.e., the whole orbit rotates in the orbital plane along the direction of satellite motion. If $63.4{}^{\circ}<\mathrm{i}\le 116.6{}^{\circ}$, the perigee regresses. For the case of $\mathrm{i} = 63.4{}^{\circ}$, or $\mathrm{i}=116.6{}^{\circ}$, the apse line does not move. These inclinations are called critical inclinations.

The phenomenon of nodal regression and perigee advancement due to Earth asphericity are effectively utilized for the two important applications of satellite orbits as explained below.

3.8.2 Sun-Synchronous Orbits

Sun-synchronous orbits are those orbits whose orbital plane makes constant angle with the Sun-Earth line, i.e. for the Sun-synchronous orbits the angle between the nodal line and the Sun-Earth line is always constant. For a defined orbit size (a) and shape (e), inclination i can be found such that $\dot{\mathsf{\varOmega}}=0.9856{}^{\circ}/\mathrm{day}$. This set of (a, e, i) defines a Sun-synchronous orbit. As the Earth moves around Sun with the angular rate of 0.9856°/day, and the nodal line also moves with the same rate, the nodal line always form a constant angle with Sun-Earth line, which is decided by the satellite applications. This is represented in Fig. 3.17.

Fig. 3.17

Sun-synchronous orbit

Such satellites, for every swath, pass through same sunlight conditions or darkness. This is particularly advantageous for Earth observation satellites to establish the correlations of various observations with respect to several phenomena such as crop growth, forest coverage, drought conditions, etc. Sun-synchronous orbits with nodal line perpendicular to the Sun-Earth line is also important. Since Sun’s declination δ is within the range $-23.5{}^{\circ}<\updelta <23.5{}^{\circ}$, by carefully selecting launch date and orbital height, such orbit remains continuously in sunlight for more than 8 months. These orbits are useful for solar power generation satellites.

3.8.3 Molniya Orbits

From the Eq. (3.146), it can be seen that if $\mathrm{i}=63.4{}^{\circ}$, or $\mathrm{i}=116.6{}^{\circ}$, then $\dot{\upomega}=0$. i.e., for such orbit, the apse line remains stationary in space. This feature was used by erstwhile USSR for communication satellite, Molniya (lightning). The Russian launch sites are at high northern latitudes, the northern most is Plesetsk at 62.8°N. As can be seen later, the lowest inclination orbit achievable for the launch from this site is 62.8°. Therefore, from such launch sites, launching satellites into geostationary orbit is costly. Also, the geostationary satellites positioned over equator cannot effectively view the far northern latitude region of erstwhile USSR. Under such situations, Molniya satellites launched into high eccentric orbit with perigee of about 500 km altitude and apogee altitude of about 40,000 km with inclination of 63.4°. The period of this orbit is about 12 h. The apogees of such orbits are placed over northern latitude to ensure that the satellite is visible over USSR for most of its period. Molniya constellation consists of 8 satellites; each separated by 45°. Each satellite is above 45°N latitude for 8 h. Typical Molniya orbit is given in Fig. 3.18.

Fig. 3.18

Molniya orbit

3.8.4 A Note on Osculating and Mean Orbital Elements

Due to continuous variation of orbital elements of short period and long period, there are two terms used for defining orbital elements: (i) osculating elements and (ii) mean orbital elements. Osculating orbital elements are the instantaneous Keplerian orbital elements. If the perturbation forces at that instant vanishes, then the orbital elements for the remaining period of time is constant, which is corresponding to the osculating element at that instant. The mean orbital elements and osculating elements are related by

$$ {\upxi}_{\mathrm{osculating}}={\upxi}_{\mathrm{mean}}+{\Delta \upxi}_{\mathrm{perturbation}} $$

(3.147)

where ξ is an orbital element (a, e, i, Ω, ω, θ). Due to the non-variation nature of mean orbital elements, satellite mission targets are on the mean orbital elements. Since the launch vehicle mission target is at a specified latitude, longitude and altitude, the launch vehicle achieved orbit is corresponding to the osculating orbital elements. Therefore, there should be suitable interface between the satellite requirements and launch vehicle mission target.

3.9 Restricted Three-Body Problem

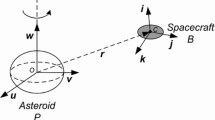
For the satellite orbit trajectories beyond Earth such as lunar mission or interplanetary mission, the satellite motion is influenced by both Earth and moon or Sun and Earth. Under such cases, the two-body problem as described in previous section is not valid and one has to adopt three-body problem as explained in this section. Consider two massive bodies m₁ and ${\mathrm{m}}_2\left({\mathrm{m}}_1>{\mathrm{m}}_2\right)$, which are under motion due to their mutual gravitational attractions about the center of mass. Now consider a small body m, which is very small compared to that of m₁ and m₂ as shown in Fig. 3.19. Motion of the third body m under the influence of the gravity attraction of bigger bodies m₁ and m₂ is called the restricted three-body problem. (Example: m₁: Earth, m₂: Moon and m: satellite or m₁: Sun, m₂: Earth and m: satellite). There is no closed form solution to this problem. Detailed discussion on such a problem is beyond the scope of this book. Certain important aspects relevant to space transportation system under such condition are briefly summarized.

Fig. 3.19

Restricted three-body problem

There are five equilibrium locations in this system, where the mass m has zero velocity and acceleration with respect to m₁ and m₂. These equilibrium locations are called liberation or Lagrange points. The equilibrium points lie in the orbital plane of ${\mathrm{m}}_1-{\mathrm{m}}_2$ system. Once a body m is placed at the liberation point, the body stays there. However, for an inertial observer, a mass m placed at such locations move around m₁ and m₂ in circular orbit.

For the Earth-Moon system, the locations of Lagrange points are given in Fig. 3.20. L₁ point of Sun–Earth system is about 1.5 million km from Earth. The L₁, L₂ and L₃ are the saddle points i.e. unstable equilibrium points. The small body occupying these locations can stay there only if there is no disturbance. L₁, L₂ and L₃ are the locations wherein the centrifugal force on the small mass m balances the combined collinear gravitational forces of Earth and Moon for three conditions. Due to unstable nature, any satellite placed in these points need fuel for keeping in that location.

Fig. 3.20

Lagrange points of Earth-Moon system

The Langrange points L₄ and L₅ are the stable equilibrium points. At these locations, the gravitational forces from the massive bodies are in the ratio as that of the masses of the bodies so that the resultant force passes through the barry center. As the barry center is the center of mass of the system as well as center of rotation of the three body system, the resultant force is the one required to keep the smaller body at the Langrange point L₄ or L₅. Any disturbance caused to the small body at this location results into stable oscillation about the equilibrium point, i.e. the small body m orbits about the equilibrium point. Thus a satellite placed in a small orbit about the stable equilibrium point stays there without any need for the fuel for station keeping. These orbits are called halo orbits. The stable equilibrium points are located at 60° with respect to the primary bodies. In nature, the Trojan asteroids occupy the stable equilibrium points L₄ and L₅ of Sun-Jupiter system.

Even though L₄ and L₅ are stable equilibrium locations, due to orbital perturbations caused by the other planetary bodies, some amount of fuel is required to keep and maintain halo orbits.

The satellites placed at the Liberation points (especially L₂ of Earth-Moon system) are useful as transit stations for interplanetary mission and for permanent space colonies (especially placed at L₄ or L₅). They also can be used as stations for permanent activities on Moon such as lunar mining etc.

3.10 Interplanetary Trajectories

In order to achieve an interplanetary mission (travel from Earth to another planet), the satellite has to escape from the Earth’s gravitational attraction. Even though the parabolic trajectory is an open trajectory which takes the satellite to infinity, if the satellite is launched with just escape velocity, at infinity, the residual velocity is zero and the satellite mission ends up with an orbit, same as that of Earth around Sun. In order to ensure that the satellite escapes from the Earth’s gravitational attraction and to reach the target planet, there must be an excessive residual velocity at infinity, which is a characteristic of hyperbolic trajectory. Therefore, to achieve interplanetary mission from Earth, the satellite has to be launched in a hyperbolic trajectory. As the distance from the Earth increases, the Earth’s gravitational attraction reduces and Sun’s gravitational attraction increases and at one point of time, the satellite enters into a heliocentric trajectory with gravitational attraction of the Sun. This heliocentric trajectory depends on the residual velocity of the vehicle when it departs the Earth’s gravitation. As the vehicle enters into the gravitational field of the target planet, the orbit becomes the planetocentric one.

The escape velocity at the time of Earth departure and trajectory during its entire journey are decided on the specific mission of the satellite. There are three types of interplanetary missions: (i) Fly-by mission, (ii) Orbiter mission and (iii) Lander mission.

In the fly-by mission, the satellite passes through the target planet at a short distance with respect to the planet and fly away further. In the orbiter mission, once the satellite is reached at a specified location and distance with respect to the target planet, propulsion system onboard the satellite is activated to reduce the velocity of the satellite to end up with an orbit around the target planet, as per the mission definition. In the case of lander mission, after reaching the orbit around the planet, the vehicle velocity is further reduced in a controlled fashion by the propulsion system. For the planets with atmosphere, the aerobreaking strategies are used to reduce the chemical propulsion requirements. Due to the high residual velocity requirements and the long distance travel, the interplanetary missions demand high energy requirements as well as longer travel time. In order to achieve the higher energy requirements and to reduce the travel time, advanced propulsion systems are required.

The main attracting bodies involved in an interplanetary trajectory are Earth, Sun and target planet. In addition, the gravitational attractions of Moon, other planets and radiation pressure act as disturbance forces to the satellite. Therefore, in reality, the interplanetary trajectories are many-body problems.

Consider an interplanetary mission from Earth to a target planet (say, Mars) as shown in Fig. 3.21. Initially, heliocentric conic section from Earth to target planet locations meeting the energy requirements and travel duration is finalized. After finalizing the requirements, the interplanetary trajectory is divided into three Keplerian conic sections as given below:

Fig. 3.21

Interplanetary trajectory conics to Mars

• 1. Geocentric hyperbolic trajectory

• 2. Heliocentric trajectory

• 3. Planetocentric hyperbolic trajectory

The velocity requirements at the interfaces and the trajectory in the three phases are decided to meet the integrated interplanetary mission requirements, i.e. the above three conic sections are patched together to arrive at the defined interplanetary trajectory. This approach is called patched conic method. After designing the trajectory with the above method, considering all the disturbance forces, their detailed trajectory analysis is carried out. While designing the interplanetary trajectory with patched conic approach, the spheres of influence plays a key role.

3.10.1 Sphere of Influence

In the patched conic approach, when a satellite follows Keplerian conic under the influence of one body (say, mass, m₂) the body is under the sphere of influence of m₂ whereas the second body (say, mass, m₁) gravitational attraction acts as disturbance to the satellite. Sphere of influence is a surface along which the influence of each body m₁ and m₂ are equal. Within the sphere of influence of m₂, the trajectory of satellite is influenced by gravitational acceleration of m₂ whereas the gravitational acceleration of m₁ is acting as disturbance.

Consider two bodies and satellite as shown in Fig. 3.22. The sphere of influence or activity sphere of m₂ is defined by

Fig. 3.22

Sphere of influence

$$ {\mathrm{r}}_{\mathrm{si}}=\mathrm{R}{\left(\frac{{\mathrm{m}}_2}{{\mathrm{m}}_1}\right)}^{2/5}\frac{1}{{\left(1+3\kern0.20em \cos {\kern-0.15em }^2\upbeta \right)}^{1/10}} $$

(3.148)

The surface is rotationally symmetric with respect to the line joining the bodies and the shape of the surface is slightly different from a sphere.

For the case of Sun-Earth system, the sphere of influence of Earth varies from 0.8 × 10⁶ km to 0.925 × 10⁶ km. For the case of Earth-Moon system, the sphere of influence of Moon varies between 58 × 10³ km and 66 × 10³ km.

3.10.2 Patched Conic Trajectory

As an example, the interplanetary trajectory from Earth to Mars is considered as shown in Fig. 3.23. The satellite velocity required at the sphere of influence of Earth to follow the heliocentric trajectory to reach Mars is ${\mathrm{V}}_{\infty \mathrm{e}}$.

Fig. 3.23

Earth-Mars trajectory

$$ {\mathbf{V}}_{\infty \mathbf{e}} = {\mathbf{V}}_1-{\mathbf{V}}_{\mathbf{e}} $$

(3.149)

where V _e is the Earth’s orbital velocity and V ₁ is the velocity at the start of the heliocentric conic near to the Earth side. Generally, at the surface of sphere of influence, the velocity of the hyperbolic trajectory equals to the hyperbolic excess (residual) velocity ${\mathbf{V}}_{\infty }$. In case additional velocity is required it can be imparted to ${\mathrm{V}}_{\infty }$ to get the required ${\mathrm{V}}_{\infty \mathrm{e}}$. Once the satellite arrives at the Mars, the planetocentric excess velocity, ${\mathbf{V}}_{\infty \mathrm{m}}$, is achieved by

$$ {\mathbf{V}}_{\infty \mathbf{m}} = {\mathbf{V}}_2-{\mathbf{V}}_{\mathbf{m}} $$

(3.150)

where V₂ is the heliocentric conic velocity at the approach and V_m is orbital velocity of Mars. If required, satellite velocity can be reduced to achieve the required ${\mathbf{V}}_{\infty \mathbf{m}}$.

By this process, the interplanetary trajectory from Earth to Mars is achieved.

3.11 Orbital Transfers and Launch Vehicle Orbit Requirements

Although this section can be a part of chapter on Mission Design or Satellite Launching, it is included here due to its close links with this chapter. Orbital transfer is an integral part of satellite mission design. Requirements of a specific orbit for a satellite depend on the application for which the satellite is intended for; it needs to be placed in the specified orbit in terms of size, shape and orientation in inertial space. As an example, remote sensing satellites need to be placed in the circular orbits with the altitude ranging from 500 to 900 km along with the inclination varying between 97° and 99°, whereas communication satellites need to be placed in the circular orbit with an altitude of about 36,000 km above the Earth over the equator (inclination = 0). The satellite orbits used for communication in the high latitude region of Earth require high eccentric orbits with critical inclination (i = 63.4°) with apogee over the specified region of Earth, whereas global navigational satellite systems need to be placed in orbits about 20,000 km with inclination about 50°.

In addition, the satellites for lunar and interplanetary missions need to depart from the Earth bound orbits at a specified time, day, month and year. Therefore, depending on the applications, it is essential to place the satellite in its specified orbit.

An efficient launch vehicle has to deliver the energy in the shortest possible time. Sometimes, although the velocity achieved by the vehicle is substantial, the altitude travelled by the vehicle may not meet the satellite requirements. Therefore, to achieve the high altitude requirement of satellite, ensuring the required velocity, the vehicle energy has to be appropriately utilized to increase the potential energy. This in turn reduces the share of kinetic energy, resulting in the reduction of payload capability of the vehicle.

Thus, for a specified launch vehicle, there is trade-off between the orbital altitude and the payload mass which can be placed in the specified orbit. To enhance the payload capability, launch vehicle always prefers to place a satellite in an orbit with lower altitude. The best performance of a launch vehicle is achieved by planar trajectory missions. To obtain the required inclination, from the launch site, a suitable launch azimuth is to be defined. Due to range safety limitations, the required launch azimuth may not be feasible and hence it is difficult to achieve the required inclination from the specified launch site. In certain cases, although the best launch azimuth is feasible, the inclination of the orbit achieved is restricted by the geographical location of launch site. For example, to achieve zero orbital inclination, the launch site has to be located over equator with an azimuth of 90°. Any deviation from this, results into different orbital inclination and this needs to be corrected by the satellite.

Therefore, an integrated optimum strategy for achieving the maximum performance is to target the launch vehicle to inject the satellite into the ‘best possible’ orbit, which achieves maximum payload. Further the satellite has to carry out the needed orbital transfers from the orbit provided by the vehicle to the final specified orbit. This needs additional fuel in satellite onboard.

Thus, launch vehicle design and mission planning is a trade-off between vehicle capability vis-à-vis extra fuel required in satellite to carry out the needed orbital transfers. The quantity of fuel in satellite depends on the type of orbital transfer maneuver needed. This section briefly explains the orbital transfer maneuvers from the satellite. It is assumed that the propulsive system used for the orbital transfer is imparting the required velocity in impulsive fashion.

3.11.1 Coplanar Circular Orbits Transfer

Assume the launch vehicle achieved orbit, O₁ is a circular orbit with radius r_c1, and the satellite required orbit O₂, is also circular orbit with radius r_c2, as shown in Fig. 3.24. Assuming O₁O₂ are coplanar (i.e., orbital inclinations are same), the minimum energy path from O₁ to O₂ is Hohmann transfer. This is a semi-elliptic trajectory with perigee tangential to the orbit altitude r_c1 of O₁ and apogee tangential to the orbit altitude r_c2 of O₂ as shown in figure.

Fig. 3.24

Coplanar circular orbits transfer

Velocity of vehicle at A on the circular orbit O1 is as derived in Eq. 3.99 is given by

$$ {\mathbf{V}}_{\mathbf{c}1}=\sqrt{\frac{\upmu}{{\mathrm{r}}_{\mathrm{c}1}}} $$

(3.151)

The parameters of Hohmann transfer ellipse as given in Fig. 3.24 are given below:

$$ {\mathrm{r}}_{\mathrm{p}}={\mathrm{r}}_{\mathrm{c}1} $$

(3.152)

$$ {\mathrm{r}}_{\mathrm{a}}={\mathrm{r}}_{\mathrm{c}2} $$

(3.153)

$$ \mathrm{a}=\frac{{\mathrm{r}}_{\mathrm{c}1}+{\mathrm{r}}_{\mathrm{c}2}}{2} $$

(3.154)

Velocity of vehicle in elliptic path is given by

$$ \mathbf{V}=\sqrt{\upmu \left(\frac{2}{\mathrm{r}}-\frac{1}{\mathrm{a}}\right)} $$

(3.155)

Velocity of the vehicle at A (perigee), if the vehicle needs to travel in Hohmann ellipse of Fig. 3.24 is given as

$$ {\mathbf{V}}_{\mathbf{A}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{c}1}}-\frac{1}{\mathrm{a}}\right)} $$

(3.156)

Therefore the velocity increment required to transfer the vehicle from the launch vehicle orbit O₁ to transfer ellipse is given as

$$ \Delta {\mathbf{V}}_{\mathbf{A}} = {\mathbf{V}}_{\mathbf{A}}-{\mathbf{V}}_{\mathbf{c}1} $$

(3.157)

Velocity of the vehicle at apogee of the transfer ellipse (B) is given by

$$ {\mathbf{V}}_{\mathbf{B}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{c}2}}-\frac{1}{\mathrm{a}}\right)} $$

(3.158)

and velocity, V_c2 of the circular orbit altitude r_c2 of O₂ is given by

$$ {\mathbf{V}}_{\mathbf{c}2}=\sqrt{\frac{\upmu}{{\mathrm{r}}_{\mathrm{c}2}}} $$

(3.159)

Therefore, the velocity increment required to transfer the vehicle from the transfer ellipse to the required satellite orbit O₂ is given by

$$ \Delta {\mathbf{V}}_{\mathbf{B}} = {\mathbf{V}}_{\mathbf{c}2} - {\mathbf{V}}_{\mathbf{B}} $$

(3.160)

Thus applying the impulsive velocity increments ΔV _A in the plane of orbit when the vehicle reaches the location A, tangential to the orbit and subsequently ΔV _B in the plane of orbit when the vehicle reaches the location at B, tangential to the orbit, the satellite will reach the final orbit O₂.

Therefore, total velocity imparted by the satellite to transfer from launch vehicle orbit to the satellite specified orbit is given by

$$ \Delta \mathbf{V} = \Delta {\mathbf{V}}_{\mathbf{A}}+\Delta {\mathbf{V}}_{\mathbf{B}} $$

(3.161)

Assuming the specific impulse, Isp (in seconds) used by the satellite propulsion system, the propellant needs to be stored in the satellite, m_p, to achieve the final orbit is given by

$$ {\mathrm{m}}_{\kern-0.20em \mathrm{p}}={\mathrm{m}}_{\mathrm{i}\ }\left[1-{\mathrm{e}}^{-\left(\frac{\Delta \mathrm{V}}{\mathrm{g}\kern0.15em \mathrm{Is}\kern-0.15em \mathrm{p}}\right)}\right] $$

(3.162)

where m_i is the mass of satellite injected by launch vehicle into initial orbit which includes useful payload, propulsion system accessories and propellant.

3.11.2 Coplanar Elliptic Orbits Transfer

In this case, the initial orbit O₁ and final orbit O₂ are ellipses with the same focus as given in Fig. 3.25. The coplanar Hohmann transfer ellipse and the locations and directions of velocity increment applications are computed as given below:

Fig. 3.25

Coplanar elliptic orbits transfer

Launch vehicle achieved orbital characteristics are: perigee radius = r_p1, apogee radius = r_a1 and ${\mathrm{a}}_1=\left({\mathrm{r}}_{\kern-0.15em \mathrm{p}1}+{\mathrm{r}}_{\mathrm{a}1}\right)/2$.

Satellite required orbital characteristics are perigee radius = r_p2, apogee radius = r_a2 and ${\mathrm{a}}_2 = \left({\mathrm{r}}_{\kern-0.15em \mathrm{p}2} + {\mathrm{r}}_{\mathrm{a}2}\right)/2$.

Perigee velocity of O₁ at A is given by

$$ {\mathbf{V}}_{\kern-0.20em \mathbf{p}1}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\kern-0.15em \mathrm{p}1}}-\frac{1}{{\mathrm{a}}_1}\right)} $$

(3.163)

The transfer ellipse is with perigee radius of r_p1 and apogee radius of r_a2. Therefore, the semi-major axis of transfer ellipse is

$$ {\mathrm{a}}_{\mathrm{t}}=\frac{{\mathrm{r}}_{\mathrm{p}1}+{\mathrm{r}}_{\mathrm{a}2}}{2} $$

(3.164)

and the perigee velocity of transfer orbit at A is given by:

$$ {\mathbf{V}}_{\mathbf{pt}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\kern-0.15em \mathrm{p}1}}-\frac{1}{{\mathrm{a}}_{\mathrm{t}}}\right)} $$

(3.165)

Therefore, the velocity increment, ΔV _A , required to be applied at A in the orbital plane along the direction of velocity to transfer the vehicle from initial orbit, O₁, to transfer orbit is given by

$$ \Delta {\mathbf{V}}_{\mathbf{A}} = {\mathbf{V}}_{\mathbf{pt}}-{\mathbf{V}}_{\kern-0.20em \mathbf{p}1} $$

(3.166)

Similarly, the apogee velocity of transfer ellipse at B is given by

$$ {\mathbf{V}}_{\mathbf{at}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{a}2}}-\frac{1}{{\mathrm{a}}_{\mathrm{t}}}\right)} $$

(3.167)

and the apogee velocity of the required orbit O₂, at B is given by

$$ {\mathbf{V}}_{\mathbf{a}2}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{a}2}}-\frac{1}{{\mathrm{a}}_2}\right)} $$

(3.168)

and therefore, the velocity increment, ΔV _B , required to be applied at B in the orbital plane along the direction of velocity to transfer the vehicle from the transfer orbit to the final required orbit, O₂, is given by

$$ \Delta {\mathbf{V}}_{\mathbf{B}} = {\mathbf{V}}_{\mathbf{a}2}-{\mathbf{V}}_{\mathbf{a}\mathbf{t}} $$

(3.169)

and the total velocity requirement is given by

$$ \Delta \mathbf{V}={\Delta \mathbf{V}}_{\mathbf{A}}+{\Delta \mathbf{V}}_{\mathbf{B}} $$

(3.170)

3.11.3 Coplanar Orbital Transfer from Ellipse to Circular Orbit

In this case, the launch vehicle is assumed to inject the satellite in an elliptic orbit O₁ with a suitable perigee and apogee altitude corresponding to the circular orbit height of the satellite. The satellite in turn circularizes the orbit to O₂. Assuming these orbits are coplanar, the incremental velocity required to be imparted by satellite is computed as follows:

The launch vehicle orbit is an elliptic one with perigee radial distance of r_p and apogee radial distance of r_a. The satellite required orbit is a circular orbit with altitude of r_a. In this case, the velocity increment need to be applied at the apogee location, A, of launch vehicle orbit along the velocity direction.

The apogee velocity of launch vehicle orbit is given by

$$ {\mathbf{V}}_{\mathbf{a}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{a}}}-\frac{1}{\mathrm{a}}\right)};\kern0.8em \mathrm{a}=\frac{{\mathrm{r}}_{\mathrm{a}}+{\mathrm{r}}_{\kern-0.15em \mathrm{p}}}{2} $$

(3.171)

The circular velocity of required orbit is given by

$$ {\mathbf{V}}_{\mathbf{c}}=\sqrt{\frac{\upmu}{{\mathrm{r}}_{\mathrm{a}}}} $$

(3.172)

and the required velocity increment ΔV _A to be applied at A along the velocity direction is given by

$$ \Delta {\mathbf{V}}_{\mathbf{A}} = {\mathbf{V}}_{\mathbf{c}} - {\mathbf{V}}_{\mathbf{A}} $$

(3.173)

3.11.4 Inclination Change of Orbital Plane

Assume that the launch vehicle injects the satellite into a circular orbit O₁ with the altitude as specified by the satellite. But it could not achieve the required inclination, and in such case, the satellite needs to maneuver the orbital plane to reach the final one, O₂, as given in Fig. 3.26.

Fig. 3.26

Inclination change of circular orbits

The inclination of the orbit is measured at equator when the satellite crosses the line of nodes. Therefore, it is essential to apply the correction maneuver at the time of equatorial crossing of the satellite. In this case, it is important not to change the magnitude of the satellite velocity but to rotate the velocity vector, V_c, in a plane normal to the original orbital plane. The incremental velocity required to change the inclination has to be applied in the normal plane with magnitude and direction as detailed below.

For simplicity, the velocity diagram of initial orbit O₁ with inclination of i₁ and final orbit O₂ with inclination of i₂ of Fig. 3.26 is reproduced in Fig. 3.27.

Fig. 3.27

Velocity diagram for change of inclination

From the figure, using trigonometrical relations, the velocity increment ΔV required to rotate the velocity vector V_c with inclination of i₁ to the velocity vector of V_c with inclination of i₂ can be computed as

$$ \Delta \mathbf{V}=\sqrt{2{{\mathbf{V}}_{\mathbf{c}}}^2\left[1- \cos \kern-0.15em \left({\mathrm{i}}_1-{\mathrm{i}}_2\right)\right]} $$

(3.174)

This velocity increment needs to be applied when the satellite crosses the equator in the plane normal to orbital plane. This has to be along the direction ψ with respect to the initial velocity vector and given by

$$ \uppsi =\frac{\uppi}{2}+\frac{\left({\mathrm{i}}_1-{\mathrm{i}}_2\right)}{2} $$

(3.175)

As per Eq. (3.174), the velocity increment required for inclination correction is proportional to the velocity of the vehicle. Due to this, at high velocities the correction velocity is rather high and the inclination correction maneuver is not beneficial. It is always advantageous to carry out the correction when the satellite is at lower velocity. Therefore, when there is large inclination correction, the preferred option is to increase the orbit size to elliptic and carry out the correction at apogee, where the velocity is less. Subsequently circularize the orbit to the required height as shown in Fig. 3.28.

Fig. 3.28

Optimum inclination correction maneuvers

The total velocity required is given below:

$$ \Delta {\mathbf{V}}_1=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{c}}}-\frac{2}{{\mathrm{r}}_{\mathrm{c}}+{\mathrm{r}}_{\mathrm{a}}}\right)}-\sqrt{\frac{\upmu}{{\mathrm{r}}_{\mathrm{c}}}} $$

(3.176)

$$ {\mathbf{V}}_{\mathbf{a}}=\sqrt{\upmu \left(\frac{2}{{\mathrm{r}}_{\mathrm{a}}}-\frac{2}{{\mathrm{r}}_{\mathrm{c}}+{\mathrm{r}}_{\mathrm{a}}}\right)} $$

(3.177)

$$ \Delta {\mathbf{V}}_2=\sqrt{2{{\mathbf{V}}_{\mathbf{a}}}^2\left(1- \cos \Delta \mathrm{i}\right)} $$

(3.178)

$$ \Delta {\mathbf{V}}_3 = \left|\Delta {\mathbf{V}}_1\right| $$

(3.179)

and therefore,

$$ \Delta \mathbf{V} = \Delta {\mathbf{V}}_1+\Delta {\mathbf{V}}_2+\Delta {\mathbf{V}}_3 $$

(3.180)

i.e.,

$$ \Delta \mathbf{V}=2\left[\sqrt{2\upmu \left(\frac{1}{{\mathrm{r}}_{\mathrm{c}}}-\frac{1}{{\mathrm{r}}_{\mathrm{c}}+{\mathrm{r}}_{\mathrm{a}}}\right)}-\sqrt{\frac{\upmu}{{\mathrm{r}}_{\mathrm{c}}}}\right]+\sqrt{4\upmu \left(\frac{1}{{\mathrm{r}}_{\mathrm{a}}}-\frac{1}{{\mathrm{r}}_{\mathrm{c}}+{\mathrm{r}}_{\mathrm{a}}}\right)\left(1- \cos \Delta \mathrm{i}\right)} $$

(3.181)

Equation (3.174) gives the incremental velocity required for correcting the inclination of the orbit directly whereas Eq. (3.181) gives the incremental velocity required for correcting the inclination through transfer ellipse. On analysis of Eqs. (3.174) and (3.181), it can be seen that for correcting inclination up to about 39°, direct correction requires less impulse whereas for correcting inclination beyond 39°, transfer ellipse method requires less incremental velocity than correcting directly. For each inclination, there will be an optimum apogee for inclination correction beyond 39° and beyond 60°, the apogee required for such maneuver is $\infty$, which is the limit.

3.11.5 Combined Orbit Size and Inclination Correction

In certain cases, from the launch vehicle achieved orbit to the satellite specified orbit, both orbit size and inclination corrections have to be carried out.

This is the typical case of orbital transfer from launch vehicle achieved Geo Transfer Orbit (GTO) to the Geo Stationary Orbit (GEO). In order to carry out the orbital corrections, it is possible to use two strategies as given in Fig. 3.29.

Fig. 3.29

Optimum correction for orbit size and inclination: (a) requirement (b) velocity change + Inclination change (c) inclination change + velocity change (d) inclination and orbits size change together

As shown in the figure two strategies are: (i) First correct for the inclination and then increase the orbit size, or (ii) First increase the orbit size and then correct for the inclination. In both these strategies, the total velocity required will be large and therefore third strategy of carrying out these maneuvers together as given in Fig. 3.29d can be adopted which demands least velocity increment.

Assuming initial orbit velocity as V_i with inclination of i_i and final orbit velocity as V_f with inclination of i_f, the optimum incremental velocity magnitude is given by

$$ \Delta \mathbf{V}=\sqrt{{{\mathbf{V}}_{\mathbf{i}}}^2+{{\mathbf{V}}_{\kern-0.20em \mathbf{f}}}^2-2{\mathbf{V}}_{\mathbf{i}}{\mathbf{V}}_{\kern-0.20em \mathbf{f}} \cos \Delta \mathrm{i}} $$

(3.182)

where

$$ \Delta \mathrm{i}={\mathrm{i}}_{\mathrm{i}}-{\mathrm{i}}_{\kern-0.15em \mathrm{f}} $$

(3.183)

and this impulsive velocity is to be applied to the vehicle when it crosses the equator in a plane perpendicular to orbital plane. This has to be done at an orientation ψ with respect to the initial orbital velocity vector V_i and is given by

$$ \uppsi =\uppi - \cos {\kern-0.20em }^{-1}\left[\frac{{{\mathrm{V}}_{\mathrm{i}}}^2+{\Delta \mathrm{V}}^2{{\hbox{-}\ \mathrm{V}}_{\kern-0.20em \mathrm{f}}}^2}{2{\mathrm{V}}_{\mathrm{i}}\ \Delta \mathrm{V}}\right] $$

(3.184)

3.11.6 Launch Vehicle GTO Requirements for Geostationary Satellite Missions

The geostationary satellites need to be placed in the circular orbit with altitude of about 36,000 km and to be placed over equator, i.e. inclination of the orbit is zero. Generally, if the launch vehicle needs to inject these satellites directly into the geostationary orbit, there will be heavy loss. In addition, due to the limitations of launch site location and launch azimuth, the finally achieved orbit may not be over equator and it will have a certain inclination with respect to the equator.

The trade-off between the launch vehicle achieved orbit and the propellant required in satellites to correct the orbit is needed. Based on such analysis, the optimum strategy for launch vehicle orbit has to be decided.

• 1. Elliptic orbit with apogee equal to the orbital height required by the satellite (i.e. 36,000 km) whereas the perigee height can be decided based on the launch vehicle capability and other operational and satellite life time constraints.

• 2. Due east launch which provides the minimum orbital inclination from the specified launch site (equal to the latitude of the launch site)

The satellite carries out the orbit size maneuver at the apogee of the launch vehicle achieved orbit as explained earlier. At the same time, the inclination correction needs to be done. The inclination correction is optimum, if it is done at the lowest velocity point of the orbit, i.e. at the apogee of the launch vehicle achieved orbit. The efficient way of achieving both these corrections is to carry out these operations together, i.e. at the apogee. At the same time, the inclination correction needs to be carried out when the vehicle crosses the equator. Therefore considering all these aspects, the launch vehicle achieved GTO is planned such that the line of apsides is over the equator, i.e. argument of perigee of launch vehicle GTO is either 180° or 0° depending upon the launch site and launch azimuth.

From the launch vehicle achieved GTO as defined earlier, satellite has to carry out the maneuver as given in Eqs. (3.182), (3.183), and (3.184) to achieve the final required orbit. Due to operational reasons and other maneuver constraints, sometimes multiple maneuver are needed when the vehicle crosses the equator at the apogee location and it is continued till the satellite reaches the required orbital height with zero inclination.