1 Introduction

In general, the motion of a probe around a celestial body (primary body) is affected by the gravitational perturbation deriving from one or more other celestial bodies and these perturbative effects can play a key role in designing orbits which are able to meet the mission requirements. This concerns both the motion around planets and moons, where the dynamic behaviour of an orbiting probe, the related stability conditions and the life times are strongly influenced, not only by the asymmetries of the gravitational field of the primary body, but also by the gravitational attraction of other celestial bodies. Some papers dealing with these problems are: Allan and Cook (1964), who analysed the case of Earth satellites; Scheeres et al. (2001), Lara and San Juan (2005), Paskowitz and Scheeres (2006), Lara and Russell (2007), Lara et al. (2007), who studied the motion of a probe orbiting Jupiter’s natural satellite Europa; Russell and Lara (2009), who investigated the dynamics around Enceladus.

In a space mission for planetary observation, a basic requirement which has to be fulfilled, and which is often influenced by the gravitational attraction deriving from other celestial bodies, lies in the possibility of obtaining cyclic observations of each zone of the celestial body around which the probe is orbiting. Such an objective, which is often realized by choosing high inclination orbits (possibly quasi-polar orbits) so as to guarantee an extended latitudinal coverage of the celestial body, can be achieved if the ground tracks of probe repeat themselves periodically (in this case the orbit is defined as periodic) (Lara 2003; Russell 2006; Russell and Lara 2007; Ortore et al. 2012; Circi et al. 2012). To this purpose, in Cinelli et al. (2015) the analytical determination of equations able to provide different typologies of periodic orbits was carried out, considering the case of a perturbing body that moves in a circular orbit lying on the equatorial plane of the primary body (as, with a good approximation, occurs for the main moons of the Solar System: Io, Europa, Ganymede, Callisto, Titan). These equations were retrieved by exploiting, for the perturbing body, the expressions found in Prado (2003) and in Broucke (2003).

In this paper an extension of this topic has been carried out. In fact, starting from the traditional expansion of the disturbing potential in Legendre polynomials up to the second order (Allan and Cook 1964), equations which provide the temporal variations of the orbit elements of the probe have been analytically gained. These equations allow the study of the probe orbit evolution in the general case in which one or more perturbing bodies describe, around the primary body, elliptical and inclined orbits. Then, introducing such equations in the periodicity condition for the probe ground track, an equation to retrieve periodic orbits has also been determined. Such an equation has been obtained considering, besides the third body influence, the perturbative effects of the primary body deriving from the even zonal harmonics up to \(J_{4}\).

The paper is organized as follows: Sect. 2 reports the analytical developments leading to equations which provide the variations of the orbit elements; Sect. 3 reports both the analytical developments which allow the determination of the equation providing periodic orbits and the extension to the case of more perturbing bodies; Sect. 4 investigates the accuracy of the results achievable by the above-mentioned equation, considering the case of Earth satellites under the influence of the luni-solar perturbation.

2 Long-term third body effects in the non-coplanar case

As is well-known, the long-term effects related to the gravitational attraction of a third body can be highlighted by averaging the disturbing potential on the positions of both probe and third body in their motions with respect to the primary body. Following the mathematical developments offered by Allan and Cook (1964), which consider the traditional expansion in Legendre polynomials up to the second order, this double averaged disturbing potential can be expressed by the relationship:

$$\begin{aligned} {\ll }U{\gg }=na^{2}U^{*} \end{aligned}$$
(1)

with:

$$\begin{aligned} U^{*}=\frac{3}{4}\frac{\mu _{\textit{III}}}{na_{\textit{III}}^3 \left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left\{ {\frac{1}{2}\left( {1-e^{2}} \right) \left( {\hat{{k}}\cdot \hat{{Z}}_{\textit{III}} } \right) ^{2}+e^{2}\left[ {1-\frac{5}{2}\left( {\hat{{e}}\cdot \hat{{Z}}_{\textit{III}} } \right) ^{2}} \right] } \right\} \end{aligned}$$
(2)

where a is the semi-major axis of the probe orbit, e is the eccentricity of the probe orbit, \(n=\sqrt{\mu _P /a^{3}}\) is the mean motion of the probe, with \(\mu _P\) gravitational constant of the primary body, \(\hat{{k}}\) is the unit vector perpendicular to the orbital plane of the probe, \(\hat{{e}}\) is the unit eccentricity vector of the probe orbit, \(\mu _{\textit{III}} \) is the gravitational constant of the third body, \(a_{\textit{III}}\) is the semi-major axis of the orbit that the third body describes with respect to the primary body, \(e_{\textit{III}}\) is the eccentricity of the orbit that the third body describes with respect to the primary body, and \(\hat{{Z}}_{\textit{III}}\) is the unit vector perpendicular to the orbital plane of the third body in its motion with respect to the primary body. Once the term \(\frac{\mu _{\textit{III}}}{a_{\textit{III}}^3}\) has been rewritten as follows:

$$\begin{aligned} \frac{\mu _{\textit{III}} }{a_{\textit{III}}^3 }=\frac{\left( \mu _P +\mu _{\textit{III}}\right) }{\left( \mu _P +\mu _{\textit{III}}\right) }\frac{\mu _{\textit{III}} }{a_{\textit{III}}^3 }=\left( {\frac{\mu _{\textit{III}} }{\mu _P +\mu _{\textit{III}} }} \right) \left( {\frac{\mu _P +\mu _{\textit{III}} }{a_{\textit{III}}^3 }} \right) =m^{\prime }n^{\prime 2} \end{aligned}$$
(3)

with \(m^{\prime }=\frac{\mu _{\textit{III}} }{\mu _P +\mu _{\textit{III}}},\) \(n^{\prime 2}=\frac{\mu _P +\mu _{\textit{III}} }{a_{\textit{III}}^3},\) and the following products have been developed:

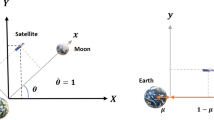
$$\begin{aligned} \left( {\hat{{k}}\cdot \hat{{Z}}_{\textit{III}} } \right) ^{2}= & {} \cos ^{2}\left( i-i^{*}\right) ,\\ \left( {\hat{{e}}\cdot \hat{{Z}}_{\textit{III}} } \right) ^{2}= & {} \left[ {\sin \omega \sin \left( i-i^{*}\right) } \right] ^{2}=\frac{1}{2}\left[ {1-\cos ^{2}\left( i-i^{*}\right) } \right] -\frac{1}{2}\cos (2\omega )\sin ^{2}\left( {i-i^{*}} \right) , \end{aligned}$$

with \(i=\) inclination of the probe orbit, \(i^{*}=\) inclination of the orbit that the third body describes with respect to the equatorial plane of the primary body, \(\Omega =\)  right ascension of the ascending node (RAAN) of the probe orbit, \(\Omega ^*=\)  right ascension of the ascending node of the perturbing body orbit (Fig. 1), Eq. 1 takes the following form:

$$\begin{aligned} {\ll } U {\gg }= & {} na^{2} U^{*}=\frac{3}{16}\frac{m^{\prime }n^{\prime 2}a^{2}}{\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left[ 2\cos ^{2}\left( i-i^{*}\right) +3e^{2}\cos ^{2}(i-i^{*})\right. \nonumber \\&\left. -\,e^{2}+5e^{2}\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) \right] \end{aligned}$$
(4)
Fig. 1
figure 1

Positions of probe and third body with respect to the primary body

Full size image

As is well-known, in order to determine the temporal variations of the orbit elements of the probe, the Lagrange planetary equations, written in the form that depends on the derivatives of the disturbing potential with respect to the Keplerian elements, can be exploited (Kozai 1959). To this end, the derivatives of Eq. (4) with respect to the orbit elements have to be calculated:

$$\begin{aligned} \frac{\partial U}{\partial a}= & {} 2\frac{U}{a}=\frac{3}{8}\frac{m^{\prime }n^{\prime 2}a}{\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left[ 2\cos ^{2}\left( i-i^{*}\right) +3e^{2}\cos ^{2}(i-i^{*})-e^{2}\right. \nonumber \\&\left. +\,5e^{2}\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) \right] \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial U}{\partial e}= & {} \frac{3}{8}\frac{m^{\prime }n^{\prime 2}a^{2}}{\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left[ {3e\cos ^{2}\left( i-i^{*}\right) -e+5e\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial U}{\partial i}= & {} \frac{3}{16}\frac{m^{\prime }n^{\prime 2}a^{2}}{\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left\{ 5e^{2}\cos (2\omega )\sin \left[ 2\left( i-i^{*}\right) \right] \right. \nonumber \\&\left. -\,2\sin \left[ 2\left( i-i^{*}\right) \right] -3e^{2}\sin \left[ 2\left( i-i^{*}\right) \right] \right\} \end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial U}{\partial \omega }= & {} -\frac{15}{8}\frac{m^{\prime }n^{\prime 2}a^{2}}{\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}e^{2}\sin (2\omega )\sin ^{2}\left( i-i^{*}\right) \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial U}{\partial \Omega }= & {} 0\end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial U}{\partial M}= & {} 0 \end{aligned}$$
(10)

where \(\omega \) is the argument of pericentre of the probe orbit and M is the mean anomaly of the probe. Thus, by substituting Eqs. (5)–(10) in the Lagrange planetary equations the long-term temporal variations of the orbit elements of the probe, due to the third body perturbation, can be retrieved:

$$\begin{aligned} \dot{a}= & {} 0 \end{aligned}$$
(11)
$$\begin{aligned} \dot{e}= & {} \frac{15}{8}\frac{m^{\prime }n^{\prime 2}e\sqrt{1-e^{2}}}{n\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\left[ {\sin (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \end{aligned}$$
(12)
$$\begin{aligned} \dot{i}= & {} -\frac{15}{8}\frac{m^{\prime }n^{\prime 2}}{n\left( 1-e_{\textit{III}}^2 \right) ^{3/2}}\frac{e^{2}}{\sqrt{1-e^{2}}}\frac{\cos i}{\sin i}\left[ {\sin (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \end{aligned}$$
(13)
$$\begin{aligned} \dot{\omega }= & {} \frac{3}{16}\frac{m^{\prime }n^{\prime 2}}{n\left( 1-e_{\textit{III}}^2 \right) ^{3/2}\sqrt{1-e^{2}}} \nonumber \\&\cdot \left\{ 2\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i^{*}\right) -1+5\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \right. \nonumber \\&\left. -\,5e^{2}\frac{\cos i}{\sin i}\cos (2\omega )\sin \left[ 2\left( i-i^{*}\right) \right] \right. \nonumber \\&\left. +\,{2\frac{\cos i}{\sin i}\sin [2(i-i^{*})]+3e^{2}\frac{\cos i}{\sin i}\sin \left[ 2\left( i-i^{*}\right) \right] } \right\} \end{aligned}$$
(14)
$$\begin{aligned} \dot{\Omega }= & {} \frac{3}{16}\frac{m^{\prime }n^{\prime 2}}{n\left( 1-e_{\textit{III}}^2 \right) ^{3/2}\sqrt{1-e^{2}}}\left[ 2\cos i\cos \left( 2i^{*}\right) -\frac{\sin \left( 2i^{*}\right) }{\sin i}\right. \nonumber \\&\left. +\,2\sin i\sin \left( 2i^{*}\right) \right] \left[ 5e^{2}\cos (2\omega )-2-3e^{2}\right] \end{aligned}$$
(15)
$$\begin{aligned} \dot{M}= & {} n-\frac{3}{8}\frac{m^{\prime }n^{\prime 2}}{n\left( 1-e_{\textit{III}}^2\right) ^{3/2}}\nonumber \\&\cdot \left\{ {2\left[ {2\cos ^{2}\left( i-i^{*}\right) +3e^{2}\cos ^{2}(i-i^{*})-e^{2}+5e^{2}\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] } \right. \nonumber \\&\left. {+\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i^{*}\right) -1+5\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] } \right\} \end{aligned}$$
(16)

Once considered for the third body a double averaged and approximated at second order disturbing potential, Eqs. (11)–(16) allow the determination of the corresponding long-term temporal variations of the probe orbit elements and of its mean anomaly in the general case of elliptical and inclined third body orbit. It is possible to note how, while the semi-major axis variation is null [Eq. (11)], the other variations do not depend on the RAAN. From these equations it is possible to re-obtain the temporal variations of the orbit elements found in Domingos et al. (2008) by assuming \(i^{*}= 0\) (case in which the third body describes an elliptical and equatorial orbit) and in Prado (2003), Broucke (2003) by also assuming \(e_{\textit{III}} =0\) (case in which the third body describes a circular and equatorial orbit).

3 Periodic orbits

The condition of periodicity on the ground track of a probe orbiting around a celestial body can be gained by solving the following equation: \(mD_n =\textit{RT}_n,\) where m is the revisit time of the same area (expressed as an integer number of nodal days of the celestial body), \(D_{n}\) is the nodal day of the celestial body, R is the number of revolutions of probe accomplished with respect to the nodal line in m nodal days and \(T_{n}\) is the nodal period of the probe. The nodal day of the celestial body can be expressed as \(D_n =2\pi /(\omega _P -\dot{\Omega })\), where \(\omega _P \) is the angular velocity of the celestial body around its polar axis, while the nodal period of probe can be found as \(T_n =2\pi /(\dot{\omega }+\dot{M})\).

As is well-known, the even zonal harmonics related to the traditional expansion of the gravitational potential of the primary body entail secular perturbations on the orbit elements involved in the periodicity condition on the ground track of probe: \(\omega \), RAAN and M (Kozai 1959). Following the mathematical developments offered by Merson (1961), and considering the zonal harmonics up to the fourth order, these variations can be expressed by the relationships:

$$\begin{aligned} \dot{\omega }= & {} \frac{3R_P ^{2}J_2 }{4}\frac{n\left( 4-5\sin ^{2}i\right) }{a^{2}\left( 1-e^{2}\right) ^{2}}+\frac{3R_P ^{4}J_2 ^{2}}{128}\frac{n\left[ 10\sin ^{2}i\left( 76-89\sin ^{2}i\right) +\left( 56-36\sin ^{2}i-45\sin ^{4}i\right) e^{2}\right] }{a^{4}\left( 1-e^{2}\right) ^{4}}\nonumber \\&-\frac{15R_P ^{4}J_4 }{32}\frac{n\left[ {16-62\sin ^{2}i+49\sin ^{4}i+\left( {18-63\sin ^{2}i+\frac{189}{4}\sin ^{4}i} \right) e^{2}} \right] }{a^{4}\left( 1-e^{2}\right) ^{4}} \end{aligned}$$
(17)
$$\begin{aligned} \dot{\Omega }= & {} -\frac{3R_P ^{2}}{2}\frac{n\cos i}{a^{2}\left( 1-e^{2}\right) ^{2}}\left\{ {J_2 -\frac{R_P ^{2}J_2 ^{2}}{16}} \right. \frac{12-80\sin ^{2}i-\left( 4+5\sin ^{2}i\right) e^{2}}{a^{2}\left( 1-e^{2}\right) ^{2}} \nonumber \\&-\!\left. {\left. {\frac{5R_P ^{2}J_4 }{16}\frac{\left( 4-7\sin ^{2}i\right) \left( 2+3e^{2}\right) }{a^{2}\left( 1-e^{2}\right) ^{2}}} \right] } \right\} \end{aligned}$$
(18)
$$\begin{aligned} \dot{M}= & {} n+\frac{3R_P ^{2}J_2 }{4}\frac{n\left( 2-3\sin ^{2}i\right) }{a^{2}\left( 1-e^{2}\right) ^{3/2}}\nonumber \\&+\,\frac{3R_P ^{4}J_2 ^{2}}{32}\frac{n\left[ {100\sin ^{2}i-131\sin ^{4}i+\left( 20-98\sin ^{2}i+67\sin ^{4}i\right) e^{2}-\frac{1}{16}\left( 280-328\sin ^{2}i+79\sin ^{4}i\right) e^{4}} \right] }{a^{4}\left( 1-e^{2}\right) ^{9/2}} \nonumber \\&-\,\frac{45R_P ^{4}J_4 }{128}\frac{ne^{2}\left( 8-40\sin ^{2}i+35\sin ^{4}i\right) }{a^{4}\left( 1-e^{2}\right) ^{7/2}} \end{aligned}$$
(19)

where \(R_P\) is the equatorial mean radius of the primary body, while \(J_{2}\) and \(J_{4}\) represent the coefficients of the first and second even zonal harmonics respectively.

By summing the variations of the orbit elements due to the zonal harmonics \(J_{2}\) and \(J_{4}\) and to the third body, the total variations of the orbit elements involved in the periodicity condition can be obtained:

$$\begin{aligned} \dot{\Omega }= & {} -\frac{3\sqrt{\mu _P }R_P ^{2}}{2}\frac{\cos i}{\left( {1-e^{2}} \right) ^{2}}\left[ {\frac{J_2 }{a^{3.5}}+\frac{b_{22} +b_4 }{a^{5.5}}+b_T a^{1.5}} \right] \end{aligned}$$
(20)
$$\begin{aligned} \dot{\omega }+\dot{M}= & {} \sqrt{\mu _P }\left[ {\frac{1}{a^{1.5}}+\frac{3R_P ^{2}}{4}\frac{1}{\left( {1-e^{2}} \right) ^{2}}\left( {\frac{c_2 }{a^{3.5}}+\frac{c_{22} +c_4 }{a^{5.5}}+c_T a^{1.5}} \right) } \right] \end{aligned}$$
(21)

In particular: Eq. (20) is obtained by summing Eqs. (15) and (18); Eq. (21) is obtained by summing Eqs. (14), (16), (17), (19). The introduced coefficients are defined as follows:

$$\begin{aligned} b_{22}= & {} -\frac{R_P ^{2}J_2 ^{2}}{16}\frac{\left( 12-80\sin ^{2}i\right) -\left( 4+5\sin ^{2}i\right) e^{2}}{\left( {1-e^{2}} \right) ^{2}}\\ b_4= & {} -\frac{5R_P ^{2}J_4 }{16}\frac{\left( 4-7\sin ^{2}i\right) \left( 2+3e^{2}\right) }{\left( {1-e^{2}} \right) ^{2}}\\ b_T= & {} \frac{{m}'{n}'^{2}}{4R_P ^{2}\mu _P }\frac{\left( 1-e^{2}\right) ^{3/2}}{\left( 1-e_{\textit{III}}^2\right) ^{3/2}}\left[ {\cos \left( 2i^{*}\right) -\frac{\sin \left( 2i^{*}\right) }{\sin (2i)}+\tan i\sin \left( 2i^{*}\right) } \right] \left[ {3e^{2}+2-5e^{2}\cos (2\omega )} \right] \\ c_2= & {} J_2 \left[ \left( 1-e^{2}\right) ^{1/2}\left( 2-3\sin ^{2}i\right) +\left( 4-5\sin ^{2}i\right) \right] \\ c_{22}= & {} \frac{R_P ^{2}J_2 ^{2}}{32}\frac{1}{\left( 1-e^{2}\right) ^{5/2}}\left\{ \left( {1-e^{2}} \right) ^{1/2}\left[ 10\sin ^{2}i(76-89\sin ^{2}i)\right. \right. \\&\left. \left. +\,\left( 56-36\sin ^{2}i-45\sin ^{4}i\right) e^{2} \right] +4\left[ \left( {100\sin ^{2}i-131\sin ^{4}i} \right) \right. \right. \\&\left. \left. +\,\left( {20-98\sin ^{2}i+67\sin ^{4}i} \right) e^{2} \right] -\frac{1}{4}(280-328\sin ^{2}i+79\sin ^{4}i)e^{4} \right\} \\ c_4= & {} \frac{15R_P ^{2}J_4 }{32}\frac{1}{\left( 1-e^{2}\right) ^{2}}\left\{ \left( 1-e^{2}\right) ^{1/2}\left[ {\left( 40\sin ^{2}i-35\sin ^{4}i-8\right) e^{2}} \right] \right. \\&\left. -\left[ {\frac{4}{3}\left( {16-62\sin ^{2}i+49\sin ^{4}i} \right) } \right. + \right. \\&\left. +\, {\left( 24-84\sin ^{2}i+63\sin ^{4}i\right) e^{2}} \right] \\ c_T= & {} \frac{m^{\prime }{n}'^{2}}{4R_P ^{2}\mu _P }\frac{\left( 1-e^{2}\right) ^{3/2}}{\left( 1-e_{\textit{III}}^2\right) ^{3/2}}\left( c_\alpha -2\sqrt{1-e^{2}}c_\beta \right) \end{aligned}$$

with:

$$\begin{aligned} c_\alpha \!= & {} \!2\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i^{*}\right) -1\!+\!5\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] -5e^{2}\frac{\cos i}{\sin i}\cos (2\omega )\sin \left[ 2\left( i-i^{*}\right) \right] \\&+\,2\frac{\cos i}{\sin i}\sin \left[ 2\left( i-i^{*}\right) \right] +3e^{2}\frac{\cos i}{\sin i}\sin \left[ 2\left( i-i^{*}\right) \right] \\ c_\beta= & {} 2\left[ {2\cos ^{2}\left( i-i^{*}\right) +3e^{2}\cos ^{2}\left( i-i^{*}\right) -e^{2}+5e^{2}\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \\&+\,\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i^{*}\right) -1+5\cos (2\omega )\sin ^{2}\left( i-i^{*}\right) } \right] \end{aligned}$$

Then, replacing Eqs. (20) and (21) in the periodicity condition \(mD_{n}=\textit{RT}_{n}\), it is possible to arrive at determining an equation which allows the retrieval of repeating ground track orbits:

$$\begin{aligned} d_T a^{7}+d_1 a^{5.5}+d_K a^{4}+d_2 a^{2}+d_4 =0 \end{aligned}$$
(22)

where \(d_T =c_T -b_T \frac{2R}{m}\cos i\) (related to the third body effects), \(d_1 =-\frac{4\omega _P }{3\sqrt{\mu _P }R_P ^{2}}\frac{R}{m}(1-e^{2})^{2}\) (related to the orbit characteristics), \(d_K =\frac{4}{3R_P ^{2}}(1-e^{2})^{2}\) (related to the Keplerian motion), \(d_2 =c_2 -J_2 \frac{2R}{m}\cos i\) (related to \(J_2 \) effects), \(d_4 =c_{22} +c_4 -(b_{22} +b_4 )\frac{2R}{m}\cos i\) (related to \(J_2 ^{2}\) and \(J_4 \) effects).

In fact, once the eccentricity, the inclination and the argument of pericentre of the orbit probe have been selected, as well as the number of nodal revolutions per nodal day (R / m),  the physically acceptable solution of Eq. (22) provides the semi-major axis of the corresponding periodic orbit.

3.1 The case of several perturbing bodies

Equation (22) can be generalized taking into consideration the case of N perturbing bodies. In fact, following the same developments as in Sect. 3, an equation formally analogous to Eq. (22) can be retrieved, where the coefficients \(b_{T}\) and \(c_{T}\) (which are the ones related to the third body effects) are now given by the sum of the contributions of the N perturbing bodies:

$$\begin{aligned} b_T= & {} \sum _{i=1}^N {b_{Ti} } =\sum _{i=1}^N \left\{ \frac{{m}^{\prime }_{i} {n}^{'2}_i}{4R_P ^{2}\mu _P }\frac{\left( 1-e^{2}\right) ^{3/2}}{\left( 1-e_{\textit{III}_i }^2 \right) ^{3/2}}\left[ \cos \left( 2i_i ^{*}\right) -\frac{\sin \left( 2i_i ^{*}\right) }{\sin (2i)}\right. \right. \nonumber \\&\left. \left. +\,\frac{\sin i}{\cos i}\sin \left( 2i_i ^{*}\right) \right] \left[ {3e^{2}+2-5e^{2}\cos (2\omega )} \right] \right\} \end{aligned}$$
(23)
$$\begin{aligned} c_T= & {} \sum _{i=1}^N {c_{Ti}}= \sum _{i=1}^N {\left[ {\frac{m^{\prime }_i {n}^{\prime 2}_i }{4R_P ^{2}\mu _P }\frac{\left( 1-e^{2}\right) ^{3/2}}{\left( 1-e_{\textit{III}_i }^2\right) ^{3/2}}\left( c_{\alpha i} -2\sqrt{1-e^{2}}c_{\beta i}\right) } \right] } \end{aligned}$$
(24)

with:

$$\begin{aligned} c_{\alpha i}= & {} 2\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i_i ^{*}\right) -1+5\cos (2\omega )\sin ^{2}\left( i-i_i ^{*}\right) } \right] \nonumber \\&-\,5e^{2}\frac{\cos i}{\sin i}\cos (2\omega )\sin \left[ 2\left( i-i_i ^{*}\right) \right] \nonumber \\&+\,2\frac{\cos i}{\sin i}\sin \left[ 2\left( i-i_i ^{*}\right) \right] +3e^{2}\frac{\cos i}{\sin i}\sin \left[ 2\left( i-i_i ^{*}\right) \right] \nonumber \\ c_{\beta i}= & {} 2\left[ {2\cos ^{2}\left( i-i_i ^{*}\right) +3e^{2}\cos ^{2}\left( i-i_i ^{*}\right) -e^{2}+5e^{2}\cos (2\omega )\sin ^{2}\left( i-i_i ^{*}\right) } \right] \nonumber \\&+\,\left( 1-e^{2}\right) \left[ {3\cos ^{2}\left( i-i_i ^{*}\right) -1+5\cos (2\omega )\sin ^{2}\left( i-i_i ^{*}\right) } \right] \nonumber \\ d_T= & {} \sum _{i=1}^N {d_{Ti} =} \sum _{i=1}^N {\left( {c_{Ti} -b_{Ti} \frac{2m}{R}\cos i} \right) } \end{aligned}$$
(25)

The coefficients \(b_{Ti} \), \(c_{Ti} \), \(d_{Ti} \), \(m^{\prime }_i \), \({n}^{\prime }_i \), \(e_{\textit{III}_{i}} \), \(i^{*}_i\) represent the contribution of the ith perturbing body.

4 Analytical and numerical results

To verify the accuracy of the results achievable by Eq. (22), the case of Earth satellites under the influence of the Sun [subscript \(i= 1\) in Eqs. (23)–(25)] and Moon [subscript \(i = 2\) in Eqs. (23)–(25)] has been considered in the present Section. The analytical results have been obtained assuming, for the probe orbit, the following conditions: \(\Omega = 0\) and \(\omega = 0.\) The same values have been considered as initial conditions for the numerical simulations.

4.1 Preliminary analysis on the perturbing effects

As is well-known, an Earth satellite, to be significantly influenced by the third body perturbation, must orbit at a considerable distance from the Earth and, at that distance, the effects deriving from the asymmetry of the gravitational field are essentially limited to the coefficient \(J_{2}\). As a matter of fact, Table 1 shows the results obtained by Eq. (22) both considering the zonal harmonics up to \(J_{4}\), according to the Earth Gravitational Model 96 (Lemoine et al. 1998), and assuming \(J_{4} = 0.\) As for the third body perturbation, the following values for the eccentricity and the inclination of the orbits described by the Sun (apparent motion) and Moon, with respect to the Earth, have been considered: \(e_{\textit{III}1} =0.01671022\) (Sun), \(e_{\textit{III}2} = 0.0554\) (Moon), \(i_{1}^{*} = 23.44^{\circ }\) (Sun) and \(i_{2}^{*} = 18.30^{\circ }\) (Moon).

Table 1 Influence of the coefficient \(J_{4}\)
Full size table

Different kinds of orbits have been taken into account. In particular, the first four cases present the same parameters of periodicity, inclination and eccentricity (but \(\omega = 0\)) as, respectively, the constellation Cosmo-SkyMed-1 (case of Low Earth Orbit), the global positioning system (GPS), the Molniya and the Tundra orbits. The absolute differences between the results obtained in the two cases (with and without \(J_{4}\)) are reported in the last column of the table. As evidence shows, in all cases of Mid and High Earth Orbit, the influence of the coefficient \(J_{4}\) is very weak and can therefore be neglected.

But there are also other coefficients in the expansion of the Earth’s gravitational potential that have the same order of magnitude as \(J_{4}\), like \(C_{22}\) and \(S_{22}\). The consideration of such coefficients in the analytical developments reported in Sect. 3 would have greatly increased the complexity of the equations and would not have allowed the determination of a polynomial equation to design periodic orbits. For this reason, their influence has been investigated through a numerical analysis. To this purpose, Table 2 reports the results obtained numerically, on different typologies of orbits, considering the following cases:

  • Case A: EGM 96 with “\(J_{2}+ J_{3}+J_{4}\)” + luni-solar effect;

  • Case B: EGM 96 with “\(J_{2 }+J_{3}+J_{4}\), \(C_{22}\) and \(S_{22}\)” + luni-solar effect;

  • Case C: EGM 96 with \((30 \times 30)\) harmonics + luni-solar effect + solar radiation pressure (considering a spherical satellite with a solar radiation pressure coefficient \(C_{\mathrm{r}} = 1\) and an area-to-mass \(\hbox {ratio} = 0.02\,\hbox {m}^{2}/\hbox {kg}\)).

Table 2 Influence of the coefficients \(C_{22}\) and \(S_{22}\) (numerical solutions)
Full size table

The results show how the influence of the coefficients \(C_{22}\) and \(S_{22}\) (as well as the one related to the solar radiation pressure) is rather weak (marked differences have been obtained at geosynchronous altitude because of the well-known resonance phenomenon associated with the elliptical shape of the Earth’s equator).

The numerical simulations have been executed by the Runge–Kutta–Fehlberg 7(8) integrator. In these simulations the positions of the Sun and Moon have been determined according to the ephemerides of these celestial bodies (DE421). The numerical values of the orbit elements have been retrieved according to the following steps:

  1. 1.

    once \(e, i, \omega \) and R / m are selected, Eq. (22) provides the initial value of semi-major axis (with \(e_{\textit{III}1}= 0.01671022, e_{\textit{III}2} = 0.0554, i_{1}^{*} = 23.44^{\circ }\), \( i_{2}^{*}=18.30^{\circ }\)). Given that the double averaging procedure, executed on the disturbing potential, eliminates the short-term effects (which, being function of the instantaneous position of the third body, consist of oscillations occurring around the corresponding long-term variation) this initial condition will represent a sort of mean value (long-term variation) for the semi-major axis;

  2. 2.

    the variations \(\dot{\Omega }\), \(\dot{\omega }\), \(\dot{M}\), associated with the periodicity condition, are numerically computed (using the above-mentioned EGM 96);

  3. 3.

    the mean values of nodal day and nodal period are obtained and, with these values, the periodicity condition (\(mD_n =\textit{RT}_n )\) is evaluated;

  4. 4.

    the precise value of semi-major axis which makes the periodicity condition satisfied is iteratively found (the iterative cycle involves points 2–4);

  5. 5.

    the solution corresponding to the gained value of semi-major axis is numerically propagated (over a long time) to verify the stability of the proposed trajectory. In this regard, the last column of Table 2 shows the maximum variations of eccentricity (\(\Delta e)\) that have been obtained, after 1 year, for the solutions belonging to Case C. The weak variations observed over the entire range of altitudes confirm the good stability of the solutions (similar results have been obtained for the variations of orbit inclination).

4.2 Effect of the lunar orbit inclination

Once established that, for satellites orbiting at an altitude higher than three Earth’s radii (where the luni-solar perturbation starts to significantly influence their motion), the only considerable effects associated with the asymmetry of the Earth’s gravitational field are limited to the harmonic \(J_{2}\), it is also important to evaluate the influence of the Moon’s orbit inclination on the results deriving from Eq. (22). To this end, Table 3 reports the values obtained in the cases of minimum (\(i_{2}^{*}=18.28^{\circ }\)) and maximum (\(i_{2}^{*}=28.58^{\circ }\)) inclination for the orbital plane of the Moon (\(e_{\textit{III}1}= 0.01671022, e_{\textit{III}2} = 0.0554, i_{1}^{*} = 23.44^{\circ }\), \(J_{4}= 0\)). Also in this case, several kinds of orbits have been taken into consideration.

Table 3 Influence of the Moon’s orbit inclination
Full size table

The results of Table 3 highlight how the effects related to the Moon’s orbit inclination become important only at very high altitudes.

4.3 Comparison between analytical and numerical results

To investigate the accuracy of the results coming from Eq. (22), a comparison with numerical results, obtained following the procedure described in Sect. 4.1 (points 1–5), has been carried out. Table 4 reports the results of this comparison, assuming \(e_{\textit{III}1} =0.01671022\), \(e_{\textit{III}2} = 0.0554\), \(i_{1}^{*} = 23.44^{\circ }\), \(i_{2}^{*} = 18.30^{\circ }\) and considering two kinds of analytical solutions:

  1. 1.

    solutions gained by Eq. (22) without considering the gravitational attraction of the Sun and Moon (\(d_{T }= 0),\) where \(\vert \Delta a\vert \) represents the absolute difference with respect to the numerical results;

  2. 2.

    solutions gained by Eq. (22) (\(\vert \Delta a\vert \) is the difference with respect to the numerical results).

Table 4 Comparison between analytical and numerical results (case A: EGM 96 with “\(J_{2}+ J_{3}+J_{4}\)” + luni-solar effect)
Full size table

As evidence shows, the results obtained by Eq. (22) are close to the ones retrieved by numerical simulations (last column of Table 4). In fact, at \(i = 15^{\circ }\) and \(i = 63.43^{\circ }\) the differences are \(<\)1.3 km, while at mid inclination these differences moderately increase (up to 4.29 km).

5 Conclusions

Taking into consideration the general case of one or more disturbing bodies moving around a primary body in elliptical and inclined orbits, the mathematical developments to analytically retrieve equations able to provide the variations of the orbit elements of the probe have been presented. Then, including the main perturbative effects related to the asymmetry of the gravitational field of the primary body, these equations have been exploited to gain periodic orbits. Considering the case of Earth satellites influenced by the luni-solar perturbation, the results retrieved by such an equation have been compared with the ones deriving from numerical simulations and the differences obtained have highlighted the accuracy of the analytical solutions.