Third-Body Perturbation Effects on Satellite Formations

Abstract

The effects of third-body perturbations on satellite formations are investigated using differential orbital elements to describe the relative motion. Absolute and differential effects of the lunar perturbation on satellite formations are derived analytically based on the simplified model of the circular restricted three-body problem. This analytical description includes averaged long-term effects on the orbital elements, including the full transformation between the osculating elements and the lunar-averaged elements, which is absent from previous research. A simplified Earth-Moon system model is used, but the results are applicable to any formation reference orbit about the Earth. Simulations are performed to determine the effects of the lunar perturbation on example formations in upper MEO, highly eccentric orbits by using the formation design criteria of Phases I and II of the NASA Magnetospheric Multiscale mission. The changes in angular differential orbital elements (δ ω, δΩ, and δ M ₀) and in science return quality due to this perturbation are compared to changes due to J ₂. The method is then expanded to include the inclination of the Moon’s orbit and results are compared to simulation using the NASA General Mission Analysis Tool.

Introduction

Long duration satellite formation flying, a critical element of upcoming science return missions [1], is a key area of current research in astrodynamics. The Keplerian (two-body) relative motion problem has essentially been solved, assuming small separations between the satellites and including arbitrary eccentricity [2–6]. However, long duration formations are impossible to design without taking into account the effect of perturbations to the Keplerian motion. Therefore, modern research is focused on accounting for disturbing forces such as the J ₂ oblateness perturbation, atmospheric drag, third-body effects, and solar radiation pressure.

J ₂ is the dominant perturbation in low-Earth orbit (LEO) and medium-Earth orbit (MEO), followed by atmospheric drag in LEO and lunisolar effects in MEO. In the upper MEO region and high-Earth orbit (HEO), third-body effects are of the same order of magnitude as J ₂. In 2003, Gim and Alfriend [7] derived the state transition matrix of relative motion including arbitrary eccentricity and first-order absolute and differential J ₂ effects using differential mean orbital elements. The present work focuses on third-body effects, in particular the lunar perturbation, using differential orbital elements as well. Differential orbital elements are a natural and convenient choice for designing general formations [8]—having been widely used throughout the literature to describe satellite relative motion for a variety of applications [9–15]—and using mean elements allows for the explicit inclusion of secular effects due to J ₂. Analytical models have many advantages over brute force, numerical simulations, such as instant adaptability to different problems, fast simulations, and most importantly the physical insight that can be gleaned from the equations themselves.

The effect of the third-body perturbation on formations in particular has not been studied much in the literature; however, the effects of lunisolar perturbations on general satellites have been studied extensively. The analysis uses perturbation methods and averaging, following a similar approach to the Brouwer theory [16] for the zonal harmonics. The first lunisolar disturbing function was developed in the 1950s by Kozai [17] and expanded by Musen et al. [18]. The previous analysis was generalized by Kaula [19], revisited by Giacaglia [20], who obtained the lunar disturbing function using orbital elements, and expanded again by Kozai [21] using orbital elements for the satellite and Cartesian coordinates for the disturbing bodies.

A simplified model was developed by Prado [22] based on the assumptions of the circular restricted three-body problem, and it is this model which will be used as a starting point for the present work. Using a similar formulation, Broucke [23] investigated the effect of lunisolar perturbations on high-altitude satellites in nearly circular orbits. More recently, Lara, San Juan, and Lòpez [24] used canonical perturbation theory to solve a higher-order lunisolar problem, including J ₂, J ₃, fifth-order lunar terms, and second-order solar terms. The effect of third-body perturbations on satellite formations has been investigated numerically in modern research, such as McLaughlin et al. [25] and Wnuk & Golebiewska [26], but analytical analyses are absent.

In the present work, absolute and differential effects of the lunar perturbation on satellite formations are derived analytically based on the simplified model of Prado [22] and the transformation between the osculating elements and the lunar-averaged elements is developed. Without this transformation, the method of averaging produces inaccurate results over time due to the effect of discrepancies in initial conditions. Later, the method is expanded to lunar orbits which are inclined relative to the ecliptic plane. Simulations are performed to determine the effects of this perturbation on example formations using the formation design criteria and techniques of Phases I and II of the NASA Magnetospheric Multiscale (MMS) mission [27–31]. The effects of the lunar perturbation are compared to the changes due to J ₂, and the results are compared to simulation using the NASA General Mission Analysis Tool (GMAT).

Dynamics

The acceleration of a satellite relative to a spherical Earth, including the gravity of the Moon, is

$$ \ddot{\mathbf{r}} = \underbrace{-\frac{Gm_{1}}{r^{3}}\mathbf{r}}_{\mathbf{f}_{g}} + \underbrace{Gm_{2}\left( \frac{1}{d^{3}}\mathbf{d} - \frac{1}{r^{\prime3}}\mathbf{r}^{\prime}\right)}_{\mathbf{f}_{d}} $$

(1)

where r is the position of satellite relative to Earth, d is the position of the Moon relative to satellite, r ^′ is position of the Moon relative to Earth, m ₁ is the mass of the Earth, m ₂ is the mass of the Moon, and G is the universal gravitational constant, assuming that the mass of the satellite is small compared to m ₁ and m ₂.

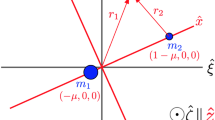
The geometry of the system is shown in Fig. 1, therefore applying the cosine law, with S denoting the angle between the Moon and the satellite as seen from the Earth, yields the relation,

Fig. 1

Geometry of the restricted three-body problem

$$ d^{2} = r^{2} + r^{\prime2} - 2rr^{\prime}\cos S $$

(2)

which can be used to eliminate the d ³ term in the denominator of Eq. (1). (Note that Fig. 1 is valid for any arbitrary lunar orbit, except for the illustration of the angle M ^′, the mean anomaly of the Moon, which is only valid when the Moon’s orbit is circular.) Collecting terms and retaining only the perturbing (non-Keplerian) terms, the disturbing potential of the Moon’s gravity can be written,

$$ R = \frac{\mu^{\prime}G\left( m_{1} + m_{2}\right)}{\sqrt{r^{2} + r^{\prime2} - 2rr^{\prime}\cos S}} $$

(3)

where

$$ \mu^{\prime} = \frac{m_{2}}{m_{1} + m_{2}} $$

(4)

and such that

$$ \mathbf{f}_{d} = \nabla R $$

(5)

Expanding Eq. (3) in Legendre polynomials about the small quantity r/r ^′ the disturbing potential can be rewritten in the more convenient form,

$$ R = \frac{\mu^{\prime} n^{\prime2} a^{\prime3}}{r^{\prime}} \sum\limits_{k=2}^{\infty} \left( \frac{r}{r^{\prime}}\right)^{k} P_{k}\left( \cos S\right) $$

(6)

where n ^′ and a ^′ are the osculating mean motion and semimajor axis, respectively, of the Moon’s reference orbit. These quantities obey the relation,

$$ n^{\prime2} a^{\prime3} = G\left( m_{1} + m_{2}\right) $$

(7)

The full gravitational potential acting on the satellite is, therefore,

$$ V = -\frac{\mu}{r} - \frac{\mu^{\prime} n^{\prime2} a^{\prime3}}{r^{\prime}} \sum\limits_{k=2}^{\infty} \left( \frac{r}{r^{\prime}}\right)^{k} P_{k}\left( \cos S\right) $$

(8)

such that

$$ \ddot{\mathbf{r}} = -\nabla V $$

(9)

Simplified Model

The dynamics presented so far are valid for any arbitrary three-body system. To allow for easy modeling and analysis of formations, a simplified model is now adopted with the following assumptions: the Earth is fixed at the center of the reference system; a formation of massless satellites orbits the Earth in an arbitrary reference orbit; the Moon is in a circular orbit about the Earth in the $\hat {\mathbf {i}}_{1}$-$\hat {\mathbf {i}}_{2}$ plane; and the motion of the satellites is assumed to be Keplerian, perturbed a small amount by the Moon’s gravity. The independent variables used to describe the satellites’ motion are the classical orbital elements, (a, e, i,Ω, ω, M ₀), and their differences (with respect to the reference orbit). Referring again to Fig. 1, the cosS term can now be determined from the orbital elements of the satellite and the mean anomaly of the Moon:

$$\begin{array}{@{}rcl@{}} \cos S & =& \cos\left( \omega+f\right)\cos\left( M^{\prime}-{\Omega}\right) + \sin\left( \omega+f\right)\cos i\sin\left( M^{\prime}-{\Omega}\right) \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} & =& \alpha\cos f + \beta\sin f \end{array} $$

(11)

where

$$\begin{array}{@{}rcl@{}} \alpha & = &\cos\omega\cos\left( M^{\prime}-{\Omega}\right) + \sin\omega\cos i\sin\left( M^{\prime}-{\Omega}\right) \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} \beta & =& -\sin\omega\cos\left( M^{\prime}-{\Omega}\right) + \cos\omega\cos i\sin\left( M^{\prime}-{\Omega}\right) \end{array} $$

(13)

There are three distinct time scales in the problem as defined. First, the period of the satellites is the shortest, over which time the variables exhibit short-period oscillations (for MMS Phase I, T ≈ 1 day; for Phase II, T ≈ 3 days). Second, over the period of the Moon (27 days) the variables exhibit medium-period oscillations. Finally, there are long-term variations in the variables, which are either non-periodic or have periods of several years.

The method presented by Prado [22] begins by first averaging Eq. (6) over one satellite period to remove the short-period oscillations:

$$ \left\langle R \right\rangle \triangleq \frac{1}{2\pi} {\int}_{0}^{2\pi} R \ dM $$

(14)

This can also be done to the non-simplified model, and is in fact the same procedure that is followed in the earlier lunar perturbation analyses. Second, the singly-averaged disturbing potential is averaged again, this time over the Moon’s period:

$$ \left\langle\left\langle R \right\rangle\right\rangle \triangleq \frac{1}{2\pi} {\int}_{0}^{2\pi} \left\langle R\right\rangle \ dM^{\prime} $$

(15)

This removes the medium-period oscillations as well as any dependence on the actual position of the Moon, which is very useful for simulation.

In Prado [22], summation terms in the expanded disturbance potential, Eq. (6), are retained up to k = 4; however, in this analysis only k = 2 terms are retained (note that the doubly-averaged k = 3 terms are zero). The resulting second-order, doubly-averaged disturbing potential is [22]

$$ \left\langle\left\langle R_{2} \right\rangle\right\rangle = \frac{\mu^{\prime} a^{2} n^{\prime2}}{16}\left[\left( 2+3e^{2}\right) \left( 3\cos^{2} i-1\right) + 15e^{2}\sin^{2} i\cos 2\omega\right] $$

(16)

Fig. 2

Comparison of secular J ₂ and averaged lunar effects on differential elements

Absolute and Differential Rates

By substituting Eq. (16) into Lagrange’s Planetary Equations, the rates of the classical orbital elements are obtained (as in Prado [22]):

$$\begin{array}{@{}rcl@{}} \dot{a} &=& 0 \end{array} $$

(17a)

$$\begin{array}{@{}rcl@{}} \dot{e} &=&\frac{15\mu^{\prime} n^{\prime2} e\eta}{8n}\sin^{2} i\sin 2\omega \end{array} $$

(17b)

$$\begin{array}{@{}rcl@{}} \dot{i} &=& -\frac{15\mu^{\prime} n^{\prime2} e^{2}}{16n\eta}\sin 2i\sin 2\omega \end{array} $$

(17c)

$$\begin{array}{@{}rcl@{}} \dot{\Omega} & =& \frac{3\mu^{\prime} n^{\prime2}\cos i}{8n\eta}\left( 5e^{2}\cos 2\omega-3e^{2}-2\right) \end{array} $$

(17d)

$$\begin{array}{@{}rcl@{}} \dot{\omega} & =& \frac{3\mu^{\prime} n^{\prime2}}{8n\eta}\left[5\cos^{2} i-\eta^{2}+ 5\left( \eta^{2}-\cos^{2} i\right)\cos 2\omega\right] \end{array} $$

(17e)

$$\begin{array}{@{}rcl@{}} \dot{M}_{0} & =& -\frac{\mu^{\prime} n^{\prime2}}{8n}\left[\left( 3e^{2}+7\right)\left( 3\cos^{2} i-1\right) + 15\left( 1+e^{2}\right)\sin^{2} i\cos^{2}\omega\right] \end{array} $$

(17f)

where η ² = 1−e ². Assuming the separation between the satellites is small, a standard assumption in satellite formation flying, the rates of the differential orbital elements can be found by taking the first variation of the rates of the absolute elements,

$$\begin{array}{@{}rcl@{}} \delta\dot{a} &=& 0\\ \delta\dot{e} &=& \frac{15\mu^{\prime} n^{\prime2}}{8n}\left[\frac{3e\eta}{2a}\sin^{2} i\sin 2\omega \ \delta a + \frac{1}{\eta}\left( 1-2e^{2}\right)\sin^{2} i\sin 2\omega \ \delta e \right. \end{array} $$

(18a)

$$\begin{array}{@{}rcl@{}} && \left.+ \ e\eta\sin 2 i\sin 2\omega\ \delta i + 2e\eta\sin^{2} i\cos 2\omega\ \delta\omega\right] \end{array} $$

(18b)

$$\begin{array}{@{}rcl@{}} \delta\dot{i} &=& -\frac{15\mu^{\prime} n^{\prime2}}{16n}\left[\frac{3e^{2}}{2a\eta}\sin 2i\sin 2\omega \ \delta a + \left( \frac{2e}{\eta}+\frac{e^{3}}{\eta^{3}}\right)\sin 2i\sin 2\omega\ \delta e \right. \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \left.\frac{2e^{2}}{\eta}\cos 2i\sin 2\omega\ \delta i + \frac{2e^{2}}{\eta}\sin 2i\cos 2\omega\ \delta\omega\right] \end{array} $$

(18c)

$$\begin{array}{@{}rcl@{}} \delta\dot{\Omega} &=& \frac{3\mu^{\prime} n^{\prime2}}{8n}\left\{\frac{3\cos i}{2a\eta} \left( 5e^{2}\cos 2\omega-3e^{2}-2\right)\delta a \right. \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \frac{e\cos i}{\eta^{3}}\left[\left( 5e^{2}\cos 2\omega-3e^{2}-2\right)+ 2\eta^{2}\left( 5\cos 2\omega-3\right)\right]\delta e \end{array} $$

(18d)

$$\begin{array}{@{}rcl@{}} && - \left.\frac{\sin i}{\eta}\left( 5e^{2}\cos 2\omega-3e^{2}-2\right)\delta i - \frac{10e^{2}}{\eta}\cos i\sin 2\omega\ \delta\omega\right\} \end{array} $$

$$\begin{array}{@{}rcl@{}} \delta\dot{\omega} &=& \frac{3\mu^{\prime} n^{\prime2}}{8n\eta^{3}}\left\{\frac{3\eta^{2}}{2a}\left[\left( 5\cos^{2} i-\eta^{2}\right)+5\left( \eta^{2}-\cos^{2} i\right)\cos 2\omega\right]\delta a \right. \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \ e\left[5\cos^{2} i-5\left( \eta^{2}+\cos^{2} i\right)\cos 2\omega + \eta^{2}\right]\delta e \end{array} $$

(18e)

$$\begin{array}{@{}rcl@{}} &&\left. - \ 5\eta^{2}\sin 2i\left( 1-\cos 2\omega\right)\delta i - 10\eta^{2}\left( \eta^{2}-\cos^{2} i\right)\sin 2\omega\ \delta\omega\right\} \end{array} $$

$$\begin{array}{@{}rcl@{}} \delta\dot{M}_{0} &=& -\frac{\mu^{\prime} n^{\prime2}}{8n}\left\{\frac{3}{2a}\left[\left( 3e^{2}+7\right)\left( 3\cos^{2} i-1\right)+15\left( 1+e^{2}\right)\sin^{2} i\cos^{2}\omega\right]\delta a \right. \end{array} $$

$$\begin{array}{@{}rcl@{}} && + \ 6e\left( 3\cos^{2} i-1+5\sin^{2} i\cos^{2}\omega\right)\delta e \end{array} $$

(18f)

$$\begin{array}{@{}rcl@{}} && \left.- 3\sin 2i\!\left[3e^{2}\!+7-5\!\left( 1+e^{2}\right)\!\cos^{2}\omega\right]\!\delta i - 15\!\left( 1+e^{2}\right)\!\sin^{2} i\sin 2\omega\ \delta\omega\right\} \end{array} $$

Canonical Transformation

Equations (17) and (18) are the rates of change of the absolute and differential classical orbital elements due to the doubly-averaged lunar perturbation. However, because the disturbing potential has been averaged, these now represent the rates of a new set of “lunar”-averaged orbital elements rather than the instantaneous osculating elements (which are what would be determined by fitting a satellite’s position and velocity to an orbit at a given time). If Eqs. (17) and (18) were applied without correcting the initial conditions for this difference, the results would become increasingly inaccurate as the equations are propagated forward in time. This concept is exactly analogous to the difference between the mean orbital elements and the osculating orbital elements in Brouwer’s near-Earth satellite theory [16].

To obtain the transformation between the lunar elements and the osculating elements, the problem is rewritten in Hamiltonian canonical form using the Delaunay variables,

$$\begin{array}{@{}rcl@{}} l &=& M \qquad\qquad~~~~~~~~~~~~~~~ L = \sqrt{\mu a}\\ g &=& \omega \qquad\qquad~~~~~~~~~~~~~~~~ G = L\eta \\ h &=& {\Omega} \qquad\qquad~~~~~~~~~~~~~~~ H = G\cos i \end{array} $$

(19)

or, in vector-matrix form, x = [l g h]^T and X = [L G H]^T. Defining the small quantity $\varepsilon = \left (a_{0}/a_{0}^{\prime }\right )^{2}$, where (⋅)₀ indicates a constant quantity (either the initial or averaged value, defined this way so that ε is a constant quantity), the Hamiltonian corresponding to Eq. (8) (up to k = 2) can be written as

$$ \mathcal{H} = \mathcal{H}_{0} + \varepsilon \mathcal{H}_{1} $$

(20)

where $\mathcal {H}_{0}$ is the two-body Hamiltonian and $\mathcal {H}_{1}$ is the first term of the disturbing potential (the k = 2 term), normalized by ε. Treating this as a Lie series in ε, the two averagings of Prado [22] can be performed as near-identity canonical transformations.

At this point, it is worth examining how each of the terms in the Hamiltonian explicitly depends on the variables of the problem. The two-body Hamiltonian, $\mathcal {H}_{0}$ is

$$ \mathcal{H}_{0} = -\frac{\mu^{2}}{2L^{2}} $$

(21)

which depends only on L. Since the equations of motion in canonical form are given by

$$ \dot{\mathbf{x}} = \frac{\partial\mathcal{H}}{\partial\mathbf{X}} \hspace{3.5cm} \dot{\mathbf{X}} = -\frac{\partial\mathcal{H}}{\partial\mathbf{x}} $$

(22)

under purely two-body motion the only variable which changes over time is the mean anomaly, l, as expected. The first-order disturbance term is

$$ \mathcal{H}_{1} = \frac{\mu^{\prime} n^{\prime}{2} {a^{\prime}{3}}}{2r^{\prime}}\left( \frac{a_{0}^{\prime}}{a_{0}}\right)^{2}\left( \frac{r}{r^{\prime}}\right)^{2} \left[3\left( \alpha\cos f + \beta\sin f\right)^{2}-1\right] $$

(23)

which depends on all six Delaunay elements through r, f, α, and β. Recall that α and β are defined in Eqs. (12) and (13), respectively; in terms of Delaunay elements these terms are

$$\begin{array}{@{}rcl@{}} \alpha &=& \cos g\cos\left( l^{\prime}-h\right) + \sin g\sin\left( l^{\prime}-h\right)\frac{H}{G} \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} \beta &=& -\sin g\cos\left( l^{\prime}-h\right) + \cos g\sin\left( l^{\prime}-h\right)\frac{H}{G} \end{array} $$

(25)

Additionally, $\mathcal {H}_{1}$ depends on the lunar parameters, most of which are constant under the assumptions of the simplified model. However, the lunar mean anomaly, l ^′, varies with a rate of n ^′ which introduces an explicit time dependence in the Hamiltonian. Therefore, the overall Hamiltonian depends explicitly on x, X, and t.

The first near-identity transformations will remove all terms depending on l from the Hamiltonian (up to first order in ε). The transformed Hamiltonian, $\mathcal {K}$, has the form

$$ \mathcal{K}(\mathbf{y},\mathbf{Y},t) = \underbrace{\mathcal{H}_{0}(\_,\mathbf{Y},\_)}_{ \mathcal{K}_{0}(\_,\mathbf{Y},\_)} + \varepsilon\underbrace{\langle\mathcal{H}_{1}\rangle(\mathbf{y},\mathbf{Y},t)}_{ \mathcal{K}_{1}(\mathbf{y},\mathbf{Y},t)} $$

(26)

where $\mathbf {y} = \left [\bar {l}\ \ \bar {g}\ \ \bar {h}\right ]^{T}$ and $\mathbf {y} = \left [\bar {l}\ \ \bar {g}\ \ \bar {h}\right ]^{T}$ are the new single-averaged variables and the (_) notation is used to show those terms which do not depend explicitly on certain variables. Note that the two-body term is unchanged and that $\mathcal {K}_{1}$ does not depend on $\bar {l}$. At first order, the equations for Lie series [32] give the relation

$$ \mathcal{K}_{1}\left( \mathbf{y},\mathbf{Y},t\right) = \mathcal{H}_{1}\left( \mathbf{y},\mathbf{Y},t\right) + L_{1} \mathcal{H}_{0} - \frac{\partial W_{1}}{\partial t} $$

(27)

where $L_{1}\mathcal {H}_{0} = \left (\mathcal {H}_{0};W_{1}\right )$ is the Lie derivative of $\mathcal {H}_{0}$ generated by W ₁ and (⋅;⋅) is the Poisson bracket with respect to the variables of interest, i.e.

$$ \left( A;B\right) = \frac{\partial A}{\partial\mathbf{y}}\frac{\partial B}{\partial\mathbf{Y}} - \frac{\partial A}{\partial\mathbf{Y}}\frac{\partial B}{\partial\mathbf{y}} $$

(28)

W ₁ is the first-order generating function for the canonical transformation. Once W ₁(y, Y, t) is determined, the transformation between the single-averaged and osculating variables is given by

$$ \mathbf{x} = \mathbf{y} + \varepsilon\frac{\partial W_{1}}{\partial\mathbf{Y}} \hspace{3.5cm} \mathbf{X} = \mathbf{Y} - \varepsilon\frac{\partial W_{1}}{\partial\mathbf{y}} $$

(29)

The inverse transformation is obtained by replacing y and Y by x and X and negating W ₁:

$$ \mathbf{y} = \mathbf{x} - \varepsilon\frac{\partial W_{1}}{\partial\mathbf{X}} \hspace{3.5cm} \mathbf{Y} = \mathbf{X} + \varepsilon\frac{\partial W_{1}}{\partial\mathbf{x}} $$

(30)

The first-order term in the Lie series expansion is, therefore,

$$\begin{array}{@{}rcl@{}} \left\langle\mathcal{H}_{1}\right\rangle\left( \mathbf{y},\mathbf{Y},t\right) &=& \mathcal{H}_{1}\left( \mathbf{y},\mathbf{Y},t\right) + \left( \mathcal{H}_{0};W_{1}\right) - \frac{\partial W_{1}}{\partial t} \\ & =& \mathcal{H}_{1}\left( \mathbf{y},\mathbf{Y},t\right) - \frac{\mu^{2}}{\bar{L}^{3}}\frac{\partial W_{1}}{\partial\bar{l}} - \frac{\partial W_{1}}{\partial t} \end{array} $$

(31)

since $\mathcal {H}_{0}$ depends only on $\bar {l}$. This yields the linear partial differential equation (PDE)

$$ \frac{\mu^{2}}{\bar{L}^{3}}\frac{\partial W_{1}}{\partial\bar{l}} + \frac{\partial W_{1}}{\partial t} = \mathcal{H}_{1}\left( \mathbf{y},\mathbf{Y},t\right) - \left\langle\mathcal{H}_{1}\right\rangle\left( \mathbf{y},\mathbf{Y},t\right) $$

(32)

which is not trivial to solve.

To address this issue, we will exploit the differences in the time scales of the problem. Since the period of the satellite is much shorter than the period of the Moon’s motion, it is reasonable to restrict our attention in this transformation to variations with respect to $\bar {l}$. In other words, assume the position of the Moon relative to the Earth is fixed throughout one orbit of the satellite and neglect the variation of W ₁ with respect to t. This yields the (approximate) simplified equation

$$ \frac{\mu^{2}}{\bar{L}^{3}}\frac{\partial W_{1}}{\partial\bar{l}} = \mathcal{H}_{1}\left( \mathbf{y},\mathbf{Y},t\right) - \left\langle\mathcal{H}_{1}\right\rangle\left( \mathbf{y},\mathbf{Y},t\right) $$

(33)

which has the general solution

$$ W_{1} = \frac{\bar{L}^{3}}{\mu^{2}}\int\left( \mathcal{H}_{1}-\left\langle\mathcal{H}_{1}\right\rangle\right) d\bar{l} + W_{1}^{\prime}\left( \_,\bar{g},\bar{h},\bar{L},\bar{G},\bar{H},t\right) $$

(34)

where $W_{1}^{\prime }$ is a constant of integration with respect to $\bar {l}$ which can be neglected at first order.

The second near-identity transformations will remove all terms depending on l ^′, i.e. t, from the Hamiltonian up to first order. The transformed Hamiltonian, $\mathcal {M}$, has the form

$$ \mathcal{M}(\mathbf{z},\mathbf{Z},\_) = \underbrace{\mathcal{H}_{0}(\_,\mathbf{Z},\_)}_{ \mathcal{M}_{0}(\_,\mathbf{Z},\_)} + \varepsilon\underbrace{\langle\langle\mathcal{H}_{1}\rangle\rangle(\mathbf{z},\mathbf{Z},\_)}_{ \mathcal{M}_{1}(\mathbf{z},\mathbf{Z},\_)} $$

(35)

where $\mathbf {z} = [\bar {\bar {l}}\ \ \bar {\bar {g}}\ \ \bar {\bar {h}}]^{T}$ and $\mathbf {z} = [\bar {\bar {l}}\ \ \bar {\bar {g}}\ \ \bar {\bar {h}}]^{T}$ are the new double-averaged or lunar variables. The two-body term is again unchanged and $\mathcal {M}_{1}$ depends on neither $\bar {\bar {l}}$ nor t. The Lie series transformation is given by

$$ \mathcal{M}_{1}(\mathbf{z},\mathbf{Z},\_) = \mathcal{K}_{1}(\mathbf{z},\mathbf{Z},t) + (\mathcal{H}_{0};\bar{W}_{1}) - \frac{\partial\bar{W}_{1}}{\partial t} $$

(36)

which leads to the linear PDE

$$ \frac{\mu^{2}}{\bar{\bar{L}}^{3}}\frac{\partial\bar{W}_{1}}{\partial\bar{\bar{l}}} + \frac{\partial\bar{W}_{1}}{\partial t} = \mathcal{K}_{1}(\mathbf{z},\mathbf{Z},t) - \langle\langle\mathcal{H}_{1}\rangle\rangle(\mathbf{z},\mathbf{Z},\_) $$

(37)

Since none of the terms on the RHS depend on $\bar {\bar {l}}$ we can assume that $\bar {W}_{1}$ also does not depend on $\bar {\bar {l}}$. Therefore, the general solution for $\bar {W}_{1}$ is given by

$$\begin{array}{@{}rcl@{}} \bar{W}_{1} &=& \int(\mathcal{K}_{1}-\langle\langle\mathcal{H}_{1}\rangle\rangle) dt + \bar{W}_{1}^{\prime}(\_,\bar{\bar{g}},\bar{\bar{h}},\bar{\bar{L}},\bar{\bar{G}},\bar{\bar{H}},\_) \\ &=& \frac{1}{n^{\prime}}\left( \int \mathcal{K}_{1} dl^{\prime} - \langle\langle\mathcal{H}_{1}\rangle\rangle l^{\prime}\right) + \bar{W}_{1}^{\prime}(\_,\bar{\bar{g}},\bar{\bar{h}},\bar{\bar{L}},\bar{\bar{G}},\bar{\bar{H}},\_) \end{array} $$

(38)

since

$$ l^{\prime} = l_{0}^{\prime} + n^{\prime} t $$

(39)

and where $\bar {W}_{1}^{\prime }$ is another constant of integration which can be neglected. The forward and inverse transformations between the lunar and single-averaged variables are obtained similarly to Eqs. (29) and (30).

Numerical Simulation

The objective of the NASA Magnetospheric Multiscale (MMS) mission is to study magnetic reconnection, charged particle acceleration, and turbulence in key boundary regions of the Earth’s magnetosphere [1]. The mission will employ a unique orbital strategy of two main phases, in which the reference orbit apogee is placed at 12 R _e and 25 R _e , respectively. With perigee of both phases at 1.2 R _e this means a highly eccentric orbit, with e = 0.81818 in Phase I and e = 0.9084 in Phase II. These high reference orbit apogees suggest that the lunar perturbation could have a significant effect on long-term formation performance, especially in Phase II [28]. The remaining reference orbital elements for MMS Phases I and II are listed in Table 1.

Table 1 MMS reference orbital elements

Both phases of the MMS mission call for a formation of four satellites, which is to form a nearly regular tetrahedron near apogee with side lengths ranging from 10 km to 400 km. The quality factor (QF) is a metric used to compare the size and shape of the instantaneous tetrahedron with a regular tetrahedron of acceptable size, and is defined on a range from 0 to 1, with 1 indicating an ideal tetrahedron [27]. The mission requires a QF which exceeds 0.7 for 80 % of the time spent in the science region of interest (RoI), which comprises all portions of the orbit within a true anomaly range of approximately ±20^∘ of apogee. For each of the following simulations, initial conditions for the three deputies were determined using the nominal formation design algorithms of Refs. [29–31] (10 km Phase I, 25 km Phase II) with no perturbations.

In general, the dynamics of satellite formations depend explicitly on both absolute and differential orbital elements. According to Eqs. (17) and (18), the lunar perturbation causes long-term changes in all of the absolute and differential elements except a and δ a. The rates are not constant, but because they are slowly varying they can be integrated semianalytically (with a very large time step) or assumed to be linear over sufficiently short time spans. The J ₂ perturbation, on the other hand, causes changes in only ω, Ω, and M ₀ and their differences. The effects of the lunar perturbation on δ ω, δΩ, and δ M ₀ are compared to J ₂ for one of the deputies in Fig. 2a, for Phase I, and 2b, for Phase II. As expected, in Phase I J ₂ has a much larger effect than the lunar perturbation; however, in Phase II they are of roughly the same order of magnitude. Despite this, the lunar perturbation seems to have little effect on average QF in the RoI (the performance metric of interest for this analysis) in either phase, as shown in Fig. 3a and b, whereas J ₂ can be seen to have a significant effect even when the J ₂ along-track drift condition [29] is applied (shown as black diamonds in the figures). In the following sections, lunar effects on the individual orbital elements will be examined for both Phases I and II, and the averaged results will be compared with numerical integration of the actual equations of motion for the simplified (circular, equatorial lunar orbit) model with $M_{0}^{\prime } = 90^{\circ }$.

Fig. 3

Comparison of average QF per RoI pass between J ₂ and averaged lunar effects

Phase I Results

Each figure in these two sections contains four sets of results: the solid blue line uses the averaged equations, Eqs. (17b) and (18), with the corrected lunar-averaged elements for initial conditions (the z-type variables); the dash-dot green line uses the same equations with (uncorrected) osculating elements for initial conditions (the x-type variables); the dashed red line uses numerical integration of the equations of motion for the indicated simulation model; and the dotted magenta line uses numerical integration of the single-averaged disturbing potential (corresponding to either Eq. (14) or (26)) with the corrected single-average elements for initial conditions (the y-type variables). M ₀ = M−n t is difficult to track over long time spans because oscillations in n induce large oscillations for large values of t. Instead,

$$ {\Delta} M = M-\bar{\bar{n}}_{0} t $$

(40)

is plotted, along with its differential value, in the following figures.

Three sets of simulations are shown in this section for the MMS Phase I reference orbit. First, the averaged lunar equations are compared to the 1st-order simplified model, that is Eq. (8) with only k = 2 terms and a circular, equatorial lunar orbit. Figure 4 shows the evolution of the reference orbital elements and Fig. 5 shows the differential elements. Note that the lunar-averaged elements correctly track the averages of a, e, δ a, and δ e, while using the uncorrected osculating elements as initial conditions for the averaged equations introduces a significant bias in each. This bias influences the rates of each of the other elements but can be seen most clearly in its effect on ΔM and δ(ΔM). For the remaining elements, there is little difference between each of the results. The effect of each of the simplifying assumptions in the Lie series analysis can be seen by noting that there is a small discrepancy between the single-averaged and the numerical integration results and an additional small discrepancy between the lunar-averaged and the single-averaged results.

Fig. 4

Averaged lunar model for Phase I compared to 1st-order simplified model

Fig. 5

Averaged lunar model for Phase I compared to 1st-order simplified model

Second, the averaged lunar equations are compared to the full-order simplified model, that is Eq. (1) with a circular, equatorial lunar orbit. Figure 6 shows the reference elements and Fig. 7 shows the differential elements. Clearly, higher-order terms in the lunar potential introduce much larger oscillations in the elements, although they do not contribute significantly to long-term changes in the average sense except in the cases of ΔM and δ(ΔM). As was noted in the previous paragraph, the now-uncorrected bias in a, e, δ a, and δ e introduces marked errors in the rates of ΔM and δ(ΔM).

Fig. 6

Averaged lunar model for Phase I compared to full-order simplified model

Fig. 7

Averaged lunar model for Phase I compared to full-order simplified model

Finally, the first simulation (comparison with 1st-order simplified model) is propagated over a longer time span to see if the averaged equations accurately predict the satellites’ motion in the long term. Only the reference elements are shown, in Fig. 8, and the semianalytic propagation performs as expected. As before, there is a predictable discrepancy between the averaged results and numerical integration, but there is no sudden divergence or large nonlinearity in the motion.

Fig. 8

Averaged lunar model for Phase I compared to 1st-order simplified model (long-term)

Phase II Results

The same three sets of simulations are shown in this section for the MMS Phase II reference orbit. First, the averaged lunar equations are compared to the 1st-order simplified model. Figure 9 shows the reference elements and Fig. 10 shows the differential elements. As with Phase I, the lunar-averaged elements correctly track the averages of a, e, δ a, and δ e, while using the uncorrected osculating elements as initial conditions introduces a significant bias in each, which has a marked effect on ΔM and δ(ΔM). The effect of each of the simplifying assumptions in the Lie series analysis can again be seen by noting that there is a small discrepancy between the single-averaged and the numerical integration results and an additional discrepancy between the lunar-averaged and the single-averaged results (most notable in ΔM and δ(ΔM)).

Fig. 9

Averaged lunar model for Phase II compared to 1st-order simplified model

Fig. 10

Averaged lunar model for Phase II compared to 1st-order simplified model

Second, the averaged lunar equations are compared to the full-order simplified model. Figure 11 shows the reference elements and Fig. 12 shows the differential elements. Again, higher-order terms in the lunar potential introduce much larger oscillations in the elements, but in Phase II there is also a noticeable effect on the long-term rates of the elements. The now-uncorrected bias in a, e, δ a, and δ e introduces large errors in the rates of ΔM and δ(ΔM).

Fig. 11

Averaged lunar model for Phase II compared to full-order simplified model

Fig. 12

Averaged lunar model for Phase II compared to full-order simplified model

Finally, the first simulation (comparison with 1st-order simplified model) is propagated over a longer time span to see if the averaged equations accurately predict the satellites’ motion in the long term. Figure 13 shows the reference elements and Fig. 14 shows the differential elements. The semianalytic propagation performs fairly well; however, there is considerably more nonlinearity in the evolution of the elements at the higher altitude of Phase II than there was in Phase I. Both the single-averaged and lunar-averaged ω and δ ω, in particular, begin to diverge after about 500 days. This extreme case (propagating for such a long time) illustrates the limitations of this method when the simplifying assumptions are being strained: for Phase II, the parameter ε ≈ 4.7×10⁻² (assumed to be small in performing the Lie series expansion) and the ratio of the satellite’s period to the lunar period is approximately 0.1 (assumed to be small in solving Eq. (32)).

Fig. 13

Averaged lunar model for Phase II compared to 1st-order simplified model (long-term)

Fig. 14

Averaged lunar model for Phase II compared to 1st-order simplified model (long-term)

High-Fidelity Verification

The analysis presented in this paper is based on a circular, equatorial lunar orbit, and it is expected that the accuracy of the predicted motion will degrade due to differences between this simplified model and actual lunar motion. It is expected that lunar orbit eccentricity (≈0.05) and inclination (≈5^∘ with respect to the ecliptic) will cause noticeable departure from the predicted motion. In particular, the lunar inclination will significantly affect the the disturbing force since it varies between about 18^∘ and 29^∘ with respect to the Earth’s equatorial plane throughout its almost 19 year nodal cycle. However, for sufficiently short time periods (compared to the nodal cycle) the lunar orbit can be assumed to have a constant orientation with respect to the geocentric equatorial frame to obtain satisfactory results.

Lunar Inclination

Retaining the assumption of a circular lunar orbit, but now including a constant right ascension of Ω^′ and inclination of i ^′, the cosine of the angle between the satellite and the Moon, Eq. (10), becomes

$$ \cos S_{i} = \alpha_{i}\cos f + \beta_{i}\sin f $$

(41)

where

$$\begin{array}{@{}rcl@{}} \alpha_{i} &=& \left( c_{\omega}c_{\Delta{\Omega}} - s_{\omega}s_{\Delta{\Omega}}c_{i}\right)c_{M^{\prime}} + \left( c_{\omega}s_{\Delta{\Omega}}c_{i^{\prime}} + s_{\omega}c_{\Delta{\Omega}}c_{i} c_{i^{\prime}} + s_{\omega}s_{i} s_{i^{\prime}}\right)s_{M^{\prime}} \end{array} $$

(42)

$$\begin{array}{@{}rcl@{}} \beta_{i} &=& -\left( s_{\omega}c_{\Delta{\Omega}} + c_{\omega}s_{\Delta{\Omega}}c_{i}\right)c_{M^{\prime}} + \left( -s_{\omega}s_{\Delta{\Omega}}c_{i^{\prime}} + c_{\omega}c_{\Delta{\Omega}}c_{i} c_{i^{\prime}} + c_{\omega}s_{i} s_{i^{\prime}}\right)s_{M^{\prime}} \end{array} $$

(43)

with s _γ = sinγ, c _γ = cosγ, and ΔΩ=Ω−Ω^′.

The first averaging of the disturbing potential, Eq. (14), and its generating function, Eq. (34), are unchanged aside from the new form of α _i and β _i , since those quantities do not depend on M. The expressions for the doubly-averaged potential, Eq. (16), and its generating function, Eq. (38), become more complicated, because of the additional trigonometric terms, but the method is identical. The same is true of the corresponding expressions for the absolute and differential element rates, Eqs. (17) and (18). With this new formulation of the problem, the results predicted by this method can now be compared to results obtained using the NASA General Mission Analysis Tool (GMAT) with a spherical Earth and lunar point mass gravity model (based on high-fidelity lunar ephemeris data).

GMAT Results

First, the conclusion drawn based on Fig. 3a and b regarding the effect of the lunar perturbation on QF performance is verified. Figure 15a and b show initial lunar orientations. As with the simplified model analysis, the lunar perturbation has little effect on QF evolution at either orbit altitude. To illustrate the effect of initial lunar orientation more distinctly, Fig. 16a and b show zoomed-in versions of the last five orbits of the previous figures. Clearly, the Moon’s actual position does not have a significant impact on overall science return quality for missions such as MMS, so it is reasonable to use averaged lunar effects in evaluating this criterion.

Fig. 15

GMAT simulations for different initial lunar mean anomalies

Fig. 16

GMAT simulations for different initial lunar mean anomalies

Second, lunar-averaged results (based on the 1st-order simplified model, including lunar inclination) are compared to simulation in GMAT for Phase I. The 100 day simulation was computed based on lunar ephemeris data starting on January 19, 2000 (Julian Date 2451562.7), during which period the average values of Ω^′ and i ^′ are approximately 10^∘ and 21^∘, respectively, and $M_{0}^{\prime } \approx 80^{\circ }$. Figure 17 shows the reference elements and Fig. 18 shows the differential elements. The simplified model does a good job predicting the average rates of the elements, with a moderate bias which affects ΔM and δ(ΔM) (although the effect is worse in the case of the uncorrected initial conditions).

Fig. 17

Averaged lunar model for Phase I compared to GMAT simulation

Fig. 18

Averaged lunar model for Phase I compared to GMAT simulation

Finally, the lunar-averaged results are compared to simulation in GMAT for Phase II over the same time period. Figure 19 shows the reference elements and Fig. 20 shows the differential elements. As with the Phase I results, the simplified model predicts the average rates of the elements well but there is a moderate bias which affects ΔM and δ(ΔM). Again, using the uncorrected initial conditions produces a greater inaccuracy.

Fig. 19

Averaged lunar model for Phase II compared to GMAT simulation

Fig. 20

Averaged lunar model for Phase II compared to GMAT simulation

Conclusion

Absolute and differential third-body perturbation effects on satellite formations were derived analytically using a simplified model, following the assumptions of the circular restricted three-body problem. The analysis and all numerical simulations are performed for the perturbing effect of the Moon; however, it is possible to adapt this method for other perturbing bodies, provided careful attention is paid to the relative time scales of the problem. The predicted lunar-averaged motion is validated by numerical integration of the simplified model and the results are compared to the effects of the J ₂ perturbation. For formations in high altitude reference orbits, such as MMS, it is essential to consider third-body effects in addition to J ₂ because they can reach the same order of magnitude. Furthermore, third-body perturbations affect e, i, δ e, and δ i whereas J ₂ does not. For comparison with simulation using more accurate lunar ephemeris data it is necessary to include the lunar inclination with respect to the equatorial plane. This is accomplished (for sufficiently short time periods) by assuming a constant orientation of the lunar orbital plane with respect to the geocentric equatorial frame. With this formulation, the lunar-averaged equations of motion perform very well compared to high-fidelity simulation. Simplified analytical models generally provide more insight than do numerical simulations, are easily adaptable to different problems, and are extremely fast to evaluate. For these reasons, it is advantageous to develop analytical methods for designing satellite formations, even if only to provide overall physical analysis and initial guesswork for high-fidelity numerical solvers/optimizers.